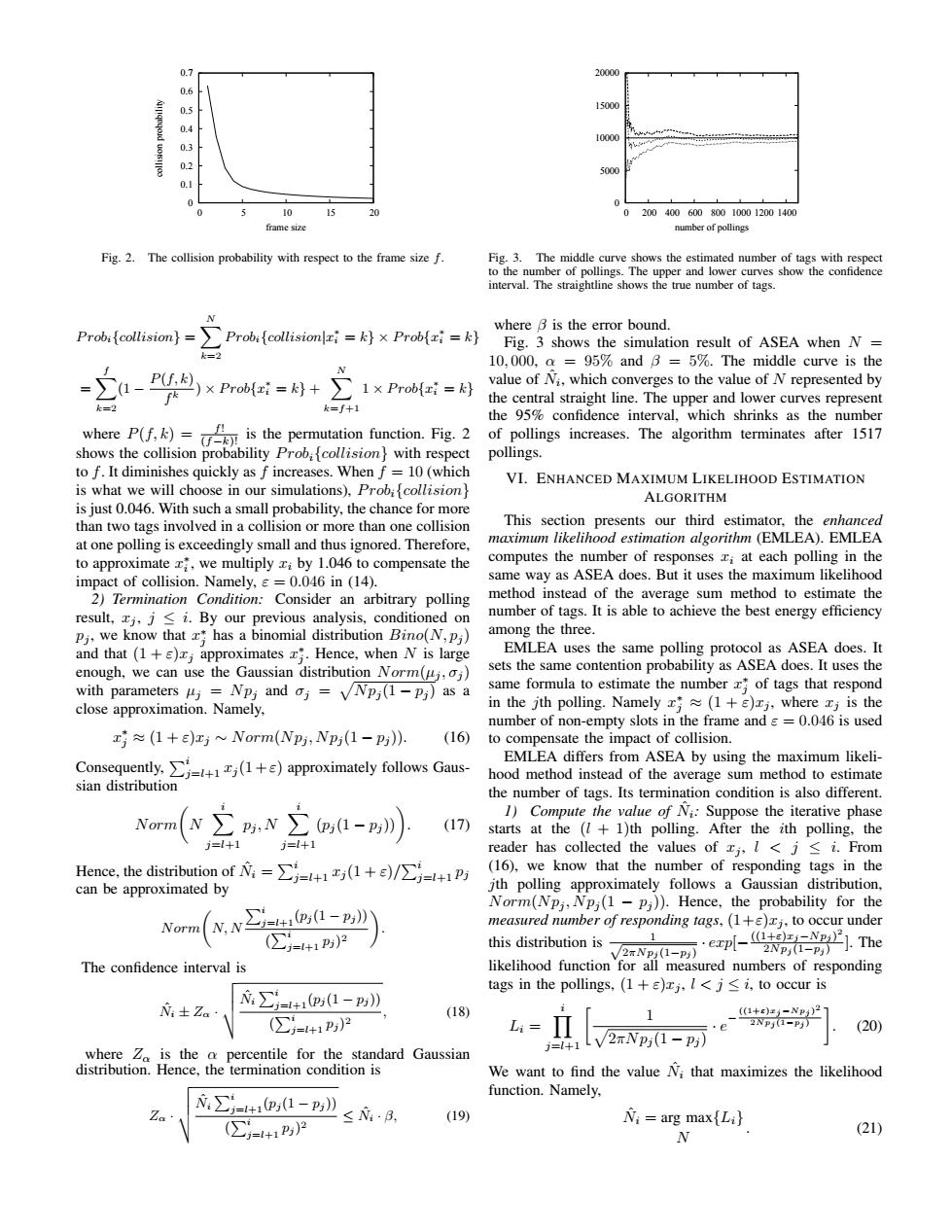
20000 1500 10000 5000 0.1 0 0 10 20 0200400600800100012001400 frame size number of pollings Fig.2.The collision probability with respect to the frame size f. Fig.3.The middle curve shows the estimated number of tags with respect to the number of pollings.The upper and lower curves show the confidence interval.The straightline shows the true number of tags where B is the error bound. Probifcollisionlri=k}x Probfi=k} Fig.3 shows the simulation result of ASEA when N k=2 10,000,a =95%and B =5%.The middle curve is the (1-P()x 1×Prob{x=k} value of Ni,which converges to the value of N represented by k=2 the central straight line.The upper and lower curves represent k=f+ the 95%confidence interval,which shrinks as the number f! where P(f,)is the permutation function.Fig.2 of pollings increases.The algorithm terminates after 1517 shows the collision probability Probfcollision}with respect pollings. to f.It diminishes quickly as f increases.When f =10(which VI.ENHANCED MAXIMUM LIKELIHOOD ESTIMATION is what we will choose in our simulations),Probifcollision ALGORITHM is just 0.046.With such a small probability,the chance for more than two tags involved in a collision or more than one collision This section presents our third estimator,the enhanced at one polling is exceedingly small and thus ignored.Therefore, maximum likelihood estimation algorithm(EMLEA).EMLEA to approximate,we multiply zi by 1.046 to compensate the computes the number of responses ri at each polling in the impact of collision.Namely,=0.046 in (14). same way as ASEA does.But it uses the maximum likelihood 2)Termination Condition:Consider an arbitrary polling method instead of the average sum method to estimate the result,j,j<i.By our previous analysis,conditioned on number of tags.It is able to achieve the best energy efficiency pj,we know that has a binomial distribution Bino(N,pj) among the three. and that(1+)j approximates Hence,when N is large EMLEA uses the same polling protocol as ASEA does.It enough,we can use the Gaussian distribution Norm(uj,oj) sets the same contention probability as ASEA does.It uses the with parameters j=NPj and oj=√/Npi(1-pi）asa same formula to estimate the number of tags that respond close approximation.Namely, in the jth polling.Namely z(1+s)zj,where xi is the number of non-empty slots in the frame and s=0.046 is used (1+E)zj~Norm(Npj,Npj(1-pj)). (16) to compensate the impact of collision. Consequently.(1+)approximately follows Gaus- EMLEA differs from ASEA by using the maximum likeli- hood method instead of the average sum method to estimate sian distribution the number of tags.Its termination condition is also different. Norm( N∑Pv∑，-》 2 1)Compute the value of Ni:Suppose the iterative phase (17) starts at the (+1)th polling.After the ith polling,the j=l+1 j=1+1 reader has collected the values of xj,I<j i.From Hence,the distribution of N=(1+)/ (16),we know that the number of responding tags in the can be approximated by jth polling approximately follows a Gaussian distribution, Norm(x,N∑i=441-》 Norm(Npj,Np;(1 -pj)).Hence,the probability for the measured number of responding tags,(1+s)xj,to occur under (∑=1+1PP this distribution is ep.The 1 2NP1-P%） The confidence interval is likelihood function for all measured numbers of responding tags in the pollings,(1+)xj,I<j<i,to occur is N:±Za :∑=+1p1-pm》 (18) (∑-+1PP Li +1lV2πNp(1-p e (20) where Zo is the a percentile for the standard Gaussian distribution.Hence,the termination condition is We want to find the value Ni that maximizes the likelihood function.Namely, Z :∑=+1(-p》 ≤N·B, (19 (∑=+1PP Ni arg max{Li} (21)0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0 5 10 15 20 collision probability frame size Fig. 2. The collision probability with respect to the frame size f. P robi{collision} = XN k=2 P robi{collision|x ∗ i = k} × P rob{x ∗ i = k} = X f k=2 (1 − P(f, k) f k ) × P rob{x ∗ i = k} + XN k=f+1 1 × P rob{x ∗ i = k} where P(f, k) = f! (f−k)! is the permutation function. Fig. 2 shows the collision probability P robi{collision} with respect to f. It diminishes quickly as f increases. When f = 10 (which is what we will choose in our simulations), P robi{collision} is just 0.046. With such a small probability, the chance for more than two tags involved in a collision or more than one collision at one polling is exceedingly small and thus ignored. Therefore, to approximate x ∗ i , we multiply xi by 1.046 to compensate the impact of collision. Namely, ε = 0.046 in (14). 2) Termination Condition: Consider an arbitrary polling result, xj , j ≤ i. By our previous analysis, conditioned on pj , we know that x ∗ j has a binomial distribution Bino(N, pj ) and that (1 + ε)xj approximates x ∗ j . Hence, when N is large enough, we can use the Gaussian distribution Norm(µj , σj ) with parameters µj = N pj and σj = p N pj (1 − pj ) as a close approximation. Namely, x ∗ j ≈ (1 + ε)xj ∼ Norm(N pj , N pj (1 − pj )). (16) Consequently, Pi j=l+1 xj (1 +ε) approximately follows Gaus￾sian distribution Normµ N X i j=l+1 pj , N X i j=l+1 (pj (1 − pj ))¶ . (17) Hence, the distribution of Nˆ i = Pi j=l+1 xj (1 + ε)/ Pi j=l+1 pj can be approximated by Normµ N, N Pi j=l+1(pj (1 − pj )) ( Pi j=l+1 pj ) 2 ¶ . The confidence interval is Nˆi ± Zα · vuut Nˆi Pi j=l+1(pj (1 − pj )) ( Pi j=l+1 pj ) 2 , (18) where Zα is the α percentile for the standard Gaussian distribution. Hence, the termination condition is Zα · vuut Nˆi Pi j=l+1(pj (1 − pj )) ( Pi j=l+1 pj ) 2 ≤ Nˆi · β, (19) 0 5000 10000 15000 20000 0 200 400 600 800 1000 1200 1400 number of pollings Fig. 3. The middle curve shows the estimated number of tags with respect to the number of pollings. The upper and lower curves show the confidence interval. The straightline shows the true number of tags. where β is the error bound. Fig. 3 shows the simulation result of ASEA when N = 10, 000, α = 95% and β = 5%. The middle curve is the value of Nˆ i , which converges to the value of N represented by the central straight line. The upper and lower curves represent the 95% confidence interval, which shrinks as the number of pollings increases. The algorithm terminates after 1517 pollings. VI. ENHANCED MAXIMUM LIKELIHOOD ESTIMATION ALGORITHM This section presents our third estimator, the enhanced maximum likelihood estimation algorithm (EMLEA). EMLEA computes the number of responses xi at each polling in the same way as ASEA does. But it uses the maximum likelihood method instead of the average sum method to estimate the number of tags. It is able to achieve the best energy efficiency among the three. EMLEA uses the same polling protocol as ASEA does. It sets the same contention probability as ASEA does. It uses the same formula to estimate the number x ∗ j of tags that respond in the jth polling. Namely x ∗ j ≈ (1 + ε)xj , where xj is the number of non-empty slots in the frame and ε = 0.046 is used to compensate the impact of collision. EMLEA differs from ASEA by using the maximum likeli￾hood method instead of the average sum method to estimate the number of tags. Its termination condition is also different. 1) Compute the value of Nˆ i: Suppose the iterative phase starts at the (l + 1)th polling. After the ith polling, the reader has collected the values of xj , l < j ≤ i. From (16), we know that the number of responding tags in the jth polling approximately follows a Gaussian distribution, Norm(N pj , N pj (1 − pj )). Hence, the probability for the measured number of responding tags, (1+ε)xj , to occur under this distribution is √ 1 2πNpj (1−pj ) · exp[− ((1+ε)xj−Npj ) 2 2Npj (1−pj ) ]. The likelihood function for all measured numbers of responding tags in the pollings, (1 + ε)xj , l < j ≤ i, to occur is Li = Y i j=l+1 · 1 p 2πN pj (1 − pj ) · e − ((1+ε)xj−Npj ) 2 2Npj (1−pj ) ¸ . (20) We want to find the value Nˆ i that maximizes the likelihood function. Namely, Nˆ i = arg max{Li} N . (21)