正在加载图片...
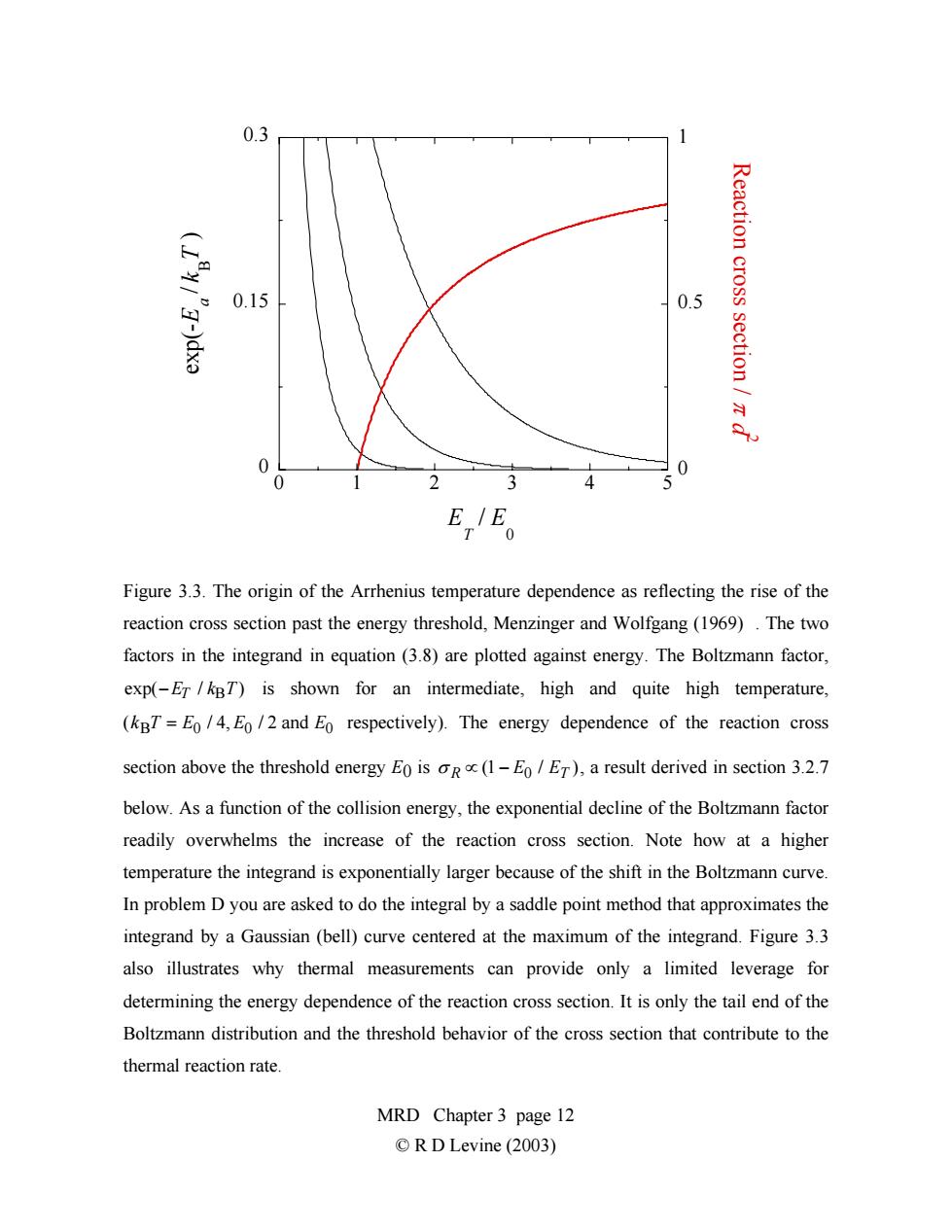
0.3 Reaction cross 0.15 0.5 section /z x 0 0 0 33 4 5 E,E。 Figure 3.3.The origin of the Arrhenius temperature dependence as reflecting the rise of the reaction cross section past the energy threshold,Menzinger and Wolfgang(1969).The two factors in the integrand in equation (3.8)are plotted against energy.The Boltzmann factor, exp(-Er/kBT)is shown for an intermediate,high and quite high temperature, (kBT=Eo/4,Eo/2 and Eo respectively).The energy dependence of the reaction cross section above the threshold energy Eo is oR(1-E/ET),a result derived in section 3.2.7 below.As a function of the collision energy,the exponential decline of the Boltzmann factor readily overwhelms the increase of the reaction cross section.Note how at a higher temperature the integrand is exponentially larger because of the shift in the Boltzmann curve. In problem D you are asked to do the integral by a saddle point method that approximates the integrand by a Gaussian(bell)curve centered at the maximum of the integrand.Figure 3.3 also illustrates why thermal measurements can provide only a limited leverage for determining the energy dependence of the reaction cross section.It is only the tail end of the Boltzmann distribution and the threshold behavior of the cross section that contribute to the thermal reaction rate. MRD Chapter 3 page 12 ©R D Levine(2003)0 0.15 0.3 0 0.5 1 012345 exp(- E a / kB T ) R e a ctio n c r o s s s e ctio n / π d 2 E T / E 0 Figure 3.3. The origin of the Arrhenius temperature dependence as reflecting the rise of the reaction cross section past the energy threshold, Menzinger and Wolfgang (1969) . The two factors in the integrand in equation (3.8) are plotted against energy. The Boltzmann factor, exp(−ET / kBT) is shown for an intermediate, high and quite high temperature, (kBT = E0 / 4, E0 / 2 and E0 respectively). The energy dependence of the reaction cross section above the threshold energy E0 is σ R ∝ (1 − E0 / ET ), a result derived in section 3.2.7 below. As a function of the collision energy, the exponential decline of the Boltzmann factor readily overwhelms the increase of the reaction cross section. Note how at a higher temperature the integrand is exponentially larger because of the shift in the Boltzmann curve. In problem D you are asked to do the integral by a saddle point method that approximates the integrand by a Gaussian (bell) curve centered at the maximum of the integrand. Figure 3.3 also illustrates why thermal measurements can provide only a limited leverage for determining the energy dependence of the reaction cross section. It is only the tail end of the Boltzmann distribution and the threshold behavior of the cross section that contribute to the thermal reaction rate. MRD Chapter 3 page 12 © R D Levine (2003)