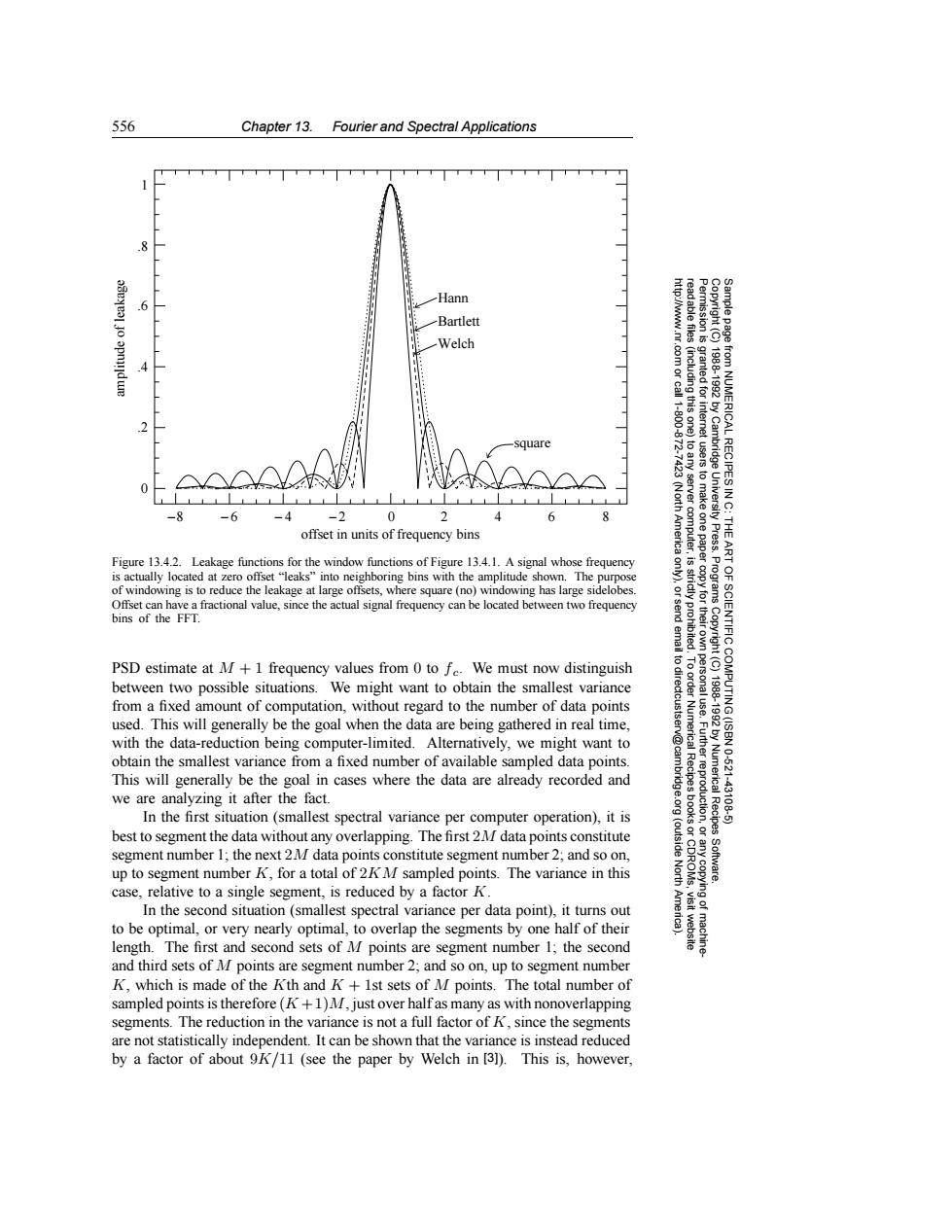
556 Chapter 13.Fourier and Spectral Applications f Hann 6 Bartlett Welch .4 .com or call 1-800-872- (including this one) square from NUMERICAL RECIPES IN C: 0 (North -8 -6 -4 -2 0 2 4 6 8 1988-1992 by Cambridge University Press. offset in units of frequency bins America to any server computer, tusers to make one paper THE Figure 13.4.2.Leakage functions for the window functions of Figure 13.4.1.A signal whose frequency ART is actually located at zero offset"leaks"into neighboring bins with the amplitude shown.The purpose 是 of windowing is to reduce the leakage at large offsets,where square (no)windowing has large sidelobes. Programs Offset can have a fractional value,since the actual signal frequency can be located between two frequency send strictly proh bins of the FFT. PSD estimate at M+1 frequency values from 0 to fe.We must now distinguish to dir between two possible situations.We might want to obtain the smallest variance from a fixed amount of computation,without regard to the number of data points OF SCIENTIFIC COMPUTING (ISBN used.This will generally be the goal when the data are being gathered in real time, 1988-1992 with the data-reduction being computer-limited.Alternatively,we might want to obtain the smallest variance from a fixed number of available sampled data points. 10-521 This will generally be the goal in cases where the data are already recorded and we are analyzing it after the fact. Fuurggoglrion In the first situation(smallest spectral variance per computer operation),it is Numerical Recipes 431985 best to segment the data without any overlapping.The first 2M data points constitute segment number 1;the next 2M data points constitute segment number 2;and so on, (outside up to segment number K,for a total of 2KM sampled points.The variance in this North Software. case,relative to a single segment,is reduced by a factor K. In the second situation (smallest spectral variance per data point),it turns out to be optimal,or very nearly optimal,to overlap the segments by one half of their visit website length.The first and second sets of M points are segment number 1;the second and third sets of M points are segment number 2;and so on,up to segment number K,which is made of the Kth and K+1st sets of M points.The total number of sampled points is therefore(K+1)M,just over halfas many as with nonoverlapping segments.The reduction in the variance is not a full factor of K,since the segments are not statistically independent.It can be shown that the variance is instead reduced by a factor of about 9K/11(see the paper by Welch in [31).This is,however,556 Chapter 13. Fourier and Spectral Applications Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). amplitude of leakage 0 .2 .4 .6 .8 1 −8 − 6 − 4 − 20 2 4 6 8 Hann Bartlett Welch offset in units of frequency bins square Figure 13.4.2. Leakage functions for the window functions of Figure 13.4.1. A signal whose frequency is actually located at zero offset “leaks” into neighboring bins with the amplitude shown. The purpose of windowing is to reduce the leakage at large offsets, where square (no) windowing has large sidelobes. Offset can have a fractional value, since the actual signal frequency can be located between two frequency bins of the FFT. PSD estimate at M + 1 frequency values from 0 to fc. We must now distinguish between two possible situations. We might want to obtain the smallest variance from a fixed amount of computation, without regard to the number of data points used. This will generally be the goal when the data are being gathered in real time, with the data-reduction being computer-limited. Alternatively, we might want to obtain the smallest variance from a fixed number of available sampled data points. This will generally be the goal in cases where the data are already recorded and we are analyzing it after the fact. In the first situation (smallest spectral variance per computer operation), it is best to segment the data without any overlapping. The first 2M data points constitute segment number 1; the next 2M data points constitute segment number 2; and so on, up to segment number K, for a total of 2KM sampled points. The variance in this case, relative to a single segment, is reduced by a factor K. In the second situation (smallest spectral variance per data point), it turns out to be optimal, or very nearly optimal, to overlap the segments by one half of their length. The first and second sets of M points are segment number 1; the second and third sets of M points are segment number 2; and so on, up to segment number K, which is made of the Kth and K + 1st sets of M points. The total number of sampled points is therefore (K + 1)M, just over half as many as with nonoverlapping segments. The reduction in the variance is not a full factor of K, since the segments are not statistically independent. It can be shown that the variance is instead reduced by a factor of about 9K/11 (see the paper by Welch in [3]). This is, however