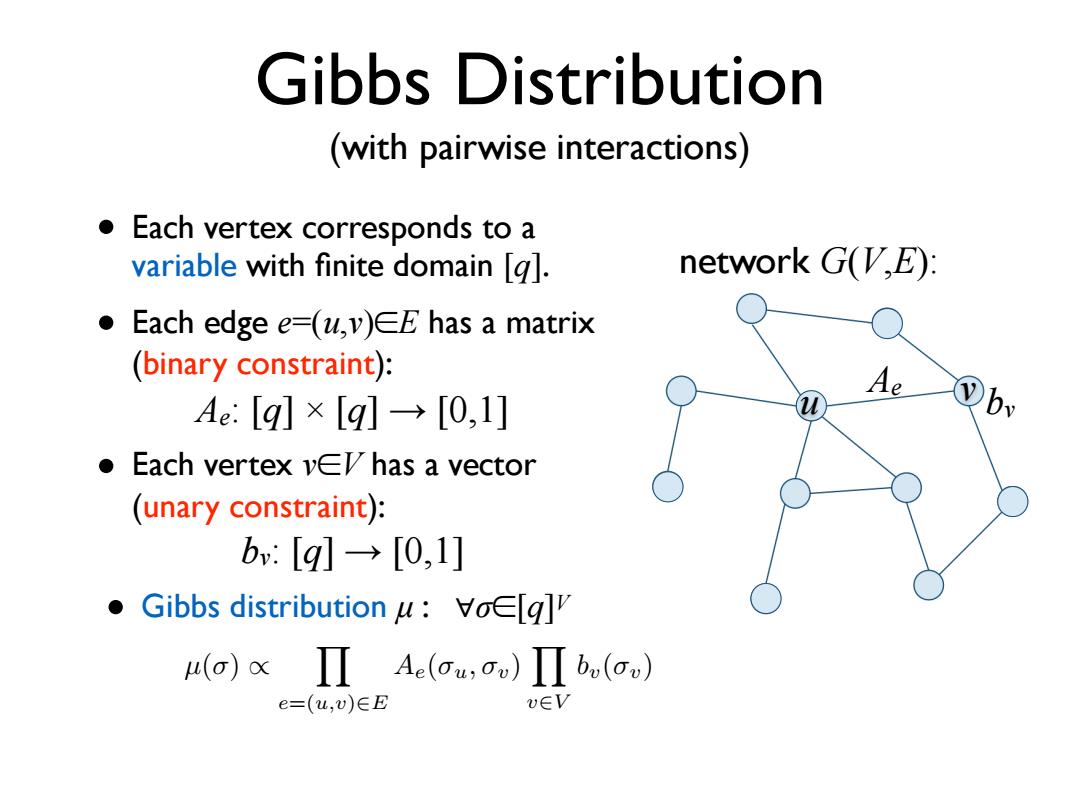
Gibbs Distribution (with pairwise interactions) Each vertex corresponds to a variable with finite domain g. network G,E): ● Each edge e=(u,v)EE has a matrix (binary constraint): Ae:[q]×[q→[0，l] bN ●Each vertex ve∈has a vector (unary constraint): bm:[g小→[0,1] Gibbs distribution u:Voelg] u(o)xIAe(o,o）Ib(ou) e=(u,v)∈E u∈VGibbs Distribution network G(V,E): • Each vertex corresponds to a variable with finite domain [q]. • Each edge e=(u,v)∈E has a matrix (binary constraint): • Each vertex v∈V has a vector (unary constraint): µ(￾) / Y e=(u,v)2E Ae(￾u, ￾v) Y v2V bv(￾v) Ae u bv v (with pairwise interactions) Ae: [q] × [q] → [0,1] bv: [q] → [0,1] • Gibbs distribution µ : ∀σ∈[q]V