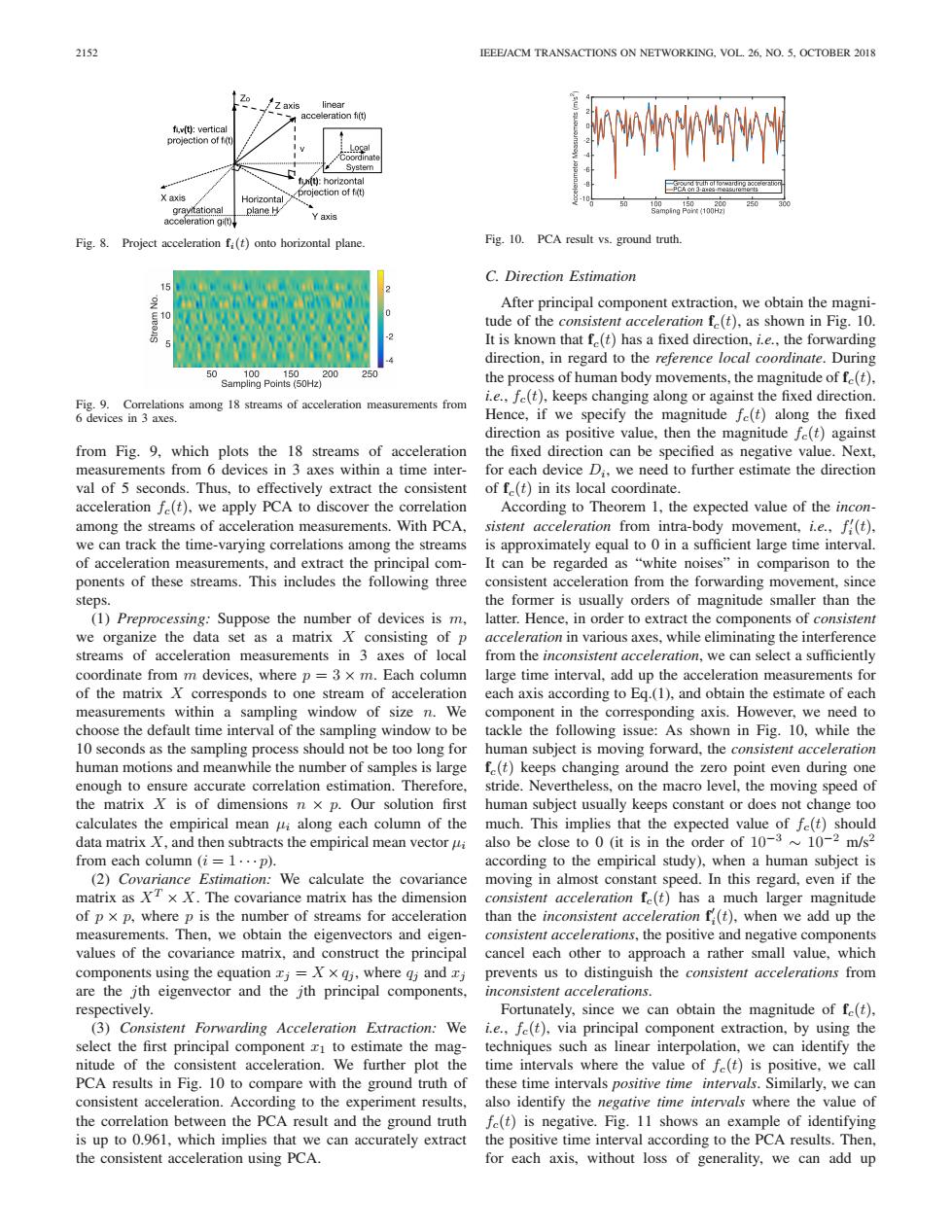
2152 IEEE/ACM TRANSACTIONS ON NETWORKING,VOL.26.NO.5.OCTOBER 2018 /Z axis linear acceleration fi(t) fiv(t):vertical projection of fi(t fiunt):horizontal n3a X axis Horizontal projection of fi(t) 250 graytational plane F npn1o acceleration gi(t) Y axis Fig.8.Project acceleration fi(t)onto horizontal plane Fig.10.PCA result vs.ground truth C.Direction Estimation 15 After principal component extraction.we obtain the magni- 复oWN tude of the consistent acceleration f(t),as shown in Fig.10. It is known that f(t)has a fixed direction,i.e..the forwarding direction,in regard to the reference local coordinate.During 50 00 50 200 25 Sampling Points(50Hz) the process of human body movements,the magnitude of fe(t). Fig.9.Correlations among 18 streams of acceleration measurements from i.e.,fe(t),keeps changing along or against the fixed direction. 6 devices in 3 axes. Hence,if we specify the magnitude fe(t)along the fixed direction as positive value,then the magnitude fe(t)against from Fig.9,which plots the 18 streams of acceleration the fixed direction can be specified as negative value.Next, measurements from 6 devices in 3 axes within a time inter- for each device D,,we need to further estimate the direction val of 5 seconds.Thus,to effectively extract the consistent of f(t)in its local coordinate. acceleration fe(t).we apply PCA to discover the correlation According to Theorem 1,the expected value of the incon- among the streams of acceleration measurements.With PCA, sistent acceleration from intra-body movement,i.e.,f(t). we can track the time-varying correlations among the streams is approximately equal to 0 in a sufficient large time interval. of acceleration measurements,and extract the principal com- It can be regarded as "white noises"in comparison to the ponents of these streams.This includes the following three consistent acceleration from the forwarding movement,since steps. the former is usually orders of magnitude smaller than the (1)Preprocessing:Suppose the number of devices is m, latter.Hence,in order to extract the components of consistent we organize the data set as a matrix X consisting of p acceleration in various axes,while eliminating the interference streams of acceleration measurements in 3 axes of local from the inconsistent acceleration,we can select a sufficiently coordinate from m devices,where p =3 x m.Each column large time interval,add up the acceleration measurements for of the matrix X corresponds to one stream of acceleration each axis according to Eq.(1),and obtain the estimate of each measurements within a sampling window of size n.We component in the corresponding axis.However,we need to choose the default time interval of the sampling window to be tackle the following issue:As shown in Fig.10,while the 10 seconds as the sampling process should not be too long for human subject is moving forward,the consistent acceleration human motions and meanwhile the number of samples is large fe(t)keeps changing around the zero point even during one enough to ensure accurate correlation estimation.Therefore. stride.Nevertheless,on the macro level,the moving speed of the matrix X is of dimensions n x p.Our solution first human subject usually keeps constant or does not change too calculates the empirical mean i along each column of the much.This implies that the expected value of fe(t)should data matrix X.and then subtracts the empirical mean vector i also be close to 0(it is in the order of 10-310-2 m/s2 from each column(i=l···p). according to the empirical study),when a human subject is (2)Covariance Estimation:We calculate the covariance moving in almost constant speed.In this regard,even if the matrix as XTx X.The covariance matrix has the dimension consistent acceleration fe(t)has a much larger magnitude of p x p,where p is the number of streams for acceleration than the inconsistent acceleration f(t),when we add up the measurements.Then,we obtain the eigenvectors and eigen- consistent accelerations,the positive and negative components values of the covariance matrix,and construct the principal cancel each other to approach a rather small value,which components using the equation j=Xx gi,where g and zj prevents us to distinguish the consistent accelerations from are the jth eigenvector and the jth principal components, inconsistent accelerations. respectively. Fortunately,since we can obtain the magnitude of fe(t), (3)Consistent Forwarding Acceleration Extraction:We i.e.,fe(t),via principal component extraction,by using the select the first principal component zi to estimate the mag- techniques such as linear interpolation,we can identify the nitude of the consistent acceleration.We further plot the time intervals where the value of fe(t)is positive,we call PCA results in Fig.10 to compare with the ground truth of these time intervals positive time intervals.Similarly,we can consistent acceleration.According to the experiment results, also identify the negative time intervals where the value of the correlation between the PCA result and the ground truth fe(t)is negative.Fig.11 shows an example of identifying is up to 0.961,which implies that we can accurately extract the positive time interval according to the PCA results.Then, the consistent acceleration using PCA. for each axis,without loss of generality,we can add up2152 IEEE/ACM TRANSACTIONS ON NETWORKING, VOL. 26, NO. 5, OCTOBER 2018 Fig. 8. Project acceleration fi(t) onto horizontal plane. Fig. 9. Correlations among 18 streams of acceleration measurements from 6 devices in 3 axes. from Fig. 9, which plots the 18 streams of acceleration measurements from 6 devices in 3 axes within a time inter￾val of 5 seconds. Thus, to effectively extract the consistent acceleration fc(t), we apply PCA to discover the correlation among the streams of acceleration measurements. With PCA, we can track the time-varying correlations among the streams of acceleration measurements, and extract the principal com￾ponents of these streams. This includes the following three steps. (1) Preprocessing: Suppose the number of devices is m, we organize the data set as a matrix X consisting of p streams of acceleration measurements in 3 axes of local coordinate from m devices, where p = 3 × m. Each column of the matrix X corresponds to one stream of acceleration measurements within a sampling window of size n. We choose the default time interval of the sampling window to be 10 seconds as the sampling process should not be too long for human motions and meanwhile the number of samples is large enough to ensure accurate correlation estimation. Therefore, the matrix X is of dimensions n × p. Our solution first calculates the empirical mean μi along each column of the data matrix X, and then subtracts the empirical mean vector μi from each column (i = 1 ··· p). (2) Covariance Estimation: We calculate the covariance matrix as XT × X. The covariance matrix has the dimension of p × p, where p is the number of streams for acceleration measurements. Then, we obtain the eigenvectors and eigen￾values of the covariance matrix, and construct the principal components using the equation xj = X ×qj , where qj and xj are the jth eigenvector and the jth principal components, respectively. (3) Consistent Forwarding Acceleration Extraction: We select the first principal component x1 to estimate the mag￾nitude of the consistent acceleration. We further plot the PCA results in Fig. 10 to compare with the ground truth of consistent acceleration. According to the experiment results, the correlation between the PCA result and the ground truth is up to 0.961, which implies that we can accurately extract the consistent acceleration using PCA. Fig. 10. PCA result vs. ground truth. C. Direction Estimation After principal component extraction, we obtain the magni￾tude of the consistent acceleration fc(t), as shown in Fig. 10. It is known that fc(t) has a fixed direction, i.e., the forwarding direction, in regard to the reference local coordinate. During the process of human body movements, the magnitude of fc(t), i.e., fc(t), keeps changing along or against the fixed direction. Hence, if we specify the magnitude fc(t) along the fixed direction as positive value, then the magnitude fc(t) against the fixed direction can be specified as negative value. Next, for each device Di, we need to further estimate the direction of fc(t) in its local coordinate. According to Theorem 1, the expected value of the incon￾sistent acceleration from intra-body movement, i.e., f i (t), is approximately equal to 0 in a sufficient large time interval. It can be regarded as “white noises” in comparison to the consistent acceleration from the forwarding movement, since the former is usually orders of magnitude smaller than the latter. Hence, in order to extract the components of consistent acceleration in various axes, while eliminating the interference from the inconsistent acceleration, we can select a sufficiently large time interval, add up the acceleration measurements for each axis according to Eq.(1), and obtain the estimate of each component in the corresponding axis. However, we need to tackle the following issue: As shown in Fig. 10, while the human subject is moving forward, the consistent acceleration fc(t) keeps changing around the zero point even during one stride. Nevertheless, on the macro level, the moving speed of human subject usually keeps constant or does not change too much. This implies that the expected value of fc(t) should also be close to 0 (it is in the order of 10−3 ∼ 10−2 m/s2 according to the empirical study), when a human subject is moving in almost constant speed. In this regard, even if the consistent acceleration fc(t) has a much larger magnitude than the inconsistent acceleration f i(t), when we add up the consistent accelerations, the positive and negative components cancel each other to approach a rather small value, which prevents us to distinguish the consistent accelerations from inconsistent accelerations. Fortunately, since we can obtain the magnitude of fc(t), i.e., fc(t), via principal component extraction, by using the techniques such as linear interpolation, we can identify the time intervals where the value of fc(t) is positive, we call these time intervals positive time intervals. Similarly, we can also identify the negative time intervals where the value of fc(t) is negative. Fig. 11 shows an example of identifying the positive time interval according to the PCA results. Then, for each axis, without loss of generality, we can add up