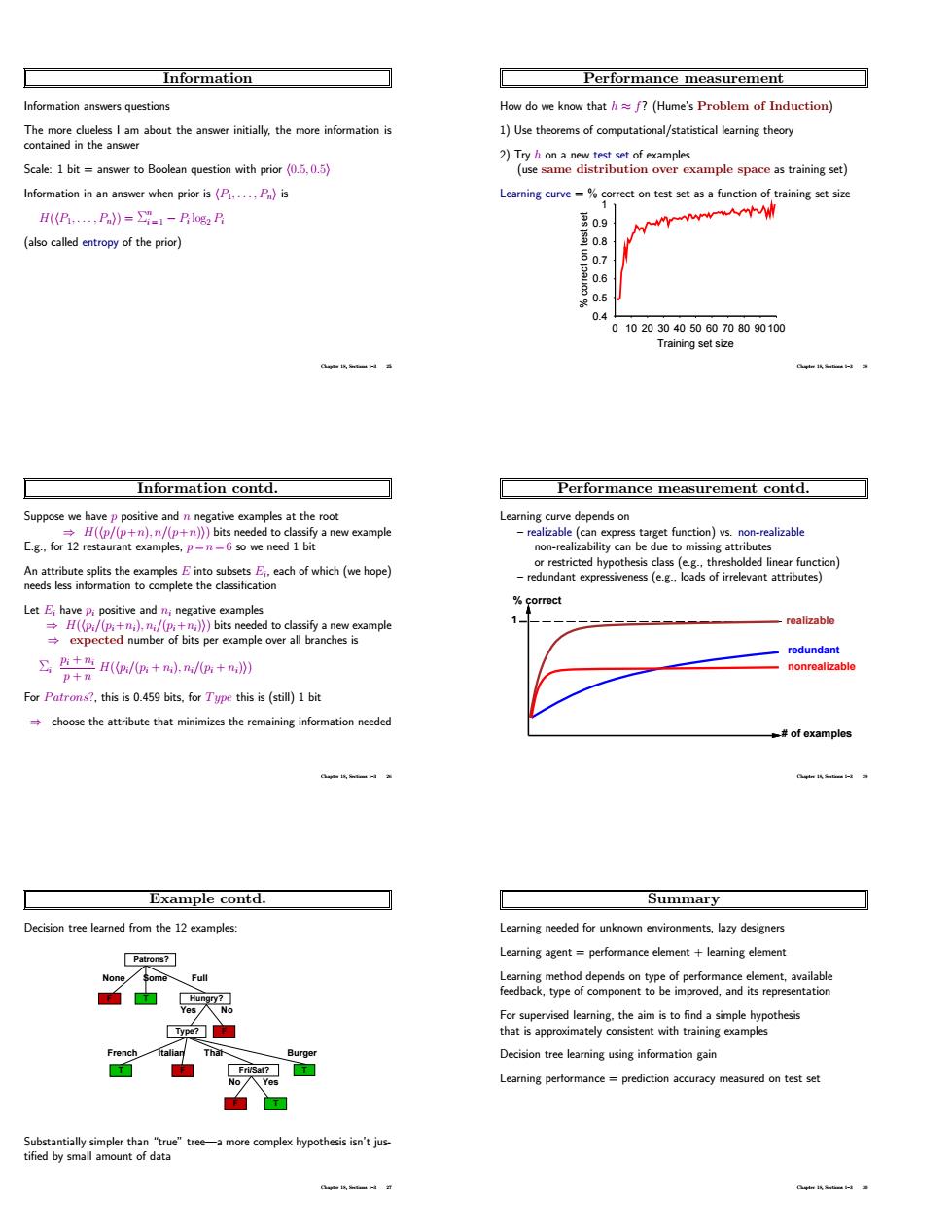
Information Performance measurement nformation answers questions How do we know thath?(Hume's Problem of Induction) answer initially.the more information i 1)Use theorems of computational/statistical learning theory 2)Tryh on a new test set of examples Scale:1 bit=answer to Boolean question with prior (0.,0.5) (use same distribution over example space as training set) Information in an answer when prior is (P....P)is Learning curve=%correct on test set as a function of training set size H(B.,P》=1-乃gB 0.9 (entropy of the prior) o8 0.7 0.6 0.5 0102030405060708090100 Training set size Information contd. Performance measurement contd. Suppose we have ppositive and rve depends o ss target function)vs.non-realizable E.g.for 12 restaurant examples,so we need 1 bit non-realizability can be due to missing attributes nt expressiveness (e.g.. rrelevant attributes) -roalizable +H(/g+)./+n》 nonrealizable p+n For Patrons?.this is 0.459 bits.for Type this is(still)1 bit choose the attribute that minimizes the remaining information needed #of examples Example contd。. Summary Decision tree leamed from the 12 examples Leaming needed for unknown environments,lazy designers Learning agent=performance element+learning element Learning method depends on type of performance element.available feedback,type of component to be improved,and its representation 奧 ftallan That Decision tree leaming using information gain Fri/Sat? No/ Learning performance=prediction accuracy measured on test se Information Information answers questions The more clueless I am about the answer initially, the more information is contained in the answer Scale: 1 bit = answer to Boolean question with prior h0.5, 0.5i Information in an answer when prior is hP1, . . . , Pni is H(hP1, . . . , Pni) = Σ n i = 1 − Pi log2 Pi (also called entropy of the prior) Chapter 18, Sections 1–3 25 Information contd. Suppose we have p positive and n negative examples at the root ⇒ H(hp/(p+n), n/(p+n)i) bits needed to classify a new example E.g., for 12 restaurant examples, p = n = 6 so we need 1 bit An attribute splits the examples E into subsets Ei , each of which (we hope) needs less information to complete the classification Let Ei have pi positive and ni negative examples ⇒ H(hpi/(pi+ni), ni/(pi+ni)i) bits needed to classify a new example ⇒ expected number of bits per example over all branches is Σi pi + ni p + n H(hpi/(pi + ni), ni/(pi + ni)i) For Patrons?, this is 0.459 bits, for Type this is (still) 1 bit ⇒ choose the attribute that minimizes the remaining information needed Chapter 18, Sections 1–3 26 Example contd. Decision tree learned from the 12 examples: No Yes Fri/Sat? None Some Full Patrons? Yes No Hungry? Type? French Italian Thai Burger F T T F F T F T Substantially simpler than “true” tree—a more complex hypothesis isn’t jus￾tified by small amount of data Chapter 18, Sections 1–3 27 Performance measurement How do we know that h ≈ f? (Hume’s Problem of Induction) 1) Use theorems of computational/statistical learning theory 2) Try h on a new test set of examples (use same distribution over example space as training set) Learning curve = % correct on test set as a function of training set size 0.4 0.5 0.6 0.7 0.8 0.9 1 0 10 20 30 40 50 60 70 80 90 100 % correct on test set Training set size Chapter 18, Sections 1–3 28 Performance measurement contd. Learning curve depends on – realizable (can express target function) vs. non-realizable non-realizability can be due to missing attributes or restricted hypothesis class (e.g., thresholded linear function) – redundant expressiveness (e.g., loads of irrelevant attributes) % correct # of examples 1 nonrealizable redundant realizable Chapter 18, Sections 1–3 29 Summary Learning needed for unknown environments, lazy designers Learning agent = performance element + learning element Learning method depends on type of performance element, available feedback, type of component to be improved, and its representation For supervised learning, the aim is to find a simple hypothesis that is approximately consistent with training examples Decision tree learning using information gain Learning performance = prediction accuracy measured on test set Chapter 18, Sections 1–3 30