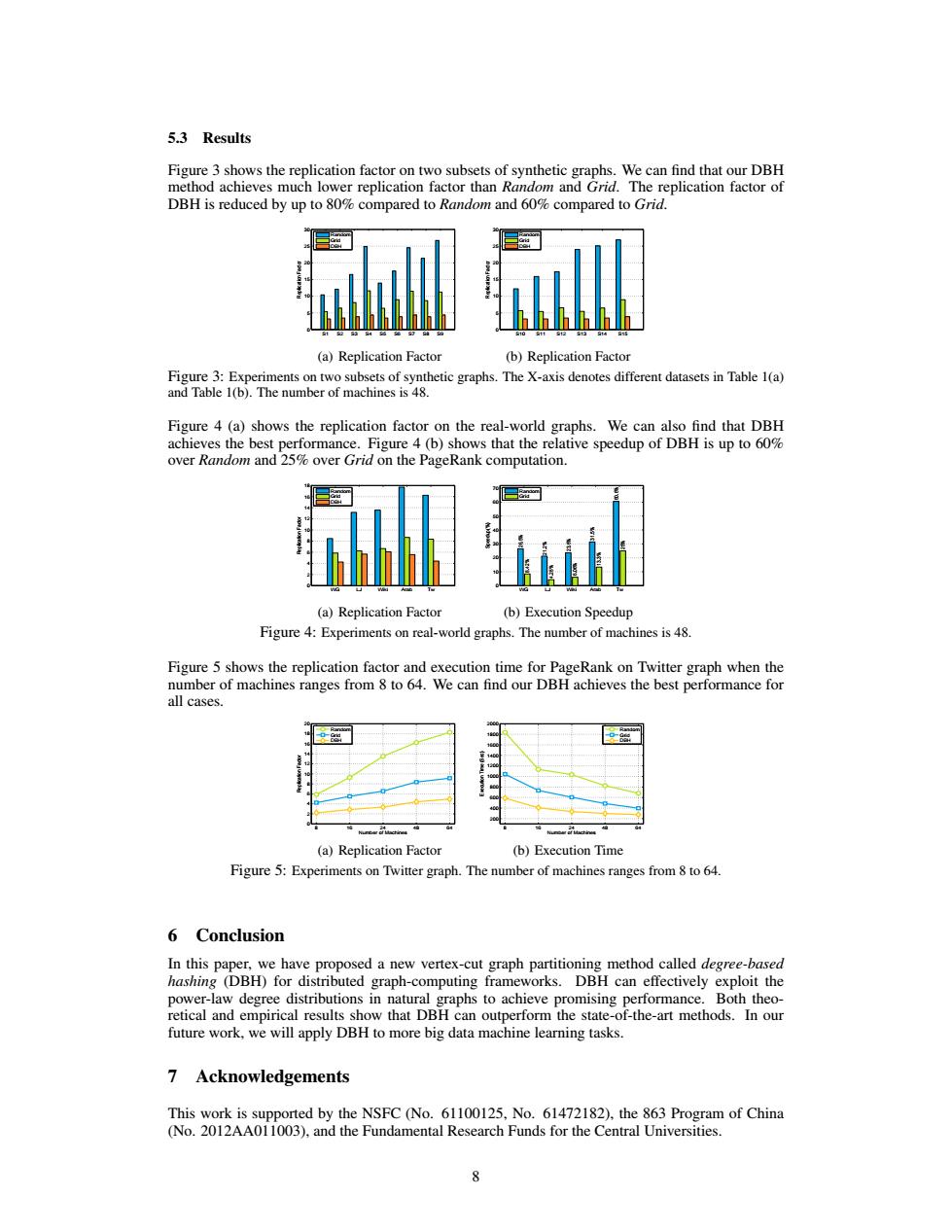
5.3 Results Figure 3 shows the replication factor on two subsets of synthetic graphs.We can find that our DBH method achieves much lower replication factor than Random and Grid.The replication factor of DBH is reduced by up to 80%compared to Random and 60%compared to Grid. (a)Replication Factor (b)Replication Factor Figure 3:Experiments on two subsets of synthetic graphs.The X-axis denotes different datasets in Table 1(a) and Table 1(b).The number of machines is 48. Figure 4(a)shows the replication factor on the real-world graphs.We can also find that DBH achieves the best performance.Figure 4(b)shows that the relative speedup of DBH is up to 60% over Random and 25%over Grid on the PageRank computation. (a)Replication Factor (b)Execution Speedup Figure 4:Experiments on real-world graphs.The number of machines is 48. Figure 5 shows the replication factor and execution time for PageRank on Twitter graph when the number of machines ranges from 8 to 64.We can find our DBH achieves the best performance for all cases. 益 (a)Replication Factor (b)Execution Time Figure 5:Experiments on Twitter graph.The number of machines ranges from 8 to 64. 6 Conclusion In this paper,we have proposed a new vertex-cut graph partitioning method called degree-based hashing (DBH)for distributed graph-computing frameworks.DBH can effectively exploit the power-law degree distributions in natural graphs to achieve promising performance.Both theo- retical and empirical results show that DBH can outperform the state-of-the-art methods.In our future work,we will apply DBH to more big data machine learning tasks. 7 Acknowledgements This work is supported by the NSFC (No.61100125,No.61472182),the 863 Program of China (No.2012AA011003),and the Fundamental Research Funds for the Central Universities.5.3 Results Figure 3 shows the replication factor on two subsets of synthetic graphs. We can find that our DBH method achieves much lower replication factor than Random and Grid. The replication factor of DBH is reduced by up to 80% compared to Random and 60% compared to Grid. S1 S2 S3 S4 S5 S6 S7 S8 S9 0 5 10 15 20 25 30 Replication Factor 1+10−12 Random Grid DBH (a) Replication Factor S10 S11 S12 S13 S14 S15 0 5 10 15 20 25 30 Replication Factor 1+10−12 Random Grid DBH (b) Replication Factor Figure 3: Experiments on two subsets of synthetic graphs. The X-axis denotes different datasets in Table 1(a) and Table 1(b). The number of machines is 48. Figure 4 (a) shows the replication factor on the real-world graphs. We can also find that DBH achieves the best performance. Figure 4 (b) shows that the relative speedup of DBH is up to 60% over Random and 25% over Grid on the PageRank computation. WG LJ Wiki Arab Tw 0 2 4 6 8 10 12 14 16 18 Replication Factor 1+10−12 Random Grid DBH (a) Replication Factor WG LJ Wiki Arab Tw 0 10 20 30 40 50 60 70 Speedup(%) 26.5% 8.42% 21.2% 4.28% 23.6% 6.06% 31.5% 13.3% 60.6% 25% 1+10−12 Random Grid (b) Execution Speedup Figure 4: Experiments on real-world graphs. The number of machines is 48. Figure 5 shows the replication factor and execution time for PageRank on Twitter graph when the number of machines ranges from 8 to 64. We can find our DBH achieves the best performance for all cases. 8 16 24 48 64 0 2 4 6 8 10 12 14 16 18 20 1+10−12 Replication Factor Number of Machines Random Grid DBH (a) Replication Factor 8 16 24 48 64 200 400 600 800 1000 1200 1400 1600 1800 2000 1+10−12 Execution Time (Sec) Number of Machines Random Grid DBH (b) Execution Time Figure 5: Experiments on Twitter graph. The number of machines ranges from 8 to 64. 6 Conclusion In this paper, we have proposed a new vertex-cut graph partitioning method called degree-based hashing (DBH) for distributed graph-computing frameworks. DBH can effectively exploit the power-law degree distributions in natural graphs to achieve promising performance. Both theo￾retical and empirical results show that DBH can outperform the state-of-the-art methods. In our future work, we will apply DBH to more big data machine learning tasks. 7 Acknowledgements This work is supported by the NSFC (No. 61100125, No. 61472182), the 863 Program of China (No. 2012AA011003), and the Fundamental Research Funds for the Central Universities. 8