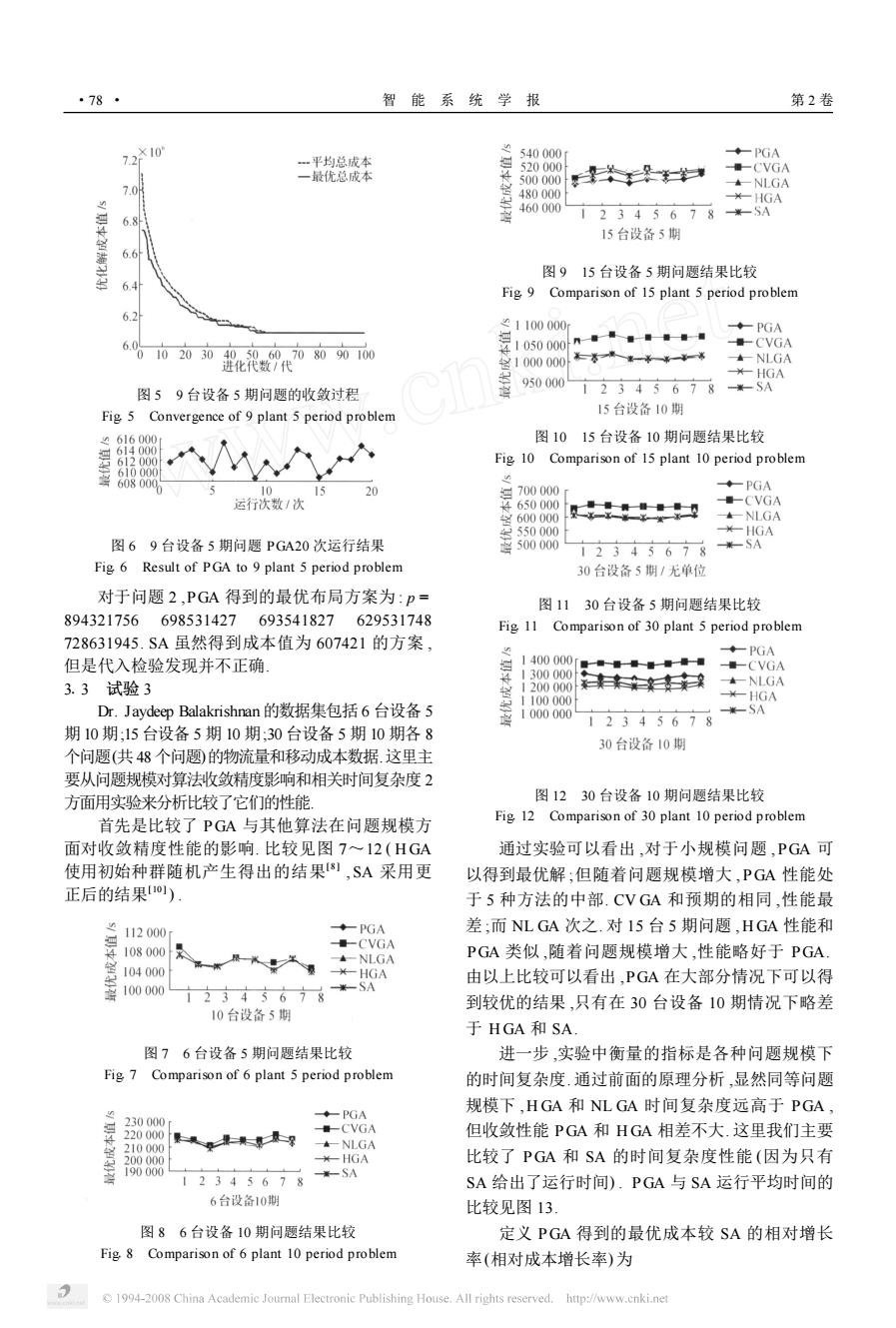
·78 智能系统学报 第2卷 7210 540000 ◆-PGA 平均总成本 延 一最优总成本 520000 500000 失x朵与 ■-CVGA 7.0 NLGA 480000 ￥-HGA 460000 68A 2345678 一SA 15台设备5期 6.6 图915台设备5期问题结果比较 6.4 Fig 9 Comparison of 15 plant 5 period problem 6.2 21100000 ◆-PGA 6.0%10203049060708090100 过，060000n110年1 ■-CVGA 士-NLGA 进化代数/代 HGA 950000 图59台设备5期问题的收敛过程 12345678米-SA Fig 5 Convergence of 9 plant 5 period problem 15台设备10期 图1015台设备10期问题结果比较 614000 612000 Fig 10 Comparison of 15 plant 10 period problem 610000 10 15 20 延700000 ◆-PGA 运行次数/次 4650000 ■CVGA 60000 ±-NLGA 安550000 ￥-1HGA 图69台设备5期问题PGA20次运行结果 500000 12345678 米-SA Fig 6 Result of PGA to 9 plant 5 period problem 30台设备5期/无单位 对于问题2，PGA得到的最优布局方案为：p= 图1130台设备5期问题结果比较 894321756698531427693541827629531748 Fig 11 Comparison of 30 plant 5 period problem 728631945.SA虽然得到成本值为607421的方案， ◆-PGA 但是代入检验发现并不正确 1400000 1300000 量数督量一■ 量-CVGA 3.3试验3 1200000 本-NLGA 1100000 HGA Dr.Jaydeep Balakrishnan的数据集包括6台设备5 1000000 米一SA 12345678 期10期：15台设备5期10期：30台设备5期10期各8 30台设备10期 个问题（共48个问题）的物流量和移动成本数据.这里主 要从问题规模对算法收敛精度影响和相关时间复杂度2 方面用实验来分析比较了它们的性能 图1230台设备10期问题结果比较 首先是比较了PGA与其他算法在问题规模方 Fig 12 Comparison of 30 plant 10 period problem 面对收敛精度性能的影响.比较见图7~12(HGA 通过实验可以看出，对于小规模问题，PGA可 使用初始种群随机产生得出的结果81，SA采用更 以得到最优解；但随着问题规模增大，PGA性能处 正后的结果) 于5种方法的中部.CVGA和预期的相同，性能最 112000 ◆-PGA 差；而NLGA次之.对15台5期问题，HGA性能和 量-CVGA ▲NLGA PGA类似，随着问题规模增大，性能略好于PGA. 104000 -HGA 由以上比较可以看出，PGA在大部分情况下可以得 100000 2345678 米-SA 到较优的结果，只有在30台设备10期情况下略差 10台设备5期 于HGA和SA. 图76台设备5期问题结果比较 进一步，实验中衡量的指标是各种问题规模下 Fig 7 Comparison of 6 plant 5 period problem 的时间复杂度.通过前面的原理分析，显然同等问题 ◆一PGA 规模下，HGA和NLGA时间复杂度远高于PGA, 230000 220000 零是果二及深 量-CVGA 但收敛性能PGA和HGA相差不大.这里我们主要 210000 本-NLGA 200000 HGA 比较了PGA和SA的时间复杂度性能（因为只有 190000 2345678 SA SA给出了运行时间).PGA与SA运行平均时间的 6台设备10期 比较见图13」 图86台设备10期问题结果比较 定义PGA得到的最优成本较SA的相对增长 Fig 8 Comparison of 6 plant 10 period problem 率（相对成本增长率）为 C 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net图 5 9 台设备 5 期问题的收敛过程 Fig15 Convergence of 9 plant 5 period problem 图 6 9 台设备 5 期问题 PGA20 次运行结果 Fig16 Result of PGA to 9 plant 5 period problem 对于问题 2 ,PGA 得到的最优布局方案为 : p = 894321756 698531427 693541827 629531748 728631945. SA 虽然得到成本值为 607421 的方案 , 但是代入检验发现并不正确. 313 试验 3 Dr. Jaydeep Balakrishnan 的数据集包括 6 台设备 5 期 10 期;15 台设备 5 期 10 期;30 台设备 5 期 10 期各 8 个问题(共 48 个问题)的物流量和移动成本数据.这里主 要从问题规模对算法收敛精度影响和相关时间复杂度 2 方面用实验来分析比较了它们的性能. 首先是比较了 PGA 与其他算法在问题规模方 面对收敛精度性能的影响. 比较见图 7～12 ( H GA 使用初始种群随机产生得出的结果[8 ] ,SA 采用更 正后的结果[10 ] ) . 图 8 6 台设备 10 期问题结果比较 Fig18 Comparison of 6 plant 10 period problem 图 7 6 台设备 5 期问题结果比较 Fig17 Comparison of 6 plant 5 period problem 图 9 15 台设备 5 期问题结果比较 Fig19 Comparison of 15 plant 5 period problem 图 10 15 台设备 10 期问题结果比较 Fig110 Comparison of 15 plant 10 period problem 图 11 30 台设备 5 期问题结果比较 Fig111 Comparison of 30 plant 5 period problem 图 12 30 台设备 10 期问题结果比较 Fig112 Comparison of 30 plant 10 period problem 通过实验可以看出 ,对于小规模问题 ,PGA 可 以得到最优解 ;但随着问题规模增大 ,PGA 性能处 于 5 种方法的中部. CV GA 和预期的相同 ,性能最 差 ;而 NL GA 次之. 对 15 台 5 期问题 , H GA 性能和 PGA 类似 ,随着问题规模增大 ,性能略好于 PGA. 由以上比较可以看出 ,PGA 在大部分情况下可以得 到较优的结果 ,只有在 30 台设备 10 期情况下略差 于 H GA 和 SA. 进一步 ,实验中衡量的指标是各种问题规模下 的时间复杂度. 通过前面的原理分析 ,显然同等问题 规模下 , H GA 和 NL GA 时间复杂度远高于 PGA , 但收敛性能 PGA 和 H GA 相差不大. 这里我们主要 比较了 PGA 和 SA 的时间复杂度性能 (因为只有 SA 给出了运行时间) . PGA 与 SA 运行平均时间的 比较见图 13. 定义 PGA 得到的最优成本较 SA 的相对增长 率(相对成本增长率) 为 · 87 · 智 能 系 统 学 报 第 2 卷