
第2卷第1期 智能系统学报 Vol.2 Ng 1 2007年2月 CAAI Transactions on Intelligent Systems Fcb.2007 基于单亲遗传算法的动态设备布局仿真研究 李波,邱枫 (天津大学管理学院,天津300072) 摘要:针对柔性生产环境下的设备布局问题,提出了一种基于单亲遗传算法原理的启发式算法.发展了一种新颖 的适用于动态设备布局的遗传换位操作算子,并提出在单期布局编码子串上应用换位概率的策略,增加了种群的多 样性.Matlab编程实现算法,通过大量仿真模拟并与其他算法进行比较分析,证实了所提出方法的有效性.提出的算 法在问题规模不大时可以迅速而准确的获得优化解,在问题规模较大时也能在较短时间(与其他算法相比)获得满 意解,因此具有较好的综合性能. 关键词:动态设备布局问题;启发式算法;单亲遗传算法 中图分类号:TP391.9文献标识码:A文章编号:16734785(2007)01-0074-06 Simulation of the dynamic plant layout problem based on partheno genetic algorithm LI Bo,QIU Feng (School of Management,Tianjin University,Tianjin 300072,China) Abstract:A heuristic algorithm based on PGA was proposed to solve the plant layout problem in flexible manufacturing systems.A new positionswitch genetic operator for DPL P was developed.Positionswitch probability strategy on single-period-layout was used to increase individuals'diversity.The effectiveness of proposed method is demonstrated by simulation examples and comparison with other approaches.Pro- posed algorithm produces optimal solutions speedily and accurately and provides acceptable solution in a reasonable time.Its performance is very good while considering both solution quality and computational time. Key words:DPLP;heuristic approach;PGA 在当今以市场为驱动的经济环境下,制造企业 备布局问题进行优化求解」 力求适应市场的变化而在竞争中立于不败之地,柔 1动态设备布局问题 性生产系统(FMS)应运而生.生产车间的设备布局 问题是柔性生产系统(或柔性生产单元)在设计初期 动态设备布局问题,包括为每一期选择一个静 必须考虑的重要问题之一.柔性即是指灵活应对市 态设备布局方案和决定是否在下一期改变这个布 场,在拉动式生产方式下,企业面临的是最终用户不 局.图1是一个单期6台(23)设备布局的例子,用 断变化的需求,静态设备布局问题(static plant lay- 236145(数字代表设备编号)来表示. out problem,SPLP)假设物料流不变,不适用于动 对实际问题进行简化,进行以下假设 态变化的环境,动态设备布局问题(dynamic plant 1)设备占地面积相同;2)设备数小于等于位置 layout problem,DPLP)在SPLP的基础上,从多时 数(小于时可通过增加虚拟设备来解决);3)设备间 期的角度出发,每个时期设备间的物料流量各不相 的单位物流运输成本相同(在此为了简化可设为 同,并考虑设备的移动成本,在总的规划时间内对设 1);4)设备的移动成本与布局方式无关(是某个常 量),5)设备间运输距离,同行或同列的设备间运距 收稿日期:20060705. 为其中心的间距、非同行或非同列的设备间运距为 基金项目:国家自然科学基金资助项目(70572045) 设备中心之间的折线距离(例如图1中设备2到设 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 1 期 智 能 系 统 学 报 Vol. 2 №. 1 2007 年 2 月 CAA I Transactions on Intelligent Systems Feb. 2007 基于单亲遗传算法的动态设备布局仿真研究 李 波 ,邱 枫 (天津大学 管理学院 ,天津 300072) 摘 要 :针对柔性生产环境下的设备布局问题 ,提出了一种基于单亲遗传算法原理的启发式算法. 发展了一种新颖 的适用于动态设备布局的遗传换位操作算子 ,并提出在单期布局编码子串上应用换位概率的策略 ,增加了种群的多 样性. Matlab 编程实现算法 ,通过大量仿真模拟并与其他算法进行比较分析 ,证实了所提出方法的有效性. 提出的算 法在问题规模不大时可以迅速而准确的获得优化解 ,在问题规模较大时也能在较短时间 (与其他算法相比) 获得满 意解 ,因此具有较好的综合性能. 关键词 :动态设备布局问题 ;启发式算法 ;单亲遗传算法 中图分类号 : TP39119 文献标识码 :A 文章编号 :167324785 (2007) 0120074206 Simulation of the dynamic plant layout problem based on partheno genetic algorithm L I Bo , QIU Feng (School of Management ,Tianjin University ,Tianjin 300072 , China) Abstract :A heuristic algorit hm based on PGA was p roposed to solve the plant layout problem in flexible manufact uring systems. A new position2switch genetic operator for DPL P was developed. Position2switch probability strategy on single2period2layout was used to increase individuals’diversity. The effectiveness of proposed method is demonstrated by simulation examples and comparison wit h ot her approaches. Pro2 posed algorit hm produces optimal solutions speedily and accurately and provides acceptable solution in a reasonable time. Its performance is very good while considering bot h solution quality and comp utational time. Keywords :DPL P; heuristic approach ; PGA 收稿日期 :2006207205. 基金项目 :国家自然科学基金资助项目(70572045) . 在当今以市场为驱动的经济环境下 ,制造企业 力求适应市场的变化而在竞争中立于不败之地 ,柔 性生产系统(FMS) 应运而生. 生产车间的设备布局 问题是柔性生产系统(或柔性生产单元) 在设计初期 必须考虑的重要问题之一. 柔性即是指灵活应对市 场 ,在拉动式生产方式下 ,企业面临的是最终用户不 断变化的需求 ,静态设备布局问题 (static plant lay2 out problem , SPL P) 假设物料流不变 ,不适用于动 态变化的环境 ,动态设备布局问题 ( dynamic plant layout p roblem , DPL P) 在 SPL P 的基础上 ,从多时 期的角度出发 ,每个时期设备间的物料流量各不相 同 ,并考虑设备的移动成本 ,在总的规划时间内对设 备布局问题进行优化求解. 1 动态设备布局问题 动态设备布局问题 ,包括为每一期选择一个静 态设备布局方案和决定是否在下一期改变这个布 局. 图 1 是一个单期 6 台(2 ×3) 设备布局的例子 ,用 236145 (数字代表设备编号) 来表示. 对实际问题进行简化 ,进行以下假设 : 1) 设备占地面积相同 ;2) 设备数小于等于位置 数(小于时可通过增加虚拟设备来解决) ;3) 设备间 的单位物流运输成本相同 (在此为了简化可设为 1) ;4) 设备的移动成本与布局方式无关 (是某个常 量) ;5) 设备间运输距离 ,同行或同列的设备间运距 为其中心的间距、非同行或非同列的设备间运距为 设备中心之间的折线距离 (例如图 1 中设备 2 到设

第1期 李波,等:基于单亲遗传算法的动态设备布局仿真研究 ·75 备4的运距为2,设备1到6的运距为3) 物流量而言最优的单期静态布局方案从多期的角度 来说很可能不是最优的.其他的一些方法比Rosen- blatt提出的DP启发式方法更好一些.如Urban提 出的一种最速下降成对交换(steepest-descent pair- wise exchange)启发式算法,这种方法类似于 图16台设备单期布局图例 CRAFT(Armour和Buffa)算法.Kusiak和Hera Fig.I 6 plant single period layout example gu1对不同的数学规划方法进行了研究.Conway 根据以上假设,结合Koopmans和Beckman的 和Venkataramanan,Balakrishnan和Cheng)用 二次分配模型四给出DPLP的数学模型: 遗传算法解决DPLP问题,Kaku和Mazzola使用了 minZ 禁忌搜索法(tabu search)l61.Baykasoglu和 Gindy!)针对DPLP问题提出一种模拟退火算法, 4Yan. 1) 利用Balakrishnan等的试验问题,他们证明这种算 法比Conway和Venkataramanan Balakrishnan和 S T. Xg=1J=1,m,1=1,“P,2 Cheng的GA算法要好.SA算法中的参数设置涉及 到确定初始温度(initial temperature)(可能在邻域 X=11=1,…n1=1“…P (3) 搜索neighborhood search中,会接受一个较差的解 Yul X(vgXsI, 决方案),温度下降速度(一个较差方案的接受概率 ij,1=1,n,1=2,…,P (4) 下降),以及反复次数(the number of iterations). 式中:P是总的时期数:n是设备台数;i,k代表布置 Balakrishnan等8)提出了一种混合遗传算法对 中的设备;j,1代表位置;f代表在第1期设备1到 DPLP进行优化计算 k物流运输成本(由于假设单位物流成本为1,f也 文中基于单亲遗传算法(partheno~genetic al- 就是设备间的物流量);d是位置j到1间的运输距 gorithm,PGA)的机理提出一种针对DPLP优化算 离;X是0,1变量,代表在第t期将设备i定位于j 法,该算法采用在一条染色体进行遗传操作的进化 位置:Y是0,1变量,代表在第1期初将设备i从 方法.并使用前人曾用的算例对算法进行测算,同时 位置j移动到位置1;A代表在第1期将设备i从 与己有算法进行比较分析 位置j移动到位置1的移动成本。 2 基于单亲遗传算法的DPLP方法 模型是在规划的总时间内,最小化每期物流成 本与设备移动成本之和.式(1)是最小化目标函数: 单亲遗传算法(PGA)是李茂军、童调生等)提 约束(2)、(3)表示在每期中每台设备都要定位于一 出的一种序号编码遗传算法(GA).PGA不同于传 个位置,每个位置都有一台设备:约束(4)表示只有 统遗传算法的是取消了传统遗传算法(TGA)序号 在连续的2期中设备的位置发生改变时,0,1变量 编码的交叉算子,代之以仅在一条染色体上操作的 Y才能取到1. 基因重组等遗传算子,简化了遗传操作,提高了计算 在n设备、t时期问题中,要计算(n)'个布局 效率,并且不要求初始群体的多样性,也不存在“早 方案的总成本才能得出最佳的解决方法.即使6设 熟收敛”问题,并且李茂军等对PGA的全局收敛性 备5期的问题也有多于1.910“种布置方案.对于 进行了研究:文献证明PGA在列车占线问题、模式 这种大规模问题,最优化方法是不适用的,需要使用 聚类问题、车辆路径问题和物流配送问题等组合优 启发式算法来得到优化解决方案」 化问题的求解中明显优于传统遗传算法(TGA). Rosenblatt(1986)用动态规划(dynamic pro 2.1编码方案 gramming,DP)方法来解决DPLP问题).他把每 单亲遗传算法采用序号编码方式,对于n台设备t 一期视为DP中的阶段(stage),一个具体的单期布 时期的动态设备布局问题(DLP),先把单期的多行静 局方案(SPLP方案)则为DP中的状态变量(state). 态布局按照设备从上到下从左到右的顺序进行编码, 由于DP方法不适用于大规模的问题,所以他又提 然后再按时期数将各期的静态布局编码顺序串接起 出了启发式DP方法,但也不是十分有效.选择一些 来.以6台(23)设备P期为例,v=[2361451123 物流成本较低的单期布局方案来构成DP可能会有 45(叶461532]代表一个动态设备布局的染色体 更好的效果,但是,由于要考虑移动成本,对于固定 串,图2描述了其编码方法(以第P期为例) 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
备 4 的运距为 2 ,设备 1 到 6 的运距为 3) . 2 3 6 1 4 5 图 1 6 台设备单期布局图例 Fig. 1 6 plant single period layout example 根据以上假设 ,结合 Koopmans 和 Beckman 的 二次分配模型[1 ]给出 DPL P 的数学模型 : min Z = ∑ P t =1 ∑ n i =1 ∑ n j = 1 ∑ n k = 1 ∑ n l = 1 f tik d tjl X tij X tkl + ∑ p t =2 ∑ n i = 1 ∑ n j = 1 ∑ n k = 1 ∑ n l =1 A tijl Ytijl , (1) S1 T1 ∑ n i =1 Xtij = 1 , j = 1 , …, n , t = 1 , …, P , (2) ∑ n j = 1 Xtij = 1 , i = 1 , …, n , t = 1 , …, P, (3) Ytijl = X( t- 1) ij X til , i , j , l = 1 , …, n , t = 2 , …, P. (4) 式中 : P 是总的时期数; n 是设备台数; i , k 代表布置 中的设备; j , l 代表位置; f tik代表在第 t 期设备 i 到 k 物流运输成本(由于假设单位物流成本为 1 , f tik也 就是设备间的物流量) ; dtjl是位置 j 到 l 间的运输距 离; Xtij是 0 ,1 变量 ,代表在第 t 期将设备 i 定位于 j 位置; Ytijl 是 0 , 1 变量 ,代表在第 t 期初将设备 i 从 位置 j 移动到位置 l ; A tijl 代表在第 t 期将设备 i 从 位置 j 移动到位置 l 的移动成本. 模型是在规划的总时间内 ,最小化每期物流成 本与设备移动成本之和. 式 (1) 是最小化目标函数 ; 约束(2) 、(3) 表示在每期中每台设备都要定位于一 个位置 ,每个位置都有一台设备 ;约束 (4) 表示只有 在连续的 2 期中设备的位置发生改变时 ,0 ,1 变量 Ytijl才能取到 1. 在 n 设备、t 时期问题中 ,要计算 ( n !) t 个布局 方案的总成本才能得出最佳的解决方法. 即使 6 设 备 5 期的问题也有多于 119 ×10 14种布置方案. 对于 这种大规模问题 ,最优化方法是不适用的 ,需要使用 启发式算法来得到优化解决方案. Rosenblatt ( 1986) 用动态规划 ( dynamic p ro2 gramming ,DP) 方法来解决 DPL P 问题[ 2 ] . 他把每 一期视为 DP 中的阶段 (stage) ,一个具体的单期布 局方案(SPL P 方案) 则为 DP 中的状态变量(state) . 由于 DP 方法不适用于大规模的问题 ,所以他又提 出了启发式 DP 方法 ,但也不是十分有效. 选择一些 物流成本较低的单期布局方案来构成 DP 可能会有 更好的效果 ,但是 ,由于要考虑移动成本 ,对于固定 物流量而言最优的单期静态布局方案从多期的角度 来说很可能不是最优的. 其他的一些方法比 Rosen2 blatt 提出的 DP 启发式方法更好一些. 如 Urban 提 出的一种最速下降成对交换 (steepest2descent pair2 wise exchange ) 启 发 式 算 法 , 这 种 方 法 类 似 于 CRAF T (Armour 和 Buffa) 算法. Kusiak 和 Hera2 gu [3 ]对不同的数学规划方法进行了研究. Conway 和 Venkataramanan [4 ] ,Balakrishnan 和 Cheng [5 ] 用 遗传算法解决 DPL P 问题 , Kaku 和 Mazzola 使用了 禁 忌 搜 索 法 ( tabu search ) [6 ] . Baykasoglu 和 Gindy [7 ]针对 DPL P 问题提出一种模拟退火算法 , 利用 Balakrishnan 等的试验问题 ,他们证明这种算 法比 Conway 和 Venkataramanan、Balakrishnan 和 Cheng 的 GA 算法要好. SA 算法中的参数设置涉及 到确定初始温度 (initial temperat ure) (可能在邻域 搜索 neighborhood search 中 ,会接受一个较差的解 决方案) ,温度下降速度 (一个较差方案的接受概率 下降) ,以及反复次数 (the number of iterations) . Balakrishnan 等[8 ] 提出 了一种 混 合 遗 传 算 法 对 DPL P 进行优化计算. 文中基于单亲遗传算法 (part heno2genetic al2 gorithm ,PGA ) 的机理提出一种针对 DPL P 优化算 法 ,该算法采用在一条染色体进行遗传操作的进化 方法. 并使用前人曾用的算例对算法进行测算 ,同时 与已有算法进行比较分析. 2 基于单亲遗传算法的 DPL P 方法 单亲遗传算法(PGA) 是李茂军、童调生等[9 ] 提 出的一种序号编码遗传算法 ( GA) . PGA 不同于传 统遗传算法的是取消了传统遗传算法 ( T GA) 序号 编码的交叉算子 ,代之以仅在一条染色体上操作的 基因重组等遗传算子 ,简化了遗传操作 ,提高了计算 效率 ,并且不要求初始群体的多样性 ,也不存在“早 熟收敛”问题 ,并且李茂军等对 PGA 的全局收敛性 进行了研究 ;文献证明 PGA 在列车占线问题、模式 聚类问题、车辆路径问题和物流配送问题等组合优 化问题的求解中明显优于传统遗传算法( TGA) . 211 编码方案 单亲遗传算法采用序号编码方式 ,对于 n台设备 t 时期的动态设备布局问题(DPLP) ,先把单期的多行静 态布局按照设备从上到下从左到右的顺序进行编码 , 然后再按时期数将各期的静态布局编码顺序串接起 来.以 6 台(2 ×3)设备 P期为例 ,v= [2 3 6 1 4 5| 1 2 3 4 5 6| …| 4 6 1 5 3 2]代表一个动态设备布局的染色体 串 ,图 2 描述了其编码方法(以第 P期为例) . 第 1 期 李 波 ,等 :基于单亲遗传算法的动态设备布局仿真研究 · 57 ·

·76· 智能系统学报 第2卷 第P期 按顺序串接起来,得到子代个体(见图3).这种遗传 操作的优点是,换位完成后,子代个体仍然是合法个 体,因为基因换位只是在每个单期布局子串上进行 (而每个单期布局子串都是一个合法的静态设备布 局方案),而且实现起来十分便捷 461532 ×10 88r 8.6 …平均总成本 图2编码方法 最优总成本 8.4 Fig 2 Code 82 8.0 2.2评价函数 78 由于DPLP求的是目标函数的极小值.而GA 7.6 7.4 选择操作是保留适应度最大的个体,因而目标函数 72 不能直接作评价函数.因此,评价函数fw(v),如式 7.0 2030 40 50 (5)定义: 进化代数/代 1 fx(vA)=1+F(vA) (5) 图36台设备5期问题的收敛过程 "是一个染色体,代表某一种设备布置方案, Fig 3 Convergence of 6 plant 5period problem F(v代表布置v的总成本(包括每期的物流成本 这里提出的基因换位遗传操作与CVGA及 和设备移动成本). NLGA的交叉遗传操作完全不同.CVGA对2个个 2.3初始种群的产生 体用单点交叉(single point crossover)a).首先,从 本算法初始种群随机产生,具体过程如下: 父代染色体中随机选择2个,然后随机选择一个点 1)构造一维自然数数组a1a=123…n],(1, 进行交叉.尽管这种交叉操作很简单而且容易执行, 2,n代表设备编号); 但可能会生成不可行的个体,必须改成可行的.例 2)随机选择a中一个元素存入v1x的1位置; 如:对于2个个体123456和125643,如果在第6个 3)删除a1×m中被选中的元素及其存储空间,即 位置交叉,就会产生2个新个体123453和125646. 变为a1×刘m.v=134…n](例如上一步选中元素 第1个个体中设备3出现2次,第2个个体中设备6 2. 出现2次,还要进行进一步的交换使它们可行,这无 重复执行,直到a为空,得到一个合法单期设备 疑增加了算法的复杂度.NLGA使用点对点交叉 布局子串ⅴ,然后把P(时期数)个单期布局子串按 (point-to-point crossover)s),2个串中每个位置上 顺序串接起来即得到DPLP的一个初始布局染色 的相应设备交换,生成许多子代设备布局(child lay 体 out),这样的结果是有些子代非法,但能保证部分子 2.4单期布局子串的基因换位操作 代可行,同样需要进行可行性检验(而且检验的运算 PGA的遗传操作包括基因换位、基因倒位、基 量很大).HGA采用DP方法进行交叉1,虽然保证 因移位等.单点基因换位是一次在一个个体上随机 了子代的可行性,当问题规模较大时,同样会遇到 选择2个位置的基因进行交换;多点基因换位是指, Rosenblatt提出的DP启发式算法遇到的问题,也 对预先给定的正整数w,取随机数i1(1≤)一次 就是将所有可行的单期静态布局全部纳入考虑范围 交换i对基因.该算法采用多点基因换位算子,w取 会很困难:不但操作较复杂,而且当选出的父代个数 int[设备台数/3]经验值) 为S=10时,一次DP交叉就要比较900个结果,交 I)基于PGA的单期布局子串基因换位 叉1000次的计算量可想而知,虽然这样交叉产生的 由于动态设备布局问题(DPLP)的特殊性,基 子代质量更好,但耗费的时间成本较高」 于PGA基因换位的原理,算法提出了一种适用于 2)单期布局子串基因换位概率的选择 DPLP的染色体单期布局子串的基因换位操作算 这里说的换位概率与传统GA中的交叉概率有 子.这种基因换位操作是先把一个DPLP的染色体 所不同,甚至与一般的PGA中的基因换位概率也 (父代个体)分解为单期的子串,然后在每个单期子 不尽相同.因为DPLP问题的特殊性,为了保证子 串上进行基因换位操作,换位完成后再把单期子串 代的可行性,在父代个体的每个单期子串上进行基 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 P 期 4 6 1 5 3 2 ↓ 4 6 1 5 3 2 图 2 编码方法 Fig12 Code 212 评价函数 由于 DPL P 求的是目标函数的极小值 ,而 GA 选择操作是保留适应度最大的个体 ,因而目标函数 不能直接作评价函数. 因此 ,评价函数 f N ( vk ) ,如式 (5) 定义 : f N ( vk ) = 1 1 + F( vk ) . (5) vk 是一个染色体 ,代表某一种设备布置方案 , F( vk ) 代表布置 vk 的总成本 (包括每期的物流成本 和设备移动成本) . 213 初始种群的产生 本算法初始种群随机产生 ,具体过程如下 : 1) 构造一维自然数数组 a1 ×n = [1 2 3 …n] , (1 , 2 , …, n 代表设备编号) ; 2) 随机选择 a 中一个元素存入 v1 ×n的 1 位置; 3) 删除 a1 ×n中被选中的元素及其存储空间 ,即 变为 a1 ×( n - 1) = [1 3 4 … n ] (例如上一步选中元素 2) . 重复执行 ,直到 a 为空 ,得到一个合法单期设备 布局子串 v,然后把 P(时期数) 个单期布局子串按 顺序串接起来即得到 DPL P 的一个初始布局染色 体. 214 单期布局子串的基因换位操作 PGA 的遗传操作包括基因换位、基因倒位、基 因移位等. 单点基因换位是一次在一个个体上随机 选择 2 个位置的基因进行交换 ;多点基因换位是指 , 对预先给定的正整数 uc ,取随机数 i(1 ≤i ≤uc ) 一次 交换 i 对基因. 该算法采用多点基因换位算子 , uc 取 int[设备台数/ 3 ](经验值) . 1) 基于 PGA 的单期布局子串基因换位 由于动态设备布局问题 (DPL P) 的特殊性 ,基 于 PGA 基因换位的原理 ,算法提出了一种适用于 DPL P 的染色体单期布局子串的基因换位操作算 子. 这种基因换位操作是先把一个 DPL P 的染色体 (父代个体) 分解为单期的子串 ,然后在每个单期子 串上进行基因换位操作 ,换位完成后再把单期子串 按顺序串接起来 ,得到子代个体(见图 3) . 这种遗传 操作的优点是 ,换位完成后 ,子代个体仍然是合法个 体 ,因为基因换位只是在每个单期布局子串上进行 (而每个单期布局子串都是一个合法的静态设备布 局方案) ,而且实现起来十分便捷. 图 3 6 台设备 5 期问题的收敛过程 Fig13 Convergence of 6 plant 5period problem 这里提出的基因换位遗传操作与 CV GA 及 NL GA 的交叉遗传操作完全不同. CV GA 对 2 个个 体用单点交叉 (single point crossover) [4 ] . 首先 ,从 父代染色体中随机选择 2 个 ,然后随机选择一个点 进行交叉. 尽管这种交叉操作很简单而且容易执行 , 但可能会生成不可行的个体 ,必须改成可行的. 例 如 :对于 2 个个体 123456 和 125643 ,如果在第 6 个 位置交叉 ,就会产生 2 个新个体 123453 和 125646. 第 1 个个体中设备 3 出现 2 次 ,第 2 个个体中设备 6 出现 2 次 ,还要进行进一步的交换使它们可行 ,这无 疑增加了算法的复杂度. NL GA 使用点对点交叉 (point2to2point crossover) [5 ] ,2 个串中每个位置上 的相应设备交换 ,生成许多子代设备布局(child lay2 out) ,这样的结果是有些子代非法 ,但能保证部分子 代可行 ,同样需要进行可行性检验(而且检验的运算 量很大) . H GA 采用 DP 方法进行交叉[ 6 ] ,虽然保证 了子代的可行性 ,当问题规模较大时 ,同样会遇到 Rosenblatt 提出的 DP 启发式算法遇到的问题 ,也 就是将所有可行的单期静态布局全部纳入考虑范围 会很困难 ;不但操作较复杂 ,而且当选出的父代个数 为 S = 10 时 ,一次 DP 交叉就要比较 900 个结果 ,交 叉1 000次的计算量可想而知 ,虽然这样交叉产生的 子代质量更好 ,但耗费的时间成本较高. 2) 单期布局子串基因换位概率的选择 这里说的换位概率与传统 GA 中的交叉概率有 所不同 ,甚至与一般的 PGA 中的基因换位概率也 不尽相同. 因为 DPL P 问题的特殊性 ,为了保证子 代的可行性 ,在父代个体的每个单期子串上进行基 · 67 · 智 能 系 统 学 报 第 2 卷

第1期 李波,等:基于单亲遗传算法的动态设备布局仿真研究 ·77 因换位操作,在此,基因换位概率是针对每个单期布 5)PGA 局子串的,而不是针对一个父代个体.试验证明单期 ①精华选择策略:②提出染色体单期布局子串 布局子串换位概率P.取在[0.2,0.4]时较好,而且 基因换位操作算子,可避免不可行解;③没置单期子 在此区间变化时,算法效果差异不大 串基因换位概率,增加种群多样性:④变异功能类似 P取0.2并不是意味着父代种群中只有大约 于NLGA外层循环的功能 20%个体进行上面所说的基因换位操作,而是所有 单期布局子串中约有20%要进行基因换位,例如对 3仿真试验 5期的问题,种群大小为100,P.=0.2,并不是只有 仿真试验分3个部分,包括试验1:Rosenb- 20个左右的个体进行基因换位,而是有100×5× latt21中的算例,一个6台设备(23)5期的动态布 0.2=l00个单期布局子串上要进行基因换位,而约局问题;试验2:Conway和Venkataramanan4中的 100个单期布局子串,随机出现在100个个体的共算例,一个9台设备(33)5期的布局问题;以及试 500个单期布局子串上 验3:对从Dr.Jaydeep Balakrishnan处取得的数据 2.5选择操作 集进行仿真试验.测算时用Matlab编程,在PMl.5 本算法选择操作包括2个部分: 600MHz的机器上运行 )从上一代群体中的N个个体和本次遗传操 3.1试验1 作产生的N个新个体共2N个体中选择适应性较 此问题已知最优解的总成本为71187,文中提 强的N个个体,类似于截断选择法: 出的基于PGA的算法(种群大小400,进化代数50) 2)把1)中选出的N个个体按其适应度值排序, 可以成功搜索到该解(见图3),图4是PGA随机运 最好的个体直接进入下一代(精华策略),其余N- 行20次得到的结果,其中7次得到71187而且得到 1个个体通过轮盘赌进行选择,适应度值高的个体 了更多的最优布置方案.CVGA从随机初始种群无 有更大的机率被选择进入下一代种群 法得到71187的解.Rosenblatt的DP方法得到的 这种选择方法虽然在一定程度上损失了种群的 最优解为71984 多样化,但可以提高算法的搜索效率 72200 2.6变异操作 71800 变异操作是随机产生新的染色体个体,以概率 71400 Pm小于0.1)替换种群中较差的个体,然后进入下 71000 68101214161820 一代. 运行次数/次 2.7各种启发式方法在搜索操作策略方面的异同 图46台设备5期问题PGA20次运行结果 1)CVGA Fig 4 Result of PGA to 6 plant 5 period problem ①遗传操作采用单点交叉;②精华选择策略;③ 由图3的一次收敛过程看到,PGA算法在迭代 抑制性可行性判断 25代前收敛,图4中7次收敛于71187的平均收敛 2)NL GA 代数小于35代,说明了算法的效率.对于此问题 ①基于内外嵌套循环,内层实现GA操作,外层 CVGA在文献中没有给出其最优解对应的布局方 随机产生新个体来替换内层遗传操作后的差的个 案,SA得到的最优布局染色体为:p=135246 体,②GA操作采用点对点交叉;③交叉后采用抑制 135246153246153246653214,PGA算法得到了更 性方法检查可行性,④辅助小概率变异 多的最优布局方案,除了p还有:p1=642531 3)HGA 642531642351642351412356,p=642531642531 ①采用联赛选择方法;②采用乐观交叉方法,③ 642351462351412356等 考虑交叉操作范围:④双亲唯一替代法,⑤启发式 3.2试验2 CRAFT变异方法 此问题最优解未知,CVGA得到的最优总成本 4)SA 为608904(选择较好的个体组成初始种群),文中提 ①采用交换方法生成相邻布局方案;②深用冷 出的算法在初始种群随机产生的情况下可以得到总 却进度表来控制寻优过程,选择合适的初始温度和 成本为608619的布局方案(取种群大小400,进化 冷却率;③2层循环,外层确定参数,内层进行相邻 代数100),收敛过程见图5.对此问题PGA运行20 布局方案的实现;④Metroplis准则的替代方法 次,得到结果见图6 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
因换位操作 ,在此 ,基因换位概率是针对每个单期布 局子串的 ,而不是针对一个父代个体. 试验证明单期 布局子串换位概率 Pc 取在[ 012 ,014 ]时较好 ,而且 在此区间变化时 ,算法效果差异不大. Pc 取 012 并不是意味着父代种群中只有大约 20 %个体进行上面所说的基因换位操作 ,而是所有 单期布局子串中约有 20 %要进行基因换位 ,例如对 5 期的问题 ,种群大小为 100 , Pc = 012 ,并不是只有 20 个左右的个体进行基因换位 ,而是有 100 ×5 × 012 = 100 个单期布局子串上要进行基因换位 ,而约 100 个单期布局子串 ,随机出现在 100 个个体的共 500 个单期布局子串上. 215 选择操作 本算法选择操作包括 2 个部分 : 1) 从上一代群体中的 N 个个体和本次遗传操 作产生的 N 个新个体共 2 N 个体中选择适应性较 强的 N 个个体 ,类似于截断选择法; 2) 把 1) 中选出的 N 个个体按其适应度值排序 , 最好的个体直接进入下一代(精华策略) ,其余 N - 1 个个体通过轮盘赌进行选择 ,适应度值高的个体 有更大的机率被选择进入下一代种群. 这种选择方法虽然在一定程度上损失了种群的 多样化 ,但可以提高算法的搜索效率. 216 变异操作 变异操作是随机产生新的染色体个体 ,以概率 Pm (小于 011) 替换种群中较差的个体 ,然后进入下 一代. 217 各种启发式方法在搜索操作策略方面的异同 1) CV GA ①遗传操作采用单点交叉 ; ②精华选择策略 ; ③ 抑制性可行性判断. 2) NL GA ①基于内外嵌套循环 ,内层实现 GA 操作 ,外层 随机产生新个体来替换内层遗传操作后的差的个 体 ; ②GA 操作采用点对点交叉 ; ③交叉后采用抑制 性方法检查可行性 ; ④辅助小概率变异. 3) H GA ①采用联赛选择方法 ; ②采用乐观交叉方法 ; ③ 考虑交叉操作范围 ; ④双亲唯一替代法 ; ⑤启发式 CRA F T 变异方法. 4) SA ①采用交换方法生成相邻布局方案 ; ②采用冷 却进度表来控制寻优过程 ,选择合适的初始温度和 冷却率 ; ③2 层循环 ,外层确定参数 ,内层进行相邻 布局方案的实现 ; ④Metroplis 准则的替代方法. 5) PGA ①精华选择策略 ; ②提出染色体单期布局子串 基因换位操作算子 ,可避免不可行解 ; ③设置单期子 串基因换位概率 ,增加种群多样性 ; ④变异功能类似 于 NL GA 外层循环的功能. 3 仿真试验 仿真试验分 3 个部分 ,包括试验 1 : Rosenb2 latt [ 2 ]中的算例 ,一个 6 台设备(2 ×3) 5 期的动态布 局问题 ;试验 2 :Conway 和 Venkataramanan [4 ] 中的 算例 ,一个 9 台设备(3 ×3) 5 期的布局问题 ;以及试 验 3 :对从 Dr1 J aydeep Balakrishnan 处取得的数据 集进行仿真试验. 测算时用 Matlab 编程 ,在PM2115 600 M Hz 的机器上运行. 311 试验 1 此问题已知最优解的总成本为 71187 ,文中提 出的基于 PGA 的算法(种群大小 400 ,进化代数 50) 可以成功搜索到该解(见图 3) ,图 4 是 PGA 随机运 行 20 次得到的结果 ,其中 7 次得到 71187 而且得到 了更多的最优布置方案. CV GA 从随机初始种群无 法得到 71187 的解. Rosenblatt 的 DP 方法得到的 最优解为 71984. 图 4 6 台设备 5 期问题 PGA20 次运行结果 Fig14 Result of PGA to 6 plant 5 period problem 由图 3 的一次收敛过程看到 ,PGA 算法在迭代 25 代前收敛 ,图 4 中 7 次收敛于 71187 的平均收敛 代数小于 35 代 ,说明了算法的效率. 对于此问题 CV GA 在文献中没有给出其最优解对应的布局方 案 , SA 得 到 的 最 优 布 局 染 色 体 为 : p = 135246 135246 153246 153246 653214 ,PGA 算法得到了更 多的 最 优 布 局 方 案 , 除 了 p 还 有 : p1 = 642531 642531 642351 642351 412356 , p2 = 642531 642531 642351 462351 412356 等. 312 试验 2 此问题最优解未知 ,CV GA 得到的最优总成本 为 608904 (选择较好的个体组成初始种群) ,文中提 出的算法在初始种群随机产生的情况下可以得到总 成本为 608619 的布局方案 (取种群大小 400 ,进化 代数 100) ,收敛过程见图 5. 对此问题 PGA 运行 20 次 ,得到结果见图 6. 第 1 期 李 波 ,等 :基于单亲遗传算法的动态设备布局仿真研究 · 77 ·
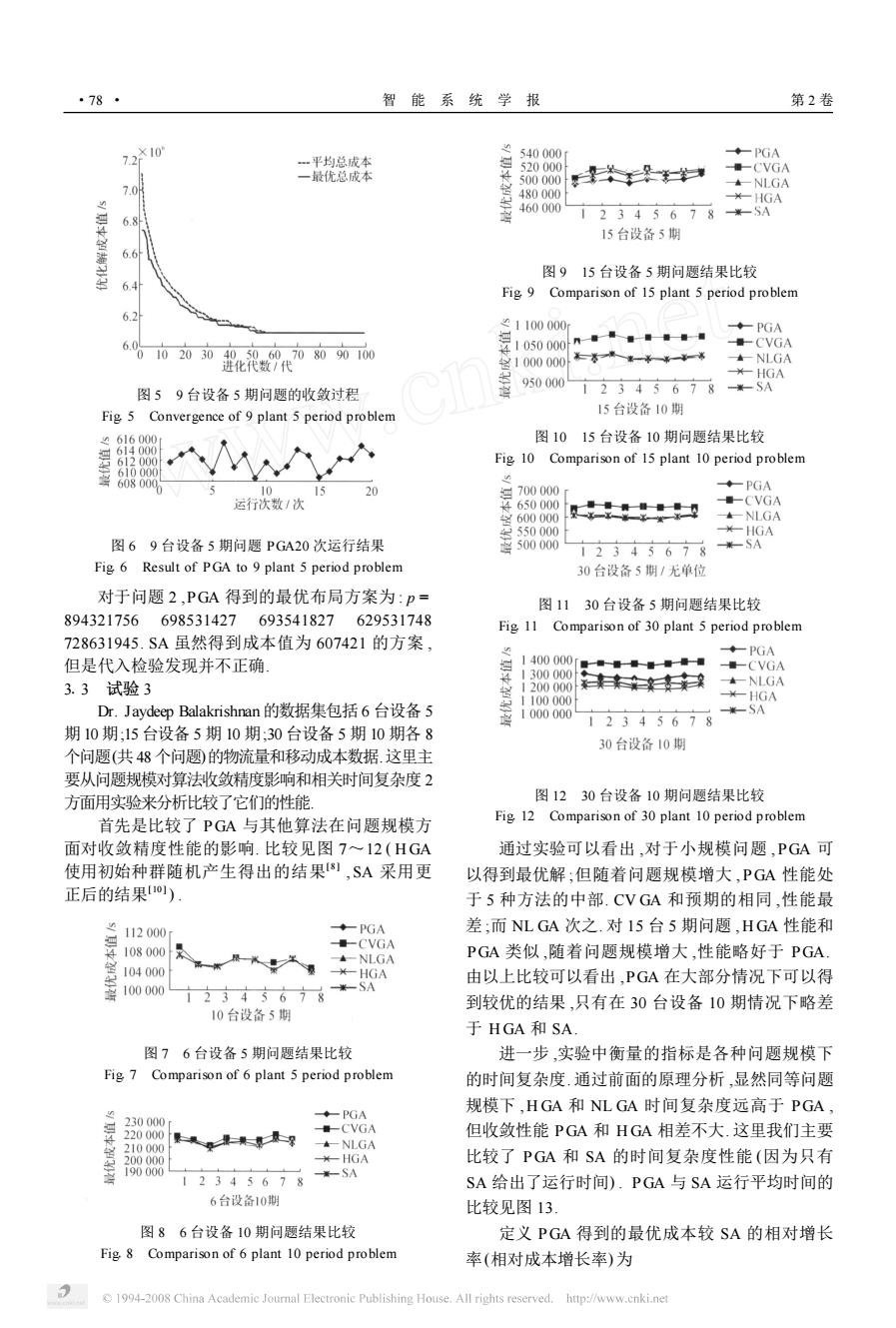
·78 智能系统学报 第2卷 7210 540000 ◆-PGA 平均总成本 延 一最优总成本 520000 500000 失x朵与 ■-CVGA 7.0 NLGA 480000 ¥-HGA 460000 68A 2345678 一SA 15台设备5期 6.6 图915台设备5期问题结果比较 6.4 Fig 9 Comparison of 15 plant 5 period problem 6.2 21100000 ◆-PGA 6.0%10203049060708090100 过,060000n110年1 ■-CVGA 士-NLGA 进化代数/代 HGA 950000 图59台设备5期问题的收敛过程 12345678米-SA Fig 5 Convergence of 9 plant 5 period problem 15台设备10期 图1015台设备10期问题结果比较 614000 612000 Fig 10 Comparison of 15 plant 10 period problem 610000 10 15 20 延700000 ◆-PGA 运行次数/次 4650000 ■CVGA 60000 ±-NLGA 安550000 ¥-1HGA 图69台设备5期问题PGA20次运行结果 500000 12345678 米-SA Fig 6 Result of PGA to 9 plant 5 period problem 30台设备5期/无单位 对于问题2,PGA得到的最优布局方案为:p= 图1130台设备5期问题结果比较 894321756698531427693541827629531748 Fig 11 Comparison of 30 plant 5 period problem 728631945.SA虽然得到成本值为607421的方案, ◆-PGA 但是代入检验发现并不正确 1400000 1300000 量数督量一■ 量-CVGA 3.3试验3 1200000 本-NLGA 1100000 HGA Dr.Jaydeep Balakrishnan的数据集包括6台设备5 1000000 米一SA 12345678 期10期:15台设备5期10期:30台设备5期10期各8 30台设备10期 个问题(共48个问题)的物流量和移动成本数据.这里主 要从问题规模对算法收敛精度影响和相关时间复杂度2 方面用实验来分析比较了它们的性能 图1230台设备10期问题结果比较 首先是比较了PGA与其他算法在问题规模方 Fig 12 Comparison of 30 plant 10 period problem 面对收敛精度性能的影响.比较见图7~12(HGA 通过实验可以看出,对于小规模问题,PGA可 使用初始种群随机产生得出的结果81,SA采用更 以得到最优解;但随着问题规模增大,PGA性能处 正后的结果) 于5种方法的中部.CVGA和预期的相同,性能最 112000 ◆-PGA 差;而NLGA次之.对15台5期问题,HGA性能和 量-CVGA ▲NLGA PGA类似,随着问题规模增大,性能略好于PGA. 104000 -HGA 由以上比较可以看出,PGA在大部分情况下可以得 100000 2345678 米-SA 到较优的结果,只有在30台设备10期情况下略差 10台设备5期 于HGA和SA. 图76台设备5期问题结果比较 进一步,实验中衡量的指标是各种问题规模下 Fig 7 Comparison of 6 plant 5 period problem 的时间复杂度.通过前面的原理分析,显然同等问题 ◆一PGA 规模下,HGA和NLGA时间复杂度远高于PGA, 230000 220000 零是果二及深 量-CVGA 但收敛性能PGA和HGA相差不大.这里我们主要 210000 本-NLGA 200000 HGA 比较了PGA和SA的时间复杂度性能(因为只有 190000 2345678 SA SA给出了运行时间).PGA与SA运行平均时间的 6台设备10期 比较见图13」 图86台设备10期问题结果比较 定义PGA得到的最优成本较SA的相对增长 Fig 8 Comparison of 6 plant 10 period problem 率(相对成本增长率)为 C 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 5 9 台设备 5 期问题的收敛过程 Fig15 Convergence of 9 plant 5 period problem 图 6 9 台设备 5 期问题 PGA20 次运行结果 Fig16 Result of PGA to 9 plant 5 period problem 对于问题 2 ,PGA 得到的最优布局方案为 : p = 894321756 698531427 693541827 629531748 728631945. SA 虽然得到成本值为 607421 的方案 , 但是代入检验发现并不正确. 313 试验 3 Dr. Jaydeep Balakrishnan 的数据集包括 6 台设备 5 期 10 期;15 台设备 5 期 10 期;30 台设备 5 期 10 期各 8 个问题(共 48 个问题)的物流量和移动成本数据.这里主 要从问题规模对算法收敛精度影响和相关时间复杂度 2 方面用实验来分析比较了它们的性能. 首先是比较了 PGA 与其他算法在问题规模方 面对收敛精度性能的影响. 比较见图 7~12 ( H GA 使用初始种群随机产生得出的结果[8 ] ,SA 采用更 正后的结果[10 ] ) . 图 8 6 台设备 10 期问题结果比较 Fig18 Comparison of 6 plant 10 period problem 图 7 6 台设备 5 期问题结果比较 Fig17 Comparison of 6 plant 5 period problem 图 9 15 台设备 5 期问题结果比较 Fig19 Comparison of 15 plant 5 period problem 图 10 15 台设备 10 期问题结果比较 Fig110 Comparison of 15 plant 10 period problem 图 11 30 台设备 5 期问题结果比较 Fig111 Comparison of 30 plant 5 period problem 图 12 30 台设备 10 期问题结果比较 Fig112 Comparison of 30 plant 10 period problem 通过实验可以看出 ,对于小规模问题 ,PGA 可 以得到最优解 ;但随着问题规模增大 ,PGA 性能处 于 5 种方法的中部. CV GA 和预期的相同 ,性能最 差 ;而 NL GA 次之. 对 15 台 5 期问题 , H GA 性能和 PGA 类似 ,随着问题规模增大 ,性能略好于 PGA. 由以上比较可以看出 ,PGA 在大部分情况下可以得 到较优的结果 ,只有在 30 台设备 10 期情况下略差 于 H GA 和 SA. 进一步 ,实验中衡量的指标是各种问题规模下 的时间复杂度. 通过前面的原理分析 ,显然同等问题 规模下 , H GA 和 NL GA 时间复杂度远高于 PGA , 但收敛性能 PGA 和 H GA 相差不大. 这里我们主要 比较了 PGA 和 SA 的时间复杂度性能 (因为只有 SA 给出了运行时间) . PGA 与 SA 运行平均时间的 比较见图 13. 定义 PGA 得到的最优成本较 SA 的相对增长 率(相对成本增长率) 为 · 87 · 智 能 系 统 学 报 第 2 卷

第1期 李波,等:基于单亲遗传算法的动态设备布局仿真研究 ·79 6000 lems and the location of economic activities [J ]Econo- 34000 ◆PGA metrica,1957(25):53.76. 2000 SA [2]ROSENBLATT M J.The dynamics of plant layout [J ] 6 0 合5期 30台10期 /5a Management Science,1986(37):272-286. [3]KUSIA K A,HERA GU S S.The facility layout problem 问题规 [J ]European Journal of Operational Research,1987 (29):229.251. 图13PGA、SA运行时间比较 [4]CONWA Y D G,VEN KATARAMANAN M A.Genetic Fig 13 Time comparison of PGA and SA search and the dynamic facility layout problem[J].Com- A=(C_PGA_c_SA)/c-PGA.(6) puters and Operations Research,1994,21(8):955- 式中:cPGA和cSA分别代表PGA和SA得到的 960. [5]BALA KRISHNAN J,CHEN G C H.Genetic search and 最优成本.△在相同规模问题时的平均值如图14所 the dynamic layout problem:an improved algorithm [J]. 示 Computers and Operations Research,2000(27):587- 593. [6]KA KU B,MAZZOLA J B,A tabur search heuristic for ◆一相对成本增长率 the plant layout problem [J ]INFORMS Journal on Computing,1997,9(4):374-384. 10期 5期 15 30台5期 5台1 30台10期 [7]BA YKASOGU A,NABIL N Z,GIND Y.A simulated 2 6 annealing algorithm for the dynamic layout problem [J]. 问题规模 Computers and Operations Research,2001(28):1403- 1426. 图14相同规模问题的相对成本增长率 [8]BALA KRISHNAN J,CHENG,C H.A hybrid genetic Fig 14 Relative cost growth rate algorithm for the dynamic plant layout problem [J ]In 从图13、14可以看到PGA运行时间随问题规 ternational Journal of Production Economics,2003(86): 模增大而增加的程度远小于SA.在大多数情况下 107.120 PGA能在可以接受的时间内得到更好的优化解.虽 [9]李茂军,童调生.单亲遗传算法及其应用研究U].湖南 然PGA在大规模设备布置问题中的优化解质量不 大学学报,1998,25(6):56·59. 如SA,但PGA的时间成本随着问题规模的增加, LI Maojun,TONG Tiaosheng.Partheno-genetic algo- rithm and its application [J ]Journal of Hunan Universi- 时间增长率远远小于SA,在30台5期的8个问题 ty,1998,25(6):56.59. 中,PGA花费的平均时间仅仅是SA的19.66%;而 [10]BA YKASOGU A,NABIL N Z.GINDY.Erratum to 在30台10期的8个问题中也只有22.87%,得到 A simulated annealing algorithm for dynamic layout 的最优成本只增加了不到4%.因此,在解决具体问 problem[J ]Computers Operation Research,2004, 题时,还要综合考虑时间成本和优化结果的质量,来 (31):313.315. 对算法进行选择」 作者简介: 李波,女,1967年生,教授,主要 4结束语 研究方向为物流系统规划、物流系统调 通过PGA算法对算例问题的实验运行,可以 度、智能计算与建模.发表学术论文30 看出PGA用于顺序编码的组合优化问题比较一般 多篇,EI检索论文9篇,参与编写教材 GA还是有一定优势的,其时间增加程度一般小于 3部. 其他算法.但在实验中发现,PGA随着编码长度的 Email libo0410 @yahoo.com.cn. 增加(问题规模的扩大)性能下降,所以对大规模设 备布局问题的布置计算,从种群多样性和时间代价 方面来看,应该进一步考虑降低时间复杂度并且增 邱枫,男,1979年生,硕士研究 大搜索空间的算法,这将是下一步研究的目标, 生,主要研究方向为物流与供应链管理、 物流系统规划」 参考文献 E mail qf ll @126.com [1]KOOPMANS T C,BECKMAN M.Assignment prob- 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 13 PGA、SA 运行时间比较 Fig113 Time comparison of PGA and SA Δ = ( C PGA c S A ) / c PGA . (6) 式中 :c_PGA 和 c_SA 分别代表 PGA 和 SA 得到的 最优成本.Δ在相同规模问题时的平均值如图 14 所 示. 图 14 相同规模问题的相对成本增长率 Fig114 Relative cost growth rate 从图 13、14 可以看到 PGA 运行时间随问题规 模增大而增加的程度远小于 SA. 在大多数情况下 PGA 能在可以接受的时间内得到更好的优化解. 虽 然 PGA 在大规模设备布置问题中的优化解质量不 如 SA ,但 PGA 的时间成本随着问题规模的增加 , 时间增长率远远小于 SA ,在 30 台 5 期的 8 个问题 中 ,PGA 花费的平均时间仅仅是 SA 的 19166 % ;而 在 30 台 10 期的 8 个问题中也只有 22187 % ,得到 的最优成本只增加了不到 4 %. 因此 ,在解决具体问 题时 ,还要综合考虑时间成本和优化结果的质量 ,来 对算法进行选择. 4 结束语 通过 PGA 算法对算例问题的实验运行 ,可以 看出 PGA 用于顺序编码的组合优化问题比较一般 GA 还是有一定优势的 ,其时间增加程度一般小于 其他算法. 但在实验中发现 ,PGA 随着编码长度的 增加(问题规模的扩大) 性能下降 ,所以对大规模设 备布局问题的布置计算 ,从种群多样性和时间代价 方面来看 ,应该进一步考虑降低时间复杂度并且增 大搜索空间的算法 ,这将是下一步研究的目标. 参考文献 : [1 ] KOOPMANS T C , BECKMAN M. Assignment prob2 lems and the location of economic activities [J ]. Econo2 metrica , 1957 (25) :53 - 76. [2 ]ROSENBLA TT M J. The dynamics of plant layout [J ]. Management Science , 1986 (37) :272 - 286. [3 ] KUSIA K A , HERA GU S S. The facility layout problem [J ]. European Journal of Operational Research , 1987 (29) :229 - 251. [4 ]CONWA Y D G, VEN KA TARAMANAN M A. Genetic search and the dynamic facility layout problem[J ]. Com2 puters and Operations Research , 1994 , 21 ( 8) : 955 - 960. [5 ]BALA KRISHNAN J , CHEN G C H. Genetic search and the dynamic layout problem : an improved algorithm [J ]. Computers and Operations Research , 2000 (27) : 587 - 593. [6 ] KA KU B , MAZZOLA J B , A tabu2search heuristic for the plant layout problem [J ]. INFORMS Journal on Computing , 1997 ,9 (4) :374 - 384. [7 ]BA YKASO GLU A , NABIL N Z , GIND Y. A simulated annealing algorithm for the dynamic layout problem [J ]. Computers and Operations Research , 2001 (28) : 1403 - 1426. [8 ]BALA KRISHNAN J , CHEN G, C H. A hybrid genetic algorithm for the dynamic plant layout problem[J ]. In2 ternational Journal of Production Economics , 2003 (86) : 107 - 120. [9 ]李茂军 ,童调生. 单亲遗传算法及其应用研究[J ]. 湖南 大学学报 ,1998 ,25 (6) : 56 - 59. L I Maojun , TON G Tiaosheng. Partheno2genetic algo2 rithm and its application [J ]. Journal of Hunan Universi2 ty , 1998 , 25 (6) : 56 - 59. [10 ]BA YKASO GLU A , NABIL N Z. GIND Y. Erratum to A simulated annealing algorithm for dynamic layout problem[J ]. Computers & Operation Research , 2004 , (31) :313 - 315. 作者简介 : 李 波 ,女 ,1967 年生 ,教授 ,主要 研究方向为物流系统规划、物流系统调 度、智能计算与建模. 发表学术论文 30 多篇 , EI 检索论文 9 篇 ,参与编写教材 3 部. E2mail : libo0410 @yahoo. com. cn. 邱 枫 ,男 , 1979 年生 ,硕士研究 生 ,主要研究方向为物流与供应链管理、 物流系统规划. E2mail : qf_ll @126. com. 第 1 期 李 波 ,等 :基于单亲遗传算法的动态设备布局仿真研究 · 97 ·