
第1卷第2期 智能系统学报 Vol.1 N2 2 2006年10月 CAAI Transactions on Intelligent Systems 0ct.2006 基于粒子群算法的神经网络短期降水预报建模研究 吴建生 (柳州师范高等专科学校数学与计算机科学系广西柳州545004) 摘要:用多样性粒子群算法优化神经网络的网络结构和连接权,获得神经网络集成个体;进一步用二次规划方法, 计算各集成个体的最优非负权系数进行组合集成,生成神经网络集成的输出结论,进行短期降水预报建模研究.以 广西全区的月降水量实例分析,结果表明该方法能有效提高系统的泛化能力 关键词:神经网络集成:粒子群优化,二次规划 中图分类号:TP183文献标识码:A文章编号:1673-4785(2006)02-0067-07 Study on the short-time rainfall prediction model of neural ensemble based on PSO algorithms WU Jiamsheng (Department of Mathematics and Computer Science,Liuzhou Teachers College,Liuzhou 545004,China) Abstract:This paper presents the evolving neural network architecture and connection weights based on Di- versity-guided Particle Swarm Optimization algorithms.The ensemble strategy is carried out by using the quadratic programming to calculate the best nomnegative weights.The weighted coefficient of each ensem- ble individual is obtained.This method can be used to establish the forecast model of the short-time rain- fall.The applied example is built with the monthly mean rainfall in the whole area of Guangxi.The result shows that this method can effectively increase the generalization ability of neural network. Key words:neural network ensemble;particle swarm optimization;quadratic program 旱涝灾害的气候预测问题是减灾防灾的重要研 成的各神经网络在该示例下的输出共同决定5刀 究课题,随着我国国民经济的高速发展.科技水平的 该方法可以显著地提高神经网络系统的泛化性能 日益提高,人们对灾害性气候的预测精度要求越来 是一种非常有效的工程化神经计算方法⑧.1o1 越高.在大气科学研究中,气候动力学方法虽然有了 粒子群优化(particle swarm optimization, 很大进展,但是天气系统的动力学模型难以客观描 PSO)是一种基于群体智能方法的进化计算技术,它 述和构造,目前天气预报业务中采用较多仍然是统 是通过个体之间的互动协作来搜寻全局最优解,其 计预报方法,从20世纪90年代以来,以神经网络方 概念简单、易于实现,既适合科学研究,又适合工程 法为代表的非线性人工智能预报建模方法,己经应 应用.利用粒子群优化算法提高神经网络的泛化 用在大气学科和气候分析等领域),神经网络与 性能是一个十分活跃的研究领域2).文中利用粒 传统的统计方法相比具有自适应和非线性影射等优 子群算法优化神经网络的结构和连接权,生成集成 良的性能得到广泛的认同,但是神经的初始连接权 个体,再用二次规划最优组合方法计算各集成个体 和网络结构选择缺乏定量的客观方法,这成为神经 的最优非负权系数进行组合集成,生成的输出结论, 网络方法在旱涝灾害的天气业务应用中的重要技术 以此建立短期降水预测模型 障碍 1 粒子群神经网络集成的基本原理 神经网络集成是用有限个神经网络对同一个问 题进行学习,集成在某输入示例下的输出由构成集 和方法 1.1粒子群神经网络的基本原理 收稿日期:200604-28. BP算法是最普遍的神经网络训练算法,由于基 基金项目:广西省教育厅资助项目(200508234) 于梯度下降的BP算法依赖于初始权值的选择, 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved htp://www.cnki.net
第 1 卷第 2 期 智 能 系 统 学 报 Vol. 1 №. 2 2006 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2006 基于粒子群算法的神经网络短期降水预报建模研究 吴建生 (柳州师范高等专科学校 数学与计算机科学系 ,广西 柳州 545004) 摘 要 :用多样性粒子群算法优化神经网络的网络结构和连接权 ,获得神经网络集成个体 ;进一步用二次规划方法 , 计算各集成个体的最优非负权系数进行组合集成 ,生成神经网络集成的输出结论 ,进行短期降水预报建模研究. 以 广西全区的月降水量实例分析 ,结果表明该方法能有效提高系统的泛化能力. 关键词 :神经网络集成 ;粒子群优化 ;二次规划 中图分类号 : TP183 文献标识码 :A 文章编号 :167324785 (2006) 0220067207 Study on the short2time rainfall prediction model of neural ensemble based on PSO algorithms WU Jian2sheng (Department of Mathematics and Computer Science , Liuzhou Teachers College , Liuzhou 545004 ,China) Abstract :This paper presents t he evolving neural network architect ure and connection weights based on Di2 versity2guided Particle Swarm Optimization algorit hms. The ensemble strategy is carried out by using t he quadratic p rogramming to calculate the best non2negative weights. The weighted coefficient of each ensem2 ble individual is obtained. This met hod can be used to establish t he forecast model of t he short2time rain2 fall. The applied example is built with the monthly mean rainfall in the whole area of Guangxi. The result shows t hat this method can effectively increase the generalization ability of neural network. Keywords :neural network ensemble ; particle swarm optimization ; quadratic program 收稿日期 :2006204228. 基金项目 :广西省教育厅资助项目(200508234) . 旱涝灾害的气候预测问题是减灾防灾的重要研 究课题 ,随着我国国民经济的高速发展. 科技水平的 日益提高 ,人们对灾害性气候的预测精度要求越来 越高. 在大气科学研究中 ,气候动力学方法虽然有了 很大进展 ,但是天气系统的动力学模型难以客观描 述和构造 ,目前天气预报业务中采用较多仍然是统 计预报方法 ,从 20 世纪 90 年代以来 ,以神经网络方 法为代表的非线性人工智能预报建模方法 ,已经应 用在大气学科和气候分析等领域[1 - 4 ] ,神经网络与 传统的统计方法相比具有自适应和非线性影射等优 良的性能得到广泛的认同 ,但是神经的初始连接权 和网络结构选择缺乏定量的客观方法 ,这成为神经 网络方法在旱涝灾害的天气业务应用中的重要技术 障碍. 神经网络集成是用有限个神经网络对同一个问 题进行学习 ,集成在某输入示例下的输出由构成集 成的各神经网络在该示例下的输出共同决定[5 - 7 ] . 该方法可以显著地提高神经网络系统的泛化性能 , 是一种非常有效的工程化神经计算方法[8 - 10 ] . 粒 子 群 优 化 ( particle swarm optimization , PSO) 是一种基于群体智能方法的进化计算技术 ,它 是通过个体之间的互动协作来搜寻全局最优解 ,其 概念简单、易于实现 ,既适合科学研究 ,又适合工程 应用[11 ] . 利用粒子群优化算法提高神经网络的泛化 性能是一个十分活跃的研究领域[12 - 13 ] . 文中利用粒 子群算法优化神经网络的结构和连接权 ,生成集成 个体 ,再用二次规划最优组合方法计算各集成个体 的最优非负权系数进行组合集成 ,生成的输出结论 , 以此建立短期降水预测模型. 1 粒子群 —神经网络集成的基本原理 和方法 111 粒子群 —神经网络的基本原理 BP 算法是最普遍的神经网络训练算法 ,由于基 于梯度下降的 BP 算法依赖于初始权值的选择[14 ] , © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·68 智能系统学报 第1卷 加之实际问题往往是极其复杂的多维曲面,所以BP 4)粒子的速度进化方程为 算法收敛速度慢而且极易陷入局部最优;另外在神 vy(1+1)vy(t)dir(an Pbes (t)- 经网络应用中,网络结构的确定基本上依赖经验,主 xy(v)))+ar(Pgbes (1)-xg(v). (3 要是采用递增或递减的试探方法来确定的网络隐节 -1. diversity 2. 本的输出具有不一致性和不可预测性,极大地限制 14 了神经网络在实际气象预报中的应用. 1 diversity(L) 粒子群算法的速度位移搜索模型操作简单, 计算复杂度低,并通过惯性权重协调全局搜索和局 (5) 部搜索,能以较大概率保证最优解,克服BP算法局 式中L为种群所含微粒的个数,」为搜索半径 部最优的缺陷,又可以提高局部区域的收敛速度,避 |M为微粒的维数,P为第i个微粒的第j个分量, 免局部搜索过程中的收敛停滞现象.为了保证种群 P,为第j个分量的平均值 的多样和过早收敛问题,文中采用J.Riget提出的 5)为保证连接结构矩阵进化后仍取0或1,依 多样性的粒子群算法i(attractive and repulsive 据文献171,连接结构位置进化方程取为 particle swarm optimizer,ARPSO)来优化神经网 1 0,r≥ 1+exp(-vg(1+1)) 络 xi(1+1) 1 粒子群神经网络的优化问题数学描述如下 1,r<1+exp-g1+) N1 n minE(w,v,.n= (6) 式中:r为0,1均匀分布的随机数.连接权位置进 化方程为 =2f,wg+91+, xg(1+1)=xg()+vg(t+1) 7) fwe 6)反复进行2)~5),直到适应度满足要求或者 达到总的进化代数(总的进化代数」 s.t w∈Rm,v∈R,0∈R,Y∈R 7)把进化后的最后一代L个体全部解码,得到 (1) L个神经网络的结构和网连接权,以其作为神经 式中:x为训练样本,x()为网络的实际输出,y() 网络的集成个体 为网络的期望输出,利用粒子群优化算法求解的二 1.2集成结论的生成 次非线性规划问题.定义适度函数为 设N个训练样本的实际输出为{y,1=1,2, F(w,v,0,》=1+min E(w,v,0,2 2) N},L个神经网络的输出:{,(),1=1,2,…N,i= 1,2,L},每个神经网络输出被赋予权重w,则集 具体实现步骤如下: 1)群体的位置和速度初始化,随机生成L个个 成输出为元=,,w,满足约束条件,0。 体,每个个体由2部分组成,第1部分是群体的位置 矩阵,第2部分对应粒子的速度矩阵:群体位置矩阵 且,=1.记e为第1个样本的误差,即 包括连接结构矩阵和权重系数矩阵,结构矩阵为二 进制变量矩阵,对应的连接权存在则该变量为1,否 e=-=y- ∑w(=∑(y:() 则为0:权重系数矩阵为浮点数矩阵,取[-2,2]上 (8) 的均匀分布随机数,它是控制网络的连接权值的大 N 小 所有训练样本的误差记为0=,P°,以其最小 2)输入训练样本,依据式1)计算每个粒子的适 求的非负权重系数w:,即求下式的解 应度,并且初始化个体经历最好位置P(),以及 min O =WT EW, 群体经历的最好位置Pet() s.t.R'W=1, (9) 3)对于每个个体,将其适应度与所经历的最好 w≥0. 位置的适应度比较,若较好,则将其作为当前最好位 式中:W=(w1,w2,w)T,R=(1,1,,1)T 置:并将其适应度与全局最好位置的适应度比较,若 ey 较好,则将其作为全局的最好位置 -)(y-yj),i,j=1,2,…L, 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved hup://www.cnki.ner
加之实际问题往往是极其复杂的多维曲面 ,所以 BP 算法收敛速度慢而且极易陷入局部最优 ;另外在神 经网络应用中 ,网络结构的确定基本上依赖经验 ,主 要是采用递增或递减的试探方法来确定的网络隐节 点[15 ] ,这些缺陷使得神经网络的训练样本和检测样 本的输出具有不一致性和不可预测性 ,极大地限制 了神经网络在实际气象预报中的应用. 粒子群算法的速度 —位移搜索模型操作简单 , 计算复杂度低 ,并通过惯性权重协调全局搜索和局 部搜索 ,能以较大概率保证最优解 ,克服 BP 算法局 部最优的缺陷 ,又可以提高局部区域的收敛速度 ,避 免局部搜索过程中的收敛停滞现象. 为了保证种群 的多样和过早收敛问题 ,文中采用 J1 Riget 提出的 多样性的粒子群算法[16 ] ( attractive and rep ulsive particle swarm optimizer , ARPSO) 来优化神经网 络. 粒子群 —神经网络的优化问题数学描述如下 : min E(w , v ,θ,γ) = 1 N1 ∑ N1 k =1 ∑ n t =1 [ yk (t) - ^yk (t) ] 2 2. (4) diversity ( L) = 1 | L | ·| R | ·∑ | L| i =1 ∑ M j = 1 ( pij - pj) 2 . (5) 式中 :| L| 为种群所含微粒的个数 ,| R| 为搜索半径 , | M| 为微粒的维数 , pij 为第 i 个微粒的第 j 个分量 , pj 为第 j 个分量的平均值. 5) 为保证连接结构矩阵进化后仍取 0 或 1 ,依 据文献[17 ] ,连接结构位置进化方程取为 xij ( t + 1) = 0 , r ≥ 1 1 + exp ( - vij ( t + 1) ) , 1 , r < 1 1 + exp ( - vij ( t + 1) ) . (6) 式中 :r 为[0 , 1 ]均匀分布的随机数. 连接权位置进 化方程为 xij ( t + 1) = xij ( t) + vij ( t + 1) . (7) 6) 反复进行 2) ~5) ,直到适应度满足要求或者 达到总的进化代数(总的进化代数 K) . 7) 把进化后的最后一代 L 个体全部解码 ,得到 L 个神经网络的结构和网络连接权 ,以其作为神经 网络的集成个体. 112 集成结论的生成 设 N 个训练样本的实际输出为{ yt , t = 1 ,2 , …, N} , L 个神经网络的输出 :{ ^yt ( i) , t = 1 ,2 , …, N , i = 1 ,2 , …, L} ,每个神经网络输出被赋予权重 wi ,则集 成输出为 yt = ∑ L i =1 wi^y t ( i) , wi 满足约束条件w i ≥0 , 且 ∑ L i = 1 wi = 1. 记 et 为第 t 个样本的误差 ,即 et = yt - ^yt = yt - ∑ L i = 1 wi^y t ( i) = ∑ L i = 1 wi ( yt - ^yt ( i) ) . (8) 所有训练样本的误差记为 Q = ∑ N t = 1 ( et) 2 , 以其最小 求的非负权重系数 wi ,即求下式的解 : min Q = W T EW , s. t. R TW = 1 , W ≥0. (9) 式中 :W = ( w1 , w2 , …, wL ) T , R = ( 1 , 1 , …, 1) T , eij = ∑ n t = 1 ( yt - yt ( i) ) ( yt - yt ( j) ) , i , j = 1 ,2 , …, L , · 86 · 智 能 系 统 学 报 第 1 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第2期 吴建生:基于粒子群算法的神经网络短期降水预报建模研究 ·69。 e11 XI 9 ·X.M+ E= 矩阵E称为信息阵.由文献 X2 XN.M+2 X= 三 eLI … * *… … 18]可知式(9)存在唯一非负最优组合权重向量,而 L XM XM+1 XN 且非负权重最优组合方法的误差平方和不大于参加 X10 Xu X1.N.M 组合的各个单项的误差平方和中最小者.根据非线 X20 X21 … X2.N.M 性规划理论,求得式9)的最优解,以其作为各集 10) ” 。年 … … 成神经网络个体的权重: Xx0 XM XM.N.M 以上的方法可以归纳为:先通过粒子群算法优 X的第1个状态向量为 化得到L个神经网络,再利用二次规划最优组合方 Xi+l X 法计算各集成个体的最优非负权系数进行组合集 Xi+2 X2 成,生成神经网络的输出结论 ,i=0,1,,N-M 2建模前的数据预处理 (11) 神经网络的输入矩阵质量一定程度上影响神经 共N-M+1个状态,X称相空间中的轨迹矩阵,矩 网络泛化能力,但是神经网络本身并不提供如何构 阵X中的元素与原序列对应关系为 造神经网络学习矩阵的方法.而如何建立合理的神 (12) 经网络输入矩阵是神经网络建模的另一项关键技术 Xm=x灯+1. X的协方差矩阵记为T,它是一个非负的对称矩 问题,是保障预测模型具有良好泛化能力和进行实 阵,其特征根也是非负的.将这些特征根按降序排列 际应用的重要条件.而且气象资料在收集过程中受 许多人为因素影响,数据本身不可避免包含噪声,由 e≥…≥ew0.矩阵T.的特征根ek对应的特 此所建立的预测模型会失真,预测结果会出现偏差 征向量E称为时间经验正交函数(time empirical 为了提高预测的准确率,需要尽量有效地减少样本 orthogonal function,T-EOF),第k个时间主成分 序列中噪声的影响 (time principal component,T-PC)定义为原始序列 文中把降水量看作一个时间序列,建立时间序 {x}在第k个时间经验正交函数上正交投影系数: 列的外推预测模型,首先采用奇异谱分析(singular spectrum analysis,SSA)方法2o1对原始降水时间序 ,2E,0≤1≤N.M:1≤k≤M 列重构,并用均生函数(mean generating function, 13) MGF)方法2对重构序列构造均生函数延拓矩阵, 任意TEOF的M个分量构成一个时间序列,反映 以其作为自变量,原始降水序列作为因变量,再利用 原始序列中的时间演变型,时间主成分是E表 偏最小二乘(partial least-squares regression,PLS) 示的时间型在原始序列的[x+1,x+2,x+M时 方法2进行处理,提取对因变量解释最强的综合变 段的权重 量作为神经网络的输入因子,原始时间序列作为输 SSA的重要功能由重建成分(reconstruction 出因子 components,RC)实现,用于在分析和预报中提取感 2.1奇异谱分析 兴趣的信息,过滤噪声,它是利用TEOF和下PC 奇异谱分析是KarhumenLoeve分解理论的发 重建一个长度为N的序列.由第k个TEOF和T 展与应用,最早应用于数字信号处理,其后被推广到 PC重建x,的成分记为x,即 海洋学、非线性动力学领域,近年来又开始应用于气 候诊断和预测中.它可以从包含噪声数据序列中提 ,,s时 M≤i≤N-M+1, 取尽可能多的可靠信息,并且有效利用周期分量重 建序列预测模型.它的好处是能够提炼出主要成分, x= a,E防,1≤i≤M-1, i,2 滤去非周期性的异常现象」 M SSA分析的对象是中心化的一维时间序列,记 ∑a,E,N-M+2≤i≤N N-i+1j-iM 为{x(),t=1,2,…,N},其M阶延迟得到矩阵X (14) RC具有叠加性,所有RC之和等于原始序列: 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
E = e11 … e1L … ω … eL1 … eLL , 矩阵 E 称为信息阵. 由文献 [18 ]可知式(9) 存在唯一非负最优组合权重向量 ,而 且非负权重最优组合方法的误差平方和不大于参加 组合的各个单项的误差平方和中最小者. 根据非线 性规划理论[19 ] ,求得式(9) 的最优解 ,以其作为各集 成神经网络个体的权重. 以上的方法可以归纳为 :先通过粒子群算法优 化得到 L 个神经网络 ,再利用二次规划最优组合方 法计算各集成个体的最优非负权系数进行组合集 成 ,生成神经网络的输出结论. 2 建模前的数据预处理 神经网络的输入矩阵质量一定程度上影响神经 网络泛化能力 ,但是神经网络本身并不提供如何构 造神经网络学习矩阵的方法. 而如何建立合理的神 经网络输入矩阵是神经网络建模的另一项关键技术 问题 ,是保障预测模型具有良好泛化能力和进行实 际应用的重要条件. 而且气象资料在收集过程中受 许多人为因素影响 ,数据本身不可避免包含噪声 ,由 此所建立的预测模型会失真 ,预测结果会出现偏差. 为了提高预测的准确率 ,需要尽量有效地减少样本 序列中噪声的影响. 文中把降水量看作一个时间序列 ,建立时间序 列的外推预测模型 ,首先采用奇异谱分析 (singular spectrum analysis , SSA) 方法[20 ]对原始降水时间序 列重构 ,并用均生函数 (mean generating f unction , M GF) 方法[21 ]对重构序列构造均生函数延拓矩阵 , 以其作为自变量 ,原始降水序列作为因变量 ,再利用 偏最小二乘 (partial least2squares regression ,PL S) 方法[ 22 ]进行处理 ,提取对因变量解释最强的综合变 量作为神经网络的输入因子 ,原始时间序列作为输 出因子. 211 奇异谱分析 奇异谱分析是 Karhumen2Loeve 分解理论的发 展与应用 ,最早应用于数字信号处理 ,其后被推广到 海洋学、非线性动力学领域 ,近年来又开始应用于气 候诊断和预测中. 它可以从包含噪声数据序列中提 取尽可能多的可靠信息 ,并且有效利用周期分量重 建序列预测模型. 它的好处是能够提炼出主要成分 , 滤去非周期性的异常现象. SSA 分析的对象是中心化的一维时间序列 ,记 为{ x ( t) , t = 1 ,2 , …, N} ,其 M 阶延迟得到矩阵 X X = x1 x2 … x N - M+1 x2 x3 … x N - M+2 … … … … x M x M+1 … x N ≡ X10 X11 … X1 , N - M X20 X21 … X2 , N - M … … … … X M0 X M1 … X M , N - M . (10) X的第 i 个状态向量为 Xi = xi+1 xi+2 … xi+ M ≡ X1 i X2 i … X Mi , i = 0 ,1 , …, N - M. (11) 共 N - M + 1 个状态 , X称相空间中的轨迹矩阵 ,矩 阵 X中的元素与原序列对应关系为 Xji = x j+1 . (12) X 的协方差矩阵记为 Tx , 它是一个非负的对称矩 阵 ,其特征根也是非负的. 将这些特征根按降序排列 e1 ≥e2 ≥…≥eM ≥0. 矩阵 Tx 的特征根 ek 对应的特 征向量 E k 称为时间经验正交函数 (time empirical ort hogonal f unction , T2EOF) ,第 k 个时间主成分 (time p rincipal component , T2PC) 定义为原始序列 { xi}在第 k 个时间经验正交函数上正交投影系数 : a k i = ∑ M j = 1 xi+ j E k j ,0 ≤i ≤N - M ;1 ≤k ≤M. (13) 任意 T2EOF 的 M 个分量构成一个时间序列 ,反映 原始序列中的时间演变型 ,时间主成分 a k i 是 E k 表 示的时间型在原始序列的[ xi + 1 , xi + 2 , …, xi + M ] T 时 段的权重. SSA 的重要功能由重建成分 ( reconstruction components ,RC) 实现 ,用于在分析和预报中提取感 兴趣的信息 ,过滤噪声 ,它是利用 T2EOF 和 T2PC 重建一个长度为 N 的序列. 由第 k 个 T2EOF 和 T2 PC 重建 xi 的成分记为 x k t ,即 x k t = 1 M ∑ M j = 1 a k i- j E k j M ≤i ≤N - M + 1 , 1 i ∑ i j = 1 a k i- j E k j ,1 ≤i ≤M - 1 , 1 N - i + 1 ∑ M j = i- N + M a k i- j E k j , N - M + 2 ≤i ≤N . (14) RC 具有叠加性 ,所有 RC 之和等于原始序列 : 第 2 期 吴建生 :基于粒子群算法的神经网络短期降水预报建模研究 · 96 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·70· 智能系统学报 第1卷 M 说偏最小二乘回归方法集多元线性回归分析、典型 x=∑1=1,2,N (15) T 相关分析和主成分分析的基本功能为一体,将数据 在实际应用中,只需要用前m个主成分即可重建原 分析方法和对模型认识分析方法有机结合.以 序列,降低噪声的干扰,达到提炼主要趋势的目的, PLS1过程说明偏最小二乘的具体计算步骤o!: 即有: 设自变量矩阵为 x,=x,m<M,1=1,2,…M.16) x11 X12 … &ST X21 Y22 … X2m 2.2均生函数方法 Xo =(Xij)nxm = 20 * 均生函数方法是将一维时间序列观测值按一定 X 的时间间隔计算均值而得到的均值生成函数,是曹 因变量矩阵为 鸿兴等在20世纪90年代初提出的一种预测方法, 它拓广了数理统计中的算术平均值的概念,建立具 yu 有多步预测能力的数学模型,能从数据中提取“自 Yo (ya)nx (21) 然”周期,因此能很好地与原序列拟合 设经过标准化的时间序列{x,1=1,2,,N}, MGF计算方法如下: 1)标准化自变量矩阵和因变量矩阵,得到标准 化数据Xo,Yo xt(i)= 1 x(i+j0,i=1,2,…,1,1≤1≤0. 2)计算主轴 xiri 17) w= ‖Xiy1'i=1,2,sT 22) 式中:NM=NT ,Q=NT(分),1为均生函数的 相应地得到第k个综合变量F,=X:1w:,F和X1 周期,Q为最大周期的长度,NT表示取整,生成如 进行普通最小二乘回归估计,回归系数P:= 下的上三角矩阵: ,并计算残差矩阵X-X1-下p,: x1(1) x21) xe(1) 3)检验交叉有效性,若G0.0975,继续计算, x2(2) x02) 18) 否则停止 4)提取T个成分F1,F2,…,F1,建立X和Y6 xe(O) 在其上的回归方程.由于F,2,…,Fr均是X的 再对其作周期性延拓,得到外延序列: 线性组合,故最终可以改写成%关于X的回归方 fi0=-1NTJ1=1,2.N+P 程 19) 3应用实例及结果分析 式中:P为预报步数,从而得到外延均生函数序列矩 阵 以广西全区6~8月(主汛期)降水量作为预测 2.3偏最小二乘回归方法 对象进行短期降水预报建模研究,样本长度为 1983年S wold及C.Albano等人首次提出了 1957~2005年共49个,其中用1957~1995年共39 偏最小二乘回归,近几十年来,它在理论方法和应用 个作为训练样本,留取1996~2005年共10个作为 方面都得到迅速发展,许多统计学家开始致力于其 检测样本,检验预测模型实用效果.采用逐年预报形 理论研究,它主要是针对多因变量对多自变量的回 式预测10个检测样本的结果,即用1957~1995年 归建模方法,在当因变量只有一个时,称其为PLS1 6月份降雨量建立的预报模型,预测1996年6月份 回归.在自变量之间存在较高相关性时,特别是样本 雨量;再用1957~1996年6月份降雨量建立的预报 个数较少,甚至样本个数小于自变量个数时,该方法 模型,预测1997年6月份雨量;依次类推直到1957 已经被证明是一种非常有效的方法, ~2004年6月份降雨量建立的预报模型,预测2005 偏最小二乘回归方法与主成分分析回归建模方 年6月份雨量 法的基本思路相同,主要区别在信息综合与筛选过 3.1基于SSA-MGF的数据预处理 程中,它不但考虑自变量的降维与信息综合,而且要 以1957~1995年6月份降雨量建立的预报模 考虑新的信息对因变量具有最佳的解释能力.可以 型,预测1996年6月份雨量为例,说明建立模型的 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved hup://www.cnki.net
xt = ∑ M k = 1 x k t t = 1 ,2 , …, N . (15) 在实际应用中 ,只需要用前 m 个主成分即可重建原 序列 ,降低噪声的干扰 ,达到提炼主要趋势的目的 , 即有 : xt = ∑ m k = 1 x k t , m < M , t = 1 ,2 , …, M. (16) 212 均生函数方法 均生函数方法是将一维时间序列观测值按一定 的时间间隔计算均值而得到的均值生成函数 ,是曹 鸿兴等在 20 世纪 90 年代初提出的一种预测方法 , 它拓广了数理统计中的算术平均值的概念 ,建立具 有多步预测能力的数学模型 ,能从数据中提取“自 然”周期 ,因此能很好地与原序列拟合. 设经过标准化的时间序列{ xt , t = 1 , 2 , …, N} , M GF 计算方法如下 : xl ( i) = 1 Nl ∑ N l - 1 j =0 x ( i + jl) , i = 1 ,2 , …, l ,1 ≤l ≤Q. (17) 式中 : Nl = IN T N l ,Q = IN T ( N 2 ) , l 为均生函数的 周期 ,Q 为最大周期的长度 ,IN T 表示取整 ,生成如 下的上三角矩阵 : X 3 = x1 (1) x2 (1) … xQ (1) x2 (2) … xQ (2) ω … x Q ( Q) . (18) 再对其作周期性延拓 ,得到外延序列 : f 1 (t) = xl[t - l ·INT( t - 1 l ) ],t = 1 ,2 , …, N + P. (19) 式中 : P 为预报步数 ,从而得到外延均生函数序列矩 阵. 213 偏最小二乘回归方法 1983 年 S1 wold 及 C1 Albano 等人首次提出了 偏最小二乘回归 ,近几十年来 ,它在理论方法和应用 方面都得到迅速发展 ,许多统计学家开始致力于其 理论研究 ,它主要是针对多因变量对多自变量的回 归建模方法 ,在当因变量只有一个时 ,称其为 PL S1 回归. 在自变量之间存在较高相关性时 ,特别是样本 个数较少 ,甚至样本个数小于自变量个数时 ,该方法 已经被证明是一种非常有效的方法. 偏最小二乘回归方法与主成分分析回归建模方 法的基本思路相同 ,主要区别在信息综合与筛选过 程中 ,它不但考虑自变量的降维与信息综合 ,而且要 考虑新的信息对因变量具有最佳的解释能力. 可以 说偏最小二乘回归方法集多元线性回归分析、典型 相关分析和主成分分析的基本功能为一体 ,将数据 分析方法和对模型认识分析方法有机结合. 以 PL S1 过程说明偏最小二乘的具体计算步骤[30 ] : 设自变量矩阵为 X0 = ( Xij ) n×m = x11 x12 … x1 m x21 x22 … x2 m … … … … x n1 x n2 … x nm . (20) 因变量矩阵为 Y0 = ( yi1 ) n×1 = y11 y21 … y n1 . (21) 1) 标准化自变量矩阵和因变量矩阵 ,得到标准 化数据 X 3 0 , Y 3 0 . 2) 计算主轴 wi = X 3 i- 1′Y 3 i- 1′ ‖X 3 i- 1′Y 3 i- 1′‖ , i = 1 ,2 , …, T. (22) 相应地得到第 k 个综合变量 Fi = X 3 i - 1 wi , Fi 和 X 3 i - 1 进行 普 通 最 小 二 乘 回 归 估 计 , 回 归 系 数 pi = X 3 i - 1′ti ‖ti ‖2 ,并计算残差矩阵 X 3 i = X 3 i - 1 - Fi p i′. 3) 检验交叉有效性 ,若Q 2 i ≥01097 5 ,继续计算 , 否则停止. 4) 提取 T 个成分 F1 , F2 , …, FT ,建立 X 3 0 和 Y 3 0 在其上的回归方程. 由于 F1 , F2 , …, FT 均是 X 3 0 的 线性组合 ,故最终可以改写成 Y0 关于 X0 的回归方 程. 3 应用实例及结果分析 以广西全区 6~8 月 (主汛期) 降水量作为预测 对象进行短期降水预报建模研究 , 样本长度为 1957~2005 年共 49 个 ,其中用 1957~1995 年共 39 个作为训练样本 ,留取 1996~2005 年共 10 个作为 检测样本 ,检验预测模型实用效果. 采用逐年预报形 式预测 10 个检测样本的结果 ,即用 1957~1995 年 6 月份降雨量建立的预报模型 ,预测 1996 年 6 月份 雨量 ;再用 1957~1996 年 6 月份降雨量建立的预报 模型 ,预测 1997 年 6 月份雨量 ;依次类推直到 1957 ~2004 年 6 月份降雨量建立的预报模型 ,预测 2005 年 6 月份雨量. 311 基于 SSA2M GF 的数据预处理 以 1957~1995 年 6 月份降雨量建立的预报模 型 ,预测 1996 年 6 月份雨量为例 ,说明建立模型的 · 07 · 智 能 系 统 学 报 第 1 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第2期 吴建生:基于粒子群算法的神经网络短期降水预报建模研究 ·71 过程,首先利用SSA-MGF方法对39个原始降水序 子个数.分别建立偏最小二乘回归模型.BP模型和 列重构,选取延迟阶数M=28,得到延迟矩阵 PSO-ANN集成模型BP模型的输入节点依据因子 X82,利用式(10)~(16)选取方差积累贡献率 个数确定,输出节点1个,隐层神经元个数和输入节 80%的值,得到重构序列.重构结果如图1所示。 点个数一样多,训练参数设置和以上相同 ×10 3.2结果对比分析 0.45r -Actual Rainfall 图2为PSO训练阶段适应度随进化次数的变 0.40 RC Rainfall 0.35 化曲线,从图可以看出适应度的最大值、平均值、最 0.30 差值随进化次数增加将趋于稳定并迅速收敛 0.25 .--Mean fitness -Best fitness 0.20 0.9r -Worest fitness 0.8 0.15 0.7 0.10 0.6 0 5 10152025303540 0.5 nla 0.4 0.3 0.2 图1原始数据和重构数据图 Fig 1 Actual data and reconstruction data 20 406080100 利用式(17)、(18)生成均生函数矩阵X9×19,再 Training/次 依照式(19)对其外延1步,生成自变量矩阵X0×9, 原始降水序列看作因变量Y×,将自变量利用偏最 图2适应度变化曲线 Fig,2 Curves of fitness in the training stage 小二乘回归处理,提取对因变量影响强的成分,在交 叉检验有效时,共提取到6个综合变量F,F, PLS模型BP模型和PSO-ANN模型对39个 F,以其建立偏最小二乘回归模型(记为PLS)为 训练样本拟合和10个预测样本的各种统计指标结 Y=0.366F+0.105F+0.097F+0.165F+ 果见表1,拟合和预测效果分别见图3和图4.从对 0.084F+0.036F6-0.0018. (23) 比统计指标和图3可以看出BP模型拟和效果最 并以这6个变量建立传统的BP模型(记为BP)和 好,它的相对误差1.48,相关系数0.9983,可以说 基于粒子群算法进化神经网络集成预报模型(记为 完全反映了训练样本的情况,其次是PSO-ANN模 PSO-ANN),分别对39个样本拟合和对1个样本预 型和PLS模型.评价一个模型的优劣看其拟合效果 报,比较结果来考察模型的效果。 是一个方面,但更重要的是看其预测效果的优劣,即 为了定量比较3种模型的效果,依据文献[23] 神经网络的泛化能力 引入以下4种误差:平均相对误差(the mean abso- 表13种模型拟和预测结果的统计评价 lute percentage error,MAPE)、均方根误差(the Table 1 The fitting and forecasting evaluate index mean squares error,MSE)、平均绝对误差(the about 39 samples of three prediction models mean absolute error,MAE)、Pearson相关系数 模型 MAPE MSE MAE PR (pearson relative coefficient.PR). PLS拟合 21.2258.20 50.000.8961 独立训练10个BP网络,每个网络都有6个输 PLS预测 27.34 86.19 77.23 0.9102 入神经元,1个输出神经元,隐层神经元个数6个, BP拟合 1.484.41 3.26 0.9983 训练参数设置:训练次数1000,学习因子为0.9,动 BP预测 31.03121.2090.97 0.8503 量因子为0.7,总体误差为0.001,训练完成后以预 PSO-ANN拟合 7.23 22.1617.67 0.9644 测结果最好者作为和PLS、PSO-ANN集成模型的 PS0ANN预测10.9245.1734.300.9271 对比实验.PSO-ANN集成模型中的参数设置为:进 化代数100,群体个数40 这3种模型的都是用SSA-MGF对原始降水量 在后续的逐年预报中,建模样本的重构是选取 序列预处理得到的建模因子,再经过LS方法对建 方差积累贡献率80%的值,得到重构序列,均生函 模因子的数据进行分解和筛选,提取对原始序列解 数外延每次外延1步,利用偏最小二乘回归提取综 释性最强的综合变量建立的非线性模型;对比表1 合变量建模因子时,以交叉有效为依据确定建模因 的拟合和预测结果,可以看出PLS模型对训练样本 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved htp://www.cnki.net
过程 ,首先利用 SSA2M GF 方法对 39 个原始降水序 列重构 , 选取延迟阶数 M = 28 , 得到延迟矩 阵 X28 ×12 ,利用式 ( 10) ~ ( 16) 选取方差积累贡献率 80 %的值 ,得到重构序列. 重构结果如图 1 所示. 图 1 原始数据和重构数据图 Fig11 Actual data and reconstruction data 利用式(17) 、(18) 生成均生函数矩阵 X 3 39 ×19 ,再 依照式(19) 对其外延 1 步 ,生成自变量矩阵 X40 ×19 , 原始降水序列看作因变量 Y40 ×1 ,将自变量利用偏最 小二乘回归处理 ,提取对因变量影响强的成分 ,在交 叉检验有效时 ,共提取到 6 个综合变量 F1 , F2 , …, F6 ,以其建立偏最小二乘回归模型(记为 PLS) 为 Y = 01366 F1 + 01105 F2 + 01097 F3 + 01165 F4 + 01084 F5 + 01036 F6 - 01001 8. (23) 并以这 6 个变量建立传统的 BP 模型 (记为 BP) 和 基于粒子群算法进化神经网络集成预报模型 (记为 PSO2ANN) ,分别对 39 个样本拟合和对 1 个样本预 报 ,比较结果来考察模型的效果. 为了定量比较 3 种模型的效果 ,依据文献[ 23 ] 引入以下 4 种误差 :平均相对误差 (the mean abso2 lute percentage error , MAPE) 、均方根误差 ( the mean squares error , MSE) 、平 均绝对误 差 ( the mean absolute error , MA E) 、Pearson 相 关 系 数 (pearson relative coefficient ,PR) . 独立训练 10 个 BP 网络 ,每个网络都有 6 个输 入神经元 ,1 个输出神经元 ,隐层神经元个数 6 个 , 训练参数设置 :训练次数 1 000 ,学习因子为 019 ,动 量因子为 017 ,总体误差为 01001 ,训练完成后以预 测结果最好者作为和 PLS、PSO2ANN 集成模型的 对比实验. PSO2ANN 集成模型中的参数设置为 :进 化代数 100 ,群体个数 40. 在后续的逐年预报中 ,建模样本的重构是选取 方差积累贡献率 80 %的值 ,得到重构序列 ,均生函 数外延每次外延 1 步 ,利用偏最小二乘回归提取综 合变量建模因子时 ,以交叉有效为依据确定建模因 子个数. 分别建立偏最小二乘回归模型. BP 模型和 PSO2ANN 集成模型 ,BP 模型的输入节点依据因子 个数确定 ,输出节点 1 个 ,隐层神经元个数和输入节 点个数一样多 ,训练参数设置和以上相同. 312 结果对比分析 图 2 为 PSO 训练阶段适应度随进化次数的变 化曲线 ,从图可以看出适应度的最大值、平均值、最 差值随进化次数增加将趋于稳定并迅速收敛. 图 2 适应度变化曲线 Fig12 Curves of fitness in the training stage1 PLS 模型、BP 模型和 PSO2ANN 模型对 39 个 训练样本拟合和 10 个预测样本的各种统计指标结 果见表 1 ,拟合和预测效果分别见图 3 和图 4. 从对 比统计指标和图 3 可以看出 BP 模型拟和效果最 好 ,它的相对误差 1148 ,相关系数 01998 3 ,可以说 完全反映了训练样本的情况 ,其次是 PSO2ANN 模 型和 PL S 模型. 评价一个模型的优劣看其拟合效果 是一个方面 ,但更重要的是看其预测效果的优劣 ,即 神经网络的泛化能力. 表 1 3 种模型拟和预测结果的统计评价 Table 1 The fitting and forecasting evaluate index about 39 samples of three prediction models 模型 MAPE MSE MA E PR PLS 拟合 21122 58120 50100 01896 1 PLS 预测 27134 86119 77123 01910 2 BP 拟合 1148 4141 3126 01998 3 BP 预测 31103 121120 90197 01850 3 PSO2ANN 拟合 7123 22116 17167 01964 4 PSO2ANN 预测 10192 45117 34130 01927 1 这 3 种模型的都是用 SSA2M GF 对原始降水量 序列预处理得到的建模因子 ,再经过 PL S 方法对建 模因子的数据进行分解和筛选 ,提取对原始序列解 释性最强的综合变量建立的非线性模型 ;对比表 1 的拟合和预测结果 ,可以看出 PL S 模型对训练样本 第 2 期 吴建生 :基于粒子群算法的神经网络短期降水预报建模研究 · 17 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
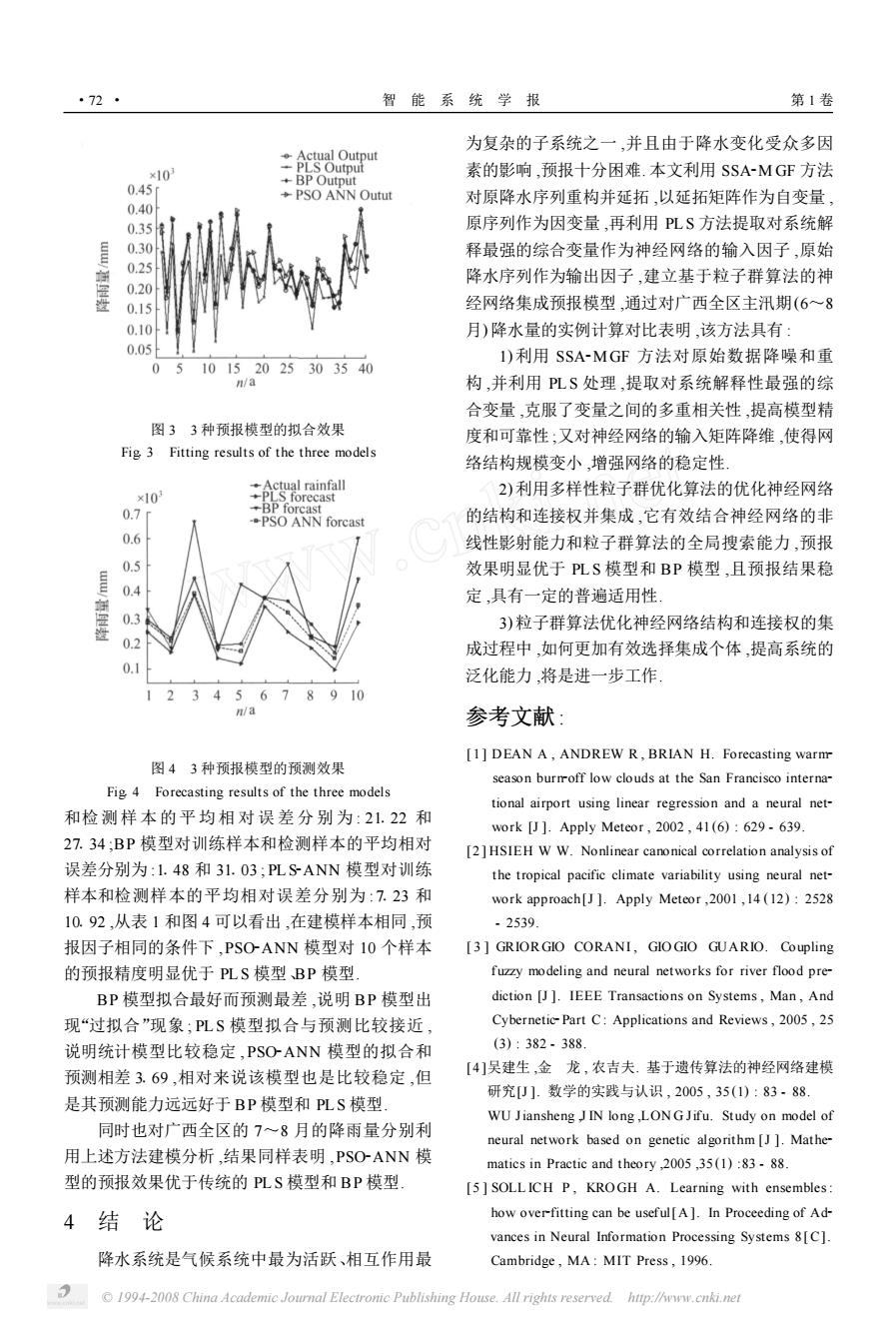
·72 智能系统学报 第1卷 为复杂的子系统之一,并且由于降水变化受众多因 Actual Output ×10 -PLS Output +BP Output 素的影响,预报十分困难.本文利用SSA-MGF方法 0.45 +PSO ANN Outut 对原降水序列重构并延拓,以延拓矩阵作为自变量 0.40 0.35 原序列作为因变量,再利用PLS方法提取对系统解 0.30 释最强的综合变量作为神经网络的输入因子,原始 0.25 降水序列作为输出因子,建立基于粒子群算法的神 0.20 0.15 经网络集成预报模型,通过对广西全区主汛期(6~8 0.10 月)降水量的实例计算对比表明,该方法具有: 0.05 1)利用SSA-MGF方法对原始数据降噪和重 0 10152025303540 n/a 构,并利用PLS处理,提取对系统解释性最强的综 合变量,克服了变量之间的多重相关性,提高模型精 图33种预报模型的拟合效果 度和可靠性,又对神经网络的输入矩阵降维,使得网 Fig 3 Fitting results of the three models 络结构规模变小,增强网络的稳定性 2)利用多样性粒子群优化算法的优化神经网络 ×10 S forecast 0.7 BP forcast PSO ANN forcast 的结构和连接权并集成,它有效结合神经网络的非 线性影射能力和粒子群算法的全局搜索能力,预报 0 效果明显优于PLS模型和BP模型,且预报结果稳 0.4 定,具有一定的普遍适用性 0.3 3)粒子群算法优化神经网络结构和连接权的集 0.2 成过程中,如何更加有效选择集成个体,提高系统的 0.1 泛化能力,将是进一步工作 45678910 n/a 参考文献: [1]DEAN A,ANDREW R,BRIAN H.Forecasting warmr 图43种预报模型的预测效果 season burmoff low clouds at the San Francisco interna- Fig 4 Forecasting results of the three models tional airport using linear regression and a neural net- 和检测样本的平均相对误差分别为:21.22和 work [J ]Apply Meteor,2002,41(6):629-639. 27.34;BP模型对训练样本和检测样本的平均相对 [2]HSIEH WW.Nonlinear canonical correlation analysis of 误差分别为:1.48和31.03;PLS-ANN模型对训练 the tropical pacific climate variability using neural net- 样本和检测样本的平均相对误差分别为:7.23和 work approach[J ]Apply Meteor,2001,14(12):2528 10.92,从表1和图4可以看出,在建模样本相同,预 .2539 报因子相同的条件下,PSO-ANN模型对10个样本 [3]GRIORGIO CORANI,GIOGIO GUARIO.Coupling 的预报精度明显优于PLS模型BP模型 fuzzy modeling and neural networks for river flood pre- BP模型拟合最好而预测最差,说明BP模型出 diction [J ]IEEE Transactions on Systems,Man,And 现“过拟合”现象,PLS模型拟合与预测比较接近, Cybernetic-Part C:Applications and Reviews,2005,25 说明统计模型比较稳定,PSO-ANN模型的拟合和 (3):382-388. 预测相差3.69,相对来说该模型也是比较稳定,但 [4]吴建生,金龙,农吉夫.基于遗传算法的神经网络建模 研究[U].数学的实践与认识,2005,35(1):83-88 是其预测能力远远好于BP模型和PLS模型 WU Jiansheng J IN longLONG Jifu.Study on model of 同时也对广西全区的7~8月的降雨量分别利 neural network based on genetic algorithm [J].Mathe- 用上述方法建模分析,结果同样表明,PSO-ANN模 matics in Practic and theory,2005,35(1):83-88. 型的预报效果优于传统的PLS模型和BP模型 [5]SOLLICH P,KROGH A.Learning with ensembles: 4 结论 how over-fitting can be useful[A ]In Proceeding of Ad- vances in Neural Information Processing Systems 8[C]. 降水系统是气候系统中最为活跃、相互作用最 Cambridge,MA:MIT Press,1996 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved htp://www.cnki.net
图 3 3 种预报模型的拟合效果 Fig13 Fitting results of the three models 图 4 3 种预报模型的预测效果 Fig14 Forecasting results of the three models 和检测样本 的平均相 对 误 差 分 别 为 : 21122 和 27134 ;BP 模型对训练样本和检测样本的平均相对 误差分别为 :1148 和 31103 ;PL S2ANN 模型对训练 样本和检测样本的平均相对误差分别为 : 7123 和 10192 ,从表 1 和图 4 可以看出 ,在建模样本相同 ,预 报因子相同的条件下 ,PSO2ANN 模型对 10 个样本 的预报精度明显优于 PL S 模型、BP 模型. BP 模型拟合最好而预测最差 ,说明 BP 模型出 现“过拟合”现象 ; PL S 模型拟合与预测比较接近 , 说明统计模型比较稳定 ,PSO2ANN 模型的拟合和 预测相差 3169 ,相对来说该模型也是比较稳定 ,但 是其预测能力远远好于 BP 模型和 PL S 模型. 同时也对广西全区的 7~8 月的降雨量分别利 用上述方法建模分析 ,结果同样表明 ,PSO2ANN 模 型的预报效果优于传统的 PL S 模型和 BP 模型. 4 结 论 降水系统是气候系统中最为活跃、相互作用最 为复杂的子系统之一 ,并且由于降水变化受众多因 素的影响 ,预报十分困难. 本文利用 SSA2M GF 方法 对原降水序列重构并延拓 ,以延拓矩阵作为自变量 , 原序列作为因变量 ,再利用 PL S 方法提取对系统解 释最强的综合变量作为神经网络的输入因子 ,原始 降水序列作为输出因子 ,建立基于粒子群算法的神 经网络集成预报模型 ,通过对广西全区主汛期(6~8 月) 降水量的实例计算对比表明 ,该方法具有 : 1) 利用 SSA2M GF 方法对原始数据降噪和重 构 ,并利用 PLS 处理 ,提取对系统解释性最强的综 合变量 ,克服了变量之间的多重相关性 ,提高模型精 度和可靠性 ;又对神经网络的输入矩阵降维 ,使得网 络结构规模变小 ,增强网络的稳定性. 2) 利用多样性粒子群优化算法的优化神经网络 的结构和连接权并集成 ,它有效结合神经网络的非 线性影射能力和粒子群算法的全局搜索能力 ,预报 效果明显优于 PL S 模型和 BP 模型 ,且预报结果稳 定 ,具有一定的普遍适用性. 3) 粒子群算法优化神经网络结构和连接权的集 成过程中 ,如何更加有效选择集成个体 ,提高系统的 泛化能力 ,将是进一步工作. 参考文献 : [ 1 ] DEAN A , ANDREW R , BRIAN H. Forecasting warm2 season burn2off low clouds at the San Francisco interna2 tional airport using linear regression and a neural net2 work [J ]. Apply Meteor , 2002 , 41 (6) : 629 - 639. [2 ] HSIEH W W. Nonlinear canonical correlation analysis of the tropical pacific climate variability using neural net2 work approach[J ]. Apply Meteor ,2001 ,14 (12) : 2528 - 2539. [ 3 ] GRIORGIO CORANI , GIO GIO GUARIO. Coupling fuzzy modeling and neural networks for river flood pre2 diction [J ]. IEEE Transactions on Systems , Man , And Cybernetic2Part C: Applications and Reviews , 2005 , 25 (3) : 382 - 388. [ 4 ]吴建生 ,金 龙 , 农吉夫. 基于遗传算法的神经网络建模 研究[J ]. 数学的实践与认识 , 2005 , 35 (1) : 83 - 88. WU Jiansheng ,J IN long ,LON G Jifu. Study on model of neural network based on genetic algorithm [J ]. Mathe2 matics in Practic and theory ,2005 ,35 (1) :83 - 88. [5 ] SOLL ICH P , KRO GH A. Learning with ensembles: how over2fitting can be useful[A ]. In Proceeding of Ad2 vances in Neural Information Processing Systems 8 [ C]. Cambridge , MA : MIT Press , 1996. · 27 · 智 能 系 统 学 报 第 1 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第2期 吴建生:基于粒子群算法的神经网络短期降水预报建模研究 ·73 [6]HANSEN L K,SALAMON P.Neural network ensem- [15 REED R.Pruning algorithms-a survey [J ]IEEE bles [J ]IEEE Transactions on Pattern Analysis and Transactions on Neural Networks,1993(4):740-747. Machine Intelligence,1990,12(10):993-1001. [16]JACQUES RIGET,JA KOB VESTERSTR.A Diversi- [7]周志华,陈世福.神经网络集成U].计算机学报,2002, ty-guided Particle Swarm Optimizer-the ARPSO [A]. 25(1):1-8. Development and Practice of Artificial Intelligence ZHOU Zhihua,CHEN Shifu.Neural nctwork ensemble Techniques[C].Durban,South Africa,1999,41-45. [J ]Chinese Journal of Computer,2002,25(1):1-8. [17]KENN EDY J,SPEARS W.Matching algorithms to [8]MAO J.A case study on bagging boosting and basic en problems:an experimental test of the particle swarm sembles of neural networks for OCR[A].In Proceedings and some genetic algorithms on the multimode problem of International Joint conference on Neural Networks generator[A].In Proceedings of IEEE International 1998[C].Anchorage,AK,1998:1828-1833 Conference on Evolutionary Computation[C].Anchor- [9]GUTTA S,WECHSL ER H.Face recognition using hy- age,Alaska,USA,1998. brid classifier systems[A].In Proceedings of Interna- [18]马永开,唐小我,杨桂元.非负权重最优组合预测方法 tional Conference Neural Network 1996 [C].Washing- 的基本理论研究J].运筹与管理,1997,6(2):1-8. ton,DC,1996:1017-1022 MA Yongkai,TANG Xiaowo.YANG Guiyuan.A [10]SOLL ICH P,IN TRA TOR N.Classification of seismic study on basic theory of the optimal combinated predic- signals by integrating ensembles of neural networks [J]. tion method of non negative weights[J ]Operations Re- IEEE Transactions Signal Processing,1998,46(5):1194 search and Management Science,1997,6(2):1-8. .1021 [19]马振华.运筹学与最优化理论[M].北京:清华大学出 [11]BONABEAU E,DORIGO M,G THERAULAZ.Im 版社,1998. spiration for optimization from social insect behavior [J]. [20]VAUTARD.SSA:a toolkit for noisy chaotic signals Nature,2000,406(6):39-42. [J].Physica D,1992,58:95-126. [12]KENNEDY J,EBERHART R C.Swarm intelligence [21]魏凤英,曹鸿兴.长期预测的数学模型及应用[M].北 M].San Francisco:Morgan Kaufmann Publishers, 京:气象出版社,1990. 2001. [22]王惠文.偏最小二乘回归方法及其应用[M].北京:国 [13]高海兵,高亮,周驰,等.基于粒子群优化的神经网 防工业出版社,1999 络训练算法研究0].电子学报,2004,32(9):1572· [23]金龙.神经网络气象预报建模理论方法与应用[M]. 1574 北京:气象出版社,2004 GAO Haibing,GAO Liang,ZHOU Chi,et al.Particle 作者简介: swarm optimization based algorithm for neural network learning[J ]Acta Electronic Sinica,2004,32(9);1572- 吴建生,男,1974年生,硕士,讲师, 1574. 主要研究方向为神经网络应用及智能优 [14]RUML HART D E,HINTON G E,WILLIAMS RJ. 化算法研究.Email:wjsh2002168@163 Learning representations by back propagating errors. com. Nature,1986,323(11):456-466. 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
[6 ] HANSEN L K , SALAMON P. Neural network ensem2 bles [J ]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 1990 ,12 (10) : 993 - 1001. [7 ]周志华 , 陈世福. 神经网络集成[J ]. 计算机学报 , 2002 , 25 (1) : 1 - 8. ZHOU Zhihua ,CHEN Shifu. Neural nctwork ensemble [J ]. Chinese Journal of Computer , 2002 ,25 (1) :1 - 8. [8 ]MAO J. A case study on bagging boosting and basic en2 sembles of neural networks for OCR[ A ]. In Proceedings of International Joint conference on Neural Networks 1998[C]. Anchorage , A K , 1998 :1828 - 1833. [9 ] GU TTA S , WECHSL ER H. Face recognition using hy2 brid classifier systems [ A ]. In Proceedings of Interna2 tional Conference Neural Network 1996 [ C ]. Washing2 ton , DC , 1996 :1017 - 1022. [10 ]SOLL ICH P , IN TRA TOR N. Classification of seismic signals by integrating ensembles of neural networks [J ]. IEEE Transactions Signal Processing ,1998 , 46 (5) :1194 - 1021. [11 ]BONABEAU E , DORIGO M , G THERAULAZ. In2 spiration for optimization from social insect behavior [J ]. Nature , 2000 , 406 (6) :39 - 42. [12 ] KENN ED Y J , EBERHART R C. Swarm intelligence [ M ]. San Francisco : Morgan Kaufmann Publishers , 2001. [13 ]高海兵 ,高 亮 ,周 驰 ,等. 基于粒子群优化的神经网 络训练算法研究[J ]. 电子学报 , 2004 , 32 (9) : 1572 - 1574. GAO Haibing , GAO Liang , ZHOU Chi ,et al. Particle swarm optimization based algorithm for neural network learning[J ]. Acta Electronic Sinica ,2004 ,32 (9) ;1572 - 1574. [14 ]RUML HART D E , HIN TON G E , WILL IAMS R J. Learning representations by back propagating errors. Nature , 1986 , 323 (11) :456 - 466. [15 ] REED R. Pruning algorithms —a survey [J ]. IEEE Transactions on Neural Networks , 1993 (4) : 740 - 747. [16 ]J ACQU ES RIGET , J A KOB VESTERSTR. A Diversi2 ty2guided Particle Swarm Optimizer2the ARPSO [ A ]. Development and Practice of Artificial Intelligence Techniques[C]. Durban , South Africa , 1999 ,41 - 45. [ 17 ] KENNED Y J , SPEARS W. Matching algorithms to problems: an experimental test of the particle swarm and some genetic algorithms on the multimode problem generator [ A ]. In Proceedings of IEEE International Conference on Evolutionary Computation [ C]. Anchor2 age , Alaska , USA , 1998. [18 ]马永开 , 唐小我 , 杨桂元. 非负权重最优组合预测方法 的基本理论研究[J ]. 运筹与管理 , 1997 , 6 (2) : 1 - 8. MA Yongkai , TAN G Xiaowo. YAN G Guiyuan. A study on basic theory of the optimal combinated predic2 tion method of non negative weights[J ]. Operations Re2 search and Management Science , 1997 ,6 (2) :1 - 8. [19 ]马振华. 运筹学与最优化理论[ M ]. 北京 :清华大学出 版社 ,1998. [20 ] VAU TARD. SSA : a toolkit for noisy chaotic signals [J ]. Physica D , 1992 , 58 : 95 - 126. [21 ]魏凤英 , 曹鸿兴. 长期预测的数学模型及应用[ M ]. 北 京 :气象出版社 , 1990. [22 ]王惠文. 偏最小二乘回归方法及其应用[ M ]. 北京 :国 防工业出版社 ,1999. [23 ]金 龙. 神经网络气象预报建模理论方法与应用[ M ]. 北京 : 气象出版社 , 2004. 作者简介 : 吴建生 ,男 ,1974 年生 ,硕士 ,讲师 , 主要研究方向为神经网络应用及智能优 化算法研究. E2mail : wjsh2002168 @163. com. 第 2 期 吴建生 :基于粒子群算法的神经网络短期降水预报建模研究 · 37 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net