
第2卷第1期 智能系统学报 Vol.2 Ng 1 2007年2月 CAAI Transactions on Intelligent Systems Fcb.2007 一种支持时间序列数据的CBR检索算法 史忠植,尹超2叶世伟 (1.中国科学院计算技术研究所智能信息处理重点实验室,北京100080:2.中国科学院研究生院信息科学与工程学院,北京 100039) 摘要:探讨了如何为CBR(基于范例的推理)增加对一种特殊的范例类型时间序列数据的支持.分析了基于谱 分析的时间序列相似度比较算法不适用于CBR检索的缺点,并在此基础上设计了一种综合性能很好的CBR检索算 法.思路是把时间序列相似度比较转化成一个卷积问题,并用DT来简化这个卷积的计算.通过对这种CBR检索算 法进行了深入的理论分析和认真的实验,结果证明,提出的算法是一个高效的算法.在这个检索算法的基础上,CBR 就能够应用到时序数据的分析推理中,具有广阔的应用前景. 关键词:基于范例的推理;时间序列数据;相似度比较 中图分类号:TP399文献标识码:A文章编号:1673-4785(2007)01-004005 A CBRalgorithm supporting time series data SHI Zhong-zhi',YIN Chao'2,YE Shi-wei? (1.Key Laboratory of Intelligent Information Processing,Institute of Computing Technology,Chinese Academy of Sciences, Beijing 100080,China:2.School of Information Science and Engineering Graduate University of Chinese Academy of Sciences, Beijing 100039,China) Abstract:This paper focuses on the retrieval algorithms of a special kind of CBR system in which cases are composed of time-series data.We introduced the classical algorithm used for processing similarity queries on time series data.This algorithm is based on the fact that DFT preserves the Euclidean distance in the time or frequency domain,and only the first few elements of the frequency sequence are significant,so the retrieval process can only use these significant elements to compute similarity degree.However,this algo- rithm has several disadvantages limiting its usage in CBR retrieval,so a new algorithm is presented for u sing batch method to compute the similarity degree.It is based on the observation that the original problem can be transformed to a convolution problem,and the circular convolution can be computed more efficiently using FFT.Theoretical analysis and experiment result prove that this algorithm is efficient and robust. The algorithm presented in this paper furnishes the CBR with the ability to process cases consist of time- series data. Key words :case-based reasoning;time series data;similarity comparison 基于范例的推理(case-based reasoning,CBR) 间信息的重要性,很多情况下,感兴趣的不仅仅是独 是实现人工智能的一种重要方法,它是对人类思维 立的快照(snapshot),而是一段连续的片段(epie 过程的模仿.CBR在如下情形下效果比较好:1)知 sode),甚至是对将来的预测.举个例子,在诊断病人 识的主要来源是经验,而不是理论;2)解决方案是可 的时候,医生不仅要了解患者目前的症状,也要了解 重用的:3)目标是求出可行解而非最优解.在过去的 其病史.医生对同样的症状最终可能会制订不同的 几年年里,CBR的研究者们已经逐渐开始注意到时 诊疗方案.最近这方面有代表性的研究包括文献[2 收稿日期:20060710. -3,16-17]等. 基金项目:国家自然科学基金资助项目(60435010,90604017, 文献[2-3]的研究都是建立在Aen在文献 60675010):国家“973”资助项目(2003CB317004). 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 1 期 智 能 系 统 学 报 Vol. 2 №. 1 2007 年 2 月 CAA I Transactions on Intelligent Systems Feb. 2007 一种支持时间序列数据的 CBR 检索算法 史忠植1 ,尹 超1 ,2 ,叶世伟2 (1. 中国科学院计算技术研究所 智能信息处理重点实验室 ,北京 100080 ;2. 中国科学院研究生院 信息科学与工程学院 ,北京 100039) 摘 要 :探讨了如何为 CBR(基于范例的推理)增加对一种特殊的范例类型 ———时间序列数据的支持. 分析了基于谱 分析的时间序列相似度比较算法不适用于 CBR 检索的缺点 ,并在此基础上设计了一种综合性能很好的 CBR 检索算 法. 思路是把时间序列相似度比较转化成一个卷积问题 ,并用 DFT 来简化这个卷积的计算. 通过对这种 CBR 检索算 法进行了深入的理论分析和认真的实验 ,结果证明 ,提出的算法是一个高效的算法. 在这个检索算法的基础上 ,CBR 就能够应用到时序数据的分析推理中 ,具有广阔的应用前景. 关键词 :基于范例的推理 ;时间序列数据 ;相似度比较 中图分类号 : TP399 文献标识码 :A 文章编号 :167324785 (2007) 0120040205 A CBR algorithm supporting time series data SHI Zhong2zhi 1 , YIN Chao 1 ,2 , YE Shi2wei 2 (1. Key Laboratory of Intelligent Information Processing , Institute of Computing Technology , Chinese Academy of Sciences , Beijing 100080 , China ;2. School of Information Science and Engineering Graduate University of Chinese Academy of Sciences , Beijing 100039 , China) Abstract :This paper focuses on the retrieval algorit hms of a special kind of CBR system in which cases are composed of time2series data. We introduced t he classical algorit hm used for processing similarity queries on time series data. This algorit hm is based on t he fact t hat DF T preserves t he Euclidean distance in t he time or frequency domain , and only the first few elements of t he frequency sequence are significant , so t he retrieval process can only use t hese significant elements to comp ute similarity degree. However , this algo2 rit hm has several disadvantages limiting its usage in CBR retrieval , so a new algorithm is presented for u2 sing batch met hod to comp ute t he similarity degree. It is based on the observation that t he original problem can be transformed to a convolution problem , and the circular convolution can be comp uted more efficiently using FF T. Theoretical analysis and experiment result prove t hat t his algorit hm is efficient and robust. The algorit hm presented in t his paper f urnishes the CBR with the ability to process cases consist of time2 series data. Keywords :case2based reasoning ; time series data ; similarity comparison 收稿日期 :2006207210. 基金项 目 : 国 家 自 然 科 学 基 金 资 助 项 目 ( 60435010 , 90604017 , 60675010) ;国家“973”资助项目(2003CB317004) . 基于范例的推理 (case2based reasoning ,CBR) 是实现人工智能的一种重要方法 ,它是对人类思维 过程的模仿. CBR 在如下情形下效果比较好 :1) 知 识的主要来源是经验 ,而不是理论 ;2) 解决方案是可 重用的 ;3) 目标是求出可行解而非最优解. 在过去的 几年年里 ,CBR 的研究者们已经逐渐开始注意到时 间信息的重要性 ,很多情况下 ,感兴趣的不仅仅是独 立的快照 (snap shot) ,而是一段连续的片段 ( epi2 sode) ,甚至是对将来的预测. 举个例子 ,在诊断病人 的时候 ,医生不仅要了解患者目前的症状 ,也要了解 其病史. 医生对同样的症状最终可能会制订不同的 诊疗方案. 最近这方面有代表性的研究包括文献[ 2 - 3 ,16 - 17 ]等. 文献[ 2 - 3 ]的研究都是建立在 Allen 在文献

第1期 史忠植,等:一种支持时间序列数据的CBR检索算法 ·41· [4]中提出的时态模型(temporal model)的基础上 len(g=n,m≥n.每个范例序列C有m-n+1个 的.文献[2]中提出了一种形式化逻辑方法来描述时 长度为n的子序列,其元素为Si]下文为了简洁 序信息,从时序模型的观点来看,这个工作特别有意 起见有时表示为y.设范例库中有N个范例序列, 义,因为该文建立的模型中融合了基于时间点的元 它们的长度不一定相等 素和基于时间间隔的元素.然而,作者却没有给出检 基于CBR的应用需要,范例库中任意范例序列 索算法,而只是声称可以采用图相似性算法来进行 C的长度m均大于查询序列Q的长度n.查询的过 相似度检索.文献[3]则是在一个具体的应用项目的 程中,需要用大小为n的滑动窗口在C上截取出子 背景下讨论了如何在CBR中应用Allen的模型,然 序列S,计算S与查询序列Q的相似度Sim(Q,S 而由于该应用的一些特殊约束,所以该文的解决方 相似度最大的几个S作为查询结果返回,这实际上 法并没有普遍适用性.Allen的时态模型是一种基 是一个子序列匹配问题, 于间隔的(interval-based).由于组合爆炸的缘故, 时间序列相似度模型对CBR的推理效果起着 这种模型只能处理一些简单的时序关系,而且相似重要作用,常用的有基于欧氏距离的,基于时间归整 性检索的计算量很大,效果也并不十分好」 (dynamic time warping)的,基于界标(landmark) 文献[16-17]引入的时态模型是基于时间序列 的,基于最长公共子序列(longest common subse 数据的,时间序列的相似度比较是个比较成熟的领 quence)的,基于分段线性化表示的,基于概率方法 域,有大量方法可以利用,比如时间规整(DTW),符 的,等等 号化,分段线型化,特征抽取降维技术等等.也正是 出于减少计算量,减少误警(false alarm)等考 因为这个原因,这2篇文章中没有过多的涉及具体 虑,文中使用了基于欧氏距离的相似度模型,即把时 的检索算法,而是侧重于设计时间序列CBR的框架 间序列看成向量,定义相似度与欧氏距离成反比,欧 和范例的存储结构.然而经过分析,CBR中的时间 氏距离越小,则相以度越大.这也是时间序列数据处 序列相似度比较具有很多特殊性,需要设计有针对 理中应用最广泛的相似度模型,但它与人类的认知 性的检索算法 模型有一定的差异,因为一些相似度很低(即欧氏距 文中选择采用的时序模型是时间序列数据,着 离很大)的序列对人类的感觉而言却是相似的 眼点不在于CBR的框架和范例的存储结构,而在于 E(Q.S) (x2 1V2 (1 针对CBR中时间序列数据的特点,利用计算机在数 值计算上的强大能力,设计高效的CBR检索算法 Sim(O,S)=-E(o.S). 文中的研究不仅参考了CBR等人工智能领域的研 计算相似度的时间复杂度为O(d,对每个范例 究成果,也很大程度上参考了时间序列数据领域的 序列需要计算m-n+1次相似度.如果直接计算的 一些成果 话,对于大小为N的范例库,一次查询需要进行N 次时间复杂度为O(n·(m-n+1))的比较.文中把 1 支持时间序列的CBR模型 这种直接计算的方法称作naive方法,并作为比较 在推广CBR时遇到的一个最大的阻碍就是难 各种算法效率的基准 于构造有效的范例库,CBR的应用首先要求从客户 2基于谱分析的相似度检索算法 的历史数据中抽取有代表性的数据构造范例库,这 个过程不可能完全由机器完成,必须有人工参与进 基于欧氏距离计算相似度的方法中,Agrawal 来.所以要向CBR增加时间序列支持,首先考虑的 等人1提出的基于离散傅里叶变换(DFT)的方法效 就是方便范例库的构造.实际应用中,用户往往只能 果比较好.离散傅立叶变换公式如下,x,是时域数 确定某一段时间内的时间序列数据有特殊的含义, 据,XF是变换域数据 但并不能确定代表这种特殊含义的精确模式,在这 i2F XF= x,exp F=0,1,…n-1, 种情况下最妥当的方法就是把这一段连续时间序列 整个作为一个范例存入范例库中 2) 文中使用的表示符号如下:范例序列为C,其长 2 =0,1,…,n-1. 度均大于某个下限,其元素表示为C11.查询序列 为Q,其长度均小于某个上限,其元素可表示为Q] 式中如果x:是实数,则(X)(F>0)一定是复数, 下文为了简洁起见有时表示为x.设len(g=m, 且Xr和X.r(F>O)一定互相共轭.模|Xr定义 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
[4 ]中提出的时态模型 (temporal model) 的基础上 的. 文献[ 2 ]中提出了一种形式化逻辑方法来描述时 序信息 ,从时序模型的观点来看 ,这个工作特别有意 义 ,因为该文建立的模型中融合了基于时间点的元 素和基于时间间隔的元素. 然而 ,作者却没有给出检 索算法 ,而只是声称可以采用图相似性算法来进行 相似度检索. 文献[3 ]则是在一个具体的应用项目的 背景下讨论了如何在 CBR 中应用 Allen 的模型 ,然 而由于该应用的一些特殊约束 ,所以该文的解决方 法并没有普遍适用性. Allen 的时态模型是一种基 于间隔的(interval - based) . 由于组合爆炸的缘故 , 这种模型只能处理一些简单的时序关系 ,而且相似 性检索的计算量很大 ,效果也并不十分好. 文献[16 - 17 ]引入的时态模型是基于时间序列 数据的 ,时间序列的相似度比较是个比较成熟的领 域 ,有大量方法可以利用 ,比如时间规整(D TW) ,符 号化 ,分段线型化 ,特征抽取降维技术等等. 也正是 因为这个原因 ,这 2 篇文章中没有过多的涉及具体 的检索算法 ,而是侧重于设计时间序列 CBR 的框架 和范例的存储结构. 然而经过分析 ,CBR 中的时间 序列相似度比较具有很多特殊性 ,需要设计有针对 性的检索算法. 文中选择采用的时序模型是时间序列数据 ,着 眼点不在于 CBR 的框架和范例的存储结构 ,而在于 针对 CBR 中时间序列数据的特点 ,利用计算机在数 值计算上的强大能力 ,设计高效的 CBR 检索算法. 文中的研究不仅参考了 CBR 等人工智能领域的研 究成果 ,也很大程度上参考了时间序列数据领域的 一些成果. 1 支持时间序列的 CBR 模型 在推广 CBR 时遇到的一个最大的阻碍就是难 于构造有效的范例库 ,CBR 的应用首先要求从客户 的历史数据中抽取有代表性的数据构造范例库 ,这 个过程不可能完全由机器完成 ,必须有人工参与进 来. 所以要向 CBR 增加时间序列支持 ,首先考虑的 就是方便范例库的构造. 实际应用中 ,用户往往只能 确定某一段时间内的时间序列数据有特殊的含义 , 但并不能确定代表这种特殊含义的精确模式 ,在这 种情况下最妥当的方法就是把这一段连续时间序列 整个作为一个范例存入范例库中. 文中使用的表示符号如下 :范例序列为 C ,其长 度均大于某个下限 ,其元素表示为 C[ i]. 查询序列 为 Q ,其长度均小于某个上限 ,其元素可表示为Q[ i] (下文为了简洁起见有时表示为 xt) . 设len( C) = m , len( Q) = n , m ≥n. 每个范例序列 C 有 m - n + 1 个 长度为 n 的子序列 S ,其元素为 S [ i](下文为了简洁 起见有时表示为 yt) . 设范例库中有 N 个范例序列 , 它们的长度不一定相等. 基于 CBR 的应用需要 ,范例库中任意范例序列 C的长度 m 均大于查询序列 Q 的长度 n. 查询的过 程中 ,需要用大小为 n 的滑动窗口在 C 上截取出子 序列 S ,计算 S 与查询序列 Q 的相似度 Sim ( Q , S) , 相似度最大的几个 S 作为查询结果返回 ,这实际上 是一个子序列匹配问题. 时间序列相似度模型对 CBR 的推理效果起着 重要作用 ,常用的有基于欧氏距离的 ,基于时间归整 (dynamic time warping) 的 ,基于界标 (landmark) 的 ,基于最长公共子序列 (longest common subse2 quence) 的 ,基于分段线性化表示的 ,基于概率方法 的 ,等等. 出于减少计算量 ,减少误警 (false alarm) 等考 虑 ,文中使用了基于欧氏距离的相似度模型 ,即把时 间序列看成向量 ,定义相似度与欧氏距离成反比 ,欧 氏距离越小 ,则相似度越大. 这也是时间序列数据处 理中应用最广泛的相似度模型 ,但它与人类的认知 模型有一定的差异 ,因为一些相似度很低(即欧氏距 离很大) 的序列对人类的感觉而言却是相似的. E( Q , S) = ∑ n- 1 t =0 ( xt - yt) 2 1/ 2 . (1) Sim( Q , S) = - E( Q , S) . 计算相似度的时间复杂度为 O( n) ,对每个范例 序列需要计算 m - n + 1 次相似度. 如果直接计算的 话 ,对于大小为 N 的范例库 ,一次查询需要进行 N 次时间复杂度为 O ( n ·( m - n + 1) ) 的比较. 文中把 这种直接计算的方法称作 naive 方法 ,并作为比较 各种算法效率的基准. 2 基于谱分析的相似度检索算法 基于欧氏距离计算相似度的方法中 ,Agrawal 等人[5 ]提出的基于离散傅里叶变换(DF T) 的方法效 果比较好. 离散傅立叶变换公式如下 , xt 是时域数 据 , X F 是变换域数据. X F = 1 n ∑ n- 1 t =0 xtexp - j2πFt n , F = 0 ,1 , …, n - 1 , (2) xt = 1 n ∑ n- 1 F=0 X Fexp j2πFt n , t = 0 ,1 , …, n - 1. 式中 :如果 xt 是实数 ,则 ( X F) ( F > 0) 一定是复数 , 且 X F 和 X n - F ( F > 0) 一定互相共轭. 模| X F | 定义 第 1 期 史忠植 ,等 :一种支持时间序列数据的 CBR 检索算法 · 14 ·
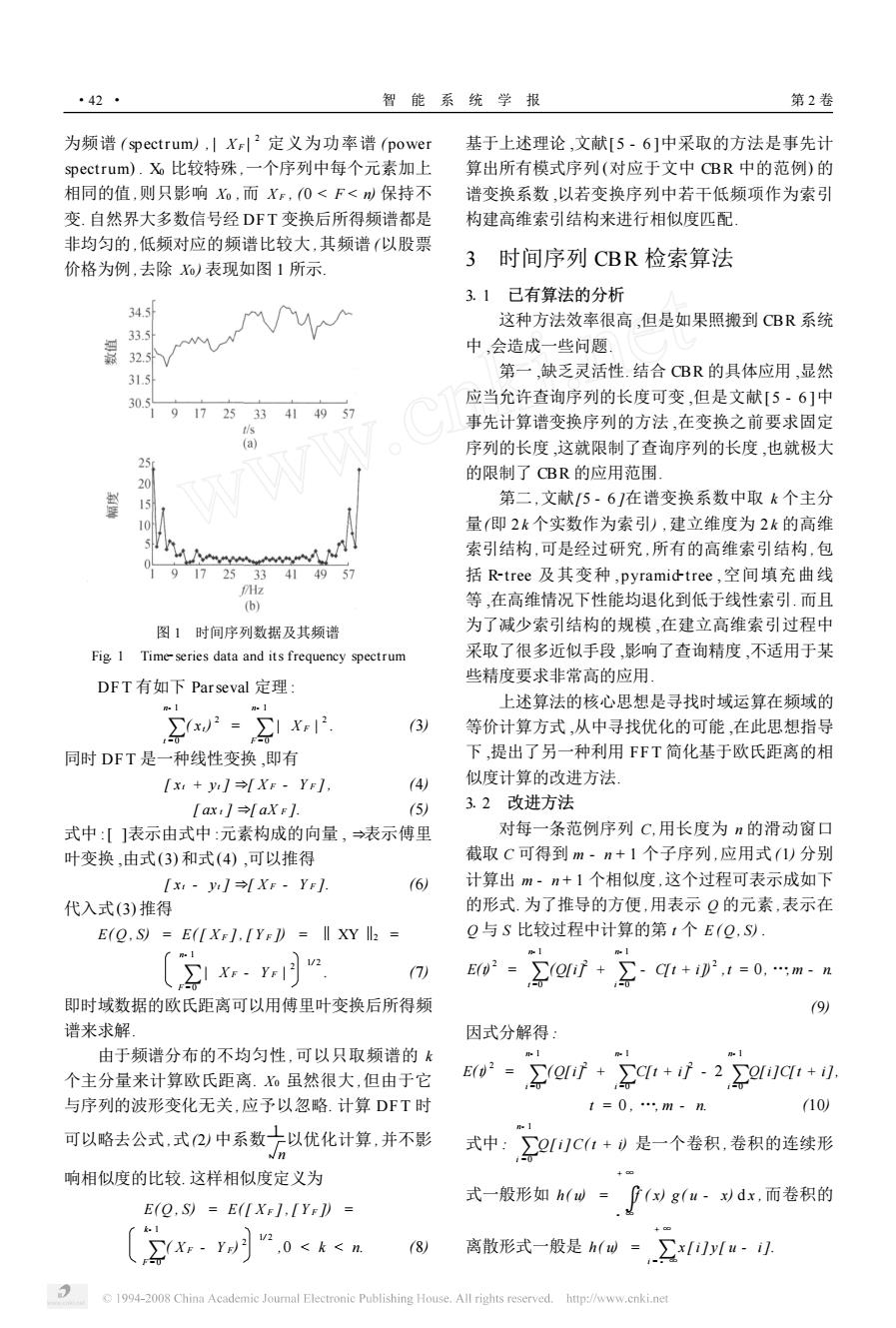
·42 智能系统学报 第2卷 为频谱(spectrum),|Xr2定义为功率谱(power 基于上述理论,文献[5-6]中采取的方法是事先计 spectrum).X比较特殊,一个序列中每个元素加上 算出所有模式序列(对应于文中CBR中的范例)的 相同的值,则只影响X,而XF,0<F<保持不 谱变换系数,以若变换序列中若干低频项作为索引 变.自然界大多数信号经DFT变换后所得频谱都是 构建高维索引结构来进行相似度匹配 非均匀的,低频对应的频谱比较大,其频谱(以股票 3 价格为例,去除Xo)表现如图1所示 时间序列CBR检索算法 3.1已有算法的分析 34.5 这种方法效率很高,但是如果照搬到CBR系统 33.5 中,会造成一些问题】 32.5 31.5 第一,缺乏灵活性.结合CBR的具体应用,显然 30.5 应当允许查询序列的长度可变,但是文献[5·6]中 25 49 事先计算谱变换序列的方法,在变换之前要求固定 (a) 序列的长度,这就限制了查询序列的长度,也就极大 25 的限制了CBR的应用范围。 第二,文献[5-6]在谱变换系数中取k个主分 量(即2k个实数作为索引),建立维度为2k的高维 5%Nw 索引结构,可是经过研究,所有的高维索引结构,包 0 9 172533 414957 括R-tree及其变种,pyramid-tree,空间填充曲线 MHz (b) 等,在高维情况下性能均退化到低于线性索引.而且 图1时间序列数据及其频谱 为了减少索引结构的规模,在建立高维索引过程中 Fig 1 Time-series data and its frequency spectrum 采取了很多近似手段,影响了查询精度,不适用于某 些精度要求非常高的应用】 DFT有如下Parseval定理 1 上述算法的核心思想是寻找时域运算在频域的 w2=,I 3 等价计算方式,从中寻找优化的可能,在此思想指导 同时DFT是一种线性变换,即有 下,提出了另一种利用FFT简化基于欧氏距离的相 [x:+]→[XF-YF1, 4) 似度计算的改进方法 [ax:1→faXF] (5) 3.2改进方法 式中:[]表示由式中:元素构成的向量,→表示傅里 对每一条范例序列C,用长度为n的滑动窗口 叶变换,由式(3)和式(4),可以推得 截取C可得到m·n+1个子序列,应用式(1)分别 Ix-]→[Xr-Yr: 6 计算出m~n+1个相似度,这个过程可表示成如下 代入式(3)推得 的形式.为了推导的方便,用表示Q的元素,表示在 E(2.S)=E([Xr1.[YE))ll XY ll Q与S比较过程中计算的第t个E(Q,Sy 1/2 (7) E0=0f++0,1=0.…mn 即时域数据的欧氏距离可以用傅里叶变换后所得频 (9) 谱来求解 因式分解得 由于频谱分布的不均匀性,可以只取频谱的k o.1 个主分量来计算欧氏距离.虽然很大,但由于它 E(2=】 0时+c+f.2,1c+1. 与序列的波形变化无关,应予以忽略.计算DFT时 1=0,m-n (10) 可以略去公式,式2)中系数十以优化计算,并不影 n 式中 ∑]C(1+)是一个卷积,卷积的连续形 响相似度的比较.这样相似度定义为 +四 式一 般形如h(w=(x)g(u-xdx,而卷积的 E(Q.S)E([Xr].[YF1)= + E(x.. 12 ,0<k<n 8 离散形式一般是h(W=∑xu·. 1994-2008 China Academic Journal Electronie Publishing House.All rights reserved.http://www.cnki.net
为频谱 ( spectrum) , | X F | 2 定义为功率谱 (power spectrum) . X0 比较特殊 ,一个序列中每个元素加上 相同的值 ,则只影响 X0 ,而 X F , (0 < F < n) 保持不 变. 自然界大多数信号经 DF T 变换后所得频谱都是 非均匀的 ,低频对应的频谱比较大 ,其频谱 (以股票 价格为例 ,去除 X0 ) 表现如图 1 所示. 图 1 时间序列数据及其频谱 Fig11 Time2series data and its frequency spectrum DF T 有如下 Parseval 定理 : ∑ n- 1 t = 0 ( xt) 2 = ∑ n- 1 F= 0 | X F | 2 . (3) 同时 DF T 是一种线性变换 ,即有 [ xt + yt ] ] [ X F - Y F ] , (4) [ ax t ] ] [ aX F ]. (5) 式中 :[ ]表示由式中 :元素构成的向量 , ] 表示傅里 叶变换 ,由式(3) 和式(4) ,可以推得 [ xt - yt ] ] [ X F - Y F ]. (6) 代入式(3) 推得 E( Q , S) = E([ X F ] ,[ Y F ]) = ‖XY‖2 = ∑ n- 1 F=0 | X F - Y F | 2 1/ 2 . (7) 即时域数据的欧氏距离可以用傅里叶变换后所得频 谱来求解. 由于频谱分布的不均匀性 ,可以只取频谱的 k 个主分量来计算欧氏距离. X0 虽然很大 ,但由于它 与序列的波形变化无关 ,应予以忽略. 计算 DFT 时 可以略去公式 ,式(2) 中系数 1 n 以优化计算 ,并不影 响相似度的比较. 这样相似度定义为 E( Q , S) = E([ X F ] ,[ Y F ]) = ∑ k- 1 F=0 ( X F - Y F) 2 1/ 2 ,0 < k < n. (8) 基于上述理论 ,文献[ 5 - 6 ]中采取的方法是事先计 算出所有模式序列 (对应于文中 CBR 中的范例) 的 谱变换系数 ,以若变换序列中若干低频项作为索引 构建高维索引结构来进行相似度匹配. 3 时间序列 CBR 检索算法 311 已有算法的分析 这种方法效率很高 ,但是如果照搬到 CBR 系统 中 ,会造成一些问题. 第一 ,缺乏灵活性. 结合 CBR 的具体应用 ,显然 应当允许查询序列的长度可变 ,但是文献[ 5 - 6 ]中 事先计算谱变换序列的方法 ,在变换之前要求固定 序列的长度 ,这就限制了查询序列的长度 ,也就极大 的限制了 CBR 的应用范围. 第二 ,文献[5 - 6 ]在谱变换系数中取 k 个主分 量(即 2 k 个实数作为索引) ,建立维度为 2 k 的高维 索引结构 ,可是经过研究 ,所有的高维索引结构 ,包 括 R2tree 及其变种 , pyramid2tree ,空间填充曲线 等 ,在高维情况下性能均退化到低于线性索引. 而且 为了减少索引结构的规模 ,在建立高维索引过程中 采取了很多近似手段 ,影响了查询精度 ,不适用于某 些精度要求非常高的应用. 上述算法的核心思想是寻找时域运算在频域的 等价计算方式 ,从中寻找优化的可能 ,在此思想指导 下 ,提出了另一种利用 FFT 简化基于欧氏距离的相 似度计算的改进方法. 312 改进方法 对每一条范例序列 C,用长度为 n 的滑动窗口 截取 C 可得到 m - n + 1 个子序列 ,应用式 (1) 分别 计算出 m - n + 1 个相似度 ,这个过程可表示成如下 的形式. 为了推导的方便 ,用表示 Q 的元素 ,表示在 Q 与 S 比较过程中计算的第 t 个 E ( Q , S) . E(t) 2 = ∑ n- 1 t =0 (Q[i] 2 + ∑ n- 1 i =0 - C[t + i]) 2 ,t = 0 , …,m - n. (9) 因式分解得 : E(t) 2 = ∑ n- 1 i =0 (Q[i] 2 + ∑ n- 1 i =0 C[t + i] 2 - 2 ∑ n- 1 i =0 Q[i]C[t + i], t = 0 , …, m - n. (10) 式中 : ∑ n- 1 i =0 Q[ i]C( t + i) 是一个卷积 ,卷积的连续形 式一般形如 h( u) = ∫ + ∞ - ∞ f ( x) g ( u - x) d x ,而卷积的 离散形式一般是 h( u) = ∑ + ∞ i = - ∞ x [ i] y[ u - i]. · 24 · 智 能 系 统 学 报 第 2 卷

第1期 史忠植,等:一种支持时间序列数据的CBR检索算法 ·43 为了把式(10)中第3项化成卷积的标准形式, 项可以事先计算并保存在范例库中,检索过程中无 构造了序列P,使得PIi1=Q(n·1·),则式9 需重复计算,第3项即式(13)中H(W,u=n-1, 可以表示为 m-1的是主要的计算.通过利用FFT,计算 -1 H(W序列的时间复杂度从O(mn)降低到 EItP =(Pli]-clu-ip. O(m+n-1))lg(m+n-)).这是一般情况下 =n-1,…,m-1. 11) 的性能,如果结合CBR的具体应用,还有进一步优 因式分解得: 化的可能:如果所有范例序列的长度m都一样,则 Eto-ictu. 对P补m~1个零得到的P是唯一的,每次查询过 程只需对P作一次FFT计算,否则N次:如果限定 - 2 P[i]Clu-i],u=n-1,m-1.(12) 查询序列长度n为固定大小,则C的每个补了n-1 个零的子序列S也可事先确定,则每个S的FFT 式(12)与式10)中的项是一一对应的,第3项单独 也可以事先计算并保存.但是无论如何优化,每次查 列出如下: 询都要计算N次频域的componentwise积和N次 R-I H(w=∑P[iCw-iu=n-1,…m-1. 反变换,而计算第3项H(,u=n-1,…m-1的 时间复杂度不会变,仍是O(m+n-1)lg(m+n- 13) 1)) 可见H(W确实是一个离散卷积(亦称线性卷积). 直接计算H(的时间复杂度为O(m) 4 数值试验 文献151中证明了一些有用的结论,第一,有限 从Yahoo财经网站上取得l00支股票,每支截 长序列的线性卷积等于循环卷积,而不产生混淆的 取10000个数据点,构造范例库.试验程序在linux 必要条件是延拓周期L≥N+M-1,式中N、M为2 (内核版本2.6)上用C实现,编译器是GCC4.0,傅 个有限长序列的长度.第2,傅里叶变换的循环卷积 立叶变换用的是FFTW3数学库 定理时域的循环卷积对应于频域的乘积.第3, 根据数据的实际意义,有时需要先作一些预处 长度为n的离散序列的FFT可以在O(dgm内完 理,比如对于股票价格序列,要调整数据以去除配股 成 和分红对价格序列的影响,使得各个不同时期的数 傅里叶变换的循环卷积定理的公式表达如下: 据具有可比性.这点不予以详述 A B =iDFT(DFT(A)*DFT(B)).(14) 一般希望图1中的频谱分布更加集中在少数几 式中:⊙为循环卷积运算21,文献12]第11章 个主分量上,这就需要对原始数据进行滤波,滤除高 有详细的说明和定义;*(点乘,componentwise 频分量,在这里采用金融技术分析中常用的滑动平 product)是这样一种运算 均法(Moving Averages)): 一个长度为n的序列和一个长度为m的序列 卷积后的序列长度为m+n-1,即式(14)中A⊙B 的长度为m+n-1,所以A、B的长度也必须为m+ 200 n-1.所以在对P和C作FFT之前,要先将2个序 150 列末端补零转化为长度为m+n-1的P和C,然 100 后进行如下的计算过程: P''=iDFT(DFT(P)*DFT(O)). 50 15) 由式(13)得到的H(W序列的长度为m-n+1,而 9 11 用式15)求得的p'⊙C长度为m+n-1,仔细分析 查询长度的对数log2(n P和C循环卷积的过程可知,p'⊙C的头n-1项 图2数值试验结果 和尾n-1项不是需要的欧氏距离,应予以舍弃」 Fig 2 experiment result 整个算法的分析如下:式12中,对于一次查询 试验结果如图所示.纵坐标表示10次不同的查 而言,第1项在整个检索过程中只要计算一次,第2 询所用时间,横坐标为查询序列长度(取对数坐标) 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
为了把式(10) 中第 3 项化成卷积的标准形式 , 构造了序列 P ,使得 P[ i] = Q( n - 1 - i) ,则式(9) 可以表示为 E[ t] 2 = ∑ n- 1 i =0 ( P[ i] - C[ u - i] 2 , u = n - 1 , …, m - 1. (11) 因式分解得 : E( t) 2 = ∑ n- 1 i =0 P[ i] 2 + ∑ n- 1 i = 0 C[ u - i] 2 - 2 ∑ n- 1 i =0 P[ i]C[ u - i] , u = n - 1 , …, m - 1. (12) 式(12) 与式(10) 中的项是一一对应的 ,第 3 项单独 列出如下 : H ( u) = ∑ n- 1 i = 0 P[ i]C[ u - i] , u = n - 1 , …, m - 1. (13) 可见 H ( u) 确实是一个离散卷积 (亦称线性卷积) . 直接计算 H ( u) 的时间复杂度为 O( m n) . 文献[15 ]中证明了一些有用的结论 ,第一 ,有限 长序列的线性卷积等于循环卷积 ,而不产生混淆的 必要条件是延拓周期 L ≥N + M - 1 ,式中 N 、M 为 2 个有限长序列的长度. 第 2 ,傅里叶变换的循环卷积 定理 ———时域的循环卷积对应于频域的乘积. 第 3 , 长度为 n 的离散序列的 FFT 可以在 O ( nlg n) 内完 成. 傅里叶变换的循环卷积定理的公式表达如下 : A á B = iDF T(DF T( A) 3 DF T( B) ) . (14) 式中 : á 为循环卷积运算[12 ] ,文献[12 ]第 11 章 有详细的说明和定义; 3 ( 点乘 , componentwise product) 是这样一种运算 : a b 3 c d = ac bd . 一个长度为 n 的序列和一个长度为 m 的序列 卷积后的序列长度为 m + n - 1 ,即式 (14) 中 A á B 的长度为 m + n - 1 ,所以 A 、B 的长度也必须为 m + n - 1. 所以在对 P 和 C 作 FF T 之前 ,要先将 2 个序 列末端补零转化为长度为 m + n - 1 的 P′和 C′. 然 后进行如下的计算过程 : P′á Q′= iDF T(DF T( P′) 3 DF T( Q′) ) . (15) 由式(13) 得到的 H ( u) 序列的长度为 m - n + 1 ,而 用式(15) 求得的 P′á C′长度为 m + n - 1 ,仔细分析 P′和 C′循环卷积的过程可知 , P′á C′的头 n - 1 项 和尾 n - 1 项不是需要的欧氏距离 ,应予以舍弃. 整个算法的分析如下 :式(12) 中 ,对于一次查询 而言 ,第 1 项在整个检索过程中只要计算一次 ,第 2 项可以事先计算并保存在范例库中 ,检索过程中无 需重复计算 ,第 3 项即式 (13) 中 H ( u) , u = n - 1 , …, m - 1 的是主要的计算. 通过利用 FF T , 计算 H ( u) 序 列 的 时 间 复 杂 度 从 O ( m n ) 降 低 到 O( ( m + n - 1) ) ·lg ( m + n - 1) ) . 这是一般情况下 的性能 ,如果结合 CBR 的具体应用 ,还有进一步优 化的可能 :如果所有范例序列的长度 m 都一样 ,则 对 P 补 m - 1 个零得到的 P′是唯一的 ,每次查询过 程只需对 P′作一次 FF T 计算 ,否则 N 次;如果限定 查询序列长度 n 为固定大小 ,则 C′的每个补了 n - 1 个零的子序列 S′也可事先确定 ,则每个 S′的 FF T 也可以事先计算并保存. 但是无论如何优化 ,每次查 询都要计算 N 次频域的 componentwise 积和 N 次 反变换 ,而计算第 3 项 H ( u) , u = n - 1 , …, m - 1 的 时间复杂度不会变 ,仍是 O( m + n - 1) ·lg ( m + n - 1) ) . 4 数值试验 从 Yahoo 财经网站上取得 100 支股票 ,每支截 取10 000个数据点 ,构造范例库. 试验程序在 linux (内核版本 216) 上用 C 实现 ,编译器是 GCC410 ,傅 立叶变换用的是 FFTW3 数学库. 根据数据的实际意义 ,有时需要先作一些预处 理 ,比如对于股票价格序列 ,要调整数据以去除配股 和分红对价格序列的影响 ,使得各个不同时期的数 据具有可比性. 这点不予以详述. 一般希望图 1 中的频谱分布更加集中在少数几 个主分量上 ,这就需要对原始数据进行滤波 ,滤除高 频分量 ,在这里采用金融技术分析中常用的滑动平 均法(Moving Averages) : ^x t = 1 w ∑ w- 1 i = 0 xt- i . 图 2 数值试验结果 Fig12 experiment result 试验结果如图所示. 纵坐标表示 10 次不同的查 询所用时间 ,横坐标为查询序列长度(取对数坐标) . 第 1 期 史忠植 ,等 :一种支持时间序列数据的 CBR 检索算法 · 34 ·

·44 智能系统学报 第2卷 图中查询时间随范例序列长度n增长最快的是na Maryland,1989 ive方法,随着查询序列长度的增长,改进方法性能 [10]BOHM C,BERCHTOLD S,KEIM D.Searching in 优势越来越明显.试验结果验证了我们前文的分析, high-dimensional spaces-index structures for improving 改进方法在时间复杂度上的表现非常好 the performance of multimedia databases[J ]ACM Com- puting Surveys,2001,33(3):322-373. 5结束语 [11 GA EDE V,GUNTHER O.Multidimensional access method[J ]ACM Computing Surveys,1998,30(2):221 文中讨论了如何为CBR增加处理时间序列数 .290. 据的能力,参考时间序列数据领域的研究成果,基于 [12]BRACEWELL R.The fourier transform and its appli- CBR的使用需要,我们设计了一种新的时间序列数 cations[M].Mc Graw-Hill,2000. 据检索算法应用于CBR.整个算法基于己有时间序 [13]史忠植.高级人工智能:第二版[M].北京:科学出版 列数据相似度匹配算法的核心思想,用卷积的方法 一社.2006. 批处理计算相似度,并用FFT简化卷积的计算过 [14]HA YKIN S,叶世伟,史忠植.神经网络原理[Ml.北 程,不仅保持了较低的时间复杂度,也增加了查询时 京:机械工业出版社,2004 的灵活性,方便了CBR的应用.我们的下一步工作 [15]吴镇扬.数字信号处理[M].北京:高等教育出版社, 2004. 是结合CBR在时间序列数据方面的具体应用,研究 [16 ]MONTANI S,PORTINALEL.Case based representa- 时间序列数据,对CBR的其他模块提出的新的要 tion and retrieval with time dependent features[A ]IC- 求,比如范例库维护等 CBR 2005[C].Chicago,IL,USA,2005. 参考文献: [17]SANCHEZ MM,CORTES U.An approach for tem- poral case-based reasoning:episode-based reasoning[A]. [1]AAMODT A,PLAZA E.Case based reasoning:founda- ICCBR 2005[C].Chicago,IL,USA,2005. tional issues,methodological variations,and system ap- 作者简介: proaches[J ]AI Communications,1994(7):56-72. 史忠植,男,1941年生,中国科学院 [2]MA J,KNIGHT B.A Framework for Historical Case- 计算所主任研究员,博士生导师.EEE Based Reasoning [A ]ICCBR 2003 [C].Trondheim, 高级会员.主要研究领域为智能科学、分 Norway,2003. 布智能、机器学习、知识工程等.1979 [3JAERE M D,AAMODT A,SKALL E P.Representing 年、1998年2001年均获中国科学院科 temporal knowledge for case-based prediction [A ]EC- 技进步二等奖,1994年获中国科学院科 CBR 2002[C].Aberdeen,Scotland,UK,2002. 技进步特等奖,2002年获国家科技进步 [4 ]ALL EN J F.Maintaining knowledge about temporal in- 二等奖 tervals[J].Communications of the ACM 1983,26(11): Email shizz @ics.ict.ac.cn. 832.843. (5]AGRAWAL R,FALOU TSOS C,SWAMI A.Efficient 尹超,男,1979年生,硕士研究生, similarity search in sequence database [A ]FODO Con- 主要研究方向为智能信息处理,基于范 ference[C].Evanston,Ilinois,1993. 例的推理技术。 [6]FALOUTSOS C,RANGANATHAN M,MANOLO- Email yinchao04 @mails.gucas.ac. POULOS Y.Fast subsequence matching in time-series database[A].Proc of the ACM SIGMOD[C].Minneap- olis,Minnesota,1994. [7]GUTTMAN A.R-trees:a dynamic index structure for spatial searching[A].Proceedings of the ACM SIGMOD 叶世伟男,1968年生,博士,副教 [C].Boston,MA,1984. 授.中国科学院研究生院信息科学与工 [8]BERCHTOLD S.,BOHM C,KRIEGEL H.The pyra 程学院;主要研方向为智能信息处理、神 mid-technique:towards breaking the curse of dimension 经计算与优化计算、认知科学等方面,在 ality[A].Proceedings of SIGMOD'98 [C].Seattle, 国内外重要刊物上发表论文20余篇」 Washington,USA,1998. [9]FALOU TSOS C,ROSEMAN S.Fractals for secondary key retrieval[R].Technical Report UMIACS-TR-89-47, CS-TR-2242,University of Maryland,College Park, 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图中查询时间随范例序列长度 n 增长最快的是 na2 ive 方法 ,随着查询序列长度的增长 ,改进方法性能 优势越来越明显. 试验结果验证了我们前文的分析 , 改进方法在时间复杂度上的表现非常好. 5 结束语 文中讨论了如何为 CBR 增加处理时间序列数 据的能力 ,参考时间序列数据领域的研究成果 ,基于 CBR 的使用需要 ,我们设计了一种新的时间序列数 据检索算法应用于 CBR. 整个算法基于已有时间序 列数据相似度匹配算法的核心思想 ,用卷积的方法 批处理计算相似度 ,并用 FF T 简化卷积的计算过 程 ,不仅保持了较低的时间复杂度 ,也增加了查询时 的灵活性 ,方便了 CBR 的应用. 我们的下一步工作 是结合 CBR 在时间序列数据方面的具体应用 ,研究 时间序列数据 ,对 CBR 的其他模块提出的新的要 求 ,比如范例库维护等. 参考文献 : [1 ]AAMODT A ,PLAZA E. Case2based reasoning : founda2 tional issues , methodological variations , and system ap2 proaches[J ]. AI Communications , 1994 (7) :56 - 72. [2 ]MA J , KNIGH T B. A Framework for Historical Case - Based Reasoning [ A ]. ICCBR 2003 [ C ]. Trondheim , Norway , 2003. [3 ]J AERE M D , AAMODT A , SKALL E P. Representing temporal knowledge for case2based prediction [ A ]. EC2 CBR 2002[C]. Aberdeen , Scotland , U K , 2002. [4 ]ALL EN J F. Maintaining knowledge about temporal in2 tervals[J ]. Communications of the ACM 1983 , 26 (11) : 832 - 843. [5 ] A GRAWAL R , FALOU TSOS C , SWAMI A. Efficient similarity search in sequence database [ A ]. FODO Con2 ference[C]. Evanston , Illinois , 1993. [6 ] FALOU TSOS C , RAN GANA THAN M , MANOLO2 POULOS Y. Fast subsequence matching in time2series database[ A ]. Proc of the ACM SIGMOD[C]. Minneap2 olis , Minnesota , 1994. [7 ] GU TTMAN A. R2trees: a dynamic index structure for spatial searching[ A ]. Proceedings of the ACM SIGMOD [C]. Boston , MA , 1984. [8 ]BERCH TOLD S. , BO HM C , KRIEGEL H. The pyra2 mid2technique : towards breaking the curse of dimension2 ality [ A ]. Proceedings of SIGMOD’98 [ C ]. Seattle , Washington , USA , 1998. [9 ] FALOU TSOS C ,ROSEMAN S. Fractals for secondary key retrieval[ R]. Technical Report UMIACS2TR289247 , CS2TR22242 , University of Maryland , College Park , Maryland , 1989. [10 ] BO HM C , BERCH TOLD S , KEIM D. Searching in high - dimensional spaces2index structures for improving the performance of multimedia databases[J ]. ACM Com2 puting Surveys ,2001 , 33 (3) : 322 - 373. [ 11 ] GA EDE V , GUN THER O. Multidimensional access method[J ]. ACM Computing Surveys , 1998 , 30 (2) :221 - 290. [12 ]BRACEWELL R. The fourier transform and its appli2 cations[ M]. Mc Graw2Hill , 2000. [13 ]史忠植. 高级人工智能 :第二版[ M ]. 北京 :科学出版 社 , 2006. [14 ] HA YKIN S , 叶世伟 , 史忠植. 神经网络原理[ M ]. 北 京 :机械工业出版社 , 2004 [15 ]吴镇扬. 数字信号处理 [ M ]. 北京 :高等教育出版社 , 2004. [16 ]MON TANI S ,PORTINAL E L. Case based representa2 tion and retrieval with time dependent features[ A ]. IC2 CBR 2005[C]. Chicago , IL , USA , 2005. [17 ] SANCHEZ M M , CORTES U. An approach for tem2 poral case2based reasoning : episode2based reasoning[A ]. ICCBR 2005[C]. Chicago , IL , USA , 2005. 作者简介 : 史忠植 , 男 ,1941 年生 ,中国科学院 计算所主任研究员 ,博士生导师. IEEE 高级会员. 主要研究领域为智能科学、分 布智能、机器学习、知识工程等. 1979 年、1998 年、2001 年均获中国科学院科 技进步二等奖 ,1994 年获中国科学院科 技进步特等奖 ,2002 年获国家科技进步 二等奖. Email :shizz @ics. ict. ac. cn. 尹 超 ,男 ,1979 年生 ,硕士研究生 , 主要研究方向为智能信息处理 ,基于范 例的推理技术. E2mail :yinchao04 @mails. gucas. ac. cn. 叶世伟 男 , 1968 年生 ,博士 ,副教 授. 中国科学院研究生院信息科学与工 程学院 ;主要研方向为智能信息处理、神 经计算与优化计算、认知科学等方面 ,在 国内外重要刊物上发表论文 20 余篇. · 44 · 智 能 系 统 学 报 第 2 卷