
第1卷第2期 智能系统学报 Vol.1 N2 2 2006年10月 CAAI Transactions on Intelligent Systems 0ct.2006 水下机器人自适应卡尔曼滤波技术研究 李晔常文田,万磊,孙玉山 (哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001) 摘要:水下机器人的位置和速度传感器受环境影响较大,数据滤波问题是运动控制的核心问题之一给出了离散 型卡尔曼滤波的基本方程,描述了卡尔曼滤波所具有的两个计算回路:增益计算回路和滤波计算回路.建立了水下 机器人状态方程和量测方程,并在此基础上采用了自适应卡尔曼滤波方法对水下机器人的传感器数据进行了滤波 分析.引入了渐消记忆指数加权方法.对时变噪声统计中,强调了新近数据的作用.避免了系统误差和量测误差统计 特性的不准确对系统滤波效果的影响.滤波效果分析表明此方法能达到很好的滤波效果. 关键词:水下机器人:卡尔曼滤波:自适应 中图分类号:TP24文献标识码:A文章编号:1673-4785(2006)02-0044-04 Research on under water vehicle ada ptive Kalman filter LI Ye ,CHANG Wemtian,WAN Lei,SUN Yushan (College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China) Abstract:AUV position and velocity sensors are affected by environment.Data filtering is one of important problems of AUV motion control.Discrete basic Kalman filter equation is given.Two loops of Kalman fil- ter:plus loop and filter loop are described.AUV state equation and measuring equation are founded.Data from AUV sensors are disposed by adaptive Kalman filter with fading exponent.Fading memory exponent is introduced.New data are emphasized for time-varied data.This method avoids inaccuracy by system er- ror and measuring error.Filter effect analysis proves that the method is effective. Key words :underwater vehicle;Kalman filter;adaptive 水下机器人普遍采用的位置传感器为短基线或优估计时充分利用了己经建立的系统运动模型,使 长基线水声定位系统,速度传感器为多普勒速度计. 滤波的实际效果更加接近真实数据的要求.但标准 影响水声定位系统精度的因素主要包括声速误差、 卡尔曼滤波方法必须清楚地知道系统噪声和量测噪 应答器响应时间的测量误差、应答器位置即间距的 声的统计特性],由于相关传感器受各种因素影响 校正误差.而影响多普勒速度计精度的因素主要包 波动很大,噪声的统计特性不易获得3!.自适应卡 括声速c、海水中的介质物理化学特性、运载器的颠 尔曼滤波器的建立,成功地解决了这一问题 簸等.由于水下机器人运行的环境复杂,水声信号的 1离散型卡尔曼滤波基本方程 噪声大,而各种水声传感器普遍存在精度较差、跳变 频繁的缺点,因此水下机器人运动控制系统中,滤波 设1(!时刻的被估计状态X()受系统噪声序 技术显得极为重要 列W(k-)驱动,驱动机理由下述方程描述: 传统上的水下机器人滤波算法采用线性平滑、 X(=Φ(k,k-1)X(k-1)+ 神经网络滤波山等.虽然在一定程度上解决了工程 T(k-)V(k-1. 1) 实践的需求.但由于没有考虑机器人系统的运动特 对X(W的量测满足线性关系,量测方程为 性,滤波效果不十分理想.卡尔曼滤波方法由于在最 Y(k)H(k)x(k)+E(k). (2) 式中:P(k,k-1)为tk-1)时刻至1(材时刻的一步 收稿日期:200601-01. 转移阵;『(k·1)为系统噪声驱动阵:H()为量测 基金项目:田家863基金资助项目(2002AA420090) 阵;E(付为量测噪声序列:V()为系统激励噪声序 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 1 卷第 2 期 智 能 系 统 学 报 Vol. 1 №. 2 2006 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2006 水下机器人自适应卡尔曼滤波技术研究 李 晔 ,常文田 ,万 磊 ,孙玉山 (哈尔滨工程大学 船舶工程学院 ,黑龙江 哈尔滨 150001) 摘 要 :水下机器人的位置和速度传感器受环境影响较大 ,数据滤波问题是运动控制的核心问题之一. 给出了离散 型卡尔曼滤波的基本方程 ,描述了卡尔曼滤波所具有的两个计算回路 :增益计算回路和滤波计算回路. 建立了水下 机器人状态方程和量测方程 ,并在此基础上采用了自适应卡尔曼滤波方法对水下机器人的传感器数据进行了滤波 分析. 引入了渐消记忆指数加权方法. 对时变噪声统计中 ,强调了新近数据的作用. 避免了系统误差和量测误差统计 特性的不准确对系统滤波效果的影响. 滤波效果分析表明此方法能达到很好的滤波效果. 关键词 :水下机器人 ;卡尔曼滤波 ;自适应 中图分类号 : TP24 文献标识码 :A 文章编号 :167324785 (2006) 0220044204 Research on underwater vehicle adaptive Kalman filter L I Ye ,CHAN G Wen2tian , WAN Lei , SUN Yu2shan (College of Shipbuilding Engineering , Harbin Engineering University , Harbin 150001 , China) Abstract :AUV position and velocity sensors are affected by environment. Data filtering is one of important problems of AUV motion control. Discrete basic Kalman filter equation is given. Two loop s of Kalman fil2 ter : plus loop and filter loop are described. AUV state equation and measuring equation are founded. Data from AUV sensors are disposed by adaptive Kalman filter with fading exponent. Fading memory exponent is introduced. New data are emp hasized for time2varied data. This met hod avoids inaccuracy by system er2 ror and measuring error. Filter effect analysis proves t hat t he met hod is effective. Keywords :underwater vehicle ; Kalman filter ; adaptive 收稿日期 :2006201201. 基金项目 :国家 863 基金资助项目(2002AA420090) . 水下机器人普遍采用的位置传感器为短基线或 长基线水声定位系统 ,速度传感器为多普勒速度计. 影响水声定位系统精度的因素主要包括声速误差、 应答器响应时间的测量误差、应答器位置即间距的 校正误差. 而影响多普勒速度计精度的因素主要包 括声速 c、海水中的介质物理化学特性、运载器的颠 簸等. 由于水下机器人运行的环境复杂 ,水声信号的 噪声大 ,而各种水声传感器普遍存在精度较差、跳变 频繁的缺点 ,因此水下机器人运动控制系统中 ,滤波 技术显得极为重要. 传统上的水下机器人滤波算法采用线性平滑、 神经网络滤波[1 ] 等. 虽然在一定程度上解决了工程 实践的需求. 但由于没有考虑机器人系统的运动特 性 ,滤波效果不十分理想. 卡尔曼滤波方法由于在最 优估计时充分利用了已经建立的系统运动模型 ,使 滤波的实际效果更加接近真实数据的要求. 但标准 卡尔曼滤波方法必须清楚地知道系统噪声和量测噪 声的统计特性[2 ] ,由于相关传感器受各种因素影响 波动很大 ,噪声的统计特性不易获得[3 - 4 ] . 自适应卡 尔曼滤波器的建立 ,成功地解决了这一问题. 1 离散型卡尔曼滤波基本方程 设 t( k) 时刻的被估计状态 X( k) 受系统噪声序 列 W ( k - 1) 驱动 ,驱动机理由下述方程描述 : X( k) = Φ( k , k - 1) X( k - 1) + Γ( k - 1) V ( k - 1) . (1) 对 X( k) 的量测满足线性关系 ,量测方程为 Y( k) = H( k) X( k) + E( k) . (2) 式中 :Φ( k , k - 1) 为 t( k - 1) 时刻至 t( k) 时刻的一步 转移阵;Γ( k - 1) 为系统噪声驱动阵; H ( k) 为量测 阵; E( k) 为量测噪声序列;V ( k) 为系统激励噪声序 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第2期 李晔,等:水下机器人自适应卡尔曼滤波技术研究 ·45· 列.同时,V(付和E()满足: K(=P(H(R'(. (6) EV(k)]=0.Cov/v(k .v(j)]= 一步预测均方误差: [V(k).V(j)]=Q(k) P(k,k-1)=Φk,k-1)P(k-1)(k,k-1)+ E[E(k)]=0.Cov/E(k)E(j)]= T(k-1)Qk-1)(k-1).7) [E(k).E(j)]R(k)& 估计均方误差: Cov[V(k).E(j)]=E[V(k ET (j)=0.(3) P(=(I-K(H(W)P(k,k-1).8) 式中:Q(材为系统噪声序列方差阵:R(材为量测噪 式4)~式8)为离散型卡尔曼滤波基本方程.只要 声序列方差阵.状态X()的估计哭(可按下述方 给定初值X和B,根据k时刻的量测值Y(材就可 程求解 递推计算得k时刻的状态估计((k=1,2,. 状态一步预测: 式(4)~(7)所描述的算法可用图1来表示,从 究(k,k-1)=Φ(k,k-1)哭(k-1). 4) 图中明显可以看出卡尔曼滤波具有2个计算回路: 状态估计: 增益计算回路和滤波计算回路).其中增益计算回 哭(W=究k,k-1)+K(付Y(材- 路是独立计算回路,而滤波计算回路依赖于增益计 H(X(k,k-1)). (5) 算回路 滤波增益: X=M.iX Pu-IP+ =k+1 K:-P (HPH+R) 文=X+K(Y-H,X) Px =(I-K:Hi)P P. 滤波计算回路 增益计算问路 图1卡尔曼滤波的两个计算回路和两个更新过程 Fig.I Two calculating loops and updating processes of Kalman filter 2 水下机器人运动状态方程和观测方 xe(k) 1 T 2 00 0 xe(k-1) 程的建立 x(k) 0 00 0 x:(k-1 2.1状态方程的建立 x(k) 0 0 1 00 0 x(k-1) 以二维运动为例,从比较全面的反映运动情况 xn(k) 0 0 0 1 T xn(k-1) 的要求考虑,选择状态向量为 x(k) 2 x若(k-1) X=[xe,xa,xt,x:,x,x,e为东向,n为北向. x(k) 00 001 x(k-1小 L00 000 建立水下机器人运动的状态方程: W(k-1) (9 X(W=Φ(k,k-1)X(k-1)+W(k-1), 式中w(k-1)为模型噪声 或 从物理意义上看,水下机器人东向和北向的位 置速度和加速度之间没有必然的联系,因而系统是 解耦的 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
列. 同时 ,V ( k) 和 E( k) 满足 : E[V ( k) ] = 0 ,Cov[V ( k) ,V ( j) ] = [V ( k) ,V T ( j) ] = Q( k)δkj , E[ E( k) ] = 0 ,Cov[ E( k) , E( j) ] = [ E( k) , E T ( j) ] = R( k)δkj , Cov[V ( k) , E( j) ] = E[V ( k) E T ( j) ] = 0. (3) 式中 :Q( k) 为系统噪声序列方差阵; R( k) 为量测噪 声序列方差阵. 状态 X( k) 的估计 X^ ( k) 可按下述方 程求解. 状态一步预测 : X^ ( k , k - 1) = Φ( k , k - 1) X^ ( k - 1) . (4) 状态估计 : X^ ( k) = X^ ( k , k - 1) + K( k) ( Y( k) - H( k) X^ ( k , k - 1) ) . (5) 滤波增益 : K( k) = P( k) H T ( k) R - 1 ( k) . (6) 一步预测均方误差 : P( k , k - 1) = Φ( k , k - 1) P( k - 1)ΦT ( k , k - 1) + Γ( k - 1) Q( k - 1)ΓT ( k - 1) . (7) 估计均方误差 : P( k) = ( I - K( k) H( k) ) P( k , k - 1) . (8) 式(4) ~式(8) 为离散型卡尔曼滤波基本方程. 只要 给定初值 X^0 和 P0 ,根据 k 时刻的量测值 Y( k) 就可 递推计算得 k 时刻的状态估计 X^ ( k) ( k = 1 ,2 , …) . 式(4) ~(7) 所描述的算法可用图 1 来表示 ,从 图中明显可以看出卡尔曼滤波具有 2 个计算回路 : 增益计算回路和滤波计算回路[5 ] . 其中增益计算回 路是独立计算回路 ,而滤波计算回路依赖于增益计 算回路. 图 1 卡尔曼滤波的两个计算回路和两个更新过程 Fig. 1 Two calculating loop s and updating processes of Kalman filter 2 水下机器人运动状态方程和观测方 程的建立 2. 1 状态方程的建立 以二维运动为例 ,从比较全面的反映运动情况 的要求考虑 ,选择状态向量为 X = [ xe , xn , x·e , x·n , ¨xe , ¨x n ] T ,e 为东向 , n 为北向. 建立水下机器人运动的状态方程 : X( k) = Φ( k , k - 1) X( k - 1) + W( k - 1) , 或 xe ( k) x·e ( k) ¨xe ( k) xn ( k) x·n ( k) ¨x n ( k) = 1 T T 2 2 0 0 0 0 1 T 0 0 0 0 0 1 0 0 0 0 0 0 1 T T 2 2 0 0 0 0 1 T 0 0 0 0 0 1 xe ( k - 1) x·e ( k - 1) ¨xe ( k - 1) xn ( k - 1) x·n ( k - 1) ¨x n ( k - 1) + W( k - 1) . (9) 式中 :W( k - 1) 为模型噪声. 从物理意义上看 ,水下机器人东向和北向的位 置、速度和加速度之间没有必然的联系 ,因而系统是 解耦的. 第 2 期 李 晔 ,等 :水下机器人自适应卡尔曼滤波技术研究 · 54 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·46· 智能系统学报 第1卷 2.2观测方程的建立 3)量测噪声均值 利用卡尔曼滤波器对系统进行最优估计,需要 建立观测方程,而观测量的选取取决于系统所能给 w=tk-Vk-)+Y因 出的状态信息,为此本文建立了以水下机器人的位 H哭(Hk-1)]. (13) 置、速度为观测量的观测方程,其形式为 4量测噪声方差阵 xe(k) R(1kR(k.V+( xe(k) Yxe(k) [1 00000 H(付P(Wk-1)H(J (14) x(k) Yre(k) 0 10000 式中:E(=Y(材-f(材-H(X(Wk-)为新息 xa(付 Yxn(k) 0 00010 阵 xn(k) Y(k 0000 第3步,交替进行计算,从而构成自适应卡尔曼 xi(付 滤波算法,流程见图2 Lx(k (k) 初始值 X0).P0).R0)0),20),q0).k-0 10 Vre(k) 输出XKK-1) 预测值X双/k-1) Vm(k 预测误差方差矩阵方程 或写成向量的形式: 计算Pkk-1D Y(k HX(k)+V(k 式中:Y(材和V(材分别为k时刻下的观测向量和观 增益方程计算(k) 测噪声向量,H为观测矩阵.在此基础上,也可以将 输入() 计算最优滤波值) 观测方程分解为东向观测方程和北向观测方程 输出《k) 3 自适应卡尔曼滤波 估计送差方程矩阵方程计算P(k) 当噪声统计特性与实际不符时特别是在工程 用自适应算法计 R(k).r(k).(k).q(k) 实际中,外界条件的变化可能使噪声统计特性是时 变的,这都会大大降低滤波的精度,甚至导致滤波发 =k+1 散).时变噪声统计估值器就是在递推滤波的同时, 图2自适应卡尔曼滤波算法 实时对系统噪声和量测噪声的统计特性进行估计 Fig.2 Architecture of adaptive Kalman filer 本文构造了一种指数加权方法的时变噪声统计估值 从统计的观点看,噪声统计估值器是算术平均 器 的,和式中每项的权系数均为1/k,但对时变噪声统 第1步,用标准的卡尔曼滤波方程计算出系统 计而言,应强调新近数据的作用,对于过于陈旧的数 状态的估计量 据应渐渐遗忘.这可用渐消记忆指数加权方法实现, 第2步,计算系统干扰均值q(),系统干扰方 即在和式中每项乘以不同的加权系数,按指数加权 差矩阵Q(付,量测噪声均值(材,量测噪声方差矩 法,选取加权系数月使之满足:A=月b,0<b<1, 阵R(付 1)系统干扰项均值为 ,9=1,这引出月=db,d=1-11-), 9为=太k.)k.)+xW则 i=0,1,,k 中(k,k.1)哭(k。1/k.1 (11) 式中:6称遗忘因子.用女代替原来的权系数 1/k,便得到指数加权渐消记忆的时变噪声统计估值 2)系统干扰项方差阵 器.其递推算法为 Q(-t1(k-vQ(k-V+ 0(=1-d.1q(k-1)+d.1[哭(W)- K(k)E(k)E (k)K (k)+P(k/k) Φ(k,k-1)突(k-1/k-)1.15) 中(k,k-1)P(k-1/k-1)D(Wk-1)1 Q(d=[1-d.)Qk-1)+d.1] (12) K(k)E(k)e (k)KT(k+P(k/k) 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.nei
2. 2 观测方程的建立 利用卡尔曼滤波器对系统进行最优估计 ,需要 建立观测方程 ,而观测量的选取取决于系统所能给 出的状态信息 ,为此本文建立了以水下机器人的位 置、速度为观测量的观测方程 ,其形式为 Y xe ( k) Yve ( k) Y xn ( k) Yvn ( k) = 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 xe ( k) x·e ( k) ¨xe ( k) xn ( k) xn ( k) x·n ( k) ¨x n ( k) + V xe ( k) V xn ( k) V ve ( k) V vn ( k) . (10) 或写成向量的形式 : Y( k) = HX ( k) + V ( k) . 式中 :Y( k) 和 V ( k) 分别为 k 时刻下的观测向量和观 测噪声向量 , H 为观测矩阵. 在此基础上 ,也可以将 观测方程分解为东向观测方程和北向观测方程. 3 自适应卡尔曼滤波 当噪声统计特性与实际不符时 ,特别是在工程 实际中 ,外界条件的变化可能使噪声统计特性是时 变的 ,这都会大大降低滤波的精度 ,甚至导致滤波发 散[6 ] . 时变噪声统计估值器就是在递推滤波的同时 , 实时对系统噪声和量测噪声的统计特性进行估计. 本文构造了一种指数加权方法的时变噪声统计估值 器. 第 1 步 ,用标准的卡尔曼滤波方程计算出系统 状态的估计量. 第 2 步 ,计算系统干扰均值 ^q ( k) ,系统干扰方 差矩阵 Q^ ( k) ,量测噪声均值 ^r ( k) ,量测噪声方差矩 阵 R^ ( k) . 1) 系统干扰项均值为 ^q( k) = 1 k ( k - 1) ^q( k - 1) + X^ ( k/ k) - Φ( k , k - 1) X^ ( k - 1/ k - 1) . (11) 2) 系统干扰项方差阵 Q^ ( k) = 1 k [ ( k - 1) Q^ ( k - 1) + K( k)ε( k)εT ( k) K T ( k) + P( k/ k) - Φ( k , k - 1) P( k - 1/ k - 1)ΦT ( k/ k - 1) ]. (12) 3) 量测噪声均值 ^r ( k) = 1 k [ ( k - 1) ^r ( k - 1) + Y( k) - H( k) X^ ( k/ k - 1) ]. (13) 4) 量测噪声方差阵 R^ ( k) = 1 k [ ( k - 1) R^ ( k - 1) +ε( k)εT ( k) - H( k) P( k/ k - 1) H T ( k) ] (14) 式中 :ε( k) = Y( k) - ^r ( k) - H ( k) X( k/ k - 1) 为新息 阵. 第 3 步 ,交替进行计算 ,从而构成自适应卡尔曼 滤波算法 ,流程见图 2. 图 2 自适应卡尔曼滤波算法 Fig. 2 Architecture of adaptive Kalman filer 从统计的观点看 ,噪声统计估值器是算术平均 的 ,和式中每项的权系数均为 1/ k ,但对时变噪声统 计而言 ,应强调新近数据的作用 ,对于过于陈旧的数 据应渐渐遗忘. 这可用渐消记忆指数加权方法实现. 即在和式中每项乘以不同的加权系数 ,按指数加权 法 ,选取加权系数βi 使之满足 : βk =βib , 0 < b < 1 , ∑ k i = 0 βi = 1 ,这引出βi = dkb i , dk = (1 - b) / ( 1 - b k - 1 ) , i = 0 ,1 , …, k. 式中 :b称遗忘因子. 用 1 - dk - 1 k - 1 代替原来的权系数 1/ k ,便得到指数加权渐消记忆的时变噪声统计估值 器. 其递推算法为 ^q( k) = (1 - dk- 1 ) ^q( k - 1) + dk- 1 [ X^ ( k/ k) - Φ( k , k - 1) X^ ( k - 1/ k - 1) ]. (15) Q^ ( k) = [ (1 - dk- 1 ) Q^ ( k - 1) + dk- 1 ] [ K( k)ε( k)εT ( k) K T ( k) + P( k/ k) - · 64 · 智 能 系 统 学 报 第 1 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
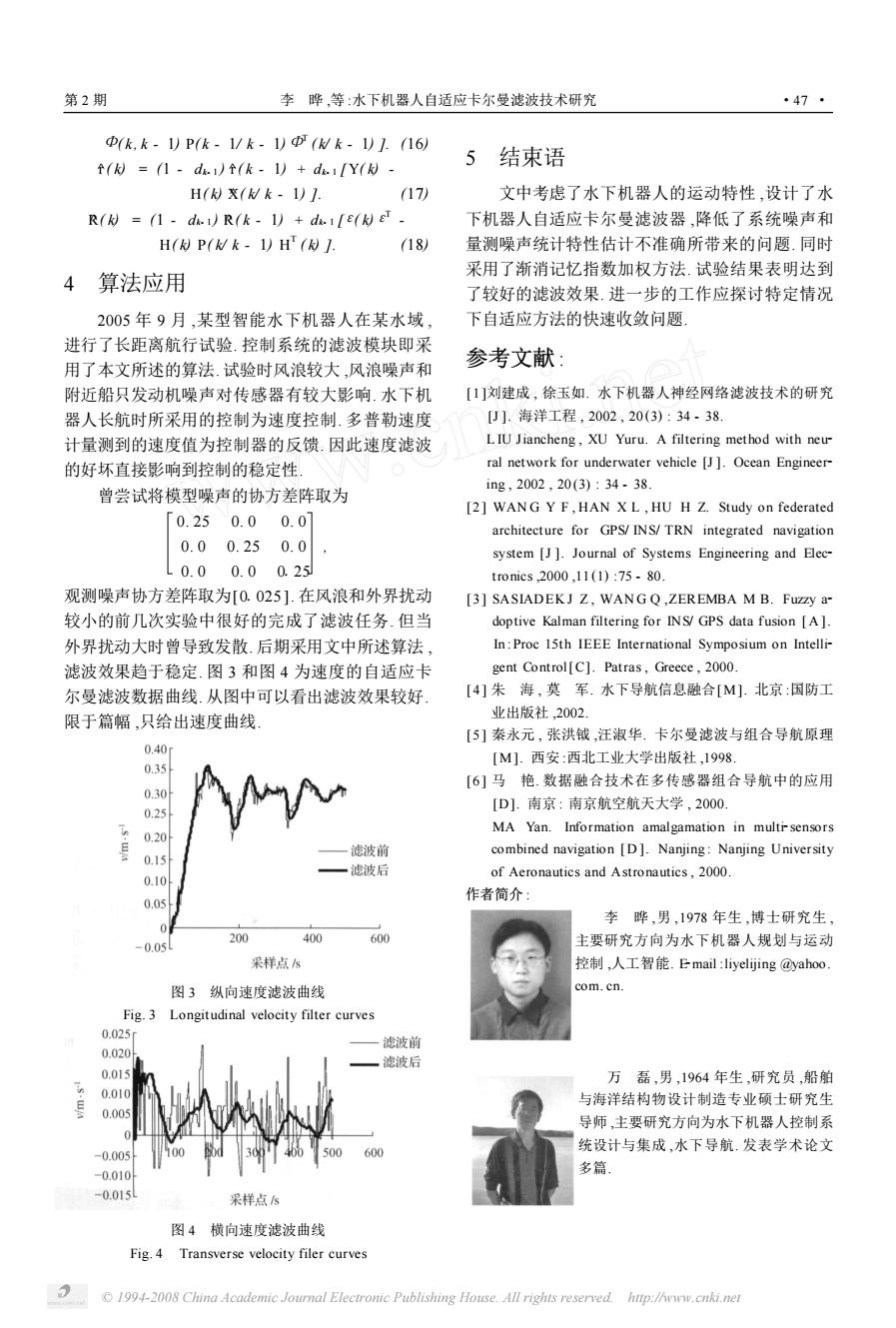
第2期 李晔,等:水下机器人自适应卡尔曼滤波技术研究 ·47· Φ(k,k-)P(k-1/k-1)D(Mk-1)1.(16) f(d=1-d.个(k-1)+d.1Y(- 5结束语 H(究(Wk-1)]. 17) 文中考虑了水下机器人的运动特性,设计了水 R(k)=(1-d.)R(k-1)+du.[e( 下机器人自适应卡尔曼滤波器,降低了系统噪声和 H(k)P(/k-1)H(] (18) 量测噪声统计特性估计不准确所带来的问题.同时 采用了渐消记忆指数加权方法.试验结果表明达到 4算法应用 了较好的滤波效果.进一步的工作应探讨特定情况 2005年9月,某型智能水下机器人在某水域, 下自适应方法的快速收敛问题 进行了长距离航行试验.控制系统的滤波模块即采 用了本文所述的算法.试验时风浪较大,风浪噪声和 参考文献: 附近船只发动机噪声对传感器有较大影响.水下机 [1]刘建成,徐玉如.水下机器人神经网络滤波技术的研究 器人长航时所采用的控制为速度控制,多普勒速度 [J].海洋工程,2002,20(3):34-38. 计量测到的速度值为控制器的反馈.因此速度滤波 LIU Jiancheng,XU Yuru.A filtering method with neu 的好坏直接影响到控制的稳定性 ral network for underwater vehicle [J].Ocean Engineer- ing,2002,20(3):34-38. 曾尝试将模型噪声的协方差阵取为 [2]WANG Y F,HAN X L,HU H Z.Study on federated 0.250.00.0 architecture for GPS/INS/TRN integrated navigation 0.00.250.0 system [J ]Journal of Systems Engineering and Elec- 0.00.00.25☒ tronics,2000,11(1):75-80. 观测噪声协方差阵取为[0.025].在风浪和外界扰动 [3]SASIADEKJ Z,WANG Q,ZEREMBA M B.Fuzzy a- 较小的前几次实验中很好的完成了滤波任务.但当 doptive Kalman filtering for INS/GPS data fusion [A]. 外界扰动大时曾导致发散.后期采用文中所述算法, In:Proc 15th IEEE International Symposium on Intelli- 滤波效果趋于稳定.图3和图4为速度的自适应卡 gent Control[C].Patras,Greece,2000. 尔曼滤波数据曲线.从图中可以看出滤波效果较好. [4]朱海,莫军.水下导航信息融合[M].北京:因防工 限于篇幅,只给出速度曲线, 业出版社,2002. [5]秦永元,张洪钺,汪淑华.卡尔曼滤波与组合导航原理 0.40 [M].西安:西北工业大学出版社,1998 0.35 [6]马艳.数据融合技术在多传感器组合导航中的应用 0.30 0.25 [D].南京:南京航空航天大学,2000 MA Yan.Information amalgamation in multi-sensors 0.20 滤波前 combined navigation [D].Nanjing:Nanjing University 0.15 ·滤波后 0.10 of Aeronautics and Astronautics,2000. 作者简介: 0.05 李晔,男,1978年生,博士研究生 200 400 600 -0.05L 主要研究方向为水下机器人规划与运动 采样点s 控制,人工智能.Email:liyelijing@yahoo. 图3纵向速度滤波曲线 com.cn. Fig.3 Longitudinal velocity filter curves 0.025 一滤波前 0.020 ,滤波后 0.015 万磊,男,1964年生,研究员,船舶 0.01 与海洋结构物设计制造专业硕士研究生 0.005 导师,主要研究方向为水下机器人控制系 统设计与集成,水下导航.发表学术论文 -0.005 600 -0.010 多篇 -0.015 采样点5 图4横向速度滤波曲线 Fig.4 Transverse velocity filer curves 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved hup://www.cnki.net
Φ( k , k - 1) P( k - 1/ k - 1)ΦT ( k/ k - 1) ]. (16) ^r ( k) = (1 - dk- 1 ) ^r ( k - 1) + dk- 1 [ Y( k) - H( k) X^ ( k/ k - 1) ]. (17) R^ ( k) = (1 - dk- 1 ) R^ ( k - 1) + dk- 1 [ε( k)εT - H( k) P( k/ k - 1) H T ( k) ]. (18) 4 算法应用 2005 年 9 月 ,某型智能水下机器人在某水域 , 进行了长距离航行试验. 控制系统的滤波模块即采 用了本文所述的算法. 试验时风浪较大 ,风浪噪声和 附近船只发动机噪声对传感器有较大影响. 水下机 器人长航时所采用的控制为速度控制. 多普勒速度 计量测到的速度值为控制器的反馈. 因此速度滤波 的好坏直接影响到控制的稳定性. 曾尝试将模型噪声的协方差阵取为 0. 25 0. 0 0. 0 0. 0 0. 25 0. 0 0. 0 0. 0 0125 , 观测噪声协方差阵取为[01025 ]. 在风浪和外界扰动 较小的前几次实验中很好的完成了滤波任务. 但当 外界扰动大时曾导致发散. 后期采用文中所述算法 , 滤波效果趋于稳定. 图 3 和图 4 为速度的自适应卡 尔曼滤波数据曲线. 从图中可以看出滤波效果较好. 限于篇幅 ,只给出速度曲线. 图 3 纵向速度滤波曲线 Fig. 3 Longitudinal velocity filter curves 图 4 横向速度滤波曲线 Fig. 4 Transverse velocity filer curves 5 结束语 文中考虑了水下机器人的运动特性 ,设计了水 下机器人自适应卡尔曼滤波器 ,降低了系统噪声和 量测噪声统计特性估计不准确所带来的问题. 同时 采用了渐消记忆指数加权方法. 试验结果表明达到 了较好的滤波效果. 进一步的工作应探讨特定情况 下自适应方法的快速收敛问题. 参考文献 : [1 ]刘建成 , 徐玉如. 水下机器人神经网络滤波技术的研究 [J ]. 海洋工程 , 2002 , 20 (3) : 34 - 38. L IU Jiancheng , XU Yuru. A filtering method with neu2 ral network for underwater vehicle [J ]. Ocean Engineer2 ing , 2002 , 20 (3) : 34 - 38. [2 ] WAN G Y F , HAN X L , HU H Z. Study on federated architecture for GPS/ INS/ TRN integrated navigation system [J ]. Journal of Systems Engineering and Elec2 tronics ,2000 ,11 (1) :75 - 80. [3 ] SASIADEK J Z , WAN G Q ,ZEREMBA M B. Fuzzy a2 doptive Kalman filtering for INS/ GPS data fusion [ A ]. In : Proc 15th IEEE International Symposium on Intelli2 gent Control[C]. Patras , Greece , 2000. [ 4 ] 朱 海 , 莫 军. 水下导航信息融合[ M]. 北京 :国防工 业出版社 ,2002. [5 ] 秦永元 , 张洪钺 ,汪淑华. 卡尔曼滤波与组合导航原理 [ M]. 西安 :西北工业大学出版社 ,1998. [6 ] 马 艳. 数据融合技术在多传感器组合导航中的应用 [D]. 南京 : 南京航空航天大学 , 2000. MA Yan. Information amalgamation in multi2sensors combined navigation [ D ]. Nanjing : Nanjing University of Aeronautics and Astronautics , 2000. 作者简介 : 李 晔 ,男 ,1978 年生 ,博士研究生 , 主要研究方向为水下机器人规划与运动 控制 ,人工智能. E2mail :liyelijing @yahoo. com. cn. 万 磊 ,男 ,1964 年生 ,研究员 ,船舶 与海洋结构物设计制造专业硕士研究生 导师 ,主要研究方向为水下机器人控制系 统设计与集成 ,水下导航. 发表学术论文 多篇. 第 2 期 李 晔 ,等 :水下机器人自适应卡尔曼滤波技术研究 · 74 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net