
第1卷第2期 智能系统学报 Vol.1№2 2006年10月 CAAI Transactions on Intelligent Systems 0ct.2006 具有一般化结构的分数阶超前校正器 汪纪锋,李元凯 (重庆邮电大学自动化学院.重庆400065) 摘要:根据分数阶系统扩展频域分析法对分数阶相位超前校正器进行建模,这一结构能使该校正器与传统整数阶 校正器一样为原系统提供一个零点和一个极点,具有任意阶次超前校正器的统一化形式.给出扩展频域超前校正器 的解析法设计步骤,并和一般频率域下不同结构的分数阶超前校正器的适用性作了分析比较和性能仿真 关键词:分数阶:超前补偿器:扩展频域分析:控制系统 中图分类号:TP13文献标识码:A文章编号:1673-4785(2006)02-0062-05 The fractional-order lead compensator with general structure WAN GJi-feng ,LI Yuam kai (College of Automation,Chongqing University of Posts and Telecommunications,Chongqing 400065,China) Abstract:The fractional-order lead compensator provided in this paper is modeled by extended frequency a- nalysis for fractional systems.It has a new structure which gives the original system one zero and one pole definitely like the integer order,and can be regarded as a generalized form of conventional compensators with arbitrary orders.Its analytical design method is given.Also,comparison and simulation are made be- tween two fractional-order lead compensators with different structures in common and extended frequency domain. Keywords fractional order;lead compensator;extended frequency analysis;control system 对于分数阶控制系统,以往的方法是将其近似的合理解释,并且依然需要系统的设计方法.文中基 为整数阶系统,然后对近似系统进行控制器设计,这于分数系统扩展频域法],提出不同于以往的分数 样就存在设计偏差,甚至不能满足原系统重要性能 阶超前校正器,这种新结构能够很好解决零极点问 如稳定性的要求,因此就有必要进行分数阶控制器 题 的研究和设计引.目前,分数阶控制器有4种提 1 法,一为TD控制器,它由积分环节、微分环节和 扩展频域模型与分数超前校正器 一个分数阶环节并联组成,其结构简单,参数较少, 整数阶系统在正负频域内的频域特性极为相 调节方便,但很难达到理想效果.二是CRONE控制 似,仅考虑系统的正频域特性即可,然而这并不适用 器.它由Oustaloup提出,己经成功地运用于实际, 于具有任意性阶次的分数阶系统,因此就有必要将 是控制器的一种理想选择,文献[5]详细论述了 区间作为整体考察其频域特性,即分数阶系统扩展 CRONE控制器.三是Podlubny提出的PTD“控制 频域法。 器61,它与TD控制器相比,前者可以获得更精确 1.1扩展频率模型 的控制性能,代价是结构较为复杂,参数较多,有3 扩展频域下的分数阶系统数学模型必须满足确 个增益和2个阶次参数.第四是超前滞后校正补偿 立分数阶系统零极点的唯一性条件].考虑分数阶 器?】,这种形式的控制器同样能够取得很好的控 方程: 制效果,但是缺乏关于控制器向系统提供的零极点 s”=Acos0+isin9=A∠0,0∈0,2r1.(1) 收稿日期:200603-30. s=A产∠9±2,k=0,1,2,4.1.(2) 基金项目:重庆市自然科学基金资助项目(CSTC2004BB2165);重庆 市教委自然科学基金资助项目(K060506). 由式1)、2)可知,原方程的所有解在s平面上均 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 1 卷第 2 期 智 能 系 统 学 报 Vol. 1 №. 2 2006 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2006 具有一般化结构的分数阶超前校正器 汪纪锋 ,李元凯 (重庆邮电大学 自动化学院 ,重庆 400065) 摘 要 :根据分数阶系统扩展频域分析法对分数阶相位超前校正器进行建模 ,这一结构能使该校正器与传统整数阶 校正器一样为原系统提供一个零点和一个极点 ,具有任意阶次超前校正器的统一化形式. 给出扩展频域超前校正器 的解析法设计步骤 ,并和一般频率域下不同结构的分数阶超前校正器的适用性作了分析比较和性能仿真. 关键词 :分数阶 ;超前补偿器 ;扩展频域分析 ;控制系统 中图分类号 : TP13 文献标识码 :A 文章编号 :167324785 (2006) 0220062205 The fractional2order lead compensator with general structure WAN G Ji2feng ,L I Yuan2kai (College of Automation ,Chongqing University of Posts and Telecommunications , Chongqing 400065 , China) Abstract :The fractional2order lead compensator provided in t his paper is modeled by extended frequency a2 nalysis for fractional systems. It has a new struct ure which gives t he original system one zero and one pole definitely like t he integer order , and can be regarded as a generalized form of conventional compensators with arbitrary orders. Its analytical design met hod is given. Also , comparison and simulation are made be2 tween two fractional2order lead compensators with different struct ures in common and extended frequency domain. Keywords :fractional order ; lead compensator ; extended frequency analysis; control system 收稿日期 :2006203230. 基金项目 :重庆市自然科学基金资助项目(CSTC2004BB2165) ;重庆 市教委自然科学基金资助项目( KJ060506) . 对于分数阶控制系统 ,以往的方法是将其近似 为整数阶系统 ,然后对近似系统进行控制器设计 ,这 样就存在设计偏差 ,甚至不能满足原系统重要性能 如稳定性的要求 ,因此就有必要进行分数阶控制器 的研究和设计[1 - 3 ] . 目前 ,分数阶控制器有 4 种提 法 ,一为 TID 控制器[4 ] . 它由积分环节、微分环节和 一个分数阶环节并联组成 ,其结构简单 ,参数较少 , 调节方便 ,但很难达到理想效果. 二是 CRON E 控制 器. 它由 Oustaloup 提出 ,已经成功地运用于实际 , 是控制器的一种理想选择 ,文献 [ 5 ] 详细论述了 CRON E 控制器. 三是 Podlubny 提出的 PI λD μ 控制 器[6 ] ,它与 TID 控制器相比 ,前者可以获得更精确 的控制性能 ,代价是结构较为复杂 ,参数较多 ,有 3 个增益和 2 个阶次参数. 第四是超前滞后校正补偿 器[7 - 8 ] ,这种形式的控制器同样能够取得很好的控 制效果 ,但是缺乏关于控制器向系统提供的零极点 的合理解释 ,并且依然需要系统的设计方法. 文中基 于分数系统扩展频域法[9 ] ,提出不同于以往的分数 阶超前校正器 ,这种新结构能够很好解决零极点问 题. 1 扩展频域模型与分数超前校正器 整数阶系统在正负频域内的频域特性极为相 似 ,仅考虑系统的正频域特性即可. 然而这并不适用 于具有任意性阶次的分数阶系统 ,因此就有必要将 区间作为整体考察其频域特性 ,即分数阶系统扩展 频域法. 1. 1 扩展频率模型 扩展频域下的分数阶系统数学模型必须满足确 立分数阶系统零极点的唯一性条件[10 ] . 考虑分数阶 方程 : s μ = A (cosθ+ i sinθ) = A ∠θ,θ∈[0 ,2π]. (1) s = A 1 μ ∠ θ+ 2 kπ μ , k = 0 ,1 ,2 , …,μ- 1. (2) 由式(1) 、(2) 可知 ,原方程的所有解在 s μ 平面上均

第2期 汪纪锋,等:具有一般化结构的分数阶超前校正器 *63* 重合于A∠0,而这些解在s平面上将以相角差2r/μ 频增益补偿,K取决于稳态性能指标.超前校正器 在各方向上形成一系列投影点.。”平面的主黎曼面 为被控系统提供一个零点和一个极点,因此式6)中 相角区间为0,2π1,图1表示了随阶次4的变化 的(T9+1或(aTs+1必须满足有效根唯一性 而收缩或扩张的s”的主黎曼面,μ=0.375时为 条件.考虑为实数,利用唯一性条件确定阶次范围 OABO,4=1时为OABC0,4=1.25时为OABC a1,4∈0.5,1.51 DO.s”平面的主黎曼面中的解为该方程的有效解. 校正器幅值与相位函数如下: 对于μ>0下的唯一有效解的条件由下式推出 A(⑨=|GGy|= 0≤0+2k知 a=arctan -5 B(“=12 1+ar四5eos受 C -10 0.5 (aTo'sin2 0 arctan 8) 虚轴 05-1-05 0.51 实轴 1+(aT叫3c0s 2 相角在频率⊙.处取极大值中。: 图1。平面的主黎曼面 dpro =0 (9) Fig.1 Main Riemann surface of s"-plane da -0m 将式8)带入式9),④由此方程确定: 因此在g2.如果系统己有足够的相角裕度,然而高 ams。+an1s1+…+4s6 频噪声太大,那么在不破坏系统稳定性的基础上,可 以谨慎选择4>凸.对于无特殊要求的通常情况,取 s9+1) 4=42即可获取所需控制性能,并能极大简化其设 5 计步骤.此外图中还表明最大相角中随参数a(系 ·Πps+ 统带宽)不同而变化的情况,当a下降,中带宽增 式中:K=/m,月=月+4,0=6+ 加,中.增大 等式右端每乘积项有且仅有一个有效复域解, 2 分数阶超前校正器的设计 即为零极点, 此方法对于在0.5,1.5]内取值的任意阶次均 1.2分数阶超前校正器 适用.为简化描述,默认4=4,不具有本质区别 基于分数阶系统模型5),分数阶超前校正器可 令式(10)中4=马,于是 表示为 G=Ka8土L (a5+1,a∈0,).(6) (T)°+(T叫+2cos 2 asin Ig 2 = π0 (1D 式中:参数a决定校正器带宽;K=a,l/a为低 (aTo°+(aT.a+2cos 2 asin 2 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
重合于 A ∠θ,而这些解在 s 平面上将以相角差2π/μ 在各方向上形成一系列投影点. s μ 平面的主黎曼面 相角区间为[0 , 2πμ] ,图 1 表示了随阶次μ的变化 而收缩或扩张的 s μ 的主黎曼面 ,μ= 01375 时为 OA B O ,μ= 1 时为 OA B CO ,μ= 1. 25 时为 OA B C2 DO. s μ 平面的主黎曼面中的解为该方程的有效解. 对于μ> 0 下的唯一有效解的条件由下式推出 : 0 ≤θ+ 2 kπ α2 . 如果系统已有足够的相角裕度 ,然而高 频噪声太大 ,那么在不破坏系统稳定性的基础上 ,可 以谨慎选择α1 >α2 . 对于无特殊要求的通常情况 ,取 α1 =α2 即可获取所需控制性能 ,并能极大简化其设 计步骤. 此外图中还表明最大相角φm 随参数 a (系 统带宽) 不同而变化的情况 , 当 a 下降 ,φm 带宽增 加 ,φm 增大. 2 分数阶超前校正器的设计 此方法对于在(0. 5 , 1. 5 ]内取值的任意阶次均 适用. 为简化描述 ,默认α1 =α2 ,不具有本质区别. 令式(10) 中α1 =α2 ,于是 ( Tω) α + ( Tω) -α + 2cos πα 2 ( aTω) α + ( aTω) -α + 2cos πα 2 = αsin πα 2 αsin πα 2 . (11) 第 2 期 汪纪锋 ,等 :具有一般化结构的分数阶超前校正器 ·63 ·

·64- 智能系统学报 第1卷 [51.这里重新考虑文献1中的控制器模型如下: 幅值曲线 C(y=K·a· +L 80 ,a∈0,1).14 a0.00 aTs l 8 相对于整数阶控制器,它能在保证系统相位裕 20 0 a>a:ap=0: 度情况下,为被控系统提供更稳定的相位曲线,使得 0.1 a<o 校正系统具有良好的鲁棒性.问题在于式(14)描述 -2 10 10 10 的校正器无法解释其应该向系统提供的关于零点和 相位曲线 极点的信息.零极点信息不明确,就无法成功运用分 1.571 0.m0.00.00】 数阶经典控制理论,包括分数阶扩展频域法和空间 根轨迹法.此外,这种结构难以对超前校正器进行时 域分析.这极大限制了它在分数阶控制系统中的深 10 10 10 10 10 入拓展与灵活应用.然而式(6)所描述的控制器可以 w/rad.s 较好地解决这些问题.它能够同整数阶控制器一样 图2超前校正器的Bode图 在原被控系统上增加一个零点和一个极点,严格的 Fig.2 Bode diagrams of lead compensator 说,它是任意阶次相位超前校正器的一般化描述.通 d1= T石 过其提供的零极点信息,分数阶系统一般分析方法 带入式7)和(8) 均得以较好应用.表1对这2种不同结构的分数阶 A()|-“.= 控制器基本特性作了比较, 0”+20os号+1 表12种不同结构分数阶超前校正器的基本特性比较 Table 1 Comparison of the basic characteristics of the two aTa)2+2(aTw-)"cos a different fractionaForder compensators 2 +1 分数系统下的分数阶控制器 (T“+1 Ts+1 K· (aTs)2+1 aTs+1 N (12) 时域线性微分方程模型(Caputo |u-“n= s定义) 有限项 无限项 扩展频域分析法 适用 不适用 a sin 2 n号 扩展频率Nyquist与对数频率稳 适用 适用 arctan arctan 定判据 +0s2 na a +cos 空间根轨迹法 适用 不适用 2 相角超前校正器的统一化形式 是 否 13) 幅值比较 等价 等价 考虑未校正系统G。(sy需进行超前相位校正,其设 最大相角比较 见图3 见图3 计步骤如下: 图3所示2种超前校正器在相应参数下其最大 1)稳态性能指标确定K.K=KWa. 相位的差别.当a∈(0.5,1)时式(14)控制器)可提 2)作原系统Bode图.确定其截止频率⊙和相 供的最大相位Φm大于式(6)控制器.a=1时它们结 角裕度中。=π+中().根据期望相角裕度决定相 构相同,性能一致,具有相同的最大相位.另外图中 角所需补偿值,中=中-中。+(5°一20) 还表明每个控制器有其不同的适用范围,可在不同 3)式8)或式13)定出相角条件: 情况下自由选择 中n=中(an). 举例说明.考虑未校正系统山: 4)式7)或式12)定出幅值条件: 2 201gA(am)=201gA。(0m)=0. G(y=s0.5s+) (15) 5)式10)或式(11)定出极值条件: 设计超前相位校正器使其速度误差指数K,= dp(y/dωl-“。=0. 20,其相位裕度保持50°左右,增益截至频率4为 6)根据性能综合需求,选择分数阶次4,4.另 10rad/s.其幅值与相位在期望截至频率2.下分别 外根据以上3个方程计算参数a,T,,从而确定2 为-8.13dB和-168.7°.利用文中第3部分的解析 个转折频率4=1/T,4=1/aT. 法得到系统频率特性如图4.图中3条曲线分别代 32种分数阶超前校正器的比较 表下列不同结构超前校正器的频率特性: 超前校正器模型的详细讨论可参考文献[1/和 Gfy=10X1±02830065 1+0.0008y065, 1994-2009 China Academie Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 2 超前校正器的 Bode 图 Fig. 2 Bode diagrams of lead compensator α1 = α2 ωm = 1 T a . 带入式(7) 和(8) A (ω) | ω=ωm = K · ( Tωm ) 2α + 2 ( Tωm ) α cos πα 2 + 1 ( aTωm ) 2α + 2 ( aTωm ) α cos πα 2 + 1 = K · 1 a α. (12) φ(ω) | ω=ωm = arctan sin πα 2 a α 2 + cos πα 2 - arctan sin πα 2 a - α 2 + cos πα 2 . (13) 考虑未校正系统 Go (s) 需进行超前相位校正 ,其设 计步骤如下 : 1) 稳态性能指标确定 K. Kc = K/ a. 2) 作原系统 Bode 图. 确定其截止频率ωco和相 角裕度φco =π+φ(ωco ) . 根据期望相角裕度决定相 角所需补偿值 ,φm =φc - φco + (5°~20°) . 3) 式(8) 或式(13) 定出相角条件 : φm = φ(ωm ) . 4) 式(7) 或式(12) 定出幅值条件 : 20lgA (ωm ) = 20lgAo (ωm ) = 0. 5) 式(10) 或式(11) 定出极值条件 : dφ(ω) / dω| ω=ωm = 0. 6) 根据性能综合需求 ,选择分数阶次α1 ,α2 . 另 外根据以上 3 个方程计算参数 a , T ,ωm ,从而确定 2 个转折频率ω1 = 1/ T ,ω2 = 1/ a T. 3 2 种分数阶超前校正器的比较 超前校正器模型的详细讨论可参考文献[1 ]和 [5 ]. 这里重新考虑文献[1 ]中的控制器模型如下 : C(s) = Kc ·a α · Ts + 1 aTs + 1 α , a ∈(0 ,1) . (14) 相对于整数阶控制器 ,它能在保证系统相位裕 度情况下 ,为被控系统提供更稳定的相位曲线 ,使得 校正系统具有良好的鲁棒性. 问题在于式 (14) 描述 的校正器无法解释其应该向系统提供的关于零点和 极点的信息. 零极点信息不明确 ,就无法成功运用分 数阶经典控制理论 ,包括分数阶扩展频域法和空间 根轨迹法. 此外 ,这种结构难以对超前校正器进行时 域分析. 这极大限制了它在分数阶控制系统中的深 入拓展与灵活应用. 然而式(6) 所描述的控制器可以 较好地解决这些问题. 它能够同整数阶控制器一样 在原被控系统上增加一个零点和一个极点 ,严格的 说 ,它是任意阶次相位超前校正器的一般化描述. 通 过其提供的零极点信息 ,分数阶系统一般分析方法 均得以较好应用. 表 1 对这 2 种不同结构的分数阶 控制器基本特性作了比较. 表 1 2 种不同结构分数阶超前校正器的基本特性比较 Table 1 Comparison of the basic characteristics of the two different fractional2order compensators 分数系统下的分数阶控制器 ( Ts) α1 + 1 ( a Ts) α2 + 1 Ts + 1 a Ts + 1 α 时域线性微分方程模型 (Caputo’ s 定义) 有限项 无限项 扩展频域分析法 适用 不适用 扩展频率 Nyquist 与对数频率稳 定判据 适用 适用 空间根轨迹法 适用 不适用 相角超前校正器的统一化形式 是 否 幅值比较 等价 等价 最大相角比较 见图 3 见图 3 图 3 所示 2 种超前校正器在相应参数下其最大 相位的差别. 当α∈(0. 5 ,1) 时式 (14) 控制器) 可提 供的最大相位φm 大于式(6) 控制器.α= 1 时它们结 构相同 ,性能一致 ,具有相同的最大相位. 另外图中 还表明每个控制器有其不同的适用范围 ,可在不同 情况下自由选择. 举例说明. 考虑未校正系统[1 ] : Go (s) = 2 s(0. 5s + 1) . (15) 设计超前相位校正器使其速度误差指数 Kv = 20 ,其相位裕度保持 50°左右 ,增益截至频率ωc 为 10 rad/ s. 其幅值与相位在期望截至频率ωc 下分别 为 - 8. 13 dB 和 - 168. 7°. 利用文中第 3 部分的解析 法得到系统频率特性如图 4. 图中 3 条曲线分别代 表下列不同结构超前校正器的频率特性 : G(s) = 10 × 1 + (0. 283 0s) 0. 635 1 + (0. 000 8s) 0. 635 , ·64 · 智 能 系 统 学 报 第 1 卷
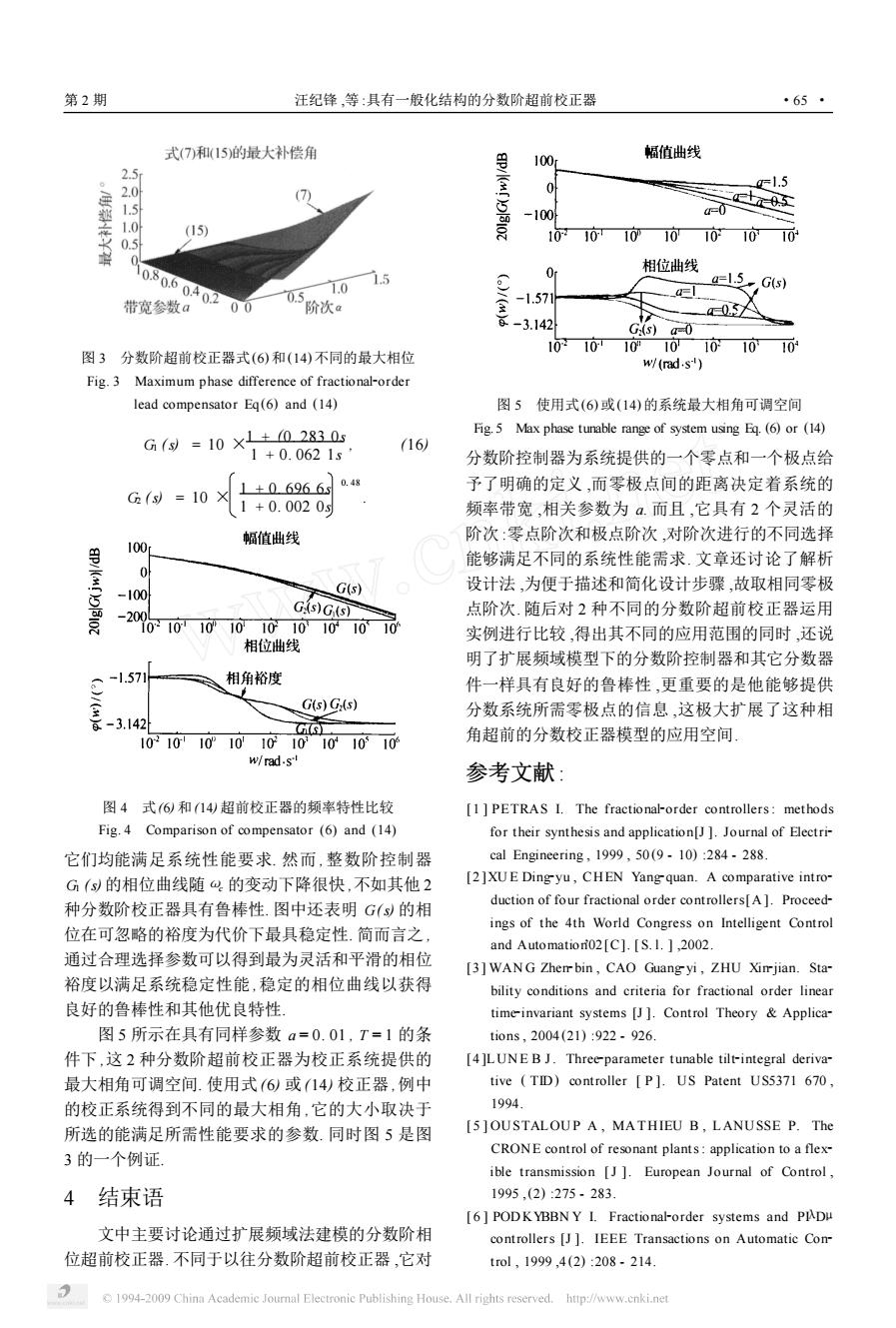
第2期 汪纪锋,等:具有一般化结构的分数阶超前校正器 *65* 式(7)和(15)的最大补偿角 幅值曲线 100 2.5 2.0 1.5 (7 1.5 e+0 -100 d=0 (15) 0.5 10210 10 10 10 1010 0.80.6040.2 1.5 2 相位曲线 1.0 a=1.5,Gs) 0.5 带宽参数a 阶次a -1.571 a=l 0 0.3A -3.142 G(s)a0 10 10 1010101010 图3分数阶超前校正器式(6)和(14)不同的最大相位 w/(rad.s) Fig.3 Maximum phase difference of fractional-order lead compensator Eq(6)and (14) 图5使用式(6)或(14)的系统最大相角可调空间 G(y=10X1±02830s Fig.5 Max phase tunable range of system using Eq.(6)or (14) 16) 1+0.0621s 分数阶控制器为系统提供的一个零点和一个极点给 予了明确的定义,而零极点间的距离决定着系统的 G(s)=10 L±06966Q4s 1+0.0020y 频率带宽,相关参数为a.而且,它具有2个灵活的 幅值出线 阶次:零点阶次和极点阶次,对阶次进行的不同选择 100r 能够满足不同的系统性能需求.文章还讨论了解析 0 G(s) 设计法,为便于描述和简化设计步骤,故取相同零极 -100 200 Gs)G(s 点阶次.随后对2种不同的分数阶超前校正器运用 01010101010101010 实例进行比较,得出其不同的应用范围的同时,还说 相位出线 明了扩展频域模型下的分数阶控制器和其它分数器 -1.571 相角裕度 件一样具有良好的鲁棒性,更重要的是他能够提供 G(s)G(s) 分数系统所需零极点的信息,这极大扩展了这种相 每-3.142 G 1021010101010101010 角超前的分数校正器模型的应用空间 w/rad.s" 参考文献: 图4式6)和14)超前校正器的频率特性比较 [1 PETRAS I.The fractional-order controllers:methods Fig.4 Comparison of compensator (6)and (14) for their synthesis and application[J ]Journal of Electri- 它们均能满足系统性能要求.然而,整数阶控制器 cal Engineering,1999,50(9-10):284.288. G(s)的相位曲线随的变动下降很快,不如其他2 [2]XUE Dingyu,CHEN Yangquan.A comparative intro- 种分数阶校正器具有鲁棒性.图中还表明G(s)的相 duction of four fractional order controllers[A].Proceed- 位在可忽略的裕度为代价下最具稳定性.简而言之, ings of the 4th World Congress on Intelligent Control and Automation02[C].[S.1.],2002. 通过合理选择参数可以得到最为灵活和平滑的相位 [3]WANG Zhemr bin,CAO Guangyi,ZHU Ximjian.Sta- 裕度以满足系统稳定性能,稳定的相位曲线以获得 bility conditions and criteria for fractional order linear 良好的鲁棒性和其他优良特性 time-invariant systems [J ]Control Theory Applica- 图5所示在具有同样参数a=0.01,T=1的条 ti0ns,2004(21):922.926. 件下,这2种分数阶超前校正器为校正系统提供的 [4]LUNE BJ.Three-parameter tunable tilt-integral deriva- 最大相角可调空间.使用式(6)或14)校正器,例中 tive (TID)controller [P].US Patent US5371 670, 的校正系统得到不同的最大相角,它的大小取决于 1994. 所选的能满足所需性能要求的参数.同时图5是图 [5]OUSTALOUP A,MATHIEU B,LANUSSE P.The 3的一个例证 CRONE control of resonant plants:application to a flex- ible transmission [J ]European Journal of Control, 4结束语 1995,(2):275-283 [6 PODKYBBN Y I.Fractional-order systems and PIDu 文中主要讨论通过扩展频域法建模的分数阶相 controllers [J ]IEEE Transactions on Automatic Con- 位超前校正器.不同于以往分数阶超前校正器,它对 trol,1999,4(2):208-214. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 3 分数阶超前校正器式(6)和(14) 不同的最大相位 Fig. 3 Maximum phase difference of fractional2order lead compensator Eq(6) and (14) G1 (s) = 10 × 1 + (0. 283 0s 1 + 0. 062 1s , (16) G2 (s) = 10 × 1 + 0. 696 6s 1 + 0. 002 0s 0. 48 . 图 4 式(6) 和(14) 超前校正器的频率特性比较 Fig. 4 Comparison of compensator (6) and (14) 它们均能满足系统性能要求. 然而 , 整数阶控制器 G1 (s) 的相位曲线随ωc 的变动下降很快 ,不如其他 2 种分数阶校正器具有鲁棒性. 图中还表明 G(s) 的相 位在可忽略的裕度为代价下最具稳定性. 简而言之 , 通过合理选择参数可以得到最为灵活和平滑的相位 裕度以满足系统稳定性能 ,稳定的相位曲线以获得 良好的鲁棒性和其他优良特性. 图 5 所示在具有同样参数 a = 0. 01 , T = 1 的条 件下 ,这 2 种分数阶超前校正器为校正系统提供的 最大相角可调空间. 使用式 (6) 或 (14) 校正器 ,例中 的校正系统得到不同的最大相角 ,它的大小取决于 所选的能满足所需性能要求的参数. 同时图 5 是图 3 的一个例证. 4 结束语 文中主要讨论通过扩展频域法建模的分数阶相 位超前校正器. 不同于以往分数阶超前校正器 ,它对 图 5 使用式(6)或(14) 的系统最大相角可调空间 Fig. 5 Max phase tunable range of system using Eq. (6) or (14) 分数阶控制器为系统提供的一个零点和一个极点给 予了明确的定义 ,而零极点间的距离决定着系统的 频率带宽 ,相关参数为 a. 而且 ,它具有 2 个灵活的 阶次 :零点阶次和极点阶次 ,对阶次进行的不同选择 能够满足不同的系统性能需求. 文章还讨论了解析 设计法 ,为便于描述和简化设计步骤 ,故取相同零极 点阶次. 随后对 2 种不同的分数阶超前校正器运用 实例进行比较 ,得出其不同的应用范围的同时 ,还说 明了扩展频域模型下的分数阶控制器和其它分数器 件一样具有良好的鲁棒性 ,更重要的是他能够提供 分数系统所需零极点的信息 ,这极大扩展了这种相 角超前的分数校正器模型的应用空间. 参考文献 : [ 1 ] PETRAS I. The fractional2order controllers: methods for their synthesis and application[J ]. Journal of Electri2 cal Engineering , 1999 , 50 (9 - 10) :284 - 288. [2 ]XU E Ding2yu , CHEN Yang2quan. A comparative intro2 duction of four fractional order controllers[A ]. Proceed2 ings of the 4th World Congress on Intelligent Control and Automation’02[C]. [ S. l. ] ,2002. [3 ] WAN G Zhen2bin , CAO Guang2yi , ZHU Xin2jian. Sta2 bility conditions and criteria for fractional order linear time2invariant systems [J ]. Control Theory & Applica2 tions , 2004 (21) :922 - 926. [4 ]LUN E B J. Three2parameter tunable tilt2integral deriva2 tive ( TID) controller [ P ]. US Patent US5371 670 , 1994. [ 5 ] OUSTALOU P A , MA THIEU B , LANUSSE P. The CRONE control of resonant plants: application to a flex2 ible transmission [J ]. European Journal of Control , 1995 ,(2) :275 - 283. [ 6 ] POD KYBBN Y I. Fractional2order systems and PλI Dμ controllers [J ]. IEEE Transactions on Automatic Con2 trol , 1999 ,4 (2) :208 - 214. 第 2 期 汪纪锋 ,等 :具有一般化结构的分数阶超前校正器 ·65 ·

·66· 智能系统学报 第1卷 [7]MONJE C A,CALDERON AJ,VINAGRE B M,et al. 作者简介: The fractional-order lead compensator [A].Computa- 汪纪锋,男,1944年生,重庆邮电大学 tional Cybernetics,Second IEEE International Confer- 教授,博士生导师,主要研究方向为复杂系 ence[C].[S.1.],2004. 统理论与应用,在因内外学术期刊上已发 [8]RA YNAUDAND H F,ZERGA INOH A.State-space 表学术论文70余篇.Email:wangif@ representartion for fractional order controllers [J].Au- cqupt.edu.cn. tomatica,2000,36(5):1017.1021. [9]WANGJi-feng,LI Yuar kai.Frequency domain analysis and applications for Fractional-order control systems 李元凯,男,1981年生,重庆邮电大学 [J].Journal of Physics:Conference series,2005,13 控制理论与控制工程专业硕士研究生.主 (5):265.273. 要研究方向为复杂系统理论与应用,在国 [10]WAN GJi-feng,LI Yuarr kai.Frequency domain stabli- 内外学术期刊上已发表多篇关于分数系 ty criteria for fractionalorder control systems [J ]Jour- 统控制的论文.Email:yuankai.i@ nal of Chongqing University (English Version),2006,1 gmail.com. (1):30-35. 图像压缩与图像处理国际研讨会 International Workshop on Image Compression and Image Processing 随着计算机技术的飞速发展,数字图像处理技术深入到社会发展的各个领域,受到了通信技术、计算机 技术和数学等各领域专家的关注和研究。 本次会议旨在为不同领域的专家提供一个良好的交流平台,会议主题涵盖图像处理的各个方面,包括图 像压缩,图像去噪,并行处理和工业应用等。研讨会将安排来自研究机构和工业应用的特邀报告和研究人员 的简短发言。会后优秀论文的作者将被邀请扩写论文并发表于英国Taylor&Francis出版社出版的杂志 《International Journal of Computer Mathematics》)或由英国科学出版社出版的杂志《ournal of Algorithms and Computational Technology》。 图像压缩与图像处理国际研讨会由福州大学数学与计算机科学学院福州-格林威治应用计算研发中心 主办,会议时间为2006年12月17日一19日,会议地点为福州大学学术交流中心,中国福建省福州市工业 路怡山大厦。会议主题包括但不限于:(1)图像和视频编码技术;(2)图像预处理技术;(3)图像和视频中的 对象识别;(4)图像处理的并行和分布算法;(S)分形、小波与图像处理;(6)PDE在图像处理中的应用,(7)图 像处理在工业和生活中的应用,如:档案管理、视频点播地下管道缺陷检测、历史文物图像恢复、遥感图像处 理等。全文截稿日期为2006年10月15日,录用通知截止日期为2006年11月15日。联系电话: 135994095660591-83717689,E mail:mqwang@fzu.edu.cn.会议网站:http:/cmcs.fzu.edu.cnl wicap/. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
[7 ]MONJ E C A , CALDERON A J , VINA GRE B M , et al. The fractional2order lead compensator [ A ]. Computa2 tional Cybernetics , Second IEEE International Confer2 ence[C]. [ S. l. ] ,2004. [8 ] RA YNAUDAND H F , ZERGAINO H A. State2space representa2tion for fractional order controllers [J ]. Au2 tomatica , 2000 ,36 (5) :1017 - 1021. [ 9 ]WAN GJi2feng , L I Yuan2kai. Frequency domain analysis and applications for Fractional2order control systems [J ]. Journal of Physics: Conference series , 2005 , 13 (5) :265 - 273. [ 10 ] WAN GJi2feng , L I Yuan2kai. Frequency domain stabli2 ty criteria for fractional2order control systems [J ]. Jour2 nal of Chongqing University ( English Version) , 2006 ,1 (1) :30 - 35. 作者简介 : 汪纪锋 ,男 ,1944 年生 ,重庆邮电大学 教授 ,博士生导师 ,主要研究方向为复杂系 统理论与应用 ,在国内外学术期刊上已发 表学 术 论 文 70 余 篇. E2mail : wangjf @ cqupt. edu. cn. 李元凯 ,男 ,1981 年生 ,重庆邮电大学 控制理论与控制工程专业硕士研究生. 主 要研究方向为复杂系统理论与应用 ,在国 内外学术期刊上已发表多篇关于分数系 统控 制 的 论 文. E2mail : yuankai. li @ gmail. com. 图像压缩与图像处理国际研讨会 International Workshop on Image Compression and Image Processing 随着计算机技术的飞速发展 , 数字图像处理技术深入到社会发展的各个领域 ,受到了通信技术、计算机 技术和数学等各领域专家的关注和研究。 本次会议旨在为不同领域的专家提供一个良好的交流平台 ,会议主题涵盖图像处理的各个方面 ,包括图 像压缩 ,图像去噪 ,并行处理和工业应用等。研讨会将安排来自研究机构和工业应用的特邀报告和研究人员 的简短发言。会后优秀论文的作者将被邀请扩写论文并发表于英国 Taylor & Francis 出版社出版的杂志 《International Journal of Comp uter Mathematics》或由英国科学出版社出版的杂志《Journal of Algorit hms and Comp utational Technology》。 图像压缩与图像处理国际研讨会由福州大学数学与计算机科学学院福州 - 格林威治应用计算研发中心 主办 ,会议时间为 2006 年 12 月 17 日 —19 日 ,会议地点为福州大学学术交流中心 ,中国福建省福州市工业 路怡山大厦。会议主题包括但不限于 : (1) 图像和视频编码技术 ; (2) 图像预处理技术 ; (3) 图像和视频中的 对象识别 ; (4) 图像处理的并行和分布算法 ; (5) 分形、小波与图像处理 ; (6) PDE 在图像处理中的应用 ; (7) 图 像处理在工业和生活中的应用 ,如 :档案管理、视频点播、地下管道缺陷检测、历史文物图像恢复、遥感图像处 理等。全文截稿日期为 2006 年 10 月 15 日 ,录用通知截止日期为 2006 年 11 月 15 日。联系电话 : 13599409566 0591 - 83717689 , E2mail : mqwang @fzu. edu. cn. 会议网站 : http :/ / cmcs. fzu. edu. cn/ wicap/ . ·66 · 智 能 系 统 学 报 第 1 卷