东北大学：【人工智能基础】中国象棋机器博弈的时间自适应分配策略研究

第1卷第2期 智能系统学报 Vol.1 N2 2 2006年10月 CAAI Transactions on Intelligent Systems 0ct.2006 中国象棋机器博弈的时间自适应分配策略研究 徐长明，南晓斐，王骄，徐心和 (东北大学人工智能与机器人研究所，辽宁沈阳110004) 摘要：时间分配问题在象棋比赛中是十分重要的策略问题，在机器博奔中也是如此。好的策略可以把宝贵的时间 资源用在“刀刃”上：此外，好的时间分配策略还要有好的自适应性，亦即对大多数比赛，无论其限时的长短、步数的 多寡，该策略都能合理利用时间。在分析和建立了时间分配的数学模型的基础上，介绍了自适应时间分配与调整的 策略和算法。时间分配问题与搜索和评估密切相关，也影响着机器博弈的风格。 关键词：机器博弈；时间分配策略；自适应 中图分类号：TP18文献标识码：A文章编号：16734785(2006)02-003905 Ada ptive time allocation strategy in computer game of Chinese Chess XU Chang-ming,NAN Xiao-fei,WANG Jiao,XU Ximhe (Institute of Artificial Intelligence and Robotics,Northeastern University,Shenyang 110004,China) Abstract:Time Allocation is a typical and important strategy problem in chess matches,so does in comput- er games.A good strategy can allocate time for each searching-step to make the best use of it.Further- more,a good allocation strategy should be adaptive,namely,fitting most contests,regardless of the length of time limit,or the number limit of steps.Based on analysing and establishing the mathematic model of time allocation,this paper introduces an adaptive algorithm of time allocation and adjustnemt. The method ties up with the searching and evalation module,and also affects the style of computer games. Key words :computer games;time allocation strategy;adaptive 正式比赛过程中，时钟是不可或缺的.每走完一 步都要按时钟，将计时切换到对手一方.时间是参赛 1时间分配的数学模型 选手的宝贵资源，也是杀手，因时间没有利用好而输 目前，中国象棋的国内外赛事中，常常采用包干 棋屡见不鲜.例如，优势情况下因为超时而输掉比 计时的方式.例如，每方基本时间60min,每走一步 赛，或者输了棋还剩余很多时间，均说明没有很好地 加时30s21 利用时间资源.因此，深入研究中国象棋机器博弈的 文中将以包干计时为例，说明时间的数学模型， 时间分配问题)很有意义，对其他棋类博弈也应有 以便更准确地刻画时间分配 借鉴意义 1)红方第k步后的总时间 时间的分配策略可以分为2大类：静态分配策 I(=T6+a·k 略和动态分配策略.首先介绍时间分配问题的数学 式中：。为各方基本时间，a为每步加时 模型，然后介绍了几种简单的静态分配策略，分析其 2)红方前k步的总计用时 优缺点，接着介绍时间的动态分配策略，最后，在“平 Tea (k)=u(i) 均配时”模型的基础上，重点介绍了机器博弈的时间 自适应分配策略 式中：u()表示第i步着法用时，1=0,1，…k 3)如果用表示红方本局总计用时(KF为 总步数，那么还有 收稿日期：20060722 Tused(Kg)=Togen Tmid Tend 1994-2008 China Academic Journal Electronie Publishing House.All rights reserved.http://www.cnki.net

第 1 卷第 2 期 智 能 系 统 学 报 Vol. 1 №. 2 2006 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2006 中国象棋机器博弈的时间自适应分配策略研究 徐长明 ,南晓斐 ,王 骄 ,徐心和 (东北大学 人工智能与机器人研究所 ,辽宁 沈阳 110004) 摘 要 :时间分配问题在象棋比赛中是十分重要的策略问题 ,在机器博弈中也是如此。好的策略可以把宝贵的时间 资源用在“刀刃”上 ;此外 ,好的时间分配策略还要有好的自适应性 ,亦即对大多数比赛 ,无论其限时的长短、步数的 多寡 ,该策略都能合理利用时间。在分析和建立了时间分配的数学模型的基础上 ,介绍了自适应时间分配与调整的 策略和算法。时间分配问题与搜索和评估密切相关 ,也影响着机器博弈的风格。 关键词 :机器博弈 ;时间分配策略 ;自适应 中图分类号 : TP18 文献标识码 :A 文章编号 :167324785 (2006) 0220039205 Adaptive time allocation strategy in computer game of Chinese Chess XU Chang2ming , NAN Xiao2fei , WAN G Jiao , XU Xin2he (Institute of Artificial Intelligence and Robotics , Northeastern University , Shenyang 110004 , China) Abstract :Time Allocation is a typical and important strategy problem in chess matches , so does in comp ut2 er games. A good strategy can allocate time for each searching - step to make the best use of it. Furt her2 more , a good allocation strategy should be adaptive , namely , fitting most contests , regardless of t he lengt h of time limit , or t he number limit of step s. Based on analysing and establishing t he mat hematic model of time allocation , t his paper introduces an adaptive algorit hm of time allocation and adjust nemt. The met hod ties up with t he searching and evalation module , and also affects the style of comp uter games. Keywords :comp uter games; time allocation strategy ; adaptive 收稿日期 :2006207222. 正式比赛过程中 ,时钟是不可或缺的. 每走完一 步都要按时钟 ,将计时切换到对手一方. 时间是参赛 选手的宝贵资源 ,也是杀手 ,因时间没有利用好而输 棋屡见不鲜. 例如 ,优势情况下因为超时而输掉比 赛 ,或者输了棋还剩余很多时间 ,均说明没有很好地 利用时间资源. 因此 ,深入研究中国象棋机器博弈的 时间分配问题[1 ] 很有意义 ,对其他棋类博弈也应有 借鉴意义. 时间的分配策略可以分为 2 大类 :静态分配策 略和动态分配策略. 首先介绍时间分配问题的数学 模型 ,然后介绍了几种简单的静态分配策略 ,分析其 优缺点 ,接着介绍时间的动态分配策略. 最后 ,在“平 均配时”模型的基础上 ,重点介绍了机器博弈的时间 自适应分配策略. 1 时间分配的数学模型 目前 ,中国象棋的国内外赛事中 ,常常采用包干 计时的方式. 例如 ,每方基本时间 60 min ,每走一步 加时 30 s [2 ] . 文中将以包干计时为例 ,说明时间的数学模型 , 以便更准确地刻画时间分配. 1) 红方第 k 步后的总时间 T red total ( k) = T0 +α·k. 式中 : T0 为各方基本时间 ,α为每步加时. 2) 红方前 k 步的总计用时 T red used ( k) = ∑ k i =1 u( i) . 式中 : u( i) 表示第 i 步着法用时 , i = 0 ,1 , …, k. 3) 如果用 T red used 表示红方本局总计用时 ( KF 为 总步数) ,那么还有 T red used ( KF) = T red open + T red mid + T red end

·40 智能系统学报 第1卷 式中：下标open,mid,end分别代表了红方在开 ◆局面1·局面2·局面3 局、中局和残局阶段的耗时」 45 Isn=pen·Kpem, 35 T=月ad·Kmd, 25 Td=民nd·Kend 式中：B为该阶段的每步平均耗时，Kpem,Kd则为开 89 101112131415 局和残局阶段的按谱走棋的步数.在有开局库和残 深度py 图3博弈树深度与节点数关系图 局库的情况下，查库的时间消耗几乎可以忽略不计 Fig.3 Relationships between depth of tree and (常常按表的时间要比查库的时间长得多).可见，开 the number of nodes searched 发内容丰富的开局库与残局库的优越性.按库中棋 从图中不难看出： 谱中给出的着法走得越多，亦即开局库越晚“脱谱”， )同一局面下时间与节点数大致成线性关系！ 残局库越早“入谱”越有利.因为不仅很少耗时，而且 与残局相比，初始局面和中局局面单位时间所搜索 还可以赢得更多的“每步加时” 的节点数要少，这是因为后者局面复杂，评估函数开 4)红方第k步后的剩余时间 销较大 Ti(材=To(材-T(k-1)-u() 2)伴随着深度的增加，博弈树搜索所花费的时 式中：T(k-1)为红方k-1步总计用时，u(为 间呈指数增长.且尤以中局花费的时间的增长速度 红方第k步用时.应该说这是最被关心的. 最快，残局的增长速度最慢 2时间的静态分配策略 3)伴随着深度的增加，要搜索的博弈树节点的 数目呈指数增长.以中局节点数目增长最快，残局增 时间的静态分配策略是根据事前给出的常量 长速度最慢 博弈树搜索的深度、己经访问过的局面数、所耗时 2.2静态分配策略 间)，来决定何时停止搜索的策略 )固定时限制：比较符合人类棋手的习惯.缺点 2.1搜索时间、搜索节点数、搜索深度之间的关系 为分析搜索时间、搜索节点数与博弈树搜索深 是在中局搜索复杂局面的层数太浅，而简化的残局 度之间关系，选3个具有代表性的局面开局、较复 常常可以搜得非常深 杂的局面较简单的残局局面)进行了测试，得出关 2)固定层数：复杂局面每出一步棋，要花费较多 系曲线如图1~3所示 的时间搜索：而简单局面，如残局则很快出步， 3)固定节点数：不容易估计，复杂局面搜索层数 ◆局面1+局面2一局面3 6 浅：简单局面搜索得过深 静态分配策略的优点在于简单，易于实现.缺点 4321 是不灵活（需要事前固定搜索时间的长度，或搜索深 0 度，或节点数)、分配不公无法兼顾简单局面与复杂 101520253035 局面)、无法预测是否会超时或者有大量时间剩余 时s 上述方法应用于比赛显得太过粗糙，但在象棋程序 图1时间与节点数关系图 的开发与调试阶段，还是非常有用的 Fig.I Relationships between used-time and the number of nodes 3时间的动态分配和调整策略 ◆局面1一局面2 ·局面3 450 时间的静态分配策略缺乏自适应性，而动态分 350 配和调整策略则根据其策略目标，为每一步着法分 250 150, 配不同的搜索时间.其中，极为简单、有效的办法是 50 “平均配时”模型 89 101112131415 深度ply 3.1“平均配时”模型分析 图2博弈树深度与时间关系图 作为棋手或机器，下棋过程中必然时刻面对2 Fig.2 Relationships between used-time and 个问题： tree's depth searched 1)下阶段时间分配：估计还有多少步，大致时间 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

式中 :下标 open , mid , end 分别代表了红方在开 局、中局和残局阶段的耗时. T red open =βopen ·Kopen , T red mid =βmid ·Kmid , T red end =βend ·Kend . 式中 :β为该阶段的每步平均耗时 , Kopen , Kend则为开 局和残局阶段的按谱走棋的步数. 在有开局库和残 局库的情况下 ,查库的时间消耗几乎可以忽略不计 (常常按表的时间要比查库的时间长得多) . 可见 ,开 发内容丰富的开局库与残局库的优越性. 按库中棋 谱中给出的着法走得越多 ,亦即开局库越晚“脱谱”, 残局库越早“入谱”越有利. 因为不仅很少耗时 ,而且 还可以赢得更多的“每步加时”. 4) 红方第 k 步后的剩余时间 T red left ( k) = T red total ( k) - T red used ( k - 1) - u( k) . 式中 : T red used ( k - 1) 为红方 k - 1 步总计用时 , u ( k) 为 红方第 k 步用时. 应该说这是最被关心的. 2 时间的静态分配策略 时间的静态分配策略是根据事前给出的常量 (博弈树搜索的深度、已经访问过的局面数、所耗时 间) ,来决定何时停止搜索的策略. 2. 1 搜索时间、搜索节点数、搜索深度之间的关系 为分析搜索时间、搜索节点数与博弈树搜索深 度之间关系 ,选 3 个具有代表性的局面 (开局、较复 杂的局面、较简单的残局局面) 进行了测试 ,得出关 系曲线如图 1～3 所示. 图 1 时间与节点数关系图 Fig. 1 Relationships between used2time and the number of nodes 图 2 博弈树深度与时间关系图 Fig. 2 Relationships between used2time and tree’s depth searched 图 3 博弈树深度与节点数关系图 Fig. 3 Relationships between depth of tree and the number of nodes searched 从图中不难看出 : 1) 同一局面下时间与节点数大致成线性关系. 与残局相比 ,初始局面和中局局面单位时间所搜索 的节点数要少 ,这是因为后者局面复杂 ,评估函数开 销较大. 2) 伴随着深度的增加 ,博弈树搜索所花费的时 间呈指数增长. 且尤以中局花费的时间的增长速度 最快 ,残局的增长速度最慢. 3) 伴随着深度的增加 ,要搜索的博弈树节点的 数目呈指数增长. 以中局节点数目增长最快 ,残局增 长速度最慢. 2. 2 静态分配策略 1) 固定时限制 :比较符合人类棋手的习惯. 缺点 是在中局搜索复杂局面的层数太浅 ,而简化的残局 常常可以搜得非常深. 2) 固定层数 :复杂局面每出一步棋 ,要花费较多 的时间搜索;而简单局面 ,如残局则很快出步. 3) 固定节点数 :不容易估计 ,复杂局面搜索层数 浅;简单局面搜索得过深. 静态分配策略的优点在于简单 ,易于实现. 缺点 是不灵活(需要事前固定搜索时间的长度 ,或搜索深 度 ,或节点数) 、分配不公(无法兼顾简单局面与复杂 局面) 、无法预测是否会超时或者有大量时间剩余. 上述方法应用于比赛显得太过粗糙 ,但在象棋程序 的开发与调试阶段 ,还是非常有用的. 3 时间的动态分配和调整策略 时间的静态分配策略缺乏自适应性 ,而动态分 配和调整策略则根据其策略目标 ,为每一步着法分 配不同的搜索时间. 其中 ,极为简单、有效的办法是 “平均配时”模型. 3. 1 “平均配时”模型分析 作为棋手或机器 ,下棋过程中必然时刻面对 2 个问题 : 1) 下阶段时间分配 :估计还有多少步 ,大致时间 · 04 · 智 能 系 统 学 报 第 1 卷

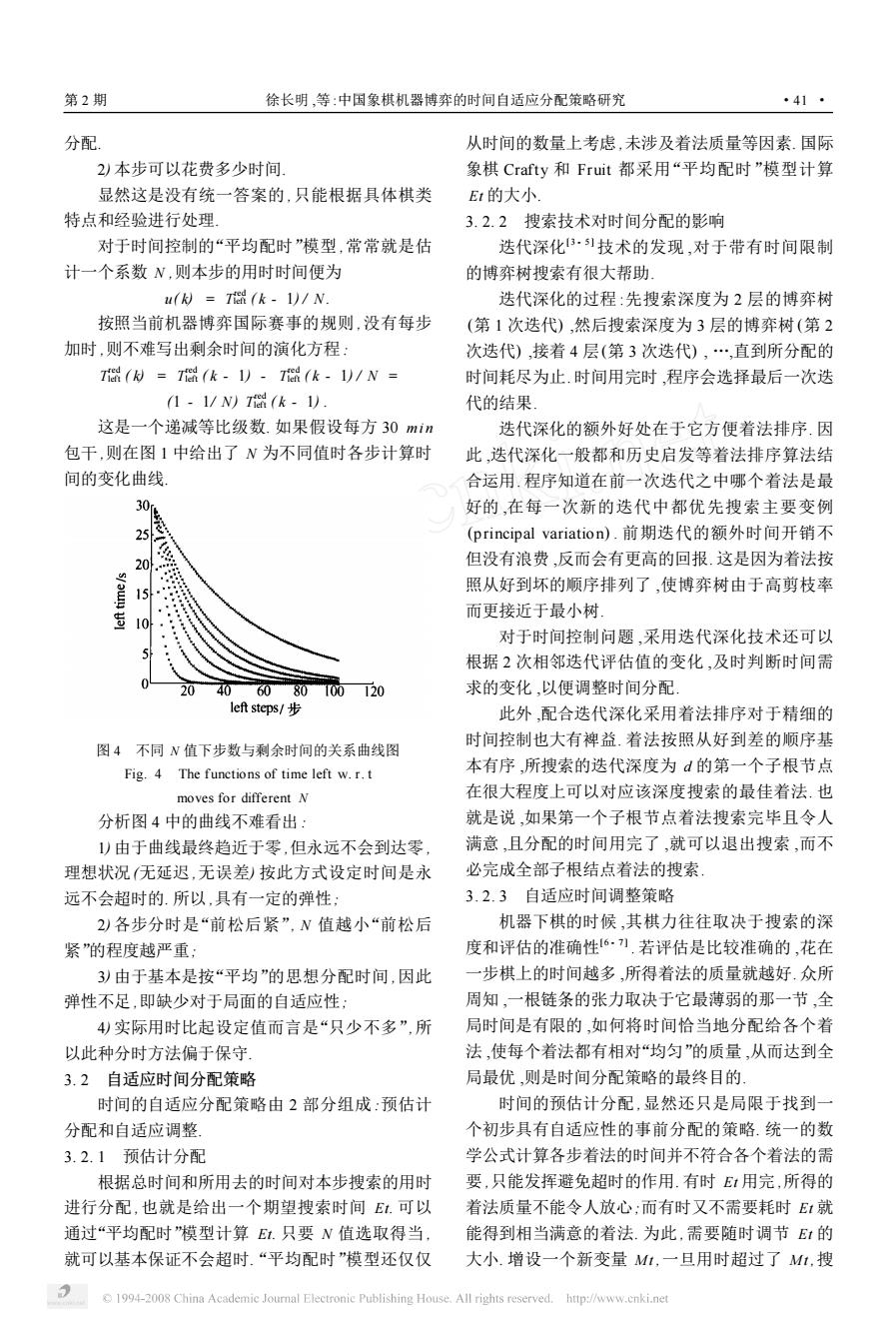
第2期 徐长明，等：中国象棋机器博弈的时间自适应分配策略研究 ·41· 分配 从时间的数量上考虑，未涉及着法质量等因素.国际 2)本步可以花费多少时间 象棋Crafty和Fruit都采用“平均配时”模型计算 显然这是没有统一答案的，只能根据具体棋类 E1的大小 特点和经验进行处理 3.2.2搜索技术对时间分配的影响 对于时间控制的“平均配时”模型，常常就是估 迭代深化)技术的发现，对于带有时间限制 计一个系数N,则本步的用时时间便为 的博弈树搜索有很大帮助」 ukd=Ti(k-1)/N」 迭代深化的过程：先搜索深度为2层的博弈树 按照当前机器博弈国际赛事的规则，没有每步 (第1次迭代)，然后搜索深度为3层的博弈树（第2 加时，则不难写出剩余时间的演化方程： 次迭代)，接着4层（第3次迭代），…，直到所分配的 I(付=T(k-1)-I(k-1)/N= 时间耗尽为止.时间用完时，程序会选择最后一次迭 1-1/N)T(k-1) 代的结果。 这是一个递减等比级数.如果假设每方30min 迭代深化的额外好处在于它方便着法排序.因 包干，则在图1中给出了N为不同值时各步计算时 此，迭代深化一般都和历史启发等着法排序算法结 间的变化曲线， 合运用.程序知道在前一次迭代之中哪个着法是最 30 好的，在每一次新的迭代中都优先搜索主要变例 25 (principal variation).前期迭代的额外时间开销不 20. 但没有浪费，反而会有更高的回报.这是因为着法按 15. 照从好到坏的顺序排列了，使博弈树由于高剪枝率 而更接近于最小树， 10 对于时间控制问题，采用迭代深化技术还可以 根据2次相邻迭代评估值的变化，及时判断时间需 20 40608010020 求的变化，以便调整时间分配 left steps/步 此外，配合迭代深化采用着法排序对于精细的 图4不同N值下步数与剩余时间的关系曲线图 时间控制也大有裨益.着法按照从好到差的顺序基 Fig.4 The functions of time left w.r.t 本有序，所搜索的迭代深度为d的第一个子根节点 moves for different N 在很大程度上可以对应该深度搜索的最佳着法.也 分析图4中的曲线不难看出： 就是说，如果第一个子根节点着法搜索完毕且令人 1)由于曲线最终趋近于零，但永远不会到达零， 满意，且分配的时间用完了，就可以退出搜索，而不 理想状况无延迟，无误差)按此方式设定时间是永 必完成全部子根结点着法的搜索 远不会超时的.所以，具有一定的弹性 3.2.3自适应时间调整策略 2)各步分时是“前松后紧”，N值越小“前松后 机器下棋的时候，其棋力往往取决于搜索的深 紧”的程度越严重， 度和评估的准确性6，刀.若评估是比较准确的，花在 3)由于基本是按“平均”的思想分配时间，因此 一步棋上的时间越多，所得着法的质量就越好.众所 弹性不足，即缺少对于局面的自适应性： 周知，一根链条的张力取决于它最薄弱的那一节，全 4)实际用时比起设定值而言是“只少不多”，所 局时间是有限的，如何将时间恰当地分配给各个着 以此种分时方法偏于保守 法，使每个着法都有相对“均匀"”的质量，从而达到全 3.2自适应时间分配策略 局最优，则是时间分配策略的最终目的 时间的自适应分配策略由2部分组成：预估计 时间的预估计分配，显然还只是局限于找到一 分配和自适应调整 个初步具有自适应性的事前分配的策略.统一的数 3.2.1预估计分配 学公式计算各步着法的时间并不符合各个着法的需 根据总时间和所用去的时间对本步搜索的用时 要，只能发挥避免超时的作用.有时E1用完，所得的 进行分配，也就是给出一个期望搜索时间E1.可以 着法质量不能令人放心；而有时又不需要耗时E1就 通过“平均配时”模型计算E1.只要N值选取得当， 能得到相当满意的着法.为此，需要随时调节E1的 就可以基本保证不会超时.“平均配时”模型还仅仅 大小.增设一个新变量M1,一旦用时超过了M1,搜 1994-2008 China Academie Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

分配. 2) 本步可以花费多少时间. 显然这是没有统一答案的 ,只能根据具体棋类 特点和经验进行处理. 对于时间控制的“平均配时”模型 ,常常就是估 计一个系数 N ,则本步的用时时间便为 u( k) = T red left ( k - 1) / N . 按照当前机器博弈国际赛事的规则 ,没有每步 加时 ,则不难写出剩余时间的演化方程 : T red left ( k) = T red left ( k - 1) - T red left ( k - 1) / N = (1 - 1/ N) T red left ( k - 1) . 这是一个递减等比级数. 如果假设每方 30 mi n 包干 ,则在图 1 中给出了 N 为不同值时各步计算时 间的变化曲线. 图 4 不同 N 值下步数与剩余时间的关系曲线图 Fig. 4 The functions of time left w. r. t moves for different N 分析图 4 中的曲线不难看出 : 1) 由于曲线最终趋近于零 ,但永远不会到达零 , 理想状况(无延迟 ,无误差) 按此方式设定时间是永 远不会超时的. 所以 ,具有一定的弹性; 2) 各步分时是“前松后紧”, N 值越小“前松后 紧”的程度越严重; 3) 由于基本是按“平均”的思想分配时间 ,因此 弹性不足 ,即缺少对于局面的自适应性; 4) 实际用时比起设定值而言是“只少不多”,所 以此种分时方法偏于保守. 3. 2 自适应时间分配策略 时间的自适应分配策略由 2 部分组成 :预估计 分配和自适应调整. 3. 2. 1 预估计分配 根据总时间和所用去的时间对本步搜索的用时 进行分配 ,也就是给出一个期望搜索时间 Et. 可以 通过“平均配时”模型计算 Et. 只要 N 值选取得当 , 就可以基本保证不会超时.“平均配时”模型还仅仅 从时间的数量上考虑 ,未涉及着法质量等因素. 国际 象棋 Crafty 和 Fruit 都采用“平均配时”模型计算 Et 的大小. 3. 2. 2 搜索技术对时间分配的影响 迭代深化[3 - 5 ] 技术的发现 ,对于带有时间限制 的博弈树搜索有很大帮助. 迭代深化的过程 :先搜索深度为 2 层的博弈树 (第 1 次迭代) ,然后搜索深度为 3 层的博弈树 (第 2 次迭代) ,接着 4 层(第 3 次迭代) , …,直到所分配的 时间耗尽为止. 时间用完时 ,程序会选择最后一次迭 代的结果. 迭代深化的额外好处在于它方便着法排序. 因 此 ,迭代深化一般都和历史启发等着法排序算法结 合运用. 程序知道在前一次迭代之中哪个着法是最 好的 ,在每一次新的迭代中都优先搜索主要变例 (principal variation) . 前期迭代的额外时间开销不 但没有浪费 ,反而会有更高的回报. 这是因为着法按 照从好到坏的顺序排列了 ,使博弈树由于高剪枝率 而更接近于最小树. 对于时间控制问题 ,采用迭代深化技术还可以 根据 2 次相邻迭代评估值的变化 ,及时判断时间需 求的变化 ,以便调整时间分配. 此外 ,配合迭代深化采用着法排序对于精细的 时间控制也大有裨益. 着法按照从好到差的顺序基 本有序 ,所搜索的迭代深度为 d 的第一个子根节点 在很大程度上可以对应该深度搜索的最佳着法. 也 就是说 ,如果第一个子根节点着法搜索完毕且令人 满意 ,且分配的时间用完了 ,就可以退出搜索 ,而不 必完成全部子根结点着法的搜索. 3. 2. 3 自适应时间调整策略 机器下棋的时候 ,其棋力往往取决于搜索的深 度和评估的准确性[ 6 - 7 ] . 若评估是比较准确的 ,花在 一步棋上的时间越多 ,所得着法的质量就越好. 众所 周知 ,一根链条的张力取决于它最薄弱的那一节 ,全 局时间是有限的 ,如何将时间恰当地分配给各个着 法 ,使每个着法都有相对“均匀”的质量 ,从而达到全 局最优 ,则是时间分配策略的最终目的. 时间的预估计分配 ,显然还只是局限于找到一 个初步具有自适应性的事前分配的策略. 统一的数 学公式计算各步着法的时间并不符合各个着法的需 要 ,只能发挥避免超时的作用. 有时 Et 用完 ,所得的 着法质量不能令人放心;而有时又不需要耗时 Et 就 能得到相当满意的着法. 为此 ,需要随时调节 Et 的 大小. 增设一个新变量 M t ,一旦用时超过了 M t ,搜 第 2 期 徐长明 ,等 :中国象棋机器博弈的时间自适应分配策略研究 · 14 ·

·42 智能系统学报 第1卷 索就要无条件停止.显然 此外，调整还可以依据其他的条件.比如，尽管 Etred MIred Ttotal (k)-Tusea (k -1), 连续的2次迭代之间的估值变差程度较大，但由于 u(k)Mtted. 本方原来的优势大，变化之后还是优于对手，那么可 Mt通常都是E1的若干倍.那么0，M)便是 以将时间延长的幅度适当缩小.总之，应该根据程序 E1的自适应调节范围， 执行过程中一些指标的变化灵活调整 一般只有在第一个子根节点着法是最佳着法， 自适应的调整策略严重依赖于评估.如果评估 且在多次迭代中都证明其足够好（如，没有Fail-low 不准确，或者由于评估模块的大量改动，可能会引起 过)的时候，才不需调整E1的大小 搜索用时的非正常波动.在对机器博弈软件的调试 在采用迭代深化的搜索算法的程序中，设搜索 过程中，曾发现由于评估的改动，导致一些平缓局面 深度为d时，得到的当前最佳着法的评估值为Eva. 在迭代深化的搜索过程中的Last_eva·Eva变化 而迭代深度为d.1的最佳着法评估值为Last 剧烈，从而使每步用时大量增加，最终超时，这是需 eva.则Last_eva-Eva反映了由d-l层迭代到d层 要注意的 的过程中，评估值变化的剧烈程度.为区别预估计分 4 时间控制策略的实现 配的Et,用新变量T表示调整之后的搜索时间，初 始时有T=E1.那么，用分段函数表示调整之后的时 为了进行时间控制，需要按前面讲述的过程进 间 行检查.若每搜索一个局面就检查一次，开销将非常 2 Et,0 Last_eva Eva <30 巨大，完全不符合象棋程序设计精打细算的特点.通 T=4Et,30 <Last eva Eva <70 常采用一个固定的节点数作为检测的单位，比如平 Mt,70≤Last_eva-Eva 均搜索速度约为100000节点/s的引擎，依据精度 注：分段函数中的评估值参照车静态子力值 要求设置每隔1000、5000、10000个节点检查一 1000)、马静态子力值400)、炮静态子力值440)、 次 兵静态子力值60)取值 还应注意到，时间分配与调整问题一方面与搜 从以上函数还可以看出，由于时间的预估计分 索和评估紧密相关，另一方面还与个人经验和喜好 配策略趋于保守，所以局面变差的时候，自适应调整 紧密相关，很难说哪个具体的时间分配和调整的方 策略可以视情况而成倍地增加搜索时间.与之相反， 案是最佳的.更确切地说，不同方案展现出不同的下 减少搜索用时应该是很谨慎的.一般只在没有风险 棋风格 或风险很小时，才减少搜索用时.下面列举几种这样 5 其他优化措施 的情况： 1)换子.对方子吃掉本方有根子，变为无根子的 在对手思考的时候，机器也可以猜测对方的应 时候，绝大多数情况都要吃掉对方子，几乎不需要多 着，并按照对方应着继续思索.如果猜测正确，那么 加考虑.但为了安全起见，可以稍用点时间继续推演 就极大地节省了时间，这种方法称为后台思考 几步.如，令搜索时间T=E/4. (Ponder).它相当于把对手的时间挪为己用，实践证 2)本方只有一个着法可选，也同样不需过多思 明是非常有效的 考，因为搜得再深也是徒劳.如，令搜索时间T= 丰富开局库，开局晚脱谱，也是节省时间的办 Ev/10 法；此外，中国象棋残局库尚不普及，目前大多数己 3)循环探测模块探测出了循环着法长将、长捉 有的残局库或多或少都存在不尽人意之处.开发出 等)，不再搜索，立刻出着。 实用的中国象棋残局库，在残局时利用残局库也有 4)能在未来连续几招之内将对方将死的着法称 同样的作用.使用数据库实质是将在线计算转化为 为杀棋.找到杀棋或自己被对方杀，不再继续搜索， 离线计算，变相地延伸了比赛时间」 立即出着」 在进行自适应调整策略的时候，要先判断是不 6结束语 是遇到了特殊情形.如果是，先按特殊情形调整，因 总结了合理分配和利用时间的方法，并建立了 为它们往往可以提前结束搜索：否则，按照分段函数 时间控制模型.实践表明，对于时间模型和配时策略 进行调整 应该给予足够的重视，这是在有限资源的条件下提 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

索就要无条件停止. 显然 , Et red < Mtred < T red total ( k) - T red used ( k - 1) , u( k) < Mtted . M t 通常都是 Et 的若干倍. 那么 (0 , M t) 便是 Et 的自适应调节范围. 一般只有在第一个子根节点着法是最佳着法 , 且在多次迭代中都证明其足够好(如 ,没有 Fail2low 过) 的时候 ,才不需调整 Et 的大小. 在采用迭代深化的搜索算法的程序中 ,设搜索 深度为 d 时 ,得到的当前最佳着法的评估值为 Eva. 而迭代深度为 d - 1 的最佳着法评估值为 Last _ eva. 则 Last_eva2Eva 反映了由 d - 1 层迭代到 d 层 的过程中 ,评估值变化的剧烈程度. 为区别预估计分 配的 Et ,用新变量 T 表示调整之后的搜索时间 ,初 始时有 T = Et. 那么 ,用分段函数表示调整之后的时 间 T = 2 Et , 0 < Last_eva2Eva < 30 4 Et , 30 ≤Last_eva2Eva < 70 Mt , 70 ≤Last_eva - Eva 注 :分 段 函 数 中 的 评 估 值 参 照 车 ( 静 态 子 力 值 1 000) 、马(静态子力值 400) 、炮(静态子力值 440) 、 兵(静态子力值 60) 取值. 从以上函数还可以看出 ,由于时间的预估计分 配策略趋于保守 ,所以局面变差的时候 ,自适应调整 策略可以视情况而成倍地增加搜索时间. 与之相反 , 减少搜索用时应该是很谨慎的. 一般只在没有风险 或风险很小时 ,才减少搜索用时. 下面列举几种这样 的情况 : 1) 换子. 对方子吃掉本方有根子 ,变为无根子的 时候 ,绝大多数情况都要吃掉对方子 ,几乎不需要多 加考虑. 但为了安全起见 ,可以稍用点时间继续推演 几步. 如 ,令搜索时间 T = Et/ 4. 2) 本方只有一个着法可选 ,也同样不需过多思 考 ,因为搜得再深也是徒劳. 如 , 令搜索时间 T = Et/ 10. 3) 循环探测模块探测出了循环着法(长将、长捉 等) ,不再搜索 ,立刻出着. 4) 能在未来连续几招之内将对方将死的着法称 为杀棋. 找到杀棋或自己被对方杀 ,不再继续搜索 , 立即出着. 在进行自适应调整策略的时候 ,要先判断是不 是遇到了特殊情形. 如果是 ,先按特殊情形调整 ,因 为它们往往可以提前结束搜索;否则 ,按照分段函数 进行调整. 此外 ,调整还可以依据其他的条件. 比如 ,尽管 连续的 2 次迭代之间的估值变差程度较大 ,但由于 本方原来的优势大 ,变化之后还是优于对手 ,那么可 以将时间延长的幅度适当缩小. 总之 ,应该根据程序 执行过程中一些指标的变化灵活调整. 自适应的调整策略严重依赖于评估. 如果评估 不准确 ,或者由于评估模块的大量改动 ,可能会引起 搜索用时的非正常波动. 在对机器博弈软件的调试 过程中 ,曾发现由于评估的改动 ,导致一些平缓局面 在迭代深化的搜索过程中的 Last _eva - Eva 变化 剧烈 ,从而使每步用时大量增加 ,最终超时 ,这是需 要注意的. 4 时间控制策略的实现 为了进行时间控制 ,需要按前面讲述的过程进 行检查. 若每搜索一个局面就检查一次 ,开销将非常 巨大 ,完全不符合象棋程序设计精打细算的特点. 通 常采用一个固定的节点数作为检测的单位 ,比如平 均搜索速度约为 100 000 节点/ s 的引擎 ,依据精度 要求设置每隔 1 000、5 000、10 000 个节点检查一 次. 还应注意到 ,时间分配与调整问题一方面与搜 索和评估紧密相关 ,另一方面还与个人经验和喜好 紧密相关 ,很难说哪个具体的时间分配和调整的方 案是最佳的. 更确切地说 ,不同方案展现出不同的下 棋风格. 5 其他优化措施 在对手思考的时候 ,机器也可以猜测对方的应 着 ,并按照对方应着继续思索. 如果猜测正确 ,那么 就极大地节省了时间 , 这种方法称为后台思考 (Ponder) . 它相当于把对手的时间挪为己用 ,实践证 明是非常有效的. 丰富开局库 ,开局晚脱谱 ,也是节省时间的办 法 ;此外 ,中国象棋残局库尚不普及 ,目前大多数已 有的残局库或多或少都存在不尽人意之处. 开发出 实用的中国象棋残局库 ,在残局时利用残局库也有 同样的作用. 使用数据库实质是将在线计算转化为 离线计算 ,变相地延伸了比赛时间. 6 结束语 总结了合理分配和利用时间的方法 ,并建立了 时间控制模型. 实践表明 ,对于时间模型和配时策略 应该给予足够的重视 ,这是在有限资源的条件下提 · 24 · 智 能 系 统 学 报 第 1 卷

第2期 徐长明，等：中国象棋机器博弈的时间自适应分配策略研究 ·43· 高棋力的一个有效措施.此外，时间分配和调整也是 作者简介： 对弈风格的一种体现 徐长明，男，1978年生，博士研究生 主要从事中国象棋的机器博弈、计算机网 参考文献： 络等的研究。Email:changmingxu@ []黄晨.解剖大象的眼睛一中国象棋程序设计探索 gmail.com EB/OL ]http:/www.elephantbase.net/computer/ele- eye_ponder.htm.2005.11. [2]王孔兴.象棋竞赛裁判手册[M].北京：人民体育出版社， 南晓斐，女，1983年生，硕士研究生。 2001 主要从事机器博弈的研究。 [3]SCHAEFFER J.The history heuristic and alphar beta search enhancements in practice[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11 (11):1203.1212. (4]REIN EFELD A,MARSLAND T A.Enhanced iterative deepening search [J].IEEE Transactions on Pattern A- 王骄，男，1978年生，博士研究 nalysis and Machine Intelligence,1994,7(7):701-710. [5]KORF R E,REID M,EDEL KAMP S.Time complexity 生，研究方向为人工智能与机器博奔。 of iterative-deepeningA[J].Artificial Intelligence,2001, 129(1.2):199.218. [6]徐心和，王骄.中国象棋计算机博弈关键技术分析U], 小型微型计算机系统，2006,27(6)：961,969 XU Xinhe,WANG Jiao.Key technologies analysis of chinese chess computer game [J].Mini-Micro Systems. 徐心和，男，1940年生，教授，博士 2006,27(6):961-969. 生导师，研究方向为控制理论与应用、系 [7]王小春.PC游戏编程[M].重庆：重庆大学出版社， 统仿真、智能机器人机器博弈等】 2002. 计算机应用研究 昂用0▣出网 ®发代安 62-68 中国科技核心期刊 全国中文核心期刊 中国科技论文统计源期刊 2007年扩容 大16开本 中国计算机学会会刊 内文320页 中国期刊方阵双效期刊 中国科学引文数据库来源期刊 高档纸张 订价每月30元 第二属国家期刊奖百种重点科技期刊 精美印制 全年360元 欢迎赐璃 欢迎订阅 地址：成都市成料西路3号邮编：610041电话：028-85249567 网址：Wwwa0cmg.00m 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

高棋力的一个有效措施. 此外 ,时间分配和调整也是 对弈风格的一种体现. 参考文献 : [1 ]黄 晨. 解剖大象的眼睛 ———中国象棋程序设计探索 [ EB/ OL ]. http :/ / www. elephantbase. net/ computer/ ele2 eye_ponder. htm. 2005. 11. [2 ]王孔兴. 象棋竞赛裁判手册[ M]. 北京 :人民体育出版社 , 2001. [3 ] SCHA EFFER J. The history heuristic and alpha2beta search enhancements in practice [J ]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 1989 , 11 (11) : 1203 - 1212. [4 ]REIN EFELD A , MARSLAND T A. Enhanced iterative2 deepening search [J ]. IEEE Transactions on Pattern A2 nalysis and Machine Intelligence , 1994 ,7 (7) :701 - 710. [5 ] KORF R E , REID M , EDEL KAMP S. Time complexity of iterative2deepening2A [J ]. Artificial Intelligence ,2001 , 129 (1 - 2) :199 - 218. [6 ]徐心和 ,王 骄. 中国象棋计算机博弈关键技术分析[J ]. 小型微型计算机系统 ,2006 ,27 (6) :961 - 969. XU Xinhe , WAN G Jiao. Key technologies analysis of chinese chess computer game [J ]. Mini2Micro Systems. 2006 ,27 (6) :961 - 969. [7 ] 王小春. PC 游戏编程 [ M ]. 重庆 : 重庆大学出版社 , 2002. 作者简介 : 徐长明 ,男 ,1978 年生 ,博士研究生 , 主要从事中国象棋的机器博弈、计算机网 络等 的 研 究。E2mail : changmingxu @ gmail. com 南晓斐 ,女 , 1983 年生 ,硕士研究生 , 主要从事机器博弈的研究。 王 骄 ,男 , 1978 年生 ,博士研究 生 ,研究方向为人工智能与机器博弈。 徐心和 ,男 ,1940 年生 ,教授 ,博士 生导师 ,研究方向为控制理论与应用、系 统仿真、智能机器人、机器博弈等. 第 2 期 徐长明 ,等 :中国象棋机器博弈的时间自适应分配策略研究 · 34 ·