
第2卷第2期 智能系统学报 Vol.2 Na 2 2007年4月 CAAI Transactions on Intelligent Systems Apr.2007 基于动态RBF神经网络的板形板 厚综合控制仿真研究 张秀玲,张志强 (燕山大学电气工程学院,河北秦皇岛066004) 摘要:基于RBF神经网络的特点提出了一种动态调节隐含层隐节点个数的方法,由2部分组成:首先以网络输出 数据的均方误差及其变化率为标准来调节隐含层节点的数目,然后调节优化隐含层节点的中心值,根据广义逆矩阵 的方法求出输出层权值.所设计的神经网络具有最少的隐含层节点数,提高了学习训练速度,构造了板形板厚综合 控制的数学模型,采用新的模型处理方法,用动态BF神经网络进行控制仿真,取得了理想的结果 关键词BF网络;动态设计;逆矩阵:板形板厚综合控制 中图分类号:TP183文献标识码:A文章编号:16734785(2007)02-006504 Simulation research on strip flatness and thickness control based on dynamic RBF neural net works ZHAN G Xiur-ling,ZHAN G Zhi-qiang (College of Electrical Engineering,Yanshan University,Qinhuangdao 066004,China) Abstract:A method to dynamically adjust the number of hidden layer nodes is proposed based on features of the RBFNN,which includes two parts:the first part is to adjust the number of hidden layer nodes based on the mean square error and change rate of network output data,and the second part is to optimize the central value of the hidden layer and find the output layer's weights based on the generalized inverse ma- trix.The newly designed RBFNN has least nodes of hidden layers and higher training speed.A mathemat- ical model for controlling strip flatness and thickness is proposed.Control simulation is executed with dy- namic RBF neural network based on new model,receiving an ideal result. Key words:RBFNN:dynamic design;inverse matrix;integrated control of strip flatness and thickness RBF神经网络是一种前向神经网络,和其他前 隐含层输出层组成.输入层把输入数据直接映射到 向网络相比,具有结构简单,全局逼近能力强,训练 隐含层;隐含层神经元的作用函数为径向对称的径 方法快速易行的优点山.RBF神经网络所研究的核 向基函数,输出层神经元的作用函数为简单的线性 心问题是确定隐含层节点数和相应数据中心以及确 函数,对隐含层神经元的输出数据进行线性加权后 定隐含层的输出权值,本文根据RBF神经网络这些 输出 特点,设计了一种动态确定隐含层节点数的方法,达 到了期望的目标,同时神经网络隐含层具有最少节 点,结构最简单;用提出的新方法设计了板形板厚综 合控制系统,进行了仿真研究, 1 RBF神经网络的结构 RBF神经网络的结构如图1所示,由输入层、 图1RBF神经网络结构图 Fig 1 Structure of RBF neural network 收稿日期:200611-04 基金项目:因家自然科学基金资助项目(50374058);燕山大学博士基 只有当输入信号在靠近作用函数的中心范围 金资助项目(B70). 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
第 2 卷第 2 期 智 能 系 统 学 报 Vol. 2 №. 2 2007 年 4 月 CAA I Transactions on Intelligent Systems Apr. 2007 基于动态 RBF 神经网络的板形板 厚综合控制仿真研究 张秀玲 ,张志强 (燕山大学 电气工程学院 ,河北 秦皇岛 066004) 摘 要 :基于 RBF 神经网络的特点提出了一种动态调节隐含层隐节点个数的方法 ,由 2 部分组成 :首先以网络输出 数据的均方误差及其变化率为标准来调节隐含层节点的数目 ,然后调节优化隐含层节点的中心值 ,根据广义逆矩阵 的方法求出输出层权值. 所设计的神经网络具有最少的隐含层节点数 ,提高了学习训练速度 ,构造了板形板厚综合 控制的数学模型 ,采用新的模型处理方法 ,用动态 RBF 神经网络进行控制仿真 ,取得了理想的结果. 关键词 :BF 网络 ;动态设计 ;逆矩阵 ;板形板厚综合控制 中图分类号 : TP183 文献标识码 :A 文章编号 :167324785 (2007) 0220065204 Simulation research on strip flatness and thickness control based on dynamic RBF neural networks ZHAN G Xiu2ling ,ZHAN G Zhi2qiang (College of Electrical Engineering , Yanshan University , Qinhuangdao 066004 , China) Abstract :A met hod to dynamically adjust t he number of hidden layer nodes is proposed based on feat ures of t he RBFNN , which includes two parts : t he first part is to adjust t he number of hidden layer nodes based on t he mean square error and change rate of network outp ut data , and the second part is to optimize t he central value of t he hidden layer and find t he outp ut layer’s weights based on t he generalized inverse ma2 trix. The newly designed RBFNN has least nodes of hidden layers and higher training speed. A mat hemat2 ical model for controlling strip flat ness and t hickness is proposed. Control simulation is executed wit h dy2 namic RBF neural network based on new model , receiving an ideal result. Keywords :RBFNN ; dynamic design ; inverse matrix ; integrated control of strip flat ness and t hickness 收稿日期 :2006211204. 基金项目 :国家自然科学基金资助项目(50374058) ;燕山大学博士基 金资助项目(B70) . RBF 神经网络是一种前向神经网络 ,和其他前 向网络相比 ,具有结构简单 ,全局逼近能力强 ,训练 方法快速易行的优点[1 ] . RBF 神经网络所研究的核 心问题是确定隐含层节点数和相应数据中心以及确 定隐含层的输出权值 ,本文根据 RBF 神经网络这些 特点 ,设计了一种动态确定隐含层节点数的方法 ,达 到了期望的目标 ,同时神经网络隐含层具有最少节 点 ,结构最简单 ;用提出的新方法设计了板形板厚综 合控制系统 ,进行了仿真研究. 1 RBF 神经网络的结构 RBF 神经网络的结构如图 1 所示 ,由输入层、 隐含层、输出层组成. 输入层把输入数据直接映射到 隐含层 ;隐含层神经元的作用函数为径向对称的径 向基函数 ,输出层神经元的作用函数为简单的线性 函数 ,对隐含层神经元的输出数据进行线性加权后 输出. 图 1 RBF 神经网络结构图 Fig11 Structure of RBF neural network 只有当输入信号在靠近作用函数的中心范围

·66· 智能系统学报 第2卷 时,隐含层节点才会产生较大的输出.隐含层中的径 T次学习后,计算e,D. 向基函数一般取为高斯函数: 2)如果eD,则说明网络结构很 据,只有在靠近中心的一小部分才被激活. 好,此时结构不变,即m=m. 输出层是对隐含层输出数据的线性映射,即 6)如果D20为给定的收敛阈值.动态结构的RBF神经网 由于当数据中心和高斯函数的宽度确定以后, 络算法可以归纳为 整个RBF网络从输入到输出就成为一个线性方程 1)首先给定初始隐含层节点数m,在网络经过 组,因此可以通过求逆矩阵的方法来确定网络的输 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
时 ,隐含层节点才会产生较大的输出. 隐含层中的径 向基函数一般取为高斯函数 : Ri ( x) = exp [ - ‖x - ci ‖2 / 2σ2 i ] , i = 1 ,2 , …, m. (1) 式中 : x 为输入向量 , ci 隐含层节点数据中心 ,σi 作 用函数所围绕中心点的宽度 , m 为隐含层节点的数 目 ,即数据中心数目 , ‖x - ci ‖为向量范数 ,表示欧 式距离. Ri ( x) 在 x = ci 时有唯一的最大值 ,随着范数的 增大 ,输出迅速地衰减到零. 因此对于给定的输入数 据 ,只有在靠近中心的一小部分才被激活. 输出层是对隐含层输出数据的线性映射 ,即 yk = ∑ m i =1 ωik R i ( x) k = 1 ,2 , …, p. (2) 式中 : p 为输出节点数 ,ωik为输出层的权值. 当隐含层节点数目比较少的时候虽然能提高系 统速度 ,但是不能达到预期效果 ,当隐含层的节点数 目较多时 ,虽然能逼近目标函数 ,但训练时间较长 , 增加了系统的冗余度 ;因此如何确定隐含层节点数 和数据中心成为 RBF 神经网络设计的重点与难点 , 本文就此问题进行了深入研究. 2 动态 RBF 神经网络的设计 整个设计过程分为 2 步进行 :首先是动态设计 RBF 的隐含层节点数目 ,可以采用随机算法选取 RBF 中心[ 2 ] ,其次是采用优化方法进行数据中心和 输出权值的优化. 211 隐含层节点数的动态设计 所谓动态 RBF 神经网络指的是在学习训练过 程中 ,隐含层的节点数目不断变化 ,结构呈现为动态 的神经网络 ,设计这种网络的目的是使网络性能在 训练过程中始终保持最优 ,最终达到最佳结构[ 3 ] . 在隐含层动态设计中 ,用网络输出的均方误差 作为网络性能评判标准 ,表达式为 e = ∑ q j = 1 ∑ p k = 1 ( ykj - y d kj ) 2 / q. (3) 式中 : q 为网络训练样本数 , ykj为输出层中第 k 个节 点的实际输出 , y d kj为输出层中第 k 个节点的期望输 出值. 在 RBF 网络训练过程中 ,经过一定的学习次 数 , T 后计算 e 和 e 的衰减率 D ,假设 D1 和 D2 分别 为在 T 次学习前和学习后的衰减率 , Ds , Df 为 2 个 给定的衰减率阈值 ,分别表示最慢和最快的衰减率. ε> 0 为给定的收敛阈值. 动态结构的 RBF 神经网 络算法可以归纳为 1) 首先给定初始隐含层节点数 m ,在网络经过 T 次学习后 ,计算 e , D1 . 2) 如果 e Df ,则说明网络结构很 好 ,此时结构不变 ,即 m = m. 6) 如果 D2 < Df ,并且 D2 < Ds ,则说明网络性 能比较差 ,不能达到期望的要求 ,此时需要增加隐含 层的节点数 ,即 m = m + 1. 7) 如果 Ds < D2 < D1 ,则说明网络性能比较差 , 需要增加节点 ,即 m = m + 1. 8) 当增加节点的时候 ,与之相连的输出权值取 很小或者为零 ,当删去节点的时候 ,删去输出均方值 最小的节点. 212 数据中心和输出权值的优化调整 21211 数据中心的优化 由于在动态设计隐含层节点数时所用的数据中 心来自于样本输入 ,并且在网络训练中该数据保持 固定不变 ,因此该数据中心可能离最优数据中心有 一定的偏差 ,为了校正这一偏差 ,需要对高斯函数的 中心进行调整和优化. 由于隐含层用的径向基函数 是高斯函数 ,只对数据中心附近的数据产生较大的 响应 ,因此在优化的时候就以数据中心周围的部分 样本为目标样本来调节该数据中心的值[4 ] . 假设某 隐含层节点的数据中心是 ci ,函数宽度为σi ,那么参 与调节的目标样本为 Xi = { ( x j , y j) | ‖x j - ci ‖ < kσi , j = 1 ,2 , …, n} . (4) k 值越大 ,则参与优化数据中心的数据就越多 , 假定( x j , yj) 是参与优化数据中心的一个样本 ,那么 数据中心对该样本的调节量为 Δci ( x j , yj) = 4 η δi Rc i ( x j) ( y j - y ( x j) )ωi . (5) 式中 :η为学习系数. 于是数据中心可用式(6) 来调整确定 : ci = ci +Δci ( x j , yj) . (6) 21212 输出权值的求解和优化 由于当数据中心和高斯函数的宽度确定以后 , 整个 RBF 网络从输入到输出就成为一个线性方程 组 ,因此可以通过求逆矩阵的方法来确定网络的输 ·66 · 智 能 系 统 学 报 第 2 卷

第2期 张秀玲,等:基于动态BF神经网络的板形板厚综合控制仿真研究 *67* 出权值.即 4)按照动态设计网络隐含层的方法训练网络, @R'y=(RTRRTy. (7) 直到隐含层节点数目达到要求为止: 式中y是RBF网络的期望输出 5)根据式(5)和式(6)优化调整隐含层节点的数 把权值看作是关于误差的函数,可用式8)对求 据中心, 出的权值进一步优化: 6)根据式(7)和式(8)优化调整隐含层输出权 方=ω+f(y%·y) 8) 值; 综上所述,BF神经网络的动态设计步骤如下: 7)算法结束 1)初始化隐含层节点个数; 3 2)应用随机算法选取RBF高斯函数的数据中 板形板厚综合控制模型 心 当机架具有工作辊弯辊板形控制和液压压下板 3)求取高斯函数的宽度; 厚控制时,板形板厚综合控制数学模型为 △h=Cp+ 9) (10) 式中:△S为辊缝的变化量,△P为轧制力的变化量,轧机,保持板形板厚综合控制数学模型的输出达到 △F为工作辊弯辊力的变化量,C为轧机纵向刚度 控制要求 系数,Cr为弯辊刚度系数,△,△G为入口、出口横 4 向张力差的改变量,H,h来料和轧后的平均厚度,E 仿真研究 为轧件的弹性模数,K为轧机横向刚度系数,K 首先,BF神经网络采用双输入双输出结构进 为横向弯辊刚度系数,△H:为轧件出口横向厚差的 行训练,输入为△H和△④,输出为△F和△S,取神 改变量,Q为轧件塑性系数 经网络具有10个隐含节点,每个隐含节点中具有2 控制的预期目标是使△h=0,△g=0,因此,令 个数据中心,分别对应输入中的△H和△④,隐含层 △h,△G均为0,将参数:△h=0,△G=0,Cp=30, 节点的输出为该节点中2个高斯函数的输出之和, Cr=28,Kr=2.6,Kp=14,Q=9.3,h=1.35,H= 采用50组数据按照上面方法进行训练,训练后发现 3,E=13.051,代入式9)和(10)得: 用8个节点就可以达到期望的效果,训练后的RBF △S+0.35714826AF=-0.31△H. (11) 神经网络数据中心和输出层权值经过优化以后如表 -0.05452563△S+0.40408882△F= 1所示 -0.05452563△H-0.45△Ha+0.10344828△④」 (12) 表1RBF神经网络的参数 1 0.35714826「△ Table 1 Parameters of RBF neural network 即 -0.054525630.40408882L△日 数据中心 输出权值 -0.31△H 064278761 001285575 1.11200181 002224004 L-0.05452563△H-0.45△H:+0.10344828△ 13) 098480775 001969616 204312282 004086246 通过矩阵求逆,得 [△「0.95402461-0.84318857 086602540001732051 -232829984-004656600 L△日L0.12873108 2.36109280J 034202014 000684040-023561254-000471225 -031△H -005452563△H-045△Ha+010344828△J -034202014-000684040 0235612540004712250 14) -086602540-001732051 232829984004656600 设△H=0.02sin(u),△Ha=0.01sin(w),△6= sin()于是,式(13)和(14)化简为 -098480775-001969616 .204312282-004086246 △S=-0.08842750sin(ut 15) -064278761.001285575-1.11200181-002224004 △F=0.23023700sin(ot). (16) 因此,在干扰作用下,通过采用RBF神经网络控制 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
出权值. 即 ω = R + y = ( R T R) - 1 R T y. (7) 式中 : y 是 RBF 网络的期望输出. 把权值看作是关于误差的函数 ,可用式(8) 对求 出的权值进一步优化 : ω = ω+ f ( ykj - y d kj ) . (8) 综上所述 ,RBF 神经网络的动态设计步骤如下 : 1) 初始化隐含层节点个数 ; 2) 应用随机算法选取 RBF 高斯函数的数据中 心 ; 3) 求取高斯函数的宽度 ; 4) 按照动态设计网络隐含层的方法训练网络 , 直到隐含层节点数目达到要求为止 ; 5) 根据式(5) 和式(6) 优化调整隐含层节点的数 据中心 ; 6) 根据式 (7) 和式 (8) 优化调整隐含层输出权 值 ; 7) 算法结束. 3 板形板厚综合控制模型 当机架具有工作辊弯辊板形控制和液压压下板 厚控制时 ,板形板厚综合控制数学模型为[6 ] Δh = CP CP + Q ΔS + Q CP + Q ΔH + CP CP + Q × ΔF CF . (9) Δσ1 = E h 1 KP × CP CP + Q (ΔH - ΔS) - 1 KP × CP CP + Q × 1 CF + 1 KF ΔF - h H ΔHd + h E Δσ0 . (10) 式中 :ΔS 为辊缝的变化量 ,ΔP 为轧制力的变化量 , ΔF 为工作辊弯辊力的变化量 , CP 为轧机纵向刚度 系数 , CF 为弯辊刚度系数 ,Δσ0 ,Δσ1 为入口、出口横 向张力差的改变量 , H , h 来料和轧后的平均厚度 , E 为轧件的弹性模数 , KP 为轧机横向刚度系数 , KF 为横向弯辊刚度系数 ,ΔHd 为轧件出口横向厚差的 改变量 , Q 为轧件塑性系数. 控制的预期目标是使Δh = 0 ,Δσ1 = 0 ,因此 ,令 Δh ,Δσ1 均为 0 ,将参数 :Δh = 0 ,Δσ1 = 0 , CP = 30 , CF = 218 , KF = 2. 6 , KP = 14 , Q = 913 , h = 1135 , H = 3 , E = 13105 [6 ] ,代入式(9) 和(10) 得 : ΔS + 01357 148 26ΔF = - 0131ΔH. (11) - 01054 525 63ΔS + 01404 088 82ΔF = - 01054 525 63ΔH - 0145ΔHd + 01103 448 28Δσ0 . (12) 即 1 01357 148 26 - 01054 525 63 01404 088 82 ΔS ΔF = - 0131ΔH - 01054 525 63ΔH - 0145ΔHd + 01103 448 28Δσ0 . (13) 通过矩阵求逆 ,得 ΔS ΔF = 01954 024 61 - 01843 188 57 01128 731 08 21361 092 80 × - 0131ΔH - 01054 525 63ΔH - 0145ΔHd + 0110344828Δσ0 . (14) 设ΔH = 0102sin (ωt) ,ΔHd = 0101sin (ωt) ,Δσ0 = sin (ωt) 于是 ,式(13) 和(14) 化简为 ΔS = - 01088 427 50sin (ωt) . (15) ΔF = 01230 237 00sin (ωt) . (16) 因此 ,在干扰作用下 ,通过采用 RBF 神经网络控制 轧机 ,保持板形板厚综合控制数学模型的输出达到 控制要求. 4 仿真研究 首先 ,RBF 神经网络采用双输入双输出结构进 行训练 ,输入为ΔH 和Δσ0 ,输出为ΔF 和ΔS ,取神 经网络具有 10 个隐含节点 ,每个隐含节点中具有 2 个数据中心 ,分别对应输入中的ΔH 和Δσ0 ,隐含层 节点的输出为该节点中 2 个高斯函数的输出之和 , 采用 50 组数据按照上面方法进行训练 ,训练后发现 用 8 个节点就可以达到期望的效果 ,训练后的 RBF 神经网络数据中心和输出层权值经过优化以后如表 1 所示. 表 1 RBF神经网络的参数 Table 1 Parameters of RBF neural network 数据中心 输出权值 01642 787 61 01012 855 75 11112 001 81 01022 240 04 01984 807 75 01019 696 16 21043 122 82 01040 862 46 01866 025 40 01017 320 51 - 21328 299 84 - 01046 566 00 01342 020 14 01006 840 40 - 01235 612 54 - 01004 712 25 - 01342 020 14 - 01006 840 40 01235 612 54 01004 712 250 - 01866 025 40 - 01017 320 51 21328 299 84 01046 566 00 - 01984 807 75 - 01019 696 16 - 21043 122 82 - 01040 862 46 - 01642 787 61 - 01012 855 75 - 11112 001 81 - 01022 240 04 第 2 期 张秀玲 ,等 :基于动态 RBF 神经网络的板形板厚综合控制仿真研究 ·67 ·
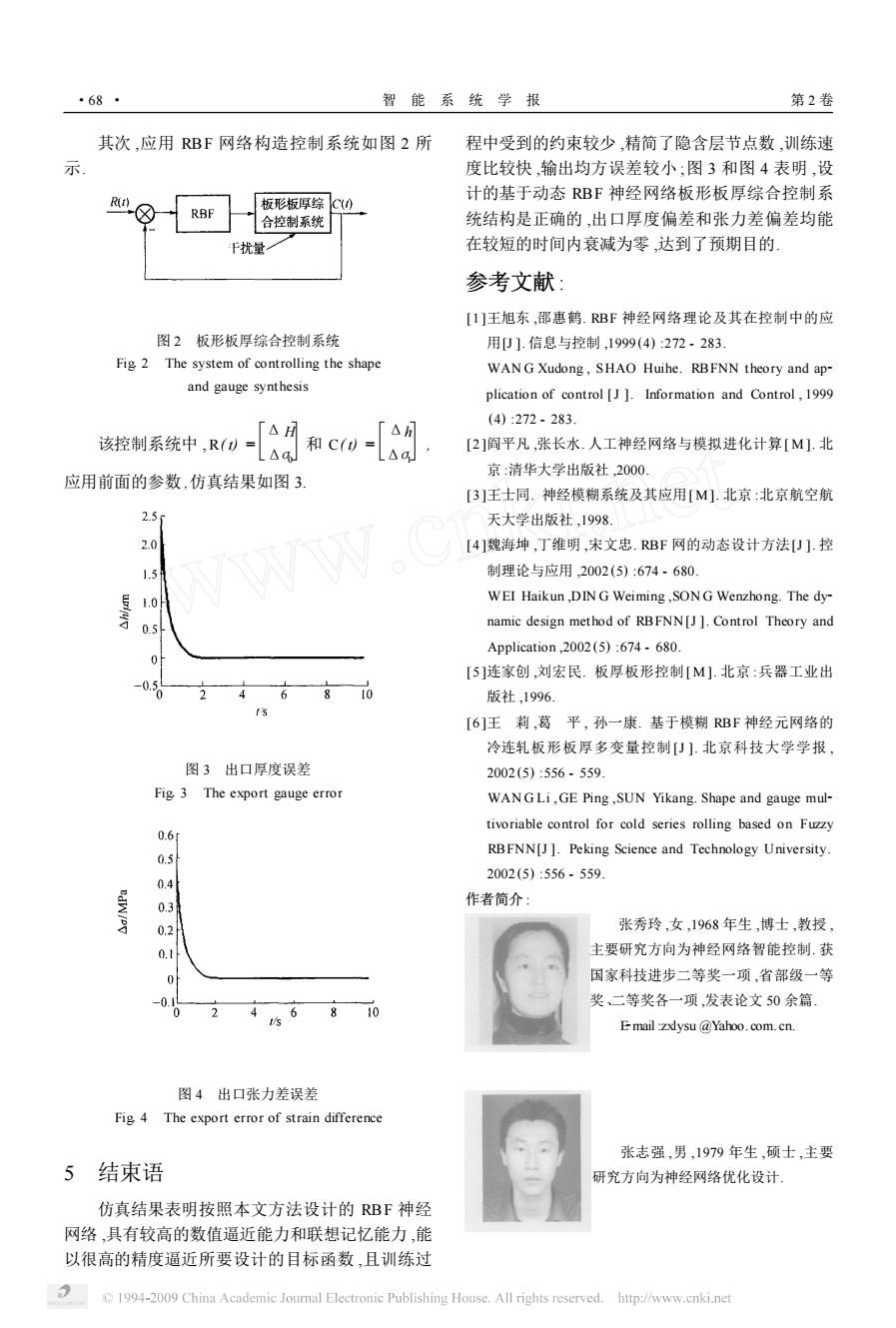
·68 智能系统学报 第2卷 其次,应用RBF网络构造控制系统如图2所 程中受到的约束较少,精简了隐含层节点数,训练速 度比较快,输出均方误差较小:图3和图4表明,设 计的基于动态RBF神经网络板形板厚综合控制系 R(n 板形板厚综C(0 RBF 合控制系统 统结构是正确的,出口厚度偏差和张力差偏差均能 F扰量 在较短的时间内衰减为零,达到了预期目的 参考文献: [1]王旭东,邵惠鹤.RBF神经网络理论及其在控制中的应 图2板形板厚综合控制系统 用U].信息与控制,1999(4):272.283. Fig 2 The system of controlling the shape WANG Xudong,SHAO Huihe.RBFNN theory and ap- and gauge synthesis plication of control [J].Information and Control,1999 (4):272.283 △H △h 该控制系统中,R()= 和C()= △J △4J [2]阎平凡,张长水.人工神经网络与模拟进化计算[M].北 京:清华大学出版社,2000。 应用前面的参数,仿真结果如图3 [3]王士同.神经模糊系统及其应用[M].北京:北京航空航 2.5 天大学出版社,1998. 2.0 4]魏海坤,丁维明,宋文忠.RBF网的动态设计方法[卩].控 1.5 制理论与应用,2002(5):674.680. 1.0 WEI Haikun ,DIN G Weiming,SONG Wenzhong.The dy- 0.5 namic design method of RBFNN[J].Control Theory and Application,2002(5):674-680. [5]连家创,刘宏民.板厚板形控制[M].北京:兵器工业出 4680 版社,1996. t's [6]王莉,葛平,孙一康.基于模糊BF神经元网络的 冷连轧板形板厚多变量控制[U].北京科技大学学报, 图3出口厚度误差 2002(5):556.559 Fig,3 The export gauge error WANGLi,GE Ping,SUN Yikang.Shape and gauge mul- tivoriable control for cold series rolling based on Fuzzy 0.61 RBFNN[J].Peking Science and Technology University. 0.4 2002(5):556.559 0.3 作者简介: 0.2 张秀玲,女,1968年生,博士,教授, 0.1 主要研究方向为神经网络智能控制.获 国家科技进步二等奖一项,省部级一等 -0. 奖、二等奖各一项,发表论文50余篇 4 .6 8 10 E mail :zxlysu @Yahoo.com.cn 图4出口张力差误差 Fig 4 The export error of strain difference 张志强,男,1979年生,硕士,主要 5结束语 研究方向为神经网络优化设计 仿真结果表明按照本文方法设计的RBF神经 网络,具有较高的数值逼近能力和联想记忆能力,能 以很高的精度逼近所要设计的目标函数,且训练过 1994-2009 China Academic Joural Electronic Publishing House.All rights reserved.http://www.cnki.net
其次 ,应用 RBF 网络构造控制系统如图 2 所 示. 图 2 板形板厚综合控制系统 Fig12 The system of controlling the shape and gauge synthesis 该控制系统中 , R( t) = ΔH Δσ0 和 C( t) = Δh Δσ1 , 应用前面的参数 ,仿真结果如图 3. 图 3 出口厚度误差 Fig13 The export gauge error 图 4 出口张力差误差 Fig14 The export error of strain difference 5 结束语 仿真结果表明按照本文方法设计的 RBF 神经 网络 ,具有较高的数值逼近能力和联想记忆能力 ,能 以很高的精度逼近所要设计的目标函数 ,且训练过 程中受到的约束较少 ,精简了隐含层节点数 ,训练速 度比较快 ,输出均方误差较小 ;图 3 和图 4 表明 ,设 计的基于动态 RBF 神经网络板形板厚综合控制系 统结构是正确的 ,出口厚度偏差和张力差偏差均能 在较短的时间内衰减为零 ,达到了预期目的. 参考文献 : [1 ]王旭东 ,邵惠鹤. RBF 神经网络理论及其在控制中的应 用[J ]. 信息与控制 ,1999 (4) :272 - 283. WAN G Xudong , SHAO Huihe. RBFNN theory and ap2 plication of control [J ]. Information and Control , 1999 (4) :272 - 283. [2 ]阎平凡 ,张长水. 人工神经网络与模拟进化计算[ M ]. 北 京 :清华大学出版社 ,2000. [3 ]王士同. 神经模糊系统及其应用[ M ]. 北京 :北京航空航 天大学出版社 ,1998. [4 ]魏海坤 ,丁维明 ,宋文忠. RBF 网的动态设计方法[J ]. 控 制理论与应用 ,2002 (5) :674 - 680. WEI Haikun ,DIN G Weiming ,SON G Wenzhong. The dy2 namic design method of RBFNN[J ]. Control Theory and Application ,2002 (5) :674 - 680. [5 ]连家创 ,刘宏民. 板厚板形控制[ M ]. 北京 :兵器工业出 版社 ,1996. [6 ]王 莉 ,葛 平 , 孙一康. 基于模糊 RBF 神经元网络的 冷连轧板形板厚多变量控制[J ]. 北京科技大学学报 , 2002 (5) :556 - 559. WAN G Li , GE Ping ,SUN Yikang. Shape and gauge mul2 tivoriable control for cold series rolling based on Fuzzy RBFNN[J ]. Peking Science and Technology University. 2002 (5) :556 - 559. 作者简介 : 张秀玲 ,女 ,1968 年生 ,博士 ,教授 , 主要研究方向为神经网络智能控制. 获 国家科技进步二等奖一项 ,省部级一等 奖、二等奖各一项 ,发表论文 50 余篇. E2mail :zxlysu @Yahoo. com. cn. 张志强 ,男 ,1979 年生 ,硕士 ,主要 研究方向为神经网络优化设计. ·68 · 智 能 系 统 学 报 第 2 卷