
第2卷第3期 智能系统学报 Vol.2№3 2007年6月 CAAI Transactions on Intelligent Systems Jun.2007 采用改进的粒子群算法训练CNNE模型 杨春玲,王来,朱敏 (哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001) 摘要:提出用人工智能算法—粒子群优化算法(PSO)对CNNE模型进行训练,并针对标准粒子群算法易限于局 部极小点的局限性,采用了一种带有梯度加速的粒子群算法,通过引入梯度信息来影响粒子速度的更新.为防止陷 入局部最优,在群体最优信息陷入停滞时,对部分粒子进行重新初始化,从而保持群体的活性,减小群体陷入局优的 可能性.采用粒子群算法训练的CNNE模型较原来的分布式最速下降法而言,在保证精度的前提下,提高了算法的 收敛速度,解决了发射率的在线实时测量问题. 关键词:CNNE模型:粒子群:梯度 中图分类号:TP183文献标识码:A文章编号:1673-4785(2007)03006706 Using the improved particle swarm optimization to train the CNNE model YANG Chumling,WAN G Jiamlai ,ZHU Min (School of Electrical Engineering and Automation,Harbin Institute of Technology,Harbin 150001,China) Abstract:An artificial intelligence algorithm-particle swarm optimization (PSO)-is proposed to train the CNNE model.To overcome a limitation of standard particle swarm optimization,which can easily be re- stricted at a local optimum point,a particle swarm optimization (PSO)algorithm with gradient acceleration was created that adds gradient information to periodically force updating of the velocities of particles. When the optimum information for the swarm is stagnant,some particles in the population are initialized a- gain to reduce the possibility of becoming trapping in a local optimum.Compared to the step steepest de- scent algorithm,training the CNNE model with the particle swarm optimization algorithm can improve the speed of convergence of the algorithm while keeping its precision,which solves the challenge of real-time measurement of emissivity. Key words:CNNE model;particle swarm optimization;gradient 光谱发射率是目标红外辐射特性的一个重要参 比较敏感,导致收敛速度较缓慢,不能满足发射率在 量.对其测量可以了解材料的红外辐射特性,这对于 线实时测量问题.因此引入一种新颖的人工智能算 材料科学的发展,从而进一步促进航天航空、国防科 法粒子群优化算法用来对CNNE模型进行训 技事业的进步有着重要意义. 练,在保证精度的前提下,大大提高了收敛速度 在文献[1-2]中,建立了激活函数可调(tuna 粒子群优化算法(partical swarm optimization, ble activation function)的组合神经网络发射率模型 PSO)是由Kennedy和Eberhart于1995年提出的 (简称TAF-CNNE模型)用于目标发射率的辨识, 一种基于群体智能(swarm intelligence)的进化计算 并用分布式最速下降法对神经网络模型进行了训 技术,其基本思想源于对鸟群捕食等群体行为的研 练.仿真结果表明该方法搜索精度高,但由于有梯度 究B,.目前,PS0己广泛应用于函数优化、神经网 运算,结构比较复杂,迭代次数较大,且对初值变化 络训练、模式分类、模糊系统控制以及其他的应用领 域.近几年的研究和实践表明,PS0在多维空间函 收稿日期:20061013. 基金项目:因家自然科学基金资助项目(60377037);黑龙江省自然科 数寻优、动态目标寻优等方面有着收敛速度快、解质 学基金资助项目(F200413). 量高、鲁棒性好等优点,特别适合工程应用) 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 3 期 智 能 系 统 学 报 Vol. 2 №. 3 2007 年 6 月 CAA I Transactions on Intelligent Systems J un. 2007 采用改进的粒子群算法训练 CNN E 模型 杨春玲 ,王目柬来 ,朱 敏 (哈尔滨工业大学 电气工程及自动化学院 ,黑龙江 哈尔滨 150001) 摘 要 :提出用人工智能算法 ———粒子群优化算法( PSO)对 CNN E 模型进行训练 ,并针对标准粒子群算法易限于局 部极小点的局限性 ,采用了一种带有梯度加速的粒子群算法 ,通过引入梯度信息来影响粒子速度的更新. 为防止陷 入局部最优 ,在群体最优信息陷入停滞时 ,对部分粒子进行重新初始化 ,从而保持群体的活性 ,减小群体陷入局优的 可能性. 采用粒子群算法训练的 CNNE 模型较原来的分布式最速下降法而言 ,在保证精度的前提下 ,提高了算法的 收敛速度 ,解决了发射率的在线实时测量问题. 关键词 :CNN E 模型 ;粒子群 ;梯度 中图分类号 : TP183 文献标识码 :A 文章编号 :167324785 (2007) 0320067206 Using the improved particle swarm optimization to train the CNNE model YAN G Chun2ling ,WAN G Jian2lai ,ZHU Min (School of Electrical Engineering and Automation , Harbin Institute of Technology , Harbin 150001 , China) Abstract :An artificial intelligence algorit hm2particle swarm optimization (PSO)2is proposed to train t he CNN E model. To overcome a limitation of standard particle swarm optimization , which can easily be re2 stricted at a local optimum point , a particle swarm optimization (PSO) algorit hm with gradient acceleration was created t hat adds gradient information to periodically force updating of t he velocities of particles. When t he optimum information for t he swarm is stagnant , some particles in t he pop ulation are initialized a2 gain to reduce t he possibility of becoming trapping in a local optimum. Compared to t he step steepest de2 scent algorit hm , training t he CNN E model with the particle swarm optimization algorit hm can improve t he speed of convergence of t he algorit hm while keeping its precision , which solves t he challenge of real2time measurement of emissivity. Keywords :CNN E model ; particle swarm optimization ; gradient 收稿日期 :2006210213. 基金项目 :国家自然科学基金资助项目(60377037) ;黑龙江省自然科 学基金资助项目( F2004213) . 光谱发射率是目标红外辐射特性的一个重要参 量. 对其测量可以了解材料的红外辐射特性 ,这对于 材料科学的发展 ,从而进一步促进航天航空、国防科 技事业的进步有着重要意义. 在文献[ 1 - 2 ]中 ,建立了激活函数可调 (tuna2 ble activation f unction) 的组合神经网络发射率模型 (简称 TAF - CNN E 模型) 用于目标发射率的辨识 , 并用分布式最速下降法对神经网络模型进行了训 练. 仿真结果表明该方法搜索精度高 ,但由于有梯度 运算 ,结构比较复杂 ,迭代次数较大 ,且对初值变化 比较敏感 ,导致收敛速度较缓慢 ,不能满足发射率在 线实时测量问题. 因此引入一种新颖的人工智能算 法 ———粒子群优化算法用来对 CNN E 模型进行训 练 ,在保证精度的前提下 ,大大提高了收敛速度. 粒子群优化算法(partical swarm optimization , PSO) 是由 Kennedy 和 Eberhart 于 1995 年提出的 一种基于群体智能(swarm intelligence) 的进化计算 技术 ,其基本思想源于对鸟群捕食等群体行为的研 究[3 - 4 ] . 目前 ,PSO 已广泛应用于函数优化、神经网 络训练、模式分类、模糊系统控制以及其他的应用领 域. 近几年的研究和实践表明 ,PSO 在多维空间函 数寻优、动态目标寻优等方面有着收敛速度快、解质 量高、鲁棒性好等优点 ,特别适合工程应用[ 5 ]

68 智能系统学报 第2卷 PSO算法在搜索的初期收敛速度很快,但在后 行大范围搜索,⊙较小适于进行小范围挖掘.对全局 期却易于陷入局部极优点,尤其当解空间为非凸集 搜索,通常较好的方法是在前期有较高的探索能力 时,这是PSO算法的主要缺点.针对这一缺点,本文 以得到合适的种子,而在后期有较高的开发能力以 在用PSO算法搜索解空间的同时加入了梯度信息, 加快收敛速度.因此,可将ω设为随时间或者迭代 从而帮助算法摆脱易于陷入局部最优点的束缚,同 次数的增加而减小.一般可用下式来确定:ω= 时又保持搜索速度快的特性,并经过仿真测试验证 Clnax Conin 了该算法的优越性 4x~最大迭代次数迭代次数,式中:4、4分 别为开始时和结束时的权重,一般取x=0.9 1粒子群算法基本原理 n=0.4. 使用PSO方法解决优化问题,即把问题的潜在 注意:粒子在第d(1≤d≤D)维的位置变化范 解定义为搜索空间中的一个“粒子”,用适应度值来 围为[-Xaa,Xmxa],速度变化范围[-Vmxw 评价这个粒子的好坏,适应度值是由目标函数唯一 Vxu],迭代中若位置和速度超过边界范围,则取边 确定的.粒子群优化算法依靠个体间的信息交换来 界值.设定较大的Vmx,可以保证粒子种群的全局搜 达到整个群体的共同演化. 索能力,V,较小则粒子种群的局部搜索能力加 首先,粒子群初始化为可行解空间的一组初始 强.通常VmxH=k Xmaxd,0.1≤k.0. 值1,然后通过迭代找到最优解.在每一次迭代中」 Maurice Clere!和F.V.D.Berght71对于PSo 粒子通过跟踪2个“极值”来更新自己:一个是该粒 的收敛性和稳定性作了初步分析,并给出一些保证 子经历过的最好位置(有最好的适应度值),即该粒 PSO算法收敛的参数条件】 子本身所找到的最优解,这个解叫做个体极值,用 PSO算法流程图如图1所示,具体步骤如下: P来表示;另一个是群体中所有粒子经历过的最 1)设定种群规模,给定求解精度和最大迭代次 数 好位置(有最好的适应度值),即整个种群目前所找 2)随机初始化粒子种群:初始化种群中所有粒 到的最优解,这个解叫做全局极值,用Gt来表示. 子的速度和位置(即可行解); 假设在一个D维的目标搜索空间中,有m个粒 3)使用根据优化问题目标定义的适应度函数对 子组成一个群体,其中第i个粒子(1=1,2,m)的 所有粒子进行评价; 位置为X,表示为X=(xm,xn,,xo)T.因为每 4)对每个粒子i,将其适应度与其经历过的最 个粒子的位置Pe,=(pe1,pea,peo)T,就 好位置P,的适应度作比较,如果较好,则将X,作 是一个潜在解,将X代入目标函数就可以计算出其 为当前的最好位置Pe,; 适应度值,根据适应度值的大小衡量其优劣.设该粒 5)对每个粒子i,将其适应度与其经历过的最 子经历过的最好位置Pe,=(peh,Pee,“ 好位置G的适应度作比较,如果较好,则将X,作 Peo)T,整个群体所有粒子经历过的最好位置为 为当前所有粒子的最好位置Gt; Get=(ge1,ge2,,gen)T,粒子i的速度表示 6根据式(1)和式2)更新粒子的速度和位置; 为V:=(a,a,)T,那么粒子i根据下面的规 7)检查是否满足迭代终止条件,若是,则终止迭 律更新自己的速度和位置: 代,求得最优值:若否,转至3),直到满足算法的迭 i=a点+arand(pe点-x) + 代终止条件为止.迭代终止条件根据具体问题设定 c rand吃(ge晴-xia), 1) 一般选为是否达到预定最大迭代次数或和)粒子群 x括=x点+结 (2) 目前为止搜索到的最优位置是否满足预定最小适应 式中:i=1,2,m;d=1,2,D:k为当前迭代次 阈值 数;rand,rand是/0,lJ区间均匀分布的随机数; 是粒子i在第k次迭代中第d维的速度:pe是粒 2 CNNE模型的粒子群算法实现 子1在第k次迭代中第d维的位置;pet是粒子i 参照文献[1]可知对CNNE模型训练的最终结 在第k次迭代中第d维的个体极值点的位置(即坐 果是得到一组最佳系数W、B1、V、B2,即待优化问 标);g音是整个种群在前k次迭代中第d维的全 题的一组最优解.而在PS0算法中,把粒子看作是 局极值点的位置.Q,Q是加速系数(或称学习因 待优化问题的潜在解,所以在用粒子群算法实现 子),分别调节向全局最好粒子和个体最好粒子方向 CNNE模型的时候,每个粒子是由系数W、B1、V、 飞行的最大步长,若太小,则粒子可能远离目标区 B2构成的 域,若太大,则会导致突然向目标区域飞去,或飞过 在CNNE模型中,取隐层节点数为6(K=6) 目标区域,合适的α,口可以加快收敛且不易陷入 可以确定权系数W为1×6维向量[w1,w2, 局部最优.ω称为惯性因子,ω较大适于对解空间进 w6],隐层偏差B1为16维向量[b1,b2,b6], 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
PSO 算法在搜索的初期收敛速度很快 ,但在后 期却易于陷入局部极优点 ,尤其当解空间为非凸集 时 ,这是 PSO 算法的主要缺点. 针对这一缺点 ,本文 在用 PSO 算法搜索解空间的同时加入了梯度信息 , 从而帮助算法摆脱易于陷入局部最优点的束缚 ,同 时又保持搜索速度快的特性 ,并经过仿真测试验证 了该算法的优越性. 1 粒子群算法基本原理 使用 PSO 方法解决优化问题 ,即把问题的潜在 解定义为搜索空间中的一个“粒子”,用适应度值来 评价这个粒子的好坏 ,适应度值是由目标函数唯一 确定的. 粒子群优化算法依靠个体间的信息交换来 达到整个群体的共同演化. 首先 ,粒子群初始化为可行解空间的一组初始 值[5 ] ,然后通过迭代找到最优解. 在每一次迭代中 , 粒子通过跟踪 2 个“极值”来更新自己 :一个是该粒 子经历过的最好位置 (有最好的适应度值) ,即该粒 子本身所找到的最优解 ,这个解叫做个体极值 ,用 Pbest来表示 ;另一个是群体中所有粒子经历过的最 好位置(有最好的适应度值) ,即整个种群目前所找 到的最优解 ,这个解叫做全局极值 ,用 Gbest来表示. 假设在一个 D 维的目标搜索空间中 ,有 m 个粒 子组成一个群体 ,其中第 i 个粒子( i = 1 ,2 , …, m) 的 位置为 Xi ,表示为 Xi = ( xi1 , xi2 , …, xiD ) T . 因为每 个粒子的位置 Pbest i = ( pbest i1 , pbest i2 , …, pbest iD ) T ,就 是一个潜在解 ,将 Xi 代入目标函数就可以计算出其 适应度值 ,根据适应度值的大小衡量其优劣. 设该粒 子经 历 过 的 最 好 位 置 Pbest i = ( pbest i1 , pbest i2 , … pbest iD ) T ,整个群体所有粒子经历过的最好位置为 Gbest = ( gbest 1 , gbest 2 , …, gbest D ) T ,粒子 i 的速度表示 为 Vi = ( vi1 , vi2 , …, viD ) T ,那么粒子 i 根据下面的规 律更新自己的速度和位置 : v k+1 id = ωv k id + c1 rand k 1 ( pbest k id - x k id ) + c2 rand k 2 ( gbest k d - x k id ) , (1) x k+1 id = x k id + v k+1 id . (2) 式中 :i = 1 ,2 , …, m ; d = 1 ,2 , …, D ; k 为当前迭代次 数;rand k 1 ,rand k 2 是[0 ,1 ]区间均匀分布的随机数; v k id 是粒子 i 在第 k 次迭代中第 d 维的速度; pbest k id 是粒 子 i 在第 k 次迭代中第 d 维的位置; pbest k id 是粒子 i 在第 k 次迭代中第 d 维的个体极值点的位置(即坐 标) ; gbest k d 是整个种群在前 k 次迭代中第 d 维的全 局极值点的位置. c1 , c2 是加速系数 (或称学习因 子) ,分别调节向全局最好粒子和个体最好粒子方向 飞行的最大步长 ,若太小 ,则粒子可能远离目标区 域 ,若太大 ,则会导致突然向目标区域飞去 ,或飞过 目标区域 ,合适的 c1 , c2 可以加快收敛且不易陷入 局部最优.ω称为惯性因子 ,ω较大适于对解空间进 行大范围搜索 ,ω较小适于进行小范围挖掘. 对全局 搜索 ,通常较好的方法是在前期有较高的探索能力 以得到合适的种子 ,而在后期有较高的开发能力以 加快收敛速度. 因此 ,可将ω设为随时间或者迭代 次数的增加而减小. 一般可用下式来确定 :ω = ωmax - ωmax - ωmin 最大迭代次数 ×迭代次数 ,式中 :ωmax 、ωmin 分 别为开始时和结束时的权重 , 一般取 ωmax = 019 , ωmin = 014. 注意 :粒子在第 d (1 ≤d ≤D) 维的位置变化范 围为 [ - Xmax id , Xmax id ] , 速度变化范围 [ - V max id , V max id ] ,迭代中若位置和速度超过边界范围 ,则取边 界值. 设定较大的 V max id 可以保证粒子种群的全局搜 索能力 , V max id 较小则粒子种群的局部搜索能力加 强. 通常 V max id = k Xmax id ,01 1 ≤k ≤110. Maurice Clere [ 6 ]和 F. V. D. Bergh [7 ] 对于 PSO 的收敛性和稳定性作了初步分析 ,并给出一些保证 PSO 算法收敛的参数条件. PSO 算法流程图如图 1 所示 ,具体步骤如下 : 1) 设定种群规模 ,给定求解精度和最大迭代次 数 ; 2) 随机初始化粒子种群 :初始化种群中所有粒 子的速度和位置(即可行解) ; 3) 使用根据优化问题目标定义的适应度函数对 所有粒子进行评价 ; 4) 对每个粒子 i ,将其适应度与其经历过的最 好位置 Pbest i的适应度作比较 ,如果较好 ,则将 Xi 作 为当前的最好位置 Pbest i ; 5) 对每个粒子 i ,将其适应度与其经历过的最 好位置 Gbest的适应度作比较 ,如果较好 ,则将 Xi 作 为当前所有粒子的最好位置 Gbest ; 6) 根据式(1) 和式(2) 更新粒子的速度和位置; 7) 检查是否满足迭代终止条件 ,若是 ,则终止迭 代 ,求得最优值;若否 ,转至 3) ,直到满足算法的迭 代终止条件为止. 迭代终止条件根据具体问题设定 , 一般选为是否达到预定最大迭代次数或(和) 粒子群 目前为止搜索到的最优位置是否满足预定最小适应 阈值. 2 CNN E 模型的粒子群算法实现 参照文献[1 ]可知对 CNN E 模型训练的最终结 果是得到一组最佳系数 W 、B1、V 、B2 ,即待优化问 题的一组最优解. 而在 PSO 算法中 ,把粒子看作是 待优化问题的潜在解 ,所以在用粒子群算法实现 CNN E 模型的时候 ,每个粒子是由系数 W 、B1、V 、 B2 构成的. 在 CNN E 模型中 ,取隐层节点数为 6 ( K = 6) . 可以确定权系数 W 为 1 ×6 维向量 [ w1 , w2 , …, w6 ] ,隐层偏差 B1 为 1 ×6 维向量[ b11 , b12 , …, b16 ] , ·68 · 智 能 系 统 学 报 第 2 卷
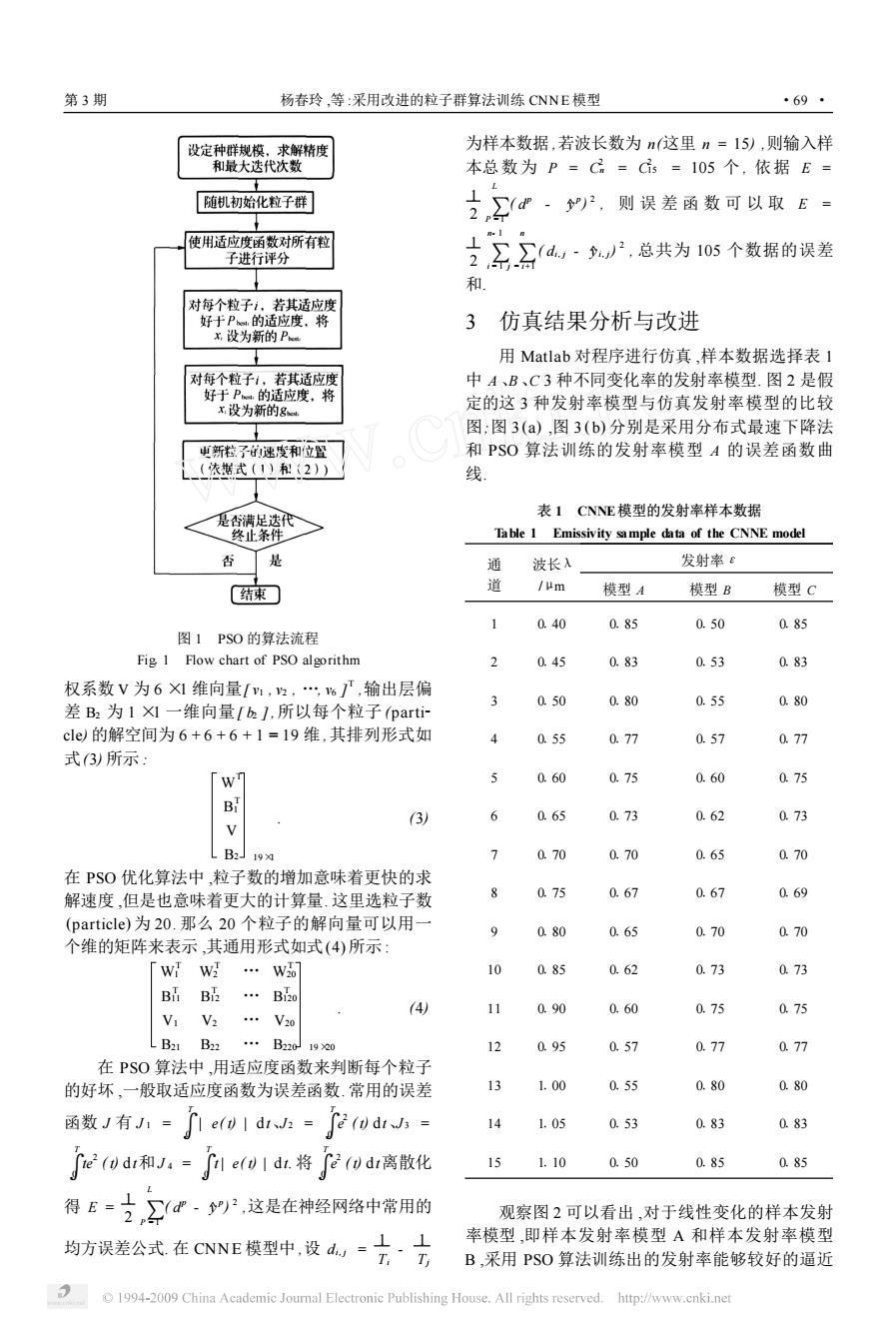
第3期 杨春玲,等:采用改进的粒子群算法训练CNNE模型 ·69· 设定种群规模,求解精度 为样本数据,若波长数为n这里n=15),则输入样 和最大迭代次数 本总数为P=C=C=105个,依据E= 随机初始化粒子群 之,Σ·,则误差函数可以取E 使用适应度函数对所有粒 1n 子进行评分 左公d,:户,总共为105个数据的误差 和 对每个粒子1,若其适应度 好于P的适应度,将 3 仿真结果分析与改进 x设为新的P 用Matlab对程序进行仿真,样本数据选择表1 对每个粒子1,若其适应度 中A、B、C3种不同变化率的发射率模型.图2是假 好于P的适应度,将 x,设为新的g 定的这3种发射率模型与仿真发射率模型的比较 图:图3(a),图3(b)分别是采用分布式最速下降法 中新粒了的速度和位置 和PSO算法训练的发射率模型A的误差函数曲 (依据式(1)和(2) 线 表1CNNE模型的发射率样本数据 是否满足迭代 终止条件 Table 1 Emissivity sample data of the CNNE model 否 是 通 波长 发射率e 道 结束 /μm 模型A 模型B 模型C 1 0.40 0.85 0.50 0.85 图1PSO的算法流程 Fig I Flow chart of PSO algorithm 2 0.45 0.83 0.53 0.83 权系数V为6X1维向量[m,,%,输出层偏 0.50 0.80 0.55 0.80 差B2为11一维向量[b],所以每个粒子(parti- cl)的解空间为6+6+6+1=19维,其排列形式如 0.55 0.77 0.57 0.77 式3)所示: w 0.60 0.75 0.60 0.75 B (3) 0.62 0.73 B2 19 0.65 0.70 在PS0优化算法中,粒子数的增加意味着更快的求 解速度,但是也意味着更大的计算量.这里选粒子数 0.67 0.69 (particle)为20.那么20个粒子的解向量可以用一 0.70 0.70 个维的矩阵来表示,其通用形式如式(4)所示: w W W2o 10 0.73 0.73 Bu B Bi20 (4) 0.75 V2 …V20 ·B2201920 12 0.95 057 0.77 0.77 在PS0算法中,用适应度函数来判断每个粒子 的好坏,一般取适应度函数为误差函数常用的误差 13 1.00 0.55 0.80 0.80 函数J有=了1ew1dh=∫Wdh 14 1.05 0.53 0.83 0.83 了e(wd和J:=le(w1d.将(wd离散化 15 1.10 0.50 0.85 0.85 得E=之,·y,这是在神经网络中常用的 观察图2可以看出,对于线性变化的样本发射 均方误差公式在CNNE模型中,设d山=六·方 率模型,即样本发射率模型A和样本发射率模型 B,采用PSO算法训练出的发射率能够较好的逼近 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
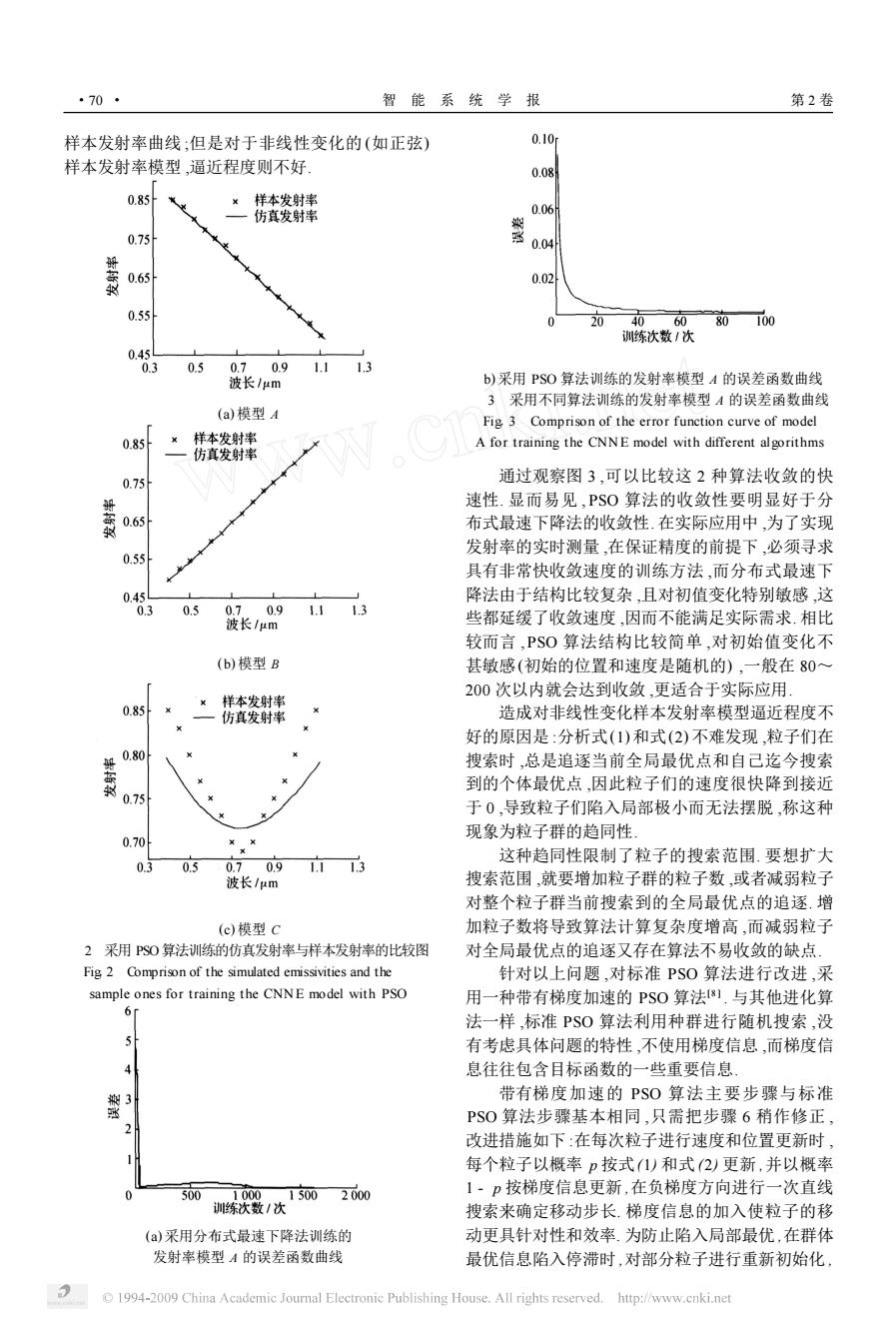
图 1 PSO 的算法流程 Fig11 Flow chart of PSO algorithm 权系数 V 为 6 ×1 维向量[ v1 , v2 , …, v6 ] T ,输出层偏 差 B2 为 1 ×1 一维向量[ b2 ] ,所以每个粒子 (parti2 cle) 的解空间为 6 + 6 + 6 + 1 = 19 维 ,其排列形式如 式(3) 所示 : W T B T 1 V B2 19×1 . (3) 在 PSO 优化算法中 ,粒子数的增加意味着更快的求 解速度 ,但是也意味着更大的计算量. 这里选粒子数 (particle) 为 20. 那么 20 个粒子的解向量可以用一 个维的矩阵来表示 ,其通用形式如式(4) 所示 : W T 1 W T 2 … W T 20 B T 11 B T 12 … B T 120 V1 V2 … V20 B21 B22 … B220 19×20 . (4) 在 PSO 算法中 ,用适应度函数来判断每个粒子 的好坏 ,一般取适应度函数为误差函数. 常用的误差 函数 J 有 J 1 =∫ T 0 | e( t) | dt、J 2 =∫ T 0 e 2 ( t) dt、J 3 = ∫ T 0 te 2 ( t) dt和J 4 =∫ T 0 t | e( t) | dt. 将∫ T 0 e 2 ( t) dt离散化 得 E = 1 2 ∑ L P =1 ( d p - ^y p ) 2 ,这是在神经网络中常用的 均方误差公式. 在 CNN E 模型中 ,设 di , j = 1 Ti - 1 Tj 为样本数据 ,若波长数为 n(这里 n = 15) ,则输入样 本总数为 P = C 2 n = C 2 15 = 105 个 , 依据 E = 1 2 ∑ L P =1 ( d p - ^y p ) 2 , 则 误 差 函 数 可 以 取 E = 1 2 ∑ n- 1 i = 1 ∑ n j = i+1 ( di , j - ^yi , j) 2 , 总共为 105 个数据的误差 和. 3 仿真结果分析与改进 用 Matlab 对程序进行仿真 ,样本数据选择表 1 中 A 、B 、C 3 种不同变化率的发射率模型. 图 2 是假 定的这 3 种发射率模型与仿真发射率模型的比较 图;图 3 (a) ,图 3 ( b) 分别是采用分布式最速下降法 和 PSO 算法训练的发射率模型 A 的误差函数曲 线. 表 1 CNNE模型的发射率样本数据 Table 1 Emissivity sample data of the CNNE model 通 道 波长λ /μm 发射率ε 模型 A 模型 B 模型 C 1 0140 0185 0150 0185 2 0145 0183 0153 0183 3 0150 0180 0155 0180 4 0155 0177 0157 0177 5 0160 0175 0160 0175 6 0165 0173 0162 0173 7 0170 0170 0165 0170 8 0175 0167 0167 0169 9 0180 0165 0170 0170 10 0185 0162 0173 0173 11 0190 0160 0175 0175 12 0195 0157 0177 0177 13 1100 0155 0180 0180 14 1105 0153 0183 0183 15 1110 0150 0185 0185 观察图 2 可以看出 ,对于线性变化的样本发射 率模型 ,即样本发射率模型 A 和样本发射率模型 B ,采用 PSO 算法训练出的发射率能够较好的逼近 第 3 期 杨春玲 ,等 :采用改进的粒子群算法训练 CNN E 模型 ·69 ·
·70 智能系统学报 第2卷 样本发射率曲线;但是对于非线性变化的(如正弦) 0.10 样本发射率模型,逼近程度则不好 0.08 0.85 样本发射率 仿真发射率 0.06 0.75 0.04 0.65 0.02 0.55 0 20 406080100 训练次数/次 0.4 0.3 05 0.70.9 1.1 1.3 波长/μm b)采用PSO算法训练的发射率模型A的误差函数曲线 3采用不同算法训练的发射率模型A的误差函数曲线 (a)模型A Fig 3 Comprison of the error function curve of model 0.85 样本发射率 A for training the CNNE model with different algorithms 仿真发射率 0.75 通过观察图3,可以比较这2种算法收敛的快 速性.显而易见,PSO算法的收敛性要明显好于分 0.65 布式最速下降法的收敛性.在实际应用中,为了实现 发射率的实时测量,在保证精度的前提下,必须寻求 0.55 具有非常快收敛速度的训练方法,而分布式最速下 0.45 降法由于结构比较复杂,且对初值变化特别敏感,这 .3 0.5 0.70.9 1.1 1.3 波长Iμm 些都延缓了收敛速度,因而不能满足实际需求.相比 较而言,P$0算法结构比较简单,对初始值变化不 (b)模型B 甚敏感(初始的位置和速度是随机的),一般在80~ 200次以内就会达到收敛,更适合于实际应用 样本发射率 0.85 仿真发射率 造成对非线性变化样本发射率模型逼近程度不 好的原因是:分析式(1)和式(2)不难发现,粒子们在 0.80 搜索时,总是追逐当前全局最优点和自己迄今搜索 到的个体最优点,因此粒子们的速度很快降到接近 0.75 于0,导致粒子们陷入局部极小而无法摆脱,称这种 现象为粒子群的趋同性 0.70 这种趋同性限制了粒子的搜索范围.要想扩大 03 0.5 0.70.91113 波长/um 搜索范围,就要增加粒子群的粒子数,或者减弱粒子 对整个粒子群当前搜索到的全局最优点的追逐.增 (c)模型C 加粒子数将导致算法计算复杂度增高,而减弱粒子 2采用PS0算法训练的仿真发射率与样本发射率的比较图 对全局最优点的追逐又存在算法不易收敛的缺点 Fig 2 Comprison of the simulated emissivities and the 针对以上问题,对标准PSO算法进行改进,采 sample ones for training the CNNE model with PSO 用一种带有梯度加速的P$0算法],与其他进化算 法一样,标准PSO算法利用种群进行随机搜索,没 有考虑具体问题的特性,不使用梯度信息,而梯度信 息往往包含目标函数的一些重要信息 带有梯度加速的PSO算法主要步骤与标准 PS0算法步骤基本相同,只需把步骤6稍作修正 改进措施如下:在每次粒子进行速度和位置更新时 每个粒子以概率p按式1)和式2)更新,并以概率 500 1000 15002000 1-p按梯度信息更新,在负梯度方向进行一次直线 训练次数/次 搜索来确定移动步长.梯度信息的加入使粒子的移 (a)采用分布式最速下降法训练的 动更具针对性和效率.为防止陷入局部最优,在群体 发射率模型A的误差函数曲线 最优信息陷入停滞时,对部分粒子进行重新初始化 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
样本发射率曲线 ;但是对于非线性变化的 (如正弦) 样本发射率模型 ,逼近程度则不好. (a) 模型 A (b) 模型 B (c) 模型 C 图 2 采用 PSO算法训练的仿真发射率与样本发射率的比较图 Fig12 Comprison of the simulated emissivities and the sample ones for training the CNN E model with PSO (a) 采用分布式最速下降法训练的 发射率模型 A 的误差函数曲线 ( b) 采用 PSO 算法训练的发射率模型 A 的误差函数曲线 图 3 采用不同算法训练的发射率模型 A 的误差函数曲线 Fig13 Comprison of the error function curve of model A for training the CNN E model with different algorithms 通过观察图 3 ,可以比较这 2 种算法收敛的快 速性. 显而易见 ,PSO 算法的收敛性要明显好于分 布式最速下降法的收敛性. 在实际应用中 ,为了实现 发射率的实时测量 ,在保证精度的前提下 ,必须寻求 具有非常快收敛速度的训练方法 ,而分布式最速下 降法由于结构比较复杂 ,且对初值变化特别敏感 ,这 些都延缓了收敛速度 ,因而不能满足实际需求. 相比 较而言 ,PSO 算法结构比较简单 ,对初始值变化不 甚敏感(初始的位置和速度是随机的) ,一般在 80~ 200 次以内就会达到收敛 ,更适合于实际应用. 造成对非线性变化样本发射率模型逼近程度不 好的原因是 :分析式(1) 和式(2) 不难发现 ,粒子们在 搜索时 ,总是追逐当前全局最优点和自己迄今搜索 到的个体最优点 ,因此粒子们的速度很快降到接近 于 0 ,导致粒子们陷入局部极小而无法摆脱 ,称这种 现象为粒子群的趋同性. 这种趋同性限制了粒子的搜索范围. 要想扩大 搜索范围 ,就要增加粒子群的粒子数 ,或者减弱粒子 对整个粒子群当前搜索到的全局最优点的追逐. 增 加粒子数将导致算法计算复杂度增高 ,而减弱粒子 对全局最优点的追逐又存在算法不易收敛的缺点. 针对以上问题 ,对标准 PSO 算法进行改进 ,采 用一种带有梯度加速的 PSO 算法[8 ] . 与其他进化算 法一样 ,标准 PSO 算法利用种群进行随机搜索 ,没 有考虑具体问题的特性 ,不使用梯度信息 ,而梯度信 息往往包含目标函数的一些重要信息. 带有梯度加速的 PSO 算法主要步骤与标准 PSO 算法步骤基本相同 ,只需把步骤 6 稍作修正 , 改进措施如下 :在每次粒子进行速度和位置更新时 , 每个粒子以概率 p 按式(1) 和式 (2) 更新 ,并以概率 1 - p 按梯度信息更新 ,在负梯度方向进行一次直线 搜索来确定移动步长. 梯度信息的加入使粒子的移 动更具针对性和效率. 为防止陷入局部最优 ,在群体 最优信息陷入停滞时 ,对部分粒子进行重新初始化 , ·70 · 智 能 系 统 学 报 第 2 卷
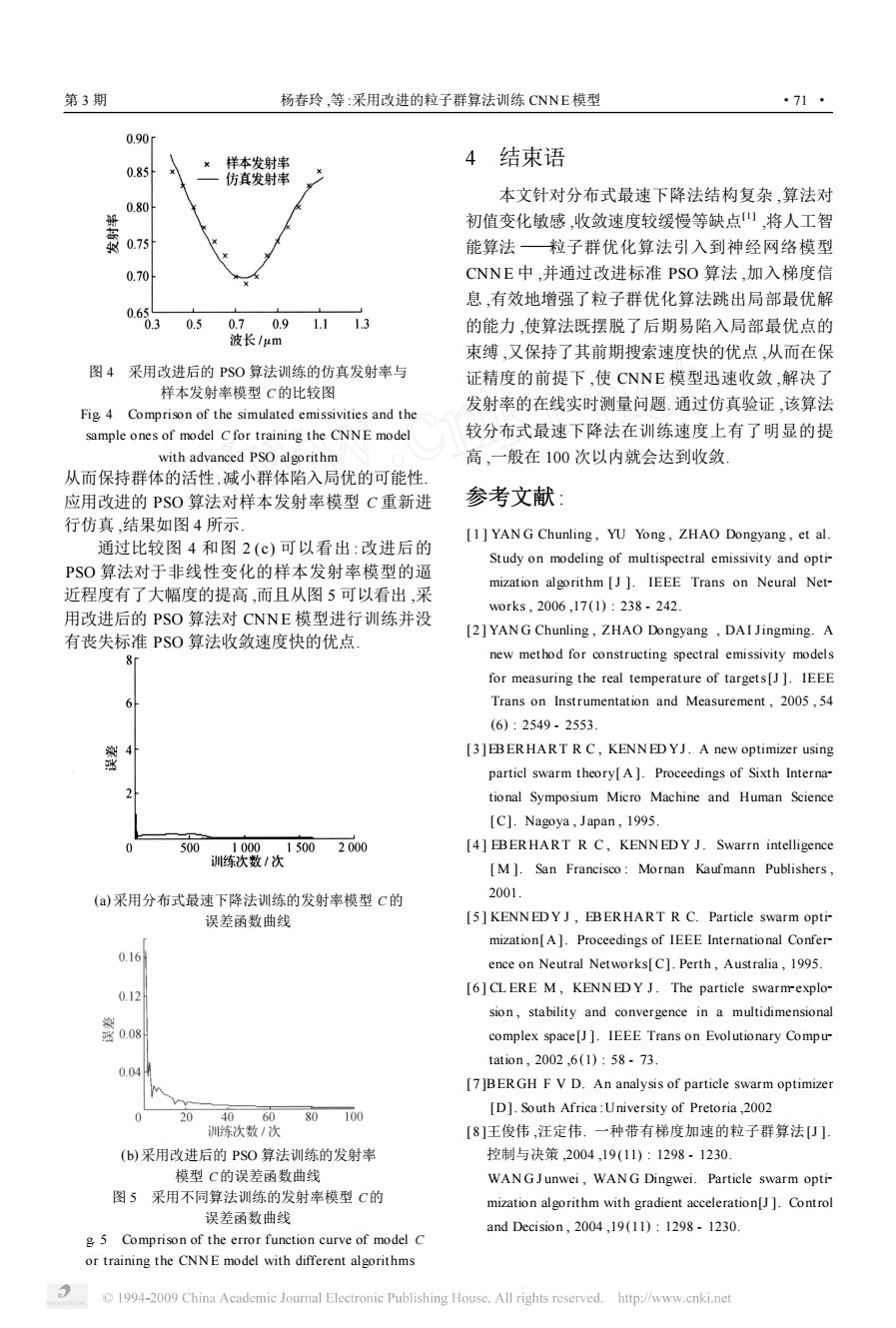
第3期 杨春玲,等:采用改进的粒子群算法训练CNNE模型 ·71 0.90r 样本发射率 4 结束语 0.85 仿真发射率 0.80A 本文针对分布式最速下降法结构复杂,算法对 初值变化敏感,收敛速度较缓慢等缺点山,将人工智 g0.75 能算法—粒子群优化算法引入到神经网络模型 0.70 CNNE中,并通过改进标准PSO算法,加入梯度信 息,有效地增强了粒子群优化算法跳出局部最优解 0.6 0.30.5 0.70.91.113 的能力,使算法既摆脱了后期易陷入局部最优点的 波长/μm 束缚,又保持了其前期搜索速度快的优点,从而在保 图4采用改进后的PSO算法训练的仿真发射率与 证精度的前提下,使CNNE模型迅速收敛,解决了 样本发射率模型C的比较图 发射率的在线实时测量问题,通过仿真验证,该算法 Fig 4 Comprison of the simulated emissivities and the sample ones of model Cfor training the CNNE model 较分布式最速下降法在训练速度上有了明显的提 with advanced PSO algorithm 高,一般在100次以内就会达到收敛 从而保持群体的活性,减小群体陷入局优的可能性」 应用改进的P$O算法对样本发射率模型C重新进 参考文献: 行仿真,结果如图4所示. [1]YAN G Chunling,YU Yong,ZHAO Dongyang,et al 通过比较图4和图2(c)可以看出:改进后的 Study on modeling of multispectral emissivity and opti- PSO算法对于非线性变化的样本发射率模型的逼 近程度有了大幅度的提高,而且从图5可以看出,采 mization algorithm [J].IEEE Trans on Neural Net- works,2006,17(1):238-242 用改进后的PSO算法对CNNE模型进行训练并没 有丧失标准PS0算法收敛速度快的优点。 [2]YANG Chunling,ZHAO Dongyang,DAI Jingming.A new method for constructing spectral emissivity models for measuring the real temperature of targets[J ]IEEE 6 Trans on Instrumentation and Measurement,2005,54 (6):2549.2553. 4 [3 ]EBERHART R C,KENNED YJ.A new optimizer using particl swarm theory[A ]Proceedings of Sixth Interna- tional Symposium Micro Machine and Human Science C].Nagoya,Japan,1995. 0 500 100015002000 [4]EBERHART R C,KENNEDY J.Swarrn intelligence 训练次数/次 M].San Francisco:Mornan Kaufmann Publishers, (a)采用分布式最速下降法训练的发射率模型C的 2001 误差函数曲线 [5]KENNEDYJ,EBERHART R C.Particle swarm opti- mization[A].Proceedings of IEEE International Confer- 0.16 ence on Neutral Networks[C].Perth,Australia,1995. 0.12 [6]CLERE M,KENNEDY J.The particle swarmrexplo- sion,stability and convergence in a multidimensional 测 0.08 complex space[J].IEEE Trans on Evolutionary Compu tation,2002,6(1):58-73. 0.04 [7]BERGH F V D.An analysis of particle swarm optimizer 80100 [D].South Africa:University of Pretoria,2002 0 20 40 60 训练次数/次 [8]王俊伟,汪定伟.一种带有梯度加速的粒子群算法U] (b)采用改进后的PSO算法训练的发射率 控制与决策,2004,19(11):1298.1230. 模型C的误差函数曲线 WANG Junwei,WANG Dingwei.Particle swarm opti- 图5采用不同算法训练的发射率模型C的 mization algorithm with gradient acceleration[J ]Control 误差函数曲线 and Decision,2004,19(11):1298.1230 g 5 Comprison of the error function curve of model C or training the CNNE model with different algorithms 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 4 采用改进后的 PSO 算法训练的仿真发射率与 样本发射率模型 C的比较图 Fig14 Comprison of the simulated emissivities and the sample ones of model C for training the CNN E model with advanced PSO algorithm 从而保持群体的活性 ,减小群体陷入局优的可能性. 应用改进的 PSO 算法对样本发射率模型 C 重新进 行仿真 ,结果如图 4 所示. 通过比较图 4 和图 2 (c) 可以看出 :改进后的 PSO 算法对于非线性变化的样本发射率模型的逼 近程度有了大幅度的提高 ,而且从图 5 可以看出 ,采 用改进后的 PSO 算法对 CNN E 模型进行训练并没 有丧失标准 PSO 算法收敛速度快的优点. (a)采用分布式最速下降法训练的发射率模型 C的 误差函数曲线 (b)采用改进后的 PSO 算法训练的发射率 模型 C的误差函数曲线 图 5 采用不同算法训练的发射率模型 C的 误差函数曲线 Fi g15 Comprison of the error function curve of model C f or training the CNN E model with different algorithms 4 结束语 本文针对分布式最速下降法结构复杂 ,算法对 初值变化敏感 ,收敛速度较缓慢等缺点[1 ] ,将人工智 能算法 ———粒子群优化算法引入到神经网络模型 CNN E 中 ,并通过改进标准 PSO 算法 ,加入梯度信 息 ,有效地增强了粒子群优化算法跳出局部最优解 的能力 ,使算法既摆脱了后期易陷入局部最优点的 束缚 ,又保持了其前期搜索速度快的优点 ,从而在保 证精度的前提下 ,使 CNN E 模型迅速收敛 ,解决了 发射率的在线实时测量问题. 通过仿真验证 ,该算法 较分布式最速下降法在训练速度上有了明显的提 高 ,一般在 100 次以内就会达到收敛. 参考文献 : [ 1 ] YAN G Chunling , YU Yong , ZHAO Dongyang , et al. Study on modeling of multispectral emissivity and opti2 mization algorithm [J ]. IEEE Trans on Neural Net2 works , 2006 ,17 (1) : 238 - 242. [2 ] YAN G Chunling , ZHAO Dongyang , DAI Jingming. A new method for constructing spectral emissivity models for measuring the real temperature of targets[J ]. IEEE Trans on Instrumentation and Measurement , 2005 , 54 (6) : 2549 - 2553. [3 ] EBERHART R C , KENN ED YJ. A new optimizer using particl swarm theory[ A ]. Proceedings of Sixth Interna2 tional Symposium Micro Machine and Human Science [C]. Nagoya , J apan , 1995. [4 ] EBERHART R C , KENN ED Y J. Swarrn intelligence [ M ]. San Francisco : Mornan Kaufmann Publishers , 2001. [5 ] KENNED Y J , EBERHART R C. Particle swarm opti2 mization[ A ]. Proceedings of IEEE International Confer2 ence on Neutral Networks[C]. Perth , Australia , 1995. [6 ] CL ERE M , KENN ED Y J. The particle swarm2explo2 sion , stability and convergence in a multidimensional complex space[J ]. IEEE Trans on Evolutionary Compu2 tation , 2002 ,6 (1) : 58 - 73. [7 ]BERGH F V D. An analysis of particle swarm optimizer [D]. South Africa :University of Pretoria ,2002 [8 ]王俊伟 ,汪定伟. 一种带有梯度加速的粒子群算法[J ]. 控制与决策 ,2004 ,19 (11) : 1298 - 1230. WAN G J unwei , WAN G Dingwei. Particle swarm opti2 mization algorithm with gradient acceleration[J ]. Control and Decision , 2004 ,19 (11) : 1298 - 1230. 第 3 期 杨春玲 ,等 :采用改进的粒子群算法训练 CNN E 模型 ·71 ·

·72· 智能系统学报 第2卷 作者简介: 杨春玲,女,1965年生,教授,博士生 王束来,男,1982年生,硕士研究生, 导师,EEE会员;东北地区高校电子技 主要研究方向为基于FPGA/CPLD的数 术研究会理事:主要研究方向为神经网络 字系统设计、人工神经网络建模等 建模及优化算法、目标红外辐射特性参数 的测量,红外图像处理、微弱信号检测及 FPGA硬件实现技术等.承担省部级科研 项目6项.在国内外发表论文40余篇,被 SCI检索5篇,主编教材4部. Email yangcl1 @hit.edu.cn. 朱敏,男,1981年生,硕士研究生主 要研究方向为红外检测。 IEEE计算智能世界大会 IEEE World Congress on Computational Intelligence (WCCI'2008) The 2008 IEEE World Congress on Computational Intelligence(WCCI 2008)will be held at the Hong Kong Convention and Exhibition Centre during June 1~6,2008.WCCI 2008 is composed of the 2008 In- ternational Joint Conference on Neural Networks (D CNN 2008),the 2008 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2008)and the 2008 IEEE Congress on Evolutionary Computation (CEC 2008).The congress will feature world-renowned plenary speakers,regular technical sessions,state-of- the-art special sessions,interactive poster sessions,moderated panel discussions,informative pre-confer- ence tutorials,themed post-conference workshops,and entertaining social functions.Researchers are invi- ted to contribute high-quality papers to WCCI 2008.All papers are to be submitted electronically through the Congress website by December 1,2007.All contributed papers will be reviewed by experts in the fields based on the criteria of originality,significance,quality,and clarity.For general inquiries,please contact General Chair Jun Wang at jwang @mae.cuhk.edu.hk.For program inquiries,contact DCNN2008 Pro- gram Chair Derong Liu at dliu @ece.uic.edu,FUZZ-IEEE2008 Program Chair Gary Feng at megfeng@ cityu.edu.hk,or CEC2008 Program Chair Zbigniew Michalewicz at zbyszek @cs.adelaide.edu.au.For more details,please visit the conference web site at http://www.wcci2008.org/. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
作者简介 : 杨春玲 ,女 ,1965 年生 ,教授 ,博士生 导师 , IEEE 会员 ;东北地区高校电子技 术研究会理事 ;主要研究方向为神经网络 建模及优化算法、目标红外辐射特性参数 的测量、红外图像处理、微弱信号检测及 FPGA 硬件实现技术等. 承担省部级科研 项目 6 项. 在国内外发表论文 40 余篇 ,被 SCI 检索 5 篇 ,主编教材 4 部. E2mail :yangcl1 @hit. edu. cn. 王目柬来 ,男 ,1982 年生 ,硕士研究生 , 主要研究方向为基于 FPGA/ CPLD 的数 字系统设计、人工神经网络建模等. 朱 敏 ,男 ,1981 年生 ,硕士研究生主 要研究方向为红外检测. IEEE 计算智能世界大会 IEEE World Co ngress o n Comp utatio nal Intelligence (WCCI′2008) The 2008 IEEE World Congress on Comp utational Intelligence (WCCI 2008) will be held at the Hong Kong Convention and Exhibition Centre during J une 1~6 , 2008. WCCI 2008 is composed of the 2008 In2 ternational Joint Conference on Neural Networks (IJ CNN 2008) , t he 2008 IEEE International Conference on Fuzzy Systems (FUZZ2IEEE 2008) and the 2008 IEEE Congress on Evolutionary Comp utation (CEC 2008) . The congress will feat ure world2renowned plenary speakers , regular technical sessions , state2of2 t he2art special sessions , interactive poster sessions , moderated panel discussions , informative pre2confer2 ence t utorials , t hemed po st2conference workshop s , and entertaining social f unctions. Researchers are invi2 ted to contribute high2quality papers to WCCI 2008. All papers are to be submitted electronically t hrough t he Congress website by December 1 , 2007. All contributed papers will be reviewed by experts in t he fields based on the criteria of originality , significance , quality , and clarity. For general inquiries , please contact General Chair J un Wang at jwang @mae. cuhk. edu. hk. For p rogram inquiries , contact IJ CNN2008 Pro2 gram Chair Derong Liu at dliu @ece. uic. edu , FUZZ2IEEE2008 Program Chair Gary Feng at megfeng @ cityu. edu. hk , or CEC2008 Program Chair Zbigniew Michalewicz at zbyszek @cs. adelaide. edu. au. For more details , please visit t he conference web site at http :/ / www. wcci2008. org/ . ·72 · 智 能 系 统 学 报 第 2 卷