
第2卷第3期 智能系统学报 Vol.2 N23 2007年6月 CAAI Transactions on Intelligent Systems Jun.2007 滞环细胞神经网络实现多涡卷混沌发生器 刘洪臣,冯勇李林静 (哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001) 摘要:提出利用2个具有滞环输出的CNN细胞实现了多涡卷混沌发生器.首先用标准CNN细胞的状态方程来表 示多涡卷混沌发生器的状态方程,通过对比来确定CNN模板的参数,用运算放大器来实现CNN细胞的状态方程及 不同形式的滞环输出方程,分别采用不同形式的滞环输出函数实现双涡卷和三涡卷混沌吸引子.本系统由运算放大 器,电阻及电容构成,易于实现集成.最后,应用Orcad Pspice进行了电路仿真,验证了结论的正确性 关键词:多涡卷;滞环函数;混沌发生器;细胞神经网络 中图分类号:TN75文献标识码:A文章编号:1673-4785(2007)03006304 Multi-scroll chaos generator based on HCNN LIU Hong-chen,FENG Yong LI Linjing (School of Electrical Engineering and Automation,Harbin Institute of Technology,Harbin 150001,China) Abstract:A realization of multi-scroll chaos generation is presented using two CNN cells with hysteresis output function in the paper.First,the CNN template can be ascertained through expressing the unstable second-order linear continuous system with the state function of CNN;Second,the state function of CNN and the hysteresis output function are realized with operational amplifier;Finally,double scroll and three scroll chaos attractor are realized using different hysteresis functions.The proposed system uses only oper- ational amplifiers,resistors and capacitors,so it's easy to be integrated.The results'validity is illustrated by the circuit simulation using Orcad Pspice. Key words:multi-scroll;hysteresis function;chaos generator;CNN 作为一种普遍存在的非线性现象,混沌的发现可靠性,防止系统的误动作.本文利用2个滞环 对科学的发展具有深远的影响.混沌行为是确定性 CNN细胞来实现多涡卷滞环混沌发生器,对实现的 因素导致的类似随机运动的行为,即一个可由确定 过程进行了分析并对电路的实现进行了阐述,最后, 性方程描述的非线性系统,其长期行为表现为明显 应用Orcad Pspice对本文的设计进行了电路仿真, 的随机性和不可预测性. 验证了结论的正确性 细胞神经网络川(CNN)是一种局域互联网络, 1 具有结构简单,易于集成等优点,使其在混沌电路领 滞环混沌发生器 域有着广泛的应用.细胞神经网络是非线性的动态 根据文献[1],无量纲滞环混沌发生器的状态方 系统,因此应用细胞神经网络可以构建混沌系统,这 程为 对研究混沌行为有着重要意义,并且为混沌电路的 仿真分析提供了一条便捷的途径 -[ 近几年来,滞环输出函数的CNN引起人们的 式中:h(x1)为滞环函数: 广泛关注1,由于滞环函数是很常用的函数,在系 1 x1≥.1, 统中引入滞环函数(或滞回比较器)可以提高系统的 h(x) -1 x1≤1, (2) 保持不变-1<x1<1. 收稿日期:200612-05. 在o和ω同为小于1的正数时有o=.d.在这 基金项目:国家自然科学基金资助项目(60474016) 种情况下,式()的特征值入=o与ω具有正实部(也 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved http://www.cnki.net
第 2 卷第 3 期 智 能 系 统 学 报 Vol. 2 №. 3 2007 年 6 月 CAA I Transactions on Intelligent Systems J un. 2007 滞环细胞神经网络实现多涡卷混沌发生器 刘洪臣 ,冯 勇 ,李林静 (哈尔滨工业大学 电气工程及自动化学院 ,黑龙江 哈尔滨 150001) 摘 要 :提出利用 2 个具有滞环输出的 CNN 细胞实现了多涡卷混沌发生器. 首先用标准 CNN 细胞的状态方程来表 示多涡卷混沌发生器的状态方程 ,通过对比来确定 CNN 模板的参数 ,用运算放大器来实现 CNN 细胞的状态方程及 不同形式的滞环输出方程 ,分别采用不同形式的滞环输出函数实现双涡卷和三涡卷混沌吸引子. 本系统由运算放大 器 ,电阻及电容构成 ,易于实现集成. 最后 ,应用 Orcad Pspice 进行了电路仿真 ,验证了结论的正确性. 关键词 :多涡卷 ;滞环函数 ;混沌发生器 ;细胞神经网络 中图分类号 : TN75 文献标识码 :A 文章编号 :167324785 (2007) 0320063204 Multi2scroll chaos generator based on HCNN L IU Hong2chen ,FEN G Yong ,L I Lin2jing (School of Electrical Engineering and Automation , Harbin Institute of Technology , Harbin 150001 ,China) Abstract :A realization of multi2scroll chaos generation is presented using two CNN cells wit h hysteresis outp ut f unction in t he paper. First , t he CNN template can be ascertained t hrough expressing t he unstable second2order linear continuous system wit h t he state f unction of CNN ; Second , t he state f unction of CNN and t he hysteresis outp ut f unction are realized with operational amplifier ; Finally , double scroll and three scroll chaos attractor are realized using different hysteresis f unctions. The proposed system uses only oper2 ational amplifiers , resistors and capacitors , so it’s easy to be integrated. The results’validity is illustrated by t he circuit simulation using Orcad Pspice. Keywords :multi2scroll ;hysteresis f unction ;chaos generator ;CNN 收稿日期 :2006212205. 基金项目 :国家自然科学基金资助项目(60474016) . 作为一种普遍存在的非线性现象 ,混沌的发现 对科学的发展具有深远的影响. 混沌行为是确定性 因素导致的类似随机运动的行为 ,即一个可由确定 性方程描述的非线性系统 ,其长期行为表现为明显 的随机性和不可预测性. 细胞神经网络[1 ] (CNN) 是一种局域互联网络 , 具有结构简单 ,易于集成等优点 ,使其在混沌电路领 域有着广泛的应用. 细胞神经网络是非线性的动态 系统 ,因此应用细胞神经网络可以构建混沌系统 ,这 对研究混沌行为有着重要意义 ,并且为混沌电路的 仿真分析提供了一条便捷的途径. 近几年来 ,滞环输出函数的 CNN 引起人们的 广泛关注[224 ] ,由于滞环函数是很常用的函数 ,在系 统中引入滞环函数(或滞回比较器) 可以提高系统的 可靠性 ,防止系统的误动作. 本文利用 2 个滞环 CNN 细胞来实现多涡卷滞环混沌发生器 ,对实现的 过程进行了分析并对电路的实现进行了阐述 ,最后 , 应用 Orcad Pspice 对本文的设计进行了电路仿真 , 验证了结论的正确性. 1 滞环混沌发生器 根据文献[1 ] ,无量纲滞环混沌发生器的状态方 程为 Ûx1 Ûx2 = σ ω - ω σ x1 x2 + 0 h( x1 ) , (1) 式中 : h( x1 ) 为滞环函数 : h( x1 ) = 1 x1 ≥- 1 , - 1 x1 ≤1 , 保持不变 - 1 < x1 < 1. (2) 在σ和ω同为小于 1 的正数时有ω= 1 - σ2 . 在这 种情况下 ,式(1) 的特征值λ=σ±jω具有正实部(也 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
·64- 智能系统学报 第2卷 就是说系统不稳定).在Q*=(“,·)和Q°= 相影响.如果用Sr(i,)表示C(i,神经元和临近 (-ω,⑨处有2个不稳定的平衡点. 其他神经元的集合,CNN网络的连接关系可以用下 式2)中的滞环函数如图1(a)所示.当x1达到 面的式子表示: 左门限值时,h(x)跳变到1;而当x1达到右门限值 S,(i,)= 时,h(x1)跳变到-1.对图1(a)所示的滞环函数变 (Ck,》,amae1k.1,11-j1}≤) 形可得到图1b)所示的滞环函数,其函数表达式如 (5 式3):将图1b)所示的滞环函数向第三象限进行 C1.1) C(1.2) C13) C14 拓展,得到图1(c所示的滞环函数,其函数表达式 如式4,由于h(x1)有3种不同取值,因此系统有 3个平衡点. C2.1) C2.2 C2.3) C2.4) h(x) C3.1) C3.2 C3.3) C3.4) C4.1) C(42) C4.3) C4.4) 图244的二维细胞神经网络的基本结构 (a)滞环函数一 6)滞环函数二 Fig.2 The 4 X4 two dimensional CNN h2(x) 细胞神经网络的通用无量纲非线性状态方程为 =+a++. (6) 式中:n为邻域细胞数,x,为状态变量,y,为细胞的 x(0 输出,标准CNN细胞的输出函数为分段线性函数, 本文取输出函数为式2)~(4)中的任一种滞环函 数,a:和s.是常数,y为门限值.在2个CNN细胞 (c)滞环函数三 全连接的情况下,动力学模型被描述为如下方程: 图1几种不同的形式的滞环函数 x1=-x1+a1y1+am22+S1x1+512X2+1, Fig.I The different kinds of hysteresis functions x2=-2+1y1+22+S21x1+S22X2+2. 0, x10 (7) h (x1)= 1 1别, (3) 式中:x1和2为状态变量,n和2为相应的输出. 保持不变,0<x1<1. 为了应用于滞环混沌发生器,系统6)中的下列参数 -1. x1≤-1, a:S必须适当选取,以得到式1)所描述的动力学 定义:h.1(x 0 x1别, 行为.比较式(1)和式7)中各项系数,并去掉无关项 保持不变,-1<x1<0 得到式8): 则拓展后的滞环函数的表达式为 x1=(1-1)1+12x2, (8) h加(x)=h(x)+h.1(x). 4) x2=S21x1+(S22-1)x2+m1y1. 式6)和式7)中各项系数为 2滞环细胞神经网络模型 1=2=0;am2=m2=Qa1=0;1=1, 标准CNN是由美国加州大学伯克莱分校的L 51=22=0+1;5m=.21=0yn=h(x1) O.Chua和L.Yang于1988年在HOPFIELD网络 这样,就用CNN的通用无量纲状态方程表示 的基础上发展的局部连接网络).CNN是一种非线 了滞环混沌发生器的状态方程,式(8)就是滞环混沌 性局域连接神经网络,由许多细胞组成.为了说明方 发生器CNN实现的状态方程模型 便,图2仅给出一个44的二维细胞神经网络. 3滞环细胞神经网络细胞模型的设计 在一个M×N的二维神经元排列空间内 C(i,(1M,1≤到≤N)表示第i行、第j列的 3.1CNN细胞状态模型运算放大器的设计 神经元,它只同周围r邻域范围内的神经元相连,而 上节中己经建立CNN的无量纲方程式(6),要 不直接相连的细胞则通过连续动态的传播效应而互 用运算放大器来实现它,必须把它变换到时间域内 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
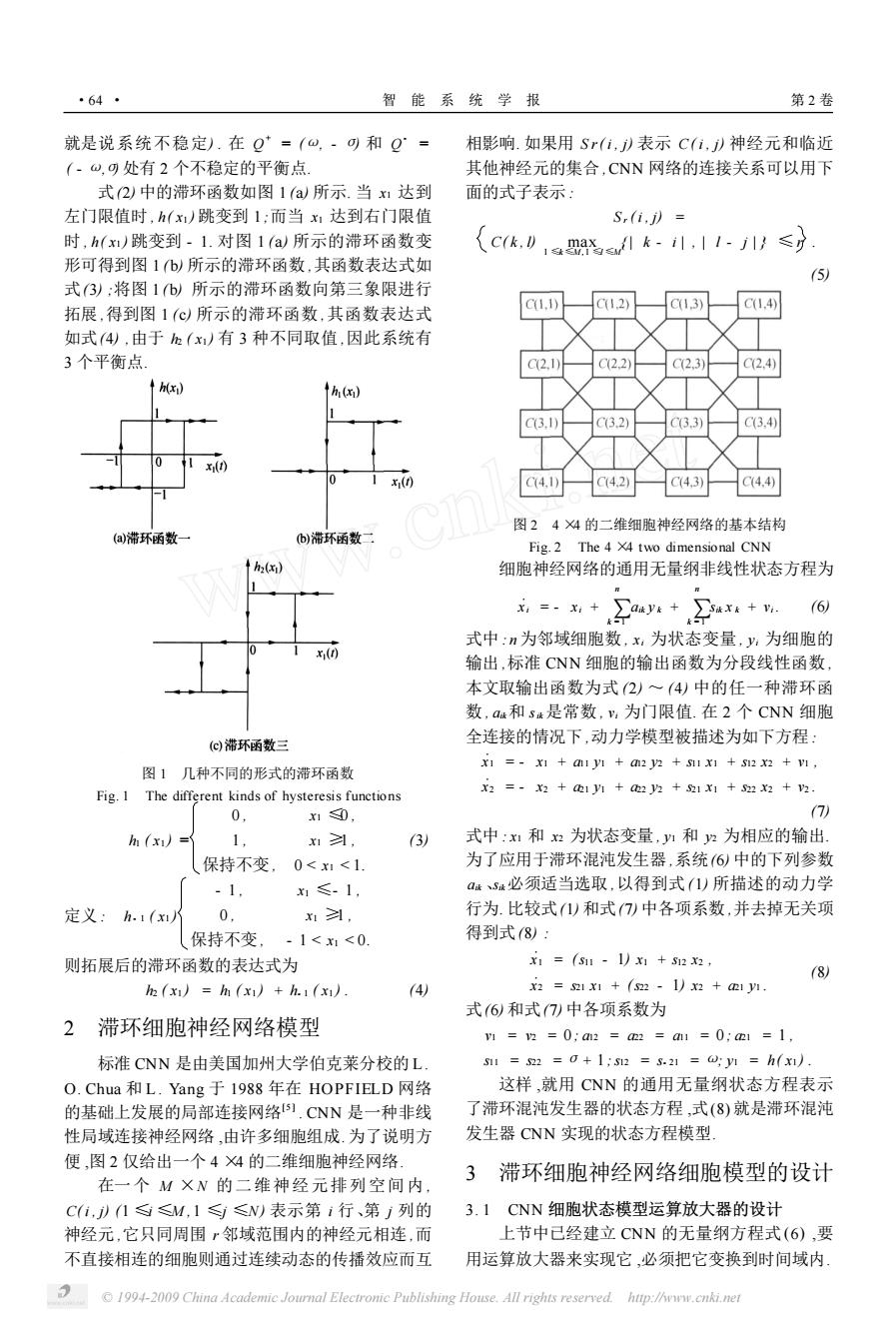
就是说系统不稳定) . 在 Q + = (ω, - σ) 和 Q - = ( - ω,σ) 处有 2 个不稳定的平衡点. 式(2) 中的滞环函数如图 1 (a) 所示. 当 x1 达到 左门限值时 , h( x1 ) 跳变到 1 ;而当 x1 达到右门限值 时 , h( x1 ) 跳变到 - 1. 对图 1 (a) 所示的滞环函数变 形可得到图 1 ( b) 所示的滞环函数 ,其函数表达式如 式(3) ;将图 1 ( b) 所示的滞环函数向第三象限进行 拓展 ,得到图 1 (c) 所示的滞环函数 ,其函数表达式 如式(4) ,由于 h2 ( x1 ) 有 3 种不同取值 ,因此系统有 3 个平衡点. 图 1 几种不同的形式的滞环函数 Fig. 1 The different kinds of hysteresis functions h1 ( x1 ) = 0 , x1 ≤0 , 1 , x1 ≥1 , 保持不变 , 0 < x1 < 1. (3) 定义 : h- 1 ( x1 ) - 1 , x1 ≤- 1 , 0 , x1 ≥1 , 保持不变 , - 1 < x1 < 0. 则拓展后的滞环函数的表达式为 h2 ( x1 ) = h1 ( x1 ) + h- 1 ( x1 ) . (4) 2 滞环细胞神经网络模型 标准 CNN 是由美国加州大学伯克莱分校的 L . O. Chua 和 L . Yang 于 1988 年在 HOPFIELD 网络 的基础上发展的局部连接网络[5 ] . CNN 是一种非线 性局域连接神经网络 ,由许多细胞组成. 为了说明方 便 ,图 2 仅给出一个 4 ×4 的二维细胞神经网络. 在一个 M ×N 的二维神经元排列空间内 , C( i , j) (1 ≤i ≤M , 1 ≤j ≤N) 表示第 i 行、第 j 列的 神经元 ,它只同周围 r 邻域范围内的神经元相连 ,而 不直接相连的细胞则通过连续动态的传播效应而互 相影响. 如果用 S r( i , j) 表示 C( i , j) 神经元和临近 其他神经元的集合 ,CNN 网络的连接关系可以用下 面的式子表示 : S r ( i , j) = C( k , l) max 1 ≤k ≤M ,1 ≤l ≤M {| k - i | , | l - j | } ≤r . (5) 图 2 4 ×4 的二维细胞神经网络的基本结构 Fig. 2 The 4 ×4 two dimensional CNN 细胞神经网络的通用无量纲非线性状态方程为 Ûx i = - xi + ∑ n k =1 aik y k + ∑ n k = 1 sik x k + vi . (6) 式中 : n 为邻域细胞数 , xi 为状态变量 , yi 为细胞的 输出 ,标准 CNN 细胞的输出函数为分段线性函数 , 本文取输出函数为式 (2) ~ (4) 中的任一种滞环函 数 , aik和 sik 是常数 , vi 为门限值. 在 2 个 CNN 细胞 全连接的情况下 ,动力学模型被描述为如下方程 : Ûx1 = - x1 + a11 y1 + a12 y2 + s11 x1 + s12 x2 + v1 , Ûx2 = - x2 + a21 y1 + a22 y2 + s21 x1 + s22 x2 + v2 . (7) 式中 : x1 和 x2 为状态变量 , y1 和 y2 为相应的输出. 为了应用于滞环混沌发生器 ,系统(6) 中的下列参数 aik 、sik必须适当选取 ,以得到式 (1) 所描述的动力学 行为. 比较式(1) 和式(7) 中各项系数 ,并去掉无关项 得到式(8) : Ûx1 = (s11 - 1) x1 + s12 x2 , Ûx2 = s21 x1 + (s22 - 1) x2 + a21 y1 . (8) 式(6) 和式(7) 中各项系数为 v1 = v2 = 0 ; a12 = a22 = a11 = 0 ; a21 = 1 , s11 = s22 =σ+ 1 ;s12 = s- 21 = ω; y1 = h( x1 ) . 这样 ,就用 CNN 的通用无量纲状态方程表示 了滞环混沌发生器的状态方程 ,式(8) 就是滞环混沌 发生器 CNN 实现的状态方程模型. 3 滞环细胞神经网络细胞模型的设计 3. 1 CNN 细胞状态模型运算放大器的设计 上节中已经建立 CNN 的无量纲方程式 (6) ,要 用运算放大器来实现它 ,必须把它变换到时间域内. ·64 · 智 能 系 统 学 报 第 2 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第3期 刘洪臣,等:滞环细胞神经网络实现多涡卷混沌发生器 *65· 令t=lRC,则有 路各参数的选取 3.2CNN滞环输出模型运算放大器的设计 图4所示为细胞输出电路,图4(a)和(b)的输 入-输出特性是图1(a)和(c)的滞环函数.对于图 9) 4(a),运算放大器U2B及其周边电阻构成滞环比较 令:=ay()+Sx()+v,则式9)可以简 器,运算放大器U2C构成比例放大器,调节R1g可将 化为 滞环比较器输出调整到所需的范围,而2D构成反 相器,因此Rg=R0 G=.立+ d·R。+R (10) 式(10)可以用运算放大器电路实现3」,图3为式 (7)所示的状态方程.细胞1和细胞2的第1级运放 (U1A和U1D)为反相求和器,实现的是将 +,+2w+ 《 反相求和,也就是式10)中的等号右边,由此可以根 据各自的放大倍数来确定U1A和U1D周边的电阻 (a)图1(a)所示滞环函数的电路模型 值,可以证明:S·1=B、 S21= R2 R -X《-M M X《M 《-X 0 3R UBA (a)细胞1 LMB24 X《M 《-X R 《 b)图【©)所示滞环函数的电路模型 图4滞环函数的电路模型 b)细胞2 Fig.4 The circuit implementation of hysteresis function 图3CNN细胞状态单元的电路实现 由于运放U2B工作在正反馈状态,因此输出只 Fig.3 The circuit implementation for the considered CNN cell 有士15V2种状态.当输出为+15V时,根据叠加 Rs an =Rug Sn2-1=R 定理(用U,和U.表示运算放大器的同相和反相输 11) 入电压,U1表示信号x1输入端的电压): U1A和U1D的输出:送入第2级运放(U1B U+R14 XU a/(R14 Ris)+Ux XRis/(R14+ 和U2A),电阻R4和电容G及电阻R1和电容C R1s)调节R2使U.=k(-15V≤5V),因此当 构成的积分电路对:进行积分便得到细胞1和细胞 U+=U.=k时输出跳变到-15V,于是得到U1= 2的状态x1和状态x2.根据U1B和U2A的输入端 列节点电流方程有 k-15XR+kXR时跳变同理,当输出为-15 R15 C+。边=0 (12) V时,输入临界跳变电压U:= 该方程式与式(10)等价,由此可知该运算放大 k+l5)XRM+kXRs.要实现图1(a)所示的滞环 R15 器模型第1级和第2级运放实现了CNN细胞的状 函数,即临界跳变点为1,令U1=·1,U=1得 态方程.电阻R、R6和运放U1C及电阻R12、R13和 k=0且R1s/R14=15/1. 运放U2B构成反相器,用以得到-x1和-x2,于是 对于图4(b),用U1+,U1.分别表示U2B的同 可得R=R、R2=R.利用上述关系即可确定电 相及反相输入电压,用U2+,U2.表示U3A的同相 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved htp://www.cnki.net
令τ= t/ RbCi ,则有 Ci = d x1 dt = - xi Rb + 1 Rb ∑ n k = 1 aik y k ( t) + ∑ n k =1 Sik x k ( t) + vi , (9) 令 z = ∑ n k = 1 aik y k ( t) + ∑ n k = 1 Sik x k ( t) + v ,则式 (9) 可以简 化为 Ci d x1 dt = - xi Rb + 1 Rb z . (10) 式(10) 可以用运算放大器电路实现[1 ,3 - 4 ] ,图 3 为式 (7) 所示的状态方程. 细胞 1 和细胞 2 的第 1 级运放 (U1A 和 U1D) 为反相求和器 ,实现的是将 - xi Rb + 1 Rb ∑ n k =1 aik y k ( t) + ∑ n k = 1 Sik x k ( t) + vi 反相求和 ,也就是式(10) 中的等号右边 ,由此可以根 据各自的放大倍数来确定 U1A 和 U1D 周边的电阻 值 ,可以证明 :S11 - 1 = R3 R1 S12 = R3 R2 S21 = R10 R7 . 图 3 CNN 细胞状态单元的电路实现 Fig. 3 The circuit implementation for the considered CNN cell S22 - 1 = R10 R8 a11 = R10 R9 . (11) U1A 和 U1D 的输出 z 送入第 2 级运放 (U1B 和 U2A) ,电阻 R4 和电容 C1 及电阻 R11 和电容 C2 构成的积分电路对 z 进行积分便得到细胞 1 和细胞 2 的状态 x1 和状态 x2 . 根据 U1B 和 U2A 的输入端 列节点电流方程有 Ci d xi dt + ( xi - z) Rb = 0. (12) 该方程式与式(10) 等价 ,由此可知该运算放大 器模型第 1 级和第 2 级运放实现了 CNN 细胞的状 态方程. 电阻 R5 、R6 和运放 U1C 及电阻 R12 、R13 和 运放 U2B 构成反相器 ,用以得到 - x1 和 - x2 ,于是 可得 R5 = R6 、R12 = R13 . 利用上述关系即可确定电 路各参数的选取. 3. 2 CNN 滞环输出模型运算放大器的设计 图 4 所示为细胞输出电路 ,图 4 (a) 和( b) 的输 入 - 输出特性是图 1 (a) 和 (c) 的滞环函数. 对于图 4 (a) ,运算放大器 U2B 及其周边电阻构成滞环比较 器 ,运算放大器 U2C 构成比例放大器 ,调节 R18可将 滞环比较器输出调整到所需的范围 ,而 2D 构成反 相器 ,因此 R19 = R20 . 图 4 滞环函数的电路模型 Fig. 4 The circuit implementation of hysteresis function 由于运放 U2B 工作在正反馈状态 ,因此输出只 有 ±15 V 2 种状态. 当输出为 + 15 V 时 ,根据叠加 定理(用 U + 和 U - 表示运算放大器的同相和反相输 入电压 ,U x1表示信号 x1 输入端的电压) : U + = R14 ×Uout / ( R14 + R15 ) + U x1 ×R15 / ( R14 + R15 ) 调节 R12使 U - = k ( - 15 V ≤k ≤15 V) ,因此当 U + = U - = k 时输出跳变到 - 15 V ,于是得到U x1 = ( k - 15) ×R14 + k ×R15 R15 时跳变. 同理 ,当输出为 - 15 V 时 , 输 入 临 界 跳 变 电 压 U′x1 = ( k + 15) ×R14 + k ×R15 R15 . 要实现图 1 ( a) 所示的滞环 函数 ,即临界跳变点为 ±1 ,令 U x1 = - 1 , U′x1 = 1 得 k = 0 且 R15 / R14 = 15/ 1. 对于图 4 ( b) ,用 U1 + , U1 - 分别表示 U2B 的同 相及反相输入电压 ,用 U2 + , U2 - 表示 U3A 的同相 第 3 期 刘洪臣 ,等 :滞环细胞神经网络实现多涡卷混沌发生器 ·65 · © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·66 智能系统学报 第2卷 及反相输入电压.调节电阻R2使U1.=k,调节电阻 细胞1.R=1000k,及=50.07k,R=50k, 2!使U2.=-k.跳变点的分析与上面双涡卷电路 R=100k,R5=R=10k,CG=104F 相同,U2B的临界跳变点为U=0,U=1,而 R7=50.07k.Rs=1000k,Rg=R1o=50k U3A的临界跳变点为U1=-1,U=0得 细胞2: R1=100k,CG2=104F, k-15/31且=0,光-0临界跳变电压为0 =1’R23 图41a) R12=R13=10k,R14=1k,R15=30k R16=150k,R1g=R19=R20=10k, 和1V 3=R2=10k,R4=B3=1k,R5=R4=30k 4仿真分析 图4b R6=R7=150k,R8=R9=R0=10k 本文以图I(a)、(c)所示的滞环函数作为CNN 5结束语 的输出函数,应用Orcad Pspice对其进行电路仿真 分析,仿真结果如图5所示」 对CNN细胞间的动力学行为的研究及用简单 20 的电路实现各种动力学行为(包括混沌行为)受到了 人们的广泛关注.本文应用2个具有滞环输出函数 的CNN细胞实现了多涡卷混沌发生器,建立了 CNN细胞的状态方程及滞环输出函数的运放模型, 并实现了双涡卷和三涡卷混沌吸引子.该系统是由 电阻、电容及运算放大器构成,因此,本文的方案易 于实现集成化.仿真结果表明本文的方案是可行的」 参考文献: 120.80.40040.8121.62024 [1]ARENA P,BAGLIO S,FORTUNA L,et al.Chua's x/V (a)双涡卷混沌吸引子的相平面图 circuit can be generated by CNN cells[J ]IEEE Trans on CAS1,1995,42(2):123.125. 20 [2]SHINJI N,TOSHIMICHI S.An RC OTA hysteresis chaos generator [J ]IEEE Trans on CAS-I,1996,43 (12):1019.1021. [3]AISSI C,SHAMS A.A CNN implementation of a hys- teresis chaos generator[A].IEEE ISCAS'99[C].Orlan- do,USA,1999. [4]ARENA P,BAGLIO S,FORTUNA L,et al.Hyper- chaos from cellular neural networks[J].Electronics Let- ters,1995,31(4):250-251. 29%5-20本$1005005101520235 [5]CHUA L O,YANGL.Cellular neural networks:theo- XNV rys[J ]IEEE Trans on CAS-I,1988,35(10):1257- b)双涡卷混沌吸引子的相平图 1272. [6]CHUA L O,YANG L.Cellular neural networks:appli- 图5混沌吸引子的相平面图 cations [J].IEEE Trans on CAS-I,1988,35(10):1273 Fig.5 The chaotic attractor .1290. 选择参数0=0.05,初始条件为 作者简介: x10)=0.5,x20)=0.根据给定的0=0.05计 刘洪臣,男,1977年生,讲师,博士研 究生,主要研究方向为细胞神经网络、非 算,d=-d=0.9987,于是电路的状态方程为 线性电路、图像处理等。 x1=-x1+1.05x1+0.9987x2, (13) Email fenmiao @hit.edu.cn. x2=-x2+y1-0.9987x1+1.05x2. 于是有11=2=1.05,s2= 0.9987,21=-0.9987,am1=am2=a2=0,a1=1 各电阻、电容的参数如下: 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
及反相输入电压. 调节电阻 R12使 U1 - = k ,调节电阻 R21使 U2 - = - k. 跳变点的分析与上面双涡卷电路 相同 , U2B 的临界跳变点为 U x1 = 0 , U′x1 = 1 , 而 U3A 的 临 界 跳 变 点 为 U x1 = - 1 , U′x1 = 0 得 k = 15/ 31且 R15 R14 = 30 1 , R24 R23 = 30 1 . 临界跳变电压为 0 和 ±1 V. 4 仿真分析 本文以图 1 (a) 、(c) 所示的滞环函数作为 CNN 的输出函数 ,应用 Orcad Pspice 对其进行电路仿真 分析 ,仿真结果如图 5 所示. 图 5 混沌吸引子的相平面图 Fig. 5 The chaotic attractor 选择参数σ= 0. 05 ,初始条件为 x1 (0) = 0. 5 , x2 (0) = 0. 根据给定的σ= 0. 05 计 算 ,ω= 1 - σ2 = 0. 998 7 ,于是电路的状态方程为 Ûx1 = - x1 + 1. 05 x1 + 0. 998 7 x2 , Ûx2 = - x2 + y1 - 0. 998 7 x1 + 1. 05 x2 . (13) 于是有 s11 = s22 = 1. 05 ,s12 = 0. 998 7 ,s21 = - 0. 998 7 , a11 = a12 = a22 = 0 , a21 = 1 各电阻、电容的参数如下 : 细胞 1 : R1 = 1 000 k , R2 = 50. 07 k , R3 = 50 k , R4 = 100 k , R5 = R6 = 10 k , C1 = 10μF, 细胞 2 : R7 = 50. 07 k , R8 = 1 000 k , R9 = R10 = 50 k , R11 = 100 k , C2 = 10μF, 图 4 (a) : R12 = R13 = 10 k , R14 = 1 k , R15 = 30 k , R16 = 150 k , R18 = R19 = R20 = 10 k , 图 4(b) : R13 = R22 = 10k , R14 = R23 = 1k , R15 = R24 = 30k , R16 = R17 = 150k , R18 = R19 = R20 = 10k 5 结束语 对 CNN 细胞间的动力学行为的研究及用简单 的电路实现各种动力学行为(包括混沌行为) 受到了 人们的广泛关注. 本文应用 2 个具有滞环输出函数 的 CNN 细胞实现了多涡卷混沌发生器 ,建立了 CNN 细胞的状态方程及滞环输出函数的运放模型 , 并实现了双涡卷和三涡卷混沌吸引子. 该系统是由 电阻、电容及运算放大器构成 ,因此 ,本文的方案易 于实现集成化. 仿真结果表明本文的方案是可行的. 参考文献 : [1 ]ARENA P , BA GL IO S , FORTUNA L , et al. Chua’s circuit can be generated by CNN cells[J ]. IEEE Trans on CAS2I , 1995 , 42 (2) :123 - 125. [2 ] SHINJ I N , TOSHIMICHI S. An RC O TA hysteresis chaos generator [J ]. IEEE Trans on CAS2I , 1996 , 43 (12) : 1019 - 1021. [3 ]AISSI C , SHAMS A. A CNN implementation of a hys2 teresis chaos generator[A ]. IEEE ISCAS’99[C]. Orlan2 do , USA , 1999. [4 ] ARENA P , BA GL IO S , FORTUNA L , et al. Hyper2 chaos from cellular neural networks[J ]. Electronics Let2 ters , 1995 , 31 (4) : 250 - 251. [5 ]CHUA L O , YAN G L. Cellular neural networks: theo2 rys[J ]. IEEE Trans on CAS2I , 1988 , 35 (10) : 1257 - 1272. [6 ]CHUA L O , YAN G L. Cellular neural networks:appli2 cations [J ] . IEEE Trans on CAS2I , 1988 , 35 (10) : 1273 - 1290. 作者简介 : 刘洪臣 ,男 ,1977 年生 ,讲师 ,博士研 究生 ,主要研究方向为细胞神经网络、非 线性电路、图像处理等. E2mail :fenmiao @hit. edu. cn. ·66 · 智 能 系 统 学 报 第 2 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net