智能系统：含有障碍物环境下多智能体系统的聚集行为.pdf_大学文库

第2卷第5期智能系统学报 Vol.2№5 2007年10月 CAAI Transactions on Intelligent Systems 0ct.2007 含有障碍物环境下多智能体系统的聚集行为王建春，谢广明 (北京大学工学院，北京100871) 摘要：研究多动态智能体系统在含有障碍物环境下的聚集行为.首先建立一类多智能体系统在有障碍物的环境下的数学模型，以描述个体在遇到障碍物时的行为特点.其次从理论上证明了整个多智能体系统聚集行为的稳定性，指出在有障碍物环境下仍然能够涌现系统的聚集行为.最后，通过数值模拟验证了有关结论的有效性关键词：多智能体系统：聚集行为：障碍物：稳定性分析中图分类号：TP13文献标识码：A文章编号：1673-4785(2007)050078-06 Aggregation behaviors of multi Agent systems in an environment with obstacles WANGJianchun,XIE Guang-ming (College of Engineering,Peking University,Beijing 100871,China) Abstract:To study aggregation behaviors of multiple dynamic Agent systems in an environment with obsta- cles,a mathematical model was established.It describes the behavioral characteristics of each Agent when meeting an obstacle.Next,the stability of aggregation behavior in an overall system was proved,showing that there is still the emergence of aggregation behavior of a whole system in an environment with obsta- cles.Finally,simulation data is given to prove the efficiency of the theory. Keywords:multi-Agent systems;aggregation behavior;obstacle;stability analysis 在自然界中，各种生物，如鸟、鱼、细菌等，无时型不仅对理解自然界有用，也有助于机器智能体的无刻不在运动，而且运动往往以群体的形式出现.在实际应用.文献[11]中给出了一个特殊的智能体运一群同类生物的运动中，个体运动极为复杂，但整体动模型，分析了运动的稳定性.文献12]对文献[11] 上往往体现出一些规律.生物学家很早就开始观察所给模型下描述智能体运动的函数作了很大的推这些运动，认识到了一些特定的规律.他们进行广，得到了该类形式下非常一般的运动模型，证明了了理论分析，建立各种数学模型，并将这些模型用于聚集行为的稳定性.考虑到在实际环境中常常存在实际的预测，得到了一些结果5割.在大多数情况智能体运动的障碍，本文建立了智能体在有障碍物下，群体的运动可看作是两两个体间相互作用的结环境下的一种运动模型.模型对描述运动的函数选果，几乎所有的模型都建立在此假设之上.实践证明择允许有相当大的任意性，并证明了群体行为的稳这样做的合理性与简洁性】.于是，用几个简单的定性，可视为文献[12]的运动模型的推广. 微分方程来表示一群生物的复杂运动，从理论上定性和定量地分析看似繁杂的、无处入手的生物群体 1模型运动.其中稳定性分析最为普遍9).随着硬件水如图1所示，M个智能体在有障碍物的平面上平的提高、仿生技术的发展，出现了以群体形式出现运动，用x1,,xM表示这M个智能体的位置，的大量的机器智能体活动.关于群体运动的数学模对于二智能体x、x,在不穿越障碍物的情况下，连收稿日期：200612-21. 接x、x的最短路径称为x、x之间的最短路径基金项目：国家自然科学基金资助项目(60404001) 记作r(x,x).r(x,x)的长度叫x、x之间的有效 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

第 2 卷第 5 期智能系统学报 Vol. 2 №. 5 2007 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2007 含有障碍物环境下多智能体系统的聚集行为王建春 ,谢广明 (北京大学工学院 ,北京 100871) 摘要 :研究多动态智能体系统在含有障碍物环境下的聚集行为. 首先建立一类多智能体系统在有障碍物的环境下的数学模型 ,以描述个体在遇到障碍物时的行为特点. 其次从理论上证明了整个多智能体系统聚集行为的稳定性 , 指出在有障碍物环境下仍然能够涌现系统的聚集行为. 最后 ,通过数值模拟验证了有关结论的有效性. 关键词 :多智能体系统 ;聚集行为 ;障碍物 ;稳定性分析中图分类号 : TP13 文献标识码 :A 文章编号 :167324785 (2007) 0520078206 Aggregation behaviors of multi2Agent systems in an environment with obstacles WAN G Jian2chun , XIE Guang2ming (College of Engineering , Peking University , Beijing 100871 , China) Abstract :To st udy aggregation behaviors of multiple dynamic Agent systems in an environment wit h obsta2 cles , a mathematical model was established. It describes t he behavioral characteristics of each Agent when meeting an obstacle. Next , the stability of aggregation behavior in an overall system was proved ,showing t hat t here is still the emergence of aggregation behavior of a whole system in an environment wit h obsta2 cles. Finally , simulation data is given to prove the efficiency of the t heory. Keywords :multi2Agent systems; aggregation behavior ; obstacle ; stability analysis 收稿日期 :2006212221. 基金项目 :国家自然科学基金资助项目(60404001) . 在自然界中 ,各种生物 ,如鸟、鱼、细菌等 ,无时无刻不在运动 ,而且运动往往以群体的形式出现. 在一群同类生物的运动中 ,个体运动极为复杂 ,但整体上往往体现出一些规律. 生物学家很早就开始观察这些运动 ,认识到了一些特定的规律[1 - 4 ] . 他们进行了理论分析 ,建立各种数学模型 ,并将这些模型用于实际的预测 ,得到了一些结果[5 - 8 ] . 在大多数情况下 ,群体的运动可看作是两两个体间相互作用的结果 ,几乎所有的模型都建立在此假设之上. 实践证明这样做的合理性与简洁性[1 - 2 ] . 于是 ,用几个简单的微分方程来表示一群生物的复杂运动 ,从理论上定性和定量地分析看似繁杂的、无处入手的生物群体运动. 其中稳定性分析最为普遍[9 - 10 ] . 随着硬件水平的提高、仿生技术的发展 ,出现了以群体形式出现的大量的机器智能体活动. 关于群体运动的数学模型不仅对理解自然界有用 ,也有助于机器智能体的实际应用. 文献[ 11 ]中给出了一个特殊的智能体运动模型 ,分析了运动的稳定性. 文献[12 ]对文献[11 ] 所给模型下描述智能体运动的函数作了很大的推广 ,得到了该类形式下非常一般的运动模型 ,证明了聚集行为的稳定性. 考虑到在实际环境中常常存在智能体运动的障碍 ,本文建立了智能体在有障碍物环境下的一种运动模型. 模型对描述运动的函数选择允许有相当大的任意性 ,并证明了群体行为的稳定性 ,可视为文献[12 ]的运动模型的推广. 1 模型如图 1 所示 , M 个智能体在有障碍物的平面上运动 ,用 x1 , x2 , …, x M 表示这 M 个智能体的位置. 对于二智能体 xi 、x j ,在不穿越障碍物的情况下 ,连接 xi 、x j 的最短路径称为 x i 、x j 之间的最短路径 , 记作 r( xi , x j) . r( xi , x j) 的长度叫 xi 、x j 之间的有效

第5期王建春，等：含有障碍物环境下多智能体系统的聚集行为。79· 距离，记作P(x,x.并用x,x)表示r(x,x在 2极短路径分析 x处的单位切向量，用(x,x表示r(x,在x 处的单位切向量，下面分析两点之间对障碍物绕行的极短路径， rx.x) 如图2所示，在x:,x两点之间有一个障碍物，直线 xx,将障碍物切下一块，记作区域D. x 图1有障碍物的环境下多智能体系统 Fig.I MultiAgent systems in an obstacle environment 图2x,x之间的极短路径 Fig.2 The shortest path between x,and x 当智能体x,不在任何障碍物边缘时，x,具有速设L(x,x)是x,x两点间从障碍物下方绕行度：x=∑g(P(x,x)(x,x,g(9是一个定义的极短路径，则直线xx)同曲线L(x,x所围成的区域E覆盖了区域D 在0，+9上的连续函数，满足：存在0<m<, 首先有：区域E是凸形.否则，如图2所示，曲当0<p<m时，g(9④，当<P时，g(p0.其线L(x,x上的一段AB凹进去，则当直线AB代替物理意义是，2个智能体足够近时相互排斥，足够远那段曲线AB时所得的L'(x,x比原先的L(x,x 时相互吸引要短，矛盾当智能体x,在某个障碍物边上时，设x,的应引理1最短路径L(x,x)除去在障碍物边上有速度为v:=∑gP(x,x)(x,x,设该点处的部分，其余部分是一些直线段，即：L(x,x)在障碍物之外的部分必是直线，障碍物的单位外法向量为n,则当，·n0时，障碍物对智能体的运动不产生影响，于是取x?=.但当，·n<0时，障碍物·n会使智能体法向方向的速度分量变为零，从而导致智能体沿障碍物切向方向运动或停止.因此，x,的速度x:取v,在切向方向的投影，也即xt=w-(w·n,则x?·n=0 若记w=∑gp(x,)B(x,x,则对任何图3引理1示意图情况都有：w·x=‖x?2,这是因为：当x?= Fig.3 A sketch for Lemma 1 时，显然y,·x:=lx:2而当x:=,-(m·n 证明如图3所示，由两点之间直线最短可知时，xr·n=0,w=xt+(w·nn,从而，·x?= 当L(x,x)的某一段AB在障碍物之外且不是直线 (xr+(w·n)nl·xr=‖xt2+(w·n)n·xr= 时，可以找到AB上足够近的两点A'、B',使川xw2 L(x,x的AB段不是直线，且连接A和B'2点对于连接x,x的最短路径，若存在障碍物，可的线段与障碍物不相交，则用直线AB替代原先的能是2种绕行障碍物方式中的某一种.将每种绕法 AB段后，可得在该种绕行方式下更短的路径，矛下的最短的路径均称为有效极短路径，简称极短路盾径，分别记为L1(x,、L2(x,x.记Lkx,x)的一般地，绕行多个障碍物的极短路径是由一些长度为S(x,x),记Ls(x,x在点x:处的单位切线段和障碍物的边界线组成，这些线段与障碍物相向量为Y(x,),k=1,2 切或相接即障碍物在直线一侧). 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

距离 ,记作ρ( xi , x j) . 并用β( xi , x j) 表示 r( xi , x j) 在 xi 处的单位切向量 ,用β( x j , xi) 表示 r( xi , x j) 在 x j 处的单位切向量. 图 1 有障碍物的环境下多智能体系统 Fig. 1 Multi2Agent systems in an obstacle environment 当智能体 xi 不在任何障碍物边缘时 , xi 具有速度 : x·i = ∑ M j = 1 j ≠i g (ρ( xi , x j) )β( xi , x j) , g (ρ) 是一个定义在(0 , + ∞) 上的连续函数 ,满足 :存在 0 < r0 < R0 , 当 0 <ρ< r0 时 , g (ρ) ≤0 ,当 R0 <ρ时 , g (ρ) ≥0. 其物理意义是 ,2 个智能体足够近时相互排斥 ,足够远时相互吸引. 当智能体 xi 在某个障碍物边上时 ,设 xi 的应有速度为 v i = ∑ M j = 1 j ≠i g (ρ( xi , x j) )β( xi , x j) ,设该点处障碍物的单位外法向量为 n ,则当 vi ·n ≥0 时 ,障碍物对智能体的运动不产生影响 ,于是取 x·i = vi . 但当 vi ·n < 0 时 ,障碍物 vi ·n 会使智能体法向方向的速度分量变为零 ,从而导致智能体沿障碍物切向方向运动或停止. 因此 , xi 的速度 x·i 取 v i 在切向方向的投影 ,也即 x·i = vi - ( vi ·n) n ,则 x·i ·n = 0. 若记 vi = ∑ M j = 1 j ≠i g (ρ( xi , x j ) )β( xi , x j ) ,则对任何情况都有 : vi ·x·i = ‖x·i ‖2 , 这是因为 :当 x·i = vi 时 ,显然 vi ·x·i = ‖x·i ‖2 ,而当 x·i = vi - ( vi ·n) n 时 , x·i ·n = 0 , vi = x·i + ( vi ·n) n , 从而 , vi ·x·i = ( x·i + ( vi ·n) n) ·x·i = ‖x·i ‖2 + ( vi ·n) n ·x·i = ‖x·i ‖2 . 对于连接 xi , x j 的最短路径 ,若存在障碍物 ,可能是 2 种绕行障碍物方式中的某一种. 将每种绕法下的最短的路径均称为有效极短路径 ,简称极短路径 ,分别记为 L1 ( xi , x j) 、L2 ( xi , x j) . 记 L k ( xi , x j) 的长度为 sk ( xi , x j) ,记 L k ( xi , x j) 在点 xi 处的单位切向量为γk ( xi , x j) , k = 1 ,2. 2 极短路径分析下面分析两点之间对障碍物绕行的极短路径. 如图 2 所示 ,在 xi , x j 两点之间有一个障碍物 ,直线 xi x j 将障碍物切下一块 ,记作区域 D. 图 2 xi , x j 之间的极短路径 Fig. 2 The shortest path between xi and x j 设 L ( xi , x j) 是 xi , x j两点间从障碍物下方绕行的极短路径 ,则直线 xi x j 同曲线 L ( xi , x j) 所围成的区域 E 覆盖了区域 D . 首先有 :区域 E 是凸形. 否则 ,如图 2 所示 ,曲线 L ( xi , x j) 上的一段A B凹进去 ,则当直线 A B 代替那段曲线A B时所得的 L′( xi , x j) 比原先的L ( xi , x j) 要短 ,矛盾. 引理 1 最短路径 L ( xi , x j) 除去在障碍物边上的部分 ,其余部分是一些直线段 ,即 :L ( xi , x j ) 在障碍物之外的部分必是直线. 图 3 引理 1 示意图 Fig. 3 A sketch for Lemma 1 证明如图 3 所示 ,由两点之间直线最短可知 , 当 L ( xi , x j) 的某一段A B在障碍物之外且不是直线时 , 可以找到 A B 上足够近的两点 A′、B′, 使 L ( xi , x j) 的A′B′段不是直线 ,且连接 A′和 B′2 点的线段与障碍物不相交 ,则用直线 A′B′替代原先的 A′B′段后 ,可得在该种绕行方式下更短的路径 ,矛盾. 一般地 ,绕行多个障碍物的极短路径是由一些线段和障碍物的边界线组成 ,这些线段与障碍物相切或相接(即障碍物在直线一侧) . 第 5 期王建春 ,等 :含有障碍物环境下多智能体系统的聚集行为 · 97 ·

引理 2 如图 4 所示 , M1 M2 是一段凸可微曲线 , N1 N2是M1 M2 的渐伸线 ,即 :取M1 M2 上任意一点 P ,过 P 作M1 M2 的切线交 N1 N2于 Q 点 ,则M1 P 的长度与直线 PQ 的长度之和为定值. 设过 Q 点的曲线N 1 N2的切线为 L ,则有 PQ ⊥L . 图 4 渐伸线 Fig. 4 Asymptote 证明见附录 A. 设 L ( xi , x j) 是 xi , x j 两点之间对障碍物的某种绕行方式下的极短路径 , 记 L ( xi , x j ) 的长度为 s( xi , x j) ,设 L ( xi , x j ) 在 xi 点处的单位切向量为 γ( xi , x j) , L ( xi , x j ) 在 x j 点处的单位切向量为 γ( xi , x j) ,则关于 s( xi , x j) 有以下的重要性质 : 引理 3 ds( xi , x j) = - γ( xi , x j) d xi - γ( x j , xi) d x j . 证明见附录 B. 3 运动的收敛性前面讨论了两点间任意一种绕行障碍物方式下的极短路径的性质 ,而有效最短路径就是某种绕行方式下的极短路径. 根据引理 3 ,可以得出引理 4. 引理 4 dρ( xi , x j) = - β( xi , x j) d xi - β( x j , xi) d x j . 下面建立一个比较普遍的收敛性定理 : 定理 1 对于 i = 1 ,2 , …, M ,limt →∞ xi ( t) 存在. 证明设 G(ρ) =∫ ρ ρ0 g (τ) dτ,其在[ r0 , R0 ]这一有界闭区间上必有最小值 ,设为 Gmin ,由条件知 :当 0 0 , 对任何 T > 0 , 存在 t′0 > t0 > T , 使得 ‖xk ( t′0 ) - xk ( t0 ) ‖ > ε, 于是 , 可找到一系列 0 ε, ( j = 1 ,2 , …) . 从而 ∫ t′j t j d dt U ( t) dt = - 2∫ t′j t j ∑ M i = 1 ‖x·i ‖2 dt ≤ - 2∫ t′j t j ‖x·k ‖2 dt ≤- 2 ‖∫ t′j t j x·k ( t) dt ‖2 = - 2 ‖xk ( t′j) - xk ( tj) ‖2 < - 2ε2 . 即 :∫ t′j t j d dt U ( t) dt < - 2ε2 . 从而 ∫ + ∞ 0 d dt U ( t) dt ≤ ∑ ∞ j = 1∫ t′j t j d dt U ( t) dt ≤ ∑ ∞ j =1 - 2ε2 = - ∞. 于是 ,limt →∞ U ( t) = - ∞, 这与 U ( t) ≥M ( M - 1) Gmin矛盾. 于是 ,对于 i = 1 ,2 , …, M ,limt →∞ xi ( t) 存在. 证毕. 4 数值模拟这里参考文献 [ 11 ] 中的函数 , 取 g (ρ) = a - bexp - ρ2 c ,在程序中 , 进一步令 a = 0101 , · 08 · 智能系统学报第 2 卷

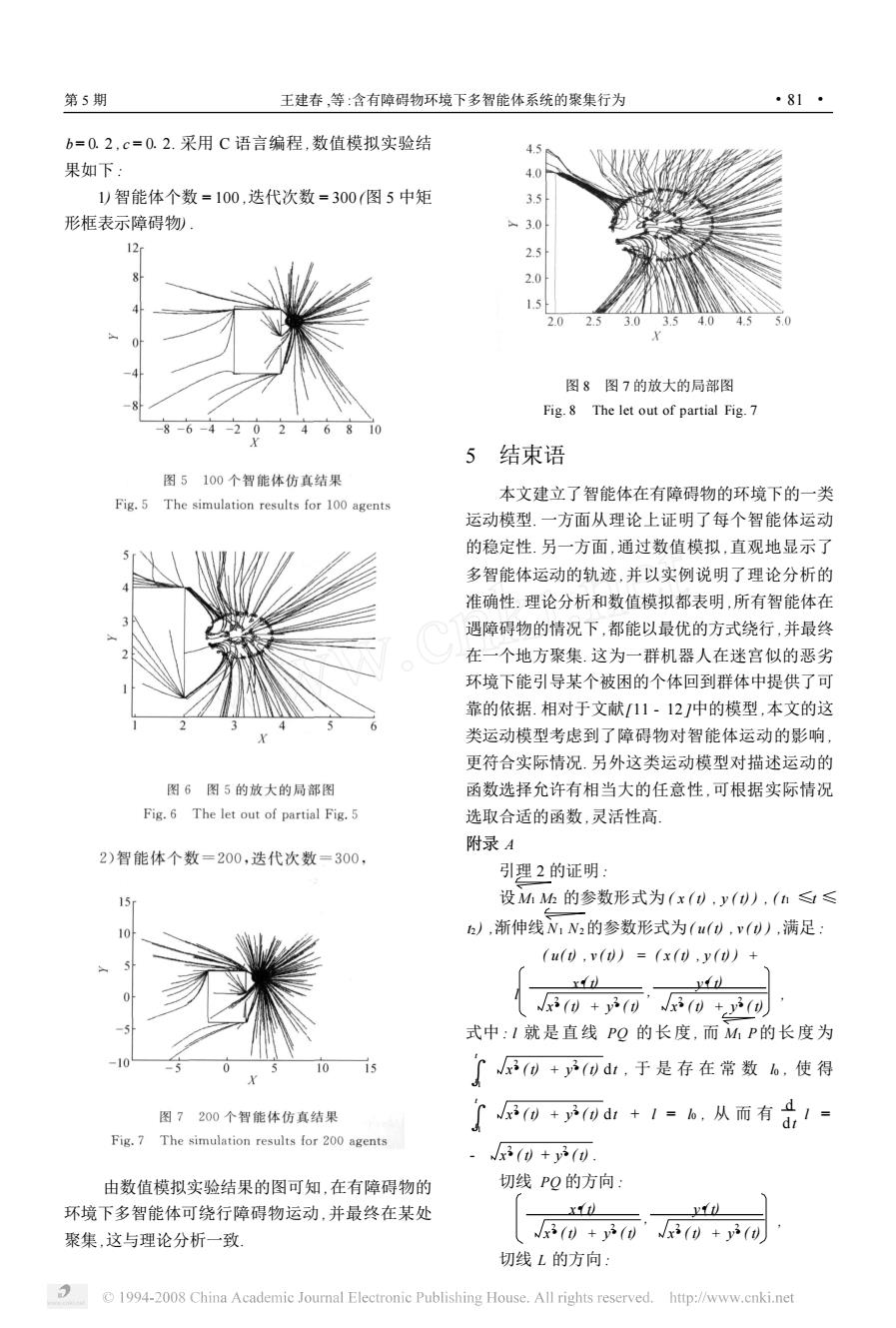
第5期王建春，等：含有障碍物环境下多智能体系统的聚集行为 ·81· b=0.2,c=0.2.采用C语言编程，数值模拟实验结 4.5 果如下：￥0 1)智能体个数=100，迭代次数=300（图5中矩 3.5 形框表示障碍物) 30 12 2.5 2.0 1.5 30 3.5 4.0 4 图8图7的放大的局部图 Fig.8 The let out of partial Fig.7 246810 5结束语图5100个智能体仿真结果本文建立了智能体在有障碍物的环境下的一类 Fig.5 The simulation results for 100 agents 运动模型.一方面从理论上证明了每个智能体运动的稳定性.另一方面，通过数值模拟，直观地显示了多智能体运动的轨迹，并以实例说明了理论分析的准确性.理论分析和数值模拟都表明，所有智能体在遇障碍物的情况下，都能以最优的方式绕行，并最终在一个地方聚集.这为一群机器人在迷宫似的恶劣环境下能引导某个被困的个体回到群体中提供了可靠的依据.相对于文献11-12]中的模型，本文的这类运动模型考虑到了障碍物对智能体运动的影响，更符合实际情况.另外这类运动模型对描述运动的图6图5的放大的局部图函数选择允许有相当大的任意性，可根据实际情况 Fig.6 The let out of partial Fig.5 选取合适的函数，灵活性高」附录A 2)智能体个数=200，迭代次数=300，引理2的证明： 15 设Mh的参数形式为(x(),y(),(n≤≤ ),渐伸线N,N2的参数形式为(u(),v(),满足： (u(),v())=(x(),y()+ 3()+y(0’x3()+3( 式中：1就是直线PQ的长度，而MP的长度为 10 15 N3()+3(dr,于是存在常数6，使得图7200个智能体仿真结果 0+0:+1=,从而有1= Fig.7 The simulation results for 200 agents x3()+y() 由数值模拟实验结果的图可知，在有障碍物的切线PQ的方向：环境下多智能体可绕行障碍物运动，并最终在某处 x 聚集，这与理论分析一致， Nx3()+3(刊 ’()+y2() 切线L的方向： 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

·82 智能系统学报第2卷 (u(0.v(0)=(ut0.vt)=(x.)+ d 由引理2知，x,和：同在障碍物边界的一条渐近线上，从而|s(x,x)-s(红，x川=o‖dxD x 于是 x3()+y()’ x3()+y( s(xx)=llx-l+s(,x)= (x刊，y1))- x3()+y3()· ‖x7-:‖+s(x,x+o(dx:D x t 而又Ix-:I=Ix-xl, x3()+y3() x3()+y3( [cos (x-x:,Y(x:,x))] xYt t N3()+y2() -(x'-x)Y(x.xj)=-Y(xi.xj)dx Nx3()+y2() 于是， xit Nx3()+y3() 3()+y2() s(xx)=s(x,,x)r(x,x)dx,+o(lldx, 略去高阶小量得： x 又因为 (d+y( 是单 x(+( s(x:dxi,xj)s(xx)=-Y(xi.xj)dxi. 位向量，从而同理， x y s(xi,xi+dx)-s(xi.xj)=-Y(x,xi dxj, N3()+3(刊与 Nx3()+y3() 从而， x y ds(x:.xj)=-(Y(xi,xj)dx:+y(xj.x)dxj). d3()+('()+y3(W 垂直，即得： 3)对于2)的退化情况或1)与2)的过渡阶段 PQ山 (如图10)，也有证毕 ds(x,xj)=-(Y(xi,xj)dxi +y(xj,x)dxj). 附录B 引理3的证明： )当L(x,x)为远离障碍物的直线时， s,x动=‖xⅡ，Y(,)=,- Xi-Xi (a)退化情况 (b)过渡情况 W=于是，有图10退化情况和过渡情况 Fig.10 Deterioration and intermediation ds(x,x)=d‖x-x‖= 女+可创参考文献： (Y(xi,xj)dx +Y(xj,x)dxj) [1 ]BREDER C M.Equations descriptive of fish schools and 2)一般情况下，L(x:,x)可能不是一条直线。 other animal aggregations [J ]Ecology,1954,35(3): 361-370 [2 WARBURTON K,LAZARUS J.Tendency-distance models of social cohesion in animal groups [J].Theoretic Biology,1991,150:473.488. [3]OKUBO A.Dynamical aspects of animal grouping: swarms[J].Schools,Flocks and Herds,1986,22 1- 94. 图9最短路径的微小变化 [4]GRUNBAUM D,O KUBO A.Modeling social animal ag- Fig.9 Shortest paths tiny change gregations[A].Frontiers in Theoretical Biology [C]. 如图9所示，L(x:,x)是由一些与障碍物相切 New York,1994. 或相接的线段和障碍物边界曲线组成的.x,改变微 [5]PARRISH J K,HAMNER W M E.Animal groups in 元dx,变为x,x:=x+dx.过x,向L(x4,x)作 three dimensions M].Cambridge:Cambridge Univ 垂线，垂足为z,则z将L(x,x)截成直线xz和 Press,1997. L(=.xj). [6]VICSEK T,CZIROK A,JACOB E,et al.Novel type of 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

d dt ( u( t) , v ( t) ) = ( u·( t) , v·( t) ) = ( x·( t) , y·( t) ) + d dt l x·( t) x·2 ( t) + y·2 ( t) , y·( t) x·2 ( t) + y·2 ( t) = ( x·( t) , y·( t) ) - x·2 ( t) + y·2 ( t) · x·( t) x·2 ( t) + y·2 ( t) , y·( t) x·2 ( t) + y·2 ( t) + l d dt x·( t) x·2 ( t) + y·2 ( t) , y·( t) x·2 ( t) + y·2 ( t) = l d dt x·( t) x·2 ( t) + y·2 ( t) , y·( t) x·2 ( t) + y·2 ( t) 又因为 x·( t) x·2 ( t) + y·2 ( t) , y·( t) x·2 ( t) + y·2 ( t) 是单位向量 ,从而 x·( t) x·2 ( t) + y·2 ( t) , y·( t) x·2 ( t) + y·2 ( t) 与 d dt x·( t) x·2 ( t) + y·2 ( t) , y·( t) x·2 ( t) + y·2 ( t) 垂直 , 即得 : PQ ⊥L . 证毕. 附录 B 引理 3 的证明 : 1) 当 L ( xi , x j ) 为远离障碍物的直线时 , s( xi , x j) = ‖xi - x j ‖,γ( xi , x j ) = x j - xi ‖xi - x j ‖ , γ( x j , xi) = xi - x j ‖xi - x j ‖ . 于是 ,有 ds( xi , x j) = d ‖xi - x j ‖ = - x j - xi ‖xi - x j ‖ d xi + xi - x j ‖xi - x j ‖ d x j = - (γ( xi , x j) d xi +γ( x j , xi) d x j) 2) 一般情况下 , L ( xi , x j) 可能不是一条直线. 图 9 最短路径的微小变化 Fig. 9 Shortest path’s tiny change 如图 9 所示 , L ( xi , x j ) 是由一些与障碍物相切或相接的线段和障碍物边界曲线组成的. xi 改变微元 d xi 变为 x′i , x′i = xi + d xi . 过 xi 向 L ( xi , x j ) 作垂线 ,垂足为 z ,则 z 将 L ( xi , x j ) 截成直线 x′iz 和 L ( z , x j) . 由引理 2 知 , xi 和 z 同在障碍物边界的一条渐近线上 ,从而 ,| s( xi , x j) - s( z , x j) | = o( ‖d xi ‖) . 于是 s( x′i , x j) = ‖x′i - z ‖+ s( z , x j) = ‖x′i - z ‖+ s( xi , x j) + o( ‖d xi ‖) 而又 ‖x′i - z ‖= ‖x′i - xi ‖, [ - cos ∠( x′i - xi ,γ( xi , x j) ) ] = - ( x′i - xi)γ( xi , x j) = - γ( xi , x j) d xi 于是 , s( x′i , xj) = s( xi , xj) - γ( xi , xj) dxi + o( ‖dx i ‖) , 略去高阶小量得 : s( xi + d xi , x j) - s( xi , x j) = - γ( xi , x j) d xi . 同理 , s( xi , x j + d x j) - s( xi , x j) = - γ( x j , xi) d x j , 从而 , ds( xi , x j) = - (γ( xi , x j) d xi +γ( x j , xi) d x j) . 3) 对于(2) 的退化情况或(1) 与 (2) 的过渡阶段 (如图 10) ,也有 ds( xi , x j) = - (γ( xi , x j) d xi +γ( x j , xi) d x j) . 图 10 退化情况和过渡情况 Fig. 10 Deterioration and intermediation 参考文献 : [1 ]BREDER C M. Equations descriptive of fish schools and other animal aggregations [J ]. Ecology , 1954 , 35 (3) : 361 - 370. [ 2 ] WARBURTON K , LAZARUS J. Tendency2distance models of social cohesion in animal groups [J ]. Theoretic Biology ,1991 , 150 :473 - 488. [ 3 ] O KUBO A. Dynamical aspects of animal grouping : swarms[J ]. Schools , Flocks and Herds , 1986 , 22 :1 - 94. [ 4 ] GRU¨NBAUM D , O KUBO A. Modeling social animal ag2 gregations[ A ]. Frontiers in Theoretical Biology [ C ]. New York ,1994. [5 ] PARRISH J K , HAMNER W M E. Animal groups in three dimensions [ M ]. Cambridge : Cambridge Univ Press , 1997. [ 6 ]VICSEK T , CZIRO K A , J ACOB E , et al. Novel type of · 28 · 智能系统学报第 2 卷

第5期王建春，等：含有障碍物环境下多智能体系统的聚集行为 ·83· phase transition in a system of self-driven particles [J ] [12]GAZI V,PASSINO K M.A class of attraction/repul- Physical Review Letters,1995,675(6):1226-1229. sion functions for stable swarm aggregations [A].IEEE [7]CZIROK A,JACOB E B,COHEN I,et al.Formation of Conference on Decision and Control [C].New York, complex bacterial colonies via self-generated vortices[J]. 2002. Phys Rev E,1996,54(2):1791-1801. 作者简介： [8]CZIROK A,STANLEY H E,VICSEK T.Spontane- 王建春，男，1985年生，硕士研究 ously ordered motion of self-propelled partciles [J ]Phys 生，主要研究方向为流体力学、多智能 A:Math,Nucl,1997,30:1375-1385. 体等」 [9]JIN K,LIANG P,BENI G.Stability of synchronized distributed control of discrete swarm structures [A].In Proceedings of IEEE International Conference on Robot- ics and Automation [C].San Diego,CA,1994. 谢广明，男，1972年生，副教授.已 [10]BENI G,LIANG P.Pattern reconfiguration in swarms 发表学术论文百余篇，其中30余篇被 convergence of a distributed asynchronous and bounded SCI收录，目前主持参与包括国家重大 iterative algorithm [J].IEEE Trans Robot Automat, 基础研究发展规划(973)、国防科工委 1996,12:485-490. 十一五计划及国家自然科学基金等多 [11 GAZI V,PASSINO K M.Stability analysis of swarms 个基金项目 [J].IEEE Transactions on Automatic Control,2003,48 E mail:guang mingxie 2007 @126. (4):692.697 com. 第二届中国Agent学术会议 The 2nd Chinese Conference on Agent 中国计算机学会人工智能与模式识别专业委员会主办、南京大学承办、苏州大学协办的第二届中国A~ gent理论与应用学术会议定于2008年4月中下旬在江苏南京举行。本次会议将聚集国内从事Agent理论与应用的研究人员和工程技术人员，广泛开展学术交流，研究发展战略，共同促进Agt理论与技术的发展和应用。一、征文范围（包括但不限于） Agent和多Agent结构多Agent系统环境与性能评价 Agent和多Agent系统的形式模型 Agent仿真基于Agent的软件工程与方法学人工社会系统 Agent协商与协调移动Agent Agent拍卖与电子市场 Agent与网格计算 Agent组织与联盟 Agent与数据挖掘 Agent通信和语言 Agent和多Agent系统应用 Agent学习与规划其他Agent理论与技术方面的内容 Agent系统的计算复杂性二、投稿要求论文未在其他会议或期刊发表过；论文应包括题目、中英文摘要、关键词、正文、参考文献等，参照《计算机研究与发展》的格式；投稿时发送电子邮件至agent.2008@nju.edu.cn,并请注明作者姓名、单位、通信地址、邮政编码、联系电话、电子邮件地址。全文截稿日期为：2007-10-31.详情请见会议网站http:/1cs. nju.edu.cn/agent2008. 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

phase transition in a system of self2driven particles[J ]. Physical Review Letters , 1995 , 675 (6) :1226 - 1229. [7 ]CZIRO K A , J ACOB E B , CO HEN I ,et al. Formation of complex bacterial colonies via self2generated vortices[J ]. Phys Rev E , 1996 , 54 (2) :1791 - 1801. [8 ] CZIRO K A , STANL EY H E , VICSEK T. Spontane2 ously ordered motion of self2propelled partciles [J ]. Phys A : Math , Nucl , 1997 , 30 : 1375 - 1385. [9 ]J IN K , L IAN G P , BENI G. Stability of synchronized distributed control of discrete swarm structures [ A ]. In Proceedings of IEEE International Conference on Robot2 ics and Automation [C]. San Diego , CA , 1994. [ 10 ]BENI G, L IAN G P. Pattern reconfiguration in swarms2 convergence of a distributed asynchronous and bounded iterative algorithm [J ]. IEEE Trans Robot Automat , 1996 , 12 : 485 - 490. [11 ] GAZI V , PASSINO K M. Stability analysis of swarms [J ]. IEEE Transactions on Automatic Control , 2003 , 48 ( 4) :692 - 697. [12 ] GAZI V , PASSINO K M. A class of attraction/ repul2 sion functions for stable swarm aggregations [ A ]. IEEE Conference on Decision and Control [ C ]. New York , 2002. 作者简介 : 王建春 ,男 , 1985 年生 ,硕士研究生 ,主要研究方向为流体力学、多智能体等. 谢广明 ,男 ,1972 年生 ,副教授. 已发表学术论文百余篇 ,其中 30 余篇被 SCI 收录 ,目前主持参与包括国家重大基础研究发展规划 (973) 、国防科工委十一五计划及国家自然科学基金等多个基金项目. E2mail :guang mingxie 2007 @126. com. 第二届中国 Agent 学术会议 The 2nd Chinese Conference on Agent 中国计算机学会人工智能与模式识别专业委员会主办、南京大学承办、苏州大学协办的第二届中国 A2 gent 理论与应用学术会议定于 2008 年 4 月中下旬在江苏南京举行。本次会议将聚集国内从事 Agent 理论与应用的研究人员和工程技术人员 ,广泛开展学术交流 ,研究发展战略 ,共同促进 Agent 理论与技术的发展和应用。一、征文范围(包括但不限于) Agent 和多 Agent 结构 Agent 和多 Agent 系统的形式模型基于 Agent 的软件工程与方法学 Agent 协商与协调 Agent 拍卖与电子市场 Agent 组织与联盟 Agent 通信和语言 Agent 学习与规划 Agent 系统的计算复杂性多 Agent 系统环境与性能评价 Agent 仿真人工社会系统移动 Agent Agent 与网格计算 Agent 与数据挖掘 Agent 和多 Agent 系统应用其他 Agent 理论与技术方面的内容二、投稿要求论文未在其他会议或期刊发表过 ;论文应包括题目、中英文摘要、关键词、正文、参考文献等 ,参照《计算机研究与发展》的格式 ;投稿时发送电子邮件至 agent2008 @nju. edu. cn ,并请注明作者姓名、单位、通信地址、邮政编码、联系电话、电子邮件地址。全文截稿日期为 :2007 - 10 - 31. 详情请见会议网站 http :/ / cs. nju. edu. cn/ agent2008. 第 5 期王建春 ,等 :含有障碍物环境下多智能体系统的聚集行为 · 38 ·