
第2卷第5期 智能系统学报 Vol.2№5 2007年10月 CAAI Transactions on Intelligent Systems 0ct.2007 基于微粒群算法的灰色预测PD控制器 吴晓威,张井岗 (太原科技大学电子与信息工程学院,山西太原030024) 摘要:针对大滞后系统,提出一种基于微粒群算法的灰色预测PD控制算法.采用灰色预测模型GMC(1,2)预测 时滞系统的输出并用微粒群算法优化PD控制器的参数.这种控制方法不需要精确的数学模型,在线估计参数少, 计算简单.仿真结果表明该方法的有效性 关键词:微粒群算法;灰色预测:PD控制器 中图分类号:TP273文献标识码:A文章编号:16734785(2007)05006305 Grey prediction PID controller based on particle s warm optimization a pproach WU Xiao-wei,ZHAN GJing gang (College of Electronics and Information Engineering,Taiyuan University of Science &Technology,Taiyuan 030024,China) Abstract:A grey prediction PID controller based on particle swarm optimization is presented for systems with long time-delay.The output of a system with time-delay is predicted by using a grey prediction model GMC(1,2)and the optimal parameters of the PID controller are obtained by using particle swarm optimiza- tion.The proposed scheme does not require a precise mathematical model.Fewer parameters must be esti- mated omline and computations are very simple.Simulation results show the effectiveness of the proposed controller Key words :particle swarm optimization;grey prediction;PID controller PD控制器因其结构简单,容易实现以及鲁棒 程,模型参数较多,计算量大.灰色预测控制的出现 性好等特点,目前在工业过程控制领域仍广泛使用. 较好地解决了这些问题 但常规PD控制器对纯滞后和参数不确定对象,难 灰色预测控制是一种将控制理论和灰色系统理 以获得满意的控制效果.为此,众多学者提出了各种 论相结合的新型控制方法.该方法需要的原始数据 改进方法.这些方法大致有3类:一类是基于智能控 少,计算简单,且不需要精确的数学模型,目前在工 制的PD控制方法,如模糊控制PD、专家PD、自 业控制中得到了广泛应用B.51.文献[11]将遗传算 适应控制器、神经网络PD控制器等,一类是基于 法和灰色预测GM(1,1)结合控制电力系统稳定器 Smith预估器的控制方法,如文献[1]是基于遗传算 取得了满意的控制效果.文献[12]将进化规划和 法的时滞系统参数辨识与时滞系统的Smith预估控 GM(1,1)结合,取得了较好的控制效果.但采用的 制算法结合:另一类是与预测控制结合的方法,如文 GM(1,1)模型仅根据系统实际输出的离散值进行 献[2]采用预测控制与遗传算法结合来控制的.这些了预测,没有考虑控制量对系统输出的影响情况,有 方法在一定程度上改进了控制效果,但存在一些问 时预测效果不佳.本文采用GMC(1,2)模型既考虑 题:第1类控制方法是根据当前的误差信号来决定 了控制量对系统输出的影响,又提高了预测精度.利 下一步的控制量,属于“事后控制”;第2类需要被控 用GMC(1,2)模型预测时滞系统输出,并采用微粒 系统具有精确的数学模型;第3类是基于CARMA 群算法优化PD参数,从而获得更好的控制性能 模型的控制算法,需要求解复杂的Diophantine方 1灰色预测控制 收稿日期:200612-01. 基金项目:山西省教育厅科技项目(20051311) 灰色预测控制通过系统行为数据系列的提取寻 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 5 期 智 能 系 统 学 报 Vol. 2 №. 5 2007 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2007 基于微粒群算法的灰色预测 PID 控制器 吴晓威 ,张井岗 (太原科技大学 电子与信息工程学院 ,山西 太原 030024) 摘 要 :针对大滞后系统 ,提出一种基于微粒群算法的灰色预测 PID 控制算法. 采用灰色预测模型 GMC(1 ,2) 预测 时滞系统的输出并用微粒群算法优化 PID 控制器的参数. 这种控制方法不需要精确的数学模型 ,在线估计参数少 , 计算简单. 仿真结果表明该方法的有效性. 关键词 :微粒群算法 ;灰色预测 ; PID 控制器 中图分类号 : TP273 文献标识码 :A 文章编号 :167324785 (2007) 0520063205 Grey prediction PID controller based on particle swarm optimization approach WU Xiao2wei , ZHAN G Jing2gang (College of Electronics and Information Engineering , Taiyuan University of Science &Technology , Taiyuan 030024 ,China) Abstract :A grey prediction PID controller based on particle swarm optimization is presented for systems with long time2delay. The outp ut of a system wit h time2delay is predicted by using a grey p rediction model GMC(1 ,2) and t he optimal parameters of t he PID controller are obtained by using particle swarm optimiza2 tion. The propo sed scheme does not require a precise mat hematical model. Fewer parameters must be esti2 mated on2line and comp utations are very simple. Simulation results show the effectiveness of t he proposed controller. Keywords :particle swarm optimization ; grey prediction ; PID controller 收稿日期 :2006212201. 基金项目 :山西省教育厅科技项目(20051311) . PID 控制器因其结构简单 ,容易实现以及鲁棒 性好等特点 ,目前在工业过程控制领域仍广泛使用. 但常规 PID 控制器对纯滞后和参数不确定对象 ,难 以获得满意的控制效果. 为此 ,众多学者提出了各种 改进方法. 这些方法大致有 3 类 :一类是基于智能控 制的 PID 控制方法 ,如模糊控制 PID、专家 PID、自 适应控制器、神经网络 PID 控制器等 ;一类是基于 Smith 预估器的控制方法 ,如文献[1 ]是基于遗传算 法的时滞系统参数辨识与时滞系统的 Smith 预估控 制算法结合 ;另一类是与预测控制结合的方法 ,如文 献[ 2 ]采用预测控制与遗传算法结合来控制的. 这些 方法在一定程度上改进了控制效果 , 但存在一些问 题 :第 1 类控制方法是根据当前的误差信号来决定 下一步的控制量 ,属于“事后控制”;第 2 类需要被控 系统具有精确的数学模型 ;第 3 类是基于 CARMA 模型的控制算法 ,需要求解复杂的 Diop hantine 方 程 ,模型参数较多 ,计算量大. 灰色预测控制的出现 较好地解决了这些问题. 灰色预测控制是一种将控制理论和灰色系统理 论相结合的新型控制方法. 该方法需要的原始数据 少 ,计算简单 ,且不需要精确的数学模型 ,目前在工 业控制中得到了广泛应用[ 3 - 15 ] . 文献[ 11 ]将遗传算 法和灰色预测 GM (1 ,1) 结合控制电力系统稳定器 , 取得了满意的控制效果. 文献 [ 12 ]将进化规划和 GM (1 ,1) 结合 ,取得了较好的控制效果. 但采用的 GM (1 ,1) 模型仅根据系统实际输出的离散值进行 了预测 ,没有考虑控制量对系统输出的影响情况 ,有 时预测效果不佳. 本文采用 GMC(1 ,2) 模型既考虑 了控制量对系统输出的影响 ,又提高了预测精度. 利 用 GMC(1 ,2) 模型预测时滞系统输出 ,并采用微粒 群算法优化 PID 参数 ,从而获得更好的控制性能. 1 灰色预测控制 灰色预测控制通过系统行为数据系列的提取寻

·64 智能系统学报 第2卷 求系统发展规律,从而按规律预测系统未来的行 为,并根据系统未来的行为趋势确定相应的控制决 (附,i=1,2,r, (5) &T 策进行预测控制,提高适应能力B5,刃 (6 1.1灰色预测模型 (0=∑0(形,i=1,2.r 这里采用文献[14]的改进灰色预测模型GMC 利用一次累加生成数据列(5)和(6),可建立 (1,2).设可测得系统的输入和输出时间序列如下: GMC(1,2)微分方程: 输入:0=(u0(1),0(2),0(), 1) dP+1+W(rp+)=b公(W+n 输出:y=(yo1),y0(2,…y@(). dt (2) 这些数据有正有负,而灰色系统建模时要求原始数 (7) 据序列必须为非负5,”.所以必须将非恒正序列变 式中:rp为滞后时间;a为发展系数,反映y的发 换为恒正序列.本文采用的变换为 展态势:系数b的大小反映控制变量“对行为变量 yg=y+川miny)l+e, 3) y的影响大小与影响极性“+”为促进,“。”为抑 =to+lmin(uo)|+£ (4) 制),1为灰色作用量,这些参数由下式估计: 式中:e为任意正常数, 对该序列(3)和(4)进行生成累加,得到一次累 (BTB)BY. (8) 加生成(1AGO)数据列 式中 "p+D+(m+2 3ww+"2 B= 2"(p+2)+ym(p+3) °+l (9) 0(m+1y+y"m+r-)+( Y=(y2),y(3),y()T (10) 式7)的解为 W(p+刊=yW(p+)e-w+ Rω E(k) PID控制器 U(k) 大滞后系统 (b (d 11 微粒群算法 用梯形公式法求上式积分得 (rp ya(rp )ea+ 灰色预测 e9(b)+ヮ+ 图1基于微粒群算法的灰色预测PD控制系统结构图 Fig.1 Block diagram of the grey prediction PID e (bu(1) (12 controller based on PSO 由于GMC(1,2)微分方程(7)是由一次累加生成数 系统输出,U(k为k时刻控制量输出,Y(m)为(k 据所建立的.故对序列进行累减生成(IAGO), m步的灰色预测值 可得预测序列,其中 根据图1,可以得到系统k时刻的预测误差 0(t+1)=g(1+1)-(.13) e(W=r(W-少m.用预测误差调节,可以有效抑制系 式(13)得到的是变换序列的预测值,对其进行逆变 统可能出现的超调 换,得到原始数列的预测值 (d=(d-0min(y)1+9.14 2 基于PSO算法的PD参数优化设计 1.2灰色预测模型算法 2.1PD控制器 通过灰色预测,将其预测值应用到PD控制算 数字PD控制在生产过程中是一种最普遍采 法中就形成了灰色预测控制算法.其闭环控制构成 用的控制方法,在治金、机械、化工等行业中获得广 如图1。 泛应用 图1中,r()为k时刻系统给定,Y(付为k时刻 传统PD离散控制算式为 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
求系统发展规律 , 从而按规律预测系统未来的行 为 , 并根据系统未来的行为趋势确定相应的控制决 策进行预测控制 ,提高适应能力[3 - 5 ,7 ] . 1. 1 灰色预测模型 这里采用文献[ 14 ]的改进灰色预测模型 GMC (1 ,2) . 设可测得系统的输入和输出时间序列如下 : 输入 : u (0) = ( u (0) (1) , u (0) (2) , …, u (0) ( r) ) , (1) 输出 : y (0) = ( y (0) (1) , y (0) (2) , …, y (0) ( r) ) . (2) 这些数据有正有负 ,而灰色系统建模时要求原始数 据序列必须为非负[3 - 5 ,7 ] . 所以必须将非恒正序列变 换为恒正序列. 本文采用的变换为 y (0) m = y (0) +| min ( y (0) ) | +ε, (3) u (0) m = u (0) +| min ( u (0) ) | +ε. (4) 式中 :ε为任意正常数. 对该序列(3) 和(4) 进行生成累加 ,得到一次累 加生成(12A GO) 数据列 : u (1) m ( i) = ∑ i k = 1 u (0) m ( k) , i = 1 ,2 , …, r, (5) y (1) m ( i) = ∑ i k = 1 y (0) m ( k) , i = 1 ,2 , …, r. (6) 利用一 次 累 加 生 成 数 据 列 ( 5 ) 和 ( 6 ) , 可 建 立 GMC(1 ,2) 微分方程 : d y (1) m ( rp + t) dt + ay (1) m ( rp + t) = bu (1) m ( t) +η. (7) 式中 :rp 为滞后时间; a 为发展系数 ,反映 y (0) 的发 展态势;系数 b的大小反映控制变量 u 对行为变量 y (0) 的影响大小与影响极性“( + ”为促进“, - ”为抑 制) ,η为灰色作用量 ,这些参数由下式估计 : a b η = (B T B) - 1 BY. (8) 式中 : B = - 1 2 ( y (1) ( rp + 1) + y (1) ( rp + 2) ) 1 2 ( u (1) (1) + u (1) (2) 1 - 1 2 ( y (1) ( rp + 2) + y (1) ( rp + 3) ) 1 2 ( u (2) (2) + u (1) (3) 1 … … … - 1 2 ( y (1) ( rp + 1 - 1) + y (1) ( rp + r) ) 1 2 ( u (1) ( r - 1) + u (1) ( r) 1 . (9) Y = ( y (0) (2) , y (0) (3) , …, y (0) ( r) ) T . (10) 式(7) 的解为 ^y (1) m ( rp + t) = y (1) m ( rp + 1) e -α( t- 1) + ∫ t 1 e - a( t-τ) ( bu (1) m (τ) +η) dτ. (11) 用梯形公式法求上式积分得 ^y (1) m ( rp + t) = y (1) m ( rp + 1) e - a( t- 1) + ∑ t- 1 τ= 2 e - a( t-τ) ( bu (1) m (τ) +η) + 1 2 (e - a( t- 1) + 1) ( bu (1) m (1) +η) . (12) 由于 GMC(1 ,2) 微分方程 (7) 是由一次累加生成数 据所建立的. 故对 ^y (1) m 序列进行累减生成( IA GO) , 可得预测序列 ^y (0) m ,其中 ^y (0) m ( t + 1) = ^y (1) m ( t + 1) - ^y (1) m ( t) . (13) 式(13) 得到的是变换序列的预测值 ,对其进行逆变 换 ,得到原始数列的预测值 ^y (0) ( k) = ^y (0) m ( k) - (| min ( y (0) ) | +ε) . (14) 1. 2 灰色预测模型算法 通过灰色预测 ,将其预测值应用到 PID 控制算 法中就形成了灰色预测控制算法. 其闭环控制构成 如图 1. 图 1 中 , r( t) 为 k 时刻系统给定 , Y ( k) 为 k 时刻 图 1 基于微粒群算法的灰色预测 PID 控制系统结构图 Fig. 1 Block diagram of the grey prediction PID controller based on PSO 系统输出 ,U ( k) 为 k时刻控制量输出 , ^Y( m) 为( k - m) 步的灰色预测值. 根据图 1 , 可以得到系统 k 时刻的预测误差. ^e( k) = r( k) - ^y m . 用预测误差调节 ,可以有效抑制系 统可能出现的超调. 2 基于 PSO 算法的 PID 参数优化设计 2. 1 PID 控制器 数字 PID 控制在生产过程中是一种最普遍采 用的控制方法 ,在冶金、机械、化工等行业中获得广 泛应用. 传统 PID 离散控制算式为 · 46 · 智 能 系 统 学 报 第 2 卷

第5期 吴晓威,等:基于微粒群算法的灰色预测PD控制器 。65· 1)确定微粒的规模,对微粒群的随机位置和速 u(k)kpe(k)+k.>e(j)+ka(e(k)e(k-1)) 度进行初始设定,并给出3个参数kp、k、k:的上界 15) 和下界: 式中:kp为比例系数,k:为积分系数,k:为微分系 2)根据式(17)计算每个微粒的适应度; 数.e()为设定值与预测量之间的偏差e(=y,- 3)对于每个粒子,将其适应值与最好位置P,的 (k+d. 适应值比较,若较好,则将其作为当前最好位置: 2.2微粒群算法原理 4)对于每个粒子,将其适应值与全局最好位置 微粒群算法(PSO)与其他进化算法相似,也是 P,的适应值比较,若较好,则将其作为当前全局最 将寻优的参数组合成群体,通过对环境的适应度来 好位置 将群体中的个体向好的区域移动.然而不像其他算 5)根据 法一样对个体使用演化算子,而是将每个个体看作 Vg(1+1)=vg()+an(Py-X()+ 是N维搜索空间中一个没有体积的微粒,结合微粒 r(Pg-Xii()). 的历史最佳位置和群体历史最佳位置信息,以一定 更新每个粒子的速度, 的速度向目标值逼近,并根据对个体和集体的飞行 i=1,n,j=1,2,3,Va代表kp的速度,V2表示k 经验的综合分析来动态调整这个速度6.8侧 的速度,Va表示ka的速度; 假设在一个N维的目标搜索空间中,有n个粒 6)如果Vg(1+1)>m,则V(1+1)=Vmx 子组成一个群体部落.其中X=(xa,x2,xm, 如果Vg(1+1)<Vm",则Vg(t+1)=": i=1,2,川,是第i个粒子在N维搜索空间中的 7)根据Xg(1+1)=Xg()+Vg(t+1),更新每 位置,V,=(a,va,vw)是第i个粒子的飞行速 个粒子的位置.其中X四m<X(1+)<m,Xm 度,P=(p,pa,pw)是第i个粒子迄今为止搜 表示PD参数的上界,Xmm表示PD参数的下界; 索到的最优位置.Pg=(P1,P2,Px)是整个粒 8)如果未达到预设最大代数,则返回2),否则 子群迄今为止搜索到的最优位置.第i个微粒速度 输出最优的PD的参数 和位置的进化方程为 V,(1+1)=w,()+an(P-X()+ 3 仿真实验 an(Px-X()), 为了验证本文提出的将微粒群算法和灰色预测 结合整定PD方法的有效性,对大滞后系统进行计 X(t+1)=X()+V:(t+1). 16) 式中:ǒ表示惯性权重,它使微粒保持运动惯性,使 算机仿真研究 为了便于比较,被控对象的传递函数为G(s)= 其具有扩展搜索空间的趋势,有助于新区域的搜索. 10 a、a均为正实数,称为加速度常数.a为调节自身 25十e.系统给定输入r1W=1(,扰动输 最好位置方向的步长,?为调节微粒向全局最好位 入为n()=0.3(-2000,采样周期均为1s,灰色 置飞行的步长.n、n是0,1]之间的随机数.为了减 预测数列长度为5,使用的样本数均为30,进化代数 少在进化过程中,微粒离开搜索空间的可能性,v 均为100,其中PD的参数kp、k、k:范围是kp∈ 通常限定于一定范围内,即vy∈[-mx,axJ.如果 0,1/,k∈0,1],ka∈0,11.在本文中惯性权重0 问题的搜索空间限定在[-xmax,xmax],则可设max= 是从0.9逐渐线性衰减到0.4,加速度常数a=2, kXmax,0.1≤k④.5. a=2,经过17代进化后得到最优解.在文献[111方 2.3基于PSO的PD参数整定 法中,染色体长度为60,交叉概率为0.8,变异概率 使用PSO优化PID的3个参数K=[kp,k,ka1 为0.02,进化76代得到最优解.在文献121中染色 是n3维.PD参数优化的目标是寻找一组优化参 体长度为61,预测步数为5,进化30代得到最优解. 数k。、k、k:使得系统快速响应,同时满足超调量 将这3种方法进行比较,得出的参数及在该参数下 小、调节时间短.采用常用的性能评价指标ISTE: 系统的性能指标见表1。 J=te(Wdr.适应度函数取为 程序的运行时间是利用Matlab的函数tic【程 序内容]toc求出的;计算机配置是Pentium4CPU f= 17) 1.7GHz,256MB内存 用于PD参数整定的PSO算法如下: 1994-2008 China Academic Journal Electronie Publishing House.All rights reserved.http://www.cnki.net
u( k) = kpe ( k) + ki ∑ k j =0 e( j) + kd ( e( k) - e( k - 1) ) . (15) 式中 : k p 为比例系数 , ki 为积分系数 , kd 为微分系 数. e( k) 为设定值与预测量之间的偏差 e ( k) = y r - ^y ( k + d) . 2. 2 微粒群算法原理 微粒群算法(PSO) 与其他进化算法相似 ,也是 将寻优的参数组合成群体 ,通过对环境的适应度来 将群体中的个体向好的区域移动. 然而不像其他算 法一样对个体使用演化算子 ,而是将每个个体看作 是 N 维搜索空间中一个没有体积的微粒 ,结合微粒 的历史最佳位置和群体历史最佳位置信息 ,以一定 的速度向目标值逼近 ,并根据对个体和集体的飞行 经验的综合分析来动态调整这个速度[16 - 18 ] . 假设在一个 N 维的目标搜索空间中 ,有 n 个粒 子组成一个群体部落. 其中 Xi = ( xi1 , xi2 , …, xin , i = 1 ,2 , …, n) ,是第 i 个粒子在 N 维搜索空间中的 位置 ,Vi = ( vi1 , vi2 , …, viN ) 是第 i 个粒子的飞行速 度 , Pi = ( pi1 , pi2 , …, piN ) 是第 i 个粒子迄今为止搜 索到的最优位置. Pg = ( pg1 , pg2 , …, pgN ) 是整个粒 子群迄今为止搜索到的最优位置. 第 i 个微粒速度 和位置的进化方程为 Vi ( t + 1) = ωVi ( t) + c1 r1 ( Pi - Xi ( t) ) + c1 r2 ( Pg - Xi ( t) ) , Xi ( t + 1) = Xi ( t) + Vi ( t + 1) . (16) 式中 :ω表示惯性权重 ,它使微粒保持运动惯性 ,使 其具有扩展搜索空间的趋势 ,有助于新区域的搜索. c1 、c2 均为正实数 ,称为加速度常数. c1 为调节自身 最好位置方向的步长 , c2 为调节微粒向全局最好位 置飞行的步长. r1 、r2 是[0 ,1 ]之间的随机数. 为了减 少在进化过程中 ,微粒离开搜索空间的可能性 , vij 通常限定于一定范围内 ,即 vij ∈[ - vmax , vmax ]. 如果 问题的搜索空间限定在[ - xmax , xmax ] ,则可设vmax = k xmax ,0. 1 ≤k ≤0. 5. 2. 3 基于 PSO 的 PID 参数整定 使用 PSO 优化 PID 的 3 个参数 K= [ k p , ki , kd ] 是 n ×3 维. PID 参数优化的目标是寻找一组优化参 数 k p 、ki 、k d 使得系统快速响应 ,同时满足超调量 小、调节时间短. 采用常用的性能评价指标 ISTE : J =∫ ∞ 0 t 2 e 2 ( t) dt . 适应度函数取为 f = 1 J . (17) 用于 PID 参数整定的 PSO 算法如下 : 1) 确定微粒的规模 ,对微粒群的随机位置和速 度进行初始设定 ,并给出 3 个参数 k p 、ki 、kd 的上界 和下界; 2) 根据式(17) 计算每个微粒的适应度; 3) 对于每个粒子 ,将其适应值与最好位置 Pi 的 适应值比较 ,若较好 ,则将其作为当前最好位置; 4) 对于每个粒子 ,将其适应值与全局最好位置 Pg 的适应值比较 ,若较好 ,则将其作为当前全局最 好位置; 5) 根据 V ij ( t + 1) = ωV ij ( t) + c1 r1 ( Pij - Xij ( t) ) + c2 r2 ( Pgj - Xij ( t) ) , 更新每个粒子的速度 , i = 1 , …, n , j = 1 ,2 ,3 ,V i1代表 k p 的速度 ,V i2表示 ki 的速度 ,V i3表示 k d 的速度; 6) 如果 V ij ( t + 1) > V max j ,则 V ij ( t + 1) = V max j , 如果 V ij ( t + 1) < V min j ,则 V ij ( t + 1) = V min j ; 7) 根据 Xij ( t + 1) = Xij ( t) + V ij ( t + 1) ,更新每 个粒子的位置. 其中 X min j < Xij ( t + 1) < X max j , X max j 表示 PID 参数的上界 , X min j 表示 PID 参数的下界; 8) 如果未达到预设最大代数 ,则返回 2) ,否则 输出最优的 PID 的参数. 3 仿真实验 为了验证本文提出的将微粒群算法和灰色预测 结合整定 PID 方法的有效性 ,对大滞后系统进行计 算机仿真研究. 为了便于比较 ,被控对象的传递函数为 G(s) = 10 25s + 1 e - 40s [13 ] . 系统给定输入 r( t) = 1 ( t) , 扰动输 入为 n( t) = 0. 3 ( t - 2 000) ,采样周期均为 1 s ,灰色 预测数列长度为 5 ,使用的样本数均为 30 ,进化代数 均为 100 ,其中 PID 的参数 k p 、ki 、k d 范围是 k p ∈ [0 ,1 ] , ki ∈[0 , 1 ] , k d ∈[0 , 1 ]. 在本文中惯性权重ω 是从 0. 9 逐渐线性衰减到 0. 4 ,加速度常数 c1 = 2 , c2 = 2 ,经过 17 代进化后得到最优解. 在文献[11 ]方 法中 ,染色体长度为 60 ,交叉概率为 0. 8 ,变异概率 为 0. 02 ,进化 76 代得到最优解. 在文献[12 ]中染色 体长度为 61 ,预测步数为 5 ,进化 30 代得到最优解. 将这 3 种方法进行比较 ,得出的参数及在该参数下 系统的性能指标见表 1. 程序的运行时间是利用 Matlab 的函数 tic [程 序内容] toc 求出的 ;计算机配置是 Pentium4 CPU 1. 7 GHz , 256 MB 内存. 第 5 期 吴晓威 ,等 :基于微粒群算法的灰色预测 PID 控制器 · 56 ·
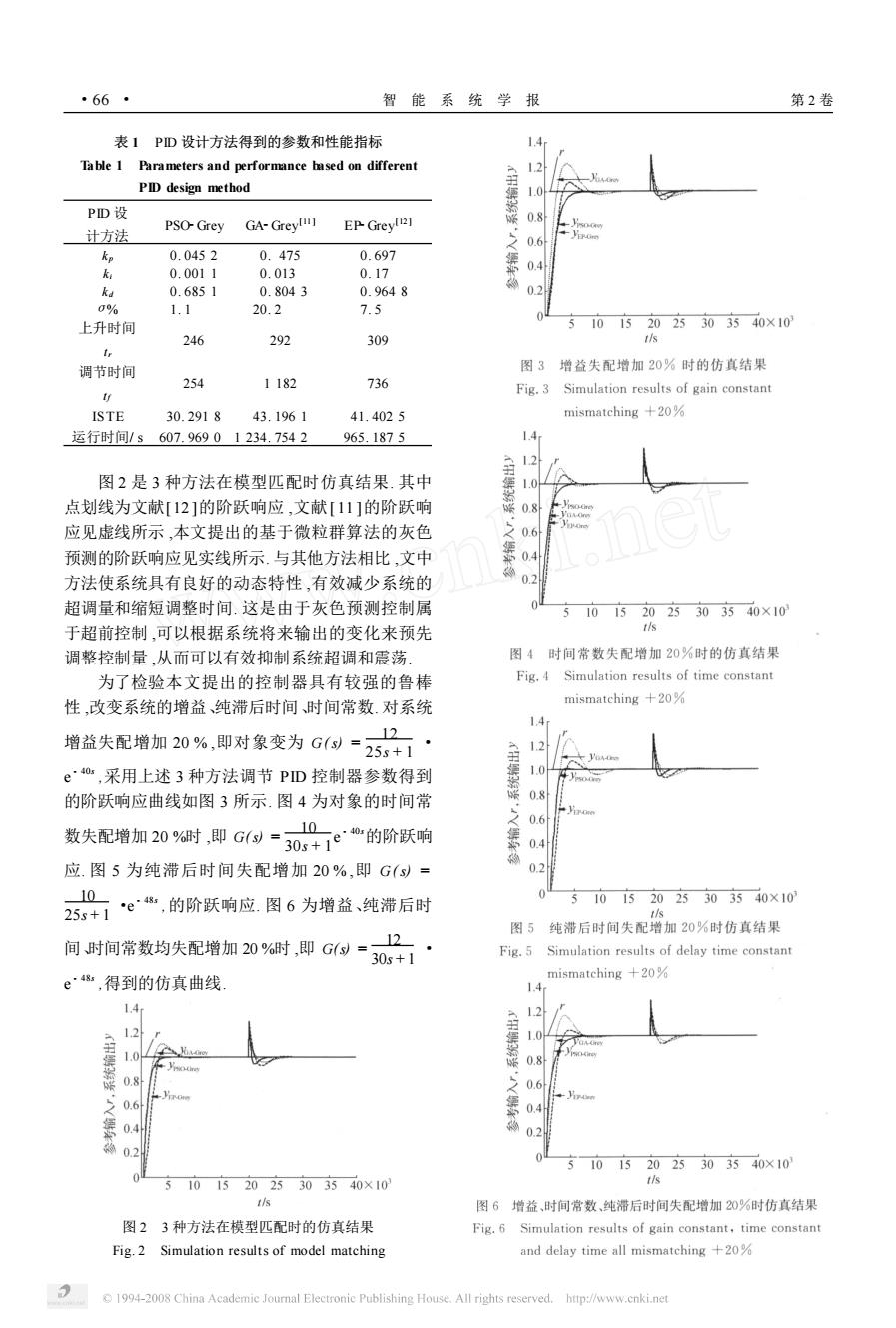
·66· 智能系统学报 第2卷 表1PD设计方法得到的参数和性能指标 14 Table 1 Parameters and performance based on different PID design method 1.0 PD设 计方法 PSO-Grey GA-Greyl11 EP-Greyl121 0.8 0.6 kp 0.0452 0.475 0.697 k 0.0011 0.013 0.17 ka 0.6851 0.8043 0.9648 02 0% 1.1 20.2 7.5 上升时间 510152025303540×10 246 292 309 1/s 调节时间 图3增益失配增加20%时的仿真结果 254 1182 736 Fig.3 Simulation results of gain constant ISTE 30.291843.1961 41.4025 mismatching +20% 运行时间/s607.96901234.7542 965.1875 1.4 图2是3种方法在模型匹配时仿真结果.其中 1.0 点划线为文献[12]的阶跃响应,文献[11]的阶跃响 0.8 iA-Cn 应见虚线所示,本文提出的基于微粒群算法的灰色 06 预测的阶跃响应见实线所示.与其他方法相比,文中 0.4 方法使系统具有良好的动态特性,有效减少系统的 02 超调量和缩短调整时间.这是由于灰色预测控制属 10152025303540×10 于超前控制,可以根据系统将来输出的变化来预先 调整控制量,从而可以有效抑制系统超调和震荡 图4时间常数失配增加20%时的仿真结果 为了检验本文提出的控制器具有较强的鲁棒 Fig.4 Simulation results of time constant 性,改变系统的增益、纯滞后时间、时间常数.对系统 mismatching十20% 14 增益失配增加20%,即对象变为G1=5片 1.2 e4a:,采用上述3种方法调节PD控制器参数得到 1.0 的阶跃响应曲线如图3所示.图4为对象的时间常 0.8 10 数失配增加20%时,即Gy=3057e'“的阶跃响 0.4 应.图5为纯滞后时间失配增加20%,即G(s)= 02 255十e,的阶跃响应.图6为增益、纯滞后时 10 510152025303540×10 g 图5纯滞后时间失配增加20%时仿真结果 12 间时间常数均失配增加20%时,即G)=30s十i· Fig.5 Simulation results of delay time constant e4,得到的仿真曲线 mismatching +20% 1.4 1.4 1.2 1.2 1.0 0.8 08 0.6 0.6 0.4 04 0.2 0 10152025303540×10 10152025303540×10 1/s 1/s 图6增益、时间常数、纯滞后时间失配增加20%时仿真结果 图23种方法在模型匹配时的仿真结果 Fig.6 Simulation results of gain constant,time constant Fig.2 Simulation results of model matching and delay time all mismatching +20% 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
表 1 PID 设计方法得到的参数和性能指标 Table 1 Parameters and performance based on different PID design method PID 设 计方法 PSO2Grey GA2Grey [11 ] EP2Grey [12 ] kp 0. 045 2 0. 475 0. 697 ki 0. 001 1 0. 013 0. 17 kd 0. 685 1 0. 804 3 0. 964 8 σ% 1. 1 20. 2 7. 5 上升时间 tr 246 292 309 调节时间 tf 254 1 182 736 ISTE 30. 291 8 43. 196 1 41. 402 5 运行时间/ s 607. 969 0 1 234. 754 2 965. 187 5 图 2 是 3 种方法在模型匹配时仿真结果. 其中 点划线为文献[ 12 ]的阶跃响应 ,文献[ 11 ]的阶跃响 应见虚线所示 ,本文提出的基于微粒群算法的灰色 预测的阶跃响应见实线所示. 与其他方法相比 ,文中 方法使系统具有良好的动态特性 ,有效减少系统的 超调量和缩短调整时间. 这是由于灰色预测控制属 于超前控制 ,可以根据系统将来输出的变化来预先 调整控制量 ,从而可以有效抑制系统超调和震荡. 为了检验本文提出的控制器具有较强的鲁棒 性 ,改变系统的增益、纯滞后时间、时间常数. 对系统 增益失配增加 20 % ,即对象变为 G(s) = 12 25s + 1 · e - 40s ,采用上述 3 种方法调节 PID 控制器参数得到 的阶跃响应曲线如图 3 所示. 图 4 为对象的时间常 数失配增加 20 %时 ,即 G(s) = 10 30s + 1 e - 40s的阶跃响 应. 图 5 为纯滞后时间失配增加 20 % ,即 G(s) = 10 25s + 1 ·e - 48s ,的阶跃响应. 图 6 为增益、纯滞后时 间、时间常数均失配增加 20 %时 ,即 G(s) = 12 30s + 1 · e - 48s ,得到的仿真曲线. 图 2 3 种方法在模型匹配时的仿真结果 Fig. 2 Simulation results of model matching · 66 · 智 能 系 统 学 报 第 2 卷

第5期 吴晓威,等:基于微粒群算法的灰色预测PD控制器 。67· LIU Dongliang,ZHAO Guangyu.Grey feedback linear- 4 结束语 ization speed control and its application in induction mo- tor[J ]Journal of Zhejiang University,2005,39 (8): 本文提出基于微粒群算法的灰色预测PD控 1164-1167 制器,将传统PD、微粒群算法和灰色预测相结合 [11]DIN G CC,LEE K T.Optimal design for power system 利用灰色预测克服时滞,利用微粒群算法优化PD dynamic stabilizer by grey prediction PID control [A]. 控制器的参数.仿真结果表明,该方法可以显著提高 IEEE ICIT'02[C].Bangkok,Thailand,2002. 系统的动态特性,有效地减少系统超调量,缩短调整 [12]LI C Y,HUANG T L.Optimal design for the grey 时间,而且具有较好的鲁棒性和适应性」 prediction PID controller for power system stabilizers by evolutionary programming[A].Proc IEEE Interna- 参考文献: tional Conference on Networking 2004 [C].Taipei, [1]张世超,姜波.基于遗传算法的时变纯滞后系统的在线 China,2004. [13]刘红军,韩璞.时变大滞后系统的自适应灰色预测 辩识与控制[U].计算机应用与软件,2005,22(5):102- 103. PD控制[U].华北电力大学学报,2004,31(5):44.47. ZHANG Shichao,J IAN G Bo.Omrline identification and LIU Hongjun,HAN Pu.Adaptive grey prediction PID control of system with time-varying time delay based on control of time-variable large delay system[J].Journal genetic algorithms[J].Computer Applications and Soft- of North China Electric Power University,2004,31 (5):44.47 ware,2005,22(5):102.103 [2]杨智,高靖.基于遗传算法的预测自整定PD控制器 [14]WU W Y,CHEN S P.A prediction method using the grey model GMC(1,n)combined with the grey relation- [)].控制与决策,2000,15(1):113-118 YANG Zhi,GAO Jing.Optimal prediction PID control- al analysis:a case study on Internet access population ler based on genetic algorithm[J].Control and Decision forecast [J ]Applied Mathematics and Computation, Metals,2000,15(1):113.118. 2005,169:198.217 [3]邓聚龙.灰色控制系统[M].武汉:华中科技大学出版社, [15]TIEN TZU-LI.A research on the deterministic grey 1987. dynamic model with multiple inputs DGDMMI(1,1,1) [4]姚向东,张立军.灰色预测控制的设计及其应用U].电 [J ]Applied Mathematics and Computation ,2003,139: 401.416. 子与自动化,1998(4):14.16 YAO Xingdong,ZHANG Lijun.Design and application [16]KAO CC,CHANGC W,FUNGR F.The self-tuning of grey prognostic controlling [J].Electronics&Auto- PID control in a slider-crank mechanism system by ap- mation,1998(4):14-16. plying particle swarm optimization approach [J ] [5]毕效辉,姚琼荟.灰色预测在过程控制中的应用卩].西南 Mechatronics,2006,16:513-522. [17]KHODIER MM.CHRISTODOULOU C G.Linear ar- 工学院学报,1997(3):11·16. BI Xiaohui,YAO Qionghui.Preliminary study on grey ray geometry synthesis with minimum sidelobe level and null control using particle swarm optimization[J ]IEEE predictive control of industrial process [J ]Journal of Southwest China Institute of Technology,1997 (3):11- Trans Antennas and Propagation,2005,53(8):2674- 2679. 16 [6]CHEN J Y.An integration design approach in PID con [18]GAIN GZL.A particle swarm optimization approach for troller [A].Proc of the Int Conf on Intelligent Process- optimum design of PID controller in AVR system[J ] ing and Manufacturing of Materials [C].Hawaii,1999. IEEE Trans on Energy Conversion,2004,19(2):384- [7]刘思峰,郭天榜.灰色系统理论及其应用[M].北京:科 391. 作者简介: 学出版社,2000. [8]张广立,付莹.一种新型自调节灰色预测控制器[J].控 吴晓威,女,1982年生,硕士研究 生,主要研究方向为智能控制和鲁棒控 制与决策,2004,19(2):212.215. 制. ZHANG Guangli,FU Ying.Novel self-adjustable grey prediction controller[J ]Control and Decision.2004.19 E mail wxwei2002467 @126.com. (2):212-215 [9]邹健,杨莹春,诸静.基于灰色模型的预测模糊控制 策略及其应用[J].中国电机工程学报,2002,22(9):12 14. ZOU Jian,YANG Yingchun,ZHU Jing.Design of Grey 张井岗,1965年生,教授,硕士生导 师,主要研究方向为鲁棒控制和智能控 model based predictive controllers and its application[J ] 制及其应用.发表学术论文60余篇,其 Proceedings of the Chinese Society for Electrical Engi- neering,2002,22(9):12-14. 中20余篇分别被EI、SCI、ISTP检索 [10]刘栋良,赵光宇.灰色反馈线性化控制及其在感应电机 调速中的应用U].浙江大学学报,2005,39(8):1164- 1167 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
4 结束语 本文提出基于微粒群算法的灰色预测 PID 控 制器 ,将传统 PID、微粒群算法和灰色预测相结合. 利用灰色预测克服时滞 ,利用微粒群算法优化 PID 控制器的参数. 仿真结果表明 ,该方法可以显著提高 系统的动态特性 ,有效地减少系统超调量 ,缩短调整 时间 ,而且具有较好的鲁棒性和适应性. 参考文献 : [1 ]张世超 ,姜 波. 基于遗传算法的时变纯滞后系统的在线 辩识与控制[J ]. 计算机应用与软件 ,2005 ,22 (5) :102 - 103. ZHAN G Shichao , J IAN G Bo. On2line identification and control of system with time2varying time delay based on genetic algorithms[J ]. Computer Applications and Soft2 ware ,2005 ,22 (5) :102 - 103. [2 ]杨 智 ,高 靖. 基于遗传算法的预测自整定 PID 控制器 [J ]. 控制与决策 ,2000 ,15 (1) :113 - 118. YAN G Zhi , GAO Jing. Optimal prediction PID control2 ler based on genetic algorithm[J ]. Control and Decision Metals , 2000 ,15 (1) :113 - 118. [3 ]邓聚龙. 灰色控制系统[ M]. 武汉 :华中科技大学出版社 , 1987. [4 ]姚向东 ,张立军. 灰色预测控制的设计及其应用[J ]. 电 子与自动化 , 1998 (4) : 14 - 16. YAO Xingdong , ZHAN G Lijun . Design and application of grey prognostic controlling [J ]. Electronics & Auto2 mation , 1998 (4) : 14 - 16. [5 ]毕效辉 ,姚琼荟. 灰色预测在过程控制中的应用[J ]. 西南 工学院学报 , 1997 (3) : 11 - 16. BI Xiaohui , YAO Qionghui . Preliminary study on grey predictive control of industrial process [J ]. Journal of Southwest China Institute of Technology , 1997 (3) :11 - 16. [6 ]CHEN J Y. An integration design approach in PID con2 troller [A ]. Proc of the Int Conf on Intelligent Process2 ing and Manufacturing of Materials [C]. Hawaii , 1999. [7 ]刘思峰 , 郭天榜. 灰色系统理论及其应用[ M ]. 北京 : 科 学出版社 , 2000. [8 ]张广立 ,付 莹. 一种新型自调节灰色预测控制器[J ]. 控 制与决策 ,2004 ,19 (2) :212 - 215. ZHAN G Guangli , FU Ying. Novel self2adjustable grey prediction controller[J ]. Control and Decision , 2004 , 19 (2) : 212 - 215. [9 ]邹 健 ,杨莹春 ,诸 静. 基于灰色模型的预测模糊控制 策略及其应用[J ]. 中国电机工程学报 ,2002 , 22 (9) :12 14. ZOU Jian , YAN G Yingchun , ZHU Jing. Design of Grey model based predictive controllers and its application[J ]. Proceedings of the Chinese Society for Electrical Engi2 neering , 2002 , 22 (9) : 12 - 14. [10 ]刘栋良 ,赵光宇. 灰色反馈线性化控制及其在感应电机 调速中的应用[J ]. 浙江大学学报 ,2005 ,39 (8) :1164 - 1167. L IU Dongliang , ZHAO Guangyu. Grey feedback linear2 ization speed control and its application in induction mo2 tor[J ]. Journal of Zhejiang University , 2005 , 39 (8) : 1164 - 1167. [11 ]DIN G C C , L EE K T. Optimal design for power system dynamic stabilizer by grey prediction PID control [ A ]. IEEE ICIT’02[C]. Bangkok , Thailand , 2002. [12 ]L I C Y , HUAN G T L. Optimal design for the grey prediction PID controller for power system stabilizers by evolutionary programming [ A ]. Proc IEEE Interna2 tional Conference on Networking 2004 [ C ]. Taipei , China , 2004. [13 ]刘红军 ,韩 璞. 时变大滞后系统的自适应灰色预测 PID 控制[J ]. 华北电力大学学报 ,2004 ,31 (5) :44 - 47. L IU Hongjun , HAN Pu . Adaptive grey prediction PID control of time2variable large delay system[J ]. Journal of North China Electric Power University , 2004 , 31 (5) :44 - 47. [14 ]WU W Y , CHEN S P. A prediction method using the grey model GMC(1 ,n) combined with the grey relation2 al analysis: a case study on Internet access population forecast [J ]. Applied Mathematics and Computation , 2005 ,169 :198 - 217. [15 ] TIEN TZU2L I. A research on the deterministic grey dynamic model with multiple inputs D GDMMI(1 ,1 ,1) [J ]. Applied Mathematics and Computation ,2003 ,139 : 401 - 416. [16 ] KAO C C , CHAN G C W , FUN G R F. The self2tuning PID control in a slider2crank mechanism system by ap2 plying particle swarm optimization approach [ J ]. Mechatronics ,2006 , 16 :513 - 522. [17 ] KHODIER M M. CHRISTODOULOU C G. Linear ar2 ray geometry synthesis with minimum sidelobe level and null control using particle swarm optimization[J ]. IEEE Trans Antennas and Propagation ,2005 ,53 (8) : 2674 - 2679. [ 18 ] GAIN G Z L. A particle swarm optimization approach for optimum design of PID controller in AVR system [J ]. IEEE Trans on Energy Conversion , 2004 , 19 (2) :384 - 391. 作者简介 : 吴晓威 , 女 , 1982 年生 , 硕士研究 生 ,主要研究方向为智能控制和鲁棒控 制. E2mail :wxwei2002467 @126. com. 张井岗 ,1965 年生 ,教授 ,硕士生导 师 ,主要研究方向为鲁棒控制和智能控 制及其应用. 发表学术论文 60 余篇 ,其 第 5 期 吴晓威 ,等 :基于微粒群算法的灰色预测 PID 控制器 · 76 · 中 20 余篇分别被 中 20 余篇分别被EI、SCI、ISTP 检索