
第2卷第3期 智能系统学报 Vol.2 Ne 3 2007年6月 CAAI Transactions on Intelligent Systems Jun.2007 使用不同的博弈树搜索算法解决 计算机围棋的吃子问题 张培刚,陈克训 (Department of Computer Science,University of North Carolina at Charlotte,Charlotte NC 28223,USA) 摘要:使用AlpharBeta搜索和proof-number(pn)搜索解决计算机围棋的吃子问题.对吃子问题形式化并给出了 简单有效的评估函数.Alpha-Beta搜索使用了包括置换表在内的各种扩展技术.pn搜索使用了包括dfpn在内的4 种变体.研究结果显示,对于解决吃子问题pn搜索优于Alpha-Beta搜索.并且搜索过程中所产生的数据的一些模式 可以帮助在结果未知的情况下对结果进行预测,所设计的算法可以用于解决单独的吃子问题或者计算机围棋比赛 中的吃子计算 关键词:计算机围棋;博弈树搜索;启发式搜索;AlphaBeta搜索proof-number搜索;吃子问题 中图分类号:TP18文献标识码:A文章编号:16734785(2007)03008407 Using different search algorithms to solve computer Go ca pturing problems ZHAN G Pei-gang ,CHEN Kehhsun (Department of Computer Science,University of North Carolina at Charlotte,Charlotte NC 28223,USA) Abstract:The capturing problem is an important tactical sub-problem in computer Go.Alpha-Beta() search and proof-number (pn)searches are used to solve computer Go capturing problems with the same e- valuation function.The performance of the capturing algorithm is favorable and practical.The algorithm could be used to solve post game capturing problems or to perform real time capturing calculations in com- puter Go tournament matches.Our results show that pmsearch is superior to-search at solving capturing problems.Some patterns can be found in the searching process that could help predict the search outcome when it is still unknown.Our work also provides a framework that could be used to solve other computer Go subproblems and other games. Keywords:computer Go:game tree search:Heuristic search:Alpha-Beta search:proof-number search; block capturing 博弈树搜索算法是博弈程序的核心组成部分」 好地解决这些战术问题 Alpha-Beta搜索是最广泛使用的博弈树搜索算法, 文中尝试使用不同的树搜索算法解决围棋的吃 pn搜索对于解决非对称博弈树问题也非常有效 子问题.首先设计和实现了Alpha-Beta搜索及其扩 面对博弈程序设计人员的一些问题包括: 展和pn搜索及其变体去解决吃子问题.进一步对 1)每种搜索算法的特性是什么?2)对于解决一 这些算法的结果进行比较并总结不同算法的特征: 类特定问题哪种搜索算法比较好?3)如何将搜索算 最后对搜索过程中产生的数据进行分析并发现一些 法嵌入博弈程序用于实时地解决问题?计算机围棋 模式可以用于对搜索结果进行预测.这个吃子算法 是当前人工智能领域的一大难题.计算机围棋包括 的表现是出色和实用的.这个算法可以用于解决单 很多战术问题例如死活问题·】、吃子问题到和连 独的吃子问题或者计算机围棋比赛中的吃子计算 接问题.构建一个强大的计算机围棋程序需要很 结果显示,对于解决吃子问题pn搜索优于Alpha Beta搜索.并且发现搜索过程中的一些模式可以帮 收稿日期:20060821. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 3 期 智 能 系 统 学 报 Vol. 2 №. 3 2007 年 6 月 CAA I Transactions on Intelligent Systems J un. 2007 使用不同的博弈树搜索算法解决 计算机围棋的吃子问题 张培刚 ,陈克训 (Department of Computer Science , University of North Carolina at Charlotte , Charlotte NC 28223 , USA) 摘 要 :使用 Alpha2Beta 搜索和 proof2number (pn) 搜索解决计算机围棋的吃子问题. 对吃子问题形式化并给出了 简单有效的评估函数. Alpha2Beta 搜索使用了包括置换表在内的各种扩展技术. pn 搜索使用了包括 df2pn 在内的 4 种变体. 研究结果显示 ,对于解决吃子问题 pn 搜索优于 Alpha2Beta 搜索. 并且搜索过程中所产生的数据的一些模式 可以帮助在结果未知的情况下对结果进行预测. 所设计的算法可以用于解决单独的吃子问题或者计算机围棋比赛 中的吃子计算. 关键词 :计算机围棋 ;博弈树搜索 ;启发式搜索 ;Alpha2Beta 搜索 ;proof2number 搜索 ;吃子问题 中图分类号 : TP18 文献标识码 :A 文章编号 :167324785 (2007) 0320084207 Using different search algorithms to solve computer Go capturing problems ZHAN G Pei2gang ,CH EN Keh2hsun (Department of Computer Science , University of North Carolina at Charlotte , Charlotte NC 28223 , USA) Abstract :The capturing problem is an important tactical sub2problem in comp uter Go. Alp ha2Beta ( ) search and proof2number (p n) searches are used to solve comp uter Go capt uring problems wit h t he same e2 valuation f unction. The performance of t he capt uring algorithm is favorable and practical. The algorit hm could be used to solve post game capt uring problems or to perform real time capt uring calculations in com2 p uter Go tournament matches. Our results show that p n2search is superior to2search at solving capt uring problems. Some patterns can be found in the searching process t hat could help predict t he search outcome when it is still unknown. Our work also provides a framework that could be used to solve ot her comp uter Go sub2problems and ot her games. Keywords : comp uter Go ; game tree search ; Heuristic search ; Alp ha2Beta search ; proof - number search ; block capt uring 收稿日期 :2006208221. 博弈树搜索算法是博弈程序的核心组成部分. Alp ha2Beta 搜索是最广泛使用的博弈树搜索算法. p n 搜索对于解决非对称博弈树问题也非常有效. 面对博弈程序设计人员的一些问题包括 : 1) 每种搜索算法的特性是什么 ? 2) 对于解决一 类特定问题哪种搜索算法比较好 ? 3) 如何将搜索算 法嵌入博弈程序用于实时地解决问题 ? 计算机围棋 是当前人工智能领域的一大难题. 计算机围棋包括 很多战术问题例如死活问题[ 1 - 2 ] 、吃子问题[3 ] 和连 接问题[4 ] . 构建一个强大的计算机围棋程序需要很 好地解决这些战术问题. 文中尝试使用不同的树搜索算法解决围棋的吃 子问题. 首先设计和实现了 Alp ha2Beta 搜索及其扩 展和 p n 搜索及其变体去解决吃子问题. 进一步对 这些算法的结果进行比较并总结不同算法的特征. 最后对搜索过程中产生的数据进行分析并发现一些 模式可以用于对搜索结果进行预测. 这个吃子算法 的表现是出色和实用的. 这个算法可以用于解决单 独的吃子问题或者计算机围棋比赛中的吃子计算. 结果显示 ,对于解决吃子问题 ,p n 搜索优于 Alp ha2 Beta 搜索. 并且发现搜索过程中的一些模式可以帮

第3期 张培刚,等:使用不同的博弈树搜索算法解决计算机围棋的吃子问题 ·85* 助在结果未知的情况下对结果进行预测.本文的工 作也为解决其他计算机围棋问题和其他博弈问题提 供了一个框架 1吃子问题 1.1计算机围棋吃子问题 围棋是一项非常古老而且受欢迎的棋类游戏 计算机围棋是人工智能中一个很吸引人的研究领 域561由于其内在复杂性,计算机围棋程序的棋力 与人相比在目前仍然大大落后.计算机围棋遇到各 图2数字标出的点是候选招法, 种类型的问题,为人工智能的各种方法提供了极佳 2是吃住目标的正确着法 的试验场.它包括许多有趣的战术问题,例如死活、 Fig 2 The candidate moves to capturing the marked 吃子和连接问题.构建一个强大的计算机围棋程序 tone,location 2 is the right move to capture the target 需要很好地解决这些战术问题 策略、终止状态检测、中间节点和叶子节点评估.然 吃子计算的目的是要得到一块棋能否被吃死或 后将使用同样的方法来产生候选着法、节点评估、终 者能否逃脱以及如何吃死或者逃脱.吃子计算对于 止状态检测并将它们用于不同的搜索算法.关于计 计算机围棋程序是基本和关键的].几乎所有的计 算机围棋和吃子问题的一些术语可以见文献[3,6] 算机围棋程序都包括吃子模块.吃子算法可以被用 于解决单独的吃子问题或者被嵌入游戏引擎进行实 1.2候选着法产生 时的吃子计算.由于在实时计算中时间是非常有限 候选着法一般靠近目标棋块或者上一手棋.一 的,所以吃子算法的效率非常重要 块棋的相关选点被定义为这块棋的气和二次气以及 吃子问题为博弈树搜索算法提供了很好的试验 对手相邻这块棋并且不大于三气的棋块的气.这里 场.一些研究者提出了一般用途的算法并且以解决 使用一个简单的评估函数,将着这手棋下在棋盘上 吃子问题作为示例8).这些算法解决吃子问题的 并且计算: 速度非常慢.为了得到更好的和更实际的结果,需要 Point Evaluation =Block's First liberties 进一步的研究 4 +Block's Second liberties 在作者以前的一项研究中,基于Alpha-Beta搜 然后选择评估值比较大的相关选点 索并高度性选择的启发式搜索被用于解决围棋的吃 考虑5种类型的棋块 子问题,得到了很好的结果).文中使用不同的搜索 1)目标棋块; 算法利用相对简单的评估函数并且考虑更多的候选 2)目标棋块的关键链; 着法以处理各种不同的可能情况 3)上一手棋所属棋块: 面对吃子问题,高水平的围棋选手一般能够很 4)对手相邻棋块; 快发现棋子的弱点并进行深而且窄的搜索.对于大 5)上一手棋的相邻棋块 多数情况,基于以前经验所形成的知识,他们能够发 每一种类型的棋块都能产生一些相关选点,在 现棋形的弱点 数目上设定了上限和下限.基本上从这5种类型的 在下面的几节将介绍候选着法的产生和排序的 棋块的相关选点中选择候选着法, 使用2种类型的目标去帮助选择候选着法:吃 子目标和逃脱目标.如果下一手棋轮目标棋块方下 是逃脱目标,否则就是吃子目标.对于不同目标候选 着法的选择策略也略有不同.例如,对于逃脱目标, 候选着法不能使目标棋块被直接征子吃掉 算法中也使用一些其他条件去排除候选着法 候选着法不能填自己的真眼.候选着法的总数被限 图1如图标出的白子是吃子的目标 制在15以下,对于绝大多数情况这是足够的 如果轮黑棋下能够被吃住 1.3节点评估 Fig I The marked white stone is the target, 使用对目标棋块的关键链的评估值作为中间节 it could be captured if black move next 点和叶子节点的评估值: 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
助在结果未知的情况下对结果进行预测. 本文的工 作也为解决其他计算机围棋问题和其他博弈问题提 供了一个框架. 1 吃子问题 111 计算机围棋吃子问题 围棋是一项非常古老而且受欢迎的棋类游戏. 计算机围棋是人工智能中一个很吸引人的研究领 域[5 - 6 ] . 由于其内在复杂性 ,计算机围棋程序的棋力 与人相比在目前仍然大大落后. 计算机围棋遇到各 种类型的问题 ,为人工智能的各种方法提供了极佳 的试验场. 它包括许多有趣的战术问题 ,例如死活、 吃子和连接问题. 构建一个强大的计算机围棋程序 需要很好地解决这些战术问题[7 ] . 吃子计算的目的是要得到一块棋能否被吃死或 者能否逃脱以及如何吃死或者逃脱. 吃子计算对于 计算机围棋程序是基本和关键的[3 ] . 几乎所有的计 算机围棋程序都包括吃子模块. 吃子算法可以被用 于解决单独的吃子问题或者被嵌入游戏引擎进行实 时的吃子计算. 由于在实时计算中时间是非常有限 的 ,所以吃子算法的效率非常重要. 吃子问题为博弈树搜索算法提供了很好的试验 场. 一些研究者提出了一般用途的算法并且以解决 吃子问题作为示例[8 - 9 ] . 这些算法解决吃子问题的 速度非常慢. 为了得到更好的和更实际的结果 ,需要 进一步的研究. 在作者以前的一项研究中 ,基于 Alp ha2Beta 搜 索并高度性选择的启发式搜索被用于解决围棋的吃 子问题 ,得到了很好的结果[3 ] . 文中使用不同的搜索 算法利用相对简单的评估函数并且考虑更多的候选 着法以处理各种不同的可能情况. 面对吃子问题 ,高水平的围棋选手一般能够很 快发现棋子的弱点并进行深而且窄的搜索. 对于大 多数情况 ,基于以前经验所形成的知识 ,他们能够发 现棋形的弱点. 图 1 如图标出的白子是吃子的目标 , 如果轮黑棋下能够被吃住 Fig11 The marked white stone is the target , it could be captured if black move next 在下面的几节将介绍候选着法的产生和排序的 图 2 数字标出的点是候选招法 , 2 是吃住目标的正确着法 Fig12 The candidate moves to capturing the marked s tone , location 2 is the right move to capture the target 策略、终止状态检测、中间节点和叶子节点评估. 然 后将使用同样的方法来产生候选着法、节点评估、终 止状态检测并将它们用于不同的搜索算法. 关于计 算机围棋和吃子问题的一些术语可以见文献[ 3 ,6 ]. 112 候选着法产生 候选着法一般靠近目标棋块或者上一手棋. 一 块棋的相关选点被定义为这块棋的气和二次气以及 对手相邻这块棋并且不大于三气的棋块的气. 这里 使用一个简单的评估函数 ,将着这手棋下在棋盘上 并且计算 : Point Evaluation = # Block’s First liberties 3 4 + # Block’s Second liberties 然后选择评估值比较大的相关选点. 考虑 5 种类型的棋块 : 1) 目标棋块 ; 2) 目标棋块的关键链 ; 3) 上一手棋所属棋块 ; 4) 对手相邻棋块 ; 5) 上一手棋的相邻棋块. 每一种类型的棋块都能产生一些相关选点 ,在 数目上设定了上限和下限. 基本上从这 5 种类型的 棋块的相关选点中选择候选着法. 使用 2 种类型的目标去帮助选择候选着法 :吃 子目标和逃脱目标. 如果下一手棋轮目标棋块方下 是逃脱目标 ,否则就是吃子目标. 对于不同目标候选 着法的选择策略也略有不同. 例如 ,对于逃脱目标 , 候选着法不能使目标棋块被直接征子吃掉. 算法中也使用一些其他条件去排除候选着法. 候选着法不能填自己的真眼. 候选着法的总数被限 制在 15 以下 ,对于绝大多数情况这是足够的. 113 节点评估 使用对目标棋块的关键链的评估值作为中间节 点和叶子节点的评估值 : 第 3 期 张培刚 ,等 :使用不同的博弈树搜索算法解决计算机围棋的吃子问题 ·85 ·

·86 智能系统学报 第2卷 Node Evaluation =Crucial chain's First lib- 小节点的最差可能值.使用这些值,很多分支可以被 erties *4+#Crucial chain's Second liberties 裁减掉 1.4终止状态测试 在儿子节点被最好排序的情况下,Alpha-Beta 算法中设定一个节点评估值的上限来进行终止 搜索为求解问题需要访问的节点数目约为w2,w 状态测试.如果节点的评估值大于这个上限,则目标 是平均候选着法的数目,d是搜索的深度.在最坏情 棋块被认为可以逃脱.如果目标棋块可以被直接吃 况下,为了求解它需要搜索整个博弈树 掉或者被征子吃掉则被认为可以吃掉 文中使用Alpha-Beta搜索及迭代加深、置换 表.每次迭代深度增加为2.关于置换表使用Zobrist 2 博弈树搜索算法 哈希161和线性探查 对于二人、零和、完备信息的棋类游戏,例如围 几种常用的用于博弈树搜索算法比较的指标 棋、象棋、国际象棋和跳棋,博弈树算法对构建一个 有:CPU时间、访问的叶子节点数、访问的所有节点 强大的博弈程序是关键的.博弈树搜索的目标是要 数.文中使用访问的所有节点数来衡量算法的表 找到极大极小博弈树或者与和树的最佳值以及最佳 现 着法序列.一般博弈树非常大以至于不能被当前的 这里使用Kano围棋系列的第3册中的吃子问 计算机所求解.降低博弈树大小的策略包括缩小候 题来检验算法效果.每一个问题的搜索时间被限制 选着法的数目以缩小展开因子、当搜索到某一深度 在200s内.表1包含了Alpha-Beta搜索不使用置 时使用评估函数以及使用搜索路径选择策略.选择 换表和使用置换表的测试结果 候选着法以及使用评估函数很大程度上取决于领域 使用置换表的算法表现比不使用置换表的算法 知识.搜索路径选择策略则一般与领域知识无关.深 表现好:使用的时间较少、访问的节点较少,将节点 度优先搜索和最佳优先搜索是最主要的2种搜索路 的最佳值存储在置换表中可以避免对同样的局面重 径选择策略 新计算,在迭代加深中使用置换表也可以帮助候选 AlpharBeta搜索是深度优先搜索算法而且是 着法排序。 当前博弈游戏程序最广泛使用的博弈树搜索算 候选着法排序的质量对Alpha-Beta搜索的效 法io..候选着法的排序对于Alpha-Beta搜索的 率是关键的.但对于不同问题很难给出统一的评估 效率是关键的.Alpha-Beta搜索有很多扩展,其中 函数去得到候选着法的最佳排序.进一步的工作可 包括迭代加深、置换表、历史启发函数等,大多数用 以使用模式数据库去帮助候选着法排序 于得到更好的候选着法排序,使用迭代加深的A: 结果发现Alpha-Beta搜索不能解决的问题主 pha-Beta搜索可以得到某一深度的最优值,这可以 要由于以下3个原因: 作为限制时间搜索下的近似解.Alpha-Beta搜索的 I)在时间限制下Alpha-Beta搜索很难搜索到 缺点是很难搜索到很深的深度 很深的深度.对于那些需要很深深度搜索才能求解 pn搜索是最佳优先搜索算法.对于非均衡树的 的问题,Alpha-Beta搜索一般用光时间从而失败. 求解,pn搜索是非常强大的2].pn搜索需要将整个 2)候选着法没有包括所有可能着法:正确着法 搜索树保存在内存中,所以内存消耗很大.近年来, 缺失 出现了一些pn搜索的深度优先搜索的变体,例如 3)解决此问题需要其他知识如连接和死活知 pn*l、df-pn和df-pn+.使用proof number 识 和disproof number的阈值,这些算法可以以深度优 先的方式去搜索博弈树,但是所展开的博弈树与pn proof-number搜索 搜索是一样的.这些深度优先的变体可以减少内存 pn搜索是最佳优先搜索算法.对于非均衡树的 的使用,但是效果与pn搜索相似 求解pn搜索是非常强大的.pn搜索的思想是总是 目前Alpha-Beta搜索及其扩展仍然是最广泛 展开那些用最小代价就可以证明或者否证与或博弈 使用的博弈树搜索算法山.pn搜索及其变体变得 树的节点2.pn搜索将节点分为2种:与节点和或 越来越流行口 节点.在每个与节点努力去否证节点,在每个或节点 努力去证明节点.在每个节点上使用2个数值: 3 Alpha-Beta搜索 proof number最少需要展开的叶子节点去证明 Alpha-Beta搜索的思想是利用Alpha值 此节点的数目;disproof number最少需要展开 对于极大节点的最差可能值和Beta值对于极 的叶子节点去否证此节点的数目.对于博弈树有时 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
Node Evaluation = # Crucial chain’s First lib2 erties 3 4 + # Crucial chain’s Second liberties 114 终止状态测试 算法中设定一个节点评估值的上限来进行终止 状态测试. 如果节点的评估值大于这个上限 ,则目标 棋块被认为可以逃脱. 如果目标棋块可以被直接吃 掉或者被征子吃掉则被认为可以吃掉. 2 博弈树搜索算法 对于二人、零和、完备信息的棋类游戏 ,例如围 棋、象棋、国际象棋和跳棋 ,博弈树算法对构建一个 强大的博弈程序是关键的. 博弈树搜索的目标是要 找到极大极小博弈树或者与和树的最佳值以及最佳 着法序列. 一般博弈树非常大以至于不能被当前的 计算机所求解. 降低博弈树大小的策略包括缩小候 选着法的数目以缩小展开因子、当搜索到某一深度 时使用评估函数以及使用搜索路径选择策略. 选择 候选着法以及使用评估函数很大程度上取决于领域 知识. 搜索路径选择策略则一般与领域知识无关. 深 度优先搜索和最佳优先搜索是最主要的 2 种搜索路 径选择策略. Alp ha2Beta 搜索是深度优先搜索算法而且是 当前博弈游戏程序最广泛使用的博弈树搜索算 法[10 - 11 ] . 候选着法的排序对于 Alp ha2Beta 搜索的 效率是关键的. Alp ha2Beta 搜索有很多扩展 ,其中 包括迭代加深、置换表、历史启发函数等 ,大多数用 于得到更好的候选着法排序. 使用迭代加深的 Al2 p ha2Beta 搜索可以得到某一深度的最优值 ,这可以 作为限制时间搜索下的近似解. Alp ha2Beta 搜索的 缺点是很难搜索到很深的深度. p n 搜索是最佳优先搜索算法. 对于非均衡树的 求解 ,p n 搜索是非常强大的[12 ] . p n 搜索需要将整个 搜索树保存在内存中 ,所以内存消耗很大. 近年来 , 出现了一些 p n 搜索的深度优先搜索的变体 ,例如 p n 3 [13 ] 、df - p n 和 df - p n + [14 ] . 使用 proof number 和 disproof number 的阈值 ,这些算法可以以深度优 先的方式去搜索博弈树 ,但是所展开的博弈树与 p n 搜索是一样的. 这些深度优先的变体可以减少内存 的使用 ,但是效果与 p n 搜索相似. 目前 Alp ha2Beta 搜索及其扩展仍然是最广泛 使用的博弈树搜索算法[11 ] . p n 搜索及其变体变得 越来越流行[1 ] . 3 Alp ha2Beta 搜索 Alp ha2Beta 搜索的思想是利用 Alp ha 值 ——— 对于极大节点的最差可能值和 Beta 值 ———对于极 小节点的最差可能值. 使用这些值 ,很多分支可以被 裁减掉[ 15 ] . 在儿子节点被最好排序的情况下 ,Alp ha2Beta 搜索为求解问题需要访问的节点数目约为 w d/ 2 , w 是平均候选着法的数目 , d 是搜索的深度. 在最坏情 况下 ,为了求解它需要搜索整个博弈树. 文中使用 Alp ha2Beta 搜索及迭代加深、置换 表. 每次迭代深度增加为 2. 关于置换表使用 Zobrist 哈希[16 ]和线性探查. 几种常用的用于博弈树搜索算法比较的指标 有 :CPU 时间、访问的叶子节点数、访问的所有节点 数[17 ] . 文中使用访问的所有节点数来衡量算法的表 现. 这里使用 Kano 围棋系列的第 3 册中的吃子问 题来检验算法效果. 每一个问题的搜索时间被限制 在 200 s 内. 表 1 包含了 Alp ha2Beta 搜索不使用置 换表和使用置换表的测试结果. 使用置换表的算法表现比不使用置换表的算法 表现好 :使用的时间较少、访问的节点较少. 将节点 的最佳值存储在置换表中可以避免对同样的局面重 新计算. 在迭代加深中使用置换表也可以帮助候选 着法排序. 候选着法排序的质量对 Alp ha2Beta 搜索的效 率是关键的. 但对于不同问题很难给出统一的评估 函数去得到候选着法的最佳排序. 进一步的工作可 以使用模式数据库去帮助候选着法排序. 结果发现 Alp ha2Beta 搜索不能解决的问题主 要由于以下 3 个原因 : 1) 在时间限制下 Alp ha2Beta 搜索很难搜索到 很深的深度. 对于那些需要很深深度搜索才能求解 的问题 ,Alp ha2Beta 搜索一般用光时间从而失败. 2) 候选着法没有包括所有可能着法 :正确着法 缺失. 3) 解决此问题需要其他知识如连接和死活知 识. 4 proof2number 搜索 p n 搜索是最佳优先搜索算法. 对于非均衡树的 求解 p n 搜索是非常强大的. p n 搜索的思想是总是 展开那些用最小代价就可以证明或者否证与或博弈 树的节点[12 ] . p n 搜索将节点分为 2 种 :与节点和或 节点. 在每个与节点努力去否证节点 ,在每个或节点 努力去证明节点. 在每个节点上使用 2 个数值 : proof number ———最少需要展开的叶子节点去证明 此节点的数目 ; disproof number ———最少需要展开 的叶子节点去否证此节点的数目. 对于博弈树有时 ·86 · 智 能 系 统 学 报 第 2 卷

第3期 张培刚,等:使用不同的博弈树搜索算法解决计算机围棋的吃子问题 ·87 可以看成是与或树,有时可以看成是极大极小树,与 搜索到更深的深度.pn搜索及其变体未能解的问题 节点通常与极小节点是一样的,或节点通常与极大 是Alpha-Beta搜索未能解的问题的子集 节点是一样的 使用pn搜索及其变体的另外一个好处是它们 近年来出现的pn`df-pn和df-pn+等变体 不需要对候选着法的排序.这也会节省相当时间 使用哈希表存储中间结果.内存消耗可以减小到哈 结果发现那些没有解决的问题主要由于以下2 希表的大小 个原因: 对于非终止节点pn搜索和df-pn将proof 1)候选着法没有包括所有可能着法:正确着法 number和disproof number设为l.Df-pn+使用 缺失 评估函数h和cost来计算proof number和dis 2)解决此问题需要其他知识如连接和死活知 proof number.类似的也可以对pn搜索使用评估函 识 数来计算proof number和disproof number,可以称 这种算法为pn+ 5结果分析 对于pn+, 5.1算法比较 pn=E dn=(x5) 对于大多数问题,pn搜索及其变体比Alpha- Beta搜索效果好.大多数问题可以在1s内被解出, 对于df-pn+, pn搜索pn+、df-pn和df-pn+没有解出的6个 cost =0,h.pn=h dn =(x25) 问题是相同的问题,他们是Alpha-Beta搜索未能解 式中:E是节点评估值,pn是proof number,dn是 出的问题的子集.在所有解出的问题中,其中13个 disproof number 问题Alpha-Beta搜索比pn搜索效果好;29个问题 这里使用pn搜索pn+、df-pn和df-pn+解 pn搜索比Alpha-Beta搜索效果好;l3个问题pn搜 决吃子问题.候选着法产生和终止状态测试与A 索和Alpha-Beta搜索表现相当.从上表也可以看 pha-Beta搜索是一样的.算法中设定了访问的节 到,pn+表现比pn搜索好,df-pn+比df-pn表现 点总数和搜索时间来限定搜索.对于df-pn和df- 好.使用评估函数计算proof number和disproof pn+,一些候选着法产生但没有被访问,所以所访 number的算法,证明和否证根节点所访问的节点数 问的节点计数显得比pn搜索和pn+要少 比较少 这里使用Kano围棋系列的第3册中的吃子问 图3一5是在限定时间下各种算法的表现比较」 题来检测算法的效果.每一个问题的搜索时间被限 可以看到搜索时间如果限定在100ms,pn+的表现 制在200s内.表1包含了测试结果 最好 从图4和图5可以看到pn搜索及其变体有基 表1不同算法解决伯o系列第3册中吃子问题的结果 本相同的表现而且比Alpha-Beta搜索表现好 Table 1 Results of different algorithms to solve 5.2吃子问题分析 capturing problems in Kano book 3) Kano系列第3册中的61个吃子问题的搜索结 求解成 求解失 果为:49个问题成功吃死,6个问题成功逃脱,6个 算法 时间/ms节点数深度 功问题败问题 问题未成功求解 算法比较 ag6无置换表 52 9 5502 28746 5.6 一→a明无置换表-*-pt 明有置换表 53 8 2785 13187 5.8 一a卵有置换表*dfpm 40 -*-pn *“df-p时 pn 55 6 2148 18607 7.2 35 pn+ 55 6 1303 10931 7.0 301 -4 df-pn 55 6 2259 5792 7.4 2 df-pn+ 55 6 16482175 6.7 30 10 表1中,时间是求解问题所用平均时间(ms); 节点数是求解问题所访问平均节点数:深度是平均 102030405060708090100 深度 时间/ms pn搜索及其变体比Alpha-Beta搜索解出了更 图3所解问题数(100ms内限制) 多的问题、花费了更少的时间、访问了更少的节点和 Fig 3 Problems solved within 100 milliseconds 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
可以看成是与或树 ,有时可以看成是极大极小树 ,与 节点通常与极小节点是一样的 ,或节点通常与极大 节点是一样的. 近年来出现的 p n 3 、df - p n 和 df - p n + 等变体 使用哈希表存储中间结果. 内存消耗可以减小到哈 希表的大小. 对于非终止节点 p n 搜索和 df - p n 将 proof number 和 disproof number 设为 1. Df - p n + 使用 评估函数 h 和 cost 来计算 proof number 和 dis2 proof number. 类似的也可以对 p n 搜索使用评估函 数来计算 p roof number 和 disproof number ,可以称 这种算法为 p n + . 对于 p n + , p n = E 2 ,dn = ( 1 E ×25) 2 . 对于 df - p n + , cost = 0 , h. p n = E 2 , h. dn = ( 1 E ×25) 2 . 式中 : E 是节点评估值 , p n 是 proof number , dn 是 disproof number. 这里使用 p n 搜索、p n + 、df - p n 和 df - p n + 解 决吃子问题. 候选着法产生和终止状态测试与 Al2 p ha - Beta 搜索是一样的. 算法中设定了访问的节 点总数和搜索时间来限定搜索. 对于 df - p n 和 df - p n + ,一些候选着法产生但没有被访问 ,所以所访 问的节点计数显得比 p n 搜索和 p n + 要少. 这里使用 Kano 围棋系列的第 3 册中的吃子问 题来检测算法的效果. 每一个问题的搜索时间被限 制在 200 s 内. 表 1 包含了测试结果. 表 1 不同算法解决 Kano 系列第 3 册中吃子问题的结果 Table 1 Results of different algorithms to solve capturing problems in Kano book 3) 算法 求解成 功问题 求解失 败问题 时间/ ms 节点数 深度 αβ无置换表 52 9 5 502 28 746 516 αβ有置换表 53 8 2 785 13 187 518 pn 55 6 2 148 18 607 712 pn + 55 6 1 303 10 931 710 df - pn 55 6 2 259 5 792 714 df - pn + 55 6 1 648 2 175 617 表 1 中 ,时间是求解问题所用平均时间 (ms) ; 节点数是求解问题所访问平均节点数 ;深度是平均 深度. p n 搜索及其变体比 Alp ha2Beta 搜索解出了更 多的问题、花费了更少的时间、访问了更少的节点和 搜索到更深的深度. p n 搜索及其变体未能解的问题 是 Alp ha2Beta 搜索未能解的问题的子集. 使用 p n 搜索及其变体的另外一个好处是它们 不需要对候选着法的排序. 这也会节省相当时间. 结果发现那些没有解决的问题主要由于以下 2 个原因 : 1) 候选着法没有包括所有可能着法 :正确着法 缺失. 2) 解决此问题需要其他知识如连接和死活知 识. 5 结果分析 511 算法比较 对于大多数问题 ,p n 搜索及其变体比 Alp ha2 Beta 搜索效果好. 大多数问题可以在 1 s 内被解出. p n 搜索、p n + 、df - p n 和 df - p n + 没有解出的 6 个 问题是相同的问题 ,他们是 Alp ha2Beta 搜索未能解 出的问题的子集. 在所有解出的问题中 ,其中 13 个 问题 Alp ha2Beta 搜索比 p n 搜索效果好 ;29 个问题 p n 搜索比 Alp ha2Beta 搜索效果好 ;13 个问题 p n 搜 索和 Alp ha2Beta 搜索表现相当. 从上表也可以看 到 ,p n + 表现比 p n 搜索好 ,df - p n + 比 df - p n 表现 好. 使用评估函数计算 proof number 和 disproof number 的算法 ,证明和否证根节点所访问的节点数 比较少. 图 3~5 是在限定时间下各种算法的表现比较. 可以看到搜索时间如果限定在 100 ms ,p n + 的表现 最好. 图 3 所解问题数(100 ms 内限制) Fig13 Problems solved within 100 milliseconds 从图 4 和图 5 可以看到 p n 搜索及其变体有基 本相同的表现而且比 Alp ha2Beta 搜索表现好. 512 吃子问题分析 Kano 系列第 3 册中的 61 个吃子问题的搜索结 果为 :49 个问题成功吃死 ,6 个问题成功逃脱 ,6 个 问题未成功求解. 第 3 期 张培刚 ,等 :使用不同的博弈树搜索算法解决计算机围棋的吃子问题 ·87 ·
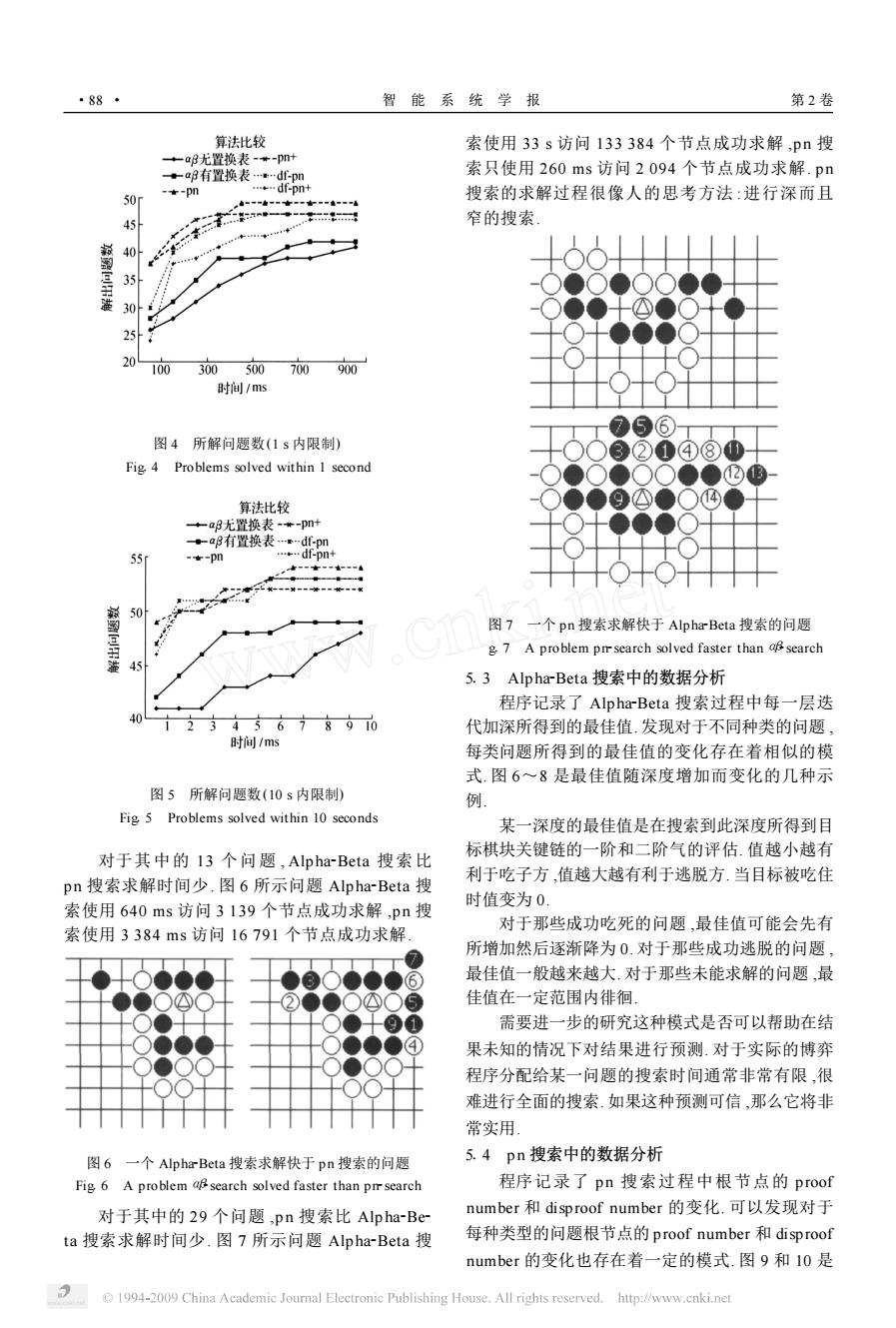
·88 智能系统学报 第2卷 算法比较 索使用33s访问133384个节点成功求解,pn搜 +a3无置换表-*-pn+ +ag有置换表…dfpn 索只使用260ms访问2094个节点成功求解.pn --pn *…df-pnt 50r 搜索的求解过程很像人的思考方法:进行深而且 45 本… 窄的搜索 治 40H 30 100 300500 700 900 时间/ms 图4所解问题数(1s内限制) 3②①④⑧0 Fig 4 Problems solved within I second 算法比较 9△ +a3无置换表-*-pn叶 。a3有置换表…df-pn 55 -★-pn +…df-pn+ 50 图7一个pn搜索求解快于AlphaBeta搜索的问题 g,7 A problem pmsearch solved faster than search 45 5.3 Alpha-Beta搜索中的数据分析 程序记录了Alpha-Beta搜索过程中每一层迭 40 345678910 代加深所得到的最佳值.发现对于不同种类的问题, 时间/ms 每类问题所得到的最佳值的变化存在着相似的模 式.图6~8是最佳值随深度增加而变化的几种示 图5所解问题数(10s内限制) 例 Fig 5 Problems solved within 10 seconds 某一深度的最佳值是在搜索到此深度所得到目 标棋块关键链的一阶和二阶气的评估.值越小越有 对于其中的I3个问题,Alpha-Beta搜索比 pn搜索求解时间少.图6所示问题Alpha-Beta搜 利于吃子方,值越大越有利于逃脱方.当目标被吃住 时值变为0, 索使用640ms访问3139个节点成功求解,pn搜 对于那些成功吃死的问题,最佳值可能会先有 索使用3384ms访问16791个节点成功求解. 所增加然后逐渐降为0.对于那些成功逃脱的问题, 6 最佳值一般越来越大.对于那些未能求解的问题,最 佳值在一定范围内徘徊· 需要进一步的研究这种模式是否可以帮助在结 果未知的情况下对结果进行预测.对于实际的博弈 程序分配给某一问题的搜索时间通常非常有限,很 难进行全面的搜索.如果这种预测可信,那么它将非 常实用 图6一个AlphaBeta搜索求解快于pn搜索的问题 5.4pn搜索中的数据分析 Fig 6 A problem search solved faster than prrsearch 程序记录了pn搜索过程中根节点的proof 对于其中的29个问题,pn搜索比Alpha-Be number和disproof number的变化.可以发现对于 ta搜索求解时间少,图7所示问题Alpha-Beta搜 每种类型的问题根节点的proof number和disproof number的变化也存在着一定的模式.图9和l0是 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 4 所解问题数(1 s 内限制) Fig14 Problems solved within 1 second 图 5 所解问题数(10 s 内限制) Fig15 Problems solved within 10 seconds 对于其中的 13 个问题 , Alp ha2Beta 搜索比 p n 搜索求解时间少. 图 6 所示问题 Alp ha2Beta 搜 索使用 640 ms 访问 3 139 个节点成功求解 ,p n 搜 索使用 3 384 ms 访问 16 791 个节点成功求解. 图 6 一个 Alpha2Beta 搜索求解快于 pn 搜索的问题 Fig16 A problemαβ2search solved faster than pn2search 对于其中的 29 个问题 ,p n 搜索比 Alp ha2Be2 ta 搜索求解时间少. 图 7 所示问题 Alp ha2Beta 搜 索使用 33 s 访问 133 384 个节点成功求解 ,p n 搜 索只使用 260 ms 访问 2 094 个节点成功求解. p n 搜索的求解过程很像人的思考方法 :进行深而且 窄的搜索. 图 7 一个 pn 搜索求解快于 Alpha2Beta 搜索的问题 Fi g17 A problem pn2search solved faster thanαβ2search 513 Alp ha2Beta 搜索中的数据分析 程序记录了 Alp ha2Beta 搜索过程中每一层迭 代加深所得到的最佳值. 发现对于不同种类的问题 , 每类问题所得到的最佳值的变化存在着相似的模 式. 图 6~8 是最佳值随深度增加而变化的几种示 例. 某一深度的最佳值是在搜索到此深度所得到目 标棋块关键链的一阶和二阶气的评估. 值越小越有 利于吃子方 ,值越大越有利于逃脱方. 当目标被吃住 时值变为 0. 对于那些成功吃死的问题 ,最佳值可能会先有 所增加然后逐渐降为 0. 对于那些成功逃脱的问题 , 最佳值一般越来越大. 对于那些未能求解的问题 ,最 佳值在一定范围内徘徊. 需要进一步的研究这种模式是否可以帮助在结 果未知的情况下对结果进行预测. 对于实际的博弈 程序分配给某一问题的搜索时间通常非常有限 ,很 难进行全面的搜索. 如果这种预测可信 ,那么它将非 常实用. 514 p n 搜索中的数据分析 程序记录了 p n 搜索过程中根节点的 proof number 和 disproof number 的变化. 可以发现对于 每种类型的问题根节点的 proof number 和 disproof number 的变化也存在着一定的模式. 图 9 和 10 是 ·88 · 智 能 系 统 学 报 第 2 卷

第3期 张培刚,等:使用不同的博弈树搜索算法解决计算机围棋的吃子问题 ·89· 成功吃死问题示例:228.sg number和disproof number一般持续增长 35 70r 成功吃死问题示例:45.5gf -p 60 -dn 20 840 民30 20 4 68 101214 10f。●鲁指。小 搜索深度 0 节点访向数 图8最佳值随深度变化(成功吃死问题示例) Fig 8 The best value of search with search deepening 1lpn搜索过程中根节点的proof number和disproof captured problem example number的变化(成功吃死问题示例) 120r 成功逃脱问题示例:15sgf Fig 11 The variation of proof number and disproof number 100H 914100 during pr search,captured problem example 804 成功逃脱问题示例:15.sg1 60 160-Pm 40 47 Dn 20 16 120 民 0 35 9i13s 且 80 搜索深度 40 图9最佳值随深度变化(成功逃脱问题示例) 0 节点访问数 Fig 9 The best value of search with search deepening, escaped problem example 图12pn搜索过程中根节点的proof number和disproof 未解出向题示例:8.sgf number的变化(成功逃脱问题示例) 40r 3333 363333 Fig 12 The variation of proof number and disproof number 30 28 during pr search,escaped problem example 20 21 需要进一步的研究这种模式是否可以帮助在结 15 果未知的情况下对结果进行预测 0 4680立14 6结束语 搜索深度 与其他相关工作比较,本文的吃子算法的表现 图10最佳值随深度变化(未能求解问题示例) 是出色的.pn搜索及其变体在解决吃子问题中有更 Fig 10 The best value of search with search deepening, 好的表现.大多数问题可以在不到1s的时间内求 unsolved problem example 解成功.这一成果可以被用于计算机围棋程序在比 随搜索访问节点数的增加根节点的proof number 赛中使用. 和disproof number的变化情况 那些未能求解的问题基本上可以归为2个原 proof number是最少需要展开的叶子节点去 因:评估函数的质量不高和需要其他类型的领域知 证明此节点的数目;disproof number是最少需要展 识如连接和死活.这需要提高评估函数的质量和使 开的叶子节点去否证此节点的数目,如果根节点的 用其他围棋战术知识: proof number变为0则目标被吃死.如果根节点的 进一步的工作包括 disproof number变为0则目标逃脱.对于那些成功 1)进一步优化吃子问题的评估函数.包括优化 吃死的问题proof number一般增加到一定的峰值 候选着法的产生、节点评估和用于pn+和df-pn+ 然后逐渐下降直到0,disproof number一般持续增 中的评估函数.机器学习的方法例如遗传算法可以 长.对于那些成功逃脱的问题,proof number一般 持续增长,disproof number一般增加到一定的峰值 引入以帮助优化评估函数 然后逐渐下降直到0.对于那些未解出的问题,proof 2)进一步研究Alpha-Beta搜索和pn搜索中的 模式及其对搜索结果的预测 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 8 最佳值随深度变化(成功吃死问题示例) Fig18 The best value ofαβ2search with search deepening , captured problem example 图 9 最佳值随深度变化(成功逃脱问题示例) Fig19 The best value ofαβ2search with search deepening , escaped problem example 图 10 最佳值随深度变化(未能求解问题示例) Fig110 The best value ofαβ2search with search deepening , unsolved problem example 随搜索访问节点数的增加根节点的 proof number 和 disproof number 的变化情况. proof number 是最少需要展开的叶子节点去 证明此节点的数目 ;disproof number 是最少需要展 开的叶子节点去否证此节点的数目. 如果根节点的 proof number 变为 0 则目标被吃死. 如果根节点的 disproof number 变为 0 则目标逃脱. 对于那些成功 吃死的问题 ,proof number 一般增加到一定的峰值 然后逐渐下降直到 0 ,disproof number 一般持续增 长. 对于那些成功逃脱的问题 ,proof number 一般 持续增长 ,disproof number 一般增加到一定的峰值 然后逐渐下降直到 0. 对于那些未解出的问题 ,proof number 和 disproof number 一般持续增长. 图 11 pn 搜索过程中根节点的 proof number 和 disproof number 的变化(成功吃死问题示例) Fig111 The variation of proof number and disproof number during pn2search , captured problem example 图 12 pn 搜索过程中根节点的 proof number 和 disproof number 的变化(成功逃脱问题示例) Fig112 The variation of proof number and disproof number during pn2search , escaped problem example 需要进一步的研究这种模式是否可以帮助在结 果未知的情况下对结果进行预测. 6 结束语 与其他相关工作比较 ,本文的吃子算法的表现 是出色的. p n 搜索及其变体在解决吃子问题中有更 好的表现. 大多数问题可以在不到 1 s 的时间内求 解成功. 这一成果可以被用于计算机围棋程序在比 赛中使用. 那些未能求解的问题基本上可以归为 2 个原 因 :评估函数的质量不高和需要其他类型的领域知 识如连接和死活. 这需要提高评估函数的质量和使 用其他围棋战术知识. 进一步的工作包括 : 1) 进一步优化吃子问题的评估函数. 包括优化 候选着法的产生、节点评估和用于 p n + 和 df - p n + 中的评估函数. 机器学习的方法例如遗传算法可以 引入以帮助优化评估函数. 2) 进一步研究 Alp ha2Beta 搜索和 p n 搜索中的 模式及其对搜索结果的预测. 第 3 期 张培刚 ,等 :使用不同的博弈树搜索算法解决计算机围棋的吃子问题 ·89 ·

·90· 智能系统学报 第2卷 3)比较Alpha-Beta搜索和pn搜索所访问的博 [11JUNGHANNS A.Are there practical alternatives to al- 弈树.研究将Alpha-Beta搜索和pn搜索结合以得 phar beta[J ]ICCA Journal,1998,21(1):14-32. 到更好的搜索效果的可能性 [12]ALLIS L V,MEUL EN M,HERIK H J.Proof-num- 4)使用本搜索框架去解决其他计算机围棋中的 ber search[J ]Artificial Intelligence,1994,66(1):91 124. 战术问题 [13]SEO M,IIDA H,UITERWU KJ W.The PN *-search 参考文献: algorithm:application to Tsume-Shogi[J ]Artificial In- telligence,2001,129(1-2):253.277. [1]KISHIMOTO A.Correct and efficient search algorithms [14]NA GAI A.Df-pn algorithm for searching and/or trees in the presence of repetitions[D].Edmonton:University and its applications [D].Tokyo:University of Tokyo, of Alberta,2005. 2002. [2]WOLF T.Forward pruning and other heuristic search [15]KNUTH D,MOORE R.Analysis of alpha-beta prun techniques in tsume go [J ]Information Sciences,2000, ing[J ]Artificial Intelligence,1975,6(4):293-326. 122(1):59.76. [16]ZOBRIST A L.A new hashing method with application [3]CHEN K,ZHAN G P.A heuristic search algorithm for for game playing [R].Techn.Rep.88,Madison: capturing problems in go [J ]ICGA Journal,2006,29 Univ.of Wisconsin,1970. (4):183.190. [17]CAMPBELL M,MARSLAND T.A comparison of [4]CHEN K.Soft and hard connectivity in go[A].Proceed- minimax tree-search algorithms [J].Artificial Intelli- ings of the 8thInternational Conference on Computer Sci- gence,1983,20(4):347.367 ence and Informatics[C].Salt Lake City,USA,2005. 作者简介: [5]BOUZY B,CAZENAVE T.Computer go:an Al orien ted survey [J].Artificial Intelligence,2001,132(1):39- 张培刚,男,1973年生,博士研究 103 生,主要研究方向为计算机围棋、人工 [6]MULL ER M.Computer go [J].Artificial Intelligence, 智能、启发式搜索和机器学习等。 2002,134(1-2):145-179. Email :pzhangl @uncc.edu [7]CHEN K.Computer go:knowledge,search,and move decision[J ]ICGA Journal 2001,24(4):203-215. [8 ]CAZENAVE T.Abstract proof search,computers and 陈克训,男,1945年生,教授,博士.主 games 2000[A].LNCS 2063[C].Hamamatsu,Japan, 要研究方向为启发式搜索、人工智能和计 2000. 算理论等.所研发的电脑围棋程序“棋慧” [9]THOMSEN T.Lambdar Search in game trees with appli- 曾两获电脑围棋世界冠军和七次夺得计 cation to go [J ]ICGA Journal,2000,23(4):203-217. 算机奥林匹亚竞赛金牌,发表论文40余 [10]CAMPBELL M,HOANE AJ,HSU F.Deep blue[J ] Artificial Intelligence,2002,134(1-2):57-83. Email :chen @uncc.edu. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
3) 比较 Alp ha2Beta 搜索和 p n 搜索所访问的博 弈树. 研究将 Alp ha2Beta 搜索和 p n 搜索结合以得 到更好的搜索效果的可能性. 4) 使用本搜索框架去解决其他计算机围棋中的 战术问题. 参考文献 : [1 ] KISHIMO TO A. Correct and efficient search algorithms in the presence of repetitions[D ]. Edmonton : University of Alberta , 2005. [2 ] WOL F T. Forward pruning and other heuristic search techniques in tsume go [J ]. Information Sciences , 2000 , 122 (1) :59 - 76. [3 ]CHEN K , ZHAN G P. A heuristic search algorithm for capturing problems in go [J ]. ICGA Journal , 2006 , 29 (4) : 183 - 190. [4 ]CHEN K. Soft and hard connectivity in go[ A ]. Proceed2 ings of the 8 th International Conference on Computer Sci2 ence and Informatics[C]. Salt Lake City ,USA ,2005. [5 ]BOUZY B , CAZENAV E T. Computer go : an AI orien2 ted survey[J ]. Artificial Intelligence , 2001 ,132 (1) :39 - 103. [6 ] MULL ER M. Computer go [J ]. Artificial Intelligence , 2002 , 134 (1 - 2) :145 - 179. [7 ]CHEN K. Computer go : knowledge , search , and move decision[J ]. ICGA Journal , 2001 ,24 (4) :203 - 215. [8 ]CAZENAV E T. Abstract proof search , computers and games 2000 [ A ]. LNCS 2063 [ C]. Hamamatsu , J apan , 2000. [ 9 ] THOMSEN T. Lambda2Search in game trees2with appli2 cation to go[J ]. ICGA Journal , 2000 ,23 (4) :203 - 217 . [10 ]CAMPBELL M , HOAN E A J , HSU F. Deep blue[J ]. Artificial Intelligence , 2002 , 134 (1 - 2) : 57 - 83. [ 11 ]J UN GHANNS A. Are there practical alternatives to al2 pha2beta[J ] . ICCA Journal ,1998 ,21 (1) :14 - 32. [12 ]ALL IS L V , MEUL EN M , HERIK H J. Proof2num2 ber search [J ]. Artificial Intelligence ,1994 ,66 (1) : 91 - 124. [ 13 ]SEO M , IIDA H , U ITERWIJ KJ W. The PN 3 2search algorithm : application to Tsume2Shogi[J ]. Artificial In2 telligence , 2001 , 129 (1 - 2) :253 - 277. [14 ]NA GAI A. Df2pn algorithm for searching and/ or trees and its applications [ D ]. Tokyo : University of Tokyo , 2002. [15 ] KNU TH D , MOORE R. Analysis of alpha2beta prun2 ing[J ]. Artificial Intelligence ,1975 ,6 (4) :293 - 326. [16 ]ZOBRIST A L. A new hashing method with application for game playing [ R ]. Techn. Rep . # 88 , Madison : Univ. of Wisconsin ,1970. [ 17 ] CAMPBELL M , MARSLAND T. A comparison of minimax tree2search algorithms [ J ]. Artificial Intelli2 gence , 1983 ,20 (4) : 347 - 367. 作者简介 : 张培刚 ,男 , 1973 年生 ,博士研究 生 ,主要研究方向为计算机围棋、人工 智能、启发式搜索和机器学习等. E2mail :pzhang1 @uncc. edu. 陈克训 ,男 ,1945 年生 ,教授 ,博士. 主 要研究方向为启发式搜索、人工智能和计 算理论等. 所研发的电脑围棋程序“棋慧” 曾两获电脑围棋世界冠军和七次夺得计 算机奥林匹亚竞赛金牌. 发表论文 40 余 篇. E2mail :chen @uncc. edu. ·90 · 智 能 系 统 学 报 第 2 卷