
第2卷第4期 智能系统学报 Vol.2№4 2007年8月 CAAI Transactions on Intelligent Systems Aug.2007 混沌卷积混合信号的预测重构盲反卷积方法 成谢锋3陈鹤鸣,马勇2,黄勇林1 (1.南京邮电大学光电工程学院,江苏南京210001;2.北京机械工业学院基础部,北京100085;3.济南大学控 制科学与工程学院,山东济南250022) 摘要:介绍了混沌序列的特性,然后利用混沌的类随机特性和盲信号处理技术,提出了一种针对混沌卷积混合信 号的预测重构盲反卷积方法.该方法充分利用了混沌的物理特性,通过对混沌卷积混合信号使用基于直接预测误差 分析所构成的混沌滤波器和基于相空间重构动力学系统方程的人工智能补偿技术去进行盲反卷积,从而实现对单 输入单输出混沌卷积信号的源信号和传输函数的盲反卷积处理.仿真实验验证了该方法的有效性和可行性. 关键词:盲反卷积:混沌:信号处理 中图分类号:TN911.7文献标识码:A文章编号:1673-4785(2007)04-006306 A blind deconvolution method for chaotic signals based on prediction and reconstruction analysis CHENG Xie-feng'3,CHEN He-ming',MA Yong?,HUANG Yong-lin' (1.Nanjing University of Posts and Telecommunications,Nanjing 210046,China;2.Division of Basic Courses,Beijing Insti- tute of Machinery,Beijing 100085,China;3.School of Control Science and Engineering,Jinan University,Jinan 250022,Chi- na) Abstract Based on the statistical characteristics of chaotic signals and blind signal processing techniques,a blind deconvolution method for chaotic signals based on prediction and reconstruction analysis is proposed. This method achieves blind deconvolution with respect to source signals and transmission functions of cha- otic signals with single-input and single-output through linear predication error analysis and artificial intel- ligence compensation.The effectiveness and feasibility of the proposed method were demonstrated in simu- lations. Key words:blind deconvolution;chaos;signal processing 混沌是复杂非线性系统中普遍存在的一种自然 行研究I.Lorenz方程、Rssler方程、Chen氏方程、 现象,如心脏系统、神经元网络、常微分方程组、二维 Logislic方程等都是研究混沌现象的经典模型.在 非线性映射均呈现典型的混沌现象.许多科学家在 应用方面也己取得许多研究成果,诸如Kaplan等人 这方面进行了较为深入的研究.1986年Goldberger 的母体中胎儿心电信号的提取2.61,Hay Kina对海 在对人体心脏进行研究后指出,健康的心脏系统是 洋杂波背景下有用信号的提取)、混沌保密通讯、混 有一定量的可变性,它对应着混沌状态,人心律频谱 沌随机波发生器、混沌振动器等.目前混沌理论的应 的1/∫分布是心脏混沌的旁证,心脏神经系统的分 用研究已从人工模拟深入到对自然界混沌现象的研 形结构是心脏混沌的有力证明山.大脑的神经元网究,因而从自然界中各种背景情况下提取和分离混 络系统是由大量的形式神经元联结而成的高度错综 沌信号就成了智能信号处理领域中的一个重要课 复杂的非线性系统,因此从神经元网络获取的信息, 题.目前对混沌信号的提取和分离已进行了较为深 如脑电波(EEG)信号也需按混沌动力学的规律进 入的研究.当混沌系统的动力学机理已知则从混合 信号中分离出混沌信号的方法是寻找一时间序列, 收稿日期:200612-28 基金项目:山东省自然科学基金资助项目(y2006G03):山东省重点科 使它满足己知的混沌动力学演化规律,又足够接近 技攻关项目(2006Gg204005). 所获取的观测序列.如果动力学机理未知,常用的 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 4 期 智 能 系 统 学 报 Vol. 2 №. 4 2007 年 8 月 CAAI Transactions on Intelligent Systems Aug. 2007 混沌卷积混合信号的预测重构盲反卷积方法 成谢锋1 ,3 ,陈鹤鸣1 ,马 勇2 ,黄勇林1 (1. 南京邮电大学 光电工程学院 ,江苏 南京 210001 ; 2. 北京机械工业学院 基础部 ,北京 100085 ; 3. 济南大学 控 制科学与工程学院 ,山东 济南 250022) 摘 要 :介绍了混沌序列的特性 , 然后利用混沌的类随机特性和盲信号处理技术 ,提出了一种针对混沌卷积混合信 号的预测重构盲反卷积方法. 该方法充分利用了混沌的物理特性 ,通过对混沌卷积混合信号使用基于直接预测误差 分析所构成的混沌滤波器和基于相空间重构动力学系统方程的人工智能补偿技术去进行盲反卷积 ,从而实现对单 输入单输出混沌卷积信号的源信号和传输函数的盲反卷积处理. 仿真实验验证了该方法的有效性和可行性. 关键词 :盲反卷积 ;混沌 ;信号处理 中图分类号 : TN911. 7 文献标识码 :A 文章编号 :167324785 (2007) 0420063206 A blind deconvolution method for chaotic signals based on prediction and reconstruction analysis CH EN G Xie2feng 1 ,3 , CH EN He2ming 1 ,MA Yong 2 , HUAN G Yong2lin 1 (1. Nanjing University of Posts and Telecommunications , Nanjing 210046 ,China ; 2. Division of Basic Courses , Beijing Insti2 tute of Machinery , Beijing 100085 , China ; 3. School of Control Science and Engineering , Jinan University , Jinan 250022 , Chi2 na) Abstract :Based on the statistical characteristics of chaotic signals and blind signal processing techniques , a blind deconvolution met hod for chaotic signals based on p rediction and reconstruction analysis is propo sed. This method achieves blind deconvolution wit h respect to source signals and transmission f unctions of cha2 otic signals wit h single2inp ut and single2outp ut t hrough linear predication error analysis and artificial intel2 ligence compensation. The effectiveness and feasibility of t he proposed method were demonstrated in simu2 lations. Keywords :blind deconvolution ; chaos ; signal processing 收稿日期 :2006212228. 基金项目 :山东省自然科学基金资助项目(y2006 G03) ;山东省重点科 技攻关项目(2006 Gg204005) . 混沌是复杂非线性系统中普遍存在的一种自然 现象 ,如心脏系统、神经元网络、常微分方程组、二维 非线性映射均呈现典型的混沌现象. 许多科学家在 这方面进行了较为深入的研究. 1986 年 Goldberger 在对人体心脏进行研究后指出 ,健康的心脏系统是 有一定量的可变性 ,它对应着混沌状态 ,人心律频谱 的 1/ f 分布是心脏混沌的旁证 ,心脏神经系统的分 形结构是心脏混沌的有力证明[ 1 ] . 大脑的神经元网 络系统是由大量的形式神经元联结而成的高度错综 复杂的非线性系统 ,因此从神经元网络获取的信息 , 如脑电波 ( EEG) 信号也需按混沌动力学的规律进 行研究[ 1 ] . Lorenz 方程、Rssler 方程、Chen 氏方程、 Logislic 方程等都是研究混沌现象的经典模型. 在 应用方面也已取得许多研究成果 ,诸如 Kaplan 等人 的母体中胎儿心电信号的提取[2 - 6 ] , Hay Kina 对海 洋杂波背景下有用信号的提取[ 7 ] 、混沌保密通讯、混 沌随机波发生器、混沌振动器等. 目前混沌理论的应 用研究已从人工模拟深入到对自然界混沌现象的研 究 ,因而从自然界中各种背景情况下提取和分离混 沌信号就成了智能信号处理领域中的一个重要课 题. 目前对混沌信号的提取和分离已进行了较为深 入的研究. 当混沌系统的动力学机理已知则从混合 信号中分离出混沌信号的方法是寻找一时间序列 , 使它满足已知的混沌动力学演化规律 ,又足够接近 所获取的观测序列[ 6 ] . 如果动力学机理未知 ,常用的 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·64 智能系统学报 第2卷 一个基本方法是相空间重构法8·).当用一个变量 0<x<1, 在不同时刻的值构成相空间,该动力系统的一个变 p( (3) 量的变化自然与此变量和系统的其他变量的相互作 0. 其他 用有关,即此变量随时间的变化隐含着整个系统的 P(x)与初值xO)无关,所以Logistic映射具有遍历 动力学规律.这样,可通过利用混沌吸引子的几何特 性 性,限定动力映射为原混沌吸引子所在流形的内部 2)混沌序列的均值x 映射,由该映射所具有的演化规律去重构动力学系 统方程,估计出混沌信号对应的轨迹,以实现混沌信 x=m太》0 N.1 号的分离提取.显然预先己知混沌动力机理,这一点 pwdx=0.5,x∈0,y. (4 对盲分离而言是不能满足的,而混沌信号与系统函 3)自相关函数A( 数卷积后己不再是和原混沌动力学方程微分同胚, N.I 所以不可能直接采用相空间重构法去恢复原混沌信 4(分=四Nx:x+r:司= 号. 本文首先介绍了混沌序列的特性,然后利用混 小时“r动d-可- 沌的类随机特性和盲信号处理技术,提出了一种针 0.125,r=0 对混沌卷积混合信号的预测重构盲反卷积方法.该 =0.1256(. (5) 0 r≠0 方法充分利用了混沌的物理特性,设计了基于直接 式中:f(x=(…f(x…,共m级 预测误差分析的混沌滤波器和基于相空间重构动力 4)互相关函数 学系统方程的补偿技术去进行盲反卷积,从而实现 任取2段混沌序列x1()、x2(刑,其互相关函 对单输入单输出混沌卷积信号的源信号和传输函数 数为 的盲反卷积处理.仿真实验验证了该方法的有效性 N.1 和可行性,并且具有速度较快、针对性强的特点。 A(r)lim- 1混沌序列的特性 (d-子=0.O 1.1混沌的定义 5)功率谱 混沌主要是研究非线性动力学系统随时间的变 W(w)= A(dek=0.125. ) 化规律.如果非线性系统是用以时间为自变量的微 t- 6)测度熵 分方程来描述,那么其离散形式为 根据Kolmogorovl)提出的测度熵: Xn+1=f(xn) 1) Kn=- 1989年Devaney给出了一种人们常用的混沌 ∑p(o,i,in)logp(o,,…il= 42 定义.设(x,p以是一紧致的度量空间,f:x→x是连 ∑4≤A, 8 续映射,称f在x上是混沌的,)∫具有对初值敏感 式中:是最大Lyapunov指数.在Logistic吸引子 依赖性:2)∫在x上拓扑传递:3)∫周期点在x中稠 情况下,当取10000点数据,嵌入空间维数为5时, 密 可计算出=(5.740.02)×101 1925年Li-Yorke给出Logistic映射的非线性 与白噪声的统计特性相比较,有如下结论 微分方程: 1)混沌信号的统计特性类同于零均值白噪声的 xa+1=4n1-xa},xn∈[0.11,μ∈f0,4]. 统计特性,所以混沌信号具有类随机性 (2 2)混沌是介于规则运动和随机运动之间的一种 当μ=3.569945672时发生倍周期分岔,导致混 特殊运动形式,当测量熵K=0时为规则运动:当测 沌 量熵K=时为随机运动;当测量熵K是大于0的 1.2混沌信号的统计特性 常数时,出现确定的混沌运动,并且随着K的增大, 1)概率分布函数P(x) 趋向真正的随机运动, H.G.Shuster证明了式(2)的概率分布密度 3)对一个混沌系统而言,它的输出是不收敛的, 函数为 输出波形是非周期的、类随机的 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
一个基本方法是相空间重构法[8 - 9 ] . 当用一个变量 在不同时刻的值构成相空间 ,该动力系统的一个变 量的变化自然与此变量和系统的其他变量的相互作 用有关 ,即此变量随时间的变化隐含着整个系统的 动力学规律. 这样 ,可通过利用混沌吸引子的几何特 性 ,限定动力映射为原混沌吸引子所在流形的内部 映射 ,由该映射所具有的演化规律去重构动力学系 统方程 ,估计出混沌信号对应的轨迹 ,以实现混沌信 号的分离提取. 显然预先已知混沌动力机理 ,这一点 对盲分离而言是不能满足的 ;而混沌信号与系统函 数卷积后已不再是和原混沌动力学方程微分同胚 , 所以不可能直接采用相空间重构法去恢复原混沌信 号. 本文首先介绍了混沌序列的特性 , 然后利用混 沌的类随机特性和盲信号处理技术 ,提出了一种针 对混沌卷积混合信号的预测重构盲反卷积方法. 该 方法充分利用了混沌的物理特性 ,设计了基于直接 预测误差分析的混沌滤波器和基于相空间重构动力 学系统方程的补偿技术去进行盲反卷积 ,从而实现 对单输入单输出混沌卷积信号的源信号和传输函数 的盲反卷积处理. 仿真实验验证了该方法的有效性 和可行性 ,并且具有速度较快、针对性强的特点. 1 混沌序列的特性 1. 1 混沌的定义 混沌主要是研究非线性动力学系统随时间的变 化规律. 如果非线性系统是用以时间为自变量的微 分方程来描述 ,那么其离散形式为 x n+1 = f ( x n ) . (1) 1989 年 Devaney 给出了一种人们常用的混沌 定义. 设( x , p) 是一紧致的度量空间 , f ∶x →x 是连 续映射 ,称 f 在 x 上是混沌的 ,1) f 具有对初值敏感 依赖性;2) f 在 x 上拓扑传递;3) f 周期点在 x 中稠 密. 1925 年 Li2Yorke 给出 Logistic 映射的非线性 微分方程 : x n+1 = μx n (1 - x n ) , x n ∈[011 ] ,μ ∈[0 ,4 ]. (2) 当μ= 3. 569 945 672 时发生倍周期分岔 ,导致混 沌. 1. 2 混沌信号的统计特性 1) 概率分布函数ρ( x) H. G. Shuster 证明了式 (2) 的概率分布密度 函数为 ρ( x) = 1 π x 1 - x , 0 < x < 1 , 0 , 其他. (3) ρ( x) 与初值 x (0) 无关 ,所以 Logistic 映射具有遍历 性. 2) 混沌序列的均值 x x = limN →∞ 1 N ∑ N - 1 i =0 x ( i) = ∫ 1 0 xρ( x) d x = 0. 5 , x ∈(0 ,1) . (4) 3) 自相关函数 A ( r) A ( r) = limN →∞ 1 N ∑ N - 1 i = 0 ( x ( i) - x ( x ( i) + r - x) = ∫ 1 0 x f m ( x)ρ( x) d x - ( x) 2 = 0. 125 , 0 , r = 0 r ≠0 = 0. 125δ( r) . (5) 式中 : f m ( x) = f ( …f ( x) …) ,共 m 级. 4) 互相关函数 任取 2 段混沌序列 x1 ( n) 、x2 ( n) ,其互相关函 数为 A ( r) = lim 1 N ∑ N - 1 i = 0 ( x1 i - x) ( x2 ( i+ r) - x) = ∫ 1 0∫ 1 0 x1 f m ( x2 )ρ( x1 )ρ( x2 ) dx1 dx2 - x 2 = 0. (6) 5) 功率谱 W ( w) = ∑ ∞ k = - ∞ A ( r) e - rwk = 0. 125. (7) 6) 测度熵 根据 Kolmogorov [ 7 ]提出的测度熵 : Kn = - i 1 , i 2∑, …, i n ρ( i0 , i1 , …, in ) log2ρ( i0 , i2 , …, in ) = ∑λi ≤λ1 , (8) 式中 :λ1 是最大 Lyap unov 指数. 在 Logistic 吸引子 情况下 ,当取 10 000 点数据 ,嵌入空间维数为 5 时 , 可计算出λ1 = (5. 74 ±0. 02) ×10 - 1 . 与白噪声的统计特性相比较 ,有如下结论 : 1) 混沌信号的统计特性类同于零均值白噪声的 统计特性 ,所以混沌信号具有类随机性. 2) 混沌是介于规则运动和随机运动之间的一种 特殊运动形式 ,当测量熵 K = 0 时为规则运动;当测 量熵 K = ∞时为随机运动;当测量熵 K 是大于 0 的 常数时 ,出现确定的混沌运动 ,并且随着 K 的增大 , 趋向真正的随机运动. 3) 对一个混沌系统而言 ,它的输出是不收敛的 , 输出波形是非周期的、类随机的. · 46 · 智 能 系 统 学 报 第 2 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第4期 成谢锋,等:混沌卷积混合信号的预测重构盲反卷积方法 ·65· Bp y(n-p)-(n-p)= 2方法描述 P y(n-p)+apy(n-p+k, 18 2.1混沌信号的反卷积预测模型与混沌滤波器 一个信号经过信道的传输,总会受信道的影响 整理得 产生延迟和衰减,比如反射地震数据中就受岩层结 Bp Bp.1(n-1)-kpep.1(n) 19) 构的影响,海洋波声数据中就含有海岸反射信息;胎 并且由式(15、19)可得,p=0时 儿心电信号经母体传递就会产生反射衰减,研究人 e(n)Bo y(n), 20) 员把这种使原始信号变得混淆的现象解释为卷积. 要同时使向前和向后误差最小,有 因此,一般情况下,传感器测得的信号是源及其衰减 dE[p (n)+Bi(n)1/okp =0. 和延迟的混合信号的线性组合,也即是卷积混合信 Ef-2Bp.1(n-1)ep.i(n kpep.(n+ 号.与瞬时混合相比,解决卷积混合问题的难度更 kpBp1(n-1)1=0, 大,更接近实际情况2 故 kp= 2E/Bm1(n-1)em.1(n)1 21) 设s()为混沌信号,h()为信道的冲击响应 E[1(W+Bn1(n-1)J 那么其卷积模型为 根据混沌的统计特性,混沌信号具有各态历经 e 特性,因此可以用时间平均近似取代集合平均 y(n h(n s(t-n. (9) 2∑IBp-1(n-l)ep-1(W] 设观测到的混沌卷积混合信号y(W的长度为M,设 22) 计一个P阶反卷积滤波器,使得s(的一个估计 (n+B(n1] (W有 由此可递推出针对混沌的反卷积滤波器的各阶系 min (n-h(n *y(n2 (10) 数 据线性预测原理,对于白噪声激励的观测序列 2.2混沌滤波器的定阶 可以用线性差分方程建模,由于混沌的类随机性,所 混沌滤波器的阶P是一个重要的问题.由于混 以对观测到的混沌卷积混合信号y(W有 沌信号具有噪声特性,根据有关文献.121的研究, P 可以使用最小描述长度判据: (=∑aty(n-d, (11) 春 min(pm)=MnG+号anM.( 23) (n-p)=->apty (n-p+k). (12) 式中:0。是预测误差,随着数据长度M的增加, 由于(m使用y(m之前的各种数据的加权线 应趋于零,当∫(P)表现出鲜明的极小值时,可确定 性组合,故称为前向预测模型,夕(n-p)使用的是 出P的值.但是,在短数据情况下,对阶次P的值通 y(W之后的数据的线性加权之和,故称为向后预测 常估值过高,并且∫(P)有时会出现多个极小值.针 模型.那么前向误差: 对混沌所具有的统计特性,通常取P为 ep(k)=y(n)-(n)= P≥D±1 24 P 式中:D为混沌动力学系统自变量的个数.总之,P y(W+aty(n-k材, (13) 值选取应通过实验反复验证,直到获得满意的效果 根据levinson所给出线性差分方程(Yule-walker方 为止 程)的递推公式1,有 2.3混沌信号的相空间重构 apk ap-1.+kpap-1.p., (14) 由于混沌信号类似于白噪声但并非真正的白噪 整理得 声,所以经过混沌滤波器复原出的信号(m并非与 ep(n)ep.1(n kpBp1(n-1). 15) 源信号s(完全相同,但与s(又基本同形,依据 式中: 混沌动力学理论,可以认为()与s(微分同胚, p-1 因此可据(重构出混沌系统的吸引子,再根据混 ep.1(n)y(n) ap.1.kv(n-k). 16) 沌吸引子光滑流形的几何特性,重构出混沌系统的 p.I 动力学方程,最终实现用这种方法去进一步恢复源 (n-1)=y(n-p)ap..ty(n-p+k. 信号的目的 17) 根据Takens!]和Sauer!)嵌入理论,s(ml构成 同理可得向后误差: 原混沌系统的可微嵌入.{s(}所在的最小流形M 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
2 方法描述 2. 1 混沌信号的反卷积预测模型与混沌滤波器 一个信号经过信道的传输 ,总会受信道的影响 产生延迟和衰减 ,比如反射地震数据中就受岩层结 构的影响 ,海洋波声数据中就含有海岸反射信息;胎 儿心电信号经母体传递就会产生反射衰减 ,研究人 员把这种使原始信号变得混淆的现象解释为卷积. 因此 ,一般情况下 ,传感器测得的信号是源及其衰减 和延迟的混合信号的线性组合 ,也即是卷积混合信 号. 与瞬时混合相比 , 解决卷积混合问题的难度更 大 ,更接近实际情况[2 - 4 ] . 设 s( n) 为混沌信号 , h ( n) 为信道的冲击响应 , 那么其卷积模型为 y ( n) = ∑ ∞ n = 0 h( n) s( t - n) , (9) 设观测到的混沌卷积混合信号 y ( n) 的长度为 M ,设 计一个 P 阶反卷积滤波器 , 使得 s ( n) 的一个估计 ^y ( n) 有 min ‖^y ( n) - h( n) 3 y ( n) ‖2 . (10) 据线性预测原理 ,对于白噪声激励的观测序列 可以用线性差分方程建模 ,由于混沌的类随机性 ,所 以对观测到的混沌卷积混合信号 y ( n) 有 ^y ( n) = - ∑ P k = 1 apk y ( n - k) , (11) ^y ( n - p) = - ∑ P k = 1 apk y ( n - p + k) . (12) 由于 ^y ( n) 使用 y ( n) 之前的各种数据的加权线 性组合 ,故称为前向预测模型 , ^y ( n - p) 使用的是 y ( n) 之后的数据的线性加权之和 ,故称为向后预测 模型. 那么前向误差 : ep ( k) = y ( n) - ^y ( n) = y ( n) + ∑ p k =1 apk y ( n - k) , (13) 根据 levinson 所给出线性差分方程( Yule2walker 方 程) 的递推公式[5 ] ,有 apk = ap- 1 , k + k p a p- 1 , p- k , (14) 整理得 ep ( n) = ep- 1 ( n) - k pB p- 1 ( n - 1) . (15) 式中 : ep- 1 ( n) = y ( n) ∑ p- 1 k = 1 ap- 1 , k y ( n - k) , (16) B p- 1 ( n - 1) = y ( n - p) + ∑ p- 1 k =1 ap- 1 , k y ( n - p + k) . (17) 同理可得向后误差 : B p = y ( n - p) - ^y ( n - p) = y ( n - p) + ∑ p k = 1 apk y ( n - p + k) , (18) 整理得 B p = B p- 1 ( n - 1) - k p e p- 1 ( n) . (19) 并且由式(15) 、(19) 可得 , p = 0 时 e0 ( n) = B0 = y ( n) , (20) 要同时使向前和向后误差最小 ,有 5E[ e 2 p ( n) + B 2 p ( n) ]/ 5k p = 0 , E[ - 2B p- 1 ( n - 1) ep- 1 ( n) + k p e 2 p- 1 ( n) + k pB 2 p- 1 ( n - 1) ] = 0 , 故 k p = 2E[ B p- 1 ( n - 1) ep- 1 ( n) ] E[ e 2 p- 1 ( n) + B 2 p- 1 ( n - 1) ] . (21) 根据混沌的统计特性 ,混沌信号具有各态历经 特性 ,因此可以用时间平均近似取代集合平均 : k p = 2 ∑n [ B p- 1 ( n - 1) ep- 1 ( n) ] ∑n [ e 2 p- 1 ( n) + B 2 p- 1 ( n - 1) ] , (22) 由此可递推出针对混沌的反卷积滤波器的各阶系 数. 2. 2 混沌滤波器的定阶 混沌滤波器的阶 P 是一个重要的问题. 由于混 沌信号具有噪声特性 ,根据有关文献[10 ,12 ] 的研究 , 可以使用最小描述长度判据 : min ( f ( p) ) = Mlnσ2 p + P 2 (ln M) . (23) 式中 :σp 是预测误差 , 随着数据长度 M 的增加 ,σp 应趋于零 ,当 f ( P) 表现出鲜明的极小值时 ,可确定 出 P 的值. 但是 ,在短数据情况下 ,对阶次 P 的值通 常估值过高 ,并且 f ( P) 有时会出现多个极小值. 针 对混沌所具有的统计特性 ,通常取 P 为 P ≥D ±1. (24) 式中 : D 为混沌动力学系统自变量的个数. 总之 , P 值选取应通过实验反复验证 ,直到获得满意的效果 为止. 2. 3 混沌信号的相空间重构 由于混沌信号类似于白噪声但并非真正的白噪 声 ,所以经过混沌滤波器复原出的信号 ^y ( n) 并非与 源信号 s( n) 完全相同 ,但与 s( n) 又基本同形 ,依据 混沌动力学理论 ,可以认为 ^y ( n) 与 s( n) 微分同胚 , 因此可据 ^y ( n) 重构出混沌系统的吸引子 ,再根据混 沌吸引子光滑流形的几何特性 ,重构出混沌系统的 动力学方程 ,最终实现用这种方法去进一步恢复源 信号的目的. 根据 Takens [ 8 ]和 Sauer [ 9 ] 嵌入理论 ,s( n) 构成 原混沌系统的可微嵌入. { s( n) }所在的最小流形 M 第 4 期 成谢锋 ,等 :混沌卷积混合信号的预测重构盲反卷积方法 · 56 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·66 智能系统学报 第2卷 与原混沌吸引子所在的流形是微分同胚,二者具有 过混沌反卷积滤波器后并非是最佳的原混沌信号恢 相同的维数.而(m并不在流形M上,但{(}在 复,但混沌信号的光滑流形之几何特性,是一个重要 R空间中与M具有差不多相同的形状.光滑流形 的先验知识,对解具有很强的限制.因而可以基于混 可以用流形上各点的局部切空间来近似,因而向流 沌的某些判据和这个特性来对盲反卷积后的估计信 形上进行投影可近似为向对应的局部切空间上投 号进行规整 影.根据文献7,91的奇异值分解(SVD)方法,设d 3)混沌信号经卷积运算后,一般已不再表现出 为重构维数,少(m)在n=m的邻域Q。内的邻近点 混沌特性,所以不能直接采用相空间重构法等手段 为(m)(i=1,2,…g,取Q>d,则s(所在流形 直接恢复原混沌信号」 的局部切空间和的估计为 2.4.2算法描述 0=1 不论是MLE算法、MMI算法,还是扩展H s(n) (25) 算法一般都要进行复杂的矩阵运算或张量运 m)·m 算】,特别是用神经网络模型实现时,存在运算收 敛速度慢,而学习速率参数的优化选择方式又对收 no) =h,,,a] 敛起决定性的作用).本文利用混沌的物理特性, 通过对混沌卷积混合信号波形的直接预测误差补偿 和光滑流形处理来实现预测重构盲反卷积,该方法 (26) 的步骤如下: 1)据观测数据y(W,经混沌反卷积滤波器给出 一个估计的°(m; 式中:0为域2。的中心,通常0(m).从矩阵A 2)利用°(m去重构动力学系统方程C(m,让 的SVD中,可确定出局部切空间的维数1,当它满 c(、°(通过庞加莱截面,对°(偏离直线分 足》+时,有∑G≈∑G.其局部切空间TM 1 1=1 布的点集,施以靠近限制,获得改造后的◇(川; 在R空间的坐标原点为so,它的一组正交基是[n, 3)利用(m和y(作反卷积,求°(: №,…血].那么由重构向量{(m}对应的流形M 4)为使得minl(d-h(m*y(l2,改造 上的点s(W可近似表示为 °(m为h(W; s/(W=0+Proj5((W-0). 27) 5)重复2)~4),当h(刊的相似系数满足要求 式中:Pojw表示向M上通过点5o的切空间投 ◇(W在庞加莱截面上为一直线分布的点集时,则停 影 止迭代: 令U,=[M,,…M],{山}-1是TwM的一 上述算法包括2个反卷积和对分离结果进行进 组单位正交基;U=[,a,a1,}1是 一步重构整理和恢复的过程.由于混沌信号的类随 Ta+)M的一组单位正交基,线性映射L:TmM→ 机性,经反卷积滤波器己获得较好的°( Ta+yM,可由LS法确定.进一步整理式(27)可得 第2次反卷积因已获得y(,°(W,求( 重构动力学系统方程1: 的方法就较多,既可再一次使用反卷积滤波器,也可 s'(n+1)ULU (n+(n+1)-ULUis'(n). 使用其他反卷积方法.本文采用的是:域除法算法: (28) Y(=H(Z☑Y(☑, 2.4单输出混沌卷积混合信号的预测重构盲反卷 故 N()=Y(/Y( 29 积算法 直接用FFT实现对序列的Z交换,然后进行 2.4.1关于混沌反卷积的讨论 频域除法,并注意对数据的去复数整理,以获取真实 在研究混沌反卷积问题时,应该注意如下特点 的(md. 1)混沌信号呈类Gauss特性,这对采用MLE 由于混沌信号所特有的物理特性,可以根据 算法、MMI算法,还是采用扩展HJ算法、ARMA °(W去重构一个动力学系统方程,并由这个系统产 模型进行盲反卷积都非常有利2,1o).对于非Gauss 生一个序列c(m,然后调整°(去逼近这个序列 卷积核,由于反卷积问题的病态,核函数的小误差可 c(m.采用的判据是用c(m和°()构造一个庞加 能导改解的重大变化 莱截面,循环让°(d的各点通过这个截面.用一个 2)混沌信号又不是真正的白噪声信号,所以经 矩形窗去限制这些点集在一条具有一定宽度的直线 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
与原混沌吸引子所在的流形是微分同胚 ,二者具有 相同的维数. 而 ^y ( n) 并不在流形 M 上 ,但{ ^y ( n) }在 R d 空间中与 M 具有差不多相同的形状. 光滑流形 可以用流形上各点的局部切空间来近似 ,因而向流 形上进行投影可近似为向对应的局部切空间上投 影. 根据文献[7 , 9 ]的奇异值分解 (SVD) 方法 ,设 d 为重构维数 , ^y ( n) 在 n = n0 的邻域Ωn 内的邻近点 为^y ( ni) ( i = 1 ,2 , …, Q) ,取 Q > d ,则 s( n) 所在流形 的局部切空间和 s0 的估计为 s0 = 1 Q ∑ Q i =1 ^y ( ni) , (25) A = ^y ( n1 ) - s0 ‖^y ( n1 ) - s0 ‖ , ^y ( n2 ) - s0 ‖^y ( n2 ) - s0 ‖ , …, ^y ( nQ ) - s0 ‖^y ( nQ ) - s0 ‖ = [ u1 , u2 , …, ud ] · σ2 1 σ2 2 ω 0d×( q- d) σ2 d v T 1 v T 2 … v T Q . (26) 式中 :s0 为域Ωn 的中心 ,通常 s0 ≠^y ( n0 ) . 从矩阵 A 的 SVD 中 ,可确定出局部切空间的维数 l ,当它满 足σ2 l µσ2 l + 1时 ,有 ∑ l i = 1 σ2 i ≈ ∑ d i = 1 σ2 i . 其局部切空间 Ts( n) M 在 R d 空间的坐标原点为s 0 ,它的一组正交基是[ u1 , u2 , …, ul ]. 那么由重构向量{ ^y ( n) } 对应的流形 M 上的点 s ( n) 可近似表示为 s′( n) = s0 + Pro j T s 0 ( M) ( ^y ( n) - s0 ) . (27) 式中 :Pro j T s 0 ( M) 表示向 M 上通过点 s 0 的切空间投 影. 令 Ul = [ u1 , u2 , …, ul ] ,{ ui} l i = 1 是 Ts( n) M 的一 组单位正交 基; Ul = [ u1 , u2 , …, ul ] , { ui } l i = 1 是 Ts( n + 1) M 的一组单位正交基 ,线性映射 L : Ts( n) M π Ts( n + 1) M ,可由 L S 法确定. 进一步整理式 (27) 可得 重构动力学系统方程[9 ] : s′( n + 1) = UlLU T l ^y ( n) + ^y ( n + 1) - UlLU T l s′( n) . (28) 2. 4 单输出混沌卷积混合信号的预测重构盲反卷 积算法 2. 4. 1 关于混沌反卷积的讨论 在研究混沌反卷积问题时 ,应该注意如下特点 : 1) 混沌信号呈类 Gauss 特性 ,这对采用 ML E 算法、MMI 算法 ,还是采用扩展 H2J 算法、ARMA 模型进行盲反卷积都非常有利[ 2 ,10 ] . 对于非 Gauss 卷积核 ,由于反卷积问题的病态 ,核函数的小误差可 能导改解的重大变化. 2) 混沌信号又不是真正的白噪声信号 ,所以经 过混沌反卷积滤波器后并非是最佳的原混沌信号恢 复 ,但混沌信号的光滑流形之几何特性 ,是一个重要 的先验知识 ,对解具有很强的限制. 因而可以基于混 沌的某些判据和这个特性来对盲反卷积后的估计信 号进行规整. 3) 混沌信号经卷积运算后 ,一般已不再表现出 混沌特性 , 所以不能直接采用相空间重构法等手段 直接恢复原混沌信号. 2. 4. 2 算法描述 不论是 ML E 算法、MMI 算法 ,还是扩展 H2J 算法 一 般 都 要 进 行 复 杂 的 矩 阵 运 算 或 张 量 运 算[1 - 2 ] ,特别是用神经网络模型实现时 ,存在运算收 敛速度慢 ,而学习速率参数的优化选择方式又对收 敛起决定性的作用[12 ] . 本文利用混沌的物理特性 , 通过对混沌卷积混合信号波形的直接预测误差补偿 和光滑流形处理来实现预测重构盲反卷积 ,该方法 的步骤如下 : 1) 据观测数据 y ( n) ,经混沌反卷积滤波器给出 一个估计的 ^y 0 ( n) ; 2) 利用 ^y 0 ( n) 去重构动力学系统方程 C( n) ,让 c( n) 、^y 0 ( n) 通过庞加莱截面 ,对 ^y 0 ( n) 偏离直线分 布的点集 ,施以靠近限制 ,获得改造后的 ^y ( n) ; 3) 利用 ^y ( n) 和 y ( n) 作反卷积 ,求 ^h 0 ( n) ; 4) 为使得 min ‖^y ( n) - h ( n) 3 y ( n) ‖2 ,改造 ^h 0 ( n) 为 ^h ( n) ; 5) 重复 2) ~4) ,当 ^h ( n) 的相似系数满足要求 , ^y ( n) 在庞加莱截面上为一直线分布的点集时 ,则停 止迭代. 上述算法包括 2 个反卷积和对分离结果进行进 一步重构整理和恢复的过程. 由于混沌信号的类随 机性 ,经反卷积滤波器已获得较好的 ^y 0 ( n) . 第 2 次反卷积因已获得 y ( n) , ^y 0 ( n) ,求 ^h 0 ( n) 的方法就较多 ,既可再一次使用反卷积滤波器 ,也可 使用其他反卷积方法. 本文采用的是 z 域除法算法 : ^Y ( z) = H ( Z) Y ( Z) , 故 H^ ( z) = ^Y ( z) / Y ( z) . (29) 直接用 FF T 实现对序列的 Z 交换 ,然后进行 频域除法 ,并注意对数据的去复数整理 ,以获取真实 的 ^h 0 ( n) . 由于混沌信号所特有的物理特性 , 可以根据 ^y 0 ( n) 去重构一个动力学系统方程 ,并由这个系统产 生一个序列 c( n) ,然后调整 ^y 0 ( n) 去逼近这个序列 c( n) . 采用的判据是用 c ( n) 和 ^y 0 ( n) 构造一个庞加 莱截面 ,循环让 ^y 0 ( n) 的各点通过这个截面 ,用一个 矩形窗去限制这些点集在一条具有一定宽度的直线 · 66 · 智 能 系 统 学 报 第 2 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
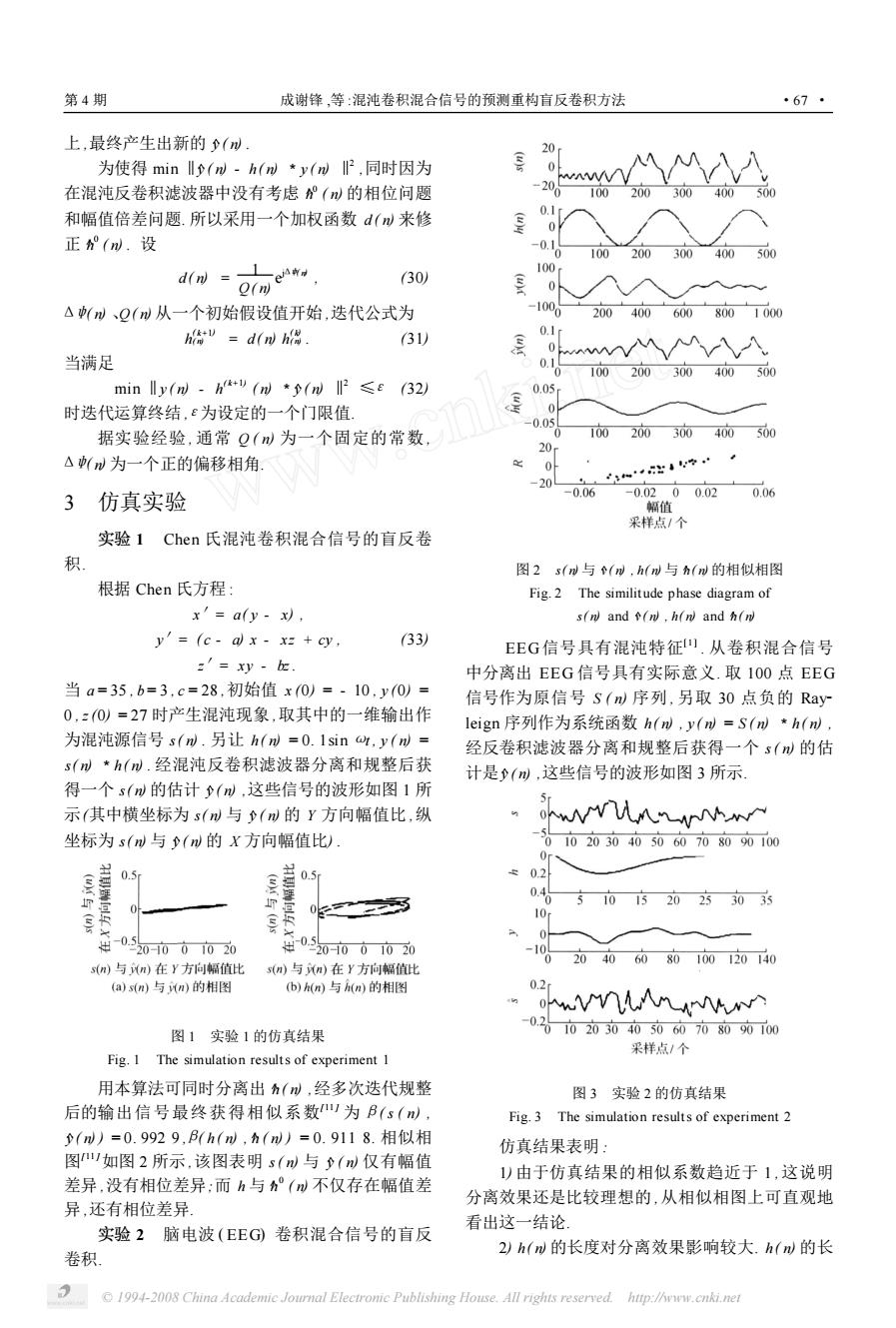
第4期 成谢锋,等:混沌卷积混合信号的预测重构盲反卷积方法 *67· 上,最终产生出新的(W. 20 为使得minl(W-h(W*y(W,同时因为 0 在混沌反卷积滤波器中没有考虑°()的相位问题 -20 100 200300400500 和幅值倍差问题.所以采用一个加权函数d()来修 0.1r 0 正°(W.设 -0.1 100200300400500 d(n e 100 (30) O(n) 0 △(W、Q(w从一个初始假设值开始,迭代公式为 -1000 2004006008001000 ho=d(n)hi 31) 0.1 当满足 wwMV 0.1 100200300400500 min lly(n)h (n(n (32) 0.05 时迭代运算终结,£为设定的一个门限值 -0.05 据实验经验,通常Q()为一个固定的常数 100200300400500 20 △(d为一个正的偏移相角. 0 -20 上和出4学… 3 仿真实验 -0.06 -0.0200.020.06 幅值 采样点/个 实验1chen氏混沌卷积混合信号的盲反卷 积 图2s(W与个(W,h(W与h(w的相似相图 根据Chen氏方程: Fig.2 The similitude phase diagram of x'=a(y-x), s(n)and(n),h(n and(n y'=(c-al x-x=+cy, (33) EEG信号具有混沌特征).从卷积混合信号 z=xy-b加 中分离出EEG信号具有实际意义.取100点EEG 当a=35,b=3,c=28,初始值x0)=·10,y0)= 信号作为原信号S(md序列,另取30点负的Ray 0,z0)=27时产生混沌现象,取其中的一维输出作 leign序列作为系统函数h(W,y(l=S(ml*h(nd, 为混沌源信号s(m.另让h(m=0.1sint,y(W= 经反卷积滤波器分离和规整后获得一个s(的估 s(刊*h(m.经混沌反卷积滤波器分离和规整后获 计是◇(m,这些信号的波形如图3所示 得一个s(m的估计(川,这些信号的波形如图1所 示(其中横坐标为s(与◇(m的y方向幅值比,纵 iwrlni 坐标为s(d与(W的X方向幅值比). 0102030405060708090100 0 0.5 0.5 0.2 0.46510120253033 10r 01 0.320-001020 ¥030市01市20 -10 020406080100120140 s(n)与n)在Y方向幅值比 s()与n)在Y方向幅值比 (a)s(n)与n)的相图 (b)h(n)与h(n)的相图 0.2r ihwvnlir 图1实验1的仿真结果 -02020304050008000 采样点/个 Fig.I The simulation results of experiment 1 用本算法可同时分离出(川,经多次迭代规整 图3实验2的仿真结果 后的输出信号最终获得相似系数)为B(s(), Fig.3 The simulation results of experiment 2 ()=0.9929,B(h(d,(l)=0.9118.相似相 仿真结果表明: 图如图2所示,该图表明s(m与(m仅有幅值 1)由于仿真结果的相似系数趋近于1,这说明 差异,没有相位差异:而h与°(不仅存在幅值差 分离效果还是比较理想的,从相似相图上可直观地 异,还有相位差异 看出这一结论 实验2脑电波(EEG卷积混合信号的盲反 卷积 2)h(刊的长度对分离效果影响较大.h(l的长 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
上 ,最终产生出新的 ^y ( n) . 为使得 min ‖^y ( n) - h( n) 3 y ( n) ‖2 ,同时因为 在混沌反卷积滤波器中没有考虑 ^h 0 ( n) 的相位问题 和幅值倍差问题. 所以采用一个加权函数 d ( n) 来修 正 ^h 0 ( n) . 设 d ( n) = 1 Q( n) e jΔψ( n) , (30) Δψ( n) 、Q( n) 从一个初始假设值开始 ,迭代公式为 h ( k+1) ( n) = d ( n) h ( k) ( n) . (31) 当满足 min ‖y ( n) - h ( k+1) ( n) 3 ^y ( n) ‖2 ≤ε (32) 时迭代运算终结 ,ε为设定的一个门限值. 据实验经验 , 通常 Q ( n) 为一个固定的常数 , Δψ( n) 为一个正的偏移相角. 3 仿真实验 实验 1 Chen 氏混沌卷积混合信号的盲反卷 积. 根据 Chen 氏方程 : x′= a( y - x) , y′= ( c - a) x - xz + cy , (33) z′= xy - bz . 当 a = 35 , b = 3 , c = 28 ,初始值 x (0) = - 10 , y (0) = 0 , z (0) = 27 时产生混沌现象 ,取其中的一维输出作 为混沌源信号 s( n) . 另让 h ( n) = 0. 1sin ωt , y ( n) = s( n) 3 h( n) . 经混沌反卷积滤波器分离和规整后获 得一个 s( n) 的估计 ^y ( n) ,这些信号的波形如图 1 所 示(其中横坐标为 s( n) 与 ^y ( n) 的 Y 方向幅值比 ,纵 坐标为 s( n) 与 ^y ( n) 的 X 方向幅值比) . 图 1 实验 1 的仿真结果 Fig. 1 The simulation results of experiment 1 用本算法可同时分离出 ^h ( n) ,经多次迭代规整 后的输出信号最终获得相似系数[11 ] 为 β( s ( n) , ^y ( n) ) = 0. 992 9 ,β( h ( n) , ^h ( n) ) = 0. 911 8. 相似相 图[11 ]如图 2 所示 ,该图表明 s( n) 与 ^y ( n) 仅有幅值 差异 ,没有相位差异;而 h 与 ^h 0 ( n) 不仅存在幅值差 异 ,还有相位差异. 实验 2 脑电波 ( EEG) 卷积混合信号的盲反 卷积. 图 2 s( n) 与 ^v ( n) , h( n) 与 ^h( n) 的相似相图 Fig. 2 The similitude phase diagram of s( n) and ^v ( n) , h( n) and ^h( n) EEG信号具有混沌特征[ 1 ] . 从卷积混合信号 中分离出 EEG 信号具有实际意义. 取 100 点 EEG 信号作为原信号 S ( n) 序列 , 另取 30 点负的 Ray2 leign 序列作为系统函数 h( n) , y ( n) = S ( n) 3 h( n) , 经反卷积滤波器分离和规整后获得一个 s( n) 的估 计是^y ( n) ,这些信号的波形如图 3 所示. 图 3 实验 2 的仿真结果 Fig. 3 The simulation results of experiment 2 仿真结果表明 : 1) 由于仿真结果的相似系数趋近于 1 ,这说明 分离效果还是比较理想的 ,从相似相图上可直观地 看出这一结论. 2) h( n) 的长度对分离效果影响较大. h ( n) 的长 第 4 期 成谢锋 ,等 :混沌卷积混合信号的预测重构盲反卷积方法 · 76 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·68· 智能系统学报 第2卷 度越接近于y(w的长度,分离的效果越好 [6]CHEN G Xiefeng,ZHANG Yong,LIU Ju.A novel blind 3)混沌卷积滤波器的阶数越大,分离结果中出 deconvolution method for singleoutput chaotic conv-olu- 现的细节波形越多,也即出现过补偿,所以阶数的选 tion mixed signal [A].International Symposium on Neu 择对分离结果影响较大, ral Networks[C].Chongqing,China,2005. [7]BENETTIN G,GAL GANI L.Kolmogorov entropy and 4结束语 numerical experiments [J ]Phys Rev 1976,14:2338- 2345. 由于混沌信号的普遍性,所以混沌卷积混合信 [8]WANG F P.Harmonic signal extraction form strong 号的盲处理技术的研究具有实用性.本文提出的预 chaotic interference [J ]Acta Phys,2001 (6):1019 测重构盲反卷积的算法充分利用了混沌的物理特 1023 性,通过对混沌卷积混合信号的直接预测误差补偿 [9]TONGL,LIU R,SOON V C,et al.Indeterminacy and 和光滑流形处理去进行盲反卷积,从而实现对单输 identifiability of blind identification [J ]IEEE Trans on 出混沌卷积信号的盲信号处理.这种针对特殊对象 Circuits and Systems,1991,38(5):499-506. 的盲反卷积方法对拓宽智能信号处理的应用范围, [10]CHENG Xiefeng,LIU Ju.A novel denoising algorithm 进一步研究这些特殊对象的性质都具有积极的现实 based on feed forward multilayer blind separation [A]. 意义 In Proc ISNN2004 [C].Dalian,China,2004. [12JUTTEN C,HERAUL TJ.Blind separation of sources, 参考文献: Part I:an adaptive algorithm based on neuromimetic [J ]Signal Processing,1991,24(4):1-10. [1]GOLDBERGER A L,WEST B J.Chaos and fractals in 作者简介: human physiology[J ]Scientific American,1990,62(3): 成谢锋,男,1956年生,教授,硕 42.49. 士生导师,主要研究方向为盲信号处 [2]刘琚,何振亚.盲源分离和盲反卷积[J].电子学报, 理、智能仪器及其应用.主持和完成省 2002,30(4):591.597. 自然科学基金、省科技攻关项目3项 LIU Ju,HE Zhenya.A survey of blind source separation 获得省科技进步二等奖1项,获得中 and blind deconvolution [J ]Acta Electronica Sinica, 国发明专利1项.发表论文30余篇, 2002,30(4):591-597. 其中被SC1收录3篇,EI收录8篇,撰 [3]BELL A J,SEJNOWSKI T J.An informatiomr maxim 写著作2部 ization approach to blind separation and blind decomvolu E mail jnucxf @163.com. tion [J ]Neural Computation,1995,7:1129-1159. [4]COMON P.Independent component analysis,a new con- 马勇,男,1983年生,硕士研究 cept [J ]Signal Processing,1994,36(4):287-314. 生,主要研究方向为非晶态合金传感 [5]HSUE J J,YAGLE A E.Blind deconvolution of sym- 技术和生物信号处理 metric noncausal impulse responses using two-sided line- ar prediction [J].Signal Processing,1994,42(6):1509 -1518 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
度越接近于 y ( n) 的长度 ,分离的效果越好. 3) 混沌卷积滤波器的阶数越大 ,分离结果中出 现的细节波形越多 ,也即出现过补偿 ,所以阶数的选 择对分离结果影响较大. 4 结束语 由于混沌信号的普遍性 ,所以混沌卷积混合信 号的盲处理技术的研究具有实用性. 本文提出的预 测重构盲反卷积的算法充分利用了混沌的物理特 性 ,通过对混沌卷积混合信号的直接预测误差补偿 和光滑流形处理去进行盲反卷积 ,从而实现对单输 出混沌卷积信号的盲信号处理. 这种针对特殊对象 的盲反卷积方法对拓宽智能信号处理的应用范围 , 进一步研究这些特殊对象的性质都具有积极的现实 意义. 参考文献 : [1 ] GOLDBERGER A L , WEST B J. Chaos and fractals in human physiology[J ]. Scientific American , 1990 , 62 (3) : 42 - 49. [2 ]刘 琚 ,何振亚. 盲源分离和盲反卷积[J ]. 电子学报 , 2002 ,30 (4) :591 - 597. L IU J u , HE Zhenya. A survey of blind source separation and blind deconvolution [J ]. Acta Electronica Sinica , 2002 , 30 (4) :591 - 597. [3 ]BELL A J , SEJ NOWSKI T J. An information2maxim2 ization approach to blind separation and blind decon2volu2 tion [J ]. Neural Computation , 1995 ,7 :1129 - 1159. [ 4 ]COMON P. Independent component analysis , a new con2 cept [J ]. Signal Processing , 1994 , 36 (4) : 287 - 314. [5 ] HSU E J J , YA GL E A E. Blind deconvolution of sym2 metric noncausal impulse responses using two2sided line2 ar prediction [J ]. Signal Processing , 1994 , 42 (6) : 1509 - 1518. [6 ]CHEN G Xiefeng , ZHAN G Yong , L IU J u. A novel blind deconvolution method for single2output chaotic conv2olu2 tion mixed signal [ A ]. International Symposium on Neu2 ral Networks[C]. Chongqing , China , 2005. [7 ]BEN ETTIN G, GAL GANI L. Kolmogorov entropy and numerical experiments [J ]. Phys Rev 1976 , 14 : 2338 - 2345. [8 ] WAN G F P. Harmonic signal extraction form strong chaotic interference [J ]. Acta Phys , 2001 ( 6 ) : 1019 - 1023. [ 9 ] TON G L , L IU R , SOON V C , et al. Indeterminacy and identifiability of blind identification [J ]. IEEE Trans on Circuits and Systems ,1991 ,38 (5) : 499 - 506. [10 ]CHEN G Xiefeng , L IU J u. A novel denoising algorithm based on feed forward multilayer blind separation [ A ]. In Proc ISNN2004 [C]. Dalian , China , 2004. [12 ]J U TTEN C , HERAUL T J. Blind separation of sources , Part I: an adaptive algorithm based on neuromimetic [J ]. Signal Processing ,1991 ,24 (4) : 1 - 10. 作者简介 : 成谢锋 ,男 , 1956 年生 ,教授 ,硕 士生导师 ,主要研究方向为盲信号处 理、智能仪器及其应用. 主持和完成省 自然科学基金、省科技攻关项目 3 项 , 获得省科技进步二等奖 1 项 ,获得中 国发明专利 1 项. 发表论文 30 余篇 , 其中被 SCI 收录 3 篇 ,EI 收录 8 篇 ,撰 写著作 2 部. E2mail :jnucxf @163. com. 马 勇 ,男 ,1983 年生 ,硕士研究 生 ,主要研究方向为非晶态合金传感 技术和生物信号处理. · 86 · 智 能 系 统 学 报 第 2 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net