
第2卷第5期 智能系统学报 Vol.2№5 2007年10月 CAAI Transactions on Intelligent Systems 0ct.2007 一类非线性不确定系统的非奇异Terminal滑模控制 姚丽萍,刘国栋 (江南大学通信与控制工程学院,江苏无锡214122) 摘要:针对一类二阶非线性系统提出新的Terminal滑模控制面以克服传统的Terminal滑模控制的奇异问题,同 时确保系统从任何初始状态能在有限时间内收敛至平衡点.进一步考虑系统参数摄动和外界扰动等不确定性因素 上界的未知性,用Lyapunov稳定性方法给出了一个带有未知性上界参数估计的自适应非奇异Terminal滑模控制 (NTSM)控制.最后通过实例比较三种滑模控制方法,仿真结果验证了非奇异Terminal滑模控制能克服传统的Ter minal滑模控制的奇异问题,并说明了自适应非奇异Terminal滑模控制的有效性和可行性 关键词:Terminal滑模控制;奇异;非线性系统,Lyapunov稳定性 中图分类号:TP273文献标识码:A文章编号:1673-4785(2007)050053-05 Non-singular Terminal sliding mode control for a class of uncertain nonlinear systems YAO Li-ping ,LIU Guo-dong (Department of Communication and Control Engineering,Southern Yangtze University,Wuxi 214122,China) Abstract:This paper presents a new Terminal sliding mode control surface for a class of second-order non- linear uncertain systems to eliminate the singularity problem in conventional terminal sliding mode con- trols,so that the system can be guaranteed to converge to an equilibrium point from any initial state within a finite time in the phase of sliding mode motion.To deal with the upper bounds of uncertainties such as systematic parameter perturbations and external disturbances,an adaptive nomsingular Terminal sliding mode (NTSM)control with parametric estimation for uncertain upper bounds was derived using Lyapunov stability theory.The simulation results of an example are investigated to show nomsingularity terminal sliding mode can elimination the singularity,and also show the feasibility and the effectiveness of the self-a- daptive method. Key words:Terminal sliding mode control;singularity:nonlinear systems;Lyapunov stability 滑模变结构控制的基本原理就是使用一个不连minal滑动模态发展起来,它是一种新型变结构控 续的高频切换控制迫使闭环系统的运动到达预先选制思想.变结构控制理论中引入Terminal滑动模态 定的滑动面或者它的一个很小的邻域上,通过控制的最直接的原因就是:Terminal滑模可以使系统的 器结构的改变以使系统达到良好的动态性能.滑模状态在“有限时间内”收敛至平衡点).Terminal滑 控制对参数摄动和外部扰动具有不敏感性,一般情模控制策略的实质在于:在滑动超平面的设计中引 况下,选择线性的滑动超平面是变结构控制理论中 入了非线性函数,非线性函数的引入使得在滑动面 最为常见的情形.这个线性的滑动超平面能够确保上系统状态能够在有限时间内收敛到零.然而传统 系统轨迹在到达滑动模态阶段以后,滑动模态的运 的Terminal滑模控制器的设计存在奇异问题,一些 动是渐近稳定的,尽管如此滑动模态仍然不会在有 避免Terminal奇异问题的解决方法己提出3).本文 限时间内收敛至零山.近年来,有限时间机理Ter 针对一类二阶非线性不确定动态系统提出非奇异 Terminal滑动模态(NTSM)控制器的设计,并通过 收稿日期:2007-0408. 提出一种新的NTSM滑模面来克服奇异问题,使得 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 5 期 智 能 系 统 学 报 Vol. 2 №. 5 2007 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2007 一类非线性不确定系统的非奇异 Terminal 滑模控制 姚丽萍 ,刘国栋 (江南大学 通信与控制工程学院 ,江苏 无锡 214122) 摘 要 :针对一类二阶非线性系统提出新的 Terminal 滑模控制面以克服传统的 Terminal 滑模控制的奇异问题 ,同 时确保系统从任何初始状态能在有限时间内收敛至平衡点. 进一步考虑系统参数摄动和外界扰动等不确定性因素 上界的未知性 ,用 Lyapunov 稳定性方法给出了一个带有未知性上界参数估计的自适应非奇异 Terminal 滑模控制 (N TSM) 控制. 最后通过实例比较三种滑模控制方法 ,仿真结果验证了非奇异 Terminal 滑模控制能克服传统的 Ter2 minal 滑模控制的奇异问题 ,并说明了自适应非奇异 Terminal 滑模控制的有效性和可行性. 关键词 : Terminal 滑模控制 ;奇异 ;非线性系统 ;Lyapunov 稳定性 中图分类号 : TP273 文献标识码 :A 文章编号 :167324785 (2007) 0520053205 Non2singular Terminal sliding mode control for a class of uncertain nonlinear systems YAO Li2ping ,L IU Guo2dong (Department of Communication and Control Engineering , Southern Yangtze University , Wuxi 214122 ,China) Abstract :This paper presents a new Terminal sliding mode control surface for a class of second2order non2 linear uncertain systems to eliminate t he singularity problem in conventional terminal sliding mode con2 trols , so t hat the system can be guaranteed to converge to an equilibrium point from any initial state wit hin a finite time in t he p hase of sliding mode motion. To deal with the upper bounds of uncertainties such as systematic parameter pert urbations and external dist urbances , an adaptive non2singular Terminal sliding mode (N TSM) control wit h parametric estimation for uncertain upper bounds was derived using Lyap unov stability theory . The simulation results of an example are investigated to show non2singularity terminal sliding mode can elimination t he singularity ,and also show the feasibility and t he effectiveness of t he self2a2 daptive met hod. Keywords :Terminal sliding mode control ; singularity ; nonlinear systems; Lyap unov stability 收稿日期 :2007204208. 滑模变结构控制的基本原理就是使用一个不连 续的高频切换控制迫使闭环系统的运动到达预先选 定的滑动面或者它的一个很小的邻域上 ,通过控制 器结构的改变以使系统达到良好的动态性能. 滑模 控制对参数摄动和外部扰动具有不敏感性 ,一般情 况下 ,选择线性的滑动超平面是变结构控制理论中 最为常见的情形. 这个线性的滑动超平面能够确保 系统轨迹在到达滑动模态阶段以后 , 滑动模态的运 动是渐近稳定的 ,尽管如此滑动模态仍然不会在有 限时间内收敛至零[1 ] . 近年来 ,有限时间机理2Ter2 minal 滑动模态发展起来 ,它是一种新型变结构控 制思想. 变结构控制理论中引入 Terminal 滑动模态 的最直接的原因就是 : Terminal 滑模可以使系统的 状态在“有限时间内”收敛至平衡点[2 ] . Terminal 滑 模控制策略的实质在于 :在滑动超平面的设计中引 入了非线性函数 ,非线性函数的引入使得在滑动面 上系统状态能够在有限时间内收敛到零. 然而传统 的 Terminal 滑模控制器的设计存在奇异问题 ,一些 避免 Terminal 奇异问题的解决方法已提出[3 ] . 本文 针对一类二阶非线性不确定动态系统提出非奇异 Terminal 滑动模态(N TSM) 控制器的设计 ,并通过 提出一种新的 N TSM 滑模面来克服奇异问题 ,使得

·54 智能系统学报 第2卷 系统处于滑动模态阶段时状态变量能够在有限时间 制不能确保x1=0、x20,奇异问题就可能发生在 内收敛至平衡点.最后利用文献[4]中提出的自适应 到达滑动模态阶段,也可能发生在到达滑动模态s= 思想,研究带有未知系统参数摄动和外界扰动等不 0后,由于计算误差和不确定项影响,系统状态不能 确定性因素上界的自适应非奇异Terminal滑模控 确保总在滑动模态,特别在平衡点(x1=0,x2=0)附 制策略 近和x1=0、?判情况下奇异问题会不时发生,因 此奇异问题在传统TSM系统下就显得非常重要 1 系统描述 2.2非奇异Terminal滑动模态(NTSM)控制 考虑如下二阶不确定非线性动态系统: 为了克服传统TSM的奇异问题已提出几种方 X1=X2 法,如在TSM和线性滑模超平面之间进行转换), x2 f(x)+g(x)+b(x)u. (1) 另一种是将轨迹转换到提前规定的区间上,在此区 式中:x=[x1,x2严表示系统状态向量,∫(x)、 间上TSM非奇异,这些方法都是间接避免奇异问 b(x0为非线性函数,g(W代表不确定项和干扰 题.本文采用如下的NTSM方法 项,且‖g(y‖g,lg>0,u为控制输入 设NTSM滑模函数为 2非奇异Terminal滑动模态 s=x1+Bx94 (6) 2.1传统Terminal滑模(TSM)控制 式中:B、p和q的定义同式2),可以看出当s=0时 传统的TSM滑模面取为下列Terminal滑模 式(6)相当于式(2).因此系统在滑动模态下达到平 向量: 衡点x1=0的时间和式(5)相同,而且由式(6)得到 s=2+月AP (2) 的$在动态系统中不会导致负幂次方,用下面的定 式中:>0为常数,p,q均为正奇数且满足p>q 理可以证明 存在TSM的充分条件为}0为 定理1对系统(1)取滑模面切换函数(6)控制 量u取为 常数.对系统1)取控制量为 u=-B'(f((sgn(s) u=-6'(xIf(x)+B4xYx2+ D (ls sgn(s)1. (3) 式中:10系统将在有限时间内到达 以确保滑动模态发生.当sO)判时,系统状态将在 NTSM,进一步讲状态量x1、x2将在有限时间内收 有限时间1,内达到滑动模态s0)=0,且满足1,≤ 敛到零 s04:当系统达到滑动模态s=0,系统动态特性 证明由()可得到 由下列非线性微分方程决定: 卫x'a=和+月x妇 §=1+B9 B g 2+P=1+tP=0. (4) 式中:x1=0为系统(4)的Terminal吸引子.设从 2+ 卫xe1(f(N+g(N+b(WW= B q x1(t)判到x1(t,+t)=0的有限时间为i,且由下 士Pxel(gN.(g+可sgn() 式给出: B g 那么 -B(p (5) s=Btx(g(Ws-l:+sgny≤ 这意味着在TSM滑模面(4)上,系统状态x1、x?在 有限时间内收敛到零 Pxf1n叫sl B q 由TSM输入控制式(3)可看出,式(3)第2项 由于p和g均为正奇数且10,让px)=Pxg1则有:当 B g 当s=0,2=-fx1P,只要q0.因此当 此项xfP1x?=-月xPgP为非奇异项.当输入控 x2o时,系统满足Lyapunov稳定性原理.将输入 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
系统处于滑动模态阶段时状态变量能够在有限时间 内收敛至平衡点. 最后利用文献[ 4 ]中提出的自适应 思想 ,研究带有未知系统参数摄动和外界扰动等不 确定性因素上界的自适应非奇异 Terminal 滑模控 制策略. 1 系统描述 考虑如下二阶不确定非线性动态系统 : Ûx1 = x2 . Ûx2 = f ( x) + g ( x) + b( x) u. (1) 式中 : x = [ x1 , x2 ] T 表示系统状态向量 , f ( x) 、 b( x) ≠0为非线性函数 , g ( x) 代表不确定项和干扰 项 ,且 ‖g ( x) ‖≤l g , l g > 0 , u 为控制输入. 2 非奇异 Terminal 滑动模态 2. 1 传统 Terminal 滑模( TSM) 控制 传统的 TSM 滑模面取为下列 Terminal 滑模 向量 : s = x2 +βx q/ p 1 . (2) 式中 :β> 0 为常数 , p , q 均为正奇数且满足 p > q. 存在 TSM 的充分条件为 1 2 d dt s 2 0 为 常数. 对系统(1) 取控制量为 u = - b - 1 ( x) [ f ( x) +β q p x q/ p- 1 1 x2 + ( l g +η) sgn (s) ] , (3) 以确保滑动模态发生. 当 s(0) ≠0 时 ,系统状态将在 有限时间 tr 内达到滑动模态 s (0) = 0 ,且满足 tr ≤ | s(0) | η ;当系统达到滑动模态 s = 0 ,系统动态特性 由下列非线性微分方程决定 : x2 +βx q/ p 1 = Ûx1 +βx q/ p 1 = 0. (4) 式中 : x1 = 0 为系统 ( 4) 的 Terminal 吸引子. 设从 x1 ( tr) ≠0 到 x1 ( ts + tr) = 0 的有限时间为 ts 且由下 式给出 : ts = p β( p - q) | x1 ( tr) | 1 - q/ p . (5) 这意味着在 TSM 滑模面(4) 上 ,系统状态 x1 、x2 在 有限时间内收敛到零. 由 TSM 输入控制式 (3) 可看出 ,式 (3) 第 2 项 包含 x q/ p - 1 1 x2 ,在 x1 = 0 , x2 ≠0 的条件下会发生奇 异问题 ,而这种情况不会发生在理想滑动模态 ,因为 当 s = 0 , x2 = - βx q/ p 1 ,只要 q 0 系统将在有限时间内到达 N TSM ,进一步讲状态量 x1 、x2 将在有限时间内收 敛到零. 证明 由(6) 可得到 Ûs = Ûx1 + 1 β p q x p/ q- 1 2 Ûx2 = x2 + 1 β p q x p/ q- 1 2 Ûx2 = x2 + 1 β p q x p/ q- 1 2 ( f ( x) + g ( x) + b( x) u) = 1 β p q x p/ q- 1 2 ( g ( x) - ( l g +η) sgn (s) ) . 那么 sÛs = 1 β p q x p/ q- 1 2 ( g ( x) s - ( l g +η) sgn (s) s) ≤ - 1 β p q x p/ q- 1 2 η| s | . 由于 p 和 q 均为正奇数且 1 0 ,让ρ( x2 ) = 1 β p q x p/ q - 1 2 则有 :当 x2 ≠0 时 , sÛs ≤- ρ( x2 )η| s| ,ρ( x2 ) ,η> 0. 因此当 x2 ≠0时 ,系统满足 Lyap unov 稳定性原理. 将输入 ·54 · 智 能 系 统 学 报 第 2 卷

第5期 姚丽萍,等:一类非线性不确定系统的非奇异Terminal滑模控制 ·55· 控制量式7)代入式1)得 方(,V=Ipx2)I·lsI, 2 =B4x+g(x(Is sgn(s) p h(,=gilp(x2)Ⅱ·s‖·lxl. 当2=0时,有 考虑Lyapunov函数为 x2 =g(x)-(I sgn(s). V=立s5+m后+m币. 当s>0时,2≤-几,当s0,>0,所以可以保证系统全局 确定性的界,并由此构造出具有继电控制项的控制 一致渐近收敛至s=0.下面讨论滑动面向量s的 律,保证系统进入滑动模态.这些界往往很难获得, 收敛率问题,根据式10)和12)可得 若控制律中的这些数据取得太大,会影响控制效率, V=s's+mm+n片≤nl知)‖· 取得太小,将不能保证滑动模态的存在.自适应控制 lls lls's+nlle(x)‖·lsⅡ 方法提供了另一种解决系统不确定性问题的有效方 或 9ng'Ipx)‖·Is‖·lxI≤ 法,可以得到已知不确定性结构的未知参数估计 -lP(x2)‖·lsl. 因此这里将结合变结构和自适应控制的各自优点, ls‖·ls‖≥op(x2)‖·lsl 并应用Terminal滑模变结构控制思想,来综合一种 或 方lPx2)‖·ls‖·lx‖+ 新型的自适应Terminal滑模控制算法7,】.此时系 nlP(x2)·lsl. 统(1)的不确定项g(xy不再满足‖g(x)‖.,即 则当s‖判时,有 不确定性的界未知,为此给出下面假设, 假设不确定性g(W满足下面的不等式: IsI≥PL·lsI±xL+2 ls‖ lgy‖≤b+nlxl. (8) 对自适应律积分得 而m、n是2个非负的未知常数,这里为了估计不 确定性g√,给出如下的简单自适应律: 元=n0,+plp()Ⅱ·lsld-n. o(t,X=g'lpx2)‖·lsl, (13) 方(,y=qi'lle(x2)‖·lsⅡ·xⅡ.例 式中:%(1,√=(1,y-n和i(1,W=n(t,W- n=n0,V+p(x)I· n是自适应参数误差,和分别为各自的正常 lsl·llx lldr-n. 14) 数自适应增益,而m(1,x和n(t,即为未知参数 则可得 心和n的自适应参数估计.由于参数b和n为常 ls‖≠0时lsIp(x2)I(%+ 数,所以式9)的自适应律也可写为 hlxl+w≥IP(x2)In (15) 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
控制量式(7) 代入式(1) 得 Ûx2 = - β q p x 2 - p/ q 2 + g ( x) - ( l g - η) sgn (s) . 当 x2 = 0 时 ,有 x2 = g ( x) - ( l g - η) sgn (s) . 当 s > 0 时 , Ûx2 ≤- η,当 s 0 ,η> 0 , 所以可以保证系统全局 一致渐近收敛至 s = 0 [9 ] . 下面讨论滑动面向量 s 的 收敛率问题 , 根据式(10) 和(12) 可得 VÛ= s TÛs + q0 r0 r · 0 + q1 r1 r · 1 ≤- η‖ρ( x2 ) ‖· ‖s ‖s TÛs + q0 r0 q - 1 0 ‖ρ( x2 ) ‖·‖s ‖ 或 q1 r1 q - 1 1 ‖ρ( x2 ) ‖·‖s ‖·‖x ‖≤ - η‖ρ( x2 ) ‖·‖s ‖. ‖s ‖·‖Ûs ‖ ≥r0 ‖ρ( x2 ) ‖·‖s ‖ 或 r1 ‖ρ( x2 ) ‖·‖s ‖·‖x ‖+ η‖ρ( x2 ) ‖·‖s ‖. 则当 ‖s ‖≠0 时 ,有 ‖s ‖ ≥ ‖ρ( x2 ) ‖·‖s ‖( r0 + r1 ‖x ‖+η) ‖s ‖ . 对自适应律积分得 r0 = r 0 (0 , x) +∫ t 0 q - 1 0 ‖ρ( x2 ) ‖·‖s ‖dt - r0 . (13) r1 = r 1 (0 , x) +∫ t 0 q - 1 1 ‖ρ( x2 ) ‖· ‖s ‖·‖x ‖dt - r1 . (14) 则可得 ‖s ‖ ≠0 时 ‖Ûs ‖ρ( x2 ) ‖( r0 + r1 ‖x ‖+η) ≥ ‖ρ( x2 ) ‖η. (15) 第 5 期 姚丽萍 ,等 :一类非线性不确定系统的非奇异 Terminal 滑模控制 ·55 ·
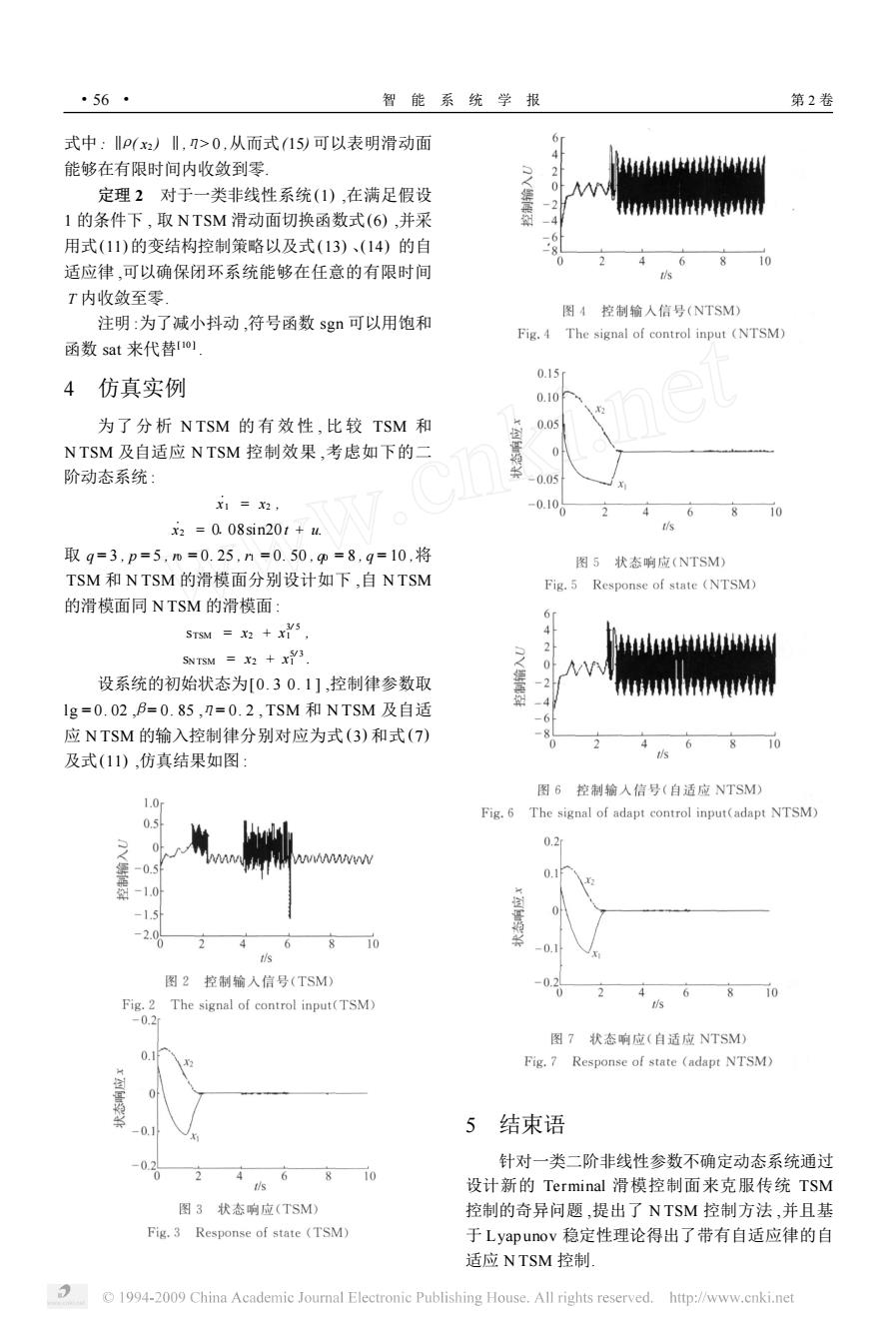
·56· 智能系统学报 第2卷 式中:‖P(x2)‖,>0,从而式(15)可以表明滑动面 61 能够在有限时间内收敛到零 Z04344 定理2对于一类非线性系统(1),在满足假设 0 2 fnnrrann 1的条件下,取NTSM滑动面切换函数式(6),并采 用式(11)的变结构控制策略以及式(13)、(14)的自 6 4 6 810 适应律,可以确保闭环系统能够在任意的有限时间 s T内收敛至零」 图4控制输人信号(NTSM) 注明:为了减小抖动,符号函数sgn可以用饱和 Fig.4 The signal of control input (NTSM) 函数sat来代替Io] 0.15 4仿真实例 0.10 为了分析NTSM的有效性,比较TSM和 0.05 NTSM及自适应NTSM控制效果,考虑如下的二 阶动态系统: -0.05 X1=x2, -0.106 4 6810 x2=0.08sin20t+u. s 取q=3,p=5,m=0.25,n=0.50,=8,g=10,将 图5状态响应(NTSM) TSM和NTSM的滑模面分别设计如下,自NTSM Fig.5 Response of state (NTSM) 的滑模面同NTSM的滑模面: 5sM=2+x, 4 2 SNTSM =X2+x3 0 设系统的初始状态为[0.30.1],控制律参数取 wwtwwwm lg=0.02,f=0.85,=0.2,TSM和NTSM及自适 应NTSM的输入控制律分别对应为式(3)和式(7) 6 810 及式(11),仿真结果如图: s 图6控制输人信号(自适应NTSM) 1.0 Fig.6 The signal of adapt control input(adapt NTSM) 0.5 0.2 wMMWW -0.5 -1.5 -2.0 6 810 tis 图2控制输入信号(TSM) -0.2 4 10 Fig.2 The signal of control input(TSM) s -0.2 图7状态响应(自适应NTSM) Fig.7 Response of state(adapt NTSM) 5结束语 6810 针对一类二阶非线性参数不确定动态系统通过 0 4 设计新的Terminal滑模控制面来克服传统TSM 图3状态响应(TSM) 控制的奇异问题,提出了NTSM控制方法,并且基 Fig.3 Response of state (TSM) 于Lyapunov稳定性理论得出了带有自适应律的自 适应NTSM控制 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
式中 : ‖ρ( x2 ) ‖,η> 0 ,从而式(15) 可以表明滑动面 能够在有限时间内收敛到零. 定理 2 对于一类非线性系统(1) ,在满足假设 1 的条件下 , 取 N TSM 滑动面切换函数式(6) ,并采 用式(11) 的变结构控制策略以及式(13) 、(14) 的自 适应律 ,可以确保闭环系统能够在任意的有限时间 T 内收敛至零. 注明 :为了减小抖动 ,符号函数 sgn 可以用饱和 函数 sat 来代替[10 ] . 4 仿真实例 为了 分 析 N TSM 的 有 效 性 , 比 较 TSM 和 N TSM 及自适应 N TSM 控制效果 ,考虑如下的二 阶动态系统 : Ûx1 = x2 , Ûx2 = 0108sin20t + u. 取 q = 3 , p = 5 , r0 = 0. 25 , r1 = 0. 50 , q0 = 8 , q = 10 ,将 TSM 和 N TSM 的滑模面分别设计如下 ,自 N TSM 的滑模面同 N TSM 的滑模面 : sTSM = x2 + x 3/ 5 1 , sN TSM = x2 + x 5/ 3 1 . 设系统的初始状态为[ 0. 3 0. 1 ] ,控制律参数取 lg = 0. 02 ,β= 0. 85 ,η= 0. 2 , TSM 和 N TSM 及自适 应 N TSM 的输入控制律分别对应为式 (3) 和式 (7) 及式(11) ,仿真结果如图 : 5 结束语 针对一类二阶非线性参数不确定动态系统通过 设计新的 Terminal 滑模控制面来克服传统 TSM 控制的奇异问题 ,提出了 N TSM 控制方法 ,并且基 于 Lyap unov 稳定性理论得出了带有自适应律的自 适应 N TSM 控制. ·56 · 智 能 系 统 学 报 第 2 卷

第5期 姚丽萍,等:一类非线性不确定系统的非奇异Terminal滑模控制 ·57· HU Jianbo,CHU Jian.Variable structure control and 参考文献: gaimscheduling contrl[D].Hangzhou:Zhejiang Universi- [1]PARK K B ,L EEJ J.Comments on a robust MIMO ter- ty,2002. minal sliding mode control scheme for rigid robot manip- [9]庄开字,褚健,苏宏业.变结构控制理论若干问题研究 ulators[J ]IEEE Trans on Automatic Control,1996,41 及其应用[D].杭州:浙江大学,2002. (4):761-762. ZHUANG Kaiyu,CHU Jian,SU Hongye.Variable [2]PARK KB,TERUO T.Terminal sliding mode control of structure control theory study and application [D].Han- second-order nonlinear uncertain system [J ]Int J of Ro- gzhou:Zhejiang University,2002. bust Nonlineat Control,1999 9(4):769-780. [10]胡建波,时满宏,庄开字,等.一类非线性系统的Termi- [3]WU Y Q,FENG X H,MAN Z H.Terminal sliding nal滑模控制[0].控制理论与应用,2005,22(3):495. mode control design for uncertain dynamic systems[J ] 498. Systems and Control Letters,1998,34(2):281-287. HU Jianbo,SHI Manhong,ZHUANG Kaiyu,et al. [4]FENG Y,YU X H,MAN Z H.Nom singular terminal Terminal sliding control for a class of nonlinear systems sliding mode control of rigid manipulators [J ]Automati- [J ]Control Theory and Application,2005,22(3):495- ca,2002,38:2159.2167. 498 (5]FENG Y,HAN F,YU X H,et al.Tracking precision a 作者简介 nalysis of terminal sliding mode control systems with sat- 姚丽萍,女,1978年生,硕士研究 uration functions [A].Advances in Variable Structure 生,主要研究方向为机器人技术 Systems:Analysis,Integration and Applications [C]. E mail xiziyidi @hotmail.com. Singapore:World Scientific.2000. 「6]姚琼荟,黄继起,吴汉松.变结构控制系统[M1.重庆:重 庆大学出版社,1997. [7]MAN Z H,YU X H.Terminal sliding mode control of mimo linear systems[J].Fundanmental Theory and Ap- plications,1997,44(11):1065.1070 刘国栋,男,1950年生,教授,硕士 [8]胡剑波,褚健.变结构控制和增益调度控制[D].杭州: 生导师,主要研究方向为人工智能与机 浙江大学,2001 器人,在国内外期刊发表论文20余篇 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
参考文献 : [1 ] PAR K K B ,L EE J J. Comments on a robust MIMO ter2 minal sliding mode control scheme for rigid robot manip2 ulators[J ]. IEEE Trans on Automatic Control ,1996 ,41 (4) :761 - 762. [2 ] PAR K K B ,TERUO T. Terminal sliding mode control of second2order nonlinear uncertain system [J ]. Int J of Ro2 bust Nonlineat Control ,1999 ,9 (4) :769 - 780. [3 ] WU Y Q , FEN G X H , MAN Z H. Terminal sliding mode control design for uncertain dynamic systems[J ] . Systems and Control Letters ,1998 ,34 (2) :281 - 287. [4 ] FEN G Y , YU X H , MAN Z H. Non2singular terminal sliding mode control of rigid manipulators [J ]. Automati2 ca ,2002 ,38 :2159 - 2167. [5 ] FEN G Y , HAN F , YU X H ,et al. Tracking precision a2 nalysis of terminal sliding mode control systems with sat2 uration functions [ A ]. Advances in Variable Structure Systems: Analysis , Integration and Applications [ C ]. Singapore : World Scientific. 2000. [6 ]姚琼荟 ,黄继起 ,吴汉松. 变结构控制系统[ M ]. 重庆 :重 庆大学出版社 ,1997. [7 ]MAN Z H , YU X H . Terminal sliding mode control of mimo linear systems[J ]. Fundanmental Theory and Ap2 plications ,1997 ,44 (11) :1065 - 1070. [8 ]胡剑波 ,褚 健. 变结构控制和增益调度控制[D ]. 杭州 : 浙江大学 ,2001. HU Jianbo , CHU Jian. Variable structure control and gain2scheduling contrl[D]. Hangzhou : Zhejiang Universi2 ty ,2002. [9 ]庄开宇 ,褚 健 ,苏宏业. 变结构控制理论若干问题研究 及其应用[D]. 杭州 :浙江大学 , 2002. ZHUAN G Kaiyu , CHU Jian , SU Hongye. Variable structure control theory study and application [D]. Han2 gzhou :Zhejiang University ,2002. [10 ]胡建波 ,时满宏 ,庄开宇 ,等. 一类非线性系统的 Termi2 nal 滑模控制[J ]. 控制理论与应用 ,2005 ,22 (3) :495 - 498. HU Jianbo , SHI Manhong , ZHUAN G Kaiyu , et al. Terminal sliding control for a class of nonlinear systems [J ]. Control Theory and Application ,2005 ,22 (3) :495 - 498. 作者简介 : 姚丽萍 ,女 ,1978 年生 ,硕士研究 生 ,主要研究方向为机器人技术. E2mail :xiziyidi @hotmail. com. 刘国栋 ,男 ,1950 年生 ,教授 ,硕士 生导师 ,主要研究方向为人工智能与机 器人 ,在国内外期刊发表论文 20 余篇. 第 5 期 姚丽萍 ,等 :一类非线性不确定系统的非奇异 Terminal 滑模控制 ·57 ·