
第2卷第5期 智能系统学报 Vol.2№5 2007年10月 CAAI Transactions on Intelligent Systems 0ct.2007 动态多目标免疫优化算法及性能测试研究 钱淑渠2张著洪 (1.贵州大学理学院,贵州贵阳550025:2.贵州安顺学院数学系,贵州安顺561000) 摘要:基于生物免疫系统的自适应学习、免疫记忆抗体多样性及动态平衡维持等功能,提出一种动态多目标免疫 优化算法处理动态多目标优化问题.算法设计中,依据自适应飞邻域及抗体所处位置设计抗体的亲和力,基于P r心to控制的概念,利用分层选择确定参与进化的抗体,经由克隆扩张及自适应高斯变异,提高群体的平均亲和力,利 用免疫记忆动态维持和Average linkage聚类方法,设计环境识别规则和记忆池,借助3种不同类型的动态多目标 测试问题,通过与出众的动态环境优化算法比较,数值实验表明所提出算法解决复杂动态多目标优化问题具有较大 潜力. 关键词:动态多目标优化,时变Pareto面;环境跟踪;自适应(邻域;免疫算法 中图分类号:TP301.6文献标识码:A文章编号:16734785(2007)05006810 Dyna mic multiobjective immune optimization algorithm and performance test QIAN Shurqu'2,ZHAN G Zhuhong (1.College of Science,Guizhou University,Guizhou 550025,China;2.Department of Mathematics,Anshun College,Anshun 561000,China) Abstract:A dynamic multi-objective immune optimization algorithm suitable for dynamic multi-objective optimization problems is proposed based on the functions of adaptive learning,immune memory,antibody diversity and dynamic balance maintenance,etc.In the design of the algorithm,the scheme of antibody af- finity was designed based on the locations of adaptive-neighborhood and antibody;antibodies participating in evolution were selected by Pareto dominance.In order to enhance the average affinity of the population, clonal proliferation and adaptive Gaussian mutation were adopted to evolve excellent antibodies.Further- more,the average linkage method and several functions of immune memory and dynamic balance mainte- nance were used to design environmental recognition rules and the memory pool.The proposed algorithm was compared against several popular multi-objective algorithms by means of three different kinds of dy- namic multi-objective benchmark problems.Simulations show that the algorithm has great potential in sol- ving dynamic multi-objective optimization problems. Keywords:dynamic multi-objective optimization;time-varying Pareto front;environment tracking;adap- tive -neighborhood;immune algorithm 动态多目标优化(dynamic multi-objective opti- 等.尽管大量静态多目标进化算法已相继提出) mization,DMO)是指优化问题的目标函数、定义 其中较为典型的2种进化算法为SPEAII31和NS 域、约束条件中至少有一个随时间而变化的多目标 GAIT,但寻求解决DMO的算法研究甚少).文 优化问题.在工程应用领域,大量此类问题急需解 献[1-2,6-7]报道了有关动态多目标进化算法的 决山,如:交通信号灯控制、机器人控制、故障诊断 研究进展.特别是Marco等在文献[2]中设计了几 种动态多目标测试问题,相应地,提出了一种邻域搜 收稿日期:200612-05. 基金项目:因家自然科学基金资助项目(60565002) 索算法(directiombased method,DBM),从性能测 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 5 期 智 能 系 统 学 报 Vol. 2 №. 5 2007 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2007 动态多目标免疫优化算法及性能测试研究 钱淑渠1 ,2 ,张著洪1 (1. 贵州大学 理学院 ,贵州 贵阳 550025 ; 2. 贵州安顺学院 数学系 ,贵州 安顺 561000) 摘 要 :基于生物免疫系统的自适应学习、免疫记忆、抗体多样性及动态平衡维持等功能 , 提出一种动态多目标免疫 优化算法处理动态多目标优化问题. 算法设计中 , 依据自适应ζ邻域及抗体所处位置设计抗体的亲和力 , 基于 Pa2 reto 控制的概念 ,利用分层选择确定参与进化的抗体 , 经由克隆扩张及自适应高斯变异 ,提高群体的平均亲和力 ,利 用免疫记忆、动态维持和 Average linkage 聚类方法 , 设计环境识别规则和记忆池 , 借助 3 种不同类型的动态多目标 测试问题 ,通过与出众的动态环境优化算法比较 , 数值实验表明所提出算法解决复杂动态多目标优化问题具有较大 潜力. 关键词 :动态多目标优化 ; 时变 Pareto 面 ; 环境跟踪 ; 自适应ζ邻域 ; 免疫算法 中图分类号 : TP301. 6 文献标识码 :A 文章编号 :167324785 (2007) 0520068210 Dynamic multi2objective immune optimization algorithm and performance test QIAN Shu2qu 1 ,2 , ZHAN G Zhu2hong 1 (1. College of Science , Guizhou University , Guizhou 550025 , China ; 2. Department of Mathematics , Anshun College , Anshun 561000 , China) Abstract :A dynamic multi2objective immune optimization algorit hm suitable for dynamic multi2objective optimization problems is proposed based on the f unctions of adaptive learning , immune memory , antibody diversity and dynamic balance maintenance , etc. In t he design of t he algorithm , t he scheme of antibody af2 finity was designed based on t he locations of adaptive2neighborhood and antibody ; antibodies participating in evolution were selected by Pareto dominance. In order to enhance t he average affinity of t he pop ulation , clonal proliferation and adaptive Gaussian mutation were adopted to evolve excellent antibodies. Furt her2 more , t he average linkage method and several f unctions of immune memory and dynamic balance mainte2 nance were used to design environmental recognition rules and t he memory pool. The p roposed algorit hm was compared against several pop ular multi2objective algorit hms by means of three different kinds of dy2 namic multi2objective benchmark problems. Simulations show that t he algorit hm has great potential in sol2 ving dynamic multi2objective optimization problems. Keywords :dynamic multi2objective optimization ; time2varying Pareto front ; environment tracking ; adap2 tive 2neighborhood ; immune algorithm. 收稿日期 :2006212205. 基金项目 :国家自然科学基金资助项目(60565002) . 动态多目标优化(dynamic multi2objective opti2 mization ,DMO) 是指优化问题的目标函数、定义 域、约束条件中至少有一个随时间而变化的多目标 优化问题. 在工程应用领域 , 大量此类问题急需解 决[1 ] , 如 : 交通信号灯控制、机器人控制、故障诊断 等. 尽管大量静态多目标进化算法已相继提出[2 ] , 其中较为典型的 2 种进化算法为 SPEA II [ 3 ] 和 NS2 GAII [4 ] , 但寻求解决 DMO 的算法研究甚少[5 ] . 文 献[1 - 2 , 6 - 7 ]报道了有关动态多目标进化算法的 研究进展. 特别是 Marco 等在文献[ 2 ]中设计了几 种动态多目标测试问题 ,相应地 ,提出了一种邻域搜 索算法 ( direction2based method ,DBM) ,从性能测

第5期 钱淑渠,等:动态多目标免疫优化算法及性能测试研究 。69= 试的角度,获得了该算法对环境的跟踪行为,但由于 衡等特点,它具有学习、记忆、识别等功能,可用于开 DMO是一类极为困难的动态优化问题,加之该算 发免疫算法,实现智能信息处理.所引用的免疫特 法属邻域搜索方法,致使其实时性需要重大改进 征和原理如下: 2006年K.Deb修改了静态的NSGAII,获得适用 )自适应性:自然界中存在的抗原类型远远多 于动态环境多目标问题求解的DNSGAIⅡ-A1,该 于生物体内的抗体种类,因此入侵生物体的抗原具 算法的自适应能力强,是一种很好的动态优化算法 有随机性和不可预测性,但免疫系统会对不同的抗 但如何利用合理的生物机理,设计有效的优化方法 原,通过免疫细胞的增殖和分化,不断地产生新的 解决DMO,仍是一个全新的课题.近来,基于免疫 抗体,最终生成亲和力较高的抗体消灭入侵抗原 机理的静态多目标免疫优化算法己有一些优越的多 2动态平衡:在应答过程中,抗原的对位与抗 目标进化算法的研究成果,,但探讨解决DMO问 体的表位以及抗体之间的表位与对位进行识别与被 题的免疫算法的研究几乎尚未启动.尚荣华等] 识别,抗体不仅识别抗原,同时又识别其他抗体和 基于克隆选择算法,利用非均匀变异抗体间距离等 被其他抗体识别,因此抗体具有识别和被识别的特 方法获得了一种克隆选择动态多目标算法(CSAD 性(二重性)。通过抗体表面的受体,抗体识别抗原, MO),并将其与DBM用于2个测试问题比较其性 抗体与抗体之间相互识别和被识别,并形成了独特 能.尽管如此,DMO免疫算法的研究仍然处于起 型免疫网络:在此网络中,被识别的抗体受到抑 步阶段,如何充分挖掘免疫系统的内在机理,选择 制,识别抗原及其他抗体的抗体得到促进和增殖 合适的免疫学原理提出更有效的算法解决DMO问 这种机制便构成了独特型免疫网络调节。网络调节 题,仍需不断努力.基于此,借鉴免疫系统的自适 能使网络中抗体的总数目获得控制,并调节各种类 应性、多样性及动态平衡维持、免疫记忆等功能,提 型的抗体在免疫系统中的数目,使所有抗体的数目 出一种新的动态多目标免疫优化算法(dynamic 达到总体上平衡。当抗原入侵免疫系统时,这种平 multiobjective immune optimization algorithm, 衡遭到破坏,应答抗原能力强的B细胞进行增殖, DMIOA),并将其与DBM,DNSGAII-A及 并导致免疫应答,待抗原被清除后,依赖于免疫网 CSADMO用于不同类型的测试问题展开比较分 络调节使抗体数目达到新的平衡。 析,数值实验结果说明了本文算法在跟踪速度和执 3)抗体多样性:免疫系统在进化过程中通过细 行效果上呈现出了一定的优越性 胞分裂、分化,抗体的二官能性,可对多种病原体产 1 问题描述 生相应的抗体.抗体的高可变区的超突变及免疫系 统浓度抑制机理,促使抗体库保存多样的抗体 考虑如下动态多目标优化问题(DMOP) 4)免疫记忆:免疫记忆是特异性免疫应答所 min f (x.(=(f(x.v .f2(x.0...fm (x.v). 特有的重要特征.当免疫系统初次遇到抗原时,淋 式中:x=(x1,x2,…,x)∈D为决策向量,DCR 巴细胞需要一定的时间进行调整,免疫应答结束后, 为定义域,:(x,)为与时间有关的子目标函数. 保留该抗原的记忆信息;当免疫系统再次遇到相同 注:本文中时间1∈1,2,,T取离散值,每一个1 或结构相似的抗原时,在联想记忆下,免疫系统提 下的优化问题就是一个环境,为环境总个数 取记忆细胞,应答速度大大提高」 定义1对于给定环境1∈T,称向量x控制向 基于以上所述,抗体动态跟踪抗原、自组织学 量记为:x<y或向量y受控于向量x,如果 习、自适应记忆的动态特性,为设计DMIOA求解 f(x,≤f(y,)∧3k,s.t.fk(x,)<fxy,), DMOP提供了新思路.在此,将问题DMOP视为 1≤i,k≤m」 环境,环境变化意指该问题随时间发生了改变.对 定义2对给定环境t∈T及有限子集XCD, 应于免疫学的术语,抗原视为环境,抗体对应给定 x`∈D,若不存在任何向量y∈X,使得x`<y,则 环境下的候选解,记亿细胞为给定环境下的抗体群 称x为1环境的非控个体.特别,若X三D,则称 中非控个体,抗体和记忆细胞均使用实数编码.在 x`为t环境的Pareto最优解 这些约定下,借助以上涉及的免疫系统特性,获得 DMOA的流程图(图1).此图由内循环和外循环 2 免疫特征及算法运行机制 2部分构成,通过环境判别规则进行切换:内循环 生物免疫系统具有分布性、自适应性和动态平 解决给定环境下的优化问题,同时对记忆集进行更 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
试的角度 ,获得了该算法对环境的跟踪行为 ,但由于 DMO 是一类极为困难的动态优化问题 ,加之该算 法属邻域搜索方法 ,致使其实时性需要重大改进. 2006 年 K. Deb 修改了静态的 NSGA II ,获得适用 于动态环境多目标问题求解的 DNSGAII - A [ 8 ] ,该 算法的自适应能力强 ,是一种很好的动态优化算法. 但如何利用合理的生物机理 , 设计有效的优化方法 解决 DMO , 仍是一个全新的课题. 近来 , 基于免疫 机理的静态多目标免疫优化算法已有一些优越的多 目标进化算法的研究成果[9 ] , 但探讨解决 DMO 问 题的免疫算法的研究几乎尚未启动. 尚荣华等[ 10 ] 基于克隆选择算法 ,利用非均匀变异、抗体间距离等 方法获得了一种克隆选择动态多目标算法 (CSAD2 MO) ,并将其与 DBM 用于 2 个测试问题比较其性 能. 尽管如此 , DMO 免疫算法的研究仍然处于起 步阶段 , 如何充分挖掘免疫系统的内在机理 , 选择 合适的免疫学原理提出更有效的算法解决 DMO 问 题 , 仍需不断努力. 基于此 , 借鉴免疫系统的自适 应性、多样性及动态平衡维持、免疫记忆等功能 ,提 出一种新的动态多目标免疫优化算法 ( dynamic multiobjective immune optimization algorit hm , DMIOA) , 并 将 其 与 DBM , DNSGA II - A 及 CSADMO 用于不同类型的测试问题展开比较分 析 , 数值实验结果说明了本文算法在跟踪速度和执 行效果上呈现出了一定的优越性. 1 问题描述 考虑如下动态多目标优化问题 (DMOP) min x ∈D ∈R n f ( x , t) = ( f 1 ( x , t) , f 2 ( x , t) , …, f m ( x , t) ) . 式中 : x = ( x1 , x2 , …, x p ) ∈D 为决策向量 , D < R n 为定义域 , f i ( x , t) 为与时间有关的子目标函数. 注 : 本文中时间 t ∈{ 1 ,2 , …, T}取离散值 , 每一个 t 下的优化问题就是一个环境 ,为环境总个数. 定义 1 对于给定环境 t ∈T , 称向量 x 控制向 量 (记为 : x < y) 或向量 y 受控于向量 x , 如果 f i ( x , t) ≤f i ( y , t) ∧ ϖ k ,s. t. f k ( x , t) < f k ( y , t) , 1 ≤i , k ≤m. 定义 2 对给定环境 t ∈T 及有限子集 X < D , x 3 ∈D , 若不存在任何向量 y ∈X , 使得 x 3 < y , 则 称 x 3 为 t 环境的非控个体. 特别 ,若 X ≡D ,则称 x 3 为 t 环境的 Pareto 最优解. 2 免疫特征及算法运行机制 生物免疫系统具有分布性、自适应性和动态平 衡等特点 ,它具有学习、记忆、识别等功能 ,可用于开 发免疫算法 ,实现智能信息处理. 所引用的免疫特 征和原理如下 : 1) 自适应性 : 自然界中存在的抗原类型远远多 于生物体内的抗体种类 ,因此入侵生物体的抗原具 有随机性和不可预测性 ,但免疫系统会对不同的抗 原 , 通过免疫细胞的增殖和分化 ,不断地产生新的 抗体 ,最终生成亲和力较高的抗体消灭入侵抗原. 2) 动态平衡 : 在应答过程中 ,抗原的对位与抗 体的表位以及抗体之间的表位与对位进行识别与被 识别 ,抗体不仅识别抗原 , 同时又识别其他抗体和 被其他抗体识别 , 因此抗体具有识别和被识别的特 性(二重性) 。通过抗体表面的受体 ,抗体识别抗原 , 抗体与抗体之间相互识别和被识别 ,并形成了独特 型免疫网络; 在此网络中 , 被识别的抗体受到抑 制 ,识别抗原及其他抗体的抗体得到促进和增殖 , 这种机制便构成了独特型免疫网络调节。网络调节 能使网络中抗体的总数目获得控制 , 并调节各种类 型的抗体在免疫系统中的数目 , 使所有抗体的数目 达到总体上平衡。当抗原入侵免疫系统时 , 这种平 衡遭到破坏 , 应答抗原能力强的 B 细胞进行增殖 , 并导致免疫应答 , 待抗原被清除后 , 依赖于免疫网 络调节使抗体数目达到新的平衡。 3) 抗体多样性 : 免疫系统在进化过程中通过细 胞分裂、分化 ,抗体的二官能性 , 可对多种病原体产 生相应的抗体. 抗体的高可变区的超突变及免疫系 统浓度抑制机理 ,促使抗体库保存多样的抗体. 4) 免疫记忆 : 免疫记忆是特异性免疫应答所 特有的重要特征. 当免疫系统初次遇到抗原时 ,淋 巴细胞需要一定的时间进行调整;免疫应答结束后 , 保留该抗原的记忆信息; 当免疫系统再次遇到相同 或结构相似的抗原时 , 在联想记忆下 , 免疫系统提 取记忆细胞 , 应答速度大大提高. 基于以上所述 , 抗体动态跟踪抗原、自组织学 习、自适应记忆的动态特性 , 为设计 DMIOA 求解 DMOP 提供了新思路. 在此 , 将问题 DMOP 视为 环境 , 环境变化意指该问题随时间发生了改变. 对 应于免疫学的术语 , 抗原视为环境 , 抗体对应给定 环境下的候选解 , 记忆细胞为给定环境下的抗体群 中非控个体 , 抗体和记忆细胞均使用实数编码. 在 这些约定下 , 借助以上涉及的免疫系统特性 , 获得 DMIOA 的流程图 (图 1) . 此图由内循环和外循环 2 部分构成 , 通过环境判别规则进行切换; 内循环 解决给定环境下的优化问题 , 同时对记忆集进行更 第 5 期 钱淑渠 ,等 :动态多目标免疫优化算法及性能测试研究 · 96 ·

·70· 智能系统学报 第2卷 新:外循环的主要作用在于更新记忆池,保存不同 6)经由算术交叉获N·N。个新抗体插入B 环境的统计特征值及产生相似、相同或新环境下的 中,并转入7) 初始抗体群.另外,在此图中,N为群体规模,B为 7)分层选择作用于B,获抗体群C 分层选择率0<B<1),N。为所获非控个体数, 8)计算C中抗体的亲和力,并实施免疫算子: 为第1环境下算法执行的当前时刻,T,表示当前环 ①以a为选择率在C中选取LaNJ个亲和力较 境保持不变的最大允许时间,“e=0”用于识别下 高的抗体构成群体D,其中0<a<B<1; 一环境是否为新环境:当为新环境时,e=0:当为 ②克隆算子V作用于D,获克隆群K: 相似或相同环境时,e=1. ③突变算子作用于K,获突变群E: ④组合B和E,计算抗体的亲和力,选取N个 初始抗体群 较高亲和力抗体构成群体F N 1≤T? 输出结果 9)若<T,则A-F,转3);若否,存储当前 y 环境的统计特征,更新记忆池,置1=1+1,转10) 非控个体群 更新记忆集 10)实施环境判别规则,判断此环境是否与以前 Y N<BN 算术交叉 的某环境相似,若是,则从记忆池中此环境对应的 记忆集中抽取m(m<S)个记忆细胞,并随机产 分层选择 生N·m2个新抗体构成当前环境的初始群体A;若 计算亲和力 否,则随机生成N个抗体构成初始群体A,转2). 克隆选择、繁殖、突变 评注该算法通过分层选择确保优秀的抗体参 ,<T? 组合 与进化,加速算法的收敛速度.4)通过记忆集来保 存非控个体,使用Average linkage聚类,防止记忆 存储统计特征 史新记忆池 集无限扩大,且有助于使所获非控面的分布较均 匀;5)和6)主要是防止算法进化中参与进化的非控 Y 相似抗体群 非相似抗体样 个体过少,导致算法搜索效果差等现象,其中,6) 是为防止进化初期所获非控个体太少而设计,交叉 方式为:分别在群体B和A中随机抽取一个抗体 图1 DMIOA的流程图 经由算术交叉获新抗体,经N·N。次便获相应数目 Fig.1 Flowchart of DMIOA 新抗体,9)依据算法实际运行的时间,确定该环境是 3算法的描述与设计 否继续进行,此更能体现算法的实时性:同时,使用 存储统计特征模块来保存不同环境的统计特征,便 3.1算法描述 于分析不同环境算法的搜索效果;10)通过判别环 基于以上免疫特征、机理及算法流程图1, 境的相似性,确定初始抗体群的产生方式,目的是 DMIOA可描述为 利用免疫系统的再次应答,加快算法在相似环境的 1)随机产生规模为N的初始抗体群A,置1= 寻优速度」 1,确定选择率a,月 3.2免疫算子模块设计 2)判断t≤T?若是,置”=0及置记忆集 1)分层选择 M,=中,转入3);否则,输出统计结果 根据群体B中抗体在群体中的受控或被控情 3)确定由A中非控个体构成的群体B,其群体 况,计算各抗体被控的个数,根据抗体的被控个数的 规模记为N. 值由小到大排序所有抗体,被控个数为0的抗体放 4)更新记忆集 在第0层,被控个数为1的放在第1层,如此,然后 ①制B中所有抗体进入M:,并清除M,中受 由低层向高层依次选择round(v)个抗体,便获抗 控个体和相同的个体 体群C,在此,round(x)是不超过x的最大整数 ②若M,的规模大于给定的值S。,则利用Av 2)亲和力 erage linkage法聚类 设A为给定环境t的抗体群,则抗体x∈A的 5)若N:<N,则转6);若否,转7) 亲和力设计为 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.ne
新; 外循环的主要作用在于更新记忆池 ,保存不同 环境的统计特征值及产生相似、相同或新环境下的 初始抗体群. 另外 , 在此图中 , N 为群体规模 ,β为 分层选择率(0 <β< 1) , Ne 为所获非控个体数 , vt 为第 t 环境下算法执行的当前时刻 , Tt 表示当前环 境保持不变的最大允许时间 ,“e = 0 ?”用于识别下 一环境是否为新环境; 当为新环境时 , e = 0 ; 当为 相似或相同环境时 , e = 1. 图 1 DMIOA 的流程图 Fig. 1 Flowchart of DMIOA 3 算法的描述与设计 3. 1 算法描述 基于以上免疫特征、机理及算法流程图 1 , DMIOA 可描述为 1) 随机产生规模为 N 的初始抗体群 A ,置 t = 1 , 确定选择率α,β. 2) 判断 t ≤T ? 若是 , 置 vt = 0 及置记忆集 Mt = <,转入 3) ; 否则 , 输出统计结果. 3) 确定由 A 中非控个体构成的群体 B , 其群体 规模记为 Ne . 4) 更新记忆集. ①复制 B 中所有抗体进入 M t , 并清除 Mt 中受 控个体和相同的个体. ②若 Mt 的规模大于给定的值 S e , 则利用 Av2 erage linkage 法聚类[11 ] . 5) 若 Ne <βN , 则转 6) ; 若否 , 转 7) . 6) 经由算术交叉获 N - Ne 个新抗体插入 B 中 , 并转入 7) . 7) 分层选择作用于 B ,获抗体群 C. 8) 计算 C中抗体的亲和力 , 并实施免疫算子 : ①以α为选择率在 C 中选取 αN 个亲和力较 高的抗体构成群体 D , 其中 0 <α<β< 1 ; ②克隆算子[11 ]作用于 D ,获克隆群 K; ③突变算子作用于 K,获突变群 E; ④组合 B 和 E , 计算抗体的亲和力 , 选取 N 个 较高亲和力抗体构成群体 F. 9) 若 vt < Tt , 则 A ←F, 转 3) ; 若否 , 存储当前 环境的统计特征 ,更新记忆池 , 置 t = t + 1 , 转 10) . 10) 实施环境判别规则 ,判断此环境是否与以前 的某环境相似 , 若是 , 则从记忆池中此环境对应的 记忆集中抽取 m2 ( m2 < Se ) 个记忆细胞 , 并随机产 生 N - m2 个新抗体构成当前环境的初始群体 A ;若 否 ,则随机生成 N 个抗体构成初始群体 A , 转 2) . 评注 该算法通过分层选择确保优秀的抗体参 与进化 , 加速算法的收敛速度. 4) 通过记忆集来保 存非控个体 , 使用 Average linkage 聚类 , 防止记忆 集无限扩大 , 且有助于使所获非控面的分布较均 匀; 5) 和 6) 主要是防止算法进化中参与进化的非控 个体过少 , 导致算法搜索效果差等现象 , 其中 , 6) 是为防止进化初期所获非控个体太少而设计 ,交叉 方式为 : 分别在群体 B 和 A 中随机抽取一个抗体 经由算术交叉获新抗体 ,经 N - Ne 次便获相应数目 新抗体 ,9) 依据算法实际运行的时间 ,确定该环境是 否继续进行 , 此更能体现算法的实时性;同时 ,使用 存储统计特征模块来保存不同环境的统计特征 , 便 于分析不同环境算法的搜索效果; 10) 通过判别环 境的相似性 ,确定初始抗体群的产生方式 , 目的是 利用免疫系统的再次应答 , 加快算法在相似环境的 寻优速度. 3. 2 免疫算子模块设计 1) 分层选择[4 ] 根据群体 B 中抗体在群体中的受控或被控情 况 ,计算各抗体被控的个数 ,根据抗体的被控个数的 值由小到大排序所有抗体 ,被控个数为 0 的抗体放 在第 0 层 ,被控个数为 1 的放在第 1 层 ,如此 ,然后 由低层向高层依次选择 round (βN) 个抗体 ,便获抗 体群 C,在此 ,round ( x) 是不超过 x 的最大整数. 2) 亲和力 设 A 为给定环境 t 的抗体群 , 则抗体 x ∈A 的 亲和力设计为 · 07 · 智 能 系 统 学 报 第 2 卷

第5期 钱淑渠,等:动态多目标免疫优化算法及性能测试研究 ·71· aff (x.raw(x.+f(x ①算法最终获得的记忆集及记忆细胞的平均 (1) 浓度 式中:raw(x,)=1+ls(x,t 1 一为抗体x在其S ②算法执行中,相邻两代的抗体群间相互的 覆盖率 (邻域内的浓度:S(x,)为该环境下,抗体群A中 6)环境判别规则 抗体x的5()邻域内,所有抗体y(y≠x)构成的集 首先随机生成m个候选解构成集合M={x' 合,即 1函≤w},然后依据下列式子确定环境t是否有 S(x,=y:f(x,)-f(y,‖≤s(), 相似环境: y∈A∧y≠xy, 0 ,1≤n()≤m, n(t) 时fx,-fx,Ⅱ ()= e(t.k) 点,n(0>m mm阳f(x,功·fX,亚刊 x'EM 式中:、为可调参数,m为大于1的正整数, 式中:k为1与1-1之间的正整数:若£(t,< n()为1环境的当前代数,此设计的目的在于使算 1025则确定满足此条件的第1个k值,并认为环 法在最终所获的非控面有较好的分布:式(1)中右 境t和环境k是相似环境,否则为非相似环境 边的第1项说明若某抗体的邻域内的抗体数较少, 4 性能测试准则 则其亲和力偏高,反之则偏低,此有助于被选中个 体分布均匀;第2项有助于提高算法的搜索性能. 给定算法A与算法B在环境t分别执行G次: 3)亲和突变 S、S分别是此两算法在该环境中第m次执行所 设x为参与突变的抗体,则其突变概率设计为 获非控解集. 1)平均覆盖率.定义映射S,S)一0,1], 即 R(x)1-ks exp af f (x)-af fma 3 af f max af f min S,S)=∈↓3∈<4 1S1 式中:0<台<I,affmax、affmin分别为抗体群中最 (5 大、最小亲和力.突变方式为多项式突变4 则在环境1下,算法A对算法B的平均覆盖率为 4)更新记忆池 G 由于随环境的变化,各环境所获的最好解之间 C(A,B=人∑p(Sd,s9 G 6 不能比较优劣:相应地,相同、相似或不同抗原所 对应的记忆细胞之间不能比较各自的优劣,这导致 若C(A,B)=1,则在环境1,算法B所获非控解集 记忆池的容量将逐渐增大:为了克服此问题,降低 完全被算法A的覆盖 算法的计算复杂度,记忆池由若干类记忆集构成, 2)平均浓度、平均覆盖.平均浓度D()和平均 具体设计如下: 覆盖H()可分别用于度量算法A所获非控解集的 将环境划分成若干类,每一类由相同或相似环 整体分布状况及覆盖的范围,基于文献[9]的设计, 境构成.?由第1类环境中各环境下算法所获记忆 它们被设计为 细胞构成,特别地,若仅由一种环境下的记忆细 1 胞构成,则表示该环境属于新环境:反之,若?由 D(=1 S (dm-dum)2 GG S-1-1c 多种环境的记忆细胞构成,则这些记忆细胞的各分 量被等价转化为0,11区间上的值,进一步,中 7) 仅保存m2个记忆细胞,若超出此数,则计算各记 H(0=士∑max{I(x.: 忆细胞的浓度),保存浓度大的m个记忆细胞 G1G1945 x',X∈Sm} (8) 5)统计特征存储 式中: 该模块用于保存算法在每一环境中获得的统计 dam min{llxx ll:xx ES, 特征,存储: 1为,1写司S1 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
af f ( x , t) = raw ( x , t) + k1 ‖f ( x , t) ‖ . (1) 式中 : raw ( x , t) = 1 1 +| S ( x , t) | 为抗体 x 在其ζ ( t) 邻域内的浓度; S ( x , t) 为该环境下 , 抗体群 A 中 抗体 x 的ζ( t) 邻域内 ,所有抗体 y( y ≠x) 构成的集 合 , 即 S ( x , t) = { y : ‖f ( x , t) - f ( y , t) ‖ ≤ζ( t) , y ∈A ∧y ≠x} , ζ( t) = k1 n( t) ,1 ≤n( t) ≤m1 , k2 m1 , n( t) > m1 . (2) 式中 : k1 、k2 为可调参数 , m1 为大于 1 的正整数 , n( t) 为 t 环境的当前代数 , 此设计的目的在于使算 法在最终所获的非控面有较好的分布; 式 (1) 中右 边的第 1 项说明若某抗体的邻域内的抗体数较少 , 则其亲和力偏高 , 反之则偏低 ,此有助于被选中个 体分布均匀; 第 2 项有助于提高算法的搜索性能. 3) 亲和突变 设 x 为参与突变的抗体 , 则其突变概率设计为 R ( x) = 1 - k3 ·exp af f ( x) - af f max af f max - af f min . (3) 式中 :0 < k3 < 1 , af f max 、af f min 分别为抗体群中最 大、最小亲和力. 突变方式为多项式突变[14 ] . 4) 更新记忆池 由于随环境的变化 , 各环境所获的最好解之间 不能比较优劣; 相应地 , 相同、相似或不同抗原所 对应的记忆细胞之间不能比较各自的优劣 , 这导致 记忆池的容量将逐渐增大; 为了克服此问题 , 降低 算法的计算复杂度 , 记忆池由若干类记忆集构成 , 具体设计如下 : 将环境划分成若干类 ,每一类由相同或相似环 境构成. τi 由第 i 类环境中各环境下算法所获记忆 细胞构成 , 特别地 , 若τi 仅由一种环境下的记忆细 胞构成 , 则表示该环境属于新环境; 反之 , 若τi 由 多种环境的记忆细胞构成 , 则这些记忆细胞的各分 量被等价转化为[0 , 1 ]区间上的值 , 进一步 , τi 中 仅保存 m2 个记忆细胞 , 若超出此数 , 则计算各记 忆细胞的浓度[13 ] , 保存浓度大的 m2 个记忆细胞. 5) 统计特征存储 该模块用于保存算法在每一环境中获得的统计 特征 , 存储 : ①算法最终获得的记忆集及记忆细胞的平均 浓度. ②算法执行中 , 相邻两代的抗体群间相互的 覆盖率. 6) 环境判别规则 首先随机生成 m0 个候选解构成集合 M = { x i , 1 ≤i ≤m0 } , 然后依据下列式子确定环境 t 是否有 相似环境 : ε( t , k) = ∑ m0 i =1 ‖f ( x i , t) - f ( x i , k) ‖ m0 max x i ∈M { ‖f ( x i , t) - f ( x i , k) ‖} . (4) 式中 : k 为 1 与 t - 1 之间的正整数; 若ε( t , k) < 10 - 215则确定满足此条件的第 1 个 k 值 , 并认为环 境 t 和环境 k 是相似环境 ,否则为非相似环境. 4 性能测试准则 给定算法 A 与算法 B 在环境 t 分别执行 G 次; S A tm 、S B tm分别是此两算法在该环境中第 m 次执行所 获非控解集. [3 ] 1) 平均覆盖率. 定义映射Φ( S A tm , S B tm ) →[0 ,1 ] , 即 Φ( S A tm , S B tm ) = | { x B ∈S B tm | ϖ x A ∈S A tm :x A < x B } | | S B tm | . (5) 则在环境 t 下 , 算法 A 对算法 B 的平均覆盖率为 C( A , B) = 1 G ∑ G k =1 Φ( S A tk , S B tk ) . (6) 若 C( A , B) = 1 , 则在环境 t , 算法 B 所获非控解集 完全被算法 A 的覆盖. 2) 平均浓度、平均覆盖. 平均浓度 D ( t) 和平均 覆盖 H ( t) 可分别用于度量算法 A 所获非控解集的 整体分布状况及覆盖的范围 ,基于文献[9 ]的设计 , 它们被设计为 D ( t) = 1 G1 ≤∑m ≤G 1 | S A tm | - 1 1 ≤i∑ ≤| S A tm | ( dtm - dtim ) 2 , (7) H ( t) = 1 G 1 ≤∑m ≤G max 1 ≤j , j ≤| S A tm | { ‖( x i - x j ) ‖: x i , x j ∈S A tm } . (8) 式中 : dtim = min i ≠j ,1 ≤j ≤| S A tm | { ‖x i - x j ‖: x i , x j ∈S A tm } , 第 5 期 钱淑渠 ,等 :动态多目标免疫优化算法及性能测试研究 · 17 ·

·72 智能系统学报 第2卷 G(t)sin(0.5t/10) 3)收敛行为 x1=(x)∈[0,11, 设X(n2)为算法A在第t环境第m次执行 xm=(x2,x3,….x0)∈「-1,11 中,第n代所得的记忆集合,则其收敛性可由下式度 量: 表2DBM对各问题在不同环境独立运行 30次所需平均时间 Pa(t)= 9) Table 2 DBM:Average run time for each environment of the given problem with respectively 30 executions /min 式中:6∈Z 环境t 1 2 34 5 67 P(i.m.0=IC()+c() 问题12.82.82.72.72.72.72.7 问题229 2.82.8 2.8 2.82.82.8 式9)表明,若lim_Pa()=0,则算法A在环境1 问题32.83.02.92.92.92.92.9 有很好的收敛性」 5数值实验 该问题的理论Pareto面满足f2=1-1.各 选取参与比较的算法为DBM,DNSGAII-A 算法在7个环境中分别独立执行30次后所获的统 及CSADMO,各算法的初始群体规模均为N=80. 计值及平均覆盖率如表3、4;此3种算法借助式 在给定环境下,指定保存此3种算法及DMIOA所 9),所获收敛行为曲线如图2,但由于DBM是一种 获非控个体的集合的规模均为80,也假定环境总个 邻域搜索算法,其结构的特殊性使得在此不能描述 数为7,即T=7.由于算法在解决给定环境优化问 出其搜索曲线,各算法在各环境中执行一次所获的 题时,其执行时间是评价动态环境优化算法的性能 非控面比较如图3.表3是各算法对各环境独立运 之一I,为此,对DNSGAII-A、CSADMO及 行30次所获非控解集的平均浓度、平均覆盖比较, DMIOA,规定其在每个环境内的执行时间T,=5s, 由此表获知:参与比较的3种算法所获非控解集的 而对于DBM,由于其结构设计的特殊性,指定每次 平均浓度较差,其中DBM最差,DNSGAⅡ-A、 执行的最大迭代数为20000,这要求DBM对每个 CSADMO稍好,而DMIOA所获效果较好;由各 测试问题在每一次执行中至少需要162s(见表2), 环境所获非控解集平均覆盖获知:DNS GAⅡ-A、 即T.=162s.各算法对每一测试问题的各环境分 CSADMO稍差,DBM及DMIOA较好.表4是各 别独立执行30次,即G=30,获相应的统计特征值 算法对各环境所获平均覆盖率比较,其中X、 及DBM在每个环境的平均执行时间(表2),DBM XDN、XS、XM分别为算法DBM、DNSGAII·-A、 的进化策略中的突变概率为0.35,梯度搜索法中停 CSADMO DMIOA所获非控解集,由此表获知: 机精度ε=0.01:其他算法参数值的选取可参考文 DMIOA与DNSGAII-A在各环境效果较接近,而 献10-11J:对于DMIOA,除了m=10外,其他 CSADMO及DBM效果较差.图2是DNSGAII- 参数如表1. A、CSADMO DMIOA对各环境独立运行30次所 获平均收敛曲线,n是实际时刻算法所对应的代 表1 DMIOA算法参数设置 Table 1 DMIOA's Parameter settings 数,由图2可知,三算法在给定时间内运行的最大代 参数aB 数均有所不同,DMIOA在较少的代数内收敛行为 k1反m 曲线接近0,而其他两算法收敛较慢.图3是各算法 值0.40.70.210.9520 100 在各环境所获非控面的点分布比较;为便于图形直 问题1FDA1PI 观,将目标函数值f2以G=0.21平移,由图获知: minf(x)=(f1(x)f2(x)) DNSGAII-A收敛较好,但其在f1接近于1的点 较难找到,而CSADMO及DBM分布较好,但收敛 s.t.fi(x x..f2 (x)=g(1- 稍差,而DMIOA所获非控面的点分布较均匀,且 与DNSGAIⅡ-A收敛行为曲线相似,此也可由表4 g(m)=1+∑(x:-G()2 获知 1994-2008 China Academie Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
dtm = 1 | S A tm | 1 ≤i∑ ≤| S A tm | dtim . 3) 收敛行为 设 X n tm ( n ≥2) 为算法 A 在第 t 环境第 m 次执行 中,第 n代所得的记忆集合, 则其收敛性可由下式度 量: PGn ( t) = 1 Gl 0 1 ≤∑m ≤G, n+1 -∑l 0 ≤i ≤n P ( i , m , t) . (9) 式中 :l0 ∈Z + , P( i , m , t) = 1 2 [ C( X i tm , X i - 1 tm ) + C( X i - 1 tm , X i tm ) ]. 式(9) 表明 , 若 lim G, n→∞ PGn ( t) = 0 , 则算法 A 在环境 t 有很好的收敛性. 5 数值实验 选取参与比较的算法为 DBM , DNSGA II - A 及 CSADMO , 各算法的初始群体规模均为 N = 80. 在给定环境下 ,指定保存此 3 种算法及 DMIOA 所 获非控个体的集合的规模均为 80 ,也假定环境总个 数为 7 ,即 T = 7. 由于算法在解决给定环境优化问 题时 ,其执行时间是评价动态环境优化算法的性能 之 一[1 ] , 为 此 , 对 DNSGAII - A 、CSADMO 及 DMIOA ,规定其在每个环境内的执行时间 Tt = 5 s, 而对于 DBM , 由于其结构设计的特殊性 ,指定每次 执行的最大迭代数为 20 000 , 这要求 DBM 对每个 测试问题在每一次执行中至少需要 162 s(见表 2) , 即 Tt = 162 s. 各算法对每一测试问题的各环境分 别独立执行 30 次 , 即 G = 30 , 获相应的统计特征值 及 DBM 在每个环境的平均执行时间 (表 2) . DBM 的进化策略中的突变概率为 0135 , 梯度搜索法中停 机精度ε= 0101 ;其他算法参数值的选取可参考文 献[10 - 11 ];对于 DMIOA , 除了 m2 = 10 外 , 其他 参数如表 1. 表 1 DMIOA算法参数设置 Table 1 DMIOA’s Parameter settings 参数 α β k1 k2 k3 m0 m1 值 0. 4 0. 7 0. 2 1 0. 95 20 100 问题 1 FDA1 [2 ] min f ( x) = ( f 1 ( x) , f 2 ( x) ) , s. t. f 1 ( xI) = xi , f 2 ( x) = g (1 - f 1 g ) , g ( xΠ) = 1 + x i∑∈x I ( xi - G( t) ) 2 , G( t) = sin (015πt/ 10) , xI = ( x1 ) ∈[0 ,1 ] , xΠ = ( x2 , x3 , …, x30 ) ∈[ - 1 ,1 ]. 表 2 DBM 对各问题在不同环境独立运行 30 次所需平均时间 Table 2 DBM : Average run time for each environment of the given problem with respectively 30 executions / min 环境 t 1 2 3 4 5 6 7 问题 1 2. 8 2. 8 2. 7 2. 7 2. 7 2. 7 2. 7 问题 2 2. 9 2. 8 2. 8 2. 8 2. 8 2. 8 2. 8 问题 3 2. 8 3. 0 2. 9 2. 9 2. 9 2. 9 2. 9 该问题的理论 Pareto 面满足 f 2 = 1 - f 1 . 各 算法在 7 个环境中分别独立执行 30 次后所获的统 计值及平均覆盖率如表 3、4 ; 此 3 种算法借助式 (9) ,所获收敛行为曲线如图 2 ,但由于 DBM 是一种 邻域搜索算法 ,其结构的特殊性使得在此不能描述 出其搜索曲线 ; 各算法在各环境中执行一次所获的 非控面比较如图 3. 表 3 是各算法对各环境独立运 行 30 次所获非控解集的平均浓度、平均覆盖比较 , 由此表获知 :参与比较的 3 种算法所获非控解集的 平均浓度较差 , 其中 DBM 最差 , DNSGA II - A 、 CSADMO 稍好 , 而 DMIOA 所获效果较好 ; 由各 环境所获非控解集平均覆盖获知 :DNSGA II - A 、 CSADMO 稍差 , DBM 及 DMIOA 较好. 表 4 是各 算法对各环境所获平均覆盖率比较 , 其中 X DB 、 X DN 、X CS 、X DM 分别为算法 DBM、DNSGAII - A 、 CSADMO、DMIOA 所获非控解集 , 由此表获知 : DMIOA 与 DNSGA II - A 在各环境效果较接近 ,而 CSADMO 及 DBM 效果较差. 图 2 是 DNSGAII - A 、CSADMO、DMIOA 对各环境独立运行 30 次所 获平均收敛曲线 , n 是实际时刻算法所对应的代 数 ,由图 2 可知 ,三算法在给定时间内运行的最大代 数均有所不同 ,DMIOA 在较少的代数内收敛行为 曲线接近 0 ,而其他两算法收敛较慢. 图 3 是各算法 在各环境所获非控面的点分布比较 ;为便于图形直 观 , 将目标函数值 f 2 以δt = 0. 2 t 平移 ,由图获知 : DNSGA II - A 收敛较好 ,但其在 f 1 接近于 1 的点 较难找到 ,而 CSADMO 及 DBM 分布较好 ,但收敛 稍差 ,而 DMIOA 所获非控面的点分布较均匀 , 且 与 DNSGA II - A 收敛行为曲线相似 ,此也可由表 4 获知. · 27 · 智 能 系 统 学 报 第 2 卷
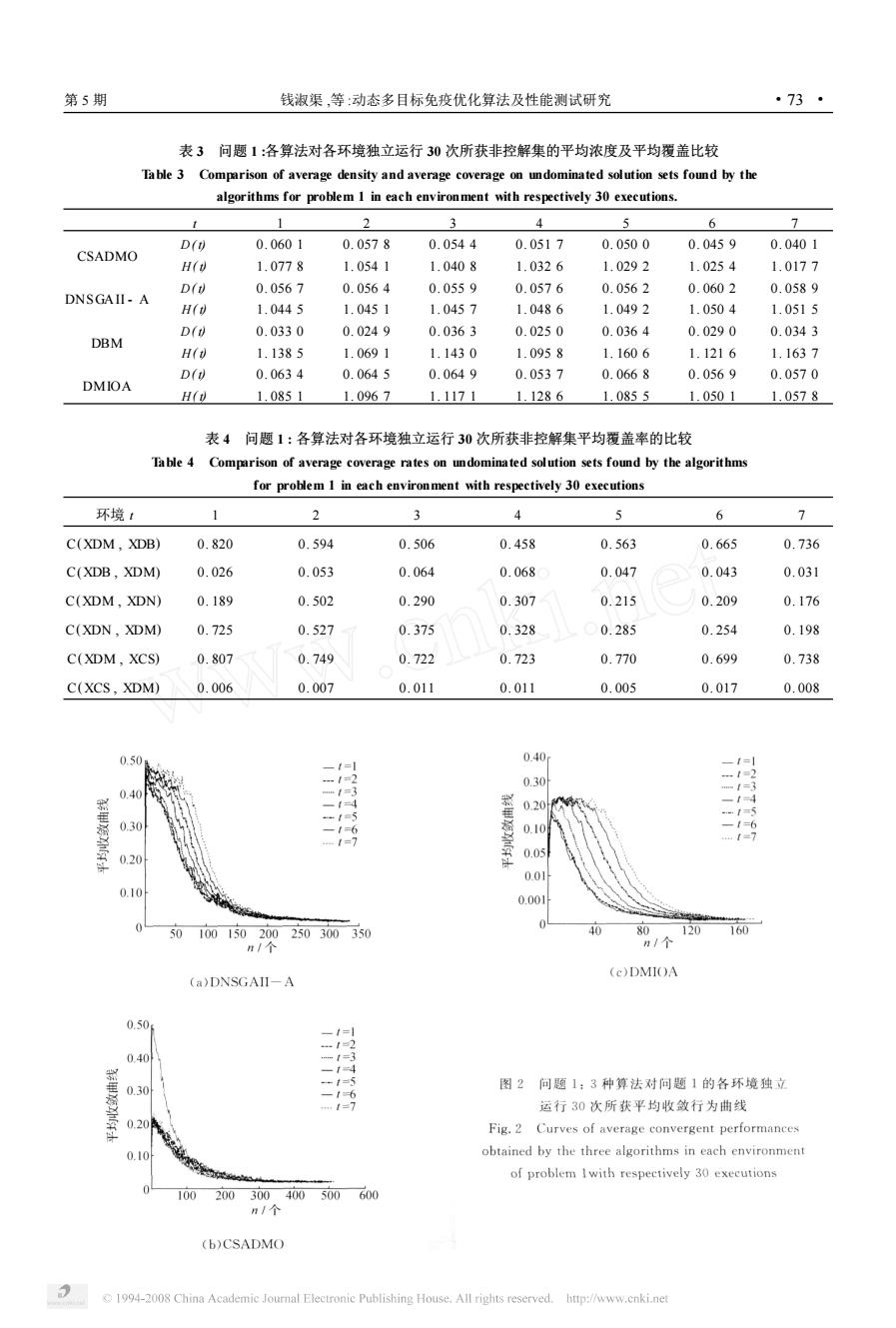
第5期 钱淑渠,等:动态多目标免疫优化算法及性能测试研究 ·73· 表3问题1:各算法对各环境独立运行30次所获非控解集的平均浓度及平均覆盖比较 Table 3 Comparison of average density and average coverage on undominated solution sets found by the algorithms for problem 1 in each environment with respectively 30 executions. 1 2 4 5 6 > D() 0.0601 0.0578 0.0544 0.0517 0.0500 0.0459 0.0401 CSADMO H(v 1.0778 1.0541 1.0408 1.0326 1.0292 1.0254 1.0177 D(1 0.0567 0.0564 0.0559 0.0576 0.0562 0.0602 0.0589 DNSGAII-A H(0 1.0445 1.0451 1.0457 1.0486 1.0492 1.0504 1.0515 D(0 0.0330 0.0249 0.0363 0.0250 0.0364 0.0290 0.0343 DBM H(0 1.1385 1.0691 1.1430 1.0958 1.1606 1.1216 1.1637 D 0.0634 0.0645 0.0649 0.0537 0.0668 0.0569 0.0570 DMIOA H() 1.0851 1.0967 1.1171 1.1286 1.0855 1.0501 1.0578 表4问题1:各算法对各环境独立运行30次所获非控解集平均覆盖率的比较 Table 4 Comparison of average coverage rates on undominated solution sets found by the algorithms for problem I in each environment with respectively 30 executions 环境t 5 6 7 C(XDM,XDB) 0.820 0.594 0.506 0.458 0.563 0.665 0.736 C(X①DB,X①M) 0.026 0.053 0.064 0.068 0.047 0.043 0.031 C(XDM,XDN) 0.189 0.502 0.290 0.307 0.215 0.209 0.176 C(XDN,X①M) 0.725 0.527 0.375 0.328 0.285 0.254 0.198 C(XDM,XCS) 0.807 0.749 0.722 0.723 0.770 0.699 0.738 C(XCS,X①M) 0.006 0.007 0.011 0.011 0.005 0.017 0.008 0.50 0.40 0.30 1=2 0.40 1=3 0.20 0.30 0.10 -1=6 1=7 0.20 0.05 0.01 0.10 0.001 50 100150200250300 350 40 80 120 160 n/个 n/个 (e)DMIOA (a)DNSGAII-A 0.50 一1=1 -t=2 0.40 …1=3 14 0.30 图2问题1:3种算法对问题1的各环境独立 运行30次所获平均收敛行为曲线 0.20 Fig.2 Curves of average convergent performances obtained by the three algorithms in each environment of problem Iwith respectively 30 executions 0 100200300400500600 n/个 (b)CSADMO 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
表 3 问题 1 :各算法对各环境独立运行 30 次所获非控解集的平均浓度及平均覆盖比较 Table 3 Comparison of average density and average coverage on undominated solution sets found by the algorithms for problem 1 in each environment with respectively 30 executions. t 1 2 3 4 5 6 7 CSADMO D( t) 0. 060 1 0. 057 8 0. 054 4 0. 051 7 0. 050 0 0. 045 9 0. 040 1 H( t) 1. 077 8 1. 054 1 1. 040 8 1. 032 6 1. 029 2 1. 025 4 1. 017 7 DNSGAII - A D( t) 0. 056 7 0. 056 4 0. 055 9 0. 057 6 0. 056 2 0. 060 2 0. 058 9 H( t) 1. 044 5 1. 045 1 1. 045 7 1. 048 6 1. 049 2 1. 050 4 1. 051 5 DBM D( t) 0. 033 0 0. 024 9 0. 036 3 0. 025 0 0. 036 4 0. 029 0 0. 034 3 H( t) 1. 138 5 1. 069 1 1. 143 0 1. 095 8 1. 160 6 1. 121 6 1. 163 7 DMIOA D( t) 0. 063 4 0. 064 5 0. 064 9 0. 053 7 0. 066 8 0. 056 9 0. 057 0 H( t) 1. 085 1 1. 096 7 1. 117 1 1. 128 6 1. 085 5 1. 050 1 1. 057 8 表 4 问题 1 : 各算法对各环境独立运行 30 次所获非控解集平均覆盖率的比较 Table 4 Comparison of average coverage rates on undominated solution sets found by the algorithms for problem 1 in each environment with respectively 30 executions 环境 t 1 2 3 4 5 6 7 C(XDM , XDB) 0. 820 0. 594 0. 506 0. 458 0. 563 0. 665 0. 736 C(XDB , XDM) 0. 026 0. 053 0. 064 0. 068 0. 047 0. 043 0. 031 C(XDM , XDN) 0. 189 0. 502 0. 290 0. 307 0. 215 0. 209 0. 176 C(XDN , XDM) 0. 725 0. 527 0. 375 0. 328 0. 285 0. 254 0. 198 C(XDM , XCS) 0. 807 0. 749 0. 722 0. 723 0. 770 0. 699 0. 738 C(XCS , XDM) 0. 006 0. 007 0. 011 0. 011 0. 005 0. 017 0. 008 第 5 期 钱淑渠 ,等 :动态多目标免疫优化算法及性能测试研究 · 37 ·
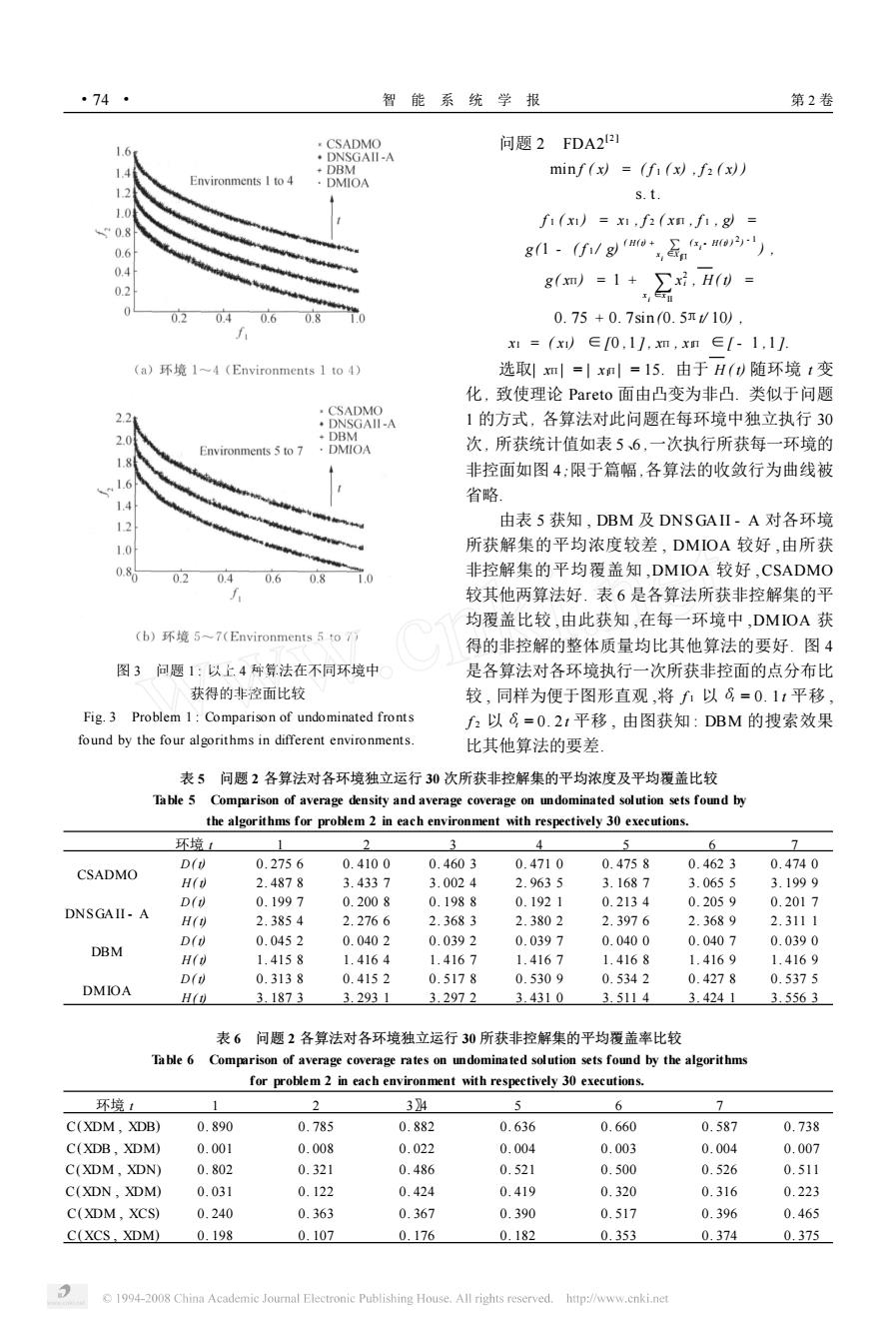
74 智能系统学报 第2卷 ¥CSADMO 1.6 问题2FDA2I ·DNSGAII-A 1.4 DBM minf(x)=(f1(x).f2(x)) Environments I to 4 ·DMIOA 1.2 s.t. 1.0 fi(x)x1,f2(xn,fi,g)= 0.8 0.6 g1-f/g0+£n. 0.4 0.2 g(xm)=1+x好,H()= ,安 0.2 0.40.6 少汽0 0.8 0.75+0.7sin0.5r/10), x1=(x∈0,1],xm,xm∈[-1,1]. (a)环境14(Environments1to4) 选取!m=|xm=15.由于H()随环境t变 化,致使理论Pareto面由凸变为非凸.类似于问题 ·CSADMO 2.2 ·DNSGAII-A 1的方式,各算法对此问题在每环境中独立执行30 2.0 +DBM Environments 5 to 7 ·DMIOA 次,所获统计值如表56,一次执行所获每一环境的 1.8 非控面如图4:限于篇幅,各算法的收敛行为曲线被 1.6 1.4 省略 12 由表5获知,DBM及DNSGAII-A对各环境 1.0 所获解集的平均浓度较差,DMIOA较好,由所获 085 020.40.60.8 1.0 非控解集的平均覆盖知,DMIOA较好,CSADMO 较其他两算法好.表6是各算法所获非控解集的平 均覆盖比较,由此获知,在每一环境中,DMIOA获 (b)环境5~7(Environments5tof 得的非控解的整体质量均比其他算法的要好.图4 图3问题1:以上.4种算法在不同环境中 是各算法对各环境执行一次所获非控面的点分布比 获得的非控面比较 较,同样为便于图形直观,将f1以8=0.11平移 Fig.3 Problem 1:Comparison of undominated fronts f2以8=0.21平移,由图获知:DBM的搜索效果 found by the four algorithms in different environments. 比其他算法的要差 表5问题2各算法对各环境独立运行30次所获非控解集的平均浓度及平均覆盖比较 Table 5 Comparison of average density and average coverage on undominated solution sets found by the algorithms for problem 2 in each environment with respectively 30 executions. 环境 1 2 3 4 5 6 7 D(v 0.2756 0.4100 0.4603 0.4710 0.4758 0.4623 0.4740 CSADMO H(v 2.4878 3.4337 3.0024 2.9635 3.1687 3.0655 3.1999 D(v 0.1997 0.2008 0.1988 0.1921 0.2134 0.2059 0.2017 DNSGAII-A H() 2.3854 2.2766 2.3683 2.3802 2.3976 2.3689 2.3111 D(0 0.0452 0.0402 0.0392 0.0397 0.0400 0.0407 0.0390 DBM H(0 1.4158 1.4164 1.4167 1.4167 1.4168 1.4169 1.4169 D(d 0.3138 0.4152 0.5178 0.5309 0.5342 0.4278 0.5375 DMIOA H(n) 3.1873 3.2931 3.2972 3.4310 3.5114 3.4241 3.5563 表6问题2各算法对各环境独立运行30所获非控解集的平均覆盖率比较 Table 6 Comparison of average coverage rates on undominated solution sets found by the algorithms for problem 2 in each environment with respectively 30 executions. 环境t 1 2 34 6 1 C(XDM,X①B) 0.890 0.785 0.882 0.636 0.660 0.587 0.738 C(XDB,XDM) 0.001 0.008 0.022 0.004 0.003 0.004 0.007 C(XDM,XDN) 0.802 0.321 0.486 0.521 0.500 0.526 0.511 C(XDN.XDM) 0.031 0.122 0.424 0.419 0.320 0.316 0.223 C(XDM.XCS) 0.240 0.363 0.367 0.390 0.517 0.396 0.465 C(XCS,XDM) 0.198 0.107 0.176 0.182 0.353 0.374 0.375 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
图 3 问题 1 : 以上 4 种算法在不同环境中 获得的非控面比较 Fig. 3 Problem 1 : Comparison of undominated fronts found by the four algorithms in different environments. 问题 2 FDA2 [2 ] min f ( x) = ( f 1 ( x) , f 2 ( x) ) s. t. f 1 ( x1 ) = x1 , f 2 ( xIΠ , f 1 , g) = g (1 - ( f 1 / g) ( H( t) + x ∑i ∈XΠI ( x i - H( t) ) 2 ) - 1 ) , g ( xΠ) = 1 + x i∑∈x II x 2 i , H ( t) = 0. 75 + 0. 7sin (0. 5πt/ 10) , xI = ( xI) ∈[0 ,1 ] , xΠ , xIΠ ∈[ - 1 ,1 ]. 选取| xΠ| = | xIΠ| = 15. 由于 H ( t) 随环境 t 变 化 , 致使理论 Pareto 面由凸变为非凸. 类似于问题 1 的方式 , 各算法对此问题在每环境中独立执行 30 次 , 所获统计值如表 5、6 ,一次执行所获每一环境的 非控面如图 4 ;限于篇幅 ,各算法的收敛行为曲线被 省略. 由表 5 获知 , DBM 及 DNSGAII - A 对各环境 所获解集的平均浓度较差 , DMIOA 较好 ,由所获 非控解集的平均覆盖知 ,DMIOA 较好 ,CSADMO 较其他两算法好. 表 6 是各算法所获非控解集的平 均覆盖比较 ,由此获知 ,在每一环境中 ,DMIOA 获 得的非控解的整体质量均比其他算法的要好. 图 4 是各算法对各环境执行一次所获非控面的点分布比 较 , 同样为便于图形直观 ,将 f 1 以δt = 0. 1 t 平移 , f 2 以δt = 0. 2t 平移 , 由图获知 : DBM 的搜索效果 比其他算法的要差. 表 5 问题 2 各算法对各环境独立运行 30 次所获非控解集的平均浓度及平均覆盖比较 Table 5 Comparison of average density and average coverage on undominated solution sets found by the algorithms for problem 2 in each environment with respectively 30 executions. 环境 t 1 2 3 4 5 6 7 CSADMO D( t) 0. 275 6 0. 410 0 0. 460 3 0. 471 0 0. 475 8 0. 462 3 0. 474 0 H( t) 2. 487 8 3. 433 7 3. 002 4 2. 963 5 3. 168 7 3. 065 5 3. 199 9 DNSGAII - A D( t) 0. 199 7 0. 200 8 0. 198 8 0. 192 1 0. 213 4 0. 205 9 0. 201 7 H( t) 2. 385 4 2. 276 6 2. 368 3 2. 380 2 2. 397 6 2. 368 9 2. 311 1 DBM D( t) 0. 045 2 0. 040 2 0. 039 2 0. 039 7 0. 040 0 0. 040 7 0. 039 0 H( t) 1. 415 8 1. 416 4 1. 416 7 1. 416 7 1. 416 8 1. 416 9 1. 416 9 DMIOA D( t) 0. 313 8 0. 415 2 0. 517 8 0. 530 9 0. 534 2 0. 427 8 0. 537 5 H( t) 3. 187 3 3. 293 1 3. 297 2 3. 431 0 3. 511 4 3. 424 1 3. 556 3 表 6 问题 2 各算法对各环境独立运行 30 所获非控解集的平均覆盖率比较 Table 6 Comparison of average coverage rates on undominated solution sets found by the algorithms for problem 2 in each environment with respectively 30 executions. 环境 t 1 2 3〗4 5 6 7 C(XDM , XDB) 0. 890 0. 785 0. 882 0. 636 0. 660 0. 587 0. 738 C(XDB , XDM) 0. 001 0. 008 0. 022 0. 004 0. 003 0. 004 0. 007 C(XDM , XDN) 0. 802 0. 321 0. 486 0. 521 0. 500 0. 526 0. 511 C(XDN , XDM) 0. 031 0. 122 0. 424 0. 419 0. 320 0. 316 0. 223 C(XDM , XCS) 0. 240 0. 363 0. 367 0. 390 0. 517 0. 396 0. 465 C(XCS , XDM) 0. 198 0. 107 0. 176 0. 182 0. 353 0. 374 0. 375 · 47 · 智 能 系 统 学 报 第 2 卷
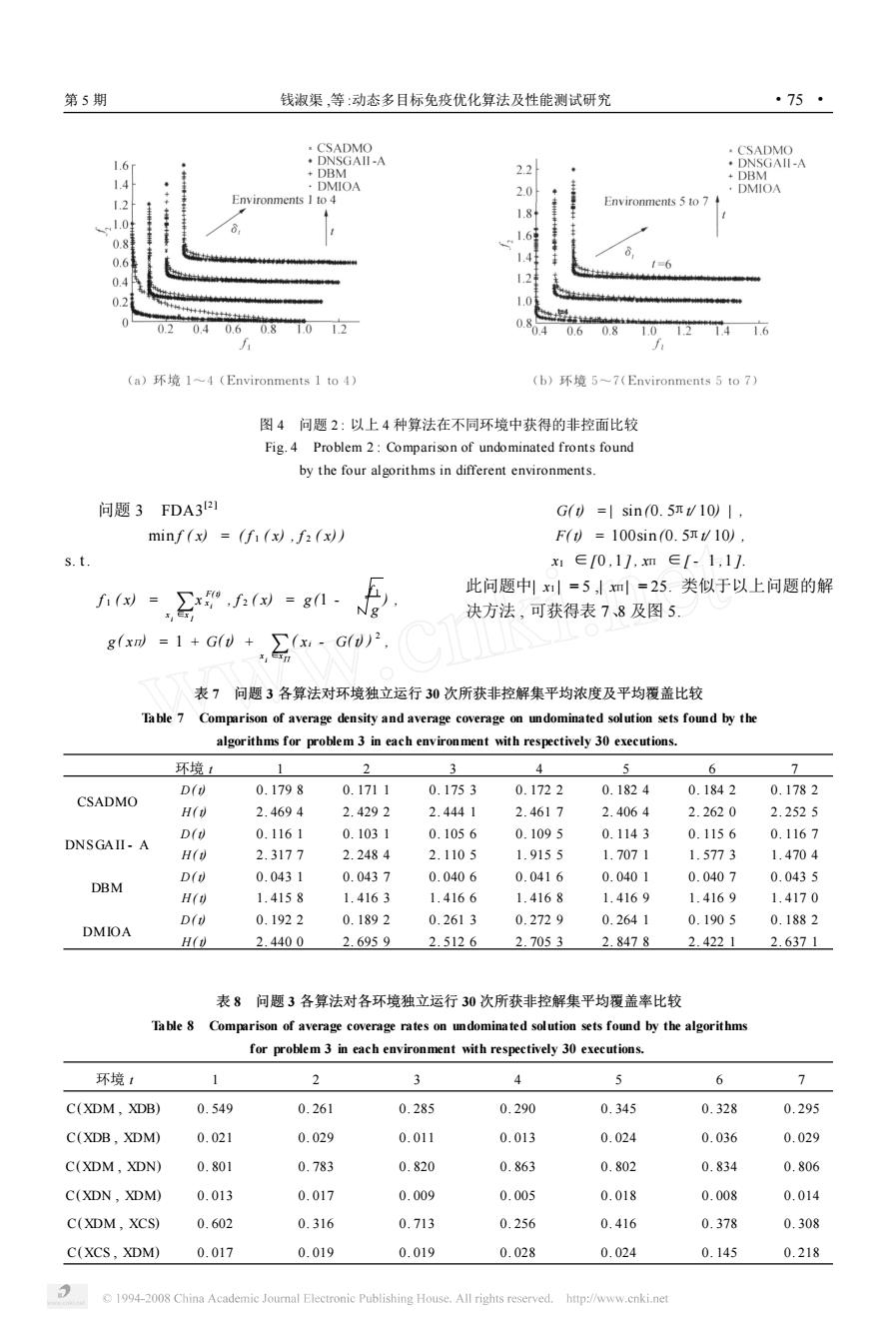
第5期 钱淑渠,等:动态多目标免疫优化算法及性能测试研究 ·75· CSADMO .CSADMO 1.6 ◆DNSGAII-A DBM 22 ·DNSGAI-A 1.4 DBM DMIOA 20 ·DMIOA Environments I to 4 Environments 5 to 7 1.8+ 10 0.8 1.6 0.6 1.41 0.4 .2 0. 1.0 0.2 0.40.608T012 0.8 4 0.60.81012T41.6 (a)环境l~4(Environments1to4) (b)环境5~7(Environments5to7) 图4问题2:以上4种算法在不同环境中获得的非控面比较 Fig.4 Problem 2:Comparison of undominated fronts found by the four algorithms in different environments. 问题3FDA3I G)=lsin0.5π/10)l, minf(x)=(f1(x),f2(x)) F()=100sin0.5r/10), s.t x1∈0,11,xm∈-1,11 fi(x)= ∑x,f2()=g1 此问题中x=5,xm=25.类似于以上问题的解 决方法,可获得表7、8及图5. g(x=1+G+∑(xG)2 表7问题3各算法对环境独立运行30次所获非控解集平均浓度及平均覆盖比较 Table 7 Comparison of average density and average coverage on undominated solution sets found by the algorithms for problem 3 in each environment with respectively 30 executions. 环境1 1 2 4 5 6 7 D(0 0.1798 0.1711 0.1753 0.1722 0.1824 0.1842 0.1782 CSADMO H(v 2.4694 2.4292 2.4441 2.4617 2.4064 2.2620 2.2525 D(0 0.1161 0.1031 0.1056 0.1095 0.1143 0.1156 0.1167 DNSGAII-A H(d 2.3177 2.2484 2.1105 1.9155 1.7071 1.5773 1.4704 D(0 0.0431 0.0437 0.0406 0.0416 0.0401 0.0407 0.0435 DBM H( 1.4158 1.4163 1.4166 1.4168 1.4169 1.4169 1.4170 D(1 0.1922 0.1892 0.2613 0.2729 0.2641 0.1905 0.1882 DMIOA H(0 2.4400 2.6959 2.5126 2.7053 2.8478 2.4221 2.6371 表8问题3各算法对各环境独立运行30次所获非控解集平均覆盖率比较 Table 8 Comparison of average coverage rates on undominated solution sets found by the algorithms for problem 3 in each environment with respectively 30 executions. 环境t 1 6 7 C(X①M,XDB) 0.549 0.261 0.285 0.290 0.345 0.328 0.295 C(XDB,XDM) 0.021 0.029 0.011 0.013 0.024 0.036 0.029 C(XDM,XDN) 0.801 0.783 0.820 0.863 0.802 0.834 0.806 C(XDN,X①DM) 0.013 0.017 0.009 0.005 0.018 0.008 0.014 C(XDM,XCS) 0.602 0.316 0.713 0.256 0.416 0.378 0.308 C(XCS,XDM) 0.017 0.019 0.019 0.028 0.024 0.145 0.218 1994-2008 China Academie Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
图 4 问题 2 : 以上 4 种算法在不同环境中获得的非控面比较 Fig. 4 Problem 2 : Comparison of undominated fronts found by the four algorithms in different environments. 问题 3 FDA3 [2 ] min f ( x) = ( f 1 ( x) , f 2 ( x) ) s. t. f 1 ( x) = x i∑∈x I x F( t) x i , f 2 ( x) = g (1 - f 1 g ) , g ( xΠ) = 1 + G( t) + x i∑∈xΠ ( xi - G( t) ) 2 , G( t) =| sin (0. 5πt/ 10) | , F( t) = 100sin (0. 5πt/ 10) , xI ∈[0 ,1 ] , xΠ ∈[ - 1 ,1 ]. 此问题中| x1 | = 5 ,| xΠ| = 25. 类似于以上问题的解 决方法 , 可获得表 7、8 及图 5. 表 7 问题 3 各算法对环境独立运行 30 次所获非控解集平均浓度及平均覆盖比较 Table 7 Comparison of average density and average coverage on undominated solution sets found by the algorithms for problem 3 in each environment with respectively 30 executions. 环境 t 1 2 3 4 5 6 7 CSADMO D( t) 0. 179 8 0. 171 1 0. 175 3 0. 172 2 0. 182 4 0. 184 2 0. 178 2 H( t) 2. 469 4 2. 429 2 2. 444 1 2. 461 7 2. 406 4 2. 262 0 2. 252 5 DNSGAII - A D( t) 0. 116 1 0. 103 1 0. 105 6 0. 109 5 0. 114 3 0. 115 6 0. 116 7 H( t) 2. 317 7 2. 248 4 2. 110 5 1. 915 5 1. 707 1 1. 577 3 1. 470 4 DBM D( t) 0. 043 1 0. 043 7 0. 040 6 0. 041 6 0. 040 1 0. 040 7 0. 043 5 H( t) 1. 415 8 1. 416 3 1. 416 6 1. 416 8 1. 416 9 1. 416 9 1. 417 0 DMIOA D( t) 0. 192 2 0. 189 2 0. 261 3 0. 272 9 0. 264 1 0. 190 5 0. 188 2 H( t) 2. 440 0 2. 695 9 2. 512 6 2. 705 3 2. 847 8 2. 422 1 2. 637 1 表 8 问题 3 各算法对各环境独立运行 30 次所获非控解集平均覆盖率比较 Table 8 Comparison of average coverage rates on undominated solution sets found by the algorithms for problem 3 in each environment with respectively 30 executions. 环境 t 1 2 3 4 5 6 7 C(XDM , XDB) 0. 549 0. 261 0. 285 0. 290 0. 345 0. 328 0. 295 C(XDB , XDM) 0. 021 0. 029 0. 011 0. 013 0. 024 0. 036 0. 029 C(XDM , XDN) 0. 801 0. 783 0. 820 0. 863 0. 802 0. 834 0. 806 C(XDN , XDM) 0. 013 0. 017 0. 009 0. 005 0. 018 0. 008 0. 014 C(XDM , XCS) 0. 602 0. 316 0. 713 0. 256 0. 416 0. 378 0. 308 C(XCS , XDM) 0. 017 0. 019 0. 019 0. 028 0. 024 0. 145 0. 218 第 5 期 钱淑渠 ,等 :动态多目标免疫优化算法及性能测试研究 · 57 ·
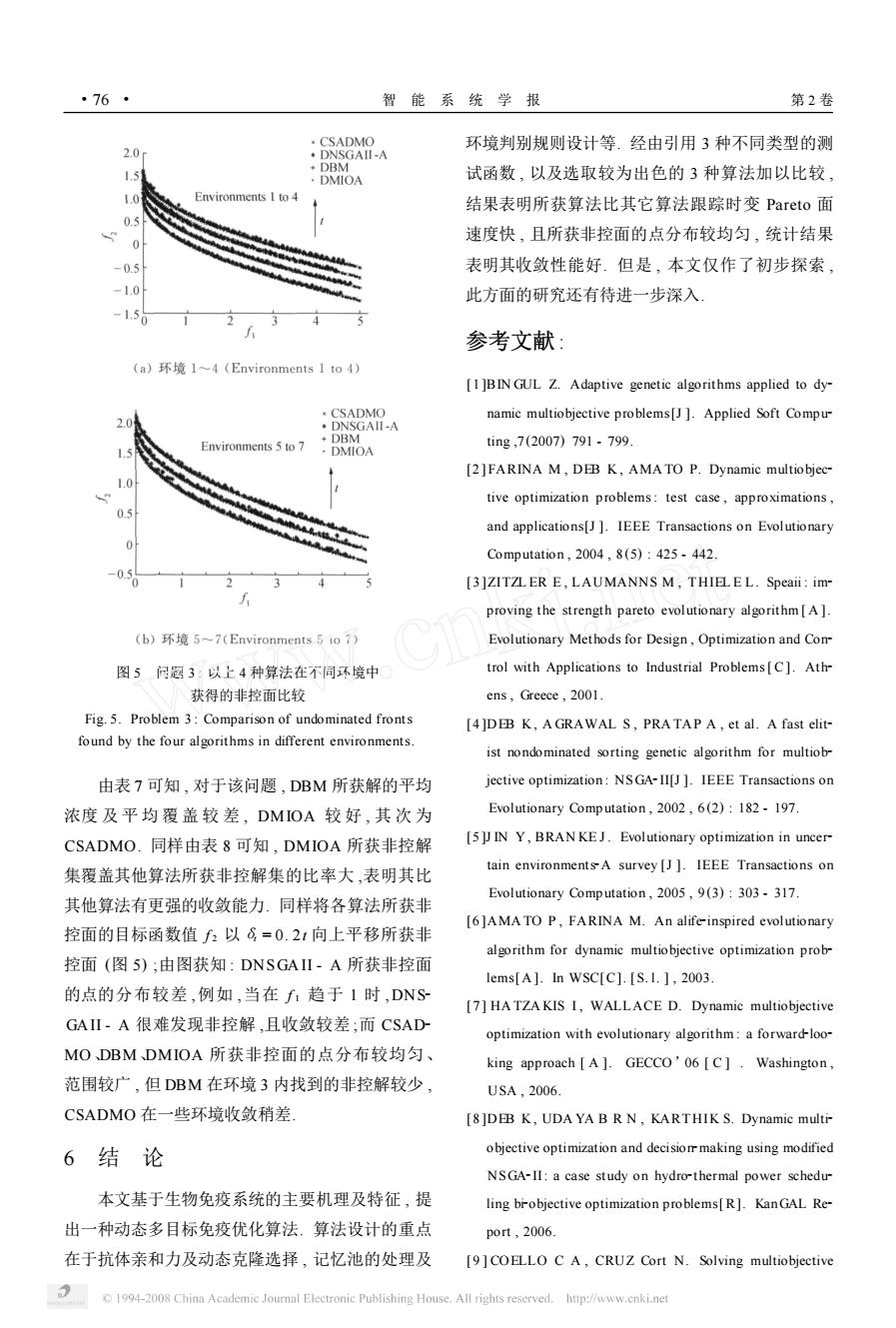
·76· 智能系统学报 第2卷 CSADMO 环境判别规则设计等.经由引用3种不同类型的测 2.0 ·DNSGAII-A 1.5 DBM ·DMIOA 试函数,以及选取较为出色的3种算法加以比较, 1.0 Environments I to 4 结果表明所获算法比其它算法跟踪时变Pareto面 0.5 速度快,且所获非控面的点分布较均匀,统计结果 0 -0.5 表明其收敛性能好.但是,本文仅作了初步探索, -1.0 此方面的研究还有待进一步深入 参考文献: (a)环境1~4(Environments1to4) [1]BIN GUL Z.Adaptive genetic algorithms applied to dy- CSADMO namic multiobjective problems[J].Applied Soft Compu ·DNSGAII-A Environments 5 to 7 DBM ting,7(2007)791-799 ·DMIOA [2]FARINA M,DEB K,AMATO P.Dynamic multiobjec- tive optimization problems:test case,approximations, and applications[J ]IEEE Transactions on Evolutionary Computation,2004,8(5):425.442. (3]ZITZL ER E,LAUMANNS M,THIELEL.Speaii:im- proving the strength pareto evolutionary algorithm[A]. (b)环境5~7(Environments5to7) Evolutionary Methods for Design,Optimization and Con- 图5问题3:以上4种算法在不同环境中 trol with Applications to Industrial Problems [C].Ath 获得的非控面比较 ens,Greece,2001. Fig.5.Problem 3:Comparison of undominated fronts [4]DEB K,A GRAWAL S,PRATAP A,et al.A fast elit- found by the four algorithms in different environments. ist nondominated sorting genetic algorithm for multiob- 由表7可知,对于该问题,DBM所获解的平均 jective optimization:NSGA-II[J ]IEEE Transactions on 浓度及平均覆盖较差,DMIOA较好,其次为 Evolutionary Computation,2002,6(2):182-197. CSADMO.同样由表8可知,DMIOA所获非控解 [5J IN Y,BRANKEJ.Evolutionary optimization in uncer- 集覆盖其他算法所获非控解集的比率大,表明其比 tain environmentsA survey [J].IEEE Transactions on Evolutionary Computation,2005,9(3):303-317 其他算法有更强的收敛能力.同样将各算法所获非 [6]AMA TO P,FARINA M.An alife-inspired evolutionary 控面的目标函数值f2以6=0.2t向上平移所获非 algorithm for dynamic multiobjective optimization prob- 控面(图5);由图获知:DNSGAII-A所获非控面 lems[A].In WSC[C].[S.1.]2003. 的点的分布较差,例如,当在f1趋于1时,DNS [7]HA TZA KIS I,WALLACE D.Dynamic multiobjective GAⅡ-A很难发现非控解,且收敛较差;而CSAD optimization with evolutionary algorithm:a forward-loo- MO DBM DMIOA所获非控面的点分布较均匀、 king approach [A ]GECCO'06 [C].Washington, 范围较广,但DBM在环境3内找到的非控解较少, USA,2006. CSADMO在一些环境收敛稍差 [8]DEB K,UDA YA B R N,KARTHIK S.Dynamic multi- 6结论 objective optimization and decisiomaking using modified NSGA-II:a case study on hydro-thermal power schedu- 本文基于生物免疫系统的主要机理及特征,提 ling br-objective optimization problems[R].KanGAL Re- 出一种动态多目标免疫优化算法.算法设计的重点 p0rt,2006. 在于抗体亲和力及动态克隆选择,记忆池的处理及 [9]COELLO C A,CRUZ Cort N.Solving multiobjective 1994-2008 China Academie Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 5 问题 3 : 以上 4 种算法在不同环境中 获得的非控面比较 Fig. 5. Problem 3 : Comparison of undominated fronts found by the four algorithms in different environments. 由表 7 可知 , 对于该问题 , DBM 所获解的平均 浓度 及 平 均 覆 盖 较 差 , DMIOA 较 好 , 其 次 为 CSADMO. 同样由表 8 可知 , DMIOA 所获非控解 集覆盖其他算法所获非控解集的比率大 ,表明其比 其他算法有更强的收敛能力. 同样将各算法所获非 控面的目标函数值 f 2 以δt = 0. 2t 向上平移所获非 控面 (图 5) ;由图获知 : DNSGAII - A 所获非控面 的点的分布较差 ,例如 ,当在 f 1 趋于 1 时 ,DNS2 GAII - A 很难发现非控解 ,且收敛较差 ;而 CSAD2 MO、DBM、DMIOA 所获非控面的点分布较均匀、 范围较广 , 但 DBM 在环境 3 内找到的非控解较少 , CSADMO 在一些环境收敛稍差. 6 结 论 本文基于生物免疫系统的主要机理及特征 , 提 出一种动态多目标免疫优化算法. 算法设计的重点 在于抗体亲和力及动态克隆选择 , 记忆池的处理及 环境判别规则设计等. 经由引用 3 种不同类型的测 试函数 , 以及选取较为出色的 3 种算法加以比较 , 结果表明所获算法比其它算法跟踪时变 Pareto 面 速度快 , 且所获非控面的点分布较均匀 , 统计结果 表明其收敛性能好. 但是 , 本文仅作了初步探索 , 此方面的研究还有待进一步深入. 参考文献 : [1 ]BIN GUL Z. Adaptive genetic algorithms applied to dy2 namic multiobjective problems[J ]. Applied Soft Compu2 ting ,7 (2007) 791 - 799. [2 ] FARINA M , DEB K , AMA TO P. Dynamic multiobjec2 tive optimization problems: test case , approximations , and applications[J ]. IEEE Transactions on Evolutionary Computation , 2004 , 8 (5) : 425 - 442. [3 ]ZITZL ER E , LAUMANNS M , THIEL E L. Speaii : im2 proving the strength pareto evolutionary algorithm[ A ]. Evolutionary Methods for Design , Optimization and Con2 trol with Applications to Industrial Problems[ C]. Ath2 ens , Greece , 2001. [4 ]DEB K , A GRAWAL S , PRA TAP A , et al. A fast elit2 ist nondominated sorting genetic algorithm for multiob2 jective optimization : NSGA2II[J ]. IEEE Transactions on Evolutionary Computation , 2002 , 6 (2) : 182 - 197. [5 ]J IN Y, BRAN KE J. Evolutionary optimization in uncer2 tain environments2A survey [J ]. IEEE Transactions on Evolutionary Computation , 2005 , 9 (3) : 303 - 317. [6 ]AMA TO P , FARINA M. An alife2inspired evolutionary algorithm for dynamic multiobjective optimization prob2 lems[A ]. In WSC[C]. [ S. l. ] , 2003. [7 ] HA TZA KIS I , WALLACE D. Dynamic multiobjective optimization with evolutionary algorithm : a forward2loo2 king approach [ A ]. GECCO’06 [ C ] . Washington , USA , 2006. [ 8 ]DEB K , UDA YA B R N , KARTHIK S. Dynamic multi2 objective optimization and decision2making using modified NSGA2II: a case study on hydro2thermal power schedu2 ling bi2objective optimization problems[ R]. KanGAL Re2 port , 2006. [9 ] COELLO C A , CRUZ Cort N. Solving multiobjective · 67 · 智 能 系 统 学 报 第 2 卷

第5期 钱淑渠,等:动态多目标免疫优化算法及性能测试研究 ·77· optimization problems using an aritificial immune system 作者简介: [J ]Genetic Programming and Evolvable Machine, 2005,6:163,190. 钱淑渠,男,1978年生,硕士,主 [10]SHANGR H,JIAOL C,GONG M G,et al.Clonal 要研究方向为智能算法 selection algorithm for dynamic multiobjective optimiza- tion[A].CIS 2005[C].Berlin:Springer-Verlag,2005. [11]黄席越,张著洪,何传江,等.现代智能算法理论及应 用[M].北京:科学出版社,2005. 张著洪,男,1966年生,副教授, 工学博士,主要研究方向为控制理论 与计算智能。 E mail sci.zhzhang @gzu.edu.cn. IEEE International Conference on Information and Automation Main Theme: The ICIA 2008 is renamed from the IEEE International Conference on Information Acquisition to provide a forum for researchers in the interdisciplinary areas of information and automation sciences and engineering. The theme of this conference is"Integration of information technologies and automation".All accepted pa- pers will be EFindexed. Cosponsors: IEEE Robotics and Automation Society National University of Defense Technology Chinese University of Hong Kong Chinese Academy of Sciences Important Dates: January 15,2008 Submission of full papers February 28,2008 Proposals of workshops/tutorials March 15,2008 Paper acceptance April 15,2008 Final Paper Submission Secretariat: Miss Pat Chan Department of Mechanical and Automation Engineering, The Chinese University of Hong Kong,Shatin,NT,Hong Kong Tcl:(852)-26098056,Fax:(852)26003.6002 Email:pchan @mae.cuhk.edu.hk 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
optimization problems using an aritificial immune system [J ]. Genetic Programming and Evolvable Machine , 2005 , 6 :163 - 190. [10 ]SHAN G R H , J IAO L C , GON G M G, et al. Clonal selection algorithm for dynamic multiobjective optimiza2 tion[ A ]. CIS 2005[C]. Berlin : Springer2Verlag , 2005. [11 ]黄席越 , 张著洪 , 何传江 ,等. 现代智能算法理论及应 用[ M]. 北京 : 科学出版社 , 2005. 作者简介 : 钱淑渠 , 男 , 1978 年生 ,硕士 , 主 要研究方向为智能算法. 张著洪 , 男 , 1966 年生 , 副教授 , 工学博士 , 主要研究方向为控制理论 与计算智能. E2mail :sci. zhzhang @gzu. edu. cn. IEEE International Conference on Information and Automation Main Theme : The ICIA 2008 is renamed from t he IEEE International Conference on Information Acquisition to provide a forum for researchers in t he interdisciplinary areas of information and automation sciences and engineering. The t heme of t his conference is " Integration of information technologies and automation" . All accepted pa2 pers will be EI2indexed. Co2sponsors : IEEE Robotics and Automation Society - National University of Defense Technology - Chinese University of Hong Kong - Chinese Academy of Sciences Important Dates : J anuary 15 , 2008 Submission of f ull papers February 28 , 2008 Proposals of workshop s/ tutorials March 15 , 2008 Paper acceptance April 15 , 2008 Final Paper Submission Secretariat : Miss Pat Chan Department of Mechanical and Automation Engineering , The Chinese University of Hong Kong , Shatin , N T , Hong Kong Tel : (852) - 26098056 , Fax : (852) 26003 - 6002 Email : pchan @mae. cuhk. edu. hk 第 5 期 钱淑渠 ,等 :动态多目标免疫优化算法及性能测试研究 · 77 ·