
第2卷第3期 智能系统学报 Vol.2№3 2007年6月 CAAI Transactions on Intelligent Systems Jun.2007 一种局加权的二维主成分分析算法 及其在人脸识别中的应用 金一,阮秋琦 (北京交通大学计算机与信息技术学院,北京100044) 摘要:提出了一种将局部特征加权与二维主成分分析相结合的局部加权的二维主成分分析方法.引入了二维局部 加权特征子空间的概念,将各类样本映射到这个局部加权特征子空间,再通过计算测试样本到加权子空间的距离进 行样本的分类.使用这种方法在OL人脸库上进行测试,结果表明,经过局部特征加权的二维主成分分析方法比普 通的二维主成分分析方法具有更优的性能,并且在提高识别率的同时算法的复杂程度并没有明显增加 关键词:二维主成分分析;局部加权;人脸识别;加权特征提取 中图分类号:TP391.4文献标识码:A文章编号:16734785(2007)03-002505 A partially weighted two dimensional PCA for face recognition JIN Yi,RUAN Qiurqi (College of Computer and Information Technology,Beijing Jiaotong University,Beijing 100044,China) Abstract:This paper proposes face recognition software that uses two-dimensional principal component a- nalysis(2DPCA)in conjunction with partial feature weighting by applying two-dimensional partial-weigh- ting to the characteristic subspace.First faces are mapped onto this partially weighted 2DPCA subspace, then the samples are classified by calculating the distance from the samples to the partially weighted 2DPCA subspace.To test this new method,ORL face databases were used and it was found that the rec- ognition rate was higher than with either 2DPCA or PCA and the computational complexity did not in- crease significantly. Key words:two-dimensional principal component analysis;partially-weighted;face recognition;weighted feature extraction 近年来,人脸识别技术因其在公安、海关、交通、 人脸识别领域取得较大成功以后,便引起人们的广 金融、医疗等领域具有广阔的发展前景和很高的社 泛关注.主成分分析法(PCA)以及随后出现的线性 会经济效益而备受关注.基于静止图像的人脸识别 判别式分析(linear discriminant analysis,LDA)B側、 受光照、表情、姿态、年龄等众多因素的影响,因此, 独立元分析(independent component analysis, 如何进行特征选择以及如何提取最有效特征就成为 ICA)等方法,其思想都是1寻找一个线性或非线 人脸识别研究领域的一个首要问题 性的空间变换,把人脸图像映射到一个低维子空间, 主成分分析法(principal component analysis, 使数据在子空间中的分布更加紧凑,从而抽取人脸 PCA)作为人脸特征提取和识别领域的一个经典算 图像的关键特征.但这些算法往往需要将二维人脸 法,在rby等和Turk等首次提出并应用于 图像表示成一个较长的一维矢量形式,图像矢量空 间的维数过高,使人脸图像特征抽取困难,并容易导 收稿日期:20060908. 基金项目:国家重点基础研究发展计划(973)资助项目 致运算复杂以及出现奇异矩阵.基于以上原因 (2004BC318005);教育部博士点基金资助项目 Yang]等人提出了一种将二维图像矩阵直接映射 (60472033). 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
第 2 卷第 3 期 智 能 系 统 学 报 Vol. 2 №. 3 2007 年 6 月 CAA I Transactions on Intelligent Systems J un. 2007 一种局部加权的二维主成分分析算法 及其在人脸识别中的应用 金 一 , 阮秋琦 (北京交通大学 计算机与信息技术学院 ,北京 100044) 摘 要 :提出了一种将局部特征加权与二维主成分分析相结合的局部加权的二维主成分分析方法. 引入了二维局部 加权特征子空间的概念 ,将各类样本映射到这个局部加权特征子空间 ,再通过计算测试样本到加权子空间的距离进 行样本的分类. 使用这种方法在 ORL 人脸库上进行测试 ,结果表明 ,经过局部特征加权的二维主成分分析方法比普 通的二维主成分分析方法具有更优的性能 ,并且在提高识别率的同时算法的复杂程度并没有明显增加. 关键词 :二维主成分分析 ;局部加权 ;人脸识别 ;加权特征提取 中图分类号 : TP391. 4 文献标识码 :A 文章编号 :167324785 (2007) 0320025205 A partially weighted two2dimensional PCA for face recognition J IN Yi , RUAN Qiu2qi (College of Computer and Information Technology , Beijing Jiaotong University , Beijing 100044 , China) Abstract :This paper proposes face recognition software t hat uses two2dimensional principal component a2 nalysis (2DPCA) in conjunction wit h partial feat ure weighting by applying two2dimensional partial2weigh2 ting to the characteristic subspace. First faces are mapped onto t his partially weighted 2DPCA subspace , t hen the samples are classified by calculating t he distance from the samples to t he partially weighted 2DPCA subspace. To test this new met hod , ORL face databases were used and it was found t hat t he rec2 ognition rate was higher than wit h eit her 2DPCA or PCA and t he comp utational complexity did not in2 crease significantly. Keywords : two2dimensional principal component analysis; partially2weighted ; face recognition ; weighted feat ure extraction 收稿日期 :2006209208. 基金 项 目 : 国 家 重 点 基 础 研 究 发 展 计 划 ( 973 ) 资 助 项 目 (2004BC318005 ) ; 教 育 部 博 士 点 基 金 资 助 项 目 (60472033) . 近年来 ,人脸识别技术因其在公安、海关、交通、 金融、医疗等领域具有广阔的发展前景和很高的社 会经济效益而备受关注. 基于静止图像的人脸识别 受光照、表情、姿态、年龄等众多因素的影响 ,因此 , 如何进行特征选择以及如何提取最有效特征就成为 人脸识别研究领域的一个首要问题. 主成分分析法 (p rincipal component analysis , PCA) 作为人脸特征提取和识别领域的一个经典算 法 ,在 Kirby 等[1 ] 和 Turk 等[2 ] 首次提出并应用于 人脸识别领域取得较大成功以后 ,便引起人们的广 泛关注. 主成分分析法 (PCA) 以及随后出现的线性 判别式分析(linear discriminant analysis , LDA) [3 ] 、 独 立 元 分 析 ( independent component analysis , ICA) [4 ]等方法 ,其思想都是[ 5 ] 寻找一个线性或非线 性的空间变换 ,把人脸图像映射到一个低维子空间 , 使数据在子空间中的分布更加紧凑 ,从而抽取人脸 图像的关键特征. 但这些算法往往需要将二维人脸 图像表示成一个较长的一维矢量形式 ,图像矢量空 间的维数过高 ,使人脸图像特征抽取困难 ,并容易导 致运算复杂以及出现奇异矩阵. 基于以上原因 , Yang [6 ]等人提出了一种将二维图像矩阵直接映射 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·26 智能系统学报 第2卷 于子空间的方法,并将其称之为二维主成分分析法 J(X)=X GX. 7 (2DPCA).2DPCA不用将二维矩阵事先转换成一 通过计算G的前d个最大特征值所对应的单位特 维向量,它计算的斜方差矩阵比PCA要小,因此 征向量,可以得到最佳的投影矩阵 2DPCA比PCA更能精确计算斜方差矩阵,而且计 2DPCA在特征抽取的过程中,并没有将人脸图 算特征向量所需要的时间也短一些 像转换成一列,而是直接投影在G,的前d个最大特 文中在二维主成分分析的基础上进行了改进, 征值所对应的单位特征向量上: 并提出了局部加权的二维主成分分析算法(PW- Y=AXk,k=1,2,…,d (8) 2DPCA),其思想是对人脸(大致在眼眉以下鼻尖以 得到的特征向量Y…Ya用U=[Y,…Ya表 上部分)的每一维特征设定一个加权系数,仍然按照 示,即为2DPCA所抽取的人脸图像的特征矩阵.易 二维图像矩阵进行计算,并以局部加权重建误差最 知U是一个mXd的图像矩阵 小为目标,计算出局部加权子空间,再根据测试样本 2 局部加权的二维主成分分析算法 点到加权子空间的距离进行分类 2DPCA与传统PCA相比,2DPCA使用图像矩 1 2DPCA算法[6 阵直接计算,其抽取的图像矩阵精确度有所提高,复 设X为一个n维单位量化的列矢量,A为一个 杂度有所降低,但是与PCA相似的是,2DPCA同样 mXn的图像矩阵,A通过线性变换: 是平等对待了人脸的每一维特征.大量心理学和生 Y=AX 1) 理学研究表明,人脸在被识别过程中,各个器官的重 直接投影到X上.于是,得到一个m维列向量Y,称 要程度是不同的,人脸的上半部分,特别是人眼所占 之为图像A的投影特征向量. 的比重相对较大.在已有的WPCA算法1中,它以 寻找一个最优的投影特征向量,使得图像A在 牺牲轮廓特征为代价,强调了某些五官特征,而根据 X方向上投影后得到的特征向量的总体离散度最 文献[2],轮廓特征在人脸识别中亦占据相当大的比 大,这个总体离散度可以通过计算其斜方差的特征 重,因此,文中根据加权2DPCA重建误差最小原 值所对应的特征向量得到: 理,提出了局部加权的二维主成分分析算法.此算法 J(X)X"S,X. 2) 取人脸大致在眼眉以下鼻尖以上部分进行局部加 斜方差矩阵表示如下: 权,既考虑到人眼作为人脸图像的关键部位的重要 S,E(Y-EY(Y-EYT 作用,又没有丢失人脸图像的整体轮廓信息 2.1局部加权2DPCA算法求解最优投影矩阵 E[AX-E(AX)[AX-E(AX)= 3) 设V=[X,…X]为变换子空间的基,U= El(A-EA X][(A-EA)X]T. Y,,YaJ为低维投影矩阵,加权的2DPCA以寻 矩阵的迹为 找最小化训练样本的重建误差的变换矩阵V为目 J(X)X [E(A-EA(A-EA X. (4) 标 因此,图像矩阵的总体散布矩阵可以表示为 G.=E(A-EA(A-EA) W=∑IA+Vw)-AP= (5) 易证,G是非奇异的,且G是一个n×n的矩阵 ((4 +VU)N((+VU).N.(9 设人脸图像有C个类,M幅训练样本,第i类 考虑到各维特征在人脸识别中所起作用不同 有训练样本图像n,个:Aa,A2,Am,训练样本 可以为每一维特征指定一个系数来代表其重要程 总数M=,样本均值为石=立,4易知 度.构造样本A:的加权重建误差计算公式: J(V.A)=wi((A +VUv).A)= 6 ((A,+VUg)-A)W((A,+VUg)-A). 此时,J(可以表示为 (10) 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
于子空间的方法 ,并将其称之为二维主成分分析法 (2DPCA) . 2DPCA 不用将二维矩阵事先转换成一 维向量 ,它计算的斜方差矩阵比 PCA 要小 ,因此 2DPCA 比 PCA 更能精确计算斜方差矩阵 ,而且计 算特征向量所需要的时间也短一些. 文中在二维主成分分析的基础上进行了改进 , 并提出了局部加权的二维主成分分析算法 (PW - 2DPCA) ,其思想是对人脸(大致在眼眉以下鼻尖以 上部分) 的每一维特征设定一个加权系数 ,仍然按照 二维图像矩阵进行计算 ,并以局部加权重建误差最 小为目标 ,计算出局部加权子空间 ,再根据测试样本 点到加权子空间的距离进行分类. 1 2DPCA 算法[ 6 ] 设 X为一个 n 维单位量化的列矢量 , A 为一个 m ×n 的图像矩阵 , A 通过线性变换 : Y = AX (1) 直接投影到 X上. 于是 ,得到一个 m 维列向量 Y,称 之为图像 A 的投影特征向量. 寻找一个最优的投影特征向量 ,使得图像 A 在 X 方向上投影后得到的特征向量的总体离散度最 大 ,这个总体离散度可以通过计算其斜方差的特征 值所对应的特征向量得到 : J ( X) = X T S x X. (2) 斜方差矩阵表示如下 : S x = E( Y - EY) ( Y - EY) T = E[ AX - E( AX) ][ AX - E( AX) ] T = (3) E[ ( A - EA) X][ ( A - EA) X] T . 矩阵的迹为 J ( X) = X T [ E( A - EA) T ( A - EA) ] X. (4) 因此 ,图像矩阵的总体散布矩阵可以表示为 Gt = E( A - EA) T ( A - EA) . (5) 易证 , Gt 是非奇异的 ,且 Gt 是一个 n ×n 的矩阵. 设人脸图像有 C 个类 , M 幅训练样本 ,第 i 类 有训练样本图像 ni 个 : A i1 , A i2 , ……, A in ,训练样本 总数 M = ∑ c i = 1 ni ,样本均值为 A = 1 M ∑ M i = 1 A i ,易知 Gt = 1 M ∑ M i = 1 ( A i - A) T ( A i - A) . (6) 此时 , J ( X) 可以表示为 J ( X) = X T Gt X. (7) 通过计算 Gt 的前 d 个最大特征值所对应的单位特 征向量 ,可以得到最佳的投影矩阵. 2DPCA 在特征抽取的过程中 ,并没有将人脸图 像转换成一列 ,而是直接投影在 Gt 的前 d 个最大特 征值所对应的单位特征向量上 : Yk = AXk , k = 1 ,2 , …, d. (8) 得到的特征向量 Y1 …, Yd 用 U = [ Y1 , …, Yd ]表 示 ,即为 2DPCA 所抽取的人脸图像的特征矩阵. 易 知 U 是一个 m ×d 的图像矩阵. 2 局部加权的二维主成分分析算法 2DPCA 与传统 PCA 相比 ,2DPCA 使用图像矩 阵直接计算 ,其抽取的图像矩阵精确度有所提高 ,复 杂度有所降低 ,但是与 PCA 相似的是 ,2DPCA 同样 是平等对待了人脸的每一维特征. 大量心理学和生 理学研究表明 ,人脸在被识别过程中 ,各个器官的重 要程度是不同的 ,人脸的上半部分 ,特别是人眼所占 的比重相对较大. 在已有的 WPCA 算法[10 ] 中 ,它以 牺牲轮廓特征为代价 ,强调了某些五官特征 ,而根据 文献[ 2 ] ,轮廓特征在人脸识别中亦占据相当大的比 重 ,因此 ,文中根据加权 2DPCA 重建误差最小原 理 ,提出了局部加权的二维主成分分析算法. 此算法 取人脸大致在眼眉以下鼻尖以上部分进行局部加 权 ,既考虑到人眼作为人脸图像的关键部位的重要 作用 ,又没有丢失人脸图像的整体轮廓信息. 2. 1 局部加权 2 D PCA 算法求解最优投影矩阵 设 V = [ X1 , …, Xd ]为变换子空间的基 , U = [ Y1 , …, Yd ]为低维投影矩阵 ,加权的 2DPCA 以寻 找最小化训练样本的重建误差的变换矩阵 V 为目 标 : J 1 (V) = ∑ P k =1 ‖( A + VU) - A ‖2 = ∑ P k = 1 ( ( A + VU) - A) T ( ( A + VU) - A) . (9) 考虑到各维特征在人脸识别中所起作用不同 , 可以为每一维特征指定一个系数来代表其重要程 度. 构造样本 A i 的加权重建误差计算公式 : J 2 (V′, A i) = ∑j w j ( ( A j + VUkj ) - A ij ) 2 = ( ( A j + VU kj ) - A ij ) T W ( ( A j + VUkj ) - A ij ) . (10) · 62 · 智 能 系 统 学 报 第 2 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第3期 金一,等:一种局部加权的二维主成分分析算法及其在人脸识别中的应用 ·27 式中w为加权对角矩阵 2DPCA算法得到的特征矩阵是一个二维矢量 0 2.3分类 W= ,4++…+n=n,寻找最优 通过局部加权2DPCA得到的特征矩阵,每一 0 幅人脸图像A都对应一个特征矩阵U,U=AV.因此 矩阵V',使得所有训练样本的加权重建误差和 可以利用最近邻法,计算每一幅测试样本与训练样 J1V)最小: 本之间的欧式距离,求出与测试样本图像欧式距离 J2N)=∑J2N',AW= 最近的训练样本图像所对应类,即为该人脸所属的 (A.4)VV-wV.D (A..4. 类 对于测试样本A,计算: 11) dw(A,W=,mi吗,dw(A,W,I5 实现算法时,可以通过寻优的方法直接计算加 则可以知道A所属的类别 权主元分析的变换矩阵V',不过这种方法运算比较 麻烦,为此在实际中,给出了一个近似算法,试验证 3试验与分析 明,这种方法同样能达到较理想的效果 文中使用的是一个具有双中心的高斯分布的函 对于一定的加权系数对角阵W,定义其加权协 数?作为加权函数对人脸图像的各维特征进行局 方差矩阵如下: 部加权,该函数为 Sx El(A-EA)X/WI(A-EA XJ.(12) 32+小-y21-)2+小21 因此,图像矩阵的总体散布矩阵可以表示为 0(i,j》=e 修 (16) G-(7w(. 13) 该函数称之为羽化函数,其特点是中间值大,文 献8中将2个羽化中心一处放在眉心(双眼连线的 但是,通过仿真试验发现,全局加权的2DPCA 中心)位置用以强调眼部信息,另外一处是嘴巴部 效果并不理想,原因是它丢失了对于识别人脸来说 位,增强嘴部的重要特征信息.文中所采用的局部加 很重要的全局信息,比如脸的轮廓可能被覆盖,因此 权2DPCA,由于它在强调双眼重要信息的同时,保 提出了局部加权的图像总体散布矩阵概念, 留了人脸轮廓信息,所以它对应的2个中心则应该 由上述推导,定义二维局部加权的图像总体散 是双眼所在的大致位置 布矩阵 3.1基于ORL人脸库的试验 M j-(p.0) o=,刀4a,+ OL人脸库是由英国剑桥大学建立,包括40 1-. J-(9.0) 人,每人10张照片,包括表情变化,微小姿态变化 ∑(Ag-A)TW(A)·A)+ 1-(pT,0 20%以内的尺度变化,戴眼镜与不戴眼镜的变化,比 j-fm.0) 较充分地反应了同一人不同人脸图像的变化和差 ∑(Ag-A)T(Ag·A)1 (14) j-(T.0 异.图像的大小均为11292.图1是ORL人脸库 式中:p、q为图像矩阵的第p、g行 的一些人脸的照片 求得的G,较大的特征值所对应的前d个特征 向量构成二维加权子空间的基V',即为局部加权的 2DPCA的最优投影矩阵 2.2局部加权2DPCA特征提取 求得局部加权的2DPCA的最优投影矩阵,可 用于特征提取.A为样本人脸图像,由 Y=AXk,k=1,2,…d, 可得投影特征矢量U'=[Y,Y?,Ya7即为图像 图1ORL人脸库的10个样本 样本A的局部加权二维主成分,显然局部加权 Fig.I 10 samples of the ORL face database 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
式中 :W 为加权对角矩阵 , W = ω1 0 ω 0 ωn ,ω1 +ω2 + …+ωn = n ,寻找最优 矩阵 V′, 使得所有训练样本的加权重建误差和 J 1 (V) 最小 : J 2 (V′) = ∑i J 2 (V′, A i) = ∑i ( A i - A) T (V′V′T - I) W (V′V′T - I) ( A i - A) . (11) 实现算法时 ,可以通过寻优的方法直接计算加 权主元分析的变换矩阵 V′,不过这种方法运算比较 麻烦 ,为此在实际中 ,给出了一个近似算法 ,试验证 明 ,这种方法同样能达到较理想的效果. 对于一定的加权系数对角阵 W ,定义其加权协 方差矩阵如下 : S x = E[ (A - EA) X ]W[ (A - EA) X] T . (12) 因此 ,图像矩阵的总体散布矩阵可以表示为 Gt = 1 M ∑ M i =1 ( Ai - A) TW( A i - A) . (13) 但是 ,通过仿真试验发现 ,全局加权的 2DPCA 效果并不理想 ,原因是它丢失了对于识别人脸来说 很重要的全局信息 ,比如脸的轮廓可能被覆盖 ,因此 提出了局部加权的图像总体散布矩阵概念. 由上述推导 ,定义二维局部加权的图像总体散 布矩阵 : G′t = 1 M ∑ M i =1 [ ∑ j = ( p ,0) j = (0 ,0) ( A ij - A) T ( Aij - A) + ∑ j = ( q,0) j = ( p+1 ,0) ( A ij - A) TW( A ij - A) + ∑ j = ( m ,0) j = ( q+1 ,0) ( A ij - A) T ( A ij - A) ]. (14) 式中 : p、q 为图像矩阵的第 p 、q 行. 求得的 G′t 较大的特征值所对应的前 d 个特征 向量构成二维加权子空间的基 V′,即为局部加权的 2DPCA 的最优投影矩阵. 2. 2 局部加权 2 D PCA 特征提取 求得局部加权的 2DPCA 的最优投影矩阵 ,可 用于特征提取. A 为样本人脸图像 ,由 Y′k = AX′k , k = 1 ,2 , …, d , 可得投影特征矢量 U′= [ Y′1 , Y′2 , …Y′d ]即为图像 样本 A 的局部加权二维主成分 , 显然局部加权 2DPCA 算法得到的特征矩阵是一个二维矢量. 2. 3 分 类 通过局部加权 2DPCA 得到的特征矩阵 ,每一 幅人脸图像 A 都对应一个特征矩阵 U ,U = AV. 因此 可以利用最近邻法 ,计算每一幅测试样本与训练样 本之间的欧式距离 ,求出与测试样本图像欧式距离 最近的训练样本图像所对应类 ,即为该人脸所属的 类. 对于测试样本 A ,计算 : dNN ( A ω3 i 3 , A) = min l ≤ω≤N min l ≤i ≤n i d NN ( A ω i , A) , (15) 则可以知道 A 所属的类别. 3 试验与分析 文中使用的是一个具有双中心的高斯分布的函 数[11 ]作为加权函数对人脸图像的各维特征进行局 部加权 ,该函数为 ω( i , j) = e - [ (i- x 1 ) 2 +( j- y 1 ) 2 ][ (i- x 2 ) 2 +( j- y 2 ) 2 ] σ2 1σ2 2 . (16) 该函数称之为羽化函数 ,其特点是中间值大 ,文 献[8 ]中将 2 个羽化中心一处放在眉心(双眼连线的 中心) 位置用以强调眼部信息 ,另外一处是嘴巴部 位 ,增强嘴部的重要特征信息. 文中所采用的局部加 权 2DPCA ,由于它在强调双眼重要信息的同时 ,保 留了人脸轮廓信息 ,所以它对应的 2 个中心则应该 是双眼所在的大致位置. 3. 1 基于 ORL 人脸库的试验 ORL 人脸库是由英国剑桥大学建立 ,包括 40 人 ,每人 10 张照片 ,包括表情变化 ,微小姿态变化 , 20 %以内的尺度变化 ,戴眼镜与不戴眼镜的变化 ,比 较充分地反应了同一人不同人脸图像的变化和差 异. 图像的大小均为 112 ×92. 图 1 是 ORL 人脸库 的一些人脸的照片. 图 1 ORL 人脸库的 10 个样本 Fig. 1 10 samples of the ORL face database 第 3 期 金 一 ,等 :一种局部加权的二维主成分分析算法及其在人脸识别中的应用 · 72 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
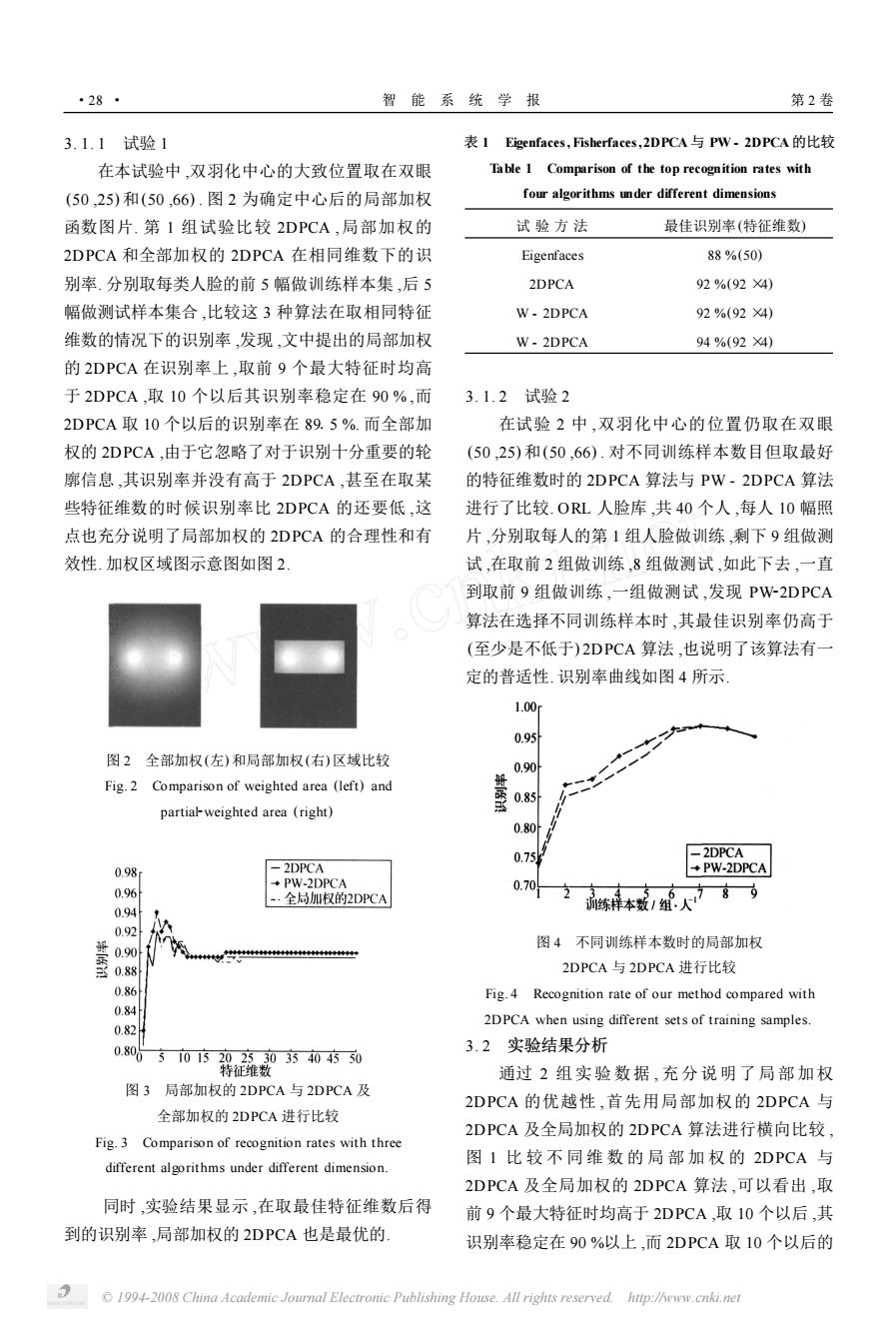
·28 智能系统学报 第2卷 3.1.1试验1 表1 Eigenfaces,Fisherfaces,2DPCA与PW.2DPCA的比较 在本试验中,双羽化中心的大致位置取在双眼 Table 1 Comparison of the top recognition rates with (50,25)和(50,66).图2为确定中心后的局部加权 four algorithms under different dimensions 函数图片.第1组试验比较2DPCA,局部加权的 试验方法 最佳识别率(特征维数) 2DPCA和全部加权的2DPCA在相同维数下的识 Eigenfaces 88%(50) 别率.分别取每类人脸的前5幅做训练样本集,后5 2DPCA 92%(92×4) 幅做测试样本集合,比较这3种算法在取相同特征 W-2DPCA 92%(92X4) 维数的情况下的识别率,发现,文中提出的局部加权 W-2DPCA 94%(92X4)】 的2DPCA在识别率上.,取前9个最大特征时均高 于2DPCA,取10个以后其识别率稳定在90%,而 3.1.2试验2 2DPCA取10个以后的识别率在89.5%.而全部加 在试验2中,双羽化中心的位置仍取在双眼 权的2DPCA,由于它忽略了对于识别十分重要的轮 (50,25)和(50,66).对不同训练样本数目但取最好 廓信息,其识别率并没有高于2DPCA,甚至在取某 的特征维数时的2DPCA算法与PW-2DPCA算法 些特征维数的时候识别率比2DPCA的还要低,这 进行了比较.ORL人脸库,共40个人,每人10幅照 点也充分说明了局部加权的2DPCA的合理性和有 片,分别取每人的第1组人脸做训练,剩下9组做测 效性.加权区域图示意图如图2 试,在取前2组做训练,8组做测试,如此下去,一直 到取前9组做训练,一组做测试,发现PW-2DPCA 算法在选择不同训练样本时,其最佳识别率仍高于 (至少是不低于)2DPCA算法,也说明了该算法有一 定的普适性.识别率曲线如图4所示 1.00 0.95 图2全部加权(左)和局部加权(右)区域比较 0.90 Fig.2 Comparison of weighted area (left)and 0.85 partial-weighted area (right) 0.80 0.75 -2DPCA 0.98 -2DPCA PW-2DPCA PW-2DPCA 0.96 0.70 -·全局加权的2DPCA 0.94 0.92 社 图4不同训练样本数时的局部加权 0.90 4炒些44t世 0.88 2DPCA与2DPCA进行比较 0.86 Fig.4 Recognition rate of our method compared with 0.84 0.82 2DPCA when using different sets of training samples. 0.806 3.2实验结果分析 5101520253035404550 特征维数 通过2组实验数据,充分说明了局部加权 图3局部加权的2DPCA与2DPCA及 2DPCA的优越性,首先用局部加权的2DPCA与 全部加权的2DPCA进行比较 2DPCA及全局加权的2DPCA算法进行横向比较 Fig.3 Comparison of recognition rates with three 图1比较不同维数的局部加权的2DPCA与 different algorithms under different dimension. 2DPCA及全局加权的2DPCA算法,可以看出,取 同时,实验结果显示,在取最佳特征维数后得 前9个最大特征时均高于2DPCA,取10个以后,其 到的识别率,局部加权的2DPCA也是最优的 识别率稳定在90%以上,而2DPCA取10个以后的 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved http://www.cnki.net
3. 1. 1 试验 1 在本试验中 ,双羽化中心的大致位置取在双眼 (50 ,25) 和(50 ,66) . 图 2 为确定中心后的局部加权 函数图片. 第 1 组试验比较 2DPCA ,局部加权的 2DPCA 和全部加权的 2DPCA 在相同维数下的识 别率. 分别取每类人脸的前 5 幅做训练样本集 ,后 5 幅做测试样本集合 ,比较这 3 种算法在取相同特征 维数的情况下的识别率 ,发现 ,文中提出的局部加权 的 2DPCA 在识别率上 ,取前 9 个最大特征时均高 于 2DPCA ,取 10 个以后其识别率稳定在 90 % ,而 2DPCA 取 10 个以后的识别率在 8915 %. 而全部加 权的 2DPCA ,由于它忽略了对于识别十分重要的轮 廓信息 ,其识别率并没有高于 2DPCA ,甚至在取某 些特征维数的时候识别率比 2DPCA 的还要低 ,这 点也充分说明了局部加权的 2DPCA 的合理性和有 效性. 加权区域图示意图如图 2. 图 2 全部加权(左) 和局部加权(右) 区域比较 Fig. 2 Comparison of weighted area (left) and partial2weighted area (right) 图 3 局部加权的 2DPCA 与 2DPCA 及 全部加权的 2DPCA 进行比较 Fig. 3 Comparison of recognition rates with three different algorithms under different dimension. 同时 ,实验结果显示 ,在取最佳特征维数后得 到的识别率 ,局部加权的 2DPCA 也是最优的. 表 1 Eigenfaces,Fisherfaces,2DPCA与 PW - 2DPCA的比较 Table 1 Comparison of the top recognition rates with four algorithms under different dimensions 试 验 方 法 最佳识别率(特征维数) Eigenfaces 88 %(50) 2DPCA 92 %(92 ×4) W - 2DPCA 92 %(92 ×4) W - 2DPCA 94 %(92 ×4) 3. 1. 2 试验 2 在试验 2 中 ,双羽化中心的位置仍取在双眼 (50 ,25) 和(50 ,66) . 对不同训练样本数目但取最好 的特征维数时的 2DPCA 算法与 PW - 2DPCA 算法 进行了比较. ORL 人脸库 ,共 40 个人 ,每人 10 幅照 片 ,分别取每人的第 1 组人脸做训练 ,剩下 9 组做测 试 ,在取前 2 组做训练 ,8 组做测试 ,如此下去 ,一直 到取前 9 组做训练 ,一组做测试 ,发现 PW22DPCA 算法在选择不同训练样本时 ,其最佳识别率仍高于 (至少是不低于) 2DPCA 算法 ,也说明了该算法有一 定的普适性. 识别率曲线如图 4 所示. 图 4 不同训练样本数时的局部加权 2DPCA 与 2DPCA 进行比较 Fig. 4 Recognition rate of our method compared with 2DPCA when using different sets of training samples. 3. 2 实验结果分析 通过 2 组实验数据 , 充分说明了局部加权 2DPCA 的优越性 ,首先用局部加权的 2DPCA 与 2DPCA 及全局加权的 2DPCA 算法进行横向比较 , 图 1 比 较 不 同 维 数 的 局 部 加 权 的 2DPCA 与 2DPCA 及全局加权的 2DPCA 算法 ,可以看出 ,取 前 9 个最大特征时均高于 2DPCA ,取 10 个以后 ,其 识别率稳定在 90 %以上 ,而 2DPCA 取 10 个以后的 · 82 · 智 能 系 统 学 报 第 2 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第3期 金一,等:一种局部加权的二维主成分分析算法及其在人脸识别中的应用 ·29· 识别率在89.5%.其次,用局部加权的2DPCA与经 [4]BARTL ETT.Face recognition by independent compo- 典的Eigenfaces,及2DPCA进行纵向比较,在最高 nent analysis [J].IEEE Transactions on Neural Net- 正确识别率方面,文中提出的局部加权的2DPCA works,2002,13(6):1450-1464. 算法的最高正确识别率均高于其他几种算法.最后, [5]刘青山.综述人脸识别中的子空间方法U].自动化学报, 2003,129(16):900-912. 文中又比较了不取不同训练样本数时候的局部加权 LIU Qingshan.A survey:subspace analysis for face rec- 的2DPCA与2DPCA算法,其最佳识别率仍高于 ognition[J ]Acta Automatica Sinica,2003,129 (16): (至少是不低于)2DPCA算法,说明了该算法有一定 900.912. 的普适性,3组实验数据同时也证明了这种强调人 [6]YANGJ,ZHANG D,YANG J Y.Two-dimensional 脸重要信息的同时仍然保留人脸轮廓信息的局部加 PCA:A new approach to appearance based face repre- 权概念的有效性 sentation and recognition [J].IEEE Transactions Pattern 4结束语 Anal Machine Intell,2004,26 (1):131-137 [7]乔字,黄席樾,柴毅.基于加权主元分析(WPCA)的 文中在2DPCA的基础上提出了一种新的局部 人脸识别J].重庆大学学报,2004,27(3):28.31. 加权的2DPCA算法,这种方法既考虑到人眼作为 QIAO Yu,HUANG Xiyue,CHAI Yi.Face recognition 人脸图像的关键部位的重要作用,同时并没有丢失 based weighted PCA[J ]Journal of Chongqing Universi- 人脸图像的轮廓信息.文中使用的以双眼为中心的 ty,2004,27(3):28-31. 高斯函数来对特征进行加权,并将其在OL人脸 [8]杨光,阮秋琦.一种新的基于加权主分量分析的人脸识 别算法[A].中国人工智能学会第11届全国学术年会 库上进行测试,结果显示,文中提出的局部加权的二 (CAAI-11)[C].武汉,中国,2005. 维主成分分析方法(PW-2DPCA)比二维主成分分 YANG Guang,RUAN Qiuqi.A new arithmetic of face 析法(2DPCA)在人脸识别中更具优势.它的优点是 recognition based on weighted PCA[A].The 11th China 将局部加权子空间的提取建立在二维特征的提取之 Artificial Intelligence Conference C].Wuhan,China, 上,不仅具有特征抽速快速而准确,还能从一定程度 2005. 上提高正确识别率.但是文中提出的算法,只能靠经 作者简介 验确定加权中心和权重的大致范围,再进行进一步 试验才能确定具体的数值,在今后的研究中,如何自 金一,女,1982年生,博士研究生, 适应地选择加权中心和权重将是一个值得进一步探 主要研究方向为图像处理、模式识别、人 考的问题 脸识别。 E mail jineejin @gmail.com. 参考文献: [1]KIRB Y M,SIROVICH L.Application of the Karhunen Loeve procedure for the characterization of human faces 阮秋琦,男,1944年生,教授,博士生 [J ]IEEE Transactions on Pattern Analysis and Ma- 导师,主要研究方向为图像处理、计算机 chine Intelligence,1990,12 (1):103-108. 视觉、模式识别、虚拟现实.曾多次获得 [2]TURK M,PEN TLAND A.Eigenfaces for recognition 省部级科技进步奖,发表论文150余篇 [J].Journal of Cognitive Neuroscience,1991,3 (1):72 出版专著3部 -86. [3]BEL HUMEUR PN,HESPANHA J P,KRIEGMAN D J.Eigenfaces vs.Fisherface:Recognition using class special linear projection[J ]IEEE Transactions on Pat- tern Analysis and Machine Intelligence,1997,19 (7): 711.720 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
识别率在 8915 %. 其次 ,用局部加权的 2DPCA 与经 典的 Eigenfaces ,及 2DPCA 进行纵向比较 ,在最高 正确识别率方面 ,文中提出的局部加权的 2DPCA 算法的最高正确识别率均高于其他几种算法. 最后 , 文中又比较了不取不同训练样本数时候的局部加权 的 2DPCA 与 2DPCA 算法 ,其最佳识别率仍高于 (至少是不低于) 2DPCA 算法 ,说明了该算法有一定 的普适性 ,3 组实验数据同时也证明了这种强调人 脸重要信息的同时仍然保留人脸轮廓信息的局部加 权概念的有效性. 4 结束语 文中在 2DPCA 的基础上提出了一种新的局部 加权的 2DPCA 算法 ,这种方法既考虑到人眼作为 人脸图像的关键部位的重要作用 ,同时并没有丢失 人脸图像的轮廓信息. 文中使用的以双眼为中心的 高斯函数来对特征进行加权 ,并将其在 ORL 人脸 库上进行测试 ,结果显示 ,文中提出的局部加权的二 维主成分分析方法 (PW22DPCA) 比二维主成分分 析法(2DPCA) 在人脸识别中更具优势. 它的优点是 将局部加权子空间的提取建立在二维特征的提取之 上 ,不仅具有特征抽速快速而准确 ,还能从一定程度 上提高正确识别率. 但是文中提出的算法 ,只能靠经 验确定加权中心和权重的大致范围 ,再进行进一步 试验才能确定具体的数值 ,在今后的研究中 ,如何自 适应地选择加权中心和权重将是一个值得进一步探 考的问题. 参考文献 : [1 ] KIRB Y M , SIROVICH L. Application of the Karhunen Loeve procedure for the characterization of human faces [J ]. IEEE Transactions on Pattern Analysis and Ma2 chine Intelligence , 1990 , 12 (1) : 103 - 108. [2 ] TUR K M , PEN TLAND A. Eigenfaces for recognition [J ]. Journal of Cognitive Neuroscience , 1991 , 3 (1) : 72 - 86. [3 ]BEL HUMEUR P N , HESPAN HA J P , KRIEGMAN D J. Eigenfaces vs. Fisherface : Recognition using class special linear projection [J ]. IEEE Transactions on Pat2 tern Analysis and Machine Intelligence , 1997 , 19 (7) : 711 - 720. [4 ] BARTL ETT. Face recognition by independent compo2 nent analysis [J ]. IEEE Transactions on Neural Net2 works , 2002 ,13 (6) : 1450 - 1464. [5 ]刘青山. 综述人脸识别中的子空间方法[J ]. 自动化学报 , 2003 , 129 (16) :900 - 912. L IU Qingshan. A survey : subspace analysis for face rec2 ognition[J ]. Acta Automatica Sinica , 2003 , 129 (16) : 900 - 912. [6 ] YAN G J , ZHAN G D , YAN G J Y. Two2dimensional PCA : A new approach to appearance based face repre2 sentation and recognition [J ]. IEEE Transactions Pattern Anal Machine Intell , 2004 , 26 (1) : 131 - 137. [7 ]乔 宇 ,黄席樾 ,柴 毅. 基于加权主元分析 (WPCA) 的 人脸识别[J ]. 重庆大学学报 ,2004 , 27 (3) :28 - 31. QIAO Yu , HUAN G Xiyue , CHAI Yi. Face recognition based weighted PCA[J ]. Journal of Chongqing Universi2 ty , 2004 , 27 (3) :28 - 31. [8 ]杨 光 ,阮秋琦. 一种新的基于加权主分量分析的人脸识 别算法[ A ]. 中国人工智能学会第 11 届全国学术年会 (CAAI - 11) [C] . 武汉 ,中国 ,2005. YAN G Guang , RUAN Qiuqi. A new arithmetic of face recognition based on weighted PCA[A ]. The 11th China Artificial Intelligence Conference [ C ]. Wuhan , China , 2005. 作者简介 : 金 一 ,女 ,1982 年生 ,博士研究生 , 主要研究方向为图像处理、模式识别、人 脸识别. E2mail :jineejin @gmail. com. 阮秋琦 ,男 ,1944 年生 ,教授 ,博士生 导师 ,主要研究方向为图像处理、计算机 视觉、模式识别、虚拟现实. 曾多次获得 省部级科技进步奖 ,发表论文 150 余篇 , 出版专著 3 部. 第 3 期 金 一 ,等 :一种局部加权的二维主成分分析算法及其在人脸识别中的应用 · 92 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net