
第2卷第4期 智能系统学报 Vol.2 Na 4 2007年8月 CAAI Transactions on Intelligent Systems Aug.2007 双足爬壁机器人壁面凹过渡步态规划研究 王洪光2,姜勇2,房立金赵明扬 (1.中国科学院沈阳自动化研究所机器人学重点实验室,辽宁沈阳110016;2.中国科学院研究生院,北京100049) 摘要:针对腿足式爬壁机器人在壁面过渡时的步态规划问题,以一种真空吸附式双足爬壁机器人为研究对象,在 步态分析的基础上,基于有限状态机建立了机器人的步态模型,进而提出了基于加权插值和BP神经网络的双足爬 壁机器人壁面凹过渡在线步态规划算法,为提高机器人壁面过渡的自主控制能力奠定了基础.仿真分析和实验结果 表明,该步态规划算法对于实际的机器人系统是有效的和可行的 关键词:双足爬壁机器人;有限状态机:壁面凹过渡;步态规划 中图分类号:TP24文献标识码:A文章编号:1673-4785(2007)04004006 Gait planning of concave transitions bet ween different slopes for bipedal wall-climbing robots WANG Hong guang'2 JIANG Yong'2,FAN GLi-jin',ZHAO Ming-yang' (1.Robotics Laboratory,Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,China;2.Grad- uate School,Chinese Academy of Sciences,Beijing 100049,China) Abstract:In order to solve the gait planning issue in wall transitions for bipedal wall-climbing robots fitted with vacuum suction cups,a gait model based on finite state machine was established after deep analysis of the robot's gait.On this basis,an omline gait planning algorithm for concave transitions was proposed based on weighted interpolation and BP neural networks.This lays a foundation for improving the ability of robots to transit complex walls under automatic control.Simulations and experiments show that the om line gait planning algorithm can successfully help wall-climbing robots complete a concave transition. Key words:bipedal wall-climbing robot;finite state machine;concave transition;gait planning 腿足式爬壁机器人是基于仿生学、机械设计、控 计的角度分析了四足爬壁机器人实现壁面过渡的步 制理论和人工智能等多学科交叉的一种特殊用途机 态可行性,但是对相应的步态规划方法并没有做深 器人.与轮式和履带式爬壁机器人相比,腿足式爬壁 入的研究J.Z.Xiao等在文献[3]中分析了微小型 机器人不仅可以在单一壁面上移动,而且也可以完 爬壁机器人CRA WL ER壁面凹过渡的步态过程, 成复杂的壁面过渡,具有较强的运动能力和灵活性, 提出了基于多传感器信息融合的步态控制方法,但 因此得到了广大研究学者的关注.所谓壁面过渡 对于步态规划中涉及的壁面交角与各个关节变量取 是指机器人从当前壁面移动到与此壁面相交一定角 值之间的关系并没有给出进一步的分析结果: 度的另外一个壁面上的过程,根据2个壁面之间交 Hyungseok Kim等在文献[4]中研究了四足爬壁机 角的大小可分为壁面凹过渡()2种情况. 过渡的步态规划问题,通过建立机器人与环境的几 针对腿足式爬壁机器人的特殊机构,如何规划 何模型分别推导出壁面凹过渡和凸过渡的各个步态 其步态以实现自主壁面过渡是此类机器人研究的一 参数的离线计算方法,对于如何实现机器人的在线 个难点问题.A.Alsalam等在文献[2]中从机构设 步态规划并未给出具体的解决办法」 收稿日期:200611-27. 本文以一种真空吸附式双足爬壁机器人为研究 基金项目:国家高技术研究发展计划资助项目(2004AA4201102) 对象,针对机器人壁面凹过渡的步态规划问题,在步 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 4 期 智 能 系 统 学 报 Vol. 2 №. 4 2007 年 8 月 CAAI Transactions on Intelligent Systems Aug. 2007 双足爬壁机器人壁面凹过渡步态规划研究 王洪光1 ,2 , 姜 勇1 ,2 ,房立金1 ,赵明扬1 (1. 中国科学院 沈阳自动化研究所机器人学重点实验室 , 辽宁 沈阳 110016 ;2. 中国科学院 研究生院 ,北京 100049) 摘 要 :针对腿足式爬壁机器人在壁面过渡时的步态规划问题 ,以一种真空吸附式双足爬壁机器人为研究对象 ,在 步态分析的基础上 ,基于有限状态机建立了机器人的步态模型 ,进而提出了基于加权插值和 BP 神经网络的双足爬 壁机器人壁面凹过渡在线步态规划算法 ,为提高机器人壁面过渡的自主控制能力奠定了基础. 仿真分析和实验结果 表明 ,该步态规划算法对于实际的机器人系统是有效的和可行的. 关键词 :双足爬壁机器人 ;有限状态机 ;壁面凹过渡 ;步态规划 中图分类号 : TP24 文献标识码 :A 文章编号 :167324785 (2007) 0420040206 Gait planning of concave transitions between different slopes for bipedal wall2climbing robots WAN G Hong2guang 1 ,2 ,J IAN G Yong 1 ,2 ,FAN G Li2jin 1 ,ZHAO Ming2yang 1 (1. Robotics Laboratory , Shenyang Institute of Automation , Chinese Academy of Sciences , Shenyang 110016 , China ; 2. Grad2 uate School ,Chinese Academy of Sciences , Beijing 100049 , China) Abstract :In order to solve t he gait planning issue in wall transitions for bipedal wall2climbing robots fitted with vacuum suction cup s , a gait model based on finite state machine was established after deep analysis of t he robot’s gait. On t his basis , an on2line gait planning algorit hm for concave transitions was proposed based on weighted interpolation and BP neural networks. This lays a foundation for improving the ability of robots to transit complex walls under automatic control. Simulations and experiments show that t he on2 line gait planning algorit hm can successf ully help wall2climbing robots complete a concave transition. Keywords :bipedal wall2climbing robot ; finite state machine ; concave transition ; gait planning 收稿日期 :2006211227. 基金项目 :国家高技术研究发展计划资助项目(2004AA4201102) . 腿足式爬壁机器人是基于仿生学、机械设计、控 制理论和人工智能等多学科交叉的一种特殊用途机 器人. 与轮式和履带式爬壁机器人相比 ,腿足式爬壁 机器人不仅可以在单一壁面上移动 ,而且也可以完 成复杂的壁面过渡 ,具有较强的运动能力和灵活性 , 因此得到了广大研究学者的关注[1 ] . 所谓壁面过渡 是指机器人从当前壁面移动到与此壁面相交一定角 度的另外一个壁面上的过程 ,根据 2 个壁面之间交 角θ的大小可分为壁面凹过渡(θπ) 2 种情况. 针对腿足式爬壁机器人的特殊机构 ,如何规划 其步态以实现自主壁面过渡是此类机器人研究的一 个难点问题. A. Alsalam 等在文献[ 2 ]中从机构设 计的角度分析了四足爬壁机器人实现壁面过渡的步 态可行性 ,但是对相应的步态规划方法并没有做深 入的研究 ;J. Z. Xiao 等在文献[ 3 ]中分析了微小型 爬壁机器人 CRAWL ER 壁面凹过渡的步态过程 , 提出了基于多传感器信息融合的步态控制方法 ,但 对于步态规划中涉及的壁面交角与各个关节变量取 值之间的关系并没有给出进一步的分析结果 ; Hyungseok Kim 等在文献[ 4 ]中研究了四足爬壁机 器人 MRWALL SPECT Ⅲ在三维环境下实现壁面 过渡的步态规划问题 ,通过建立机器人与环境的几 何模型分别推导出壁面凹过渡和凸过渡的各个步态 参数的离线计算方法 ,对于如何实现机器人的在线 步态规划并未给出具体的解决办法. 本文以一种真空吸附式双足爬壁机器人为研究 对象 ,针对机器人壁面凹过渡的步态规划问题 ,在步

第4期 王洪光,等:双足爬壁机器人壁面凹过渡步态规划研究 ·41· 态分析和建立有限状态机(finite state machine, 距传感器用来测定机器人壁面过渡的环境数据;模 FSM)模型的基础上,利用神经网络的学习能力,提 式传感器用来区分机器人的运动模式.机器人与基 出了基于加权插值和BP神经网络的双足爬壁机器 站之间通过无线蓝牙模块进行实时通讯。 人壁面凹过渡在线步态规划算法 2机器人步态建模 1双足爬壁机器人 2.1壁面凹过渡的步态分析 双足爬壁机器人本体采用五自由度(RRPRR) 双足爬壁机器人可以通过2个吸盘足的交替吸 三电机驱动的欠驱动机构设计,利用2个真空吸盘 附和各个关节的配合灵活地实现尺蠖式爬行和转 足实现机器人的壁面吸附功能).如图1所示.旋转 向,并且能够在夹角满足一定范围的凹交叉壁面之 关节1和5使爬壁机器人具有2个俯仰自由度,这间实现过渡运动,机器人从当前位置运动到与所在 2个自由度分别由2台电机独立驱动;机身通过移壁面相交一定角度B∈45°,1809的另外一个壁面 动关节3实现一个伸缩自由度,由一个电机驱动使 的整个过渡步态如图2所示。 机器人可以借助两腿的伸展和收缩达到移动的目 的;旋转关节2和4是2个被动关节,它们在机器人 的腿和足之间产生2个水平回转自由度,使机器人 具备转向能力:另外,旋转关节2和4产生的2个水 平回转自由度是通过与移动关节3运动耦合来实现 的 (b (d) fe (f) 旋转关节2 旋转关节4 (g) (h) m 转动关节3 图2壁面凹过渡 旋转关节1 旋转关节 Fig 2 Concave transition 吸然足 吸欧足2 7 运动过程为: 1)机器人移动到距离目标壁面为L(红外测距 图1双足爬壁机器人及其机构简图 传感器检测值)的位置,移动关节3收缩至最短; Fig 1 Bipedal climbing robot and mechanism sketch 2)释放吸盘足2; 双足爬壁机器人的控制系统采用TI公司的 3)旋转关节1逆时针旋转Y1角度,旋转关节5 TMS320F2812DSP芯片作为中央处理器.关节电 逆时针旋转Y2角度 机和真空泵电机的驱动选用TI公司的SN754410 4)移动关节3伸长至1,使吸盘足2触及目标壁 芯片.2台直流伺服电机均安装光电码盘,可以对每 面; 个关节的运动实施位置和速度闭环控制.集成在机 5)启动真空泵使吸盘足2牢牢吸附在目标壁面 器人本体上的传感器包括:1个零位开关、4个触觉 上 传感器、2个压力传感器、2个红外测距传感器和2 6)释放吸盘足1; 个模式传感器.零位开关用来识别机器人的参考零 7)移动关节3收缩至1m,旋转关节1逆时针旋 位置:触觉传感器用来反馈两吸盘足与壁面的接触 转1角度: 状态;压力传感器用来检测气路中的负压值;红外测 8)旋转关节5逆时针旋转角度: 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
态分析和建立有限状态机 (finite state machine , FSM) 模型的基础上 ,利用神经网络的学习能力 ,提 出了基于加权插值和 BP 神经网络的双足爬壁机器 人壁面凹过渡在线步态规划算法. 1 双足爬壁机器人 双足爬壁机器人本体采用五自由度 ( RRPRR) 三电机驱动的欠驱动机构设计 ,利用 2 个真空吸盘 足实现机器人的壁面吸附功能[5 ] . 如图 1 所示. 旋转 关节 1 和 5 使爬壁机器人具有 2 个俯仰自由度 ,这 2 个自由度分别由 2 台电机独立驱动 ;机身通过移 动关节 3 实现一个伸缩自由度 ,由一个电机驱动使 机器人可以借助两腿的伸展和收缩达到移动的目 的 ;旋转关节 2 和 4 是 2 个被动关节 ,它们在机器人 的腿和足之间产生 2 个水平回转自由度 ,使机器人 具备转向能力 ;另外 ,旋转关节 2 和 4 产生的 2 个水 平回转自由度是通过与移动关节 3 运动耦合来实现 的. 图 1 双足爬壁机器人及其机构简图 Fig11 Bipedal climbing robot and mechanism sketch 双足爬壁机器人的控制系统采用 TI 公司的 TMS320F2812 DSP 芯片作为中央处理器. 关节电 机和真空泵电机的驱动选用 TI 公司的 SN754410 芯片. 2 台直流伺服电机均安装光电码盘 ,可以对每 个关节的运动实施位置和速度闭环控制. 集成在机 器人本体上的传感器包括 :1 个零位开关、4 个触觉 传感器、2 个压力传感器、2 个红外测距传感器和 2 个模式传感器. 零位开关用来识别机器人的参考零 位置 ;触觉传感器用来反馈两吸盘足与壁面的接触 状态 ;压力传感器用来检测气路中的负压值 ;红外测 距传感器用来测定机器人壁面过渡的环境数据 ;模 式传感器用来区分机器人的运动模式. 机器人与基 站之间通过无线蓝牙模块进行实时通讯. 2 机器人步态建模 211 壁面凹过渡的步态分析 双足爬壁机器人可以通过 2 个吸盘足的交替吸 附和各个关节的配合灵活地实现尺蠖式爬行和转 向 ,并且能够在夹角满足一定范围的凹交叉壁面之 间实现过渡运动. 机器人从当前位置运动到与所在 壁面相交一定角度β∈[ 45°, 180°) 的另外一个壁面 的整个过渡步态如图 2 所示. 图 2 壁面凹过渡 Fig12 Concave transition 运动过程为 : 1) 机器人移动到距离目标壁面为 L (红外测距 传感器检测值) 的位置 ,移动关节 3 收缩至最短 lmin ; 2) 释放吸盘足 2 ; 3) 旋转关节 1 逆时针旋转γ1 角度 ,旋转关节 5 逆时针旋转γ2 角度 ; 4) 移动关节 3 伸长至 l ,使吸盘足 2 触及目标壁 面 ; 5) 启动真空泵使吸盘足 2 牢牢吸附在目标壁面 上 ; 6) 释放吸盘足 1 ; 7) 移动关节 3 收缩至 lmin ,旋转关节 1 逆时针旋 转γ1 角度; 8) 旋转关节 5 逆时针旋转γ2 角度; 第 4 期 王洪光 ,等 :双足爬壁机器人壁面凹过渡步态规划研究 ·41 ·

·42 智能系统学报 第2卷 9)启动真空泵使吸盘足1牢牢吸附在目标壁面 4逆时针转动,“111”非法状态, 上 Js(joint5)关节5的运动状态:“o0”表示静止或 上述壁面凹过渡步态可用函数表示为 吸盘足自动微调(AR=1),“01”表示关节5顺时针 G=g(L,,,) 转动,“10”表示关节5逆时针转动,“11”非法状态 式中:B是相交壁面的夹角;L、、?和1是步态规 SC(suction cup1)吸盘足1的状态:“0”表示 划的待定参数 吸盘足1释放,“1”表示吸盘足1吸附 2.2基于FSM的步态建模 SCz(suction cup2)吸盘足2的状态:“0”表示 FSM由有限个状态和相互之间的转移构成,机 吸盘足2释放,“1"”表示吸盘足2吸附 器人在任何时候只能处于给定数目的状态中的一 AR(adaptive regulate)吸盘足姿态自调整:“o” 个.当接收到一个输入事件时,FSM产生一个输出, 表示终止自调整程序,“1”表示启动自调整程序 同时也可能伴随着状态的转移. ST(stage)基本步态阶段:“0”表示处于基本步 双足爬壁机器人步态规划的FSM模型表示为 态的前半程阶段,“1"”表示处于基本步态的后半程阶 M=(Q,2,6,m,日. 段 式中:Q代表机器人运动步态的有限状态集合, 根据上述双足爬壁机器人步态规划FSM模型 廿q∈Q,g,为M的一个状态;2代表机器人运动过 的状态向量定义,可以得到壁面凹过渡时机器人的 程的输入状态集合:∈Q表示机器人的初始状态: F三Q代表机器人的终止状态集合:状态转移函数 状态(十六进制表示)转移路径,如图3所示 6:Q×2-Q,则6(4,a=g表示当输入为a∈2 0180C 0xI808 0x1C08 0x1828 0x18C8 0x180A 时,机器人的状态从g转移到q.FSM模型的状态 0x1807 0x1825 0xIC05 0x1905 01805 0x180D 向量由8个元素组成,占据2个字节(共16位, 其中15~13位取“0”),如表1所示 图3壁面凹过渡FSM转移路径 表1SM状态向量 Fig 3 FSM path of concave transition Table 1 FSM state vectors 3机器人步态规划算法 元素 位 LM 12,11 3.1相关参数 J 10,9 当双足爬壁机器人要实现在相交角度为B∈ J23 8,7,6 [45°,6=105°的2个壁面之间的过渡时,如图4(a) J5 5,4 SC 3 所示,一方面,过渡起始位置与目标壁面的距离L SC 2 不能过长,否则,即使移动关节3的伸长量1达到最 AR 大值Lx,吸盘足也无法完全接触到目标壁面:另一 ST 0 方面,为避免运动机构与墙壁发生干涉,要求R< LM(locomotion mode)机器人的运动模式: L1和R<L2,则L不能过短.基于规则的参数L分 “00”"表示参考零位置静止模式,“01”表示尺蠖式爬 段取值如下: 行模式,“10”表示转向模式,“11”表示壁面过渡模 IFB∈A=45°,g],THEN L=m1; 式 IFB∈A,g],THEN L=m; J1(joint1)关节1的运动状态:“00”表示静止或 吸盘足自动微调(AR=1),“01”表示关节1顺时针 IFB∈0.1,A.=105],THEN L=mm1 转动,“10”表示关节1逆时针转动,“11”非法状态。 其中45°=4<4<…<0n.1<0。=105°,常数m, J234(joint2,3and4)关节2、3和4的运动状 m2,,mm1是通过离线试验确定的 态:“000”表示静止或吸盘足自动微调(AR=1), 当双足爬壁机器人要实现在相交角度为B∈ “001”表示关节2顺时针转动,“010”表示关节2逆 105°,1807的2个壁面之间的过渡时,如图4(b)所 示,则参数L的取值为 时针转动,“011”表示关节3伸长,“100”表示关节3 收缩,“101”表示关节4顺时针转动,“110”表示关节 2 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
9) 启动真空泵使吸盘足 1 牢牢吸附在目标壁面 上. 上述壁面凹过渡步态可用函数表示为 Gβ = g (L ,γ1 ,γ2 , l) . 式中 :β是相交壁面的夹角; L 、γ1 、γ2 和 l 是步态规 划的待定参数. 212 基于 FS M 的步态建模 FSM 由有限个状态和相互之间的转移构成 ,机 器人在任何时候只能处于给定数目的状态中的一 个. 当接收到一个输入事件时 ,FSM 产生一个输出 , 同时也可能伴随着状态的转移. 双足爬壁机器人步态规划的 FSM 模型表示为 M = ( Q ,Ω,δ, q0 , F) . 式中 : Q 代表机器人运动步态的有限状态集合 , Πqi ∈Q , qi 为 M 的一个状态;Ω代表机器人运动过 程的输入状态集合; q0 ∈Q 表示机器人的初始状态; F ΑQ 代表机器人的终止状态集合;状态转移函数 δ:Q ×Ω→Q ,则δ( qi , a) = qj 表示当输入为 a ∈Ω 时 ,机器人的状态从 qi 转移到 qj . FSM 模型的状态 向量 qi 由 8 个元素组成 ,占据 2 个字节 (共 16 位 , 其中 15~13 位取“0”) ,如表 1 所示. 表 1 FSM 状态向量 Table 1 FSM state vectors 元素 位 LM 12 ,11 J 1 10 ,9 J 2 ,3 ,4 8 ,7 ,6 J 5 5 ,4 SC1 3 SC2 2 AR 1 ST 0 LM (locomotion mode ) 机器人的运动模式 : “00”表示参考零位置静止模式“, 01”表示尺蠖式爬 行模式“, 10”表示转向模式 “, 11”表示壁面过渡模 式. J 1 (joint 1) 关节 1 的运动状态“: 00”表示静止或 吸盘足自动微调(AR = 1) “, 01”表示关节 1 顺时针 转动“, 10”表示关节 1 逆时针转动“, 11”非法状态. J 2 ,3 ,4 (joint 2 , 3 and 4) 关节 2、3 和 4 的运动状 态“: 000”表示静止或吸盘足自动微调 ( AR = 1) , “001”表示关节 2 顺时针转动“, 010”表示关节 2 逆 时针转动“, 011”表示关节 3 伸长“, 100”表示关节 3 收缩“, 101”表示关节 4 顺时针转动“, 110”表示关节 4 逆时针转动“, 111”非法状态. J 5 (joint 5) 关节 5 的运动状态“: 00”表示静止或 吸盘足自动微调(AR = 1) “, 01”表示关节 5 顺时针 转动“, 10”表示关节 5 逆时针转动“, 11”非法状态. SC1 (suction cup 1) 吸盘足 1 的状态 “: 0”表示 吸盘足 1 释放“, 1”表示吸盘足 1 吸附. SC2 (suction cup 2) 吸盘足 2 的状态 “: 0”表示 吸盘足 2 释放“, 1”表示吸盘足 2 吸附. AR(adaptive regulate) 吸盘足姿态自调整“: 0” 表示终止自调整程序“, 1”表示启动自调整程序. ST(stage) 基本步态阶段“: 0”表示处于基本步 态的前半程阶段“, 1”表示处于基本步态的后半程阶 段. 根据上述双足爬壁机器人步态规划 FSM 模型 的状态向量定义 ,可以得到壁面凹过渡时机器人的 状态(十六进制表示) 转移路径 ,如图 3 所示. 图 3 壁面凹过渡 FSM 转移路径 Fig13 FSM path of concave transition 3 机器人步态规划算法 311 相关参数 当双足爬壁机器人要实现在相交角度为β∈ [45°,δ= 105°]的 2 个壁面之间的过渡时 ,如图 4 (a) 所示 ,一方面 ,过渡起始位置与目标壁面的距离 L 不能过长 ,否则 ,即使移动关节 3 的伸长量 l 达到最 大值 L max ,吸盘足也无法完全接触到目标壁面;另一 方面 ,为避免运动机构与墙壁发生干涉 ,要求 R1 < L1 和 R2 < L2 ,则 L 不能过短. 基于规则的参数 L 分 段取值如下 : IFβ∈[θ1 = 45°θ, 2 ] ,T HEN L = m1 ; IFβ∈[θ2 ,θ3 ] , T HEN L = m2 ; … IFβ∈[θn - 1 θ, n = 105°] , T HEN L = mn - 1 . 其中 45°=θ1 <θ2 < …<θn - 1 <θn = 105°, 常数 m1 , m2 , …, mn - 1是通过离线试验确定的. 当双足爬壁机器人要实现在相交角度为β∈ [105°,180°]的 2 个壁面之间的过渡时 ,如图 4 ( b) 所 示 ,则参数 L 的取值为 L = d ·tan β- π 2 + c ·r. ·42 · 智 能 系 统 学 报 第 2 卷

第4期 王洪光,等:双足爬壁机器人壁面凹过渡步态规划研究 ·43· 式中:d是红外测距传感器的安装位置到吸盘腔底 3.2步态规划算法 的距离,r是吸盘腔底的直径,常数C是安全系数 通过离线步态规划,双足爬壁机器人可以自主 实现相交角度为4∈(45°,75°,105°,135°,165?的 壁面凹过渡,相应的步态可用函数表示为 G=gLg,hg,g,lo),i=1,2,3,4,5 对于B∈(45°,180J的任意凹交叉壁面,机器人实现 自主壁面过渡的在线步态规划算法如下: )确定与B相邻的日和0,1,即日0 4= 1, B=0 0-E 1+01.0 B0 1, B=0 1- 0-E B<0, 8-1-0 (b)B∈105°,1807 图4过渡起始位置与目标壁面的距离 0=g+9a 2 Fig 4 Distance between original position 3)计算旋转关节1和5的转动角度h,: and object slope 40+104 在壁面凹过渡时,双足爬壁机器人的旋转关节 2 1的旋转角度片和旋转关节5的旋转角度2与壁 s=180°.B-hB. 面夹角B的关系如图5所示,其中片=∠ACB, 4)根据规则确定参数L; h=∠ABC,a=∠ACB+∠ABC,a+B=180°, 5)基于神经网络的训练和学习,利用多个BP 1+3+B=180° 神经网络对旋转角度h、s和移动变量1B的关系 曲线如图6所示)进行分段拟合,计算移动关节3 的伸长量:拟合曲线是根据离线规划获得的相关 数据绘制的, 75 70 价5价 45 40 35 45505560657075808590 旋转关节1、5旋转角度之和) 图5B与参数竹和的关系 (a)45°e+g909 Fig5 Relations of Band parameters片, 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
式中 : d 是红外测距传感器的安装位置到吸盘腔底 的距离 , r 是吸盘腔底的直径 ,常数 C是安全系数. (a)β∈[45°,105°] (b)β∈[105°,180°] 图 4 过渡起始位置与目标壁面的距离 Fig14 Distance between original position and object slope 在壁面凹过渡时 ,双足爬壁机器人的旋转关节 1 的旋转角度γ1 和旋转关节 5 的旋转角度γ2 与壁 面夹角β的关系如图 5 所示 , 其中γ1 = ∠ACB , γ2 = ∠AB C ,α = ∠ACB + ∠AB C ,α+β = 180°, γ1 +γ2 +β = 180°. 图 5 β与参数γ1 和γ2 的关系 Fig15 Relations ofβand parametersγ1 ,γ2 312 步态规划算法 通过离线步态规划 ,双足爬壁机器人可以自主 实现相交角度为θi ∈{ 45°, 75°, 105°, 135°, 165°} 的 壁面凹过渡 ,相应的步态可用函数表示为 Gθi = g (Lθi ,γ1θi ,γ1θi , lθi ) , i = 1 ,2 ,3 ,4 ,5. 对于β∈[45°,180°]的任意凹交叉壁面 ,机器人实现 自主壁面过渡的在线步态规划算法如下 : 1) 确定与β相邻的θi 和θi + 1 ,即θi θ, 1 , β =θ, 1 + θi+1 - β θi+1 - θi , β θ, 1 , β =θ, 1 - θi+1 - β θi+1 - θi , β <θ, θ= θi +θi+1 2 . 3) 计算旋转关节 1 和 5 的转动角度γ1β ,γ2β: γ1β = ω1γ1θi +ω2γ1θi+1 2 , γ2β = 180°- β- γ1β. 4) 根据规则确定参数 Lβ; 5) 基于神经网络的训练和学习 ,利用多个 BP 神经网络对旋转角度γ1β、γ2β和移动变量 lβ 的关系 曲线(如图 6 所示) 进行分段拟合 ,计算移动关节 3 的伸长量 lβ;拟合曲线是根据离线规划获得的相关 数据绘制的. (a) 45°≤γ1β +γ2β ≤90° 第 4 期 王洪光 ,等 :双足爬壁机器人壁面凹过渡步态规划研究 ·43 ·
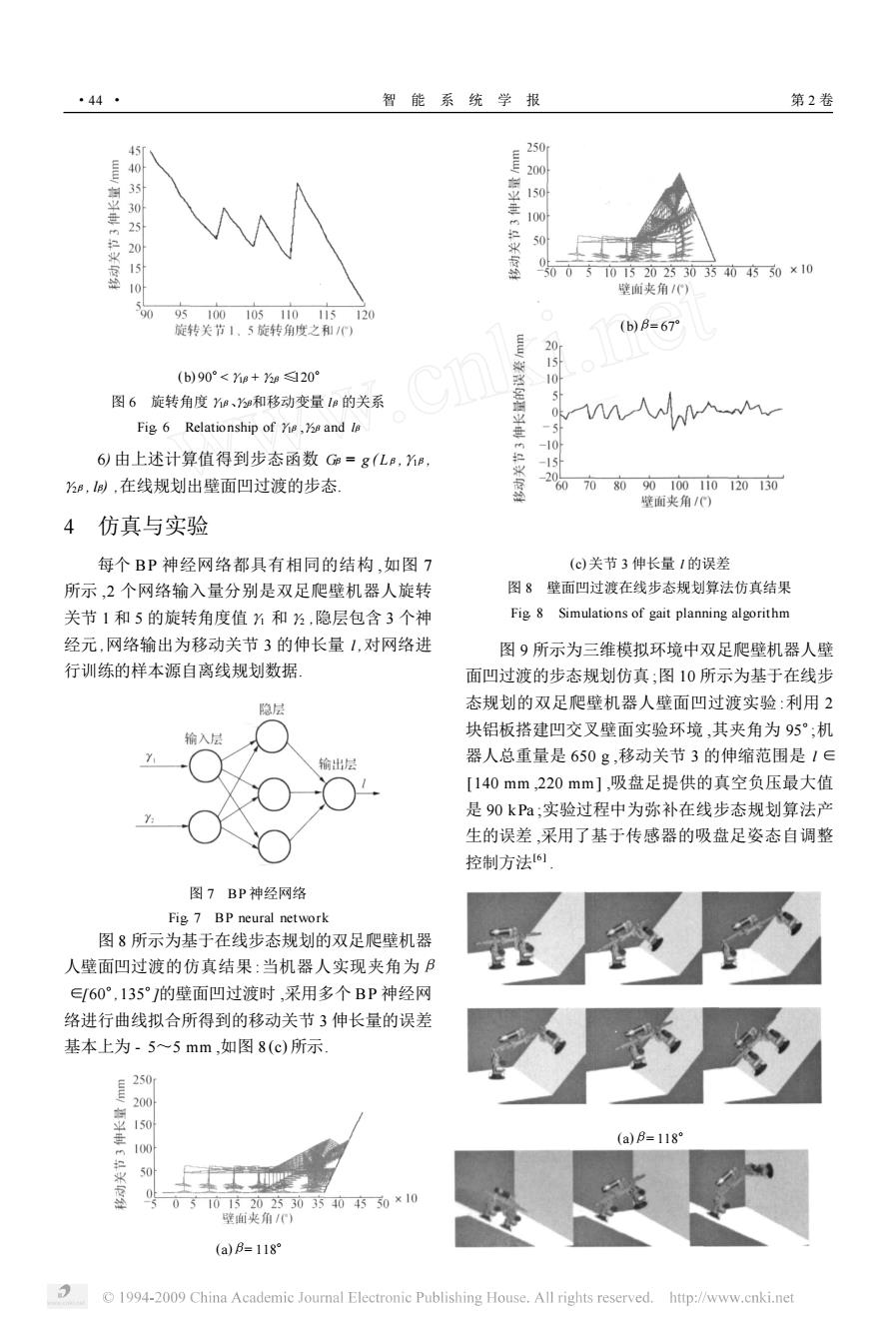
·44 智能系统学报 第2卷 45 250 200 30250 150 100 500了10152023303方404$50×10 10 壁面夹角/) 90 95100105110115120 旋转关节1、5旋转角度之和心) (b)B=67 0 15 (b)90°<a+1g☒209 图6旋转角度he、9和移动变量1e的关系 5 Fig 6 Relationship of Yis,and le -10 6)由上述计算值得到步态函数G=g(L,当B, ,),在线规划出壁面凹过渡的步态. -20607080 90100110120130 壁面夹角/) 4仿真与实验 每个BP神经网络都具有相同的结构,如图7 (c)关节3伸长量1的误差 所示,2个网络输入量分别是双足爬壁机器人旋转 图8壁面凹过渡在线步态规划算法仿真结果 关节1和5的旋转角度值1和,隐层包含3个神 Fig 8 Simulations of gait planning algorithm 经元,网络输出为移动关节3的伸长量1,对网络进 图9所示为三维模拟环境中双足爬壁机器人壁 行训练的样本源自离线规划数据, 面凹过渡的步态规划仿真:图10所示为基于在线步 隐层 态规划的双足爬壁机器人壁面凹过渡实验:利用2 输入层 块铝板搭建凹交叉壁面实验环境,其夹角为95°;机 输出层 器人总重量是650g,移动关节3的伸缩范围是1∈ [140mm,220mm],吸盘足提供的真空负压最大值 是90kPa,实验过程中为弥补在线步态规划算法产 生的误差,采用了基于传感器的吸盘足姿态自调整 控制方法1 图7BP神经网络 Fig 7 BP neural network 图8所示为基于在线步态规划的双足爬壁机器 人壁面凹过渡的仿真结果:当机器人实现夹角为B ∈60°,135°J的壁面凹过渡时,采用多个BP神经网 络进行曲线拟合所得到的移动关节3伸长量的误差 基本上为-5~5mm,如图8(c)所示 250 200 100 (a)B=118 上 01052025050务50×10 壁面夹角/) (a)B=118 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
(b) 90°<γ1β +γ2β ≤120° 图 6 旋转角度γ1β、γ2β和移动变量 lβ 的关系 Fig16 Relationship of γ1β ,γ2β and lβ 6) 由上述计算值得到步态函数 Gβ = g ( Lβ ,γ1β, γ2β , lβ) ,在线规划出壁面凹过渡的步态. 4 仿真与实验 每个 BP 神经网络都具有相同的结构 ,如图 7 所示 ,2 个网络输入量分别是双足爬壁机器人旋转 关节 1 和 5 的旋转角度值γ1 和γ2 ,隐层包含 3 个神 经元 ,网络输出为移动关节 3 的伸长量 l ,对网络进 行训练的样本源自离线规划数据. 图 7 BP 神经网络 Fig17 BP neural network 图 8 所示为基于在线步态规划的双足爬壁机器 人壁面凹过渡的仿真结果 :当机器人实现夹角为β ∈[60°,135°]的壁面凹过渡时 ,采用多个 BP 神经网 络进行曲线拟合所得到的移动关节 3 伸长量的误差 基本上为 - 5~5 mm ,如图 8 (c) 所示. (a)β= 118° (b)β= 67° (c)关节 3 伸长量 l 的误差 图 8 壁面凹过渡在线步态规划算法仿真结果 Fig18 Simulations of gait planning algorithm 图 9 所示为三维模拟环境中双足爬壁机器人壁 面凹过渡的步态规划仿真 ;图 10 所示为基于在线步 态规划的双足爬壁机器人壁面凹过渡实验 :利用 2 块铝板搭建凹交叉壁面实验环境 ,其夹角为 95°;机 器人总重量是 650 g ,移动关节 3 的伸缩范围是 l ∈ [140 mm ,220 mm] ,吸盘足提供的真空负压最大值 是 90 kPa ;实验过程中为弥补在线步态规划算法产 生的误差 ,采用了基于传感器的吸盘足姿态自调整 控制方法[6 ] . (a)β= 118° ·44 · 智 能 系 统 学 报 第 2 卷

第4期 王洪光,等:双足爬壁机器人壁面凹过渡步态规划研究 ·45· ground to vertical wall movement [A ]Proceedings TENCON2000[C].[s.1.J,2000. [3 XIAO Jizhong,XI Ning,XIAO Jun,TAN Jindong. Multi-sensor referenced gait control of a miniature climbing robot [A ]IEEE/RSJ International Conference on Intelligent Robots and Systems [C].[s.1.],2003. (b)B=67 [4]HYUNGSEOK K,TAEHUN K,VO GL,HYOUK R 图93D模拟环境中壁面凹过渡仿真 C.Gait planning of quadruped walking and climbing ro- bot for locomotion in 3D environment [A].IEEE Inter- Fig 9 Simulations of concave transition in 3D national Conference on Robotics and Automation [C]. Spain,2005. [5]XIAO J Z,XIAO J,XI N.Minimal power control of a miniature climbing robot [A].Proceedings of the IEEE/ ASME International Conference on Advanced Intelligent Mechatronics [C].New York,USA,2003. [6JIANG Yong,WANG Hongguang,FANGLijin,ZHAO Mingyang.A novel approach to fault detection and iden tification in suction foot control of a climbing robot [A]. Proceedings of the IEEE/RSI International Conference on Intelligent Robots and Systems [C].Beijing,2006. 作者简介: 图10机器人壁面凹过渡实验 王洪光,男,1965年生,研究员,博士 Fig 10 Experiments of concave transition 生导师,主要研究方向为机器人机构学、特 for climbing robot 种机器人及机电一体化技术,主持和参加 实验结果证明,在凹交叉壁面夹角角度已知的 完成了国家自然科学基金、国家863计划、 前提下,基于本文提出的在线步态规划算法,双足爬 九五攻关国家重大科学工程及企业委托 壁机器人能够自主地实现壁面凹过渡 等研究与应用课题多项;获得发明和实用 新型专利10余项,获辽宁省技术发明二等 5结束语 奖1项,沈阳市科技进步二等奖1项,发表 论文30余篇 本文通过对双足爬壁机器人壁面凹过渡步态的 Email hgwang @sia.cn. 分析,建立了基于FSM的步态模型,并在此基础上 提出了基于加权插值和BP神经网络的在线步态规 划算法,实现了机器人的自主壁面凹过渡.通过仿真 分析和实验,证明了该算法的有效性和可行性.本文 姜勇,男,1975年生,博士,主要 所提出的方法对壁面夹角的检测精度有较高的要 研究方向为移动机器人运动规划与控 求,并且不适用于壁面凸过渡的情况.在未来的工作 制、智能控制,发表学术论文10余篇. 中,将进一步研究壁面夹角的测定方法,以及探讨壁 面凸过渡乃至更复杂环境的步态规划方法, 参考文献: [1]肖立,佟仕忠,丁启敏,吴俊生.爬壁机器人的现状与 房立金,男,1965年生,博士,研究 员,主要研究方向为离散自动控制、并联 发展].自动化博览,2005,22(1):81-84. 机器人、机器人控制.1998年获中国科 XIAO Li,TONG Shizhong,DIN G Qimin,WU Junsh- 学院自然科学三等奖一项,1999年获沈 eng.The current situation and development of the wall- 阳市科技进步二等奖一项;2002年获解 climbing robot [J ]Automation Panorama,2005,22 放军总参二等奖一项:申请专利10余 (1):81-84. 项,发表学术论文10余篇 [2]ALSALAMEH AA S,AMIN S H M,MAMAT R. Mechanical design of a quadruped robot for horizontal 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
(b)β= 67° 图 9 3D 模拟环境中壁面凹过渡仿真 Fig19 Simulations of concave transition in 3D 图 10 机器人壁面凹过渡实验 Fig110 Experiments of concave transition for climbing robot 实验结果证明 ,在凹交叉壁面夹角角度已知的 前提下 ,基于本文提出的在线步态规划算法 ,双足爬 壁机器人能够自主地实现壁面凹过渡. 5 结束语 本文通过对双足爬壁机器人壁面凹过渡步态的 分析 ,建立了基于 FSM 的步态模型 ,并在此基础上 提出了基于加权插值和 BP 神经网络的在线步态规 划算法 ,实现了机器人的自主壁面凹过渡. 通过仿真 分析和实验 ,证明了该算法的有效性和可行性. 本文 所提出的方法对壁面夹角的检测精度有较高的要 求 ,并且不适用于壁面凸过渡的情况. 在未来的工作 中 ,将进一步研究壁面夹角的测定方法 ,以及探讨壁 面凸过渡乃至更复杂环境的步态规划方法. 参考文献 : [1 ]肖 立 ,佟仕忠 ,丁启敏 , 吴俊生. 爬壁机器人的现状与 发展[J ]. 自动化博览 , 2005 , 22 (1) : 81 - 84. XIAO Li , TON G Shizhong , DIN G Qimin , WU J unsh2 eng. The current situation and development of the wall2 climbing robot [J ]. Automation Panorama , 2005 , 22 (1) : 81 - 84. [2 ] ALSALAMEH A A S , AMIN S H M , MAMA T R. Mechanical design of a quadruped robot for horizontal ground to vertical wall movement [ A ]. Proceedings TENCON 2000[C]. [s. l. ] ,2000. [3 ] XIAO Jizhong , XI Ning , XIAO J un , TAN Jindong. Multi2sensor referenced gait control of a miniature climbing robot [ A ]. IEEE/ RSJ International Conference on Intelligent Robots and Systems [C]. [s. l. ] ,2003. [4 ] H YUN GSEO K K , TA EHUN K , VO G L , H YOU K R C. Gait planning of quadruped walking and climbing ro2 bot for locomotion in 3D environment [ A ]. IEEE Inter2 national Conference on Robotics and Automation [ C ]. Spain , 2005. [5 ]XIAO J Z , XIAO J , XI N. Minimal power control of a miniature climbing robot [ A ]. Proceedings of the IEEE/ ASME International Conference on Advanced Intelligent Mechatronics [C]. New York , USA , 2003. [6 ]J IAN G Yong , WAN G Hongguang , FAN GLijin , ZHAO Mingyang. A novel approach to fault detection and iden2 tification in suction foot control of a climbing robot [A ]. Proceedings of the IEEE/ RSJ International Conference on Intelligent Robots and Systems [C]. Beijing ,2006. 作者简介 : 王洪光 ,男 ,1965 年生 ,研究员 ,博士 生导师 ,主要研究方向为机器人机构学、特 种机器人及机电一体化技术 ,主持和参加 完成了国家自然科学基金、国家 863 计划、 九五攻关、国家重大科学工程及企业委托 等研究与应用课题多项 ;获得发明和实用 新型专利 10 余项 ;获辽宁省技术发明二等 奖 1 项 ,沈阳市科技进步二等奖 1 项 ,发表 论文 30 余篇. E2mail :hgwang @sia. cn. 姜 勇 ,男 ,1975 年生 ,博士 ,主要 研究方向为移动机器人运动规划与控 制、智能控制 ,发表学术论文 10 余篇. 房立金 ,男 ,1965 年生 ,博士 ,研究 员 ,主要研究方向为离散自动控制、并联 机器人、机器人控制. 1998 年获中国科 学院自然科学三等奖一项 ;1999 年获沈 阳市科技进步二等奖一项 ;2002 年获解 放军总参二等奖一项 ;申请专利 10 余 项 ,发表学术论文 10 余篇. 第 4 期 王洪光 ,等 :双足爬壁机器人壁面凹过渡步态规划研究 ·45 ·