
第2卷第5期 智能系统学报 Vol.2 Na 5 2007年10月 CAAI Transactions on Intelligent Systems 0ct.2007 基于遗传算法的大规模矩形件优化排样 马炫,张亚龙 (西安理工大学自动化与信息工程学院陕西西安710048) 摘要:大规模矩形件优化排样是一个典型的组合优化问题,属于NP-hard问题,实际工程中对一个排样方案一般 有满足“一刀切”的工艺要求,“一刀切”要求增加了对排样的约束.提出的优化算法,将矩形匹配分割算法作为遗传 算法染色体的解码器实现一个排样方案,用遗传算法进行排样方案的全局搜索.算例比较表明,该算法可以求得满 足“一刀切”约束的最优解 关键词:遗传算法;矩形件排样;组合优化 中图分类号:TP301文献标识码:A文章编号:1673-4785(2007)05004805 A genetic algorithm for the layout of large scale rectangular parts MA Xuan,ZHAN G Ya-long (School of Automation and Information Engineering,Xi'an University of Technology,Xi'an 710048,China) Abstract:The optimal layout of large scale rectangular parts is a combinatorial optimization problem,a typ- ical NP-hard one.In practical engineering,quire cutting is often requested,which increases the constraints in the determination of a layout.To satisfy quire cutting requirements,in this paper,an optimization algo- rithm is proposed wherein a rectangular matching and segmentation algorithm is employed as a decoder of chromosomes in a genetic algorithm to determine placement.A global optimal solution for placement can be achieved with this genetic algorithm.Simulation results confirmed the validity of the proposed algo- rithm. Key words:genetic algorithm;rectangular parts layout;combinatorial optimization 矩形件排样是指在给定尺寸的矩形板材上,排了排样的约束条件,而且切割时会产生一定的切缝 放多规格多数量的矩形件时,如何排放可以使板材 宽度.这些都会对排样结果产生影响.文中将矩形匹 的利用率最大.这是一个典型的组合优化问题,在工 配分割算法的局部搜索和遗传算法的全局搜索相结 业领域如冲裁件排样造船、车辆、家具生产、玻璃切 合,提出了一种满足“一刀切”工艺要求的矩形件排 割等行业都存在大量的排样问题.求解最优排样方 样优化算法.设计的编码方法和具有方向交叉的交 案是一个NP-hard问题,至今尚未找到多项式时间叉算子改善了遗传算法的搜索性能.通过算例比较】 算法.因此,对于大规模排样问题,在可接受的时间 表明了算法的有效性 内快速找到次优解的算法引起了人们的关注.很多 学者在这方面做了卓有成效的研究工作文献[1- 1矩形件排样优化算法 3]分别提出了排样问题的遗传算法;文献[4]提出了 1.1排样优化问题 将遗传算法和模拟退火算法结合的遗传模拟退火算 矩形件在矩形板材上的排样问题,可以分为2 法;文献「5]提出了启发式排样算法等等.在实际工 类:一类是在单一板材上排样,称为单排,其中包括 程中,对一个排样方案中的矩形件进行切割时,经常 卷材,卷材可以看成在宽度方向有约束而在长度方 会提出满足“一刀切”的下料工艺要求,如玻璃切割、 向没有约束的矩形板材:还有一类是在多块矩形板 厚型金属板材切割等.“一刀切”的要求实际上增加 材上的排样,称为套排.显然,套排比单排更加复杂 这里主要研究套排问题,排样优化问题可以描述成 收稿日期:200611-18. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 卷第 5 期 智 能 系 统 学 报 Vol. 2 №. 5 2007 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2007 基于遗传算法的大规模矩形件优化排样 马 炫 ,张亚龙 (西安理工大学 自动化与信息工程学院 ,陕西 西安 710048) 摘 要 :大规模矩形件优化排样是一个典型的组合优化问题 ,属于 NP2hard 问题. 实际工程中对一个排样方案一般 有满足“一刀切”的工艺要求“, 一刀切”要求增加了对排样的约束. 提出的优化算法 ,将矩形匹配分割算法作为遗传 算法染色体的解码器实现一个排样方案 ,用遗传算法进行排样方案的全局搜索. 算例比较表明 ,该算法可以求得满 足“一刀切”约束的最优解. 关键词 :遗传算法 ;矩形件排样 ;组合优化 中图分类号 : TP301 文献标识码 :A 文章编号 :167324785 (2007) 0520048205 A genetic algorithm for the layout of large scale rectangular parts MA Xuan , ZHAN G Ya2long (School of Automation and Information Engineering , Xi′an University of Technology , Xi′an 710048 ,China) Abstract :The optimal layout of large scale rectangular parts is a combinatorial optimization p roblem , a typ2 ical N P2hard one. In practical engineering , quire cutting is often requested , which increases t he constraints in t he determination of a layout. To satisfy quire cutting requirements , in t his paper , an optimization algo2 rit hm is proposed wherein a rectangular matching and segmentation algorit hm is employed as a decoder of chromo somes in a genetic algorithm to determine placement. A global optimal solution for placement can be achieved with t his genetic algorit hm. Simulation results confirmed t he validity of t he proposed algo2 rit hm. Keywords :genetic algorit hm ; rectangular parts layout ; combinatorial optimization 收稿日期 :2006211218. 矩形件排样是指在给定尺寸的矩形板材上 ,排 放多规格多数量的矩形件时 ,如何排放可以使板材 的利用率最大. 这是一个典型的组合优化问题 ,在工 业领域如冲裁件排样、造船、车辆、家具生产、玻璃切 割等行业都存在大量的排样问题. 求解最优排样方 案是一个 N P2hard 问题 ,至今尚未找到多项式时间 算法. 因此 ,对于大规模排样问题 ,在可接受的时间 内快速找到次优解的算法引起了人们的关注. 很多 学者在这方面做了卓有成效的研究工作. 文献[ 1 - 3 ]分别提出了排样问题的遗传算法 ;文献[4 ]提出了 将遗传算法和模拟退火算法结合的遗传模拟退火算 法 ;文献[ 5 ]提出了启发式排样算法等等. 在实际工 程中 ,对一个排样方案中的矩形件进行切割时 ,经常 会提出满足“一刀切”的下料工艺要求 ,如玻璃切割、 厚型金属板材切割等.“一刀切”的要求实际上增加 了排样的约束条件 ,而且切割时会产生一定的切缝 宽度. 这些都会对排样结果产生影响. 文中将矩形匹 配分割算法的局部搜索和遗传算法的全局搜索相结 合 ,提出了一种满足“一刀切”工艺要求的矩形件排 样优化算法. 设计的编码方法和具有方向交叉的交 叉算子改善了遗传算法的搜索性能. 通过算例比较 , 表明了算法的有效性. 1 矩形件排样优化算法 1. 1 排样优化问题 矩形件在矩形板材上的排样问题 ,可以分为 2 类 :一类是在单一板材上排样 ,称为单排 ,其中包括 卷材 ,卷材可以看成在宽度方向有约束而在长度方 向没有约束的矩形板材 ;还有一类是在多块矩形板 材上的排样 ,称为套排. 显然 ,套排比单排更加复杂. 这里主要研究套排问题 ,排样优化问题可以描述成 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第5期 马炫,等:基于遗传算法的大规模矩形件优化排样 。49 在给定多块矩形板材上如何排放多个矩形件,即把 切”要求 每个矩形件排放在哪块板材上,排在板材的什么位 综上所述,按准“一刀切”的要求排样,可以最大 置,是横排还是竖排等,确定一个可以使板材的利用 限度地提高板材的利用率因此,算法设计主要考虑 率达到最大的排样方案.其数学表示如下: 满足准“一刀切”的排样优化问题 设有一个矩形件集合fB,i=1,2,,n,其面 1.3遗传算法 积集合为/};一个板材集合fA},j=1,2,m,其 遗传算法作为一种全局数值优化方法,被广泛 面积集合为{a};排料优化问题就是寻找一个板材 应用于组合优化问题,对大规模矩形件排样优化问 集合{A},j=1,2,…k,k≤m,其面积集合为{a}, 题也显示出了明显的优势1引 及其上的矩形件的放置布局,使以下目标函数达到 矩形件在板材左下角的排法及板材的切法可以 最大值: 有4种,如图2所示.图中的虚线表示切割方向,图 2(a)为横排竖切,图2(b)为横排横切,图2(c)为竖 F=max (1) 排竖切,图2(d)为竖排横切.显然,在解决优化排样 问题中,矩形件的排法和板材的切法直接影响到优 (2 化结果.因此,把板材和矩形件的编号序列和方向作 在布局中要求: 为染色体中的信息,用矩形匹配分割算法实现一个 1)B,、B,互不重叠,i,j=1,2,…n,i为: 染色体所表示的排样方案,进行局部搜索;再用遗传 2)B:必须位于板材内i=1,2,n 算子实现全局搜索,是算法设计的主要思想 3)满足一定的工艺要求 1.2“一刀切”约束 “一刀切”是指在切割一个排样方案中的矩形件 时,沿矩形件边的切割线可以将板材分割成2部分, 称切割线是贯通的.排样方案中的“一刀切”约束有 (a)横排竖切 (b)横排横切 以下2种情况: 1)完全“一刀切”.在排样方案中,沿任一矩形件 边的切割线都是贯通的,这种情况如图1(a)所示. 将矩形件在板材上连续横排或连续纵排6)],容易实 现“一刀切”且切割效率最高,但排样结果不一定是 (c)竖排竖切 (b)竖排横切 最优的,特别是在多规格且同一种规格的矩形件数 量比较少的情况下,完全“一刀切”使板材的利用率 图2矩形件排放与切法 不够高 Fig.2 Placement and cutting of a part 2)准“一刀切”.在排样方案中至少有一条切割 1.3.1编码 线是贯通的,切割后形成的2块板材也分别至少有 编码就是用字符串形式表示问题空间的一个可 一条切割线是贯通的,以保证可以将板材上的全部 行解,称之为染色体.一个染色体应该表示出问题空 矩形件以贯通方式切割,如图1(b)、(c)所示.图1 间的有关信息.文献[2]的编码方法没有反映出矩形 (c)中,先沿a线切割后,再沿b线即可“一刀切”,然 件排放的方向信息,仅由矩形匹配算法确定方向,影 后再分别沿c线和d线切割.这样就可以切割出所 响了遗传算法的全局搜索性能.对于排样问题,一个 有矩形件.因此,认为这样的排样方案也满足“一刀 染色体表示的一个排放方案,既要表明哪个矩形件 h 排入哪块板材,又要表明矩形件是横排还是竖排.为 此,设计一个具有2层形式的染色体编码: 213,524136 010,011000 第1层的字符代表顺序,“,”之前的字符表示板材顺 (a)完全*一刀切“ (b)准“一刀切 (c准“一刀切 序(例中表示有3块板材),“,”之后的字符表示矩形 图1“一刀切”示例 件的排放顺序.第2层的字符表示板材和矩形件的 Fig.I Example of quire cutting 放置方向,“0”表示按原方向排放,“1”表示旋转90° 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
在给定多块矩形板材上如何排放多个矩形件 ,即把 每个矩形件排放在哪块板材上 ,排在板材的什么位 置 ,是横排还是竖排等 ,确定一个可以使板材的利用 率达到最大的排样方案. 其数学表示如下 : 设有一个矩形件集合{ Bi} , i = 1 , 2 , …, n ,其面 积集合为{ bi} ;一个板材集合{ A j} , j = 1 ,2 , …, m ,其 面积集合为{ aj} ;排料优化问题就是寻找一个板材 集合{ A′f } , j = 1 ,2 , …, k , k ≤m ,其面积集合为{ a′j } , 及其上的矩形件的放置布局 ,使以下目标函数达到 最大值 : F = max ∑ n i =1 bi / ∑ k j = 1 a′j , (1) ∑ n i =1 bi ≤ ∑ k j =1 a′j . (2) 在布局中要求 : 1) Bi 、B j 互不重叠 , i , j = 1 ,2 , …, n , i ≠j ; 2) Bi 必须位于板材内 i = 1 ,2 , …, n; 3) 满足一定的工艺要求. 1. 2 “一刀切”约束 “一刀切”是指在切割一个排样方案中的矩形件 时 ,沿矩形件边的切割线可以将板材分割成 2 部分 , 称切割线是贯通的. 排样方案中的“一刀切”约束有 以下 2 种情况 : 1) 完全“一刀切”. 在排样方案中 ,沿任一矩形件 边的切割线都是贯通的 ,这种情况如图 1 (a) 所示. 将矩形件在板材上连续横排或连续纵排[6 ] ,容易实 现“一刀切”且切割效率最高 ,但排样结果不一定是 最优的 ,特别是在多规格且同一种规格的矩形件数 量比较少的情况下 ,完全“一刀切”使板材的利用率 不够高. 图 1 “一刀切”示例 Fig. 1 Example of quire cutting 2) 准“一刀切”. 在排样方案中至少有一条切割 线是贯通的 ,切割后形成的 2 块板材也分别至少有 一条切割线是贯通的 ,以保证可以将板材上的全部 矩形件以贯通方式切割 ,如图 1 ( b) 、(c) 所示. 图 1 (c) 中 ,先沿 a 线切割后 ,再沿 b线即可“一刀切”,然 后再分别沿 c 线和 d 线切割. 这样就可以切割出所 有矩形件. 因此 ,认为这样的排样方案也满足“一刀 切”要求. 综上所述 ,按准“一刀切”的要求排样 ,可以最大 限度地提高板材的利用率. 因此 ,算法设计主要考虑 满足准“一刀切”的排样优化问题. 1. 3 遗传算法 遗传算法作为一种全局数值优化方法 ,被广泛 应用于组合优化问题 ,对大规模矩形件排样优化问 题也显示出了明显的优势[1 - 3 ] . 矩形件在板材左下角的排法及板材的切法可以 有 4 种 ,如图 2 所示. 图中的虚线表示切割方向 ,图 2 (a) 为横排竖切 ,图 2 ( b) 为横排横切 ,图 2 (c) 为竖 排竖切 ,图 2 (d) 为竖排横切. 显然 ,在解决优化排样 问题中 ,矩形件的排法和板材的切法直接影响到优 化结果. 因此 ,把板材和矩形件的编号序列和方向作 为染色体中的信息 ,用矩形匹配分割算法实现一个 染色体所表示的排样方案 ,进行局部搜索 ;再用遗传 算子实现全局搜索 ,是算法设计的主要思想. 图 2 矩形件排放与切法 Fig. 2 Placement and cutting of a part 1. 3. 1 编 码 编码就是用字符串形式表示问题空间的一个可 行解 ,称之为染色体. 一个染色体应该表示出问题空 间的有关信息. 文献[2 ]的编码方法没有反映出矩形 件排放的方向信息 ,仅由矩形匹配算法确定方向 ,影 响了遗传算法的全局搜索性能. 对于排样问题 ,一个 染色体表示的一个排放方案 ,既要表明哪个矩形件 排入哪块板材 ,又要表明矩形件是横排还是竖排. 为 此 ,设计一个具有 2 层形式的染色体编码 : 2 1 3 , 5 2 4 1 3 6 0 1 0 , 0 1 1 0 0 0 第 1 层的字符代表顺序“, ,”之前的字符表示板材顺 序(例中表示有 3 块板材) “, ,”之后的字符表示矩形 件的排放顺序. 第 2 层的字符表示板材和矩形件的 放置方向“, 0”表示按原方向排放“, 1”表示旋转 90° 第 5 期 马 炫 ,等 :基于遗传算法的大规模矩形件优化排样 ·49 · © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·50· 智能系统学报 第2卷 后排放, 取乃交叉点开始的基因顺序为1、6、7、5、2、3、 上述染色体的排样方案可能是第5、24号矩形 4,消除中已有的1、3、5,得到6、7、2、4,按此顺序决 件排入第2块板材,第1、3号矩形件排入第1块板 定x,O变为 材,第6号矩形件排入第3块板材.对于每个染色体 01:123,13516724) 所表示的排样方案由矩形匹配分割算法具体确定 同理可得: 也就是说,在遗传算法中通过调用矩形匹配分割算 02:132,234|6715) 法实现每个染色体所表示的排样方案.比如,对于上 2)方向交叉 述染色体,先选2号板材将矩形件排样,2号板材排 如果板材先旋转90°,根据矩形匹配分割算法 满后再将剩余的矩形件在1号板材上排样,1号板 中始终采用沿矩形件的竖边切割的规定,实际上是 材排满后再选3号板材对其余的矩形件排样 对板材实现了沿矩形件的横向切割.同样,矩形件放 如果只在一块板材上排样,可将板材部分的字 入板材时旋转90°可以调整矩形件的横排和竖排」 符全部设置为0.对于卷材,可将染色体中第2层板 因此,方向交叉只对染色体第2层的字符进行操作 材部分的字符全设为0,并将矩形匹配分割算法中 交叉方法如下: 的分割方向设为竖切,就可以实现矩形件在卷材上 设父代染色体为 的排样.这样,上述2层形式的染色体编码就可以具 123,1352467 P: 有比较广泛的适用性,为算法既可以应用于套排,也 010,0110100 可应用于单排提供了方便 132,2341675 1.3.2适应度函数 110,1001001 己有文献中用一个排样方案的板材利用率即板 交叉后的子代染色体O的第1层为P的第1 材上排放的矩形件的面积与板材面积之比的大小衡 层,第2层为P的第1层字符在B中所对应的第 量一个染色体的优劣,然而,余料面积相同而形状不 2层的0.1值.染色体O2的第1层为B的第1层 同,其可利用性是不同的,利用率应当包含余料面积 第2层为B的第1层字符在A中所对应的第2层 的大小和形状2个要素.因此,在适应度函数中采用 的0,1值.这样,得到子染色体如下: 了一个余料的长宽比例系数(0<B),当长和宽 123,1352467 相等时B最大 101,1011000 13.3交叉 132,2341675 由于矩形件的排放顺序和排放方向均产生不同 O2 001,011000 的排样结果,因此,设计了包括顺序交叉和方向交叉 1.3.4变异 的交叉算子在执行每次交叉操作时,随机确定是顺 由于板材横切或竖切的改变都将改变剩余矩形 序交叉还是方向交叉 的形状,从而使以后的排放方式发生变化.因此,变 1)顺序交叉 异操作只对染色体的第2层实施变异操作.根据变 顺序交叉只在染色体的第1层进行.在染色体 异概率在种群中随机选择出染色体和染色体的基因 长度范围内随机产生一个交叉点,这个点可能在板 位,对该位的基因值反转变异,即若为0,则变为1, 材部分也可能在矩形件部分.如果在板材部分就只 若为1,则变为0.由于变异操作,板材或矩形件的方 对板材顺序实施交叉,而矩形件部分保持不变.如果 向发生了变化,这样就需要对于变异点以后的剩余 在矩形件部分就只对矩形件部分实施交叉,而板材 矩形和矩形件重新调用矩形匹配分割算法, 部分保持不变.进行交叉操作时是保留交叉点前部 1.4矩形匹配分割算法 还是后部,每次也随机确定.交叉方法如下:设2个 为了实现“一刀切”,在剩余矩形匹配算法1的 父代染色体的第1层为 基础上提出了矩形匹配分割算法,按照先进行矩形 P:123,135|2467), 匹配后进行板材分割的原则进行.即首先在矩形件 P:132,234|1675) 中搜索与板材的一个边匹配程度最近的一个矩形件 “”为交叉位置,即对矩形件部分进行交叉.若保留 放入板材的左下角,然后再把板材分成2部分.由于 交叉点前部分,得到: 板材和矩形件都可旋转,因此,这里规定板材的切割 0:123,1351×××, 方向为竖切.算法主要步骤如下: 0:132,234|×××为 1)读入板材的长L和宽W,所有矩形件的长1 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
后排放. 上述染色体的排样方案可能是第 5、2、4 号矩形 件排入第 2 块板材 ,第 1、3 号矩形件排入第 1 块板 材 ,第 6 号矩形件排入第 3 块板材. 对于每个染色体 所表示的排样方案由矩形匹配分割算法具体确定. 也就是说 ,在遗传算法中通过调用矩形匹配分割算 法实现每个染色体所表示的排样方案. 比如 ,对于上 述染色体 ,先选 2 号板材将矩形件排样 ,2 号板材排 满后再将剩余的矩形件在 1 号板材上排样 ,1 号板 材排满后再选 3 号板材对其余的矩形件排样. 如果只在一块板材上排样 ,可将板材部分的字 符全部设置为 0. 对于卷材 ,可将染色体中第 2 层板 材部分的字符全设为 0 ,并将矩形匹配分割算法中 的分割方向设为竖切 ,就可以实现矩形件在卷材上 的排样. 这样 ,上述 2 层形式的染色体编码就可以具 有比较广泛的适用性 ,为算法既可以应用于套排 ,也 可应用于单排提供了方便. 1. 3. 2 适应度函数 已有文献中用一个排样方案的板材利用率即板 材上排放的矩形件的面积与板材面积之比的大小衡 量一个染色体的优劣 ,然而 ,余料面积相同而形状不 同 ,其可利用性是不同的 ,利用率应当包含余料面积 的大小和形状 2 个要素. 因此 ,在适应度函数中采用 了一个余料的长宽比例系数β(0 <β≤1) ,当长和宽 相等时 ,β最大. 1. 3. 3 交 叉 由于矩形件的排放顺序和排放方向均产生不同 的排样结果 ,因此 ,设计了包括顺序交叉和方向交叉 的交叉算子. 在执行每次交叉操作时 ,随机确定是顺 序交叉还是方向交叉. 1) 顺序交叉 顺序交叉只在染色体的第 1 层进行. 在染色体 长度范围内随机产生一个交叉点 ,这个点可能在板 材部分也可能在矩形件部分. 如果在板材部分就只 对板材顺序实施交叉 ,而矩形件部分保持不变. 如果 在矩形件部分就只对矩形件部分实施交叉 ,而板材 部分保持不变. 进行交叉操作时是保留交叉点前部 还是后部 ,每次也随机确定. 交叉方法如下 :设 2 个 父代染色体的第 1 层为 P1 : (1 2 3 , 1 3 5 | 2 4 6 7) , P2 : (1 3 2 , 2 3 4 | 1 6 7 5) . “| ”为交叉位置 ,即对矩形件部分进行交叉. 若保留 交叉点前部分 ,得到 : O1 : (1 2 3 , 1 3 5 | × × × ×) , O2 : (1 3 2 , 2 3 4 | × × × ×) . 取 P2 交叉点开始的基因顺序为 1、6、7、5、2、3、 4 ,消除中已有的 1、3、5 ,得到 6、7、2、4 ,按此顺序决 定 x , O1 变为 O1 : (1 2 3 , 1 3 5 | 6 7 2 4) . 同理可得 : O2 : (1 3 2 , 2 3 4 | 6 7 1 5) . 2) 方向交叉 如果板材先旋转 90°,根据矩形匹配分割算法 中始终采用沿矩形件的竖边切割的规定 ,实际上是 对板材实现了沿矩形件的横向切割. 同样 ,矩形件放 入板材时旋转 90°可以调整矩形件的横排和竖排. 因此 ,方向交叉只对染色体第 2 层的字符进行操作. 交叉方法如下 : 设父代染色体为 P1 : 1 2 3 , 1 3 5 2 4 6 7 0 1 0 , 0 1 1 0 1 0 0 , P2 : 1 3 2 , 2 3 4 1 6 7 5 1 1 0 , 1 0 0 1 0 0 1 . 交叉后的子代染色体 O1 的第 1 层为 P1 的第 1 层 ,第 2 层为 P1 的第 1 层字符在 P2 中所对应的第 2 层的 0 ,1 值. 染色体 O2 的第 1 层为 P2 的第 1 层 , 第 2 层为 P2 的第 1 层字符在 P1 中所对应的第 2 层 的 0 ,1 值. 这样 ,得到子染色体如下 : O1 : 1 2 3 , 1 3 5 2 4 6 7 1 0 1 ,1 0 1 1 0 0 0 , O2 : 1 3 2 , 2 3 4 1 6 7 5 0 0 1 , 0 1 1 0 0 0 1 . 1. 3. 4 变 异 由于板材横切或竖切的改变都将改变剩余矩形 的形状 ,从而使以后的排放方式发生变化. 因此 ,变 异操作只对染色体的第 2 层实施变异操作. 根据变 异概率在种群中随机选择出染色体和染色体的基因 位 ,对该位的基因值反转变异 ,即若为 0 ,则变为 1 , 若为 1 ,则变为 0. 由于变异操作 ,板材或矩形件的方 向发生了变化 ,这样就需要对于变异点以后的剩余 矩形和矩形件重新调用矩形匹配分割算法. 1. 4 矩形匹配分割算法 为了实现“一刀切”,在剩余矩形匹配算法[7 ] 的 基础上提出了矩形匹配分割算法 ,按照先进行矩形 匹配后进行板材分割的原则进行. 即首先在矩形件 中搜索与板材的一个边匹配程度最近的一个矩形件 放入板材的左下角 ,然后再把板材分成 2 部分. 由于 板材和矩形件都可旋转 ,因此 ,这里规定板材的切割 方向为竖切. 算法主要步骤如下 : 1) 读入板材的长 L 和宽 W ,所有矩形件的长 l ·50 · 智 能 系 统 学 报 第 2 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
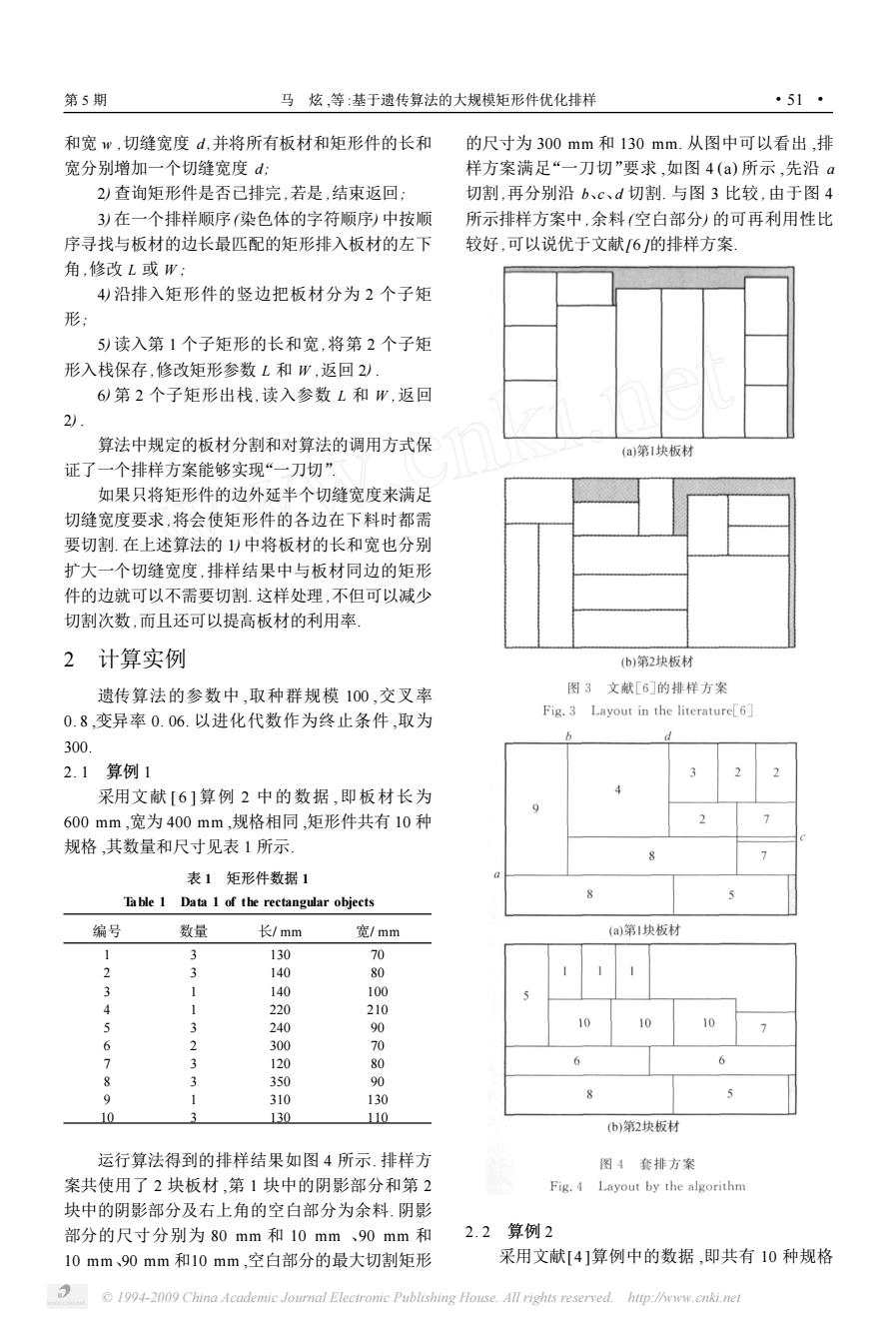
第5期 马炫,等:基于遗传算法的大规模矩形件优化排样 ·51· 和宽w,切缝宽度d,并将所有板材和矩形件的长和 的尺寸为300mm和130mm.从图中可以看出,排 宽分别增加一个切缝宽度d: 样方案满足“一刀切”要求,如图4(a)所示,先沿a 2)查询矩形件是否己排完,若是,结束返回: 切割,再分别沿b、c、d切割.与图3比较,由于图4 3)在一个排样顺序(染色体的字符顺序)中按顺 所示排样方案中,余料(空白部分)的可再利用性比 序寻找与板材的边长最匹配的矩形排入板材的左下 较好,可以说优于文献[6的排样方案 角,修改L或W: 4)沿排入矩形件的竖边把板材分为2个子矩 形: 5)读入第1个子矩形的长和宽,将第2个子矩 形入栈保存,修改矩形参数L和W,返回2). 6)第2个子矩形出栈,读入参数L和W,返回 2· 算法中规定的板材分割和对算法的调用方式保 (a)第1块板材 证了一个排样方案能够实现“一刀切”, 如果只将矩形件的边外延半个切缝宽度来满足 切缝宽度要求,将会使矩形件的各边在下料时都需 要切割.在上述算法的1)中将板材的长和宽也分别 扩大一个切缝宽度,排样结果中与板材同边的矩形 件的边就可以不需要切割.这样处理,不但可以减少 切割次数,而且还可以提高板材的利用率。 2计算实例 (b)第2块板材 遗传算法的参数中,取种群规模100,交叉率 图3文献[6]的排样方案 Fig.3 Layout in the literature6] 0.8,变异率0.06.以进化代数作为终止条件,取为 d 300. 2.1算例1 3 采用文献[6]算例2中的数据,即板材长为 9 600mm,宽为400mm,规格相同,矩形件共有10种 规格,其数量和尺寸见表1所示。 8 7 表1矩形件数据1 Table 1 Data 1 of the rectangular objects 5 编号 数量 长/mm 宽/mm (a)第1块板材 1 3 130 70 2 3 140 80 1 140 100 4 220 210 5 3 240 90 10 6 300 70 1 3 120 o 6 350 90 9 1 310 130 8 5 10 3 130 110 (b)第2块板材 运行算法得到的排样结果如图4所示.排样方 图4套排方案 案共使用了2块板材,第1块中的阴影部分和第2 Fig.4 Layout by the algorithm 块中的阴影部分及右上角的空白部分为余料.阴影 部分的尺寸分别为80mm和10mm、90mm和 2.2算例2 10mm、90mm和10mm,空白部分的最大切割矩形 采用文献[4]算例中的数据,即共有10种规格 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
和宽 w ,切缝宽度 d ,并将所有板材和矩形件的长和 宽分别增加一个切缝宽度 d ; 2) 查询矩形件是否已排完 ,若是 ,结束返回; 3) 在一个排样顺序(染色体的字符顺序) 中按顺 序寻找与板材的边长最匹配的矩形排入板材的左下 角 ,修改 L 或 W ; 4) 沿排入矩形件的竖边把板材分为 2 个子矩 形; 5) 读入第 1 个子矩形的长和宽 ,将第 2 个子矩 形入栈保存 ,修改矩形参数 L 和 W ,返回 2) . 6) 第 2 个子矩形出栈,读入参数 L 和 W ,返回 2) . 算法中规定的板材分割和对算法的调用方式保 证了一个排样方案能够实现“一刀切”. 如果只将矩形件的边外延半个切缝宽度来满足 切缝宽度要求 ,将会使矩形件的各边在下料时都需 要切割. 在上述算法的 1) 中将板材的长和宽也分别 扩大一个切缝宽度 ,排样结果中与板材同边的矩形 件的边就可以不需要切割. 这样处理 ,不但可以减少 切割次数 ,而且还可以提高板材的利用率. 2 计算实例 遗传算法的参数中 ,取种群规模 100 ,交叉率 0. 8 ,变异率 0. 06. 以进化代数作为终止条件 ,取为 300. 2. 1 算例 1 采用文献 [ 6 ] 算例 2 中的数据 ,即板材长为 600 mm ,宽为 400 mm ,规格相同 ,矩形件共有 10 种 规格 ,其数量和尺寸见表 1 所示. 表 1 矩形件数据 1 Table 1 Data 1 of the rectangular objects 编号 数量 长/ mm 宽/ mm 1 3 130 70 2 3 140 80 3 1 140 100 4 1 220 210 5 3 240 90 6 2 300 70 7 3 120 80 8 3 350 90 9 1 310 130 10 3 130 110 运行算法得到的排样结果如图 4 所示. 排样方 案共使用了 2 块板材 ,第 1 块中的阴影部分和第 2 块中的阴影部分及右上角的空白部分为余料. 阴影 部分的尺寸分别为 80 mm 和 10 mm 、90 mm 和 10 mm、90 mm 和10 mm ,空白部分的最大切割矩形 的尺寸为 300 mm 和 130 mm. 从图中可以看出 ,排 样方案满足“一刀切”要求 ,如图 4 (a) 所示 ,先沿 a 切割 ,再分别沿 b、c、d 切割. 与图 3 比较 ,由于图 4 所示排样方案中 ,余料 (空白部分) 的可再利用性比 较好 ,可以说优于文献[6 ]的排样方案. 2. 2 算例 2 采用文献[4 ]算例中的数据 ,即共有 10 种规格 第 5 期 马 炫 ,等 :基于遗传算法的大规模矩形件优化排样 ·51 · © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·52· 智能系统学报 第2卷 的矩形件,其数量及尺寸的数据如表2所示.在卷材 CAO Ju,FENG Song.The application of genetic algo- 上排样,卷材宽度为600mm.运行算法得到的排样 rithm in rectangular object optimal layout [J].Computer 结果如图5所示,卷材的使用长度为1150mm,小 Engineering and Application,1999,5(2):5-7. 于文献[4]的卷材长度1245mm [2]杨威,罗阳,刘胜青.大规模矩形零件优化套排的遗 传算法[U].四川大学学报(工程科学版),2001,33(5) 表2矩形件数据2 59.62. Table 2 Data 2 of the rectangular objects YANG Wei,LUO Yang,LIU Shengqing.Genetic algo- 编号 数量 长/mm 宽/mm rithm for large scale rectangular object optimal embed 5 40 40 20 placement[J].Journal of Sichuan University (Engineer- % 78 15 6 ing science edition),2001,33(5):59-62. 2 19 50 30 [3]韩喜君,丁根宏.基于改进遗传算法的矩形件优化排样 59 50 25 [U].计算机工程与应用,2006,42(25):63.65. 6 64 50 40 HAN Xijun,DING Genhong.The optimum packing of 35 18 6 rectangles based on improved genetic algorithm [J ] 15 26 45 Computer Engineering and Application,2006,42(25): 2 49 35 15 63.65 3 66 60 40 [4]杨彩,史俊友,顾海明.基于遗传模拟退火算法的矩形 80 80 40 件排样[U].青岛科技大学学报,2004,25(5):452·456. YANG Cai,SHIJunyou,GU Haiming.Packing of rec- tangular using genetic simulated annealing algorithm[J]. Journal of Qingdao University of Science and Technolo- gy,2004,25(5):452-456. [5]罗意平,刘军,李兵,等.一个实用的矩形件优化排样 启发式算法U].工程图学学报,2003,24(4):50.58 150 LUO Yiping,LIU Jun,LI Bing,et al.A practical heu 图5卷材上的排样方案 ristic algorithm for rectangle parts packing problem[J]. Fig.5 Layout on the roll Journal of Engineering Graphics,2003,24(4):50-58. 3结束语 [6]陶献伟,王华昌,李志刚.基于填充算法的矩形件排样优 化求解U].中国机械工程,2003,14(13):1104.1108. 针对已有遗传算法中存在由于编码信息不全而 TAO Xianwei,WANG Huachang,LI Zhigang.Optimal 产生的算法搜索性能不够好的问题,以及实际生产 solution of rectangular part layout based on rectangle fill- 中对排样方案的“一刀切”工艺要求,文中设计了一 ing algorithm[J].China Mechanical Engineering,2003 个具有2层形式的染色体编码,并在遗传算法中调 14(13):1104.1108 用改进后的矩形匹配分割算法实现一个具体排样方 [7]邢文训,谢金星.现代优化计算方法[M],2版.北京:清 华大学出版社,2005. 案.矩形匹配分割算法和遗传算法都是解决矩形件 作者简介: 排样问题的有效方法,前者具有局部搜索性能强而 马炫,男,1962年生,工学博士, 后者全局搜索性能好.将二者结合的算法可以更有 副教授硕士生导师,主要研究方向为智 效地解决大规模多规格的板材和矩形件的排样优化 能信息处理、模式识别.在国内外刊物上 问题.计算实例表明了文中提出的算法可以找到比 发表论文10余篇,著有译著1部. 较好的排样方案.由于算法可以实现板材的“一刀 Email maxuan @xaut.edu.cn 切”要求,并考虑了下料工艺中的切缝宽度问题,不 仅可以应用于不同规格板材的套排,还可用于单块 板材及卷材,具有更好的适用性和实用性.算法已制 成软件在实际生产中应用】 张亚龙,男,1976年生,硕士研究 参考文献: 生,主要研究方向为遗传算法及应用. [1]曹炬,冯松.遗传算法在矩形件优化排样中的应用 [U].计算机工程与应用,1999,5(2):5.7 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
的矩形件 ,其数量及尺寸的数据如表 2 所示. 在卷材 上排样 ,卷材宽度为 600 mm. 运行算法得到的排样 结果如图 5 所示 ,卷材的使用长度为 1 150 mm ,小 于文献[ 4 ]的卷材长度 1 245 mm. 表 2 矩形件数据 2 Table 2 Data 2 of the rectangular objects 编号 数量 长/ mm 宽/ mm 5 40 40 20 8 78 15 6 12 19 50 30 1 59 50 25 6 64 50 40 9 35 18 6 15 26 45 15 2 49 35 15 3 66 60 40 4 80 80 40 图 5 卷材上的排样方案 Fig. 5 Layout on the roll 3 结束语 针对已有遗传算法中存在由于编码信息不全而 产生的算法搜索性能不够好的问题 ,以及实际生产 中对排样方案的“一刀切”工艺要求 ,文中设计了一 个具有 2 层形式的染色体编码 ,并在遗传算法中调 用改进后的矩形匹配分割算法实现一个具体排样方 案. 矩形匹配分割算法和遗传算法都是解决矩形件 排样问题的有效方法 ,前者具有局部搜索性能强而 后者全局搜索性能好. 将二者结合的算法可以更有 效地解决大规模多规格的板材和矩形件的排样优化 问题. 计算实例表明了文中提出的算法可以找到比 较好的排样方案. 由于算法可以实现板材的“一刀 切”要求 ,并考虑了下料工艺中的切缝宽度问题 ,不 仅可以应用于不同规格板材的套排 ,还可用于单块 板材及卷材 ,具有更好的适用性和实用性. 算法已制 成软件在实际生产中应用. 参考文献 : [1 ]曹 炬 ,冯 松. 遗传算法在矩形件优化排样中的应用 [J ]. 计算机工程与应用 ,1999 ,5 (2) : 5 - 7. CAO J u , FEN G Song. The application of genetic algo2 rithm in rectangular object optimal layout [J ]. Computer Engineering and Application , 1999 ,5 (2) : 5 - 7. [2 ]杨 威 ,罗 阳 ,刘胜青. 大规模矩形零件优化套排的遗 传算法[J ]. 四川大学学报 ( 工程科学版) ,2001 ,33 (5) : 59 - 62. YAN G Wei , LUO Yang , L IU Shengqing. Genetic algo2 rithm for large scale rectangular object optimal embed placement[J ]. Journal of Sichuan University ( Engineer2 ing science edition) , 2001 ,33 (5) :59 - 62. [3 ]韩喜君 ,丁根宏. 基于改进遗传算法的矩形件优化排样 [J ]. 计算机工程与应用 ,2006 ,42 (25) :63 - 65. HAN Xijun , DIN G Genhong. The optimum packing of rectangles based on improved genetic algorithm [ J ]. Computer Engineering and Application , 2006 , 42 (25) : 63 - 65. [4 ]杨 彩 ,史俊友 ,顾海明. 基于遗传模拟退火算法的矩形 件排样[J ]. 青岛科技大学学报 ,2004 ,25 (5) :452 - 456. YAN G Cai , SHI J unyou , GU Haiming. Packing of rec2 tangular using genetic simulated annealing algorithm[J ]. Journal of Qingdao University of Science and Technolo2 gy , 2004 ,25 (5) :452 - 456. [5 ]罗意平 ,刘 军 ,李 兵 ,等. 一个实用的矩形件优化排样 启发式算法[J ]. 工程图学学报 ,2003 ,24 (4) :50 - 58. LUO Yiping , L IU J un , L I Bing ,et al. A practical heu2 ristic algorithm for rectangle parts packing problem[J ]. Journal of Engineering Graphics , 2003 , 24 (4) : 50 - 58. [6 ]陶献伟 ,王华昌 ,李志刚. 基于填充算法的矩形件排样优 化求解[J ]. 中国机械工程 ,2003 ,14 (13) : 1104 - 1108. TAO Xianwei , WAN G Huachang , L I Zhigang. Optimal solution of rectangular part layout based on rectangle fill2 ing algorithm[J ]. China Mechanical Engineering , 2003 , 14 (13) : 1104 - 1108. [7 ]邢文训 ,谢金星. 现代优化计算方法[ M ]. 2 版. 北京 :清 华大学出版社 ,2005. 作者简介 : 马 炫 ,男 ,1962 年生 ,工学博士 , 副教授 ,硕士生导师 ,主要研究方向为智 能信息处理、模式识别. 在国内外刊物上 发表论文 10 余篇 ,著有译著 1 部. E2mail : maxuan @xaut. edu. cn. 张亚龙 ,男 ,1976 年生 ,硕士研究 生 ,主要研究方向为遗传算法及应用. ·52 · 智 能 系 统 学 报 第 2 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net