
第3卷第2期 智能系统学报 Vol.3№2 2008年4月 CAAI Transactions on Intelligent Systems Apr.2008 TSP冰晶算法 周蓝海,蔡东风 (沈阳航空工业学院知识工程中心,辽宁沈阳110034) 摘要:TSP即旅行商问题,是一个典型的NP困难问题,随问题规模的增加,获得最优解的代价呈指数级增长.受自 然智能的启发,冰晶算法首次模拟湖水降温时湖面冰晶的生长过程,在亚稳态区内维持适宜的饱和度来尝试解决 TSP问题.冰晶生长的过程就是TSP路径形成的过程,试验表明,这是一种快速有效的TSP问题近似算法,可在O (kog)时间复杂度下获得可行解,同时该算法适用于并行计算,可对开环动态、大规模的TSP问题实时求解。 关键词:旅行商问题;冰晶;树枝晶;凸壳;非确定多项式 中图分类号:TP301.5文献标识码:A文章编号:16734785(2008)02-0167-06 Solving the TSP problem with a crystal algorithm ZHOU Lamhai,CAI Dong feng Knowledge Engineering Research Center,Shenyang Institute of Aeronautical Engineering,Shenyang 110034,China) Abstract:The traveling salesman problem (TSP)is a typical NP problem.The optimal solution can be costly to obtain as computational requirements of the problem increase exponentially with complexity.This paper proposes a new method for solving TSP problems.With this method,we simulated the growth process of crystals on the surface of a lake as the temperature of the water decreased.In the metastable re- gion we maintained an appropriate degree of saturation and found the growth process of the crystals was the same as the process of forming a TSP path.The proposed method is an appropriate algorithm for sol- ving TSP problems quickly and effectively,obtaining feasible solutions under O(knlogn)complexity.It can also be used in parallel computation,generating real-time solutions for opemlooped,dynamic,and large-scale TSP problems. Key words :traveling salesman problem;ice crystal;dendrite;convex hull;nondeterministic polynomialm 随着网络、通讯、宽带、物流等技术的发展,网络力学与动力学等多种因素影响,是复杂物理现象相 数据优先,电网电力调度,卫星信号中继,国际物流 互作用的结果.冰晶现象是描述自然界液态水降温 配送,多处理器协同等领域,要求能够快速对目标 凝固,结晶长大的过程,具有能量最小原则的特征, TSP现象进行正确和精确的定位,及时获得有效的 在过冷却水滴和冰晶共存的水面,如果存在E< 解决途径 e<Es(E表示饱和水汽压,e表示水汽压,i表示冰,s TsP问题被证明是一个NP-hard问题.目前 表示过冷却水),冰晶就会凝结而不断长大,冰水共 解决TSP问题有蚂蚁算法!、遗传算法、粒子群算 存相互渗透.冰晶算法模拟自然湖面冰晶的生长过 法)及弹性网络等,在有限的时空复杂度下获得近 程来尝试解决TSP问题,并取得较好的试验结果, 似解或次(最)优解.迭代的求解方式,在大规模有实 1 时性要求的场合,就显得力不从心,有待寻求更高效 试验模型 的算法, TSP冰晶算法的提出是基于以下3个假设: 晶体生长是一种动态相变过程,受晶体生长热 假设1元素属性一致的前提下,系统边界层 的元素对系统的干扰很大,系统内元素只会产生局 收稿日期:2007-0625. 基金项目:教育部科学技术研究重点资助项目(207148) 部扰动,复杂存在于系统的边缘。 通讯作者:周蓝海,Email:zhlanhai@l63.com. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3 卷第 2 期 智 能 系 统 学 报 Vol. 3 №. 2 2008 年 4 月 CAA I Transactions on Intelligent Systems Apr. 2008 TSP 冰晶算法 周蓝海 , 蔡东风 (沈阳航空工业学院 知识工程中心 ,辽宁 沈阳 110034) 摘 要 : TSP 即旅行商问题 ,是一个典型的 NP 困难问题 ,随问题规模的增加 ,获得最优解的代价呈指数级增长. 受自 然智能的启发 ,冰晶算法首次模拟湖水降温时 ,湖面冰晶的生长过程 ,在亚稳态区内维持适宜的饱和度来尝试解决 TSP 问题. 冰晶生长的过程就是 TSP 路径形成的过程 ,试验表明 ,这是一种快速有效的 TSP 问题近似算法 ,可在 O ( knlogn) 时间复杂度下获得可行解 ,同时该算法适用于并行计算 ,可对开环、动态、大规模的 TSP 问题实时求解. 关键词 :旅行商问题 ;冰晶 ;树枝晶 ;凸壳 ;非确定多项式 中图分类号 : TP301. 5 文献标识码 :A 文章编号 :167324785 (2008) 0220167206 Solving the TSP problem with a crystal algorithm ZHOU Lan2hai , CAI Dong2feng ( Knowledge Engineering Research Center , Shenyang Institute of Aeronautical Engineering ,Shenyang 110034 ,China) Abstract :The traveling salesman p roblem ( TSP) is a typical NP problem. The optimal solution can be costly to obtain as comp utational requirements of the problem increase exponentially wit h complexity. This paper proposes a new met hod for solving TSP problems. Wit h t his met hod , we simulated t he growt h process of crystals on t he surface of a lake as t he temperature of the water decreased. In t he metastable re2 gion we maintained an appropriate degree of sat uration and found t he growth process of t he crystals was t he same as the p rocess of forming a TSP pat h. The proposed met hod is an appropriate algorit hm for sol2 ving TSP problems quickly and effectively , obtaining feasible solutions under O ( knlog n) complexity. It can also be used in parallel comp utation , generating real2time solutions for open2looped , dynamic , and large2scale TSP p roblems. Keywords :traveling salesman problem ;ice crystal ;dendrite ;convex hull ;nondeterministic polynomialm 收稿日期 :2007206225. 基金项目 :教育部科学技术研究重点资助项目(207148) . 通讯作者 :周蓝海. E2mail :zhlanhai @163. com. 随着网络、通讯、宽带、物流等技术的发展 ,网络 数据优先 ,电网电力调度 ,卫星信号中继 ,国际物流 配送 ,多处理器协同等领域 ,要求能够快速对目标 TSP 现象进行正确和精确的定位 ,及时获得有效的 解决途径. TSP 问题被证明是一个 NP2hard [ 1 ] 问题. 目前 解决 TSP 问题有蚂蚁算法[ 2 ] 、遗传算法、粒子群算 法[3 ]及弹性网络等 ,在有限的时空复杂度下获得近 似解或次(最) 优解. 迭代的求解方式 ,在大规模有实 时性要求的场合 ,就显得力不从心 ,有待寻求更高效 的算法. 晶体生长是一种动态相变过程 ,受晶体生长热 力学与动力学等多种因素影响 ,是复杂物理现象相 互作用的结果. 冰晶现象是描述自然界液态水降温 凝固 ,结晶长大的过程 ,具有能量最小原则的特征 , 在过冷却水滴和冰晶共存的水面 ,如果存在 Ei < e < Es ( E 表示饱和水汽压 , e 表示水汽压 ,i 表示冰 ,s 表示过冷却水) ,冰晶就会凝结而不断长大 ,冰水共 存相互渗透. 冰晶算法模拟自然湖面冰晶的生长过 程来尝试解决 TSP 问题 ,并取得较好的试验结果. 1 试验模型 TSP 冰晶算法的提出是基于以下 3 个假设 : 假设 1 元素属性一致的前提下 ,系统边界层 的元素对系统的干扰很大 ,系统内元素只会产生局 部扰动 ,复杂存在于系统的边缘

·168 智能系统学报 第3卷 假设2:晶体形成过程中,晶界微偏聚动力和晶 1.2冰晶效应 间脆性断裂等现象不会对晶格点阵的整体布局产生 1.2.1冰晶形成 蝴蝶效应,忽略该算法在最坏情况下获得可行解的 冰晶是自然界很平常的物理现象.液体凝固包 难度 括晶核的形成和长大,晶核的形成是液体中的一些 假设3:固相的冰晶内不存在扩散现象,忽略凝 原子的动能减少到足以使这些原子固定于晶格点阵 固界面曲率等因素对凝固前沿的影响,以此来简化 上时发生的晶体成核现象,如水结冰 冰晶生长所谓的能量函数, 原子的大小、形态及相邻原子间键合的性质,会 TSP问题与冰晶现象的相似性分析,如表1, 导致一种最低能量的单晶组态,决定了原子在晶体 值得一提的是其中冰晶生长的过程就是TSP路径 中规则的周期性排列,温度和压力的不同,会有不同 形成的过程 的晶体结构1湖面结冰则是以湖畔为依托冰晶不 断的向湖中心生长,直到湖面冰封的过程 表1特征相似性分析 1.2.2树枝晶体 Table I Similarity analysis of the characteristics 湖岸的表面一般都有凹凸部分,水会均匀地浸 序号 冰晶算法 TSP(计算几何) 透湖岸,并吸附着空气和湿气,导致晶胚的活性较 CFI 湖面 地图(凸壳域) CF2 湖畔 国界(凸壳边界) 大,与水全接触的湖畔的晶核,可以优先生长。 CF3 晶胞 城市(点集) CF4 冰晶生长 路径形成 CF5 临界冰渣 诱导走向歧途的城市 CF6 微风吹拂湖面 局部约束扰动 1.1形成湖畔 1.1.1凸壳定义 平面(E)中点集S的凸壳是包含S的最小 图2树枝晶的生长 凸集,凸壳是S计算几何中最普遍、最基本的一种 Fig,2 Growth of the dendrite 结构,它不仅有许多自身的特征,还是构造其他几何 形体的有效工具.本文采用Gramham扫描算法,如 凝固初期,晶粒在生长过程中与相邻晶粒接触 果点集有n个点,时空开销主要涉及角度排序,需要 形成凝固壳,先沿着湖岸横向生长,形成树枝晶的树 O(Hog列时间) 干和分支,竞争过程中优先生长的分支在横向又生 1.1.2围建湖岸 出子分支形成树枝晶,如图2所示,其阴影部分表示 令V=(,2,,ym)代表由v个晶核组成 己结冰区域, 的一个矢量,存储凸壳的顶点并以此为基础形成湖 计算机模拟晶体生长,本文采用距离函数代替 岸,为湖水中晶胞提供一个结冰的容器 能量函数,控制晶体生长的过程,令Ew(p)为第1 凸壳的抽象形态如图1,其中每一个圆点表示 特征点对应凝固前沿的每条边是否结冰的判定依 一个城市,黑色的圆点表示湖畔的晶核,白色的圆点 据,点x、y代表该边的2个端点.E(p)=Da+ 表示湖面游离的晶胞,外围样条虚线表示的人工围 Do Dsy-A(dn da),pr min{Ex (p)(i=1. 建的湖岸,直线段虚线表示点集的凸壳边界 2,k,…2.其中:D表示点x和点y的距离: d和dm分别表示i点与其最近点、次近点的距离:A =0,1),取0为绝对代价,取1为相对代价;pk表 示获得能量最小值的ⅰ点,该点可以凝固结冰;k是 一个待定值,指需要计算的每个城市最邻近城市的 0 数目,均匀分布的TSP问题取30~60就可以,不均 匀的分布适当取大一点,要保证在k邻图中不会出 现孤立的岛.E,(p)控制树枝晶的生长并进行过程 图1湖畔模型结构 扫描,所得记录即所求TSP可行解,晶胞全部结冰 Fig 1 Structure of the lakefront model 后,图2所示湖中心未结冰区域的边界就是所求 TSP问题的可行解路径 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
假设 2 :晶体形成过程中 ,晶界微偏聚动力和晶 间脆性断裂等现象不会对晶格点阵的整体布局产生 蝴蝶效应 ,忽略该算法在最坏情况下获得可行解的 难度. 假设 3 :固相的冰晶内不存在扩散现象 ,忽略凝 固界面曲率等因素对凝固前沿的影响 ,以此来简化 冰晶生长所谓的能量函数. TS P 问题与冰晶现象的相似性分析 ,如表 1 , 值得一提的是其中冰晶生长的过程就是 TS P 路径 形成的过程. 表 1 特征相似性分析 Table 1 Similarity analysis of the characteristics 序号 冰晶算法 TSP(计算几何) CF1 湖面 地图(凸壳域) CF2 湖畔 国界(凸壳边界) CF3 晶胞 城市(点集) CF4 冰晶生长 路径形成 CF5 临界冰渣 诱导走向歧途的城市 CF6 微风吹拂湖面 局部约束扰动 111 形成湖畔 11111 凸壳定义 平面( E 2 ) 中点集 S 的凸壳[4 ] 是包含 S 的最小 凸集 ,凸壳是 S 计算几何中最普遍、最基本的一种 结构 ,它不仅有许多自身的特征 ,还是构造其他几何 形体的有效工具. 本文采用 Gramham 扫描算法 ,如 果点集有 n 个点 ,时空开销主要涉及角度排序 ,需要 O( nlog n) 时间[5 ] . 11112 围建湖岸 令 V = ( v1 , v2 , v3 , …, vm ) 代表由 v 个晶核组成 的一个矢量 ,存储凸壳的顶点并以此为基础形成湖 岸 ,为湖水中晶胞提供一个结冰的容器. 凸壳的抽象形态如图 1 ,其中每一个圆点表示 一个城市 ,黑色的圆点表示湖畔的晶核 ,白色的圆点 表示湖面游离的晶胞 ,外围样条虚线表示的人工围 建的湖岸 ,直线段虚线表示点集的凸壳边界. 图 1 湖畔模型结构 Fig11 Structure of the lakefront model 112 冰晶效应 11211 冰晶形成 冰晶是自然界很平常的物理现象. 液体凝固包 括晶核的形成和长大 ,晶核的形成是液体中的一些 原子的动能减少到足以使这些原子固定于晶格点阵 上时发生的晶体成核现象 ,如水结冰. 原子的大小、形态及相邻原子间键合的性质 ,会 导致一种最低能量的单晶组态 ,决定了原子在晶体 中规则的周期性排列 ,温度和压力的不同 ,会有不同 的晶体结构[6 ] . 湖面结冰则是以湖畔为依托冰晶不 断的向湖中心生长 ,直到湖面冰封的过程. 11212 树枝晶体 湖岸的表面一般都有凹凸部分 ,水会均匀地浸 透湖岸 ,并吸附着空气和湿气 ,导致晶胚的活性较 大 ,与水全接触的湖畔的晶核 ,可以优先生长. 图 2 树枝晶的生长 Fig12 Growth of the dendrite 凝固初期 ,晶粒在生长过程中与相邻晶粒接触 形成凝固壳 ,先沿着湖岸横向生长 ,形成树枝晶的树 干和分支 ,竞争过程中优先生长的分支在横向又生 出子分支形成树枝晶 ,如图 2 所示 ,其阴影部分表示 已结冰区域. 计算机模拟晶体生长 ,本文采用距离函数代替 能量函数 ,控制晶体生长的过程 ,令 Exy ( pi) 为第 i 特征点对应凝固前沿的每条边是否结冰的判定依 据 ,点 x、y 代表该边的 2 个端点. Exy ( pi) = Dix + Diy - Dxy - λ( df i + dsi ) , pk = min{ Exy ( pi) } ( i = 1 , 2 , …, k , …,2 k) . 其中 : Dxy 表示点 x 和点 y 的距离; df i和 dsi分别表示 i 点与其最近点、次近点的距离;λ = { 0 , 1} ,取 0 为绝对代价 ,取 1 为相对代价; pk 表 示获得能量最小值的 i 点 ,该点可以凝固结冰; k 是 一个待定值 ,指需要计算的每个城市最邻近城市的 数目 ,均匀分布的 TSP 问题取 30~60 就可以 ,不均 匀的分布适当取大一点 ,要保证在 k 邻图中不会出 现孤立的岛. Exy ( pi) 控制树枝晶的生长并进行过程 扫描 ,所得记录即所求 TSP 可行解 ,晶胞全部结冰 后 ,图 2 所示湖中心未结冰区域的边界就是所求 TSP 问题的可行解路径. ·168 · 智 能 系 统 学 报 第 3 卷

第2期 周蓝海,等:TSP冰晶算法 ·169· 1.2.3局部扰动 范围内求点Pk,(如果做扰动的话,在此处加入扰动 初期模型的试验结果表明,在冰晶生长的过程 函数即可),将P按照xy确定的位置加入点集V, 中,单一依靠距离函数的判定,效果不很理想.自然 删除P中该点 冰晶生长会出现一些临界冰渣,某个区域很难简单 Mi++,goto 3) 判定它是已结冰,还是未结冰,这种混沌现象会影响 5)路径输出:计算回路的长度并输出C 冰晶的继续生长,并诱导路径的错误走向.无序向有 算法终止 序的转化,本文采用微风吹拂湖面,对可能引导进入 时间复杂度:1)为0(log)时间,2)为 歧途的晶胞做局部扰动,扰动后如果小晶胞仍处于 O(klog),k为求n个点的前k个近邻点的时间开 结冰状态,就认定它已正常结冰,扰动的时间复杂度 销系数.3)、4)共小于O(knlogn),5)为常数时间,所 为O(kd 以该算法总的时间复杂度为O(kogm)时间, 2试验设计 3结果分析 本文选取的试验数据是国际TSPL IB和台湾某 本试验选取国际TSPLIB提供的数据和台湾 大学提供的参考数据」 清华大学咨询工程系的部分测试结果 冰晶算法框图如图3。 为了便于比较,对一些TSP求解的近似算法的 初始化点集A 效率有一个直观的认识,表2给出台湾清华大学提 供的参考数据劉.其中“弹性网络”表示1987年由 计算凸壳得到点集 Durbin和Willshaw提出了算法,其精髓是:想象弹 计算点集A的k~邻近 性网络是一个橡皮筋,会自动收缩到最小张力的状 m++ 态,“蚂蚁”表示“蚂蚁算法”,“基因”表示“基因算 mj=n 求P并加入点集严 法”,“人脑"”表示人工一笔画对平面点集求TSP路 径,城市数目比较少时,该算法比较理想.表中百分 输出 比“%”代表试验的结果比参考解高出多少,“”表示 Y 绘图[输出边集即TSP路径 数据空缺,“平均比”表示某算法比参考解高出的百 分比的平均值.“蚂蚁”取得了很好的成绩,平均比为 “2.84%”,2次获得参考解.冰晶算法是一个确定性 图3程序框图 Fig 3 Process diagram 局部算法,平均比为“1.59%” 算法实现: 表2其他TSP模型的试验比较 n表示城市的总数目,mj表示当前点集V中城 Table 2 Comparison of other TSP models 号 市的数目,C表示动态的凝固边界集 试验结果比参考解高出的部分 TSP 输入:给定点集A,包括n个点的坐标P,(x, 弹性网络蚂蚁基因人脑冰品 y)及各点之间的距离Dg,i,j=1,2,n Att48 5.812.863.04.412.19 输出:经过n个点的一条旅行回路C及此回路 Berlin52 6901.52 7.45.18267 的长度 E101 9.107.6414.2883 218 主要步骤为 E151 3.37 441 4.48.98 209 1)围建湖岸.求n个点的凸壳.设V=fm,, St70 4163425.97.031.47 V阿}是凸壳的顶点集,P={p,p2,:pa.画}是 Ulysses16 1.30 0 1.05 012 剩余点集,C=/M2,2内,4,Vv}是凝固 Ulysses22 1.57 0 03 0.45 前沿的动态边界集,初始值为凸壳的边集,j=1,2, 平均比 4.602.845.035.911.59 2)确定搜索范围.求n个点的邻近 试验选取了TSPL IB提供的68个TSP问题, 3)判断是否完全结冰.ifmj=n then C即所求 其中包含了一些有疑问的解,如bays29、gr202等测 回路,goto5); 试数据.冰晶算法直接计算的结果偏离程度不容乐 else goto 4). 观,平均比为8.006%,见表3,其中“参考解”表示目 4)冰晶生长.根据距离函数E(p),在K邻近 前TSPL IB所提供的最短路径长度.“冰晶”表示在 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
11213 局部扰动 初期模型的试验结果表明 ,在冰晶生长的过程 中 ,单一依靠距离函数的判定 ,效果不很理想. 自然 冰晶生长会出现一些临界冰渣 ,某个区域很难简单 判定它是已结冰 ,还是未结冰 ,这种混沌现象会影响 冰晶的继续生长 ,并诱导路径的错误走向. 无序向有 序的转化 ,本文采用微风吹拂湖面 ,对可能引导进入 歧途的晶胞做局部扰动 ,扰动后如果小晶胞仍处于 结冰状态 ,就认定它已正常结冰 ,扰动的时间复杂度 为 O( kn) . 2 试验设计 本文选取的试验数据是国际 TSPL IB 和台湾某 大学提供的参考数据. 冰晶算法框图如图 3. 图 3 程序框图 Fig13 Process diagram 算法实现 : n 表示城市的总数目 , m j 表示当前点集 V 中城 市的数目 , C 表示动态的凝固边界集. 输入 :给定点集 A ,包括 n 个点的坐标 p i ( xi , yi) 及各点之间的距离 Dij , i , j = 1 ,2 , …, n. 输出 :经过 n 个点的一条旅行回路 C 及此回路 的长度. 主要步骤为 1) 围建湖岸. 求 n 个点的凸壳. 设 V = { v1 , v2 , …, vmj}是凸壳的顶点集 , P = { p1 , p2 , …, pn - mj } 是 剩余点集 , C = { v1 v2 , v2 v3 , v3 v4 , …, vmj v 1 } 是凝固 前沿的动态边界集 ,初始值为凸壳的边集 , j = 1 , 2 , …. 2) 确定搜索范围. 求 n 个点的 K2邻近. 3) 判断是否完全结冰. if m j = n t hen C 即所求 回路 , goto 5) ; else goto 4) . 4) 冰晶生长. 根据距离函数 Exy ( pi) ,在 K2邻近 范围内求点 Pk , (如果做扰动的话 ,在此处加入扰动 函数即可) ,将 Pk 按照 x y 确定的位置加入点集 V , 删除 P 中该点. Mj + + ,goto 3) . 5) 路径输出 :计算回路的长度并输出 C. 算法终止. 时间 复 杂 度 : 1 ) 为 O ( nlog n) 时 间 , 2 ) 为 O( knlog n) , k 为求 n 个点的前 k 个近邻点的时间开 销系数. 3) 、4) 共小于 O( k nlog n) ,5) 为常数时间 ,所 以该算法总的时间复杂度为 O( knlog n) 时间. 3 结果分析 本试验选取国际 TSPL IB 提供的数据[7 ]和台湾 清华大学咨询工程系的部分测试结果. 为了便于比较 ,对一些 TSP 求解的近似算法的 效率有一个直观的认识 ,表 2 给出台湾清华大学提 供的参考数据[8 ] . 其中“弹性网络”表示 1987 年由 Durbin 和 Willshaw 提出了算法 ,其精髓是 :想象弹 性网络是一个橡皮筋 ,会自动收缩到最小张力的状 态“, 蚂蚁”表示“蚂蚁算法”“, 基因”表示“基因算 法”“, 人脑”表示人工一笔画对平面点集求 TSP 路 径 ,城市数目比较少时 ,该算法比较理想. 表中百分 比“%”代表试验的结果比参考解高出多少“, 2”表示 数据空缺“, 平均比”表示某算法比参考解高出的百 分比的平均值.“蚂蚁”取得了很好的成绩 ,平均比为 “2184 %”,2 次获得参考解. 冰晶算法是一个确定性 局部算法 ,平均比为“1159 %”. 表 2 其他 TSP 模型的试验比较 Table 2 Comparison of other TSP models % TSP 试验结果比参考解高出的部分 弹性网络 蚂蚁 基因 人脑 冰晶 Att48 5181 2186 310 4141 2119 Berlin52 6190 1152 714 5118 2167 Eil101 9110 7164 1412 8183 2118 Ei151 3137 4141 414 8198 2109 St70 4116 3142 519 7103 1147 Ulysses16 1130 0 2 1105 0112 Ulysses22 1157 0 013 2 0145 平均比 4160 2184 5103 5191 1159 试验选取了 TSPL IB 提供的 68 个 TSP 问题 , 其中包含了一些有疑问的解 ,如 bays29、gr202 等测 试数据. 冰晶算法直接计算的结果偏离程度不容乐 观 ,平均比为 81006 % ,见表 3 ,其中“参考解”表示目 前 TSPL IB 所提供的最短路径长度.“冰晶”表示在 第 2 期 周蓝海 ,等 : TSP 冰晶算法 ·169 ·
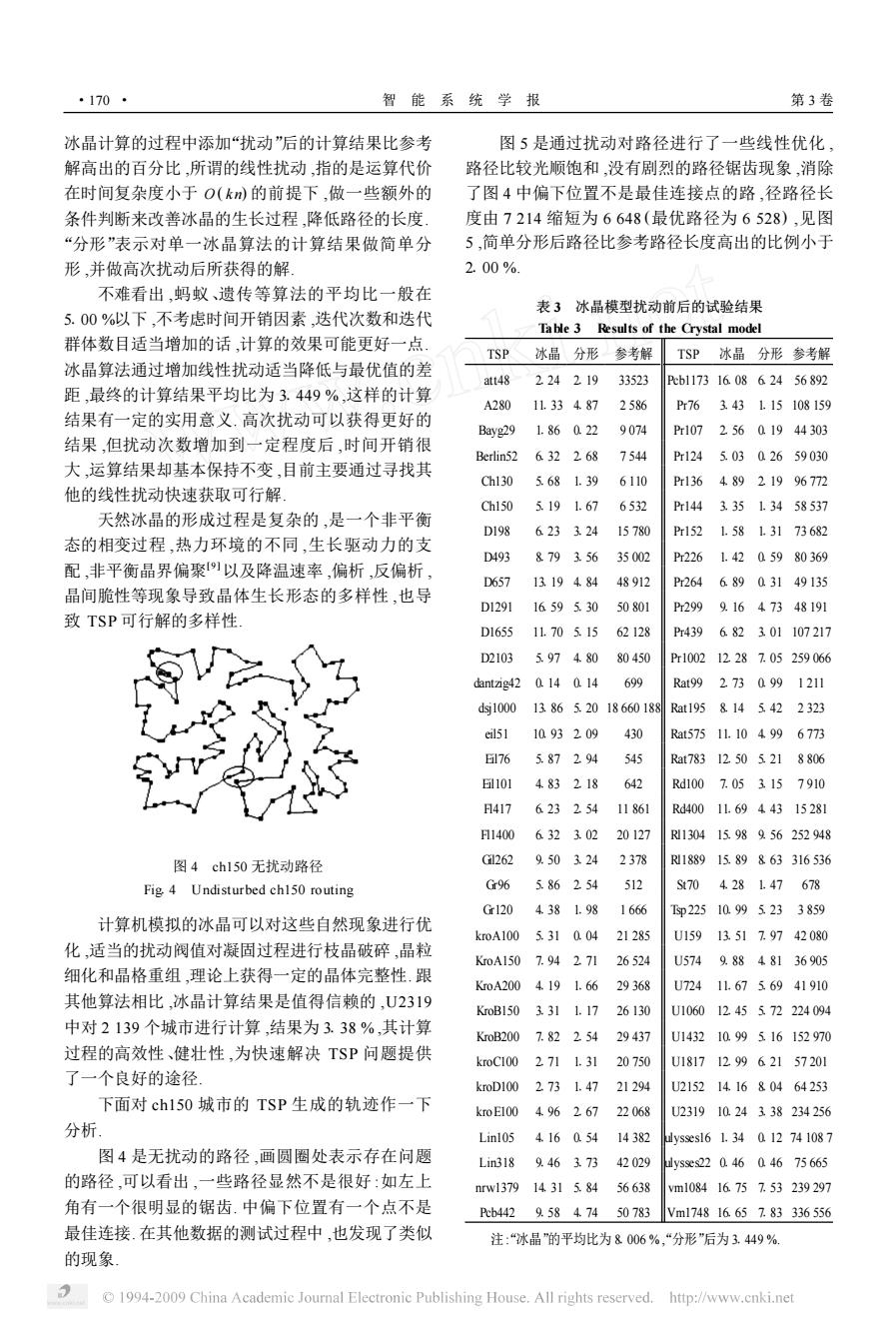
·170· 智能系统学报 第3卷 冰晶计算的过程中添加“扰动”后的计算结果比参考 图5是通过扰动对路径进行了一些线性优化, 解高出的百分比,所谓的线性扰动,指的是运算代价 路径比较光顺饱和,没有剧烈的路径锯齿现象,消除 在时间复杂度小于O(km)的前提下,做一些额外的 了图4中偏下位置不是最佳连接点的路,径路径长 条件判断来改善冰晶的生长过程,降低路径的长度 度由7214缩短为6648(最优路径为6528),见图 “分形”表示对单一冰晶算法的计算结果做简单分 5,简单分形后路径比参考路径长度高出的比例小于 形,并做高次扰动后所获得的解 2.00%. 不难看出,蚂蚁、遗传等算法的平均比一般在 表3冰晶模型扰动前后的试验结果 5.00%以下,不考虑时间开销因素,迭代次数和迭代 Table 3 Results of the Crystal model 群体数目适当增加的话,计算的效果可能更好一点。 TSP 冰晶分形参考解 TSP冰晶分形参考解 冰晶算法通过增加线性扰动适当降低与最优值的差 att48224219 33523 Pb1173160862456892 距,最终的计算结果平均比为3.449%,这样的计算 A28011.33487 2586 P-763431.15108159 结果有一定的实用意义.高次扰动可以获得更好的 Bayg29 1.860.22 9074 Pr107 2.560.1944303 结果,但扰动次数增加到一定程度后,时间开销很 Berlin526322.68 7544 Pr12450302659030 大,运算结果却基本保持不变,目前主要通过寻找其 Ch1305.681.39 6110 P-13648921996772 他的线性扰动快速获取可行解」 Ch150 5.191.67 6532 Pr14433513458537 天然冰晶的形成过程是复杂的,是一个非平衡 D198 6233.24 15780 Pr1521.581.3173682 态的相变过程,热力环境的不同,生长驱动力的支 D493 8793.56 35002 Pr2261.4205980369 配,非平衡晶界偏聚以及降温速率,偏析,反偏析, D657 13.19484 48912 Pr26468903149135 晶间脆性等现象导致晶体生长形态的多样性,也导 D1291 16595.30 50801 P2999.1647348191 致TSP可行解的多样性 D165511.705.15 62128 P-439682301107217 D2103 5.974.80 80450 Pr100212.287.05259066 dantzig420.14014 699 Rat992.730991211 ds100013865.2018660188别Rat1958.145422323 eil51 1093209 430 Rat57511.104996773 176 5.87294 545 Rat78312.505218806 E101 4.83218 642 Rd1007.05315 7910 H417623254 11861 Rd40011.6944315281 FH14006323.02 20127 130415989.56252948 图4ch150无扰动路径 G2629.503.24 2378 18891589863316536 Fig 4 Undisturbed ch150 routing Gr96 5.86254 512 S704281.47678 Gr1204381.98 1666 Tp22510995233859 计算机模拟的冰晶可以对这些自然现象进行优 kroA1005.31004 21285 U15913.517.9742080 化,适当的扰动阀值对凝固过程进行枝晶破碎,晶粒 KoA1507.94271 26524 U5749.8848136905 细化和晶格重组,理论上获得一定的晶体完整性.跟 KoA2004.191.66 29368 U72411.6756941910 其他算法相比,冰晶计算结果是值得信赖的,U2319 KoB1503.311.17 26130 U106012.45572224094 中对2139个城市进行计算,结果为3.38%,其计算 KoB2007.82254 29437 U14321099516152970 过程的高效性、健壮性,为快速解决TSP问题提供 kroC1002711.31 20750 U1817129962157201 了一个良好的途径 kroD1002.731.4721294 U215214.1680464253 下面对ch150城市的TSP生成的轨迹作一下 kroE1004.962.67 22068 U23191024338234256 分析 Lin105 4160.54 14382 ulysses161.34012741087 图4是无扰动的路径,画圆圈处表示存在问题 Lin3189.463.73 42029 ulysses2204604675665 的路径,可以看出,一些路径显然不是很好:如左上 nrw137914.315.84 56638 vm108416757.53239297 角有一个很明显的锯齿.中偏下位置有一个点不是 Pb4429.584.7450783 Vm174816657.83336556 最佳连接.在其他数据的测试过程中,也发现了类似 注:“冰晶”的平均比为8006%,“分形”后为3.449% 的现象 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
冰晶计算的过程中添加“扰动”后的计算结果比参考 解高出的百分比 ,所谓的线性扰动 ,指的是运算代价 在时间复杂度小于 O ( kn) 的前提下 ,做一些额外的 条件判断来改善冰晶的生长过程 ,降低路径的长度. “分形”表示对单一冰晶算法的计算结果做简单分 形 ,并做高次扰动后所获得的解. 不难看出 ,蚂蚁、遗传等算法的平均比一般在 5100 %以下 ,不考虑时间开销因素 ,迭代次数和迭代 群体数目适当增加的话 ,计算的效果可能更好一点. 冰晶算法通过增加线性扰动适当降低与最优值的差 距 ,最终的计算结果平均比为 31449 % ,这样的计算 结果有一定的实用意义. 高次扰动可以获得更好的 结果 ,但扰动次数增加到一定程度后 ,时间开销很 大 ,运算结果却基本保持不变 ,目前主要通过寻找其 他的线性扰动快速获取可行解. 天然冰晶的形成过程是复杂的 ,是一个非平衡 态的相变过程 ,热力环境的不同 ,生长驱动力的支 配 ,非平衡晶界偏聚[9 ]以及降温速率 ,偏析 ,反偏析 , 晶间脆性等现象导致晶体生长形态的多样性 ,也导 致 TSP 可行解的多样性. 图 4 ch150 无扰动路径 Fig14 Undisturbed ch150 routing 计算机模拟的冰晶可以对这些自然现象进行优 化 ,适当的扰动阀值对凝固过程进行枝晶破碎 ,晶粒 细化和晶格重组 ,理论上获得一定的晶体完整性. 跟 其他算法相比 ,冰晶计算结果是值得信赖的 ,U2319 中对 2 139 个城市进行计算 ,结果为 3138 % ,其计算 过程的高效性、健壮性 ,为快速解决 TSP 问题提供 了一个良好的途径. 下面对 ch150 城市的 TSP 生成的轨迹作一下 分析. 图 4 是无扰动的路径 ,画圆圈处表示存在问题 的路径 ,可以看出 ,一些路径显然不是很好 :如左上 角有一个很明显的锯齿. 中偏下位置有一个点不是 最佳连接. 在其他数据的测试过程中 ,也发现了类似 的现象. 图 5 是通过扰动对路径进行了一些线性优化 , 路径比较光顺饱和 ,没有剧烈的路径锯齿现象 ,消除 了图 4 中偏下位置不是最佳连接点的路 ,径路径长 度由 7 214 缩短为 6 648 (最优路径为 6 528) ,见图 5 ,简单分形后路径比参考路径长度高出的比例小于 2100 %. 表 3 冰晶模型扰动前后的试验结果 Table 3 Results of the Crystal model TSP 冰晶 分形 参考解 TSP 冰晶 分形 参考解 att48 2124 2119 33523 Pcb1173 16108 6124 56 892 A280 11133 4187 2 586 Pr76 3143 1115 108 159 Bayg29 1186 0122 9 074 Pr107 2156 0119 44 303 Berlin52 6132 2168 7 544 Pr124 5103 0126 59 030 Ch130 5168 1139 6 110 Pr136 4189 2119 96 772 Ch150 5119 1167 6 532 Pr144 3135 1134 58 537 D198 6123 3124 15 780 Pr152 1158 1131 73 682 D493 8179 3156 35 002 Pr226 1142 0159 80 369 D657 13119 4184 48 912 Pr264 6189 0131 49 135 D1291 16159 5130 50 801 Pr299 9116 4173 48 191 D1655 11170 5115 62 128 Pr439 6182 3101 107 217 D2103 5197 4180 80 450 Pr1002 12128 7105 259 066 dantzig42 0114 0114 699 Rat99 2173 0199 1 211 dsj1000 13186 5120 18 660 188 Rat195 8114 5142 2 323 eil51 10193 2109 430 Rat575 11110 4199 6 773 Eil76 5187 2194 545 Rat783 12150 5121 8 806 Eil101 4183 2118 642 Rd100 7105 3115 7 910 Fl417 6123 2154 11 861 Rd400 11169 4143 15 281 Fl1400 6132 3102 20 127 Rl1304 15198 9156 252 948 Gil262 9150 3124 2 378 Rl1889 15189 8163 316 536 Gr96 5186 2154 512 St70 4128 1147 678 Gr120 4138 1198 1 666 Tsp 225 10199 5123 3 859 kroA100 5131 0104 21 285 U159 13151 7197 42 080 KroA150 7194 2171 26 524 U574 9188 4181 36 905 KroA200 4119 1166 29 368 U724 11167 5169 41 910 KroB150 3131 1117 26 130 U1060 12145 5172 224 094 KroB200 7182 2154 29 437 U1432 10199 5116 152 970 kroC100 2171 1131 20 750 U1817 12199 6121 57 201 kroD100 2173 1147 21 294 U2152 14116 8104 64 253 kroE100 4196 2167 22 068 U2319 10124 3138 234 256 Lin105 4116 0154 14 382 ulysses16 1134 0112 74 108 7 Lin318 9146 3173 42 029 ulysses22 0146 0146 75 665 nrw1379 14131 5184 56 638 vm1084 16175 7153 239 297 Pcb442 9158 4174 50 783 Vm1748 16165 7183 336 556 注“: 冰晶”的平均比为 81006 %“, 分形”后为 31449 %. ·170 · 智 能 系 统 学 报 第 3 卷

第2期 周蓝海,等:TSP冰晶算法 ·171· 用其轨道行为的不可预测性,对系统初始状态极端 敏感的依赖性,,来获得具有混沌态特征的TSP路 径并获得了可信的成绩.很多自然界中的物理明显 地是以分形的形式生成的,分支重复地分裂产生更 小的分支,,特别是最原始的植物,像地衣、苔藓、 海藻,看起来都像分形,冰晶生长也是一样的.总的 来说,这一方法和试验的结果还是可取的 4结束语 针对TSP问题,采用冰晶算法进行了路径生成 图5ch150简单分形后路径 试验,简单分形扰动后试验结果的平均比一般在 Fig.5 Fractal ch152 routiag 4.00%以下,对TSP问题的求解比较有效,并且冰 晶算法的较低时间复杂度和计算的可并行性保证了 它求解的高效性 同时也可看出,该算法得到的可行解都具有一 个特点:就是路径围出一个单连通区域,实际上 TSP问题的解显然没有此限制,也就是说该算法在 TSP问题整个解空间的一个子空间中寻找可行解, 而最(次)优解是不是就在这个子空间中有待进一步 验证,如果不是,即便加入扰动,也不能从根本上解 决该问题,得到的结果只是一般意义上的可行解. 目前还不能证明该算法的有效程度,可以参考 的是:支撑树加完美匹配算法是到目前为止所见到 的,具有最好性能保证的多项式时间近似算法山 其时间复杂度为O(m),其路径长度满足STM() (a)TSPLIB提供的 (b)冰品算法计算结果 A.5OPT(),STM()表示该算法找到环游的 Gr202参考解 权,OPT()表示最优环游权.而其他贪婪算法一般 图6Gr202参考路径 时间复杂度为O()所得环游的权不会大于最优环 Fig.6 Gr202 referenced routing 游权的2倍 在时间开销上,这里不做详细比较.在普通的 对于有疑问的路径,简单分析一下TSPL IB提 PC机上,包含路径图像动态显示的时间开销在内, 供的Gr202参考解,见图6(a)所示,该路径长度为 冰晶算法在小于1s的时间可以轻松地计算500个 550,路径不存在交叉,整体结构紧凑,不存在明显的 城市的TSP问题,而以速度和可靠性著称的弹性网 路径问题,相对比较饱和光滑,但不足的是路径中保 络时间开销接近120s.其他算法,如蚂蚁算法就更 留了一条很长的边,并且由于该边的出现导致路径 长一些 的右上角出现了一个锯齿,如圆圈标记所示 冰晶算法是一种对自然智能简单的模拟,试验 冰晶算法的计算结果见图6(b)所示,跟参考解 数据的有限和单一特征的模拟,使得试验结果存在 不同的地方比较明显,主要是保留了2条比较长的 一定的不足,同时,也看到随着城市数量的增加,计 边,如圆圈标记所示.整体比较光滑,局部存在的路 算的结果与参考解的比例有增大的趋向,进一步的 径缺陷人脑比较难识别,路径长度为495,比 实验表明它受线性扰动强度和扰动范围的影响,当 TSPL IB提供的参考路径短10%. 城市数量增加后,通过增大线性扰动O(k)中的系 通过对68个TSPL IB不同数据的测试分析,平 数k一般可以获得更好的解,“分形”可有效降低该 均比的分布情况比较均衡,ulysses16获得了 情况下获得可行解的难度.目前,冰晶算法在降低时 0.12%的成绩.随线性约束的增加,计算结果不断降 间开销、降低空间开销提高准确度所碰到的主要障 低,采用分形思想来实现对冰晶生长过程的扰动,利 碍是跟计算几何相关的问题没有得到很好解决,下 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
对于有疑问的路径 ,简单分析一下 TSPL IB 提 供的 Gr202 参考解 ,见图 6 (a) 所示 ,该路径长度为 550 ,路径不存在交叉 ,整体结构紧凑 ,不存在明显的 路径问题 ,相对比较饱和光滑 ,但不足的是路径中保 留了一条很长的边 ,并且由于该边的出现导致路径 的右上角出现了一个锯齿 ,如圆圈标记所示. 冰晶算法的计算结果见图 6 (b) 所示 ,跟参考解 不同的地方比较明显 ,主要是保留了 2 条比较长的 边 ,如圆圈标记所示. 整体比较光滑 ,局部存在的路 径缺 陷 人 脑 比 较 难 识 别 , 路 径 长 度 为 495 , 比 TSPL IB 提供的参考路径短 10 %. 通过对 68 个 TSPL IB 不同数据的测试分析 ,平 均比 的 分 布 情 况 比 较 均 衡 , ulysses16 获 得 了 0112 %的成绩. 随线性约束的增加 ,计算结果不断降 低 ,采用分形思想来实现对冰晶生长过程的扰动 ,利 用其轨道行为的不可预测性 ,对系统初始状态极端 敏感的依赖性[9 ] ,来获得具有混沌态特征的 TSP 路 径并获得了可信的成绩. 很多自然界中的物理明显 地是以分形的形式生成的 ,分支重复地分裂产生更 小的分支[10 ] ,特别是最原始的植物 ,像地衣、苔藓、 海藻 ,看起来都像分形 ,冰晶生长也是一样的. 总的 来说 ,这一方法和试验的结果还是可取的. 4 结束语 针对 TSP 问题 ,采用冰晶算法进行了路径生成 试验 ,简单分形扰动后试验结果的平均比一般在 4100 %以下 ,对 TSP 问题的求解比较有效 ,并且冰 晶算法的较低时间复杂度和计算的可并行性保证了 它求解的高效性. 同时也可看出 ,该算法得到的可行解都具有一 个特点 : 就是路径围出一个单连通区域 ,实际上 TSP 问题的解显然没有此限制 ,也就是说该算法在 TSP 问题整个解空间的一个子空间中寻找可行解 , 而最(次) 优解是不是就在这个子空间中有待进一步 验证 ,如果不是 ,即便加入扰动 ,也不能从根本上解 决该问题 ,得到的结果只是一般意义上的可行解. 目前还不能证明该算法的有效程度 ,可以参考 的是 :支撑树加完美匹配算法是到目前为止所见到 的 ,具有最好性能保证的多项式时间近似算法[11 ] , 其时间复杂度为 O ( n 3 ) ,其路径长度满足 STM (Ι) ≤115 OPT (Ι) , STM (Ι) 表示该算法找到环游的 权 ,OPT(Ι) 表示最优环游权. 而其他贪婪算法一般 时间复杂度为 O( n 2 ) 所得环游的权不会大于最优环 游权的 2 倍. 在时间开销上 ,这里不做详细比较. 在普通的 PC 机上 ,包含路径图像动态显示的时间开销在内 , 冰晶算法在小于 1 s 的时间可以轻松地计算 500 个 城市的 TSP 问题 ,而以速度和可靠性著称的弹性网 络时间开销接近 120 s. 其他算法 ,如蚂蚁算法就更 长一些. 冰晶算法是一种对自然智能简单的模拟 ,试验 数据的有限和单一特征的模拟 ,使得试验结果存在 一定的不足 ,同时 ,也看到随着城市数量的增加 ,计 算的结果与参考解的比例有增大的趋向 ,进一步的 实验表明它受线性扰动强度和扰动范围的影响 ,当 城市数量增加后 ,通过增大线性扰动 O ( k n) 中的系 数 k 一般可以获得更好的解 “, 分形”可有效降低该 情况下获得可行解的难度. 目前 ,冰晶算法在降低时 间开销、降低空间开销、提高准确度所碰到的主要障 碍是跟计算几何相关的问题没有得到很好解决 ,下 第 2 期 周蓝海 ,等 : TSP 冰晶算法 ·171 ·

·172· 智能系统学报 第3卷 一步计划增加试验数据,在结晶的混沌状态中寻找 [7]GERHARD R.TSPL IB EB/OL ][1997-02-19 ]ht- 某些确定性因素,来降低与参考解的差距,主要从以 tp://elib.zib.de/pub/mp-testdata/tsp/tsplib/tsplib.ht- 下几方面深入研究:1)引入晶界偏聚,晶间脆性约 ml 束,2)寻找其他线性扰动提高精确度,3)改善冰晶生 [8]WU Ruiqian,L IN Huijuan JIANG Fengyi.Final project for neural Network EB/OL ]1997-12-28 ]http:/ 长的能量函数;4)TSPL IB参考解验证;5)平面TSP wayne.cs.nthu.edu.tw/~roland/nn/report fe.html. 冰晶并行算法 [9]PEITGEN HO,RICHLET P H.The beauty of frac- 参考文献: tals:images of complex dynamical systems M].New York Springer-Verlag,1986. [1]GAREY M R,JOHNSON D S.Computers and intracta [I0]KENNETHJ.分形几何数学基础及其应用[M]. bility a guide to the theory of NP-completeness M]. 曾文曲,译.沈阳:东北大学出版社,1991。 San Francisco:Freeman W H,1979. [11]陈志平,徐宗本.计算机数学计算复杂性理论与 [2]DORIGO M,MANIEZZO V,COLORNI A.The ant NP、CNP难问题的求解[M].北京:科学出版社,2001. system:optimization by a colony of cooperating agents 作者简介 [J ]IEEE Transactions on Systems,Man and Cyber- 周蓝海,男,1980年生,硕士研究生 netics,1996(1):2941. 主要研究方向为人工智能、知识工程、机器 [3]KENNEDYJ,EBERHART R C.Particle swarm opti- 翻译,发表论文4篇. mization [Cl//Proceedings of IEEE International Con ference on Neutral Net works,Perth,Australia,1995: 1942-1948. [4]KIR KPA TRICK D G,SEIDEL R.The ultimate planar convex hull al gorithm[J ]SIAMI Comput,1986,15:287- 299. 蔡东风,男,1958年生教授,获东京大 [5]周培德.计算几何:算法分析与设计[M].北京:清华大 学工学博士学位,主要研究方向为人工智 学出版社,2000. 能、自然语言处理、信息检索.近年来完成 [6]徐庭栋非平衡晶界偏聚动力学和晶间脆性断裂[M], 科研项目20余项,发表学术论文60余篇」 北京:科学出版社,2006 The Fourth International Conference on Advanced Data Mining and Applications (ADMA 2008) 第四届国标高性能数据挖掘与应用大会 The 4 th International Conference on Advanced Data Mining and Applications (ADMA2008)aims at bringing together the experts on data mining in the world,and provides a leading international forum for the dissemination of original research results in data mining,spanning applications,algorithms,software and systems,and different applied disciplines with potential in data mining. Key Topics We invite authors to submit papers on any topics of advanced data mining and applications,including but not limited to: Advanced Data Mining Topics:1)Grand challenges of data mining;2)Parallel and distributed data min- ing algorithms;3)Mining on data streams;4)Graph and subgraph mining;5)Spatial data mining;6)Text, video,multimedia data mining;7)Web mining;8)High performance data mining algorithms;9)Correlation mining;10)Bench marking and evaluations;11)Interactive data mining;Data-mining-ready structures and pre-processing;12)Data mining visualization;13)Information hiding in data mining;14)Security and privacy issues;15)Competitive analysis of mining algorithms. Data Mining Applications (applied data mining in following listed areas):1)Database administration, indexing,performance tuning;2)Grid computing;3)DNA Sequencing,Bioinformatics,Genomics,and bio- metrics;4)mage interpretations;5)Ecommerce and Web services;6)Medical informatics;7)Disaster predic- tion;8)Remote monitoring;9)Financial market analysis;10)Online filtering. Web site:http://cs.scu.edu.cn/~adma08 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
一步计划增加试验数据 ,在结晶的混沌状态中寻找 某些确定性因素 ,来降低与参考解的差距 ,主要从以 下几方面深入研究 :1) 引入晶界偏聚 ,晶间脆性约 束 ;2) 寻找其他线性扰动提高精确度 ;3) 改善冰晶生 长的能量函数 ;4) TSPL IB 参考解验证 ;5) 平面 TSP 冰晶并行算法. 参考文献 : [1 ] GAREY M R , JO HNSON D S. Computers and intracta2 bility : a guide to the theory of NP2completeness [ M ]. San Francisco : Freeman W H , 1979. [2 ] DORIGO M , MANIEZZO V , COLORNI A. The ant system : optimization by a colony of cooperating agents [J ]. IEEE Transactions on Systems , Man and Cyber2 netics , 1996 (1) :29241. [3 ] KENN ED Y J , EBERHART R C. Particle swarm opti2 mization [ C]/ / Proceedings of IEEE International Con2 ference on Neutral Net works , Perth , Australia , 1995 : 194221948. [4 ] KIR KPA TRICK D G, SEIDEL R. The ultimate planar convex hull algorithm[J ]. SIAMJ Comput ,1986 ,15 :2872 299. [5 ] 周培德. 计算几何 :算法分析与设计[ M ]. 北京 :清华大 学出版社 , 2000. [6 ] 徐庭栋. 非平衡晶界偏聚动力学和晶间脆性断裂[ M ]. 北京 :科学出版社 , 2006. [7 ] GERHARD R. TSPL IB [ EB/ OL ]. [ 1997202219 ]. ht2 tp :/ / elib. zib. de/ pub/ mp2testdata/ tsp/ tsplib/ tsplib. ht2 ml. [8 ] WU Ruiqian , L IN Huijuan ,J IAN G Fengyi. Final project for neural Network [ EB/ OL ]. [ 1997212228 ]. http :/ / wayne. cs. nthu. edu. tw/ ~roland/ nn/ report_fc. html. [9 ] PEITGEN H O , RICHL ET P H. The beauty of frac2 tals: images of complex dynamical systems [ M ]. New York :Springer2Verlag ,1986. [10 ] KENNETH J. 分形几何 ———数学基础及其应用[ M ]. 曾文曲 ,译. 沈阳 :东北大学出版社 ,1991. [11 ]陈志平 ,徐宗本. 计算机数学 ———计算复杂性理论与 NP、CNP 难问题的求解[ M]. 北京 :科学出版社 , 2001. 作者简介 : 周蓝海 ,男 ,1980 年生 ,硕士研究生 , 主要研究方向为人工智能、知识工程、机器 翻译 ,发表论文 4 篇. 蔡东风 ,男 ,1958 年生 ,教授 ,获东京大 学工学博士学位 ,主要研究方向为人工智 能、自然语言处理、信息检索. 近年来完成 科研项目 20 余项 ,发表学术论文 60 余篇. The Fourth International Conference on Advanced Data Mining and Applications ( ADMA 2008) 第四届国际高性能数据挖掘与应用大会 The 4 t h International Conference on Advanced Data Mining and Applications (ADMA2008) aims at bringing toget her t he experts on data mining in t he world , and provides a leading international forum for t he dissemination of original research results in data mining , spanning applications , algorit hms , software and systems , and different applied disciplines wit h potential in data mining. Key Topics : We invite aut hors to submit papers on any topics of advanced data mining and applications , including but not limited to : Advanced Data Mining Topics:1) Grand challenges of data mining ;2) Parallel and distributed data min2 ing algorit hms;3) Mining on data streams;4) Grap h and subgrap h mining ;5) Spatial data mining ;6) Text , video , multimedia data mining ;7) Web mining ;8) High performance data mining algorit hms;9) Correlation mining ;10)Bench marking and evaluations; 11) Interactive data mining ;Data2mining2ready structures and pre2p rocessing ;12) Data mining visualization ;13) Information hiding in data mining ;14) Security and privacy issues;15) Competitive analysis of mining algorit hms. Data Mining Applications (applied data mining in following listed areas) :1) Database administration , indexing , performance tuning ;2) Grid comp uting ;3) DNA Sequencing , Bioinformatics , Genomics , and bio2 metrics;4) mage interpretations;5) E2commerce and Web services;6) Medical informatics;7) Disaster predic2 tion ;8) Remote monitoring ;9) Financial market analysis;10) Online filtering. Web site :http :/ / cs. scu. edu. cn/ ~adma08 ·172 · 智 能 系 统 学 报 第 3 卷