
第3卷第2期 智能系统学报 Vol.3 Na 2 2008年4月 CAAI Transactions on Intelligent Systems Apr.2008 克隆粒子群算法的镜像层叠 滤波器的优化设计 赵春晖,肖晓俊 (哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001) 摘要:层叠滤波器是一种具有层叠性和阈值分解性的滑动窗非线性数字滤波器.层叠滤波器的优化设计过程关键 就是对正布尔函数优化.本文利用了克隆粒子群优化算法的全局寻优能力和免疫系统的免疫信息处理机制,改善了 粒子群优化算法摆脱局部极值点的能力,提高了算法进化过程中的收敛速度和精度.仿真实验的结果也表明,该算 法在正布尔函数的优化效果得到了显著改善,收敛加快,试验结果表明该算法设计的层叠滤波器具有良好的细节保 持能力和去噪声能力,有效地改善了滤波性能. 关键词:镜像阈值分解:正布尔函数(PBF):层叠滤波器:克隆选择:粒子群 中图分类号:TN911.26文献标识码:A文章编号:1673-4785(2008)02-0129-06 Optimizing stacked filters with mirrored threshold decomposition using an improved clone selection and PSO algorithm ZHAO Chumhui,XIAO Xiao-jun (College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China) Abstract:Stack filters are a class of nonlinear digital filters with sliding windows.Their two main proper- ties are threshold decomposition and stacking.Optimal design of these filters requires optimization of a positive Boolean function (PBF).Optimization of stacked filters using traditional algorithms is easily trapped in a local optimum.To prevent this in recent years the bionic clone selection and PSO algorithms were proposed.The combination of these two algorithms avoids the problem of falling into a local mini- mum,greatly improving convergence speed and accuracy.Experimental results show that optimally stacked filters effectively suppress noise while retaining details of images and enhancing filtering capability Keywords:mirrored threshold decomposition;positive Boolean function (PBF);stacked filters;clone se- lection algorithm:Particle swarm optimization(PSO) 层叠滤波器是一类基于正布尔函数的非线性数 镜像层叠滤波器的优化还没有深入研究,而且镜像 字滤波器,阈值分解和层叠特性是它的2个主要特 层叠滤波器的优化比传统的层叠滤波器优化要困难 性山,被广泛地应用在信号和图像处理中.近些年来 得多,为了解决这个问题,本文采用了克隆选择和粒 提出一种新的镜像层叠滤波器,拓展了层叠滤波器 子群结合的方法, 应用范围).文献[3]在镜像阈值分解的基础上,根 粒子群优化算法(particle swarm optimization, 据判决向量确定正布尔函数,提出一种快速镜像层 PSO)在进化初期收敛速度快,在进化后期收敛速度 叠滤波器优化方法,改善了滤波器的性能,具有更好 明显变慢,同时算法收敛到一定精度时,无法继续优 的细节保持能力.文献[4]把克隆算法应用于优化传 化,搜索结果会有较大波动,因此算法所能达到的精 统的层叠滤波器,取得了较好的滤波效果.然而对于 度较差.把克隆的免疫信息处理机制(多样性、克隆、 免疫自我调节、免疫记忆等)引入到粒子群优化算法 收稿日期:2007-0920 基金项目:国家自然科学基金资助项目(60672034)。 中,在粒子群优化算法的基本框架上,结合免疫系统 通讯作者:赵春晖.zhaochunhui@hrbeu.edu.cn. 的免疫信息处理机制给出了克隆粒子群优化算法 1994-2009 China Academic Journal Electronie Publishing House.All rights reserved.http://www.cnki.net
第 3 卷第 2 期 智 能 系 统 学 报 Vol. 3 №. 2 2008 年 4 月 CAA I Transactions on Intelligent Systems Apr. 2008 克隆粒子群算法的镜像层叠 滤波器的优化设计 赵春晖 , 肖晓俊 (哈尔滨工程大学 信息与通信工程学院 ,黑龙江 哈尔滨 150001) 摘 要 :层叠滤波器是一种具有层叠性和阈值分解性的滑动窗非线性数字滤波器. 层叠滤波器的优化设计过程关键 就是对正布尔函数优化. 本文利用了克隆粒子群优化算法的全局寻优能力和免疫系统的免疫信息处理机制 ,改善了 粒子群优化算法摆脱局部极值点的能力 ,提高了算法进化过程中的收敛速度和精度. 仿真实验的结果也表明 ,该算 法在正布尔函数的优化效果得到了显著改善 ,收敛加快 ,试验结果表明该算法设计的层叠滤波器具有良好的细节保 持能力和去噪声能力 ,有效地改善了滤波性能. 关键词 :镜像阈值分解 ;正布尔函数(PBF) ;层叠滤波器 ;克隆选择 ;粒子群 中图分类号 : TN911. 26 文献标识码 :A 文章编号 :167324785 (2008) 0220129206 Optimizing stacked filters with mirrored threshold decomposition using an improved clone selection and PSO algorithm ZHAO Chun2hui , XIAO Xiao2jun (College of Information and Communication Engineering , Harbin Engineering University , Harbin 150001 ,China) Abstract :Stack filters are a class of nonlinear digital filters wit h sliding windows. Their two main proper2 ties are threshold decomposition and stacking. Optimal design of these filters requires optimization of a positive Boolean f unction ( PBF) . Optimization of stacked filters using traditional algorithms is easily trapped in a local optimum. To prevent t his in recent years t he bionic clone selection and PSO algorit hms were proposed. The combination of t hese two algorit hms avoids the problem of falling into a local mini2 mum , greatly improving convergence speed and accuracy. Experimental results show t hat optimally stacked filters effectively suppress noise while retaining details of images and enhancing filtering capability. Keywords :mirrored t hreshold decomposition ; positive Boolean f unction (PBF) ; stacked filters; clone se2 lection algorit hm ; Particle swarm optimization (PSO) 收稿日期 :2007209220. 基金项目 :国家自然科学基金资助项目(60672034) . 通讯作者 :赵春晖. zhaochunhui @hrbeu. edu. cn. 层叠滤波器是一类基于正布尔函数的非线性数 字滤波器 ,阈值分解和层叠特性是它的 2 个主要特 性[1 ] ,被广泛地应用在信号和图像处理中. 近些年来 提出一种新的镜像层叠滤波器 ,拓展了层叠滤波器 应用范围[2 ] . 文献[ 3 ]在镜像阈值分解的基础上 ,根 据判决向量确定正布尔函数 ,提出一种快速镜像层 叠滤波器优化方法 ,改善了滤波器的性能 ,具有更好 的细节保持能力. 文献[ 4 ]把克隆算法应用于优化传 统的层叠滤波器 ,取得了较好的滤波效果. 然而对于 镜像层叠滤波器的优化还没有深入研究 ,而且镜像 层叠滤波器的优化比传统的层叠滤波器优化要困难 得多 ,为了解决这个问题 ,本文采用了克隆选择和粒 子群结合的方法. 粒子群优化算法(particle swarm optimization , PSO) 在进化初期收敛速度快 ,在进化后期收敛速度 明显变慢 ,同时算法收敛到一定精度时 ,无法继续优 化 ,搜索结果会有较大波动 ,因此算法所能达到的精 度较差. 把克隆的免疫信息处理机制(多样性、克隆、 免疫自我调节、免疫记忆等) 引入到粒子群优化算法 中 ,在粒子群优化算法的基本框架上 ,结合免疫系统 的免疫信息处理机制给出了克隆粒子群优化算法

·130· 智能系统学报 第3卷 这种克隆粒子群优化算法结合了粒子群优化算法具 解和镜像阈值分解后的二值序列经过处理后叠加恢 有的全局寻优能力、实现简单和免疫系统的免疫信 复而成,镜像层叠滤波器输出定义为 息处理机制,从而避免了粒子群优化算法易于陷入 局部极值点的缺点,提高了进化后期算法的收敛速 5,w支 度和精度.仿真结果说明所提出的克隆粒子群优化 这里x和s,i=1,2,N,是式(1)和2)中定义 算法优于粒子群优化算法 的阈值分解的结果,函数f()是有2N个变量的 正布尔函数(PBF) 1层叠滤波器及镜像阈值分解原理 1.2层叠滤波器的优化设计策略 层叠滤波过程可概括为阈值分解、二值滤波和 设S(W、N(m和X(d分别为原始信号、噪声信 叠加合成3个步骤,即首先将多值信号通过阈值分 号和观测信号,$(·)代表层叠滤波器,Y(川为层叠 解转化为相对简单的一系列二值信号,然后对每一 滤波器输出信号.图1给出了层叠滤波器最优模型, 级的二值信号序列进行滤波,最后将二值输出信号 此时设滤波窗W大小为N=2K+1. 叠加以得到最终输出信号值 Sn) 1.1镜像层叠滤波器基本理论 R(n) Y(n) G.) S.) 在传统阈值分解的基础上,提出了镜像阈值分 解的层叠滤波器.与传统阈值分解不同,镜像阈值分 N(n) 解允许对负的实数信号进行处理.假设有这样一个 实数抽样序列X(1),X2),·,X(N),这里X()∈ 图1层叠滤波器最优模型 Q,并且Q={-M,…,0,M,不同于阈值分解 Fig I Optimal stack filter model 的传统形式,向量X的镜像阈值分解是由2部分组 根据最小误差准则,结构元约束最优层叠滤波 成的,每一部分有2M个二进制向量.第1部分与传 器应满足下列条件,当r=1时,满足MAE误差准 统阈值分解的定义相同,即 则,当r=2时,满足MSE误差准则 x1,X°,:x C(Sr)EI S(n)-Ss(R(n), (3) 这里x的第1个元素的定义为 f(x)≥f(a),x1≥2. (4 1,X(动≥m, x=T(X()={.1 1) 式4)代表层叠性约束条件 else. 显然如果式(3达到最小值,则完成了基于 第2部分由镜像向量$的阈值分解形式构成, MAE准则层叠滤波器的最优化设计.因此,层叠滤 X的镜像向量S定义为 波器的优化问题被转化为求式3)的最小值问题.根 S=fS1)S2…S(N)1= 据阈值分解性质,可将式3)转化为式5): 「-X1)-X2·-X(N)1. MAE(Sy)=Ell S(n)Sy(R(n)]= S的阈值分解产生了第2部分的分解信号 sM+1,s°,s“,这里s的第i个元素的定义为 ∑Es(w·f(r(W)I] (5) t-. si=T(S(i))= 1,-X(d≥m,2 式中:s(和t(d分别是期望信号S(m和输入信 -1, else. 号RW的阈值分解信号,期望信号S()和输入信 为了符号的方便,向量X在m级上的镜像阈值 号R(W都属于Q.根据信号估计理论和贝叶斯判决 分解可以表示为一个长度为2N的二值向量.第1 理论,进一步将式5)转化为式(6)的形式: 部分的N个分量对应的是二值向量xm,而第2部 分的N个分量对应的是二值向量s,所以它的定义 MAE(Sy)c(-1,a,)Ps(1/a)+ 式为 C1,a)1-P(1/a)) (6) T"(W=[x;s]=[x";s"1 基于镜像阈值分解的二进制向量,每一组二进 式中:C(-1,a)为当输入信号为a时,理想信号为 制向量都服从层叠性.即镜像阈值分解后的二进制 1,判断为-1的误判代价:C(1,a)为当输入信号为 向量序列: a,时,理想信号为-1,判断为1的误判代价 x1,X°,x"和s1,°,s" Pr(1/a)是输入为a时,输出为1的概率;1- 这组二进制向量满足部分排序: Pr(1/a)是输入为a时,输出为-1概率. [x;s1≤[x,s1,i≥j 在实际应用中,C(-1,a)可估算为理想输出为 层叠滤波器的输出是输入抽样向量经过阈值分 -1时,a在观测信号中出现的次数;C(1,a)可估 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
这种克隆粒子群优化算法结合了粒子群优化算法具 有的全局寻优能力、实现简单和免疫系统的免疫信 息处理机制 ,从而避免了粒子群优化算法易于陷入 局部极值点的缺点 ,提高了进化后期算法的收敛速 度和精度. 仿真结果说明所提出的克隆粒子群优化 算法优于粒子群优化算法. 1 层叠滤波器及镜像阈值分解原理 层叠滤波过程可概括为阈值分解、二值滤波和 叠加合成 3 个步骤 ,即首先将多值信号通过阈值分 解转化为相对简单的一系列二值信号 ,然后对每一 级的二值信号序列进行滤波 ,最后将二值输出信号 叠加以得到最终输出信号值. 111 镜像层叠滤波器基本理论 在传统阈值分解的基础上 ,提出了镜像阈值分 解的层叠滤波器. 与传统阈值分解不同 ,镜像阈值分 解允许对负的实数信号进行处理. 假设有这样一个 实数抽样序列 X (1) , X (2) , …, X ( N) ,这里 X ( i) ∈ Q ,并且 Q = { - M , …, 0 , …, M} ,不同于阈值分解 的传统形式 ,向量 X的镜像阈值分解是由 2 部分组 成的 ,每一部分有 2 M 个二进制向量. 第 1 部分与传 统阈值分解的定义相同 ,即 x - M+1 , …, x 0 , …, x M . 这里 x m 的第 i 个元素的定义为 x m i = T m ( X ( i) ) = 1 , X ( i) ≥m , - 1 , else. (1) 第 2 部分由镜像向量 S 的阈值分解形式构成 , X的镜像向量 S 定义为 S = [ S (1) S (2) … S ( N) ] = [ - X (1) - X (2) … - X ( N) ]. S 的阈值分解产生了第 2 部分的分解信号 s - M + 1 , …,s 0 , …,s M ,这里 s m 的第 i 个元素的定义为 s m i = T m ( S ( i) ) = 1 , - X ( i) ≥m , - 1 , else. (2) 为了符号的方便 ,向量 X在 m 级上的镜像阈值 分解可以表示为一个长度为 2 N 的二值向量. 第 1 部分的 N 个分量对应的是二值向量 x m ,而第 2 部 分的 N 个分量对应的是二值向量 s m ,所以它的定义 式为 T m ( X) = [ x;s] m = [ x m ;s m ]. 基于镜像阈值分解的二进制向量 ,每一组二进 制向量都服从层叠性. 即镜像阈值分解后的二进制 向量序列 : x - M+1 , …, x 0 , …, x M 和 s - M+1 , …,s 0 , …,s M . 这组二进制向量满足部分排序 : [ x i ;s i ] ≤[ x j ,s j ] , i ≥j. 层叠滤波器的输出是输入抽样向量经过阈值分 解和镜像阈值分解后的二值序列经过处理后叠加恢 复而成 ,镜像层叠滤波器输出定义为 S f ( X1 , …, X N ) = 1 2 ∑ M m = - M+1 f ( x m 1 , …, x m N ;s m 1 , …,s m N ) . 这里 x m i 和 s m i , i = 1 ,2 , …, N ,是式 (1) 和 (2) 中定义 的阈值分解的结果 ,函数 f ( ·) 是有 2 N 个变量的 正布尔函数(PBF) [4 ] . 112 层叠滤波器的优化设计策略 设 S( n) 、N ( n) 和 X( n) 分别为原始信号、噪声信 号和观测信号 , S( ·) 代表层叠滤波器 , Y( n) 为层叠 滤波器输出信号. 图 1 给出了层叠滤波器最优模型 , 此时设滤波窗 W 大小为 N = 2 K + 1. 图 1 层叠滤波器最优模型 Fig11 Optimal stack filter model 根据最小误差准则 ,结构元约束最优层叠滤波 器应满足下列条件 ,当 r = 1 时 ,满足 MA E 误差准 则 ,当 r = 2 时 ,满足 MSE 误差准则. C( S f ) = E{| S( n) - Sf ( R( n) ) | r } , (3) f ( x1 ) ≥f ( x2 ) , x1 ≥x2 . (4) 式(4) 代表层叠性约束条件. 显然如果式 ( 3) 达到最小值 , 则完成了基于 MA E 准则层叠滤波器的最优化设计. 因此 ,层叠滤 波器的优化问题被转化为求式(3) 的最小值问题. 根 据阈值分解性质 ,可将式(3) 转化为式(5) : MA E( S f ) = E[| S( n) - S f ( R( n) ) | ] = ∑ M t = - M+1 E[| s t ( n) - f ( r t ( n) ) | ]. (5) 式中 :s t ( n) 和 r t ( n) 分别是期望信号 S ( n) 和输入信 号 R( n) 的阈值分解信号 ,期望信号 S ( n) 和输入信 号 R( n) 都属于 Q. 根据信号估计理论和贝叶斯判决 理论 ,进一步将式(5) 转化为式(6) 的形式 : MA E( S f ) = ∑ N 3 j = 1 C( - 1 ,αj) Pf (1/αj) + C(1 ,αj) (1 - Pf (1/αj) ) . (6) 式中 :C( - 1 , aj) 为当输入信号为 aj 时 ,理想信号为 1 ,判断为 - 1 的误判代价; C(1 , aj) 为当输入信号为 aj 时 , 理想信号为 - 1 , 判断为 1 的 误判代价. Pf (1/ aj) 是输入为 aj 时 , 输出为 1 的概率; 1 - Pf (1/ aj) 是输入为 aj 时 ,输出为 - 1 概率. 在实际应用中 , C( - 1 , aj) 可估算为理想输出为 - 1 时 , aj 在观测信号中出现的次数; C(1 , aj ) 可估 ·130 · 智 能 系 统 学 报 第 3 卷

第2期 赵春晖,等:基于克隆粒子群算法的镜像层叠滤波器的优化设计 ·131· 算为理想输出为1时,a,在观测信号中出现的次 子的位置代表解空间的一个候选解,粒子的位置通 数.Pr1/a)=0or1,所以P可以看成是一个布 过速度来调整,解的优劣程度由适应度函数决定,将 尔函数真值表.此外,由于层叠滤波器具有层叠特 一个粒子的位置带入一个目标函数就可以计算出其 性,表达式7)成立: 适应值.其中,第i个粒子在d维解空间的位置表示 Pr1/a)≤Pr1/a),a≤a. 7) 为X,=(Xn,Xa,Xa).粒子在搜索空间单位位 因此,基于MAE准则的层叠滤波器优化问题, 移由速度决定V,=(Ⅳ1,Va,,Vad),初始速度是随 可进一步改写成与布尔函数真值表相关的表达式, 机产生的,选取0,1]之间的随机数.在每一次迭代 该式作为优化过程中的目标函数 中,粒子通过动态地跟踪2个极值来更新其速度和 位置:第1个是粒子从初始到当前迭代次数搜索产 MAE(S)=C(-1,aj)Pr(1/a)+ 生的最优解,个体极值:第2个是粒子种群目前的最 C1,a)1-Pr(1/a), 优解,全局极值,其更新公式为 Pr(1/a)≤P1/a),g≤a. w Xvi +a xrand(x(pid-xh)+ Pr(1/a)=0,1,j: c Xrand()x(gid-xh), (9) 所以层叠滤波器的核心问题是正布尔函数,确 x洁)=x+ (10) 定了正布尔函数,就可以确定层叠滤波器.对于一个 kX业m-1业mnl 1) 有N个输入变量的正布尔函数,对于镜像阈值分解 K 来说,阈值分解输出二进制向量长度为2N,但不是 式中:p:=(pm,pa,pa)为个体极值;G=(ga, 所有2N种可能的二进制向量都出现在输出端,其 g2,ga)为全局极值.w是衰减因子,wmx、wmm分 镜像阈值分解后的二进制向量的个数为 别取0.9和0.1;k表示进化到第k代,为K总的进 N=23)-2 化代数1 即正布尔函数对应真值表的长度为N,这里N为滤 因为层叠滤波器是一种数字滤波器,优化的是 波窗的尺寸.正布尔函数又可以用一个判决向量, 正布尔函数,所以本文采用一种离散二进制粒子群 即正布尔函数真值表D来表示: 算法来进行优化,则粒子的位置更新公式更改为 D [D(1)D(N)1. if <sig(v),thenx=1;elsex=0, 式中:D()=f(a),a为正布尔函数输入的一种可 能取值,其长度为2N sg'=1+ep,∈f0.l17 其中代价函数C的计算:首先初始化,对任意i (12) 置C,=0,然后由噪声图像、镜像图像和期望图像训 克隆选择算法借助生物学免疫系统的抗体克隆 练C迭代的具体过程:在1时刻对噪声图像和镜像 选择机理构造适用于人工智能的克隆算子,此算法 图像取窗值,根据噪声图像窗值中心点的位置,得到 考虑了免疫应答中亲和力的成熟,可以用来解决复 1时刻期望图像的值,然后对它们进行镜像阈值分 杂问题.对比遗传算法,克隆选择算法在编码机制和 解.设x=「a;]为t时刻输入图像的二进制窗向 评价函数的构造上基本一致,但搜索的策略和步骤 量,若1时刻期望图像对应的值取为0,则G= 有所不同,而且通过免疫记忆机制,该算法可以保存 C-1,否则C=C,+1.这时C的长度为22,其中 各个局部最优解 有22.N·个位置是不起作用的 2.2算法实现步骤及参数分析 综上所述,这种求代价函数最小化的问题可以 本文在基本粒子群算法的基础上,将其基本算 转化成解决二进制线性的方式,其具体的形式为 子结合克隆算法进行改进,并结合镜像层叠滤波器 N" 理论,基于这种改进型克隆选择粒子群算法对层叠 min∑CD(d,D(d=0or1. 8) 滤波器进行优化设计,其具体算法如下: 式中:系数C是依赖于输入与期望信号设想的统计 1)初始化种群:在Matlab中初始化种群就是要 模型的权值,也可以理解为当a,出现在滤波窗中 产生随机矩阵,确定每个抗体的初始位置和速度,用 时,正布尔函数f()输出判决为1的判决代价. X表示粒子群的当前位置,V为速度,m是种群个 数.在层叠滤波器中就是要产生一个随机矩阵,来表 2改进的克隆粒子群算法 示式(8)中的C,C中的元素要满足正布尔函数编码 2.1离散PSO算法和克隆选择算法 要求,其中C就对应于这里的X,设L是镜像窗口 PS0算法首先随机初始化为一群粒子,每个粒 长度,如取N=5则L=2×N,就随机产生X长度 1994-2009 China Academie Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
算为理想输出为 1 时 , aj 在观测信号中出现的次 数. Pf (1/ aj) = 0 or 1 ,所以 Pf 可以看成是一个布 尔函数真值表. 此外 , 由于层叠滤波器具有层叠特 性 ,表达式(7) 成立 : Pf (1/αj) ≤ Pf (1/αi) ,αj ≤αi . (7) 因此 ,基于 MA E 准则的层叠滤波器优化问题 , 可进一步改写成与布尔函数真值表相关的表达式 , 该式作为优化过程中的目标函数[425 ] . MA E( S f ) = ∑ N 3 j = 1 C( - 1 ,αj) Pf (1/αj) + C(1 ,αj) (1 - Pf (1/αj) ) , Pf (1/αj) ≤ Pf (1/αi) ,αj ≤αi , Pf (1/αj) = 0 ,1 , Πj. 所以层叠滤波器的核心问题是正布尔函数 ,确 定了正布尔函数 ,就可以确定层叠滤波器. 对于一个 有 N 个输入变量的正布尔函数 ,对于镜像阈值分解 来说 ,阈值分解输出二进制向量长度为 2 N ,但不是 所有 2 N 种可能的二进制向量都出现在输出端 ,其 镜像阈值分解后的二进制向量的个数为 N 3 = 2 (3 N ) - 2 N . 即正布尔函数对应真值表的长度为 N ,这里 N 为滤 波窗的尺寸. 正布尔函数又可以用一个判决向量 , 即正布尔函数真值表 D 来表示 : D = [ D (1) …D ( N 3 ) ]. 式中 : D ( i) = f ( ai) , ai 为正布尔函数输入的一种可 能取值 ,其长度为 2 N . 其中代价函数 C的计算 :首先初始化 ,对任意 i 置 Ci = 0 ,然后由噪声图像、镜像图像和期望图像训 练 C. 迭代的具体过程 :在 t 时刻对噪声图像和镜像 图像取窗值 ,根据噪声图像窗值中心点的位置 ,得到 t 时刻期望图像的值 ,然后对它们进行镜像阈值分 解. 设 xi = [α;β]为 t 时刻输入图像的二进制窗向 量 ,若 t 时刻期望图像对应的值取为 0 , 则 Ci = Ci - 1 ,否则 Ci = Ci + 1. 这时 C 的长度为 2 2 N ,其中 有 2 2 N - N 3 个位置是不起作用的. 综上所述 ,这种求代价函数最小化的问题可以 转化成解决二进制线性的方式 ,其具体的形式为 min ∑ N 3 i = 1 CiD ( i) , D ( i) = 0 or 1. (8) 式中 :系数 Ci 是依赖于输入与期望信号设想的统计 模型的权值 ,也可以理解为当 αi 出现在滤波窗中 时 ,正布尔函数 f ( ·) 输出判决为 1 的判决代价. 2 改进的克隆粒子群算法 211 离散 PS O 算法和克隆选择算法 PSO 算法首先随机初始化为一群粒子 ,每个粒 子的位置代表解空间的一个候选解 ,粒子的位置通 过速度来调整 ,解的优劣程度由适应度函数决定 ,将 一个粒子的位置带入一个目标函数就可以计算出其 适应值. 其中 ,第 i 个粒子在 d 维解空间的位置表示 为 Xi = ( Xi1 , Xi2 , …, Xid ) . 粒子在搜索空间单位位 移由速度决定 Vi = (V i1 ,V i2 , …,V id ) ,初始速度是随 机产生的 ,选取[0 ,1 ]之间的随机数. 在每一次迭代 中 ,粒子通过动态地跟踪 2 个极值来更新其速度和 位置 :第 1 个是粒子从初始到当前迭代次数搜索产 生的最优解 ,个体极值;第 2 个是粒子种群目前的最 优解 ,全局极值 ,其更新公式为 v k+1 id = w ×v k id + c1 ×rand () ×( pid - x k id ) + c2 ×rand () ×( gid - x k id ) , (9) x k+1 id = x k id + v k+1 id , (10) w = wmax - k ×( wmax - wmin ) K . (11) 式中 : pi = ( pi1 , pi2 , …, pid ) 为个体极值; Gi = ( gi1 , gi2 , …, gid ) 为全局极值. w 是衰减因子 , wmax 、wmin分 别取 019 和 011 ; k 表示进化到第 k 代 ,为 K 总的进 化代数[6 ] . 因为层叠滤波器是一种数字滤波器 ,优化的是 正布尔函数 ,所以本文采用一种离散二进制粒子群 算法来进行优化 ,则粒子的位置更新公式更改为 ifρk+1 id < sig ( v k+1 id ) ,then x k+1 id = 1 ;else x k+1 id = 0 , sig ( v k+1 id ) = 1 1 + exp ( - v k+1 id ) ,ρk+1 id ∈[0 ,1 ]. (12) 克隆选择算法借助生物学免疫系统的抗体克隆 选择机理构造适用于人工智能的克隆算子 ,此算法 考虑了免疫应答中亲和力的成熟 ,可以用来解决复 杂问题. 对比遗传算法 ,克隆选择算法在编码机制和 评价函数的构造上基本一致 ,但搜索的策略和步骤 有所不同 ,而且通过免疫记忆机制 ,该算法可以保存 各个局部最优解[4 ] . 212 算法实现步骤及参数分析 本文在基本粒子群算法的基础上 ,将其基本算 子结合克隆算法进行改进 ,并结合镜像层叠滤波器 理论 ,基于这种改进型克隆选择粒子群算法对层叠 滤波器进行优化设计 ,其具体算法如下 : 1) 初始化种群 :在 Matlab 中初始化种群就是要 产生随机矩阵 ,确定每个抗体的初始位置和速度 ,用 X表示粒子群的当前位置 ,V 为速度 , m 是种群个 数. 在层叠滤波器中就是要产生一个随机矩阵 ,来表 示式(8) 中的 C, C中的元素要满足正布尔函数编码 要求 ,其中 C 就对应于这里的 X ,设 L 是镜像窗口 长度 ,如取 N = 5 则 L = 2 ×N ,就随机产生 X 长度 第 2 期 赵春晖 ,等 :基于克隆粒子群算法的镜像层叠滤波器的优化设计 ·131 ·
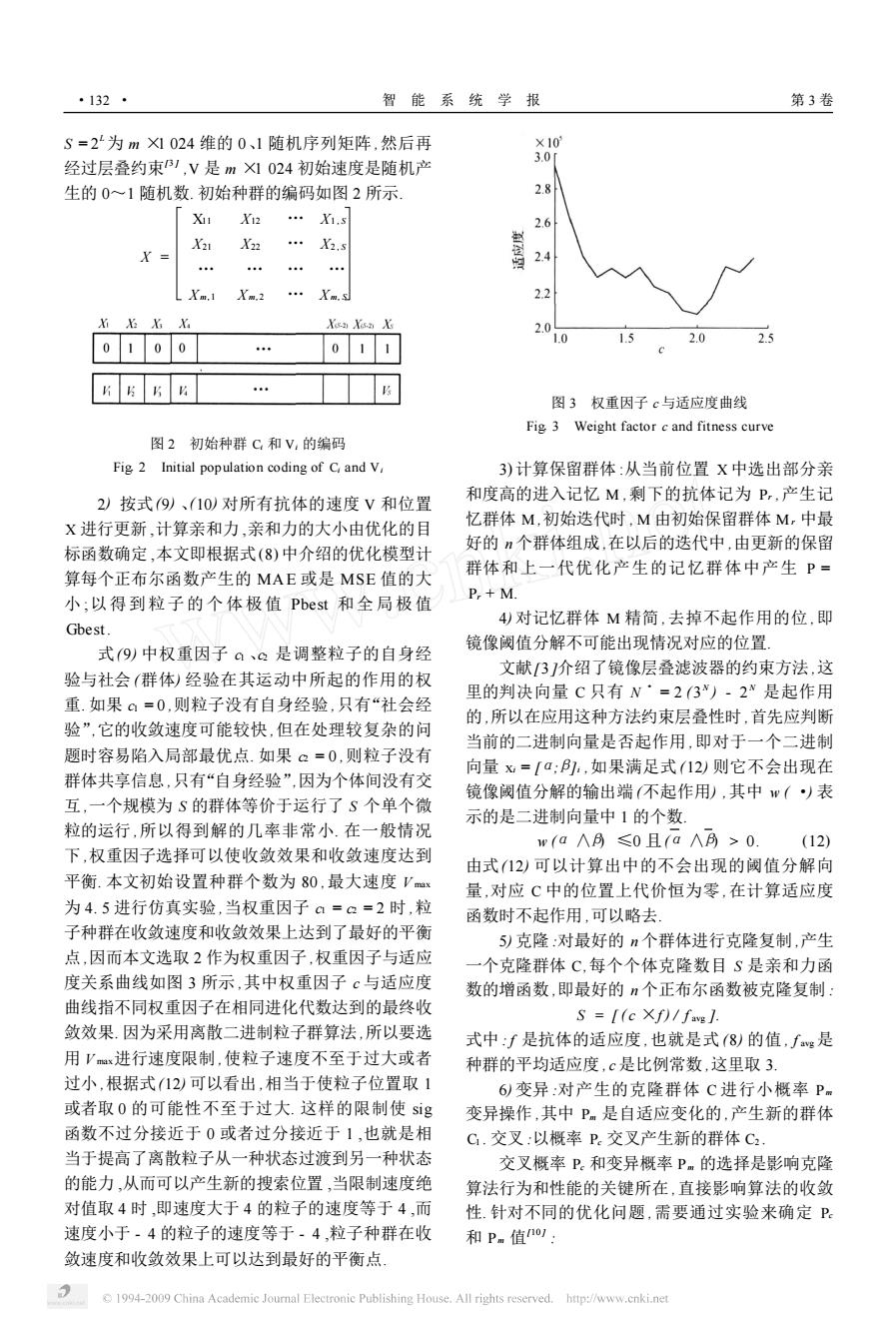
·132· 智能系统学报 第3卷 S=2为mX1024维的0、1随机序列矩阵,然后再 ×10 经过层叠约束1,V是mX1024初始速度是随机产 3.0 生的0~1随机数.初始种群的编码如图2所示. 2.8 Xi X12 …Xi.s 2.6 X21 X22 …X2s X 2.4 … Xm.1 Xm.2 Xm.s 22 Xi X:X Xa Xes-2 Xis-2 Xs 2.0 2.5 0100 011 1.0 2.0 片5⅓6 图3权重因子c与适应度曲线 Fig 3 Weight factor c and fitness curve 图2初始种群C和V:的编码 Fig 2 Initial population coding of C and V, 3)计算保留群体:从当前位置X中选出部分亲 2)按式9)、(10)对所有抗体的速度V和位置 和度高的进入记忆M,剩下的抗体记为P,产生记 X进行更新,计算亲和力,亲和力的大小由优化的目 忆群体M,初始迭代时,M由初始保留群体M,中最 标函数确定,本文即根据式(8)中介绍的优化模型计 好的n个群体组成,在以后的迭代中,由更新的保留 群体和上一代优化产生的记忆群体中产生P= 算每个正布尔函数产生的MAE或是MSE值的大 P,+M. 小;以得到粒子的个体极值Pbest和全局极值 4)对记忆群体M精简,去掉不起作用的位,即 Gbest 镜像阈值分解不可能出现情况对应的位置, 式9)中权重因子Q、Q是调整粒子的自身经 文献3]介绍了镜像层叠滤波器的约束方法,这 验与社会(群体)经验在其运动中所起的作用的权 里的判决向量C只有N·=2(3)-2是起作用 重.如果©=0,则粒子没有自身经验,只有“社会经 的,所以在应用这种方法约束层叠性时,首先应判断 验”,它的收敛速度可能较快,但在处理较复杂的问 当前的二进制向量是否起作用,即对于一个二进制 题时容易陷入局部最优点.如果α=0,则粒子没有 向量x=[a:],如果满足式12)则它不会出现在 群体共享信息,只有“自身经验”,因为个体间没有交 镜像阈值分解的输出瑞(不起作用),其中w()表 互,一个规模为S的群体等价于运行了S个单个微 示的是二进制向量中1的个数 粒的运行,所以得到解的几率非常小.在一般情况 w(a∧月≤0且(a∧月>0. (12) 下,权重因子选择可以使收敛效果和收敛速度达到 由式(12)可以计算出中的不会出现的阈值分解向 平衡.本文初始设置种群个数为80,最大速度Vx 量,对应C中的位置上代价恒为零,在计算适应度 为4.5进行仿真实验,当权重因子a=a=2时,粒 函数时不起作用,可以略去 子种群在收敛速度和收敛效果上达到了最好的平衡 5)克隆:对最好的n个群体进行克隆复制,产生 点,因而本文选取2作为权重因子,权重因子与适应 一个克隆群体C,每个个体克隆数目S是亲和力函 度关系曲线如图3所示,其中权重因子c与适应度 数的增函数,即最好的n个正布尔函数被克隆复制: 曲线指不同权重因子在相同进化代数达到的最终收 S=[(c xf)/fave ] 敛效果.因为采用离散二进制粒子群算法,所以要选 式中:f是抗体的适应度,也就是式(8)的值,fg是 用Vmx进行速度限制,使粒子速度不至于过大或者 种群的平均适应度,c是比例常数,这里取3 过小,根据式(12)可以看出,相当于使粒子位置取1 6)变异:对产生的克隆群体C进行小概率P 或者取0的可能性不至于过大.这样的限制使sg 变异操作,其中Pm是自适应变化的,产生新的群体 函数不过分接近于0或者过分接近于1,也就是相 C.交叉:以概率P.交叉产生新的群体C2. 当于提高了离散粒子从一种状态过渡到另一种状态 交叉概率P.和变异概率Pm的选择是影响克隆 的能力,从而可以产生新的搜索位置,当限制速度绝 算法行为和性能的关键所在,直接影响算法的收敛 对值取4时,即速度大于4的粒子的速度等于4,而 性.针对不同的优化问题,需要通过实验来确定P 速度小于-4的粒子的速度等于·4,粒子种群在收 和Pm值11: 敛速度和收敛效果上可以达到最好的平衡点 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
S = 2 L为 m ×1 024 维的 0、1 随机序列矩阵 ,然后再 经过层叠约束[3 ] ,V 是 m ×1 024 初始速度是随机产 生的 0~1 随机数. 初始种群的编码如图 2 所示. X = X11 X12 … X1 , S X21 X22 … X2 , S … … … … X m ,1 X m ,2 … X m , S 图 2 初始种群 Ci 和 Vi 的编码 Fig12 Initial population coding of Ci and Vi 2) 按式(9) 、(10) 对所有抗体的速度 V 和位置 X 进行更新 ,计算亲和力 ,亲和力的大小由优化的目 标函数确定 ,本文即根据式(8) 中介绍的优化模型计 算每个正布尔函数产生的 MA E 或是 MSE 值的大 小 ;以得到粒子的 个体极值 Pbest 和全局极 值 Gbest. 式(9) 中权重因子 c1 、c2 是调整粒子的自身经 验与社会 (群体) 经验在其运动中所起的作用的权 重. 如果 c1 = 0 ,则粒子没有自身经验 ,只有“社会经 验”,它的收敛速度可能较快 ,但在处理较复杂的问 题时容易陷入局部最优点. 如果 c2 = 0 ,则粒子没有 群体共享信息 ,只有“自身经验”,因为个体间没有交 互 ,一个规模为 S 的群体等价于运行了 S 个单个微 粒的运行 ,所以得到解的几率非常小. 在一般情况 下 ,权重因子选择可以使收敛效果和收敛速度达到 平衡. 本文初始设置种群个数为 80 ,最大速度 V max 为 4. 5 进行仿真实验 ,当权重因子 c1 = c2 = 2 时 ,粒 子种群在收敛速度和收敛效果上达到了最好的平衡 点 ,因而本文选取 2 作为权重因子 ,权重因子与适应 度关系曲线如图 3 所示 ,其中权重因子 c 与适应度 曲线指不同权重因子在相同进化代数达到的最终收 敛效果. 因为采用离散二进制粒子群算法 ,所以要选 用 V max进行速度限制 ,使粒子速度不至于过大或者 过小 ,根据式(12) 可以看出 ,相当于使粒子位置取 1 或者取 0 的可能性不至于过大. 这样的限制使 sig 函数不过分接近于 0 或者过分接近于 1 ,也就是相 当于提高了离散粒子从一种状态过渡到另一种状态 的能力 ,从而可以产生新的搜索位置 ,当限制速度绝 对值取 4 时 ,即速度大于 4 的粒子的速度等于 4 ,而 速度小于 - 4 的粒子的速度等于 - 4 ,粒子种群在收 敛速度和收敛效果上可以达到最好的平衡点. 图 3 权重因子 c 与适应度曲线 Fig13 Weight factor c and fitness curve 3) 计算保留群体 :从当前位置 X 中选出部分亲 和度高的进入记忆 M ,剩下的抗体记为 Pr ,产生记 忆群体 M ,初始迭代时 , M 由初始保留群体 M r 中最 好的 n 个群体组成 ,在以后的迭代中 ,由更新的保留 群体和上一代优化产生的记忆群体中产生 P = Pr + M. 4) 对记忆群体 M 精简 ,去掉不起作用的位 ,即 镜像阈值分解不可能出现情况对应的位置. 文献[3 ]介绍了镜像层叠滤波器的约束方法 ,这 里的判决向量 C 只有 N 3 = 2 ( 3 N ) - 2 N 是起作用 的 ,所以在应用这种方法约束层叠性时 ,首先应判断 当前的二进制向量是否起作用 ,即对于一个二进制 向量 xi = [α;β]i ,如果满足式 (12) 则它不会出现在 镜像阈值分解的输出端 (不起作用) ,其中 w ( ·) 表 示的是二进制向量中 1 的个数. w (α ∧β) ≤0 且(α ∧β) > 0. (12) 由式(12) 可以计算出中的不会出现的阈值分解向 量 ,对应 C 中的位置上代价恒为零 ,在计算适应度 函数时不起作用 ,可以略去. 5) 克隆 :对最好的 n 个群体进行克隆复制 ,产生 一个克隆群体 C,每个个体克隆数目 S 是亲和力函 数的增函数 ,即最好的 n 个正布尔函数被克隆复制 : S = [ ( c ×f ) / f avg ]. 式中 : f 是抗体的适应度 ,也就是式 (8) 的值 , f avg是 种群的平均适应度 , c 是比例常数 ,这里取 3. 6) 变异 :对产生的克隆群体 C 进行小概率 P m 变异操作 ,其中 Pm 是自适应变化的 ,产生新的群体 C1 . 交叉 :以概率 Pc 交叉产生新的群体 C2 . 交叉概率 Pc 和变异概率 P m 的选择是影响克隆 算法行为和性能的关键所在 ,直接影响算法的收敛 性. 针对不同的优化问题 ,需要通过实验来确定 Pc 和 P m 值[10 ] : ·132 · 智 能 系 统 学 报 第 3 卷

第2期 赵春晖,等:基于克隆粒子群算法的镜像层叠滤波器的优化设计 ·133 ·Bf'-f型 P.= fmux-favg f'≥fe 表1PSO、Kelong和PSO Kelong算法优化性能比较 ble 1 PSO,Kelong and PSOKelong optimization comparison favg. 噪声概率 类型 MAE MSE ·i卫f≥j 0.10 PSO 29485 866183 fmax favg 0.10 Kelong 22511 75.0663 p<favg. 0.10 PSO Kelong 21898 63.7912 式中:fm为群体中最大的适应度值;fa为每代群 0.15 PSO 3.7454 97.2551 体的平均适应度值;∫为要交叉的2个个体中较大 的适应度值;∫为要变异个体的适应度值 0.15 Kelong 2.9753 92.7346 7)淘汰:删除C中退化的个体,更新保留群体 0.15 PSO Kelong 25941 82.5847 P,由新的群体G中适应度增加的个体替换P,原 0.20 PSO 4.3862 137.2733 始个体组成新的个体,恢复M中去掉的位,本文中 0.20 Kelong 3.7517 118.5237 由于层叠滤波器要满足层叠性的要求,因此要对新 0.20 PSO Kelong 3.1264 983756 产生的布尔函数进行层叠性的约束, 10 8)进化:用C中的1个较好的群体替换P中 9r 1个适应度最差的群体 8 -PSO --Kelong 9)根据式(9)和(10),利用粒子的个体极值 7 PSOKelong 6 pbest和全局极值gbest进行各粒子速度和位置的 更新,在更新的过程中,要对新产生的粒子的位置进 行层叠性的约束,以保证其为正布尔函数,计算适应 度,若迭代收敛,则输出最好的群体即最优的正布尔 函数用于滤波,否则返回步骤2) 100 200300 400 500 进化代数 3实验结果与分析 用前文确定的参数和算子,优化基于镜像阈值 图4收敛曲线 分解的层叠滤波器重建被椒盐噪声污染的图像.采 Fig 4 Convergence curves 用窗口尺寸为15的层叠滤波器处理被噪声污染 在噪声增加为15%和20%时,处理结果表明, 的256256卫星云图,在噪声概率分别为0.10、 MAE和MSE的值均变化不大,这说明本文算法具 0.150.20时,在MAE准则下计算出重建后图像 有较强的去噪能力,并且算法具有稳定的收敛性.图 的MAE和MSE值,并与PSO算法和克隆算法优 4中的收敛曲线可以看出,改进的克隆粒子群算法 化结果作比较. 很快趋于收敛,只需进化130代就可以达到最优解 试验结果数据如表1所示.图4给出了10%椒 图5给出了各种算法下的去噪效果图,由图可以直 盐噪声条件下,PSO算法、克隆算法(Kelong)和克 观地看出,图5(e)的滤波效果最好,细节保持也更 隆粒子群算法(PSO Kelong)的收敛曲线,图4给出 好,图像边缘更清晰。 了10%椒盐噪声条件下,上面3种算法的去噪效果 图.比较图4的曲线可以看出,克隆算法较粒子群算 法有更好的收敛特性,取得了更好的滤波性能, 由表1中数据可以看出,在镜像阈值分解下,粒 子群算法搜索能力较差,容易陷入局部最优,克隆算 法收敛较平稳,本文克隆粒子群算法(PSO Kelong) 比粒子群算法和克隆算法取得了更好的滤波特性, 收敛加快,MAE和MSE值都得到了进一步减小 这就是说图像的噪声进一步降低,而且图像的细节 保持能力也得到了提高, (a)cloud图像 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
Pc = pc 1 - ( pc 1 - pc 2 ) ( f′- f avg ) f max - f avg , f′≥f avg , pc 1 , f′< f avg . Pm = pm1 - ( pm1 - pm2 ) ( f max - f) f max - f avg , f ≥f avg , pm1 , f′< f avg . 式中 : f max为群体中最大的适应度值; f avg 为每代群 体的平均适应度值; f 为要交叉的 2 个个体中较大 的适应度值; f 为要变异个体的适应度值. 7) 淘汰 :删除 C2 中退化的个体 ,更新保留群体 Pr ,由新的群体 C2 中适应度增加的个体替换 Pr 原 始个体组成新的个体 ,恢复 M 中去掉的位 ,本文中 由于层叠滤波器要满足层叠性的要求 ,因此要对新 产生的布尔函数进行层叠性的约束. 8) 进化 :用 C 中的 n1 个较好的群体替换 P 中 n1 个适应度最差的群体. 9) 根据式 ( 9) 和 ( 10) ,利用粒子的个体极值 p best 和全局极值 gbest 进行各粒子速度和位置的 更新 ,在更新的过程中 ,要对新产生的粒子的位置进 行层叠性的约束 ,以保证其为正布尔函数. 计算适应 度 ,若迭代收敛 ,则输出最好的群体即最优的正布尔 函数用于滤波 ,否则返回步骤 2) . 3 实验结果与分析 用前文确定的参数和算子 ,优化基于镜像阈值 分解的层叠滤波器重建被椒盐噪声污染的图像. 采 用窗口尺寸为 1 ×5 的层叠滤波器处理被噪声污染 的 256 ×256 卫星云图 ,在噪声概率分别为 0110、 0115、0120 时 ,在 MA E 准则下计算出重建后图像 的 MA E 和 MSE 值 ,并与 PSO 算法和克隆算法优 化结果作比较. 试验结果数据如表 1 所示. 图 4 给出了 10 %椒 盐噪声条件下 ,PSO 算法、克隆算法 ( Kelong) 和克 隆粒子群算法 (PSO Kelong) 的收敛曲线 ;图 4 给出 了 10 %椒盐噪声条件下 ,上面 3 种算法的去噪效果 图. 比较图 4 的曲线可以看出 ,克隆算法较粒子群算 法有更好的收敛特性 ,取得了更好的滤波性能. 由表 1 中数据可以看出 ,在镜像阈值分解下 ,粒 子群算法搜索能力较差 ,容易陷入局部最优 ,克隆算 法收敛较平稳 ,本文克隆粒子群算法 (PSO Kelong) 比粒子群算法和克隆算法取得了更好的滤波特性 , 收敛加快 ,MA E 和 MSE 值都得到了进一步减小 , 这就是说图像的噪声进一步降低 ,而且图像的细节 保持能力也得到了提高. 表 1 PSO、Kelong 和 PSOKelong 算法优化性能比较 Table 1 PSO, Kelong and PSOKelong optimization comparison 噪声概率 类型 MAE MSE 0110 0. 10 0. 10 PSO 21948 5 861618 3 Kelong 21251 1 751066 3 PSO Kelong 21189 8 631791 2 0115 0. 15 0. 15 PSO 31745 4 971255 1 Kelong 21975 3 921734 6 PSO Kelong 21594 1 821584 7 0120 0. 20 0. 20 PSO 41386 2 1371273 3 Kelong 31751 7 1181523 7 PSO Kelong 31126 4 981375 6 图 4 收敛曲线 Fig14 Convergence curves 在噪声增加为 15 %和 20 %时 ,处理结果表明 , MA E 和 MSE 的值均变化不大 ,这说明本文算法具 有较强的去噪能力 ,并且算法具有稳定的收敛性. 图 4 中的收敛曲线可以看出 ,改进的克隆粒子群算法 很快趋于收敛 ,只需进化 130 代就可以达到最优解. 图 5 给出了各种算法下的去噪效果图 ,由图可以直 观地看出 ,图 5 (e) 的滤波效果最好 ,细节保持也更 好 ,图像边缘更清晰. (a) cloud 图像 第 2 期 赵春晖 ,等 :基于克隆粒子群算法的镜像层叠滤波器的优化设计 ·133 ·

·134· 智能系统学报 第3卷 4结束语 本文将克隆算法和粒子群算法相结合,并对该 算法根据应用的需要作了各种改进.加入了自适应 算子,能够根据优化的结果实时地改变变异概率,为 克服各种算法在镜像条件下容易陷入局部最优解的 问题,实验结果表明,最优结果比PSO和克隆算法 要好,改进的算法具有更强寻优能力,层叠滤波器在 图像的细节保持能力和去除噪声能力上都有很大的 提高.该算法收敛速度更快,很快地达到全局最优, (b)加噪10%图像 具有更强的稳定性 参考文献: [1]CO YLE EJ,LIN J H.Stack filters and the mean abso- lute error criterion[J].IEEE Transaction on Signal Pro- cessing,1988,36(8):12441254. [2]PARADES J L,ARCE GR.Optimization of stack filters based on mirrored threshold decomposition[J].IEEE Transaction on Signal Procession,2001,49(6):1179- 1188. [3]崔颖,赵春晖.基于镜像阈值分解的层叠滤波器优化 [J].哈尔滨工程大学学报,2006,27(6):904-907. (c)PSO滤波图像 CUI Ying,ZHAO Chunhui.Optimization of stack filters based on mirrored threshold decomposition [J ]Journal of Harbin Engineering University,2006,27(6):904- 907. [4]赵春晖,孙莉,付正威.基于克隆选择算法的层叠滤波 器的优化设计D].哈尔滨工程大学学报,2007,28(4): 454-460 ZHAO Chunhui,SUN Li,FU Zhengwei.Optimizing stack filters through a clone selection algorithm [J ] Journal of Harbin Engineering University,2007,28(4): 454460. [5]PARADES J L,ARCE G R.Stack filters,stack smoothers,and mirrored threshold decomposition [J ] (d)Kelong滤波图像 IEEE Transactions on Signal Processing,1999,47 (10):2757-2767. [6]吴静敏,左洪福.基于免疫粒子群算法的组合预测方法 [U].系统工程理论方法应用,2006,15(3):229233. WU Jingmin,ZUO Hongfu.A combined forecasting method base on PSO with immunity algorithms [J ]Sys- tems Engineering Theory Methodology Applications, 2006,15(3):229233 作者简介: 赵春晖男,1965年生,教授、博士生导 师,主要研究方向为智能信息处理技术、图 像处理.获省部级科技奖5项,发表论文 180多篇,出版著作3部。 (e)PSOKelong滤波图像 图5去噪效果图 Fig.5 Noise removal results 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.ne
4 结 束 语 本 文 将 克 隆 算 法 和 粒 子 群 算 法 相 结 合 , 并 对 该 算 法 根 据 应 用 的 需 要 作 了 各 种 改 进 . 加 入 了 自 适 应 算 子 , 能 够 根 据 优 化 的 结 果 实 时 地 改 变 变 异 概 率 , 为 克 服 各 种 算 法 在 镜 像 条 件 下 容 易 陷 入 局 部 最 优 解 的 问 题 , 实 验 结 果 表 明 , 最 优 结 果 比 P S O 和 克 隆 算 法 要 好 , 改 进 的 算 法 具 有 更 强 寻 优 能 力 , 层 叠 滤 波 器 在 图 像 的 细 节 保 持 能 力 和 去 除 噪 声 能 力 上 都 有 很 大 的 提 高 . 该 算 法 收 敛 速 度 更 快 , 很 快 地 达 到 全 局 最 优 , 具 有 更 强 的 稳 定 性 . 参 考 文 献 : [ 1 ] C O YL E E J , L IN J H . S t a c k fi l t e r s a n d t h e m e a n a b s o 2 l u t e e r r o r c r i t e r i o n [ J ] . I E E E T r a n s a c t i o n o n S i g n a l P r o 2 c e s s i n g , 1 9 8 8 , 3 6 ( 8 ) : 1 2 4 4 2 1 2 5 4 . [ 2 ] P A R A D E S J L , A R C E G R . O p t i m i z a t i o n o f s t a c k fi l t e r s b a s e d o n m i r r o r e d t h r e s ho l d d e c o mp o s i t i o n [ J ] . I E E E T r a n s a c t i o n o n S i g n a l P r o c e s s i o n , 2 0 0 1 , 4 9 ( 6 ) : 1 1 7 9 2 1 1 8 8 . [ 3 ] 崔 颖 , 赵 春 晖 . 基 于 镜 像 阈 值 分 解 的 层 叠 滤 波 器 优 化 [ J ] . 哈 尔 滨 工 程 大 学 学 报 , 2 0 0 6 , 2 7 ( 6 ) : 9 0 4 2 9 0 7 . C U I Yi n g , Z H A O C h u n h u i . O p t i m i z a t i o n o f s t a c k fi l t e r s b a s e d o n m i r r o r e d t h r e s ho l d d e c o mp o s i t i o n [ J ] . J o u r n a l o f H a r b i n E n g i n e e r i n g U n i v e r s i t y , 2 0 0 6 , 2 7 ( 6 ) : 9 0 4 2 9 0 7 . [ 4 ] 赵 春 晖 , 孙 莉 , 付 正 威 . 基 于 克 隆 选 择 算 法 的 层 叠 滤 波 器 的 优 化 设 计 [ J ] . 哈 尔 滨 工 程 大 学 学 报 , 2 0 0 7 , 2 8 ( 4 ) : 4 5 4 2 4 6 0 . Z H A O C h u n h u i , S U N L i , F U Zh e n g w e i . O p t i m i z i n g s t a c k fi l t e r s t h r o u g h a c l o n e s e l e c t i o n a l g o r i t h m [ J ] . J o u r n a l o f H a r b i n E n g i n e e r i n g U ni v e r s i t y , 2 0 0 7 , 2 8 ( 4 ) : 4 5 4 2 4 6 0 . [ 5 ] P A R A D E S J L , A R C E G R . S t a c k fi l t e r s , s t a c k s mo o t h e r s , a n d m i r r o r e d t h r e s h o l d d e c o mp o s i t i o n [ J ] . I E E E T r a n s a c t i o n s o n S i g n a l P r o c e s s i n g , 1 9 9 9 , 4 7 ( 1 0 ) : 2 7 5 7 2 2 7 6 7 . [ 6 ] 吴 静 敏 , 左 洪 福 . 基 于 免 疫 粒 子 群 算 法 的 组 合 预 测 方 法 [ J ] . 系 统 工 程 理 论 方 法 应 用 , 2 0 0 6 , 1 5 ( 3 ) : 2 2 9 2 2 3 3 . W U J i n g m i n , Z U O H o n gf u . A c o m b i n e d fo r e c a s t i n g m e t ho d b a s e o n P S O w i t h i m m u n i t y a l go r i t h m s [ J ] . S y s 2 t e m s E n g i n e e r i n g T h e o r y · M e t h o do l o g y A p p l i c a t i o n s , 2 0 0 6 , 1 5 ( 3 ) : 2 2 9 2 2 3 3 . 作 者 简 介 : 赵 春 晖 男 , 1 9 6 5 年 生 , 教 授 、 博 士 生 导 师 , 主 要 研 究 方 向 为 智 能 信 息 处 理 技 术 、 图 像 处 理 . 获 省 部 级 科 技 奖 5 项 , 发 表 论 文 1 8 0 多 篇 , 出 版 著 作 3 部 . · 1 3 4 · 智 能 系 统 学 报 第 3 卷