
第3卷第3期 智能系统学报 Vol 3 Na 3 2008年6月 CAA I Transactions on Intelligent Systems Jun 2008 多分辨小波过程神经网络及其应用研究 李洋,钟诗胜 (哈尔滨工业大学机电工程学院,黑龙江哈尔滨150001) 摘要:以小波多分辨分析为理论基础,结合过程神经网络模型,建立了具有分层、多分辨和局部学习特性的多分辨 小波过程神经网络.该网络充分利用小波函数和尺度函数互补的特性,以及过程神经网络可以处理连续输入信号的 能力,能够很好地解决复杂的非线性时间序列的预测问题.给出了相应的学习算法,并以航空发动机排气温度裕度 状态监视为例,利用多分辨小波过程神经网络进行预测.结果表明,多分辨小波过程神经网络收敛速度快、精度高」 同时也为航空发动机排气温度裕度状态监视问题提供了一种有效的方法 关键词:过程神经元;多分辨分析;多分辨小波过程神经网络:学习算法;发动机状态监测 中图分类号:1P183文献标识码:A文章编号:1673-4785(2008)03-0211-05 Research on multi-resolution wavelet process neural networks and applica tions L I Yang,ZHONG Shi-sheng (Deparment ofMechanical and Electrical Engineering,Harbin Institute of Technobgy,Harbin 150001,China) Abstract:We propose a multiresolution wavelet process neural nework (MW PNN)based on wavelet multiresolu- tion analysis theory and the process neural netork model It combines their characteristics of delam ination,multi- resolution,and bcal leaming capability The netork,making full use of the comp lementary characteristic ofwave- let function and scale function,as well as the ability to handle continuous input signals,can orecast complicated nonlinear tme sequences The network's leaming algorithm is given Using an example of state monitoring of ex- haust gas temperature margins of aeroengines,forecasting was perfomed using the multi-resolution wavelet process neural network It was found that the proposed network exhibited good convergence and high accuracy,providing an effective way for state monitoring of exhaust gas temperatures of aeroengines Keywords:process neuron;multiresolution analysis multiresolution wavelet process neural netork,leaming algo- rithm;condition monitoring of aeroengine system 小波分析是当前应用数学中一个迅速发展的新 了过程神经元网络模型.过程神经元与传统神经元 领域.小波在紧支集中能任意逼近非线性连续函数 不同之处在于过程神经元的输入和权值可以是时变 的特性和它在时频域都有分辨的特点,使得以小波 的,其聚合运算中既有对空间的多输入聚合,也有对 分析理论为基础构造的小波神经网络更适合于学习 时间过程的积累.过程神经元网络是人工神经元网 局部非线性和快速变化的函数).小波神经网络 络在时间域上的扩展,放宽了传统神经元网络模型 避免了传统神经网络机构设计的盲目性,因而具有对输入的同步瞬时限制,因此,对于求解与过程有关 较强的逼近、容错能力)然而,在许多复杂的系统 的众多实际问题有着广泛的应用价值1.将过程神 中,许多系统的输入是依赖于时间变化的连续函数, 经网络和小波多分辨分析理论相结合,在文献 其输出值既依赖于输入函数的空间聚合,又与时间 [1·6的基础上,提出了多分辨小波过程神经网络 的累计效应密切相关.针对这一问题,文献【4提出 模型.其输入和权值是时变的,其聚合运算既有对空 间的多输入聚合,也有对时间过程的积累.多分辨小 收稿日期:2007-12-10 基金项目:国家自然科学基金资助项目(60572174) 波过程神经网络充分利用小波函数和尺度函数互补 通讯作者:李洋.Emai让ansysman(@126cmm 的特性,把尺度函数和小波函数共同包含在网络中, 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved http://www.cnki.net
第 3卷第 3期 智 能 系 统 学 报 Vol. 3 №. 3 2008年 6月 CAA I Transactions on Intelligent System s Jun. 2008 多分辨小波过程神经网络及其应用研究 李 洋 , 钟诗胜 (哈尔滨工业大学 机电工程学院 ,黑龙江 哈尔滨 150001) 摘 要 :以小波多分辨分析为理论基础 ,结合过程神经网络模型 ,建立了具有分层、多分辨和局部学习特性的多分辨 小波过程神经网络. 该网络充分利用小波函数和尺度函数互补的特性 ,以及过程神经网络可以处理连续输入信号的 能力 ,能够很好地解决复杂的非线性时间序列的预测问题. 给出了相应的学习算法 ,并以航空发动机排气温度裕度 状态监视为例 ,利用多分辨小波过程神经网络进行预测. 结果表明 ,多分辨小波过程神经网络收敛速度快、精度高. 同时也为航空发动机排气温度裕度状态监视问题提供了一种有效的方法. 关键词 :过程神经元 ;多分辨分析 ;多分辨小波过程神经网络 ;学习算法 ;发动机状态监测 中图分类号 : TP183 文献标识码 : A 文章编号 : 167324785 (2008) 0320211205 Research on multi2resolution wavelet process neural networks and applications L I Yang, ZHONG Shi2sheng (Department ofMechanical and Electrical Engineering, Harbin Institute of Technology, Harbin 150001, China) Abstract:We p ropose a multiresolution wavelet p rocess neural network (MWPNN ) based on wavelet multiresolu2 tion analysis theory and the p rocess neural network model. It combines their characteristics of delam ination, multi2 resolution, and local learning capability. The network, making full use of the comp lementary characteristic ofwave2 let function and scale function, as well as the ability to handle continuous input signals, can forecast comp licated nonlinear time sequences. The network’s learning algorithm is given. U sing an examp le of state monitoring of ex2 haust gas temperature margins of aeroengines, forecasting was performed using the multi2resolution wavelet p rocess neural network. It was found that the p roposed network exhibited good convergence and high accuracy, p roviding an effective way for state monitoring of exhaust gas temperatures of aeroengines. Keywords: p rocess neuron; multiresolution analysis; multiresolution wavelet p rocess neural network; learning algo2 rithm; condition monitoring of aeroengine system 收稿日期 : 2007212210. 基金项目 :国家自然科学基金资助项目 (60572174). 通讯作者 :李 洋. E2mail: ansysman@126. com. 小波分析是当前应用数学中一个迅速发展的新 领域. 小波在紧支集中能任意逼近非线性连续函数 的特性和它在时频域都有分辨的特点 ,使得以小波 分析理论为基础构造的小波神经网络更适合于学习 局部非线性和快速变化的函数 [ 122 ] . 小波神经网络 避免了传统神经网络机构设计的盲目性 ,因而具有 较强的逼近、容错能力 [ 3 ] . 然而 ,在许多复杂的系统 中 ,许多系统的输入是依赖于时间变化的连续函数 , 其输出值既依赖于输入函数的空间聚合 ,又与时间 的累计效应密切相关. 针对这一问题 ,文献 [ 4 ]提出 了过程神经元网络模型. 过程神经元与传统神经元 不同之处在于过程神经元的输入和权值可以是时变 的 ,其聚合运算中既有对空间的多输入聚合 ,也有对 时间过程的积累. 过程神经元网络是人工神经元网 络在时间域上的扩展 ,放宽了传统神经元网络模型 对输入的同步瞬时限制 ,因此 ,对于求解与过程有关 的众多实际问题有着广泛的应用价值 [ 5 ] . 将过程神 经网络和小波多分辨分析理论相结合 , 在文献 [ 126 ]的基础上 ,提出了多分辨小波过程神经网络 模型. 其输入和权值是时变的 ,其聚合运算既有对空 间的多输入聚合 ,也有对时间过程的积累. 多分辨小 波过程神经网络充分利用小波函数和尺度函数互补 的特性 ,把尺度函数和小波函数共同包含在网络中 , © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·212· 智能系统学报 第3卷 先在粗分辨率下对信号进行逼近,而后由粗到细逐 虑空间L2(R)中的一个闭子空间序列V,基于 渐增加节点来保证逼近精度.由于各基函数的相互 多分辨分析理论,空间V有如下分解: 正交性,使得在训练过程中添加网络节点而不影响 Vn=Vm1回W1='m2⊙W2⊙Wm1= 己训练好的网络权值,可使网络学习时间大大缩短 V。⊙W。⊙W,⊙…⊙Wm. (4) 多分辨小波过程神经网络可以处理时变信号,从而 式中: 避免了传统神经网络结在解决大容量非线性时变系 。=anφ。=22Φ(zx-l,m,n∈Z. 统的信号处理问题时存在的不适应性,使得网络能 够很好的解决复杂的非线性时间序列的预测问题, W。=panf中n=22中zx-,m,n∈Z}. (5) 1多分辨小波过程神经网络 式中:中(x)、中(x)分别是尺度函数和小波函数,子 11过程神经元 空间V。、W。、…W.相互正交 过程神经元是由过程输入信号加权,时间、空间 因此,在给定分辨率2“下,任意非线性函数 二维聚合和阈值激励输出4部分运算组成.与传统 f(x)∈L(R),可由式6)近似分解 神经元不同之处在于过程神经元的输入和连接权可 f(x)≈(x)=∑.中m(x)+ 以是时变函数,过程神经元增加了一个对于时间的 聚合算子,其聚合运算既有对输入信号的空间加权 12w2 聚集,也有对时间过程效应的累积.过程神经元模型 g.d..以 (6) 的结构如图1所示 13多分辨小波过程神经网络模型 x,()w,() 根据多分辨分析思想,可以构造具有这样功能 ()"(D 的多分辨小波过程神经网络.将小波函数和尺度函 K(·) F(·) 数共同作为过程神经网络的隐层激励函数,充分利 xn(t) ,(t) 用二者互补的特性,建立具有分层、多分辨和局部学 图1过程神经元结构图 习特性的多分辨小波过程神经网络.多分辨小波过 Fig 1 Structure of process neuron 程神经网络的结构如图2所示 过程神经元输入与输出之间的映射关系为 y=fw(t)⊙X()⊙K()-.(1) X()() 式中:X()=(x),为(),…xn()为过程神经 元的输入矢量,W()=w1(),w2(),,wn()) 为相应的连接权矢量,“⊙表示某种空间聚合运 算,可取为A()=w(⊙X()=∑x(,(, 11 “⊙”表示某种时间聚合运算,可取为 A()⊙K)=。K)d,为过程神经元的 图2分辨小波过程神经网络模型 输出阈值 Fig 2 Multiresolution wavelet process neural netork 12多分辨分析 model 函数中(x)∈L(R),其通过伸缩平移可产生一 组小波函数基」 该网络首先在最粗的分辨率下学习输入输出映 射关系,然后依次被训练在越来越高的分辨率下学 中。6(x划 (2) a 习,直到达到所要求的精度。 式中:a、b分别为伸缩、平移尺度因子.其二进制离 基于多分辨分析的小波过程神经网络,其网络 散小波族可表示为 隐节点激活函数有2种类型:尺度函数和小波函数 中n.n(x)=2"中(2"x-,m,n∈Z 网络输出为 M.1 2m-IL 3) 式中:m为伸缩尺度,n为小波的平移离散步长.考 y=买oW+4电= 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. htip://www.cnki.net
先在粗分辨率下对信号进行逼近 ,而后由粗到细逐 渐增加节点来保证逼近精度. 由于各基函数的相互 正交性 ,使得在训练过程中添加网络节点而不影响 已训练好的网络权值 ,可使网络学习时间大大缩短. 多分辨小波过程神经网络可以处理时变信号 ,从而 避免了传统神经网络结在解决大容量非线性时变系 统的信号处理问题时存在的不适应性 ,使得网络能 够很好的解决复杂的非线性时间序列的预测问题. 1 多分辨小波过程神经网络 1. 1 过程神经元 过程神经元是由过程输入信号加权 ,时间、空间 二维聚合和阈值激励输出 4部分运算组成. 与传统 神经元不同之处在于过程神经元的输入和连接权可 以是时变函数 ,过程神经元增加了一个对于时间的 聚合算子 ,其聚合运算既有对输入信号的空间加权 聚集 ,也有对时间过程效应的累积. 过程神经元模型 的结构如图 1所示. 图 1 过程神经元结构图 Fig. 1 Structure of p rocess neuron 过程神经元输入与输出之间的映射关系为 y = f (W ( t) ) © X ( t) ª K (·) - θ). (1) 式中 : X ( t) = ( x1 ( t) , x2 ( t) , …, xn ( t) ) 为过程神经 元的输入矢量 , W ( t) = (w1 ( t) , w2 ( t) , …, wn ( t) ) 为相应的连接权矢量 ,“© ”表示某种空间聚合运 算 ,可取为 A ( t) =W ( t) © X ( t) = ∑ n i =1 xi ( t) wi ( t) , “ª ”表 示 某 种 时 间 聚 合 运 算 , 可 取 为 A ( t) ª K (·) = ∫ T 0 A ( t) K (·) dt ,θ为过程神经元的 输出阈值. 1. 2 多分辨分析 函数 ψ( x) ∈L 2 (R ) ,其通过伸缩平移可产生一 组小波函数基 : ψa, b ( x) = 1 a ψ( x - b a ) . (2) 式中 : a、b分别为伸缩、平移尺度因子. 其二进制离 散小波族可表示为 ψm, n ( x) = 2 - mψ(2 - m x - n) , m , n ∈ Z 2 . (3) 式中 : m 为伸缩尺度 , n为小波的平移离散步长. 考 虑空间L 2 (R )中的一个闭子空间序列 { Vj } j∈z ,基于 多分辨分析理论 ,空间 Vm 有如下分解 : Vm = Vm - 1 © Wm - 1 = Vm - 2 © Wm - 2 © Wm - 1 = V0 © W0 © W1 © … © Wm - 1 . (4) 式中 : Vm = span{φm n = 2 m 2φ(2 m x - n) , m , n ∈ Z }, Wm = span{ψm n = 2 m 2ψ(2 m x - n) , m , n ∈ Z } . (5) 式中 :φ( x)、ψ( x) 分别是尺度函数和小波函数 ,子 空间 V0、W0、…、Wm - 1相互正交. 因此 ,在给定分辨率 2 - M下 , 任意非线性函数 f ( x) ∈L 2 (R ) ,可由式 (6)近似分解 : f ( x) ≈ fM ( x) = ∑ L m =0 c0nφ0n ( x) + ∑ M - 1 m =0 ∑ 2 m - 1L n =0 dm nψm n ( x) . (6) 1. 3 多分辨小波过程神经网络模型 根据多分辨分析思想 ,可以构造具有这样功能 的多分辨小波过程神经网络. 将小波函数和尺度函 数共同作为过程神经网络的隐层激励函数 ,充分利 用二者互补的特性 ,建立具有分层、多分辨和局部学 习特性的多分辨小波过程神经网络. 多分辨小波过 程神经网络的结构如图 2所示. 图 2 分辨小波过程神经网络模型 Fig. 2 Multiresolution wavelet p rocess neural network model 该网络首先在最粗的分辨率下学习输入输出映 射关系 ,然后依次被训练在越来越高的分辨率下学 习 ,直到达到所要求的精度. 基于多分辨分析的小波过程神经网络 ,其网络 隐节点激活函数有 2种类型 :尺度函数和小波函数 , 网络输出为 y = ∑ L k =0 c0kφ0k ( x) + ∑ M - 1 m =0 ∑ 2 m - 1L k =0 dm kψm k ( x) = ·212· 智 能 系 统 学 报 第 3卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第3期 李洋,等:多分辨小波过程神经网络及其应用研究 ·213· 2i2"。E 个层次上实现,分辨率越高,得到的逼近精度越高, ()wkdt-))+ 但计算量花费也越大.在较粗的分辨率下逼近,虽然 42中2"。 逼近精度较差,但工作量要比细分辨率下的工作量 小得多.因此,可考虑将细分辨率下的逼近问题转化 (7 为粗的分辨率下的逼近问题.这就是构造多分辨小 式中:x()为多分辨小波过程神经网络的输入函 波过程神经网络学习算法的基本思想 数矢量,w()为隐层第k个尺度函数隐节点激活 考虑函数f(x)在尺度m=M上的逼近问题.首 函数与输入层第个单元的连接权函数,()为隐 先在最粗尺度m=0上对函数f(x)的进行逼近.对 层第k个小波函数隐节点激活函数与输入层第个 于一维输入函数,最粗尺度下的网格系由2个网格 单元的连接权函数,为0尺度下,隐层第k个尺度 点组成,最细尺度m=M的选取则与采样频率有关, 函数隐节点激活函数与输出层单元的连接权值,d: 即最细网格间距应等于最小非零采样频率,顺次较 为m尺度下,隐层第k个小波函数隐节点激活函数 细分解尺度下的网格系均由上一尺度网格系中间隔 与输出层单元的连接权值,y为网络输出 挑一构成,图3描述了各尺度之间网格系的关系. 2多分辨小波过程神经网络学习算法 X×××××××× 21 函数正交基展开 由式(7)可以看出过程神经网络的时间累积运 + 算比较复杂,为此引入一组合适的正交基函数将输 0 入函数和连接权函数同时展开,以达到简化时间 123456789一 累积运算的目的. 位置k 设(),(),…b(,…为C([0,T])空间 图3多分辨小波网格系示意图 上一组标准正交基函数,为输入空间的任意函数,由 Fig 3 The sketch map of multiresolution wavelet grid- 数学分析理论则有 ding series x()= dib(o. 在最粗尺度m=0上对函数f(x的逼近可表示 为 (t= 26(w, (8 f(x)≈无(x (x). (10) va(v= b(o 在较细尺度m=1下,f(x)∈V,=,⊙W其函数逼 式中:w、分别为w、:(关于p()的展开式 近为 系数 fx)≈f(x) 根据正交函数的性质,有 oa (s) 。手w4f0d 1,p=4 11) 、0,p≠4 继续提高分辨率,尺度依次m=2,m=3,…逼近 因此,式(7)可以转化为 误差越来越小,直到满足逼近精度要求为止 M.1 2m-IL 尺度m=M时, 24-IL ()-B. M.1 2m-L .12w-1L a+gd电 (12) 4:2i2“2dd 多分辨小波过程神经网络的学习算法可描述如图4 (9) 3 22学习过程 航空发动机EGT状态监视 多分辨分析是一种逐层逼近的分析工具,可以 飞机发动机排气温度(EGT),是飞机发动机的 利用其提供的多层次信息,把大规模计算分解在多 重要状态参数.由于发动机部件性能衰退或故障均 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
∑ L k =0 c0k 2 - m 2 (φ(2 - m ∫ T 0 ∑ n i =1 xi ( t) wik tdt - k) ) + ∑ M - 1 m =0 ∑ 2 m - 1 k =0 dm k 2 - m 2 (ψ(2 - m ∫ T 0 ∑ n i =1 xi ( t) vik ( t) dt - k) ). (7) 式中 : xi ( t) 为多分辨小波过程神经网络的输入函 数矢量 , wik ( t)为隐层第 k个尺度函数隐节点激活 函数与输入层第 i个单元的连接权函数 , vik ( t)为隐 层第 k个小波函数隐节点激活函数与输入层第 i个 单元的连接权函数 , c0k为 0尺度下 ,隐层第 k个尺度 函数隐节点激活函数与输出层单元的连接权值 , dm k 为 m 尺度下 ,隐层第 k个小波函数隐节点激活函数 与输出层单元的连接权值 , y为网络输出. 2 多分辨小波过程神经网络学习算法 2. 1 函数正交基展开 由式 (7)可以看出过程神经网络的时间累积运 算比较复杂 ,为此引入一组合适的正交基函数将输 入函数和连接权函数同时展开 [ 7 ] ,以达到简化时间 累积运算的目的. 设 b1 ( t) , b2 ( t) , …, bp ( t) , …为 C ( [0, T ])空间 上一组标准正交基函数 ,为输入空间的任意函数 ,由 数学分析理论则有 xi ( t) = ∑ P p =1 a P i bP ( t) , wik ( t) = ∑ P p =1 w P ik bP ( t) , vik ( t) = ∑ P p =1 v P ik bP ( t) . (8) 式中 : w P ik、v P ik分别为 wik、vik ( t) 关于 bP ( t)的展开式 系数. 根据正交函数的性质 ,有 ∫ T 0 bP ( t) bq ( t) dt = 1, p = q; 0, p ≠ q. . 因此 ,式 (7)可以转化为 y = ∑ L k =0 c0kφ0k ( x) + ∑ M - 1 m =0 ∑ 2 m - 1 L k =0 dm kψm k ( x) = ∑ L k =0 c0k 2 m 2φ(2 - m ∑ n i =1 ∑ P p =1 a p iw p ik dt - k) + ∑ M - 1 m =0 ∑ 2m - 1L k =0 dm k 2 - m 2ψ(2 - m ∑ n i =1 ∑ P p =1 a p i v p ik dt - k). (9) 2. 2 学习过程 多分辨分析是一种逐层逼近的分析工具 ,可以 利用其提供的多层次信息 ,把大规模计算分解在多 个层次上实现 ,分辨率越高 ,得到的逼近精度越高 , 但计算量花费也越大. 在较粗的分辨率下逼近 ,虽然 逼近精度较差 ,但工作量要比细分辨率下的工作量 小得多. 因此 ,可考虑将细分辨率下的逼近问题转化 为粗的分辨率下的逼近问题. 这就是构造多分辨小 波过程神经网络学习算法的基本思想. 考虑函数 f ( x)在尺度 m =M 上的逼近问题. 首 先在最粗尺度 m = 0上对函数 f ( x)的进行逼近. 对 于一维输入函数 ,最粗尺度下的网格系由 2个网格 点组成 ,最细尺度 m =M 的选取则与采样频率有关 , 即最细网格间距应等于最小非零采样频率 ,顺次较 细分解尺度下的网格系均由上一尺度网格系中间隔 挑一构成 ,图 3描述了各尺度之间网格系的关系. 图 3 多分辨小波网格系示意图 Fig 3 The sketch map of multiresolution wavelet grid2 ding series 在最粗尺度 m = 0上对函数 f ( x)的逼近可表示 为 f ( x) ≈ f0 ( x) = ∑ L k =0 c0kφ0k ( x). (10) 在较细尺度 m = 1下 , f ( x) ∈V1 =V0 ©W0其函数逼 近为 f ( x) ≈ f1 ( x) = ∑ L k =0 c0kφ0k ( x) + ∑ L k =0 d0kψ0k . (11) 继续提高分辨率 ,尺度依次 m = 2, m = 3, ……逼近 误差越来越小 ,直到满足逼近精度要求为止. 尺度 m =M 时 , fM ( x) = fM - 1 ( x) ∑ 2 M - 1L k =0 dM - 1, kψM - 1, k ( x) = ∑ L k =0 c0kφ0k ( x) + ∑ M - 1 m =0 ∑ 2 m - 1 L k =0 dm kψm k ( x). (12) 多分辨小波过程神经网络的学习算法可描述如图 4. 3 航空发动机 EGT状态监视 飞机发动机排气温度 ( EGT) ,是飞机发动机的 重要状态参数. 由于发动机部件性能衰退或故障均 第 3期 李 洋 ,等 :多分辨小波过程神经网络及其应用研究 ·213· © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
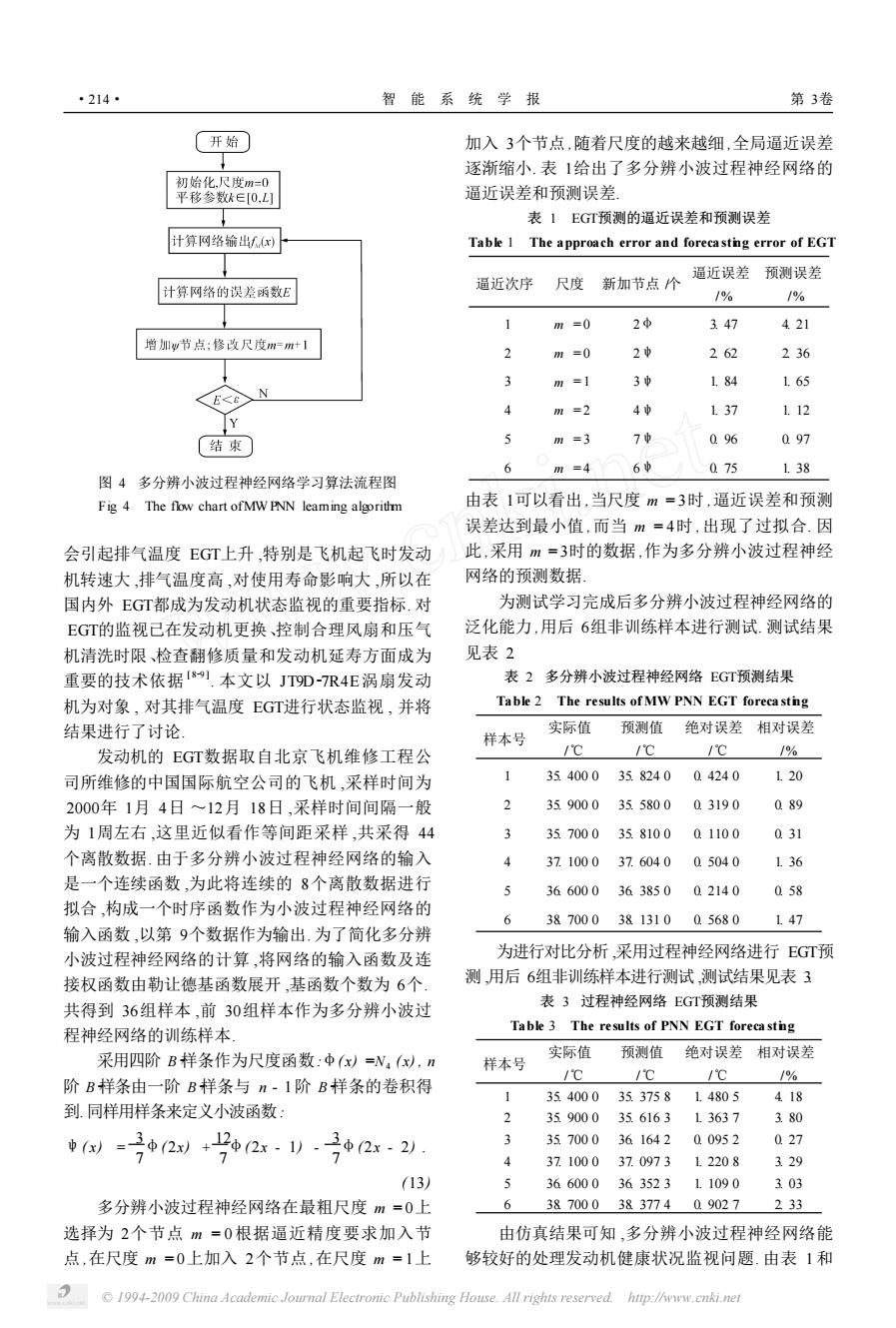
·214· 智能系统学报 第3卷 开始 加入3个节点,随着尺度的越来越细,全局逼近误差 逐渐缩小.表1给出了多分辨小波过程神经网络的 初始化,尺度m=0 平移参数k∈[0,L 逼近误差和预测误差 表1EGT预测的逼近误差和预测误差 计算网络输出f:)上 Table 1 The approach error and forecastng error of EGT 逼近误差预测误差 计算网络的误差函数E 逼近次序尺度 新加节点个 1% 1% 1 m=0 2中 347 421 增加w节点:修改尺度m=m+1 2 m=0 2中 262 236 3 m=1 3中 184 1.65 N F<E m=2 4中 137 1.12 结束 J m=3 7中 096 097 6 m=4 6中 075 1.38 图4多分辨小波过程神经网络学习算法流程图 Fig 4 The flow chart ofMW PNN leaming algorithm 由表1可以看出,当尺度m=3时,逼近误差和预测 误差达到最小值,而当m=4时,出现了过拟合,因 会引起排气温度EGT上升,特别是飞机起飞时发动 此,采用m=3时的数据,作为多分辨小波过程神经 机转速大,排气温度高,对使用寿命影响大,所以在 网络的预测数据 国内外EGT都成为发动机状态监视的重要指标.对 为测试学习完成后多分辨小波过程神经网络的 EGT的监视已在发动机更换、控制合理风扇和压气 泛化能力,用后6组非训练样本进行测试.测试结果 机清洗时限、检查翻修质量和发动机延寿方面成为 见表2 重要的技术依据[8).本文以JT9D-7R4E涡扇发动 表2多分辨小波过程神经网络EGT预测结果 机为对象,对其排气温度EGT进行状态监视,并将 Table 2 The results of MW PNN EGT forecastng 结果进行了讨论 实际值 样本号 预测值绝对误差相对误差 发动机的EGT数据取自北京飞机维修工程公 /℃ /℃ /℃ /6 司所维修的中国国际航空公司的飞机,采样时间为 354000 35.8240 04240 1.20 2000年1月4日~12月18日,采样时间间隔一般 359000 35.5800 03190 089 为1周左右,这里近似看作等间距采样,共采得44 3 357000 35.8100 01100 031 个离散数据.由于多分辨小波过程神经网络的输入 4 37.1000 37.6040 05040 1.36 是一个连续函数,为此将连续的8个离散数据进行 36600036385002140 058 拟合,构成一个时序函数作为小波过程神经网络的 6 38700038131005680 1.47 输入函数,以第9个数据作为输出.为了简化多分辨 小波过程神经网络的计算,将网络的输入函数及连 为进行对比分析,采用过程神经网络进行EGT预 接权函数由勒让德基函数展开,基函数个数为6个 测,用后6组非训练样本进行测试,测试结果见表3 共得到36组样本,前30组样本作为多分辨小波过 表3过程神经网络EGT预测结果 程神经网络的训练样本. Table 3 The results of PNN EGT forecastng 采用四阶B样条作为尺度函数:中(x)=N,(x),n 实际值 预测值 绝对误差相对误差 样本号 /℃ /℃ /℃ /% 阶B样条由一阶B样条与n-1阶B样条的卷积得 1 35400035.375814805 418 到.同样用样条来定义小波函数: 35900035616313637 3.80 1似=02划+42).2-2 3 35700036164200952 027 7 7 4 37100037.097312208 329 (13) 5 3660003635231.1090 303 多分辨小波过程神经网络在最粗尺度m=0上 638700038377409027233 选择为2个节点m=0根据逼近精度要求加入节 由仿真结果可知,多分辨小波过程神经网络能 点,在尺度m=0上加入2个节点,在尺度m=1上 够较好的处理发动机健康状况监视问题.由表1和 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved http://www.cnki.net
图 4 多分辨小波过程神经网络学习算法流程图 Fig. 4 The flow chart ofMW PNN learning algorithm 会引起排气温度 EGT上升 ,特别是飞机起飞时发动 机转速大 ,排气温度高 ,对使用寿命影响大 ,所以在 国内外 EGT都成为发动机状态监视的重要指标. 对 EGT的监视已在发动机更换、控制合理风扇和压气 机清洗时限、检查翻修质量和发动机延寿方面成为 重要的技术依据 [ 829 ] . 本文以 JT9D27R4E涡扇发动 机为对象 , 对其排气温度 EGT进行状态监视 , 并将 结果进行了讨论. 发动机的 EGT数据取自北京飞机维修工程公 司所维修的中国国际航空公司的飞机 ,采样时间为 2000年 1月 4日 ~12月 18日 ,采样时间间隔一般 为 1周左右 ,这里近似看作等间距采样 ,共采得 44 个离散数据. 由于多分辨小波过程神经网络的输入 是一个连续函数 ,为此将连续的 8个离散数据进行 拟合 ,构成一个时序函数作为小波过程神经网络的 输入函数 ,以第 9个数据作为输出. 为了简化多分辨 小波过程神经网络的计算 ,将网络的输入函数及连 接权函数由勒让德基函数展开 ,基函数个数为 6个. 共得到 36组样本 ,前 30组样本作为多分辨小波过 程神经网络的训练样本. 采用四阶 B 2样条作为尺度函数:φ( x) =N4 ( x) , n 阶 B 2样条由一阶 B 2样条与 n - 1阶 B 2样条的卷积得 到.同样用样条来定义小波函数: ψ( x) = 3 7 φ(2x) + 12 7 φ(2x - 1) - 3 7 φ(2x - 2) . (13) 多分辨小波过程神经网络在最粗尺度 m = 0上 选择为 2个节点 m = 0根据逼近精度要求加入节 点 ,在尺度 m = 0上加入 2个节点 ,在尺度 m = 1上 加入 3个节点 ,随着尺度的越来越细 ,全局逼近误差 逐渐缩小. 表 1给出了多分辨小波过程神经网络的 逼近误差和预测误差. 表 1 EGT预测的逼近误差和预测误差 Table 1 The approach error and foreca sting error of EGT 逼近次序 尺度 新加节点 /个 逼近误差 /% 预测误差 /% 1 m = 0 2φ 3. 47 4. 21 2 m = 0 2ψ 2. 62 2. 36 3 m = 1 3ψ 1. 84 1. 65 4 m = 2 4ψ 1. 37 1. 12 5 m = 3 7ψ 0. 96 0. 97 6 m = 4 6ψ 0. 75 1. 38 由表 1可以看出 ,当尺度 m = 3时 ,逼近误差和预测 误差达到最小值 ,而当 m = 4时 ,出现了过拟合. 因 此 ,采用 m = 3时的数据 ,作为多分辨小波过程神经 网络的预测数据. 为测试学习完成后多分辨小波过程神经网络的 泛化能力 ,用后 6组非训练样本进行测试. 测试结果 见表 2. 表 2 多分辨小波过程神经网络 EGT预测结果 Table 2 The results of MW PNN EGT foreca sting 样本号 实际值 /℃ 预测值 /℃ 绝对误差 /℃ 相对误差 /% 1 35. 400 0 35. 824 0 0. 424 0 1. 20 2 35. 900 0 35. 580 0 0. 319 0 0. 89 3 35. 700 0 35. 810 0 0. 110 0 0. 31 4 37. 100 0 37. 604 0 0. 504 0 1. 36 5 36. 600 0 36. 385 0 0. 214 0 0. 58 6 38. 700 0 38. 131 0 0. 568 0 1. 47 为进行对比分析 ,采用过程神经网络进行 EGT预 测 ,用后 6组非训练样本进行测试 ,测试结果见表 3. 表 3 过程神经网络 EGT预测结果 Table 3 The results of PNN EGT foreca sting 样本号 实际值 /℃ 预测值 /℃ 绝对误差 /℃ 相对误差 /% 1 35. 400 0 35. 375 8 1. 480 5 4. 18 2 35. 900 0 35. 616 3 1. 363 7 3. 80 3 35. 700 0 36. 164 2 0. 095 2 0. 27 4 37. 100 0 37. 097 3 1. 220 8 3. 29 5 36. 600 0 36. 352 3 1. 109 0 3. 03 6 38. 700 0 38. 377 4 0. 902 7 2. 33 由仿真结果可知 ,多分辨小波过程神经网络能 够较好的处理发动机健康状况监视问题. 由表 1 和 ·214· 智 能 系 统 学 报 第 3卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第3期 李洋,等:多分辨小波过程神经网络及其应用研究 ·215· 表2可以看出,过程神经网络的预测结果误差较大, cedure neural netorks[J ]Engineering Science,2000,2 小波过程神经网络的误差却控制在较小的范围内: (12):40-44 过程神经网络预测EGT的测试结果的平均相对误 [5许少华,何新贵.基于函数正交基展开的过程神经网络 差为282%,多分辨小波过程神经网络预测EGT的 学习算法[J1计算机学报,2004,27(5):645650 测试结果的平均相对误差仅为Q97%.这说明过程 XU Shaohua,HE Xingui Leaming algorithms of process neural netorks based on orthogonal function basis expan- 神经网络对于像发动机这样复杂的非线性系统,其 sion[J ]Chinese Joumal of Computers,2004,27 (5): 泛化能力低于多分辨小波过程神经网络 645-650 多分辨小波过程神经网络可以通过小波细节的 [6何新贵,梁久祯,许少华.过程神经网络的训练及其应用 添加不断提高学习精度,这样可以建立多分辨小波 [J]中国工程科学,2001,3(4):31-35 过程神经网络和逼近精度之间的明确关系.另外,多 HE Xingui,LANG Jiuzhen,XU Shaohua Leaming and 分辨小波过程神经网络可以通过学习算法得到网络 applications of procedure neural netorks[J ]Engineering 的权值,还可以逐步选择最为合适的网络隐含层节 Science,.2001,3(4):3135 点神经元数目,从而使多分辨小波过程神经网络有 [7柳重堪.正交函数及其应用M】.北京:国防工业出版 很强的建模能力和函数逼近能力」 社.1982:16 [8贺尔铭,宋力涛.EGT影响因素分析及提高EGT裕度的 4结论 措施[J]航空维修,1999,6:20-21 HE Em ing.SONGLitaa Analysis of EGT and measures b 1)提出了多分辨小波过程神经网络模型,它是 increase the EGT margin [J].Aviation Maintenance,1999 基于小波多分辨分析和过程神经网络建立的一类新 (6):20-21. 型前馈网络,该模型以多分辨分析为理论基础,来 [9]付尧明.民用涡扇发动利在使用和维护中的EGT裕度 指导网络的结构和参数的选取,并且具有处理时变 管理[J]航空维修,2005(1):44-45 信号的能力,因而对于求解与过程有关的问题,具有 FU Yaom ing Management of EGT margin of civil turbofan 较强的逼近能力和容错性 in the use and maintenance J ]Aviation Maintenance, 2)航空发动机EGT是发动机在使用和维护过 2005(1):44-45 程中一个非常重要的性能参数,对飞机的安全飞行 作者简介: 李洋,男,1978年生,博士研究 起着重要的作用.针对EGT受许多复杂因素的影响 生,主要研究方向为人工智能及其应 且随时间而变化难以确定其变化规律,采用多分辨 用、故障诊断等,发表论文8篇,SC检 小波过程神经网络方法较好地解决了此问题,对于 索3篇,E检索3篇,1篇被STP检索. 时变和不确定性的航空发动机状态监视问题具有重 要的意义。 参考文献: 钟诗胜,男,1964年生,哈尔滨工业 [1 ]ZHANGQ inghua,BENV EN ISTE A.Wavelet netorks[J]. 大学威海分校副校长,教授,博士生导 IEEE Transactions on Neural Netorks,1992,3(6):889- 师,博士,主要研究方向为制造业信息 898 化、人工智能理论与应用、数控设备研 [2 ]ZHANG Q inghua Using wavelet netork in nonparametric 发等.主持并完成国家863研究项目2 estmaton J ]IEEE Transactons on Neural Neworks, 项,参加国家863研究项目3项,主持 1997,2(8):227-236 和参加国家自然科学基金项目各1项, [3 ]ZHANG J,WALTER G,M AO Y.Wavelet neural netorks 主持过多项省(部)级研究项目,曾担任国家863/CM$重点 for function leaming[J].IEEE Transactions on Signal Pro- 应用示范工程项目一HEC-CMS工程的副总设计师,曾 cessing.1995,43(6):1485-1497. 获黑龙江省级科技进步奖2项,黑龙江省教学成果奖1项, [4何新贵,梁久祯.过程神经网络的若干理论问题[J] 国家版权局计算机软件著作权登记2套,获专利1项,荣获 中国工程科学,2000,2(12):40-44 黑龙江省CMS应用示范工程先进工作者称号.出版专著1 HE X ingui,L ANG Jiuzhen Some theoretical issues on po- 部,发表论文100余篇,被SCkE检索30余篇 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
表 2可以看出 ,过程神经网络的预测结果误差较大 , 小波过程神经网络的误差却控制在较小的范围内. 过程神经网络预测 EGT的测试结果的平均相对误 差为 2. 82% ,多分辨小波过程神经网络预测 EGT的 测试结果的平均相对误差仅为 0. 97%. 这说明过程 神经网络对于像发动机这样复杂的非线性系统 ,其 泛化能力低于多分辨小波过程神经网络. 多分辨小波过程神经网络可以通过小波细节的 添加不断提高学习精度 ,这样可以建立多分辨小波 过程神经网络和逼近精度之间的明确关系. 另外 ,多 分辨小波过程神经网络可以通过学习算法得到网络 的权值 ,还可以逐步选择最为合适的网络隐含层节 点神经元数目 ,从而使多分辨小波过程神经网络有 很强的建模能力和函数逼近能力. 4 结 论 1)提出了多分辨小波过程神经网络模型 ,它是 基于小波多分辨分析和过程神经网络建立的一类新 型前馈网络 , 该模型以多分辨分析为理论基础 ,来 指导网络的结构和参数的选取 ,并且具有处理时变 信号的能力 ,因而对于求解与过程有关的问题 ,具有 较强的逼近能力和容错性. 2) 航空发动机 EGT是发动机在使用和维护过 程中一个非常重要的性能参数 ,对飞机的安全飞行 起着重要的作用. 针对 EGT受许多复杂因素的影响 且随时间而变化难以确定其变化规律 ,采用多分辨 小波过程神经网络方法较好地解决了此问题 ,对于 时变和不确定性的航空发动机状态监视问题具有重 要的意义. 参考文献 : [ 1 ] ZHANGQ inghua, BENVEN ISTE A. W avelet networks[J ]. IEEE Transactions on Neural Networks, 1992, 3 (6) : 8892 898. [ 2 ] ZHANG Q inghua. U sing wavelet network in nonparametric estimation [ J ]. IEEE Transactions on Neural Networks, 1997, 2 (8) : 2272236. [ 3 ] ZHANG J, WALTER G, M IAO Y. W avelet neural networks for function learning[J ]. IEEE Transactions on Signal Pro2 cessing, 1995, 43 (6) : 148521497. [ 4 ]何新贵 , 梁久祯. 过程神经网络的若干理论问题 [J ]. 中国工程科学 , 2000, 2 (12) : 40244. HE Xingui, L IANG Jiuzhen. Some theoretical issues on p ro2 cedure neural networks[ J ]. Engineering Science, 2000, 2 (12) : 40244. [ 5 ]许少华 , 何新贵. 基于函数正交基展开的过程神经网络 学习算法 [J ]. 计算机学报 , 2004, 27 (5) : 6452650. XU Shaohua, HE Xingui. Learning algorithm s of p rocess neural networks based on orthogonal function basis expan2 sion [ J ]. Chinese Journal of Computers, 2004, 27 ( 5 ) : 6452650. [ 6 ]何新贵 ,梁久祯 ,许少华. 过程神经网络的训练及其应用 [J ]. 中国工程科学 , 2001, 3 (4) : 31235. HE Xingui, L IANG Jiuzhen, XU Shaohua. Learning and app lications of p rocedure neural networks[J ]. Engineering Science, 2001, 3 (4) : 31235. [ 7 ]柳重堪. 正交函数及其应用 [M ]. 北京 :国防工业出版 社 , 1982: 126. [ 8 ]贺尔铭 ,宋力涛. EGT影响因素分析及提高 EGT裕度的 措施 [J ]. 航空维修 , 1999, 6: 20221. HE Erm ing, SONG L itao. Analysis of EGT and measures to increase the EGT margin [J ]. Aviation Maintenance, 1999 (6) : 20221. [ 9 ]付尧明. 民用涡扇发动利在使用和维护中的 EGT裕度 管理 [J ]. 航空维修 , 2005 (1) : 44245. FU Yaoming. Management of EGT margin of civil turbofan in the use and maintenance [ J ]. Aviation Maintenance, 2005 (1) : 44245. 作者简介 : 李 洋 ,男 , 1978年生 ,博士研究 生 ,主要研究方向为人工智能及其应 用、故障诊断等 ,发表论文 8篇 , SCI检 索 3篇 , EI检索 3篇 , 1篇被 ISTP检索. 钟诗胜 ,男 , 1964年生 ,哈尔滨工业 大学威海分校副校长 ,教授 ,博士生导 师 ,博士 ,主要研究方向为制造业信息 化、人工智能理论与应用、数控设备研 发等. 主持并完成国家 863研究项目 2 项 ,参加国家 863研究项目 3项 ,主持 和参加国家自然科学基金项目各 1项 , 主持过多项省 (部 )级研究项目 ,曾担任国家 863 /CIMS重点 应用示范工程项目 ———HEC2CIMS II工程的副总设计师 ,曾 获黑龙江省级科技进步奖 2项 ,黑龙江省教学成果奖 1项 , 国家版权局计算机软件著作权登记 2套 ,获专利 1项 ,荣获 黑龙江省 CIMS应用示范工程先进工作者称号. 出版专著 1 部 ,发表论文 100余篇 ,被 SCI、EI检索 30余篇. 第 3期 李 洋 ,等 :多分辨小波过程神经网络及其应用研究 ·215· © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net