
第3卷第5期 智能系统学报 Vol 3 Na 5 2008年10月 CAA I Transactions on Intelligent Systems 0ct2008 一种基于种群多样度的实数编码并行遗传算法 刘胜,李高云,孙天英 哈尔滨工程大学自动化学院,黑龙江哈尔滨150001) 摘要:为了改善遗传算法的收敛性能,提出了一种基于个体适应度的种群多样性度量函数,恰当地反映了遗传算 法的进化阶段,预报了早熟收敛的趋势.设计了基于种群多样度函数的迁移算子和交叉算子,并对交叉、变异概率等 进行了动态调整,构成了具有多层迁移特点的实数编码并行遗传算法.通过和其他优秀遗传算法对测试函数的验证 比较结果表明,该算法对于解决遗传算法中早熟、收敛速度慢等问题具有优越的性能」 关键词:遗传算法;种群多样性:迁移算子;实数编码 中图分类号:TP18文款标识码:A文章编号:1673-4785(2008)05-042306 A real coding parallel genetic algor ithm based on diversity of popula tion L U Sheng,LI Gao-yun,SUN Tian-ying (College of Autmation,Harbin Engineering University,Harbin,150001,China) Abstract:In order to mprove the convergence perfomance of genetic algorithms,a function measuring population diversity on the basis of the degree of ind ividual adap tability was needed This measuring function must reflect the evolutionary stage of the genetic algorithm and orecast premature trends appropriately.We designed am igration op- erator and crossover operaor based on diversity of population functions,and made dynam ic adjusments on cross- over and mutation probabilities This structured a parallel genetic algorithm with real coding and a multi-layer mi gration operator Comparative experments were made on benchmark functions The results showed that this algo- rithm is obviously superior to other genetic algorithms in overcom ing problems such as prematurity and slow conver gence Keywords:genetic algorithm;diversity of population;m igration operator,real coding 遗传算法是受生物进化理论启发的搜索算法, 能充分利用其他子群体的信息,同样不利于提高解 是由Holland在19世纪70年代提出来的),其本身 的质量.管宇等分析了迁移算子在整个算法收敛过 具备良好的并行设计结构,不易陷入局部最优,并且 程中的重要作用,提出一种基于模式定理的迁移策 不依赖于梯度信息,因此特别适用于处理高度复杂 略MS,提高了算法的时间性能s).Marin等采用集 的非线性问题,并在函数优化、参数辨识、模式识别、 中式方案,从各进程在其子群体中执行G4,并周 自动控制等许多领域得到广泛地应用.然而,遗传算 期地将最好的部分结果发送给主进程,在网络上所 法作为一种随机搜索方法,存在局部领域搜索不敏 作的实验表明,运行速度以接近线性加速比增加.但 感,早熟收敛,寻优速度慢等诸多不足之处.为了改 迁移时机的把握还需作进一步的研究.Baun的方 善性能,人们进行了大量的研究,并提出了许多解决 案)是当GA在区域上产生早熟收敛时,才进行迁 的方案.J.Liening博士通过大量的实验发现2):过 移.Knoger等则采用了另一种途径,每当一个区域中 多以及过频繁的迁移会破坏子群体的多样性,致使 发现一个改进的个体,就异步地执行迁移操作6 多个搜索进程集中到相同的区域,不利于提高解的 本文在以上基础上,提出了一种新的种群多样度度 质量:过少的迁移以及迁移频率过低,使各子群体不 量函数,并基于此设计引入迁移算子的实数并行遗 传算法,同时对实数交叉等方面也做了改进.算例结 收稿日期:20080301 基金项目:黑龙江省自然科学基金资助项目(A200419)」 果表明,该算法具有良好的防止早熟特性,并且增强 通信作者:李高云.Emai让ligaoyun@hrbeu edu cn 了全局最优解的搜索能力,能较快地搜索到全局最 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3卷第 5期 智 能 系 统 学 报 Vol. 3 №. 5 2008年 10月 CAA I Transactions on Intelligent System s Oct. 2008 一种基于种群多样度的实数编码并行遗传算法 刘 胜 ,李高云 ,孙天英 (哈尔滨工程大学 自动化学院 ,黑龙江 哈尔滨 150001) 摘 要 :为了改善遗传算法的收敛性能 ,提出了一种基于个体适应度的种群多样性度量函数 ,恰当地反映了遗传算 法的进化阶段 ,预报了早熟收敛的趋势. 设计了基于种群多样度函数的迁移算子和交叉算子 ,并对交叉、变异概率等 进行了动态调整 ,构成了具有多层迁移特点的实数编码并行遗传算法. 通过和其他优秀遗传算法对测试函数的验证 比较 ,结果表明 ,该算法对于解决遗传算法中早熟、收敛速度慢等问题具有优越的性能. 关键词 :遗传算法 ;种群多样性 ;迁移算子 ;实数编码 中图分类号 : TP18 文献标识码 : A 文章编号 : 167324785 (2008) 0520423206 A real coding parallel genetic algorithm based on diversity of population L IU Sheng, L I Gao2yun, SUN Tian2ying (College of Automation, Harbin Engineering University, Harbin, 150001, China) Abstract: In order to imp rove the convergence performance of genetic algorithm s, a function measuring population diversity on the basis of the degree of individual adap tability was needed. This measuring function must reflect the evolutionary stage of the genetic algorithm and forecast p remature trends app rop riately. We designed a m igration op2 erator and crossover operator based on diversity of population functions, and made dynam ic adjustments on cross2 over and mutation p robabilities. This structured a parallel genetic algorithm with real coding and a multi2layer m i2 gration operator. Comparative experiments were made on benchmark functions. The results showed that this algo2 rithm is obviously superior to other genetic algorithm s in overcom ing p roblem s such as p rematurity and slow conver2 gence. Keywords: genetic algorithm; diversity of population; m igration operator; real coding 收稿日期 : 2008203201. 基金项目 :黑龙江省自然科学基金资助项目 (A200419). 通信作者 :李高云. E2mail: ligaoyun@hrbeu. edu. cn. 遗传算法是受生物进化理论启发的搜索算法 , 是由 Holland在 19世纪 70年代提出来的 [ 1 ] ,其本身 具备良好的并行设计结构 ,不易陷入局部最优 ,并且 不依赖于梯度信息 ,因此特别适用于处理高度复杂 的非线性问题 ,并在函数优化、参数辨识、模式识别、 自动控制等许多领域得到广泛地应用. 然而 ,遗传算 法作为一种随机搜索方法 ,存在局部领域搜索不敏 感 ,早熟收敛 ,寻优速度慢等诸多不足之处. 为了改 善性能 ,人们进行了大量的研究 ,并提出了许多解决 的方案. J. L iening博士通过大量的实验发现 [ 2 ] :过 多以及过频繁的迁移会破坏子群体的多样性 ,致使 多个搜索进程集中到相同的区域 ,不利于提高解的 质量 ;过少的迁移以及迁移频率过低 ,使各子群体不 能充分利用其他子群体的信息 ,同样不利于提高解 的质量. 管宇等分析了迁移算子在整个算法收敛过 程中的重要作用 ,提出一种基于模式定理的迁移策 略 SMS,提高了算法的时间性能 [ 3 ] . Marin等采用集 中式方案 [ 4 ] ,从各进程在其子群体中执行 GA,并周 期地将最好的部分结果发送给主进程 ,在网络上所 作的实验表明 ,运行速度以接近线性加速比增加. 但 迁移时机的把握还需作进一步的研究. Braun的方 案 [ 5 ]是当 GA在区域上产生早熟收敛时 ,才进行迁 移. Kroger等则采用了另一种途径 ,每当一个区域中 发现一个改进的个体 ,就异步地执行迁移操作 [ 6 ] . 本文在以上基础上 ,提出了一种新的种群多样度度 量函数 ,并基于此设计引入迁移算子的实数并行遗 传算法 ,同时对实数交叉等方面也做了改进. 算例结 果表明 ,该算法具有良好的防止早熟特性 ,并且增强 了全局最优解的搜索能力 ,能较快地搜索到全局最
·424· 智能系统学报 第3卷 优解, 调形式,这恰好符合了种群多样度的各项要求, 本文为了检测种群多样度函数D值的性能,做 1一种新的种群多样性度量 了以下检验,在第次随机产生10000个[0,1之 在遗传算法中,人们最关注的问题之一就是它 间的随机数,然后用1替换其中的100个随机数, 的过早收敛.近几年的研究发现:种群只有在保持一 i∈[1,100,分别计算种群多样度D的值,得到随 定的多样性的基础上才能进化,过早收敛总是与种 机种群多样度曲线,如图2所示 群中个体趋同、种群多样性(population diversity,. 0.14入 PD)的迅速下降有密切的关系.遗传算法中多个遗 0.12 传算子参数需要根据种群的D进行自适应地调 0.10 整因此,如何合理、有效地刻画种群的多样性是遗 0.08 0.06 传算法急需解决的问题.常用的测度方法是采用海 0.04 明距离,但海明距离通常只适合二进制编码,从计算 0.02 量的角度来讲,海明距离方法运算量又显得较大.因 0102030405060708090100 此,本文从个体表现性的角度出发,根据个体适应度 测试次数 来定义了一种可以应用到各类遗传算法,而且能恰 图2随机种群多样度 当充分反映种群多样性的度量函数 Fig 2 Diversity of random population function 假设种群pop含有M个个体,分别为P,P, P,其所对应的适应度值为无,,…,石,那么种 测试曲线中,D值逐渐较稳定的从Q14左右降 群的平均适应度可记为 为O,表明本文提出的D函数对于种群的多样度具 1-h M 有极良好的反映性能.当D越接近于1,种群的多样 1) 性就越高,越不易于陷入早熟;反之接近于0时,种 则种群的多样度定义为 群很可能陷入到局部最优解之中,这时就需要采取 。姑2的 其他有效的方式来使遗传算法跳出该局部最优解。 (2) 由于在遗传算法设计适应度函数时,为了选择 2基于种群多样度的迁移算子 的方便且具有意义,一般情况下廿1满足≥0,那 生物界具有大规模的迁移习性,通过这种行为 么就有f≥0,由此可以得到: 往往使种群得到极大的发展,而遗传算法本质上是 -f-f≤方-f≤f+f (3) 一种模拟生物进化的过程,本文从中得到启发,设计 所以,0≤f-f升≤6+f升得到: 了迁移算子改进遗传算法, 1≥-≥0 然而,迁移时机很难把握.进一步分析遗传算 4) f+f 法,由于选择算子的作用,加之人们对遗传算法收敛 从而得到0≤D≤1,种群多样度函数的曲线如 性的要求,较为理想的遗传算法的种群多样性呈现 图1所示 出总体缓慢递减,随后逐步稳定的一个过程.当遗传 D 算法早期陷入到局部最优解时,解将在这一局部最 优解集中,同时遗传算法的多样性会呈现出较快下 降的态势.依据以上特点,本文采用监测种群多样度 D函数的变化,从而适时的引入迁移算子,解决迁移 时机很难把握的难题 当种群多样度函数D低于某一预先设定的值 入(T)=中.中T'/I时,对种群po即进行整体迁移替 0 换,即将种群中个体适应度最差的(100n入)%,用相 应的种群来替换更新,称此种操作为整体迁移算子 图1种群多样度函数 (T为当前种群代数,为延拓代数,规定为进化种 Fig I Diversity of population function 群代数的15倍,中为整体迁移因子,在下面的测试 当远离时,多样度函数值趋近于1,而接 实验中取中为0065.12为150,n=3). 近于0时,其值同样接近于1,且呈现出以为中心单 整体迁移算子的引入实质是为了使种群保持一 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
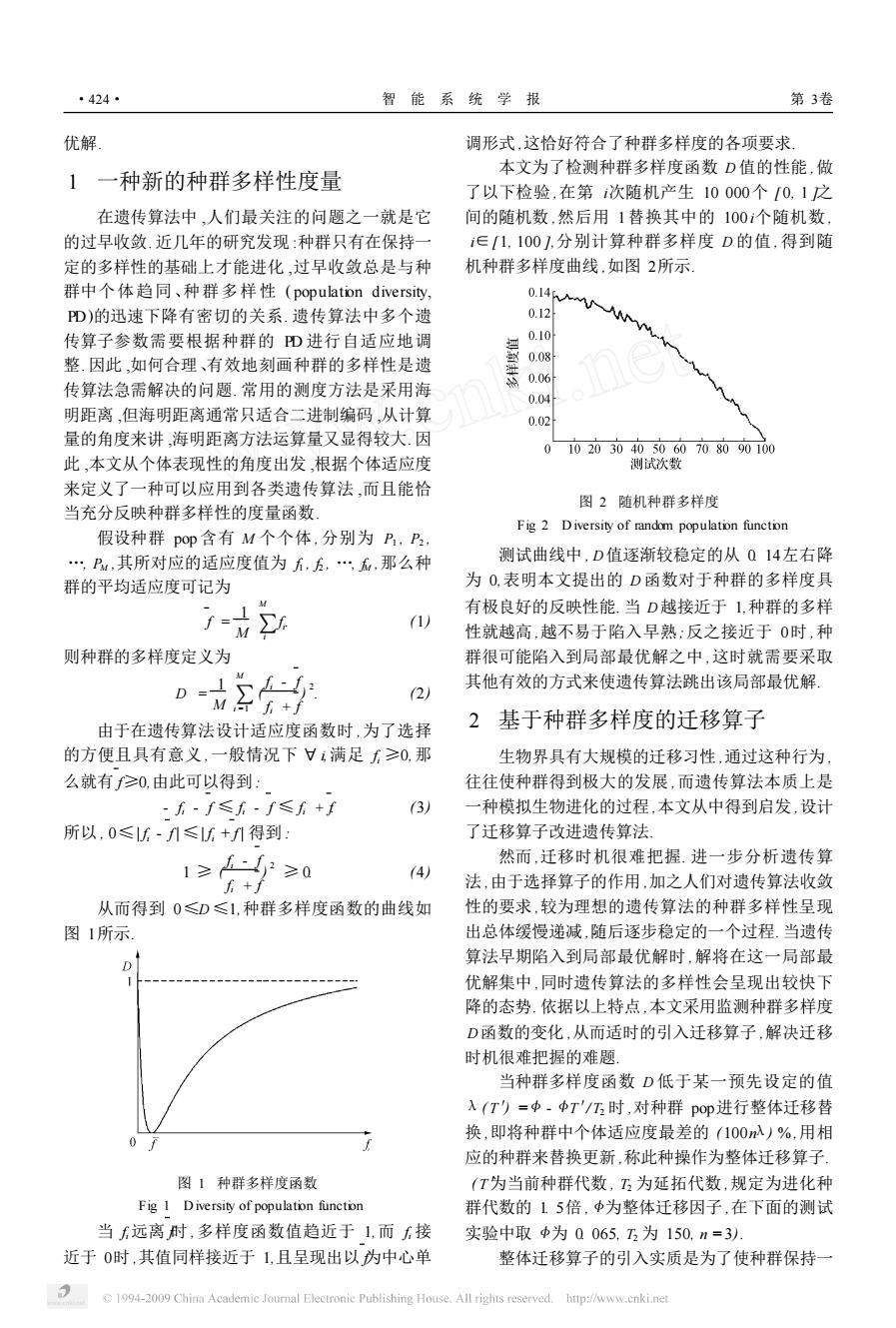
优解. 1 一种新的种群多样性度量 在遗传算法中 ,人们最关注的问题之一就是它 的过早收敛. 近几年的研究发现 :种群只有在保持一 定的多样性的基础上才能进化 ,过早收敛总是与种 群中个体趋同、种群多样性 ( population diversity, PD)的迅速下降有密切的关系. 遗传算法中多个遗 传算子参数需要根据种群的 PD 进行自适应地调 整. 因此 ,如何合理、有效地刻画种群的多样性是遗 传算法急需解决的问题. 常用的测度方法是采用海 明距离 ,但海明距离通常只适合二进制编码 ,从计算 量的角度来讲 ,海明距离方法运算量又显得较大. 因 此 ,本文从个体表现性的角度出发 ,根据个体适应度 来定义了一种可以应用到各类遗传算法 ,而且能恰 当充分反映种群多样性的度量函数. 假设种群 pop 含有 M 个个体 , 分别为 P1 , P2 , …, PM ,其所对应的适应度值为 f1 , f2 , …, fM ,那么种 群的平均适应度可记为 f = 1 M ∑ M i fi . (1) 则种群的多样度定义为 D = 1 M ∑ M i =1 ( fi - f fi + f ) 2 . (2) 由于在遗传算法设计适应度函数时 ,为了选择 的方便且具有意义 ,一般情况下 Π i,满足 fi ≥0,那 么就有 f≥0,由此可以得到 : - fi - f ≤ fi - f ≤ fi + f. (3) 所以 , 0≤| fi - f | ≤| fi + f | 得到 : 1 ≥ ( fi - f fi + f ) 2 ≥ 0. (4) 从而得到 0≤D ≤1,种群多样度函数的曲线如 图 1所示. 图 1 种群多样度函数 Fig. 1 D iversity of population function 当 fi 远离 f时 ,多样度函数值趋近于 1,而 fi 接 近于 0时 ,其值同样接近于 1,且呈现出以 f为中心单 调形式 ,这恰好符合了种群多样度的各项要求. 本文为了检测种群多样度函数 D 值的性能 ,做 了以下检验 ,在第 i次随机产生 10 000个 [ 0, 1 ]之 间的随机数 ,然后用 1替换其中的 100 i个随机数 , i∈[1, 100 ],分别计算种群多样度 D 的值 , 得到随 机种群多样度曲线 ,如图 2所示. 图 2 随机种群多样度 Fig. 2 D iversity of random population function 测试曲线中 , D值逐渐较稳定的从 0. 14左右降 为 0,表明本文提出的 D 函数对于种群的多样度具 有极良好的反映性能. 当 D越接近于 1,种群的多样 性就越高 ,越不易于陷入早熟;反之接近于 0时 ,种 群很可能陷入到局部最优解之中 ,这时就需要采取 其他有效的方式来使遗传算法跳出该局部最优解. 2 基于种群多样度的迁移算子 生物界具有大规模的迁移习性 ,通过这种行为 , 往往使种群得到极大的发展 ,而遗传算法本质上是 一种模拟生物进化的过程 ,本文从中得到启发 ,设计 了迁移算子改进遗传算法. 然而 ,迁移时机很难把握. 进一步分析遗传算 法 ,由于选择算子的作用 ,加之人们对遗传算法收敛 性的要求 ,较为理想的遗传算法的种群多样性呈现 出总体缓慢递减 ,随后逐步稳定的一个过程. 当遗传 算法早期陷入到局部最优解时 ,解将在这一局部最 优解集中 ,同时遗传算法的多样性会呈现出较快下 降的态势. 依据以上特点 ,本文采用监测种群多样度 D函数的变化 ,从而适时的引入迁移算子 ,解决迁移 时机很难把握的难题. 当种群多样度函数 D 低于某一预先设定的值 λ( T′) = < - <T′/ T2 时 ,对种群 pop进行整体迁移替 换 ,即将种群中个体适应度最差的 ( 100nλ) % ,用相 应的种群来替换更新 ,称此种操作为整体迁移算子. ( T′为当前种群代数 , T2 为延拓代数 ,规定为进化种 群代数的 1. 5倍 , <为整体迁移因子 ,在下面的测试 实验中取 <为 0. 065, T2 为 150, n = 3). 整体迁移算子的引入实质是为了使种群保持一 ·424· 智 能 系 统 学 报 第 3卷

第5期 刘胜,等:一种基于种群多样度的实数编码并行遗传算法 ·425. 定的多样度,调整种群的多样度按期望的梯度下降 下 有利于遗传算法的全局收敛.整体迁移算子引入准 =对+1-D)川场-…d (5 则示意图如图3所示 、=店+1+D)1场-"d 式中:D为种群多样度的大小.相比于文献「9],该 算法除了保持原有算法的优点外,由于在遗传算法 初期D较大,而在后期会逐渐减小,因此在算法初 期扩大了搜索的范围,而在算法后期加速了算法的 收敛,提高了算法的整体性能 B 32参数的自适应调整 一方面,为了使遗传算法具有更强的鲁棒性、全 局最优性和效率,当算法提前收敛时,加大P和A: 在算法后期减小P和A:另一方面,为了保持优良 图3迁移算子引入准则示意图 个体,不能对所有的个体采取同一个?和A,本文 Fig 3 Migration operator mport rule 结合Striniras的自适应交叉和变异率,对其进行改 图3中,T为进化代数,T,为种群总进化代数 进设计R和A,如下: 图中AB线以上即1区)为期望的种群多样度变化 Pemax-Pcmin 域,随着种群代数的进化呈现出线性递减规律:若在 ep ((12)) +Pcmin' 点ax≤g 进化的过程中多样度低于AB线即2区)时,遗传 P e·石n 算法有可能陷入到局部最优解当中,在此种情况下 Pcmm 点ax>e 需要对种群中的最差个体进行随机替换.遵循陷入 (6) 早熟代数越早,替换越多种群的原则,本文采用正比 PmmPmn 于多样度函数下降斜率替换的策略 2· 一+Pmm 点an≤fie 上述设计方式的优点在于: 1 exp((1-- 人e·石n 1)由于种群多样度函数具有监测作用,预报了 Pa min 点ax≤fg 遗传算法陷入早熟的可能性概率和时间: 7) 2)一旦陷入到早熟状态,可以根据所处进化阶 式中:A=9903438,点x、右m分别为交叉的2个个体 段的不同情况,自适应地控制随机迁移算子引入的 的高、低适应度值,为该群体的平均适应度 多寡; P:mm、Pmn、Pa max P min为个人设定的交叉最大概 3)可以根据计算的要求,动态地调整种群延拓 率、交叉最小概率、变异最大概率、变异最小概率.本 代数的大小,方便对选择压力进行自适应地调节 文在下面的测试过程中本文取子群体Pmx、Pm血 3并行遗传算法算子设计及其流程 Pma、Pmn为1、0、Q01、0,取主群体Pmax、Peman P.max、Pmmn为07、0、00005、0 31基于种群多样度的交叉算子改进 33算法并行结构设计及其流程 在文献「9中给出了关于交叉算子的改进算 算法采用并行结构,共有3个子种群,并由此产 法,但其计算的方案并未根据遗传算法的进化过程 生一个主群体和一个融合种群.本文提出“整体迁 进行动态地调节.而实际过程中,当种群进化到一定 移算子+相互迁移”的思想,即各个子群体本身实 阶段后,就必须在所搜索到的个体中进行重点的搜 现由上文提出的整体迁移算子,并在进化过程中,子 索,而不应该与算法初期搜索的方式一样.由于种群 群体间也进行种群相互迁移.其迁出迁入的个数由 多样度函数恰当地反映了遗传算法的进化阶段,因 各种群进化效果决定0),但其迁移总数目保持不 此本文将多样度函数嵌入到交叉策略中,对于文献 变,具体如式(8)所示: [9中的搜索方式进行改进 E afuist +bf+df (8) 2个待交叉个体为x、x,判断其适应度的高低, 式中:为种群最优个体的适应度;为种群的平均 并记为石咖人,相应的个体记为:xx令交叉的搜 适应度:△为相邻2次个体迁移间种群平均适应度 索方向d,即一个个体沿着方向d从区域 的变化,表示种群的进化速度;a、bc为常数,且 a+b+c=1,一般取a>b>c 人向另一个区域石前进,则实数交叉策略操作如 迁移后的种群大小由式(9)决定 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
定的多样度 ,调整种群的多样度按期望的梯度下降 有利于遗传算法的全局收敛. 整体迁移算子引入准 则示意图如图 3所示. 图 3 迁移算子引入准则示意图 Fig. 3 M igration operator import rule 图 3中 , T为进化代数 , T1 为种群总进化代数. 图中 AB 线以上 (即 1区 )为期望的种群多样度变化 域 ,随着种群代数的进化呈现出线性递减规律;若在 进化的过程中多样度低于 AB 线 (即 2区 )时 ,遗传 算法有可能陷入到局部最优解当中 ,在此种情况下 需要对种群中的最差个体进行随机替换. 遵循陷入 早熟代数越早 ,替换越多种群的原则 ,本文采用正比 于多样度函数下降斜率替换的策略. 上述设计方式的优点在于 : 1)由于种群多样度函数具有监测作用 ,预报了 遗传算法陷入早熟的可能性概率和时间; 2)一旦陷入到早熟状态 ,可以根据所处进化阶 段的不同情况 ,自适应地控制随机迁移算子引入的 多寡; 3)可以根据计算的要求 ,动态地调整种群延拓 代数的大小 ,方便对选择压力进行自适应地调节. 3 并行遗传算法算子设计及其流程 3. 1 基于种群多样度的交叉算子改进 在文献 [ 9 ]中给出了关于交叉算子的改进算 法 ,但其计算的方案并未根据遗传算法的进化过程 进行动态地调节. 而实际过程中 ,当种群进化到一定 阶段后 ,就必须在所搜索到的个体中进行重点的搜 索 ,而不应该与算法初期搜索的方式一样. 由于种群 多样度函数恰当地反映了遗传算法的进化阶段 ,因 此本文将多样度函数嵌入到交叉策略中 ,对于文献 [9 ]中的搜索方式进行改进. 2个待交叉个体为 xi、xj ,判断其适应度的高低 , 并记为 fhigh、flow ,相应的个体记为 : xh、xl . 令交叉的搜 索方向 d = fhigh - flow fhigh ,即一个个体沿着方向 d从区域 flow向另一个区域 fhigh前进 ,则实数交叉策略操作如 下 : x t+1 h = x t l + (1 - D ) ·| x t h - x t l |·d, x t+1 l = x t h + (1 + D ) ·| x t h - x t l |·d. (5) 式中 : D为种群多样度的大小. 相比于文献 [ 9 ],该 算法除了保持原有算法的优点外 ,由于在遗传算法 初期 D较大 ,而在后期会逐渐减小 ,因此在算法初 期扩大了搜索的范围 ,而在算法后期加速了算法的 收敛 ,提高了算法的整体性能. 3. 2 参数的自适应调整 一方面 ,为了使遗传算法具有更强的鲁棒性、全 局最优性和效率 ,当算法提前收敛时 ,加大 pc 和 pm , 在算法后期减小 pc 和 pm ;另一方面 ,为了保持优良 个体 ,不能对所有的个体采取同一个 pc 和 pm ,本文 结合 Striniras的自适应交叉和变异率 ,对其进行改 进设计 pc 和 pm ,如下 [ 8 ] : Pc = Pc max - Pc min 1 + exp (A (1 - 2 (favg - fmax ) favg - fmin ) ) + Pc min , fmax ≤ favg . Pc min , fmax > favg . (6) Pm = Pm max - Pm min 1 + exp (A (1 - 2 (favg - fmax ) favg - fmin ) ) + Pm min , fmax ≤ favg . Pm min , fmax ≤ favg . (7) 式中 : A = 9. 903 438, fmax、fm in分别为交叉的 2个个体 的高、低适应度值 , favg为该群体的平均适应度 , Pc max、Pc m in、Pm max、Pm m in为个人设定的交叉最大概 率、交叉最小概率、变异最大概率、变异最小概率. 本 文在下面的测试过程中本文取子群体 Pc max、Pc m in、 Pm max、Pm m in为 1、0、0. 01、0, 取主群体 Pc max、Pc m in、 Pm max、Pm m in为 0. 7、0、0. 000 5、0. 3. 3 算法并行结构设计及其流程 算法采用并行结构 ,共有 3个子种群 ,并由此产 生一个主群体和一个融合种群. 本文提出“整体迁 移算子 +相互迁移 ”的思想 ,即各个子群体本身实 现由上文提出的整体迁移算子 ,并在进化过程中 ,子 群体间也进行种群相互迁移. 其迁出、迁入的个数由 各种群进化效果决定 [ 10211 ] ,但其迁移总数目保持不 变 ,具体如式 (8)所示 : E = afelist + b f + cΔf. (8) 式中 : felist为种群最优个体的适应度; f为种群的平均 适应度;Δf为相邻 2次个体迁移间种群平均适应度 的变化 , 表示种群的进化速度; a、b、c为常数 , 且 a + b + c = 1,一般取 a > b > c. 迁移后的种群大小由式 (9)决定. 第 5期 刘 胜 ,等 :一种基于种群多样度的实数编码并行遗传算法 ·425·

·426- 智能系统学报 第3卷 3 E pop size=3 9 4算例分析 E 数值函数测试不需要专门的领域知识,且能很 所设计的MPGA主要算法过程描述如下 好地反映算法本身的实际效能,因此精选了2个测 1)初始化子种群P、P2、P: 试函数,从不同的角度来检测本文设计算法的性能 2选择各个子种群中适应度较高的前13个 2个函数如下分别如下: 体构成主进化群体A F=100(-2+(1-)2, 3)选择各个子种群中适应度较高的前13个 -512≤x≤512 (10) 体构成融合群体B; s㎡2层+及.05 4)从融合群体中选择,替换每个子群体中的最 差的1/3个体: 5=05,7+0001居+ -512≤x,≤512 (11 5)检测各个子群体多样度,并相应调整各遗传 当上述函数满足-512≤x,≤512时,F,最小 算子,当种群多样度低于入(T)时,实现自适应整体 值位于0,0)点,F的最大值位于(0,0)点.F是 迁移算子: 一个快速变化的多模态函数,有无数个局部极大值 6)检测主群体多样度,是否需要进行子群体间 点,且全局最优点周围有一圈脊,取值均为 的互相迁移,若需要则进行互相迁移, 0990283,可以参考图5的三维模型,其越接近于 7)各个子群体、主群体进行选择、交叉、变异等 原点,函数变化越剧烈,在最优点附近形成很密、很 遗传操作: 陡的振荡峰,可以很好考察函数的全局最优收敛性 8)检测子群体最优个体是否优于主群体,倘若 是,则用最优个体替换掉主群体最差个体: 0.9 9)检验主群体是否满足设计计算指标,满足则 1.0 0.8 0.8 停止运算,否则转到2步 0.6 0.6 程序流程图如图4所示 0.4 0.5 0.4 0.3 初始化3个子种群 0.2 遗传操作参数设首 01 -55 求取各个个 选择每个子种群的 体适应度值 前13,生成主种群 A和融合群B 图5F三维曲线图 Fig 5 F three-dmensional curves 替换最差个体 为了比较各个算法的具体性能,本文分别采用 种样多样度监测 计算λ(T) D-争 5种方法对以上2个函数进行测试,其中算法1为 a(T)=中TyT 标准的遗传算法:算法2为文献[7提出的算法:算 根据D调整 子群D≥A(T 整体迁移 法3为文献[9提出的算法,算法4采用本文提出 交叉算子 青 Y 的不含有整体迁移算子的MPGA,算法5为本文提 根据式(6).(7), 主样D2≥A(T N 相互迁移 出的MPGA,MPGA具体的参数设置如表1所示 调整交叉、变 异算子 表1 MPGA参数设定 选择、交叉、变异 Table 1 Parameter setting of M PGA 等遗传操作 MPGA参数 是否满足指标 停止迭代 子群体的迁移频率代 10 N 子群体迁移百分比/% 20 种群代数加1 算法结求 子群体的规模 50 选择策略 最优保留 编码方式 实数编码 图4算法结构流程图 种群代数 100 Fig 4 Flw chart of algorithm 1994-2009 China Academic Journal Electronie Publishing House.All rights reserved.http://www.cnki.net
pop size′i = Ei ∑ 3 i =1 Ei ·∑ 3 i =1 pop sizei . (9) 所设计的 MPGA主要算法过程描述如下 : 1)初始化子种群 P1、P2、P3 ; 2)选择各个子种群中适应度较高的前 1 /3个 体构成主进化群体 A; 3) 选择各个子种群中适应度较高的前 1 /3个 体构成融合群体 B; 4) 从融合群体中选择 ,替换每个子群体中的最 差的 1 /3个体; 5) 检测各个子群体多样度 ,并相应调整各遗传 算子 ,当种群多样度低于 λ( T′)时 ,实现自适应整体 迁移算子; 6) 检测主群体多样度 ,是否需要进行子群体间 的互相迁移 ,若需要则进行互相迁移; 7) 各个子群体、主群体进行选择、交叉、变异等 遗传操作; 8) 检测子群体最优个体是否优于主群体 ,倘若 是 ,则用最优个体替换掉主群体最差个体; 9) 检验主群体是否满足设计计算指标 ,满足则 停止运算 ,否则转到 2)步. 程序流程图如图 4所示. 图 4 算法结构流程图 Fig. 4 Flow chart of algorithm 4 算例分析 数值函数测试不需要专门的领域知识 ,且能很 好地反映算法本身的实际效能 ,因此精选了 2个测 试函数 ,从不同的角度来检测本文设计算法的性能 , 2个函数如下分别如下 : F1 = 100 ( x 2 1 - x2 ) 2 + (1 - x1 ) 2 , - 5. 12 ≤ xi ≤ 5. 12, (10) F2 = 0. 5 - sin 2 x 2 1 + x 2 2 - 0. 5 (1 + 0. 001 ( x 2 1 + x 2 2 ) ) 2 , - 5. 12 ≤ xi ≤ 5. 12. (11) 当上述函数满足 - 5. 12≤xi ≤5. 12时 , F1 最小 值位于 ( 0, 0)点 , F2 的最大值位于 ( 0, 0)点. F2 是 一个快速变化的多模态函数 ,有无数个局部极大值 点 , 且 全 局 最 优 点 周 围 有 一 圈 脊 , 取 值 均 为 0. 990 283,可以参考图 5的三维模型 ,其越接近于 原点 ,函数变化越剧烈 ,在最优点附近形成很密、很 陡的振荡峰 ,可以很好考察函数的全局最优收敛性. 图 5 F2 三维曲线图 Fig. 5 F2 three2dimensional curves 为了比较各个算法的具体性能 ,本文分别采用 5种方法对以上 2个函数进行测试 ,其中算法 1为 标准的遗传算法;算法 2为文献 [ 7 ]提出的算法;算 法 3为文献 [ 9 ]提出的算法 ,算法 4采用本文提出 的不含有整体迁移算子的 MPGA,算法 5为本文提 出的 MPGA,MPGA具体的参数设置如表 1所示. 表 1 M PGA参数设定 Table 1 Param eter setting of M PGA MPGA参数 子群体的迁移频率 /代 10 子群体迁移百分比 /% 20 子群体的规模 50 选择策略 最优保留 编码方式 实数编码 种群代数 100 ·426· 智 能 系 统 学 报 第 3卷

第5期 刘胜,等:一种基于种群多样度的实数编码并行遗传算法 ·427 其中整体迁移算子、自适应交叉、变异参数己经 代左右达到了预期收敛精度,而算法5在48代左右 由前面几节给出,这里不再累述.本文运用以上算 就达到了预期收敛精度.表明MPGA算法(算法5) 法,对每个测试函数都重复计算100次 具有较好的防止早熟、跳出局部最优解的能力 由于仿真曲线数目众多,下面给出针对F,函数 针对以上各种算法具有随机性的因素,本文对 测试的其中一次仿真曲线图,如图6所示.其中,横 以上算法做了统计性的测试,统计结果如表2所示 坐标为迭代次数,纵坐标为算法进化精度 给出了对上述5种算法测试的统计性能比较.从 0.12 表2中可看出,尽管函数具有多峰性、凹凸性和连续 0.10 性,MPGA找到全局最优解的概率还是较大的,比其 他4种算法均有所改善.MPGA达到精度的平均代 0.0 数比文献中其他算法有所降低,特别是在处理非线 0.06 性严重的F测试函数时,其性能更加的明显,这进 004 一步说明了MPGA在处理高度非线性函数寻优时 0.02 的优越性.与算法4相比较,由于其加入了整体迁移 算子,因此对于早熟现象有更好的解决能力,在算法 1020 30405060708090100 迭代次数 陷入早熟的时候,整体迁移算子给予了种群二次发 展的机会,使其跳出了测试函数的局部最优解, 图6收敛精度曲线 发挥了整体迁移算子对多样度调整的性能,但在运 Fig 6 Curves of convergence precision 算时间的比较上,由于MPGA采用了较多的算子, 从图6中可以清晰看到,在进化30代以后,收 相比于其他算法,其计算时间略微有所增加,但增加 敛几乎处于了停滞状态,此时种群个体趋同,种群多 的幅度很小,相对于计算效率而言,这样的损耗是值 样度值迅速下降:算法1、2和3在此次仿真中最终 得的(本算法实现环境为P4处理器,28G主频, 没能达到预期的收敛精度:本次仿真中算法4在75 256M内存). 表2各个函数性能测试 Table 2 Test of each funetion capability 收敛次数达到精度平均代数 达到指定精度平均运行时间/s 函数 精度 算法1算法2算法3算法4算法5算法1算法2算法3算法4算法5 F 000001 43/80 77/61 83/59 91/43 100/40015 018 017 018 019 F 000001 32/93 55/90 5294 70/90 91/95041 047 050052 053 [J]计算机学报,2003,5(3):294-301 5结束语 GJAN Yu,XU Baowen Parallel genetic algorithms with 本文提出了一种新的种群多样度度量函数,基 schema m igration[Jl.Chinese Joumal of Computers,2003. 于在适当的时机引入整体迁移算子,并利用多样度 5(3):294-301 进行交叉方式的改进,采用二层迁移的并行结构体 [4 ]AKRA S Expermental results in distributed genetic algo- rithms C ]/Applied Corporate Computing Monterrey, 系,对于改善遗传算法的性能具有一定程度的提高, Mexico.1994:99-108 且可以很方便地在其他各类遗传算法中实现 [5 ]BRAUN H.On solving trasvelling salesnan p roblms by ge- 参考文献: netic algorithms[M].Berlin:Springer-Verlag,1991:129- 133 [1 ]HOLLAND J H.Adap tation in natural and artificial system s [6]KROGER B,SCHW ENDERL NG P,VORNBERGER O. [M ]Cam bridge,Massachusetts:M IT Press,1992:87-95. Parallel genetic packing of rectangles[M ]Berlin:Springer- [2]LIEN IG J.A parallel genetic algrithm or permance driv- Verlag,1991:160-164 en VLSI routing[J].IEEE Trans on EC,1997,1(1):29- [7 SR N NAS M,PA TNA IK L M.Adaptive probabilities of 39 crossover and mutation in genetic abgrithms [J].EEE [3管宇,徐宝文.基于模式迁移策略的并行遗传算法 Transanctions on Systems,Man and Cybemetic,1994,24 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
其中整体迁移算子、自适应交叉、变异参数已经 由前面几节给出 ,这里不再累述. 本文运用以上算 法 ,对每个测试函数都重复计算 100次. 由于仿真曲线数目众多 ,下面给出针对 F2 函数 测试的其中一次仿真曲线图 ,如图 6所示. 其中 ,横 坐标为迭代次数 ,纵坐标为算法进化精度. 图 6 收敛精度曲线 Fig. 6 Curves of convergence p recision 从图 6中可以清晰看到 ,在进化 30代以后 ,收 敛几乎处于了停滞状态 ,此时种群个体趋同 ,种群多 样度值迅速下降;算法 1、2和 3在此次仿真中最终 没能达到预期的收敛精度;本次仿真中算法 4在 75 代左右达到了预期收敛精度 ,而算法 5在 48代左右 就达到了预期收敛精度. 表明 MPGA算法 (算法 5) 具有较好的防止早熟、跳出局部最优解的能力. 针对以上各种算法具有随机性的因素 ,本文对 以上算法做了统计性的测试 ,统计结果如表 2所示 , 给出了对上述 5种算法测试的统计性能比较. 从 表 2中可看出 ,尽管函数具有多峰性、凹凸性和连续 性 ,MPGA找到全局最优解的概率还是较大的 ,比其 他 4种算法均有所改善. MPGA达到精度的平均代 数比文献中其他算法有所降低 ,特别是在处理非线 性严重的 F2 测试函数时 ,其性能更加的明显 ,这进 一步说明了 MPGA 在处理高度非线性函数寻优时 的优越性. 与算法 4相比较 ,由于其加入了整体迁移 算子 ,因此对于早熟现象有更好的解决能力 ,在算法 陷入早熟的时候 ,整体迁移算子给予了种群二次发 展的机会 ,使其跳出了 F2 测试函数的局部最优解 , 发挥了整体迁移算子对多样度调整的性能 ,但在运 算时间的比较上 ,由于 MPGA 采用了较多的算子 , 相比于其他算法 ,其计算时间略微有所增加 ,但增加 的幅度很小 ,相对于计算效率而言 ,这样的损耗是值 得的 (本算法实现环境为 P4 处理器 , 2. 8G主频 , 256M内存 ). 表 2 各个函数性能测试 Table 2 Test of each function capab ility 函数 精度 收敛次数 /达到精度平均代数 算法 1 算法 2 算法 3 算法 4 算法 5 达到指定精度平均运行时间 /s 算法 1 算法 2 算法 3 算法 4 算法 5 F1 0. 000 01 43 /80 77 /61 83 /59 91 /43 100 /40 0. 15 0. 18 0. 17 0. 18 0. 19 F2 0. 000 01 32 /93 55 /90 52 /94 70 /90 91 /95 0. 41 0. 47 0. 50 0. 52 0. 53 5 结束语 本文提出了一种新的种群多样度度量函数 ,基 于在适当的时机引入整体迁移算子 ,并利用多样度 进行交叉方式的改进 ,采用二层迁移的并行结构体 系 ,对于改善遗传算法的性能具有一定程度的提高 , 且可以很方便地在其他各类遗传算法中实现. 参考文献 : [ 1 ]HOLLAND J H . Adap tation in natural and artificial system s [M ]. Cambridge,Massachusetts:M IT Press, 1992: 87295. [ 2 ]L IEN IG J. A parallel genetic algorithm for performance driv2 en VLSI routing[J ]. IEEE Trans on EC, 1997, 1 (1) : 292 39. [ 3 ]管 宇 ,徐宝文. 基于模式迁移策略的并行遗传算法 [J ]. 计算机学报 , 2003, 5 (3) : 2942301. GUAN Yu, XU Baowen. Parallel genetic algorithm s with schema m igration[J ]. Chinese Journal of Computers, 2003, 5 (3) : 2942301. [ 4 ]AKIRA S. Experimental results in distributed genetic algo2 rithms [ C ] / / App lied Corporate Computing. Monterrey, Mexico, 1994: 992108. [ 5 ]BRAUN H. On solving trasvelling salesman p roblem s by ge2 netic algorithms[M ]. Berlin: Sp ringer2Verlag, 1991: 1292 133. [ 6 ] KROGER B, SCHW ENDERL ING P, VORNBERGER O. Parallel genetic packing of rectangles[M ]. Berlin: Sp ringer2 Verlag, 1991: 1602164. [ 7 ] SR IN IVAS M, PATNA IK L M. Adap tive p robabilities of crossover and mutation in genetic alogorithms [J ]. IEEE Transanctions on System s, Man and Cybernetic, 1994, 24 第 5期 刘 胜 ,等 :一种基于种群多样度的实数编码并行遗传算法 ·427·

·428· 智能系统学报 第3卷 (4):655-677 [8陈小平,于盛林.实数遗传算法交叉策略的改进[J]电 作者简介: 子学报,2003,1(1):71-74 刘胜,男,1957年生,教授,博士 CHEN Xiaoping.YU Shenglin mprovement on crossover 生导师,曾获国防科学技术进步三等 strategy of real-valued genetic algorithm [J].Acta Electron- 奖中国船舶工业集团科技进步三等 ica Sinica,2003,1(1):71-74 奖、黑龙江省科技进步二等奖.主要研 [9]吴好阳,朱长春,刘建华.自适应遗传算法改进种群早熟 究方向为智能控制、鲁棒控制、船舶姿 收敛[J]西安交通大学学报,1999,33(11):27-30 态控制」 WU Haoyang,ZHU Changchun,L U J ianhua Adaptive ge- netic algorithm to mprove group premature convergence 李高云,男,1981年生,博士研究 [J ]Joumal of Xi'an Jiaotong University,1999,33(11) 生,主要研究方向为智能控制、故障诊 27-30 断与容错控制、船舶姿态控制」 [10黄晓峰,潘立登,陈标华,等.用改进的实数编码遗传算 法估计反应动力学参数[J]高校化学工程学报,1999, 13(1):50-55 HUANG Xiaofeng.PAN Lideng,CHEN Biaohua,et al. Estmating reaction kinetics parameters with an mproved 孙天英,男,1981年生,硕士研究 realcoded genetic algorithm [J].Joumal of Chemn ical En- 生,主要研究方向为智能控制、船舶姿 gineering of Chinese University,1999,13(1):50-55. 态控制。 [11李波,邱枫.基于单亲遗传算法的动态设备布局仿 真研究[J1智能系统学报,2007,2(1):74-79. LI Bo,QU Feng Smulation of the dynam ic plantlayout problem besed on partheno genetic algorithm [J]CAAI Transactions on Intelligent System,2007,2(1):74-79 2009EEE机电一体化与自动化国际会议 The 2009 IEEE Iterna tional Conference on M echa tron ics and Automa tion ICMA 2009) The 2009 IEEE Intemational Conference on Mechatronics and Automation IMA 2009)will take place in Changchun,Jilin,China from August 9 to August 12,2009.The objective of KMA 2009 is to provide a fonm for researchers,educators,engineers,and govemment officials involved in the general areas of mechatronics,robot ics,automation and sensors to dissem inate their latest research results and exchange views on the future research di- rections of these fields The ppics of interest include,but not lm ited to the following -Intelligent mechatronics,robotics,biom metics,automation and control systems -opto-electronic elements and Materials,laser technobgy and laser processing -Elements,structures,mechanisns,and applications ofm icro and nano systems Teleoperation,telerobotics,hap tics,and teleoperated semi-autonomous systems Sensor design,multi-sensor data fusion algorithms and wireless sensor networks -B iomedical and rehabilitation engineering,prosthetics and artificial organs -Control system modeling and smulation techniques and methodologies -AL intelligent control,neuro-control,fuzzy control and their app lications -Industrial automation,process control,manufacturing process and automation All papersmust be subm itted in PDF omat prepared strictly follwing the IEEE PDF Requirements for Crea- ting PDF Documents for IEEE Xp bre*.The standard number of pages is6 and the maxium page lim it is 8 pages with extra payment for the to extra pages See detailed instructions in the conference web site All paper accepted by IEEE IMA 2009 will be indexed by EI and included in IEEE Xplore". Website:http://www.ieee-icma org/ 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
(4) : 6552677. [ 8 ]陈小平 ,于盛林. 实数遗传算法交叉策略的改进 [J ]. 电 子学报 , 2003, 1 (1) : 71274. CHEN Xiaop ing, YU Shenglin. Imp rovement on crossover strategy of real2valued genetic algorithm [J ]. Acta Electron2 ica Sinica, 2003, 1 (1) : 71274. [ 9 ]吴好阳 ,朱长春 ,刘建华. 自适应遗传算法改进种群早熟 收敛 [J ]. 西安交通大学学报 , 1999, 33 (11) : 27230. WU Haoyang, ZHU Changchun, L IU Jianhua. Adap tive ge2 netic algorithm to imp rove group p remature convergence [J ]. Journal of Xi’an Jiaotong University, 1999, 33 (11) : 27230. [ 10 ]黄晓峰 ,潘立登 ,陈标华 ,等. 用改进的实数编码遗传算 法估计反应动力学参数 [J ]. 高校化学工程学报 , 1999, 13 (1) : 50255. HUANG Xiaofeng, PAN L ideng, CHEN Biaohua, et a1. Estimating reaction kinetics parameters with an imp roved realcoded genetic algorithm [J ]. Journal of Chem ical En2 gineering of Chinese University, 1999, 13 (1) : 50255. [ 11 ]李 波 ,邱 枫. 基于单亲遗传算法的动态设备布局仿 真研究 [J ]. 智能系统学报 , 2007, 2 (1) : 74279. L I Bo, Q IU Feng. Simulation of the dynam ic p lantlayout p roblem besed on partheno genetic algorithm [ J ]. CAA I Transactions on Intelligent System, 2007, 2 (1) : 74279. 作者简介 : 刘 胜 ,男 , 1957年生 ,教授 ,博士 生导师 ,曾获国防科学技术进步三等 奖、中国船舶工业集团科技进步三等 奖、黑龙江省科技进步二等奖. 主要研 究方向为智能控制、鲁棒控制、船舶姿 态控制. 李高云 ,男 , 1981 年生 ,博士研究 生 ,主要研究方向为智能控制、故障诊 断与容错控制、船舶姿态控制. 孙天英 ,男 , 1981 年生 ,硕士研究 生 ,主要研究方向为智能控制、船舶姿 态控制. 2009 IEEE机电一体化与自动化国际会议 The 2009 IEEE Interna tiona l Conference on M echa tron ics and Automa tion ( ICMA 2009) The 2009 IEEE International Conference on Mechatronics and Automation ( ICMA 2009) will take p lace in Changchun, Jilin, China from August 9 to August 12, 2009. The objective of ICMA 2009 is to p rovide a forum for researchers, educators, engineers, and government officials involved in the general areas of mechatronics, robot2 ics, automation and sensors to dissem inate their latest research results and exchange views on the future research di2 rections of these fields. The top ics of interest include, but not lim ited to the following: - Intelligent mechatronics, robotics, biom imetics, automation and control system s - op to2electronic elements and Materials, laser technology and laser p rocessing - Elements, structures, mechanism s, and app lications of m icro and nano system s - Teleoperation, telerobotics, hap tics, and teleoperated sem i - autonomous system s - Sensor design, multi2sensor data fusion algorithm s and wireless sensor networks - Biomedical and rehabilitation engineering, p rosthetics and artificial organs - Control system modeling and simulation techniques and methodologies - A I, intelligent control, neuro2control, fuzzy control and their app lications - Industrial automation, p rocess control, manufacturing p rocess and automation A ll papers must be subm itted in PDF format p repared strictly following the IEEE PDF Requirements for Crea2 ting PDF Documents for IEEE Xp lore Ó . The standard number of pages is 6 and the maximum page lim it is 8 pages with extra payment for the two extra pages. See detailed instructions in the conference web site. A ll paper accep ted by IEEE ICMA 2009 will be indexed by E I and included in IEEE Xp lore Ó . W ebsite: http: / /www. ieee2icma. org/ ·428· 智 能 系 统 学 报 第 3卷