
第3卷第6期 智能系统学报 Vol.3 No.6 2008年12月 CAAI Transactions on Intelligent Systems Dec.2008 规则分层约简算法 尹林子12,阳春华,柱卫华,李勇刚 (1.中南大学信息科学与工程学院,湖南长沙410083:2.中南大学物理科学与技术学院,湖南长沙410083) 摘要:针对传统粗糙集方法处理问题时所遇到的离散化以及属性约简的NP难题,将粗糙集中下近似概念与分层 思想相结合,提出一种新的粗糙集数据处理方法一规则分层约简算法HRR.该算法直接从决策表中提取规则,利 用对规则进行约简来代替属性约简,以避开NP推题,同时针对传统离散化算法对不同离散化区间采取不同编码的 局限,实现了不同区间的聚类编码,并在此基础上提出等价决策表的概念.实例表明,HRR算法在计算量以及性能上 具有非常明显的优势, 关键词:全局启发;规则约简:粗糙集;等价决策表 中图分类号:TP18文献标识码:A文章编号:1673-4785(2008)06049206 Hierarchical reduction of rules YIN Lin-zi2,YANG Chun-hua',GUI Wei-hua',LI Yong-gang (1.School of Information Science and Engineering,Central South University,Changsha 410083,China;2.School of Physics Science and Technology,Central South University,Changsha 410083,China) Abstract:In order to resolve the NP-hard problem in the discretization,or reduction process,using traditional rough set theory,a new data processing approach for the rough set process-hierarchical reduction of rule (HRR) was formulated.It integrates the low approximation of the rough set and the hierarchical methods.Rules are extrac- ted directly from decision tables and rule reduction is used to replace attribute reduction for evading the NP-hard problem.Also,the same clustering code is used for different segments,while the traditional method must use dif- ferent codes for different clustering segments.An equivalent decision table is also put forward.Some examples il- lustrate its obvious advantage in computational time and performance. Keywords:whole heuristic;reduction of rules;rough set;equivalent decision table 粗糙集理论是20世纪80年代由波兰的Pawlak性.首先,连续属性的最优离散化问题是一个NP 教授提出的一种新型的处理模糊性和不确定性知识(non-deterministic polynomial)难题3)],因此对具有 的数学工具,并且具有不需要外界信息和先验知 丰富样本的信息系统而言,求得最优离散化结果的 识的独特优势[2].目前,粗糙集理论同神经网络、模 时间开销将是令人无法忍受的;其次,Wong和Ziar 糊理论、专家系统、遗传算法和证据理论等结合已被 ko已经证明找出一个决策表的最小约简也是NP难 应用于知识获取、数据挖掘、信息融合、决策分析和 题41;第三,通过传统算法得到的规则是一种被动 决策支持、模式识别、机器学习、故障诊断和控制算 的规则,它完全取决于离散化以及属性约简过程,而 法获取等各种应用领域.粗糙集对数据处理的流程 这些过程的处理目标往往又不是针对最简的规则, 如下:先把数据离散化、编码、形成决策表、约简决策 因此传统算法得到的规则有可能不是最简的. 表之后再提取规则.思想在于利用最简的决策表来 为了解决属性约简的P难题,很多学者展开 提取最简的规则.但是这种传统的方法有一些局限 了相关的研究,采用启发式算法以避免NP难题,主 收稿日期:2008-03-17. 要包括矩阵类方法、属性重要度方法以及分层约简 基金项目:国家自然科学重点基金资助项目(60634020):国家自然科 方法等.如文献[5]基于二进制可辩识矩阵进行属 学基金资助项目(60874069). 通信作者:尹林子.E-mail:nihaoylz@126.com 性约简,取得了良好的效果;文献[6]分析属性约简

第6期 尹林子,等:规则分层约简算法 ·493· 与条件信息量的关系,定义新的属性重要性,并以此 面有3个三好学生,2个五好学生;山2队里面有3个 为启发信息,给出了计算新的条件信息量的高效算 五好学生,还有2个差学生;d队里面有5个差学 法;文献[7]模拟人类认知的分层递阶原则,将信息 生.那么,可以把每一个队伍(d,d2,d)看成是决策 系统或决策系统的知识在由部分属性所构成的多种 属性d的一个决策属性值,存在一个条件属性c的 层次和多种粒度上表示出来,然后分别对各个属性 属性值则是三好学生c1,五好学生c2以及差学生c 层次进行递阶约简,具有较强的实用性和较好的动 这3个值,而每一个学生作为一个样本含有一个条 态特性,但该算法中属性层次划分的依据不是来源 件属性c,一个决策属性d.则对于d1队来说,它针 于数据分析,而是基于数据采集难度、成本以及实时 对条件属性c的下近似为:三好学生c;五好学生在 性等,对应用的场合有所依赖. 边界.也就是说,一旦某一个学生是三好学生c1,那 本文从另一个角度出发,利用规则约简来代替 么他肯定在d,队,而如果它是五好学生,则可能在 属性约简,提出了规则分层约简算法HRR(hierar- d1队,也可能在d2队. chical reduction of rule):首先利用下近似从决策表 这样就为规则的提取提供了一种思路,即一旦 分层提取规则,然后对规则进行约简,并通过规则约 某一个条件属性值为某个决策属性值的下近似(即 简过程得到新的数据离散化聚类,在此基础上形成 正域),那么,肯定可以使用这个条件属性值作为该 等价决策表.本算法的优势在于避开了NP难题,同 决策值的一个充分规则:因此,可以将下近似理解为 时又不需要任何先验知识,避免了属性分层约简算 可以进行决策的关键特征, 法的层次划分依赖问题, 然后利用分层思想,将决策表中提取出规则的 相关样本删除,重新再寻找下近似,一直到决策属性 1 粗糙集的基本概念 值只有一个值或者所有样本均已经被规则提取.如 决策表:一个决策表S可以定义为四元组S= 果这两个条件不能满足,并且不能提取新的规则,则 〈U,A,Vf),其中:U为论域;A=CUD,C,D分别为 意味着原始的决策表可能为含有不相容情况等特殊 关于U的条件和决策属性集;V=UaeCuD Va,V.表 情况,剩下的样本为特殊样本 示属性a的值域;f:U×(CUD)→V是一个信息 在本算法中,对提取的规则结构进行了新的定义. 函数,即对任意x∈U,a∈CUD,有f八x,a)∈V 定义1规则的表示方法为:S:C,->D(X); 不可分辨关系:对于子集B∈A,则B在U上的 C:为规则的前件;D:为规则的后件;X1为本规则所适 不可分辨关系定义为 应的样本集合,称为规则S的关联样本集 IND =(x,x')EUI a E B,a(x)=a(x'). 规则分层提取算法如下: 等价类:对于元素x∈U,它的等价类定义为 1)将原始决策表根据条件以及决策属性值对 [x]a={yI(x,y)∈WD(B). 论域进行划分,获得U/a,aeA以及U/D; 下近似与上近似:对于任意一个对象集合X∈U 2)找到每一个条件属性相对于每个决策属性 以及属性集合B∈A.X的B下近似定义为:B,X= 值的下近似,提取规则,如果提取失败,则提取结束, {xI[x]g∈X},X的B上近似定义为:BX= 否则执行步骤3); {xl[x]a∩X≠0}. 3)将规则的关联样本删除; B.X实际上是由那些根据已有知识判断肯定 4)判断样本集是否为空或者决策属性值只有 属于X的对象所组成的最大的集合,也称为X的正 一个,是则结束,否则,返回步骤2). 域(positive region). 算法分析:步骤1)可以采用文献[8]中的算法 2 HRR算法 E实现,其时间复杂度为O(1U12),最坏情况下为 IU1·(IU川-1)/2.步骤2)可以将U/a中的子集与 HRR算法包括了3个部分:基于下近似的规则 U/D子集比较,一旦U/a中的某个子集为U/D某 分层提取、规则约简以及基于规则的聚类, 个子集的子集,则U/a中的该子集为所寻找的下近 2.1基于下近似的规则分层提取 似.该过程的实现方法如下:设 下近似是粗糙集里面一个最基本的概念.例如: U/a={A1,A2,…,An}, 集X相对于属性B的下近似是所有在B属性下肯 U/D={X,X2,…,Xm}. 定属于X的对象集合,假设有3个队伍,d1队伍里 1)对于uad∈A:,寻找X满足uaa∈X;

494 智能系统学报 第3卷 2)对于A:的其他样本u∈A:,一旦u生X, 2.2规则约简与聚类原则 则A不是X的子集,结束;如果A:中的所有样本均 从上面的实例可以看出,分层提取所得到的规 包含在X中,则A:为X的子集, 则往往存在冗余,需要约简,规则约简的基础是基于 可见,在最坏情况下的计算量为1U1+(IA:I- 规则关联样本集的隶属关系。顺序为:先行后列,先 1)1X1.由于IA:1,IXI≤IU1,时间复杂度为 同属性后不同属性,约简的过程可以遵循以下的一 0(1U12).因此,结合步骤1)以及步骤2)得到每层 些定理进行,同时,在约简的时候将产生相应的聚类 规则提取的时间复杂度为O(1U12).假设进行了n 约束, 次分层提取,则规则提取的总的时间复杂度为 定义2聚类约束:P:C[v]->C[o](X), C[]为约束的前件,C[w]为约束的后件,X,为本 名010.其中:U,1=1U1,1u1为第i-1 约束所适应的样本集合,即样本X,对应C属性的 次分层提取之后剩下的样本数目. 属性值v转化为w. 考虑文献[9]中的决策表,见表1,条件属性集 定理1如果有某个条件属性在同一层的不同 C={a,b,c,决策属性集D={d},U={#1,#2,#3, 属性值指向同一个决策属性值,即S:C,-> 料,5}.运用HHR算法提取规则。 D(X)且S2:C2->D(X2),则这两条规则可以合 表1决策表1 并,新规则的关联样本为X=XUX2· Tablel Decision table 1 聚类原则1:对于定理1中的规则合并,被约掉 U 的规则的前件可以转换成任何一个值,考虑最大聚 b d 1 0 2 类的情况,应该将其改为保留规则的前件,并产生对 1 #2 2 0 3 1 应的聚类约束。 粥 1 2 1 1 定理2于规则S:C:->D(X),如果同一层 料 2 1 3 0 与其具有相同后件的其他规则集S(X)={S 揽 1 0 3 0 C->D,(X),C≠C,D=D,X=UX满足X1S 首先,根据决策属性将U划分为2个子集,即 X,则规则S:可以约掉。 U/R={X1,X;Xg={#4,#5},X1={#1,#2,#3}. 聚类原则2:对于定理1中约掉的规则,其前件 可以寻找到相关于X,的下近似为b2和c1,c2,相关 可以转换成任何一个值,考虑最大聚类的情况,应该 于X,的下近似为b.因此,可以提取出第1层规则: 将其转化为该属性值中有但是没有在规则中出现过 b2->X1(#3),c1->X1(#3),c2->X1(#1), 的属性值。 b1->X(#料).将含有第1层规则的样本删除,得到 考虑聚类原则1,可以得到定理3. 表2. 定理3第i层某个规则S1:C:->D(X1),第 表2抽取第1层规则之后的决策表 i+1层的规则中与S1具有不同后件的规则集 Table 2 Decision table after first abstraction S+1(X)={SIC->D(X),D≠D:,X=UX},且 U b d S的关联样本集X,的属性中不含有C,则规则S 2 2 0 3 1 可以转到第i+1层. 证明规则S1:C:->D(X)如果要转到下一 5 1 0 3 0 层,则要保证该规则与规则集S:+1没有冲突,即不会 此时,X1={#2},X。={#5}.寻找X,的下近似 产生规则歧义,因为在第i+1层引入了新的样本集 有a2·X2的下近似有a1·因此,第2层的规则为: X1,因此,需要保证X,中每一个样本的所有属性中 a2->X1(#2),a1->X(#5).将与第2层规则相 不含有C值,否则,肯定会产生冲突.由此得证, 关的样本删除,由于此时样本集为空,因此,算法结 定理4在规则里面出现过的条件属性为冗余 束.得到了规则表述如下: 属性,可以约掉。 表3规则表 聚类原则3:对于规则里面没有出现过的条件 Table 3 Rule table 属性值,可以将其聚类为同一个值。 b2->X1(#粉),c1->X(粉),C2->X(#1), 定理5对于最后一层的规则,如果后件一致, b1->X(料); 均为D,则倒数第二层中规则后件为D:的规则可 a2->X1(#2),a1->X(5) 以转到最后一层;同时,最后一层的规则以及属性不

第6期 尹林子,等:规则分层约简算法 ·495· 需要保留, 约束条件,那么,在考虑相容性不变的情况下,可以 对于表1所提取出来的规则,可以利用上述定 把等价决策表认为是原来决策表经过离散聚类之后 理进行约简. 形成的,即在相容性不变基础上的数据离散化过程 第1层,先考虑同属性约简,c1和c2均可以用 的可能结果之一 来判断X,因此,可以将c属性的属性值1和2统一 等价决策表与传统的最简决策表相比可能会更 起来,即可以将1变成2或者将2变成1,这样的改 简单,比如对决策表1的规则提取,以传统的观点来 变在现有规则下不会产生歧义. 看,其决策表已经是最简的,无法做属性以及样本约 假设约掉c2->X(#粗),即将决策表中的c2变 简;但是通过HRR算法,可以把样本#粗和粉化为重 成c1,得到c1->X(#1,#).再来考虑不同属性约 复样本,从而减少了样本数目.也可以利用等价决策 简,规则b2->X1(3),c1->X1(#1,#粉),b2的关 表直接用传统的方法提取规则,该规则与HRR算法 联样本集为{3},c1的关联样本集为{#1,3},因此 得到的规则本质上是一致的,但是泛化能力相对弱 规则b2->X,可以约掉,b2可以转换为任何一个 一些因此,可以根据需要任意选取哪一种形式的规 值.考虑到粗糙集的连续数据离散化过程,应该将 则 b2转换为b属性已有的且未在规则中出现过的值, HRR算法的流程图以及与传统算法流程图的 所以,本例中b,应该转换为b。.因此,得到了约简的 比较见表1. 规则如表4. 表4约简规则表 Table 4 The concise rule table 原始 分层扯 规则 分层最 决策表 收规则 约简 简规则 c1->X(#粗,3),b->X(料): a2->X1(#2),a1->x(5). 离散系 等价 最简 相应的聚类约束为:c[2]->c[1](1); 类综码 决策表 规则 b[2]->b[0](3). 定义3等价决策表:将原始决策表按照基于 下近似提取的分层规则进行约简所获得的聚类约束 图1HRR算法的流程图 Fig.1 Flow chart of HRR 进行重编码,获得新的决策表称为原始决策表的等 价决策表, 此时得到的等价决策表如表5所示 表5等价决策表 原始 离散聚 届性 获取 决策表 类绵码 约简 规则 Table 5 Equivalence decision table U b d 图2传统算法的流程图 #1 0 2->1 Fig.2 Flow chart of traditional rough set 2 2 0 3 3 HRR算法应用与比较 #3 2->0 1 3.1与分层递阶属性约简算法的比较 #料 HRR算法吸收了分层递阶的思想,但是与其他 5 0 0 的分层递阶属性约简算法不相同.通常的分层递阶约 可见,如果该决策表来自于连续数据的离散化, 简算法属于一种局部启发式算法,如文献[10]在规则 则可以修改离散化的聚类规则,将b2和c2的编码 的判断上采用了基于条件属性选择的判断方法,先查 去掉;从而可以达到诚少离散化断点的目的,得到更 看某一组条件属性,将相容部分提取规则,对于不相 优的离散聚类集,同时,在等价决策表中,样本#1和 容部分则转入下一组属性处理.它的缺点是: 3是相同的,因此减少了决策表的样本数目. 1)属性值组的划分以及选择问题.属性分组的 2.3等价决策表研究 顺序对最后的约简结果有重要的影响,排在前面的 等价决策表有2个约束条件:一个是约简得到 属性很难被约掉;因此,由一个不合适的属性分组情 的规则;还有一个是规则约简时所产生的聚类约束. 况所产生的属性约简效果不一定好.文献[10]基于 只有在这2个前提下才是等价的.如果抛开这2个 数据采集难度、成本以及实时性等来划分,但是这种
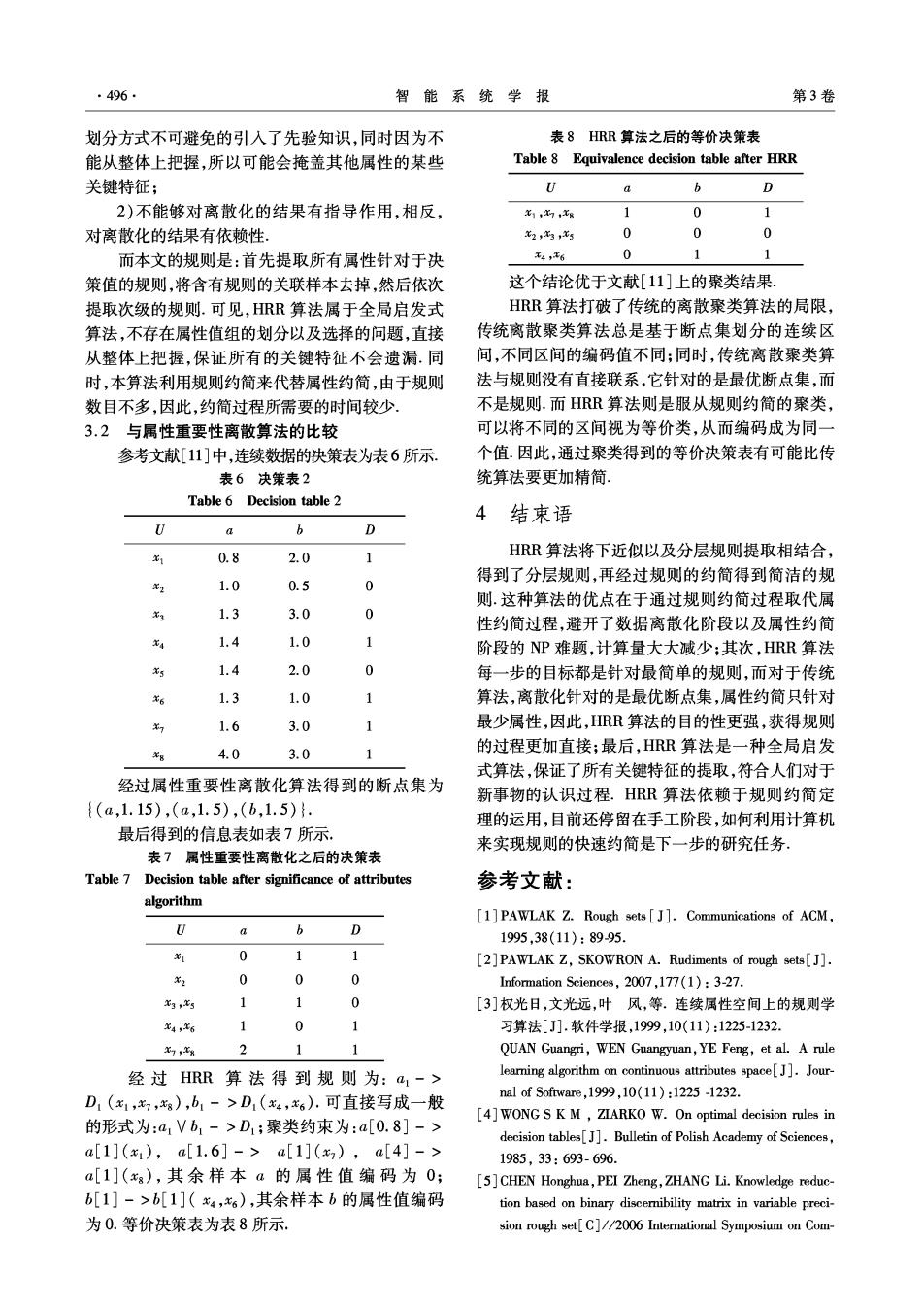
·496 智能系统学报 第3卷 划分方式不可避免的引入了先验知识,同时因为不 表8HRR算法之后的等价决策表 能从整体上把握,所以可能会掩盖其他属性的某些 Table 8 Equivalence decision table after HRR 关键特征; C a b 2)不能够对离散化的结果有指导作用,相反, x1,,8 0 1 对离散化的结果有依赖性. 2,X3,5 0 0 0 而本文的规则是:首先提取所有属性针对于决 4,¥6 0 1 1 策值的规则,将含有规则的关联样本去掉,然后依次 这个结论优于文献[11]上的聚类结果, 提取次级的规则.可见,HRR算法属于全局启发式 HRR算法打破了传统的离散聚类算法的局限, 算法,不存在属性值组的划分以及选择的问题,直接 传统离散聚类算法总是基于断点集划分的连续区 从整体上把握,保证所有的关键特征不会遗漏.同 间,不同区间的编码值不同;同时,传统离散聚类算 时,本算法利用规则约简来代替属性约简,由于规则 法与规则没有直接联系,它针对的是最优断点集,而 数目不多,因此,约简过程所需要的时间较少 不是规则.而HRR算法则是服从规则约简的聚类, 3.2与属性重要性离散算法的比较 可以将不同的区间视为等价类,从而编码成为同 参考文献[11]中,连续数据的决策表为表6所示. 个值.因此,通过聚类得到的等价决策表有可能比传 表6决策表2 统算法要更加精简, Table 6 Decision table 2 4结束语 a D 0.8 2.0 HRR算法将下近似以及分层规则提取相结合, 1 得到了分层规则,再经过规则的约简得到简洁的规 1.0 0.5 0 则这种算法的优点在于通过规则约简过程取代属 1.3 3.0 0 性约简过程,避开了数据离散化阶段以及属性约简 1.4 1.0 1 阶段的NP难题,计算量大大减少;其次,HRR算法 5 1.4 2.0 0 每一步的目标都是针对最简单的规则,而对于传统 1.3 1.0 2 算法,离散化针对的是最优断点集,属性约简只针对 1.6 3.0 最少属性,因此,HRR算法的目的性更强,获得规则 4.0 3.0 的过程更加直接;最后,HRR算法是一种全局启发 式算法,保证了所有关键特征的提取,符合人们对于 经过属性重要性离散化算法得到的断点集为 新事物的认识过程.HRR算法依赖于规则约简定 {(a,1.15),(a,1.5),(b,1.5)}. 理的运用,目前还停留在手工阶段,如何利用计算机 最后得到的信息表如表7所示 来实现规则的快速约简是下一步的研究任务. 表7属性重要性离散化之后的决策表 Table 7 Decision table after significance of attributes 参考文献: algorithm [1]PAWLAK Z.Rough sets [J].Communications of ACM, U a b D 1995,38(11):8995. 1 0 1 1 [2]PAWLAK Z,SKOWRON A.Rudiments of rough sets[J]. 0 0 0 Information Sciences,2007,177(1):3-27. 3,5 1 1 0 [3]权光日,文光远,叶风,等.连续属性空间上的规则学 4,¥6 1 0 1 习算法[J].软件学报,1999,10(11):1225-1232. ,8 2 1 1 QUAN Guangri,WEN Guangyuan,YE Feng,et al.A rule 经过HRR算法得到规则为:a,-> learning algorithm on continuous attributes space[J].Jour- nal of Software,1999,10(11):1225-1232. D1(x1,,),b1->D1(x4,6).可直接写成一般 [4]WONG S K M,ZIARKO W.On optimal decision rules in 的形式为:a1Vb1->D1;聚类约束为:a[0.8]-> decision tables[].Bulletin of Polish Academy of Sciences, a[1](x),a[1.6]->a[1](x),a[4]-> 1985,33:693-696. a[1](x),其余样本a的属性值编码为0; [5]CHEN Honghua,PEI Zheng,ZHANG Li.Knowledge reduc- b[1]->b[1](x4,x6),其余样本b的属性值编码 tion based on binary discemibility matrix in variable preci- 为0.等价决策表为表8所示. sion rough set[C]//2006 Interational Symposium on Com-

第6期 尹林子,等:规则分层约简算法 497. munications and Information Technologies.Bangkok,Thai- 作者简介: 1and.2006:949-954. 尹林子,男,1980年生,讲师,博士 [6]钱进,叶飞跃,孟样萍,等.一种基于新的条件信息量 主要研究方向为智能信息处理与人工 的属性约简算法[J].系统工程与电子技术,2007,12: 智能.发表学术论文5篇. 2154-2157. QIAN Jin,YE Feiyue,MENG Xiangping,et al.Attribute reduction algorithm based on newconditional information quantity[J].Systems Engineering and Electronics,2007, 12:2154-2157. 阳春华,女,1965年生,教授,博士 [7]LI Yurong,QIAO Bin.Hierarchical reduction algorithm of 生导师.中国有色金属学会计算机学 rough sets[C]//Proceedings of Sixth International Confer- 术委员会秘书长,中国自动化学会应用 ence on Intelligent Systems Design and Applications.Jinan, 专业委员会委员,中国人工智能学会智 China,2006,1:497-502. 能控制与智能管理专业委员会委员,湖 [8]GUAN J W,BELL D A.Rough computational methods for 南省自动化学会常务理事等.主要研究 information systems[J].Artificial Intelligence,1998,105 方向为智能信息处理、复杂工业过程建模、仿真与优化、智能 (1/2):77-103. 自动化控制系统等.主持国家自然科学基金、国家863计划、 [9]裴小兵,吴涛,陆永忠.最小化决策规则集的计算方法 国家高技术产业化等国家和省部级科研项目30多项.获国 [J].智能系统学报,2007,2(6):6567. 家科技进步二等奖2项,省部级科技进步奖12项,申请和授 PEI Xiaobing,WU Tao,LU Yongzhong.Calculating method 权国家发明专利15项.发表学术论文180余篇,被SC1、E for a minimal set of decision rules J].CAAI Transactions 等收录100余篇, on Intelligence Systems,2007,2(6):65-67. 桂卫华,男,1950年生,教授,博士 [10]乔斌,李玉榕,蒋静坪.粗糙集理论的分层递阶约简 生导师.中国自动化学会理事,中国自 算法及其信息论基础[J].控制理论与应用,2004,21 动化学会技术过程故障诊断专业委员 (2):195-199. 会副主任委员,过程控制专业委员会常 QIAO Bin,LI Yurong,JIANG Jingping.Hierarchical re- 务理事,中国有色金属学会理事,计算 duction approach of rough sets theory and its basis on the 机学术委员会主任委员,湖南省自动化 information theory [J].Control Theory Applications, 学会理事长.主要研究方向为复杂工业过程建模、控制与优 2004,21(2):195-199. 化、工业大系统理论、故障诊断技术.主持国家自然科学基金 [11]候利娟,王国胤,聂能,等.粗糙集理论中的离散化问 重点项目、国家863和973计划、国家高技术产业化项目45 题[J].计算机科学,2000,12(27):8994. 项.获国家科技进步二等奖2项,省部级科技进步奖15项, HOU Lijuan,WANG Guoyin,NIE Neng,et al.Discreti- 申请和授权国家发明专利16项.发表学术论文400余篇,其 zation in rough set theory[J].Computer Science,2000,12 中SCI收录55篇,EI收录165篇,出版专著、译著各2部. (27):8994