
第3卷第6期 智能系统学报 Vol.3 No.6 2008年12月 CAAI Transactions on Intelligent Systems Dec.2008 采样点个数对T-S模糊建模精度的影响 刘福才,陈超,张彦柳 (燕山大学工业计算机控制工程河北省重,点实验室,河北秦皇岛066004) 摘要:在模糊建模中所取的采样点个数会对辨识出的模型精度产生影响,在只给出有限个数据采样点且数据分布 不能人为控制的情况下怎样选取最优的采样点个数是模糊辨识中要解决的问题之一通过采样点个数变化的模糊 辨识算法来研究模糊建模中采样点个数对模型描述性能的影响.基于TS模糊模型,采用对称三角形模糊划分和 “网格对角线法”提取模糊规则,通过对DIS0系统和Mackey-Glass无序时间序列进行建模,给出模糊模型训练性能 指标和检验性能指标随采样点个数增加的变化趋势曲线。 关键词:模糊辨识;样本点个数;三角形隶属函数;网格对角线法;T-S模糊模型 中图分类号:TP15文献标识码:A文章编号:16734785(2008)060541-07 The influence of sampling points on the descriptive performance of T-S fuzzy modeling LIU Fu-cai,CHEN Chao,ZHANG Yan-liu (Key Lab.of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao 066004,China) Abstract:The number of sampling points in fuzzy modeling has a substantial influence on the accuracy of models. If the sampled data is limited and its distribution not properly controlled,choice of the optimal number of sampling points creates significant problems in fuzzy identification.The author proposed a fuzzy identification algorithm with varied sampling points to investigate the influence of the number of sampling points on descriptive performance. Based on the T-S fuzzy model,we extracted the fuzzy rules by using the symmetrical triangular fuzzy division and the net-diagonal method.By modeling the DISO system and the Mackey-Glass chaotic time-series,we concluded that training and testing performance indexes in fuzzy models will increase with increased numbers of sampling points. Keywords:fuzzy identification;number of sampling points;triangular membership function;net-diagonal method; T-S fuzzy model 自Zadeh创立模糊理论以来,已经成功应用于 给出有限个数据采样点且数据的分布不能人为控制 许多控制领域.Zadeh提出了一种有效的方法来描 的情况下怎样选取最优的采样点个数这一问题, 述不能用精确数学模型表达的复杂或病态系统.由 模糊辨识是根据系统的输入输出数据对模型进行建 于非线性系统的复杂动态特性,并且模糊系统是一 模的,模糊模型的辨识分为结构辨识和参数辨识.长 个年轻的领域,在应用模糊模型对非线性系统进行 期以来,人们对模糊辨识的研究多集中于采用何种 建模时仍有很多尚待解决的问题.如模糊系统的不 方法进行结构和参数的辨识才能提高辨识精度和缩 同学习算法的提出,算法的收敛性分析,及学习完成 短辨识时间5刃.本文将从输入输出采样点出发,讨 后模糊系统的性能分析等14.本文主要研究了只 论只给出有限个数据采样点且数据分布随机的情况 下能达到所需精度的最小采样点个数和采样点个数 收稿日期:2007-10-31. 对模型精度的影响,即围绕着基于T-S(Takagi--Suge 基金项目:国家863计划资助项目. 通信作者:刘福才.E-mai:fo_xh@263.com o)模型对非线性系统进行模糊建模时,所取采样

542. 智能系统学报 第3卷 点的个数对模型描述性能的影响进行研究与分析. 的简单方法,该方法使得描述非线性系统的模糊规 1模糊辨识 则数只与输入变量的模糊划分数有关,而与输入变 量数目无关即规则的数目随输入空间模糊划分数 1.1T-S模糊模型 按一定的比例增大,而不是呈指数型增长,避免了规 模糊模型的辨识由结构辨识和参数辨识两部分 则爆炸 组成.其中,结构辨识又分为前提结构和结论结构的 图1中给出了一模糊系统(输入为1,2,输出 辨识;参数辨识也分为前提参数和结论参数的辨识, 为y)在K=2时的模糊划分情形. 在本文中模糊模型采用T-S模型,模糊划分(可 完成前提结构及前提参数辨识)采用三角形划分方 K=2 small 法,结论参数辨识采用递推最小二乘算法.Takagi和 large Sugeno于1985年提出了著名的T-S模糊模型,其形 M 式如下: R':if x is Aa and x2 is An and..and x,is Ar 图1输入空间的不同划分 then yi =po pix +p2x2++p;x, Fig.1 Different division of the input space 其中:R是第i条模糊规则,xk是模糊模型的第k个 每一个输入变量划分为两个模糊集合.若按传 输入变量,4是变量x的第j个模糊子集,y:是第i 统的模糊概念,模糊规则数将为2=4:然而这里采 条规则的输出,卫是实系数 用“模糊网格对角线法”,只有两个模糊规则被使用 1.2模糊划分 并具有如下形式: 可将一些隶属函数的形式(三角形、梯形和钟 R':if is small and x2 is small2. 形)应用在前提模糊集合中,三角形型隶属函数是 then yi=po +pix +px2 模糊控制中常用的一种隶属函数,由于它的形状仅 R2:if x is large and x2 is largez. 与直线斜率有关,属于直线型隶属函数,在应用软件 then y2 =po +pix +pix 实现模糊控制器时,直线型隶属函数比较简单,并耗 1.3 结论参数辨识算法 费较少的计算时间,控制系统的实时性比曲线形隶 系统的输出可表示为 属函数要好;因此适合于有隶属函数在线调整的自 适应模糊辨识与控制. y= 在本文中的隶属函数采用对称三角形模糊集 4,=,(, 合,每一个输入空间取相等的划分.每一个输人空间 x的间隔区间[M,M]是通过不同的K(见图1) 1={1,2,…,r,i=1,2,…,c 划分获得的,其中 这里:w,是由前面的模糊划分得出的,Π为模糊化 M=min{xp|p=1,2,…,m, 算子,通常采用取小运算。 定义 Mg=maxp=1,2,…,m. (1) 其隶属函数可简单按下式计算: =(p-M)/(M-M), 于是模糊系统输出为 喝=1-, j=1,2,…,rp=1,2,…,m (2) y=名, 为了简化模糊模型,本文在提取模糊规则时采 用“模糊网格对角线方法”3).所有的模糊系统都遇 ∑a,(p6+pix1+p吃+…+px,)= 到维数灾难:规则爆炸,对于大多数函数来说,都需 [01D1x1…⊙1x,…00x1…ox,]X 要模糊系统提供相当多的规则去逼近.规则的数目 [p%pp…p6pip]T (3) 随着输入输出变量数目的增多呈指数型增长,而不 将V对输入输出数据代入上式可得到一矩阵等式 是按一定的比例增大.“模糊网格对角线法”是在输 Y=XP. 人空间网格划分的基础上提出的一种提取模糊规则 其中:P是L=(r+I)c维结论参数向量;Y,X是
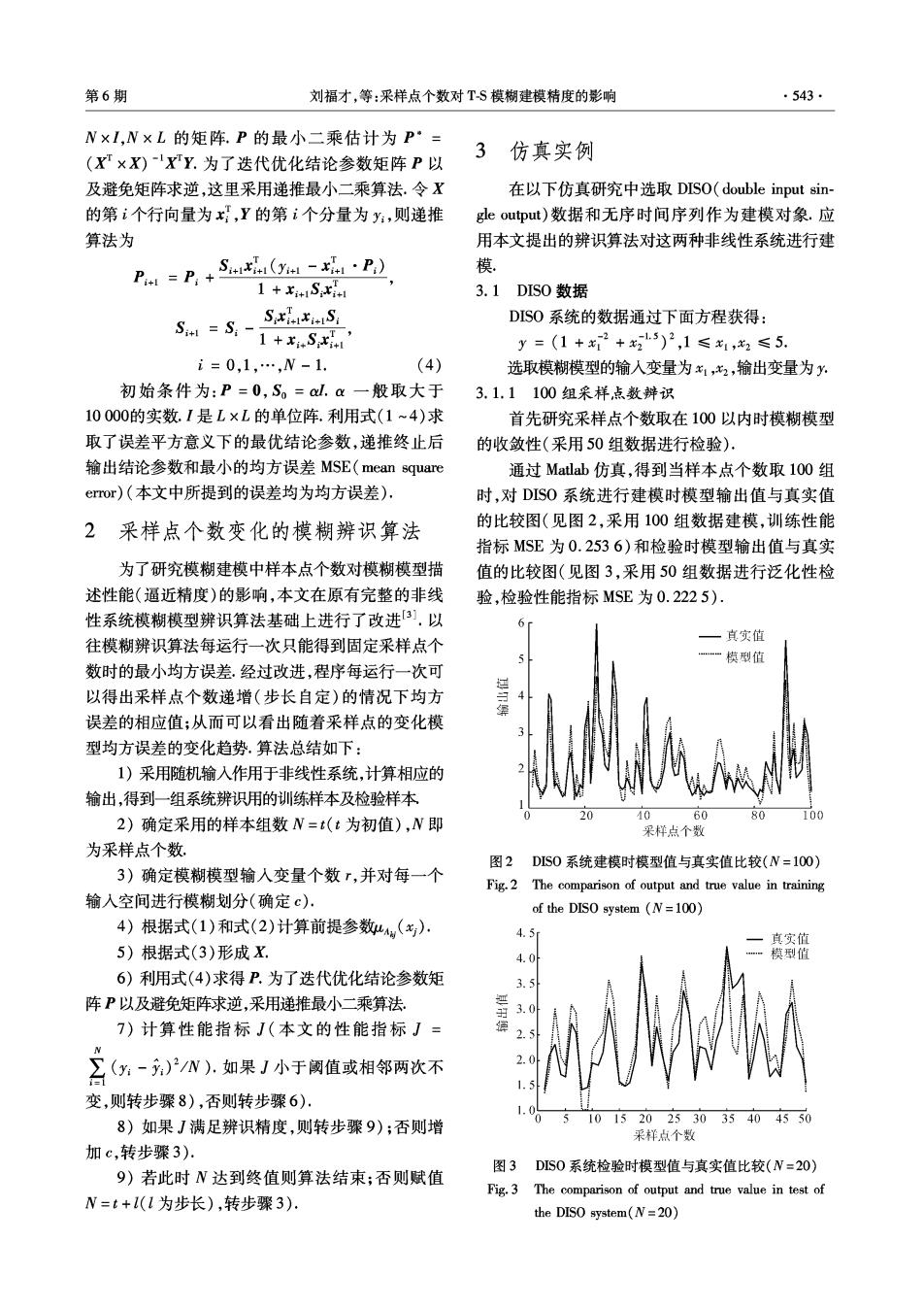
第6期 刘福才,等:采样点个数对TS模糊建模精度的影响 ·543· N×I,N×L的矩阵.P的最小二乘估计为P·= (X×X)xY.为了迭代优化结论参数矩阵P以 3仿真实例 及避免矩阵求逆,这里采用递推最小二乘算法.令X 在以下仿真研究中选取DISO(double input sin- 的第个行向量为x,Y的第i个分量为y,则递推 le output)数据和无序时间序列作为建模对象.应 算法为 用本文提出的辨识算法对这两种非线性系统进行建 P=P+S4e(u-4·P) 模。 1+Si 3.1DIS0数据 SXixiS DISO系统的数据通过下面方程获得: Sm=S-1+S y=(1+x2+x25)2,1≤x1,2≤5. i=0,1,…,W-1. (4) 选取模糊模型的输人变量为x1,x2,输出变量为y, 初始条件为:P=0,So=al,a一般取大于 3.1.1100组采样,点数辩识 10000的实数.I是L×L的单位阵.利用式(1~4)求 首先研究采样点个数取在100以内时模糊模型 取了误差平方意义下的最优结论参数,递推终止后 的收敛性(采用50组数据进行检验). 输出结论参数和最小的均方误差MSE(mean square 通过Matlab仿真,得到当样本点个数取100组 eor)(本文中所提到的误差均为均方误差). 时,对DISO系统进行建模时模型输出值与真实值 2采样点个数变化的模糊辨识算法 的比较图(见图2,采用100组数据建模,训练性能 指标MSE为0.2536)和检验时模型输出值与真实 为了研究模糊建模中样本点个数对模糊模型描 值的比较图(见图3,采用50组数据进行泛化性检 述性能(逼近精度)的影响,本文在原有完整的非线 验,检验性能指标MSE为0.2225). 性系统模糊模型辨识算法基础上进行了改进3).以 —其实值 往模糊辨识算法每运行一次只能得到固定采样点个 一模型值 数时的最小均方误差.经过改进,程序每运行一次可 以得出采样点个数递增(步长自定)的情况下均方 误差的相应值:从而可以看出随着采样点的变化模 型均方误差的变化趋势.算法总结如下: 1)采用随机输入作用于非线性系统,计算相应的 输出,得到一组系统辨识用的训练样本及检验样本 10 60 80 100 2)确定采用的样本组数N=t(t为初值),N即 采样点个数 为采样点个数. 图2DIS0系统建模时模型值与真实值比较(N=100) 3)确定模糊模型输人变量个数「,并对每一个 Fig.2 The comparison of output and true value in training 输入空间进行模糊划分(确定c). of the DISO system (N=100) 4)根据式(1)和式(2)计算前提参数4,(). 4.5 ,真实值 5)根据式(3)形成X. 4.0 模型值 6)利用式(4)求得P.为了迭代优化结论参数矩 3.5 阵P以及避免矩阵求逆,采用递推最小二乘算法, 3.0 7)计算性能指标J(本文的性能指标J= 2.5 名(-)N).如果J小于阈值或相邻两次不 2.0 1.5 变,则转步骤8),否则转步骤6). 1. 8)如果J满足辨识精度,则转步骤9);否则增 05101520253035404550 采样点个数 加c,转步骤3). 图3 DIS0系统检验时模型值与真实值比较(N=20) 9)若此时N达到终值则算法结束;否则赋值 Fig.3 The comparison of output and true value in test of N=t+1(1为步长),转步骤3). the DISO system(N=20)
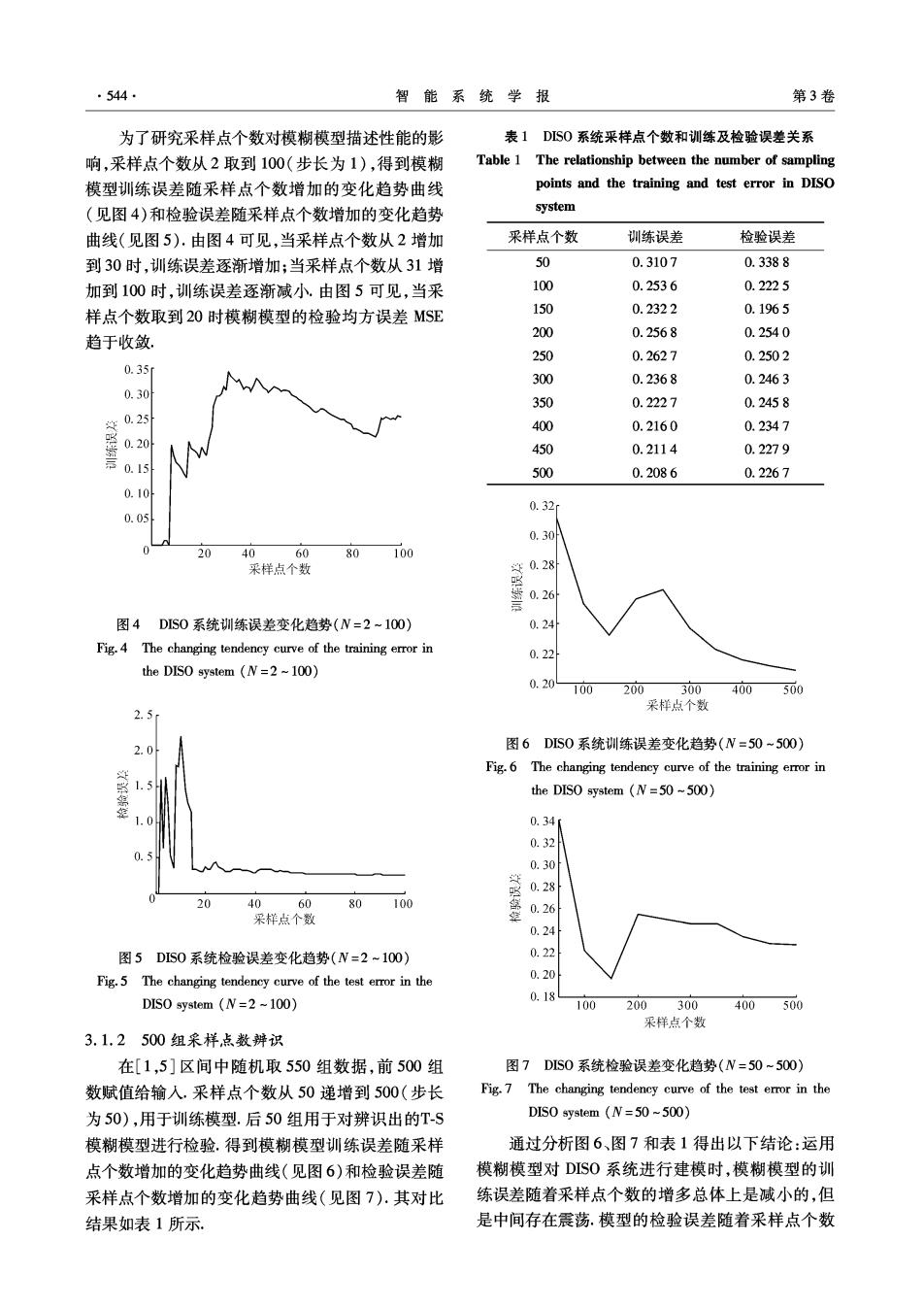
544 智能系统学报 第3卷 为了研究采样点个数对模糊模型描述性能的影 表1DIS0系统采样点个数和训练及检验误差关系 响,采样点个数从2取到100(步长为1),得到模糊 Table 1 The relationship between the number of sampling 模型训练误差随采样点个数增加的变化趋势曲线 points and the training and test error in DISO (见图4)和检验误差随采样点个数增加的变化趋势 system 曲线(见图5).由图4可见,当采样点个数从2增加 采样点个数 训练误差 检验误差 到30时,训练误差逐渐增加;当采样点个数从31增 50 0.3107 0.3388 加到100时,训练误差逐渐减小.由图5可见,当采 100 0.2536 0.2225 样点个数取到20时模糊模型的检验均方误差MSE 150 0.2322 0.1965 200 0.2568 0.2540 趋于收敛 250 0.2627 0.2502 0.35 300 0.2368 0.2463 0.30 350 0.2227 0.2458 0.25 400 0.2160 0.2347 0.20 450 0.2114 0.2279 0.15 500 0.2086 0.2267 0.10 0.32 0.05 0.30 20 40 60 80 100 采样点个数 年0.28 图4DIS0系统训练误差变化趋势(N=2~100) 0.24 Fig.4 The changing tendency curve of the training error in 0.22 the DISO system (N=2~100) 0.204 100 200 300 400500 采样点个数 2.5 2.0 图6DIS0系统训练误差变化趋势(N=50~500) Fig.6 The changing tendency curve of the training error in the DISO system (N=50~500) 0.34 0.32 0.30 0.28 20 40 60 80 100 采样点个数 0.26 0.24 图5DIS0系统检验误差变化趋势(V=2-100) 0.22 Fig.5 The changing tendency curve of the test error in the 0.20 DISO system (N=2 ~100) 0.18 100 200300 400500 采样点个数 3.1.2500组采样点数辩识 在[1,5]区间中随机取550组数据,前500组 图7DIS0系统检验误差变化趋势(N=50~500) 数赋值给输入,采样点个数从50递增到500(步长 Fig.7 The changing tendency curve of the test error in the 为50),用于训练模型.后50组用于对辨识出的T-S DISO system (N=50~500) 模糊模型进行检验.得到模糊模型训练误差随采样 通过分析图6、图7和表1得出以下结论:运用 点个数增加的变化趋势曲线(见图6)和检验误差随 模糊模型对DIS0系统进行建模时,模糊模型的训 采样点个数增加的变化趋势曲线(见图7).其对比 练误差随着采样点个数的增多总体上是减小的,但 结果如表1所示. 是中间存在震荡.模型的检验误差随着采样点个数
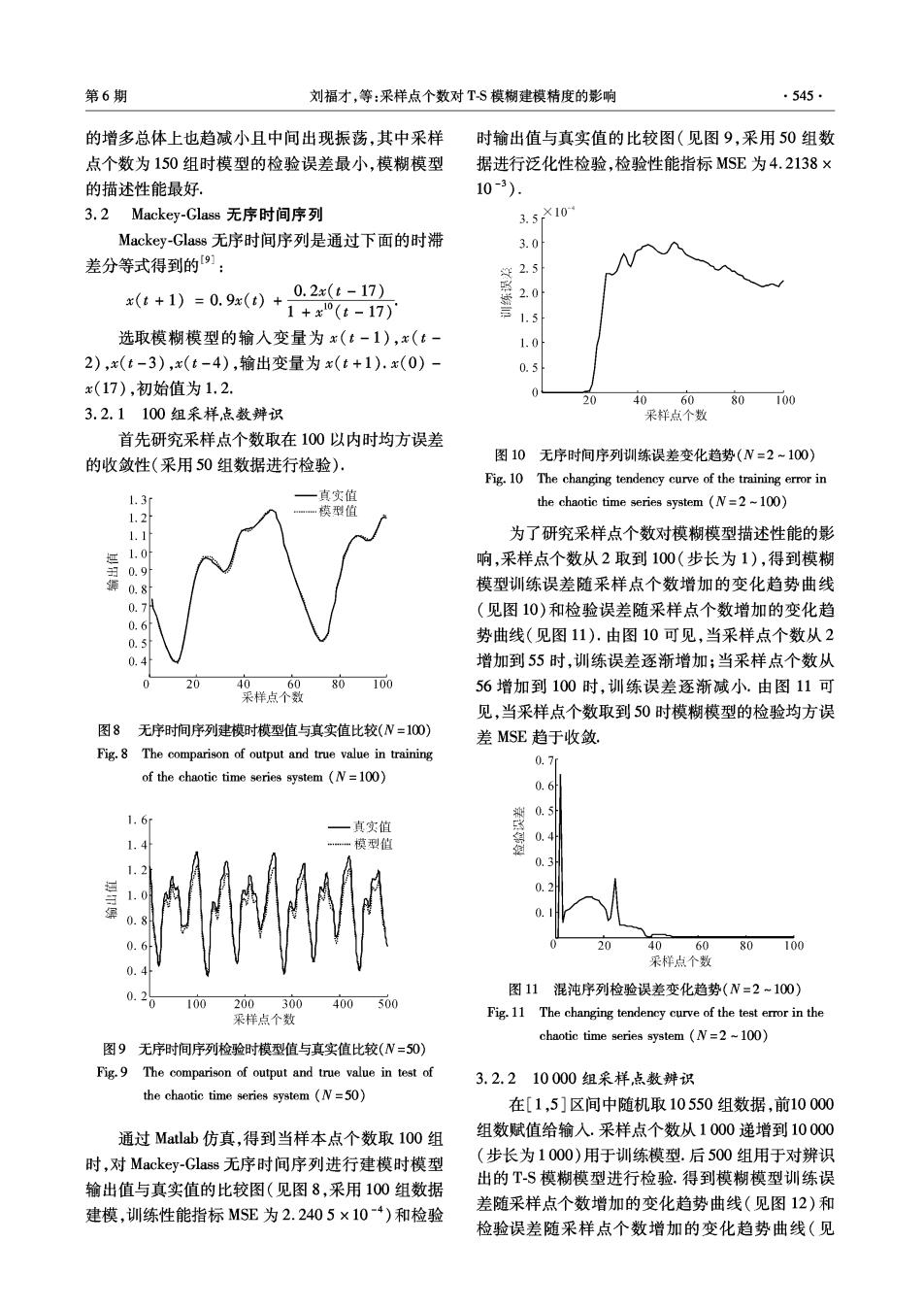
第6期 刘福才,等:采样点个数对TS模糊建模精度的影响 ·545· 的增多总体上也趋减小且中间出现振荡,其中采样 时输出值与真实值的比较图(见图9,采用50组数 点个数为150组时模型的检验误差最小,模糊模型 据进行泛化性检验,检验性能指标MSE为4.2138× 的描述性能最好. 10-3). 3.2 Mackey-Glass无序时间序列 3.5×10 Mackey-Glass无序时间序列是通过下面的时滞 3.0 差分等式得到的: (t+1)=0.9x()+0.2x(t-17) 2.0 1+x0(t-17) 1.5 选取模糊模型的输入变量为x(t-1),x(t- 1.0 2),x(t-3),x(t-4),输出变量为x(t+1).x(0)- 0.5 x(17),初始值为1.2. 20 406080100 3.2.1100组采样,点数辩识 采样点个数 首先研究采样点个数取在100以内时均方误差 图10无序时间序列训练误差变化趋势(N=2~100) 的收敛性(采用50组数据进行检验). Fig.10 The changing tendency curve of the training error in 1.3i 一真实值 模型值 the chaotic time series system (N=2~100) 1.2 1.1 为了研究采样点个数对模糊模型描述性能的影 1.0 响,采样点个数从2取到100(步长为1),得到模糊 0.9 0.8 模型训练误差随采样点个数增加的变化趋势曲线 0.7 (见图10)和检验误差随采样点个数增加的变化趋 0.6 0.5 势曲线(见图11).由图10可见,当采样点个数从2 04 增加到55时,训练误差逐渐增加;当采样点个数从 20 406080100 采样点个数 56增加到100时,训练误差逐渐减小.由图11可 见,当采样点个数取到50时模糊模型的检验均方误 图8无序时间序列建模时模型值与其实值比较(N=100) 差MSE趋于收敛. Fig.8 The comparison of output and true value in training 0.7 of the chaotic time series system (N=100) 0.6 0.5 一真实值 ☒ 模型值 0.4 0.3 0.2 0 40 60 80 100 采样点个数 图11混沌序列检验误差变化趋势(N=2~100) 100 200300400500 采样点个数 Fig.11 The changing tendency curve of the test error in the chaotic time series system (N=2 ~100) 图9无序时间序列检验时模型值与真实值比较(N=50) Fig.9 The comparison of output and true value in test of 3.2.210000组采样,点数辨识 the chaotic time series system (N=50) 在[1,5]区间中随机取10550组数据,前10000 通过Matlab仿真,得到当样本点个数取l00组 组数赋值给输入.采样点个数从1000递增到10000 时,对Mackey-Glass无序时间序列进行建模时模型 (步长为1000)用于训练模型.后500组用于对辨识 出的T-S模糊模型进行检验.得到模糊模型训练误 输出值与真实值的比较图(见图8,采用100组数据 差随采样点个数增加的变化趋势曲线(见图12)和 建模,训练性能指标MSE为2.2405×10-4)和检验 检验误差随采样点个数增加的变化趋势曲线(见
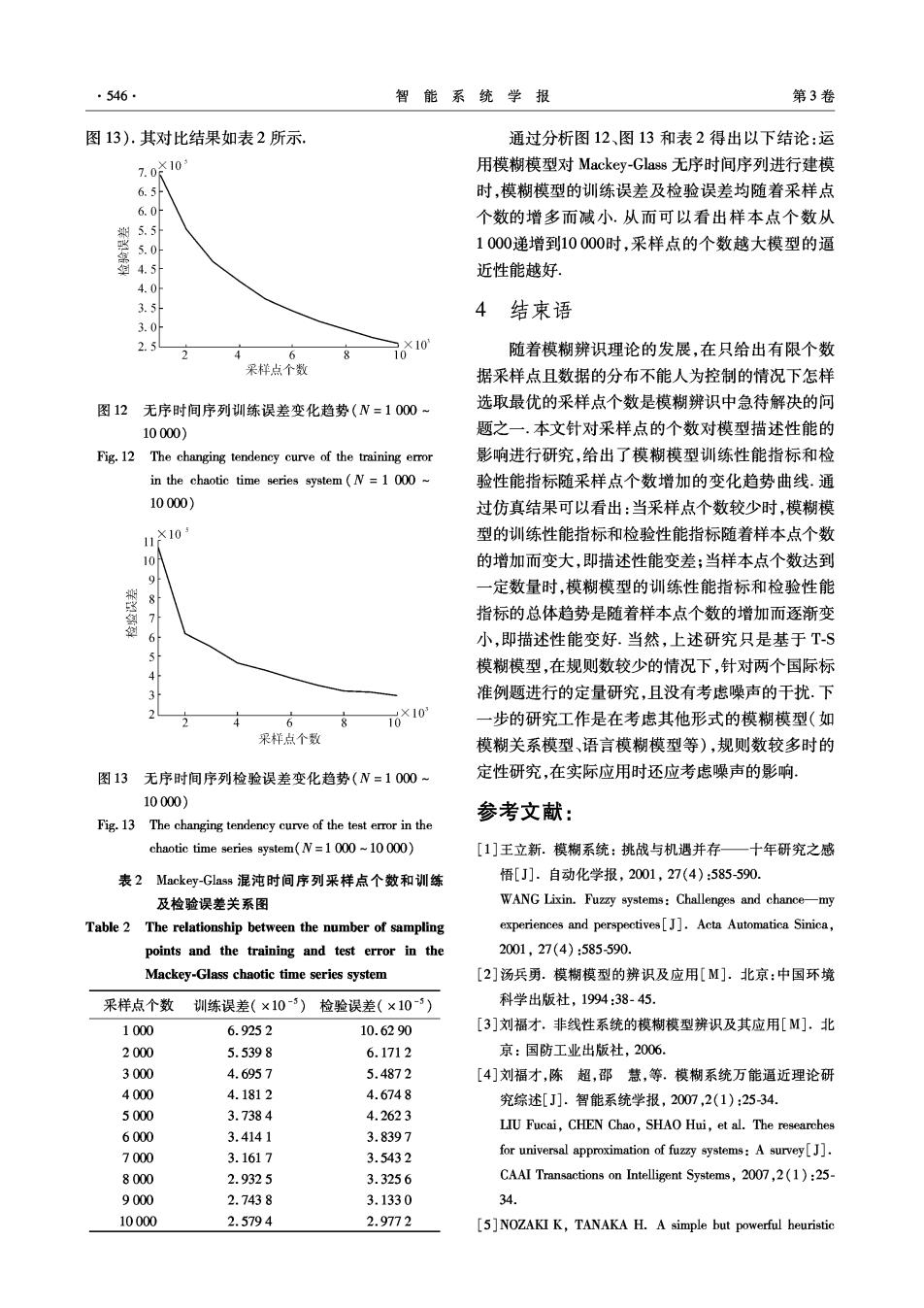
.546. 智能系统学报 第3卷 图13).其对比结果如表2所示 通过分析图12、图13和表2得出以下结论:运 7010 用模糊模型对Mackey-Glass无序时间序列进行建模 6.5 时,模糊模型的训练误差及检验误差均随着采样点 6.0 个数的增多而减小.从而可以看出样本点个数从 5.0 1000递增到10000时,采样点的个数越大模型的逼 4.5 近性能越好. 4.0 3.5 4结束语 3.0 2.5 4 ×10 6 10 随着模糊辨识理论的发展,在只给出有限个数 采样点个数 据采样点且数据的分布不能人为控制的情况下怎样 图12无序时间序列训练误差变化趋势(N=1000~ 选取最优的采样点个数是模糊辨识中急待解决的问 10000) 题之一.本文针对采样点的个数对模型描述性能的 Fig.12 The changing tendency curve of the training error 影响进行研究,给出了模糊模型训练性能指标和检 in the chaotic time series system(N =1 000~ 验性能指标随采样点个数增加的变化趋势曲线.通 10000) 过仿真结果可以看出:当采样点个数较少时,模糊模 11X105 型的训练性能指标和检验性能指标随着样本点个数 10 的增加而变大,即描述性能变差;当样本点个数达到 9 一定数量时,模糊模型的训练性能指标和检验性能 8 指标的总体趋势是随着样本点个数的增加而逐渐变 6 小,即描述性能变好.当然,上述研究只是基于T-S 模糊模型,在规则数较少的情况下,针对两个国际标 3 准例题进行的定量研究,且没有考虑噪声的干扰.下 2 6 一步的研究工作是在考虑其他形式的模糊模型(如 采样点个数 模糊关系模型、语言模糊模型等),规则数较多时的 图13无序时间序列检验误差变化趋势(N=1000~ 定性研究,在实际应用时还应考虑噪声的影响, 10000) 参考文献: Fig.13 The changing tendency curve of the test error in the chaotic time series system(N=1 000~10000) [1]王立新.模糊系统:挑战与机遇并存一十年研究之感 表2 Mackey-Glass混沌时间序列采样点个数和训练 悟[J].自动化学报,2001,27(4):585-590. 及检验误差关系图 WANG Lixin.Fuzzy systems:Challenges and chance-my Table 2 The relationship between the number of sampling experiences and perspectives[J].Acta Automatica Sinica, points and the training and test error in the 2001,27(4):585590. Mackey-Glass chaotic time series system [2]汤兵勇.模糊模型的辨识及应用[M].北京:中国环境 采样点个数训练误差(×10-5)检验误差(×10-5) 科学出版社,1994:38-45. 1000 6.9252 10.6290 [3]刘福才.非线性系统的模糊模型辨识及其应用[M].北 2000 5.5398 6.1712 京:国防工业出版社,2006, 3000 4.6957 5.4872 [4]刘福才,陈超,邵慧,等.模糊系统万能逼近理论研 4000 4.1812 4.6748 究综述[J].智能系统学报,2007,2(1):25-34 5000 3.7384 4.2623 LIU Fucai,CHEN Chao,SHAO Hui,et al.The researches 6000 3.4141 3.8397 7000 3.1617 3.5432 for universal approximation of fuzzy systems:A survey[J]. 8000 2.9325 3.3256 CAAI Transactions on Intelligent Systems,2007,2(1):25- 9000 2.7438 3.1330 34. 10000 2.5794 2.9772 [5]NOZAKI K,TANAKA H.A simple but powerful heuristic

第6期 刘福才,等:采样点个数对TS模糊建模精度的影响 .547. method for generating fuzzy rules from numerical data J. 作者简介: Fuzzy Sets Syst,1997,86(2):251-270. 刘福才,男,1966年生,教授,博士 [6]岳玉芳,毛剑琴.一种基于TS模型的快速自适应建模 生导师.主要研究方向为模糊辨识与 方法[J].控制与决策,2002,17(2):155-158 预测控制、军事测控技术、电力拖动及 YUE Yufang,MAO Jiangin.Fast adaptive modeling based 其计算机控制等.发表学术论文120余 on T-S model[J].Control and Decision,2002,17(2): 篇,出版专著1部。 155-158. [7]刘福才,关新平,裴润.基于一种新模糊模型的非线性 陈超,女,1982年生,硕士研究 系统模糊辨识[J].控制理论与应用,2003,20(1):113 生.主要研究方向为模糊辨识与模糊控 116 制 LIU Fucai,GUAN Xinping,PEI Run.Fuzzy identification based on a new fuzzy model for nonlinear systems[J].Con- trol Theory Application,2003,20(1):113-116. [8]TAKAGI T,SUGENO M.Fuzzy identification of systems 张彦柳,女,1984年生,硕士研究 and its application to modeling and control[J].IEEE Trans 生.主要研究方向为模糊建模与图像处 Syst,Man,Cybern,1985,15(1):116-132. 理技术 [9 ]LO J C,YANG C H.A heuristic error-feedback leaming al- gorithm for fuzzy modeling[J].IEEE Trans Syst,Man,Cy- bem,1999,29(6):686691. The Seventh IEEE International Conference on Control Automation 第7届EEE控制与自动化国际会议 The 7th IEEE International Conference on Control and Automation (ICCA09)will be held on December 9-11,2009,in Christchurch, New Zealand.The conference is jointly organized by the IEEE Control Systems Chapter,Singapore and IEEE South New Zealand Sec- tion,and technically sponsored by IEEE Control Systems Society and University of Canterbury,New Zealand.It is to create a forum for scientists and practicing engineers throughout the world to present the latest research findings and ideas in the areas of control and auto- mation. ICCA Proceedings are included in EI Compendex,IEEE Xplore and ISI Proceedings (ISTP). Topics of interest include but not limited to Modeling of Complex Systems Smart Structures Learning Systems Discrete Event Systems Optimal Control Linear Systems Nonlinear Systems and Control Robust and Contro Adaptive Control Fuzzy and Neural Systems Intelligent and AI Based Control Estimation and Identification Real-time Systems Fault Detection Process Control Instrumentation Robotics Motion Control Integrated Manufacturing Automated Guided Vehicles Flexible Manufacturing Systems Control Education Sensor/data fusion Factory Modeling and Automation Process Automation Control Applications Petri-Nets and Applications Man-machine Interactions Multi-agent systems Micro and Nano Systems Sensor networks and networked control Important Dates Deadline for Manuscript Submissions:April 1,2009 Notification of Acceptance:July 1,2009 Submission of Final Papers:September 1,2009 Wesite:http://www.ieee-icca.org http://hdd.ece.nus.edu.sg/-icca09/ E-mail:icca2009@ntu.edu.sg