
第3卷第6期 智能系统学报 Vol.3 No.6 2008年12月 CAAI Transactions on Intelligent Systems Dec.2008 采用脉冲宽度检测的自适应滤波算法 林其伟 (华侨大学信息科学与工程学院,福建泉州362021) 摘要:在对图像中干扰噪声模型分析的基础上,提出基于脉冲宽度和噪声模型检测的自适应噪声滤波算法,通过 判定干扰噪声的脉冲宽度及分布密度来确定滤波器窗口的大小及类型,从而有效去除复合型干扰噪声.实验结果表 明所提出的算法操作简单,对实际图像的处理效果优于一般常用噪声平滑滤波器的输出结果. 关键词:噪声模型;噪声密度;自适应;滤波 中图分类号:TP301.6,TN911.73文献标识码:A文章编号:16734785(2008)06054804 An adaptive filtering algorithm with impulse width testing LIN Qi-wei School of Information Science and Technology,Huagiao University,Quanzhou 362021,China) Abstract:An adaptive noise filtering algorithm was developed that uses impulse width and noise model detection. With this method,we determine the types and sizes of the windows of the noise filter by the impulse widths and their distribution densities,so that composite noise can be effectively removed from images and the detail of the im- age can be preserved.The algorithm has been tested with several images.Experimental results indicate that the proposed algorithm is easy to use and the output image quality of the proposed algorithm is superior to that of com- monly used noise filters. Keywords:noise model;noise density;adaptability;filtering 数字图像中的去噪是图像处理时最常见的问对非脉冲型噪声进行处理.这些算法以数学理论为 题,也是十分棘手的问题.对图像中噪声清除的效果依托,同时考虑像素领域的统计特性和人眼的视觉 好坏将直接影响后续的处理,因而在进行相应的图特性以及最佳滤波准则,在去除图像中干扰噪声的 像处理或分析之前通常要对图像进行去噪预处理. 基础上较好地保护了图像的边缘.上述多数算法在 对实际图像而言,由于传输或编、解码过程经常引人 特定的应用场合可达到较好的效果,但算法比较费 脉冲型的干扰噪声并伴随有非脉冲型的干扰噪声 时.文献[5]提出了一种改进的自适应中值滤波算 (如高斯白噪声等),对这两种不同类型的噪声所产 法,该算法对不同的图像区域,相应地采用不同的 生的复合噪声用单一的滤波器难以同时检出并加以 算子和权值,使得算法自适应于图像内容,从而在 消除.对此,研究人员提出过多种应对措施,如文 信噪比性能方面有所改善.本文在对图像中干扰噪 献[2]提出的自适应保细节中值滤波器,文献[3]提 声模型进行分析的基础上,对Li等的滤波方案进 出的脉冲噪声去除的灰度形态学模型,Lin和Wl 行了改进和简化,提出了基于脉冲宽度和噪声模型 so41提出了基于噪声宽度检测的可变长度中值滤 检测的自适应滤波算法,在去除图像中的较大密度 波器,该方案先滤除正、负向脉冲干扰噪声,然后再 脉冲干扰和非脉冲型干扰噪声方面有较好的效果, 同时可较好地保持图像的细节.实验结果表明所提 收稿日期:2007-10-15. 基金项目:福建省自然科学基金计划资助项目(A0610022):国务院 出的算法操作简单,对实际图像的处理效果优于一 侨办科研基金资助项目(06QZR03) 般常用噪声滤波器的输出结果 通信作者:林其伟.E-mail:win@hqw.ed血.cm

第6期 林其伟:采用脉冲宽度检测的自适应滤波算法 ·549· 冲型的干扰噪声,则检测干扰脉冲的宽度.根据检测 1 噪声分析 的结果决定所用的滤波器窗口的宽度,以达到既消 设像素x(m,n)为原图像在(m,n)处的取值, 除脉冲型干扰又减轻非脉冲型干扰影响,同时也较 它受噪声干扰的概率为P. 好地保持图像细节的目的.由上述思路得到的算法 当像素受噪声干扰时记为x'(m,n),若被脉冲 步骤如下: 型噪声干扰时,x'(m,n)的取值变为P(受负向脉 1)干扰噪声类型的检测.对图像中是否存在非 冲干扰时)成P(被正向脉冲干扰时), 脉冲型于扰噪声的检测,采用区域方差比较法来实 y(m,n)是受干扰的图像,则 现.为此将图像分割成几个子图像,计算各子图像的 「x'(m,n),概率为P; 方差,是否满足 y(m,n)= (1) lx(m,n),概率为P. [oi>Ta1,i=(1,…,W); (4) 已知对均值为零,方差为σ的正态分布噪声而 lo-o>Ta,iJj=1,…,N,i≠ji 言,当采用中值滤波器时输出的噪声方差为 这里:o(i=1,…,N)为各子图像计算所得方 。4w(而g+”,为 差,T,T2为由对图像的知识所确定的两个阈值.一 2 (2) 般认为:若σ比较大,则图像变化剧烈,存在脉冲型 噪声干扰的可能性就大;反之,若σ小于某一阈值, 式中:σ为输入噪声功率,W为中值滤波器的窗口, 则图像变化不是很剧烈,存在脉冲型噪声干扰的可 m为输入噪声均值,(m)为输人噪声密度函数, 能性就小.而Ta用于衡量相邻图像子块变化的剧烈 若采用均值滤波器时,输出噪声方差σ:为 程度是否一致,当其变化小于某一阈值时,则认为图 (3) 像子块之间变化的剧烈程度相近,此时对应的图像 l 从式(2)、(3)可知,中值滤波器的输出噪声与输入 本身细节较多,而不是由脉冲型干扰噪声所引起, 噪声的密度分布状况有关,而均值滤波器的输出噪 若式(4)的条件满足,则认为所处理的图像中 声与输入噪声的密度分布状况无关,中值滤波器对 存在脉冲型干扰噪声,此时进入步骤2):若式(4)的 脉冲干扰的消除效果比较理想,而均值滤波器则对 条件不满足,则认为所处理的图像不存在脉冲型干 忧噪声,则直接转步骤3),使用均值平滑算法处理 高斯白噪声的消除有较好的效果.因此,对于随机噪 来降低图像中非脉冲型噪声干扰的影响。 声的抑制来说,中值滤波器的性能不如均值平滑滤 波器;而对独立的脉冲性干扰噪声,特别是宽度小于 2)进行脉冲宽度的检测.定义检测指标h-1, W2的相对较远的脉冲干扰,中值滤波器的噪声滤 h,v-1,为 波效果较好.在对图像中的噪声进行抑制时,需要针 [h:=x,m+i-l-无,m+i, 对噪声的分布特性来选择合适的滤波器类型, h1=名am一花,m-1, (5) :=+i-l,m一七+i,m, 2采用噪声脉冲宽度检测的自适应滤 -1=xn,m一x4-l,m 波算法 这里,i=1,2,…,出a-和x-1n分别为滤波器 窗口在位置(n,m-1)和(n-1,m)处的灰度值. 若希望在去除脉冲干扰的同时对非脉冲性的干 下面以水平方向为例,说明对脉冲宽度进行检 扰噪声也有较好的抑制效果,而对原图像的有用信 测的操作。 息的影响同时又为最小,可以通过对干扰噪声脉冲 利用h1和h:,可检出脉冲宽度为“1”的噪声. 宽度和类型的检测来设计滤波算法.为此,本文在 a)如果h1>T1且h-1>T,或h1<-T1且 Lin提出的自适应中值滤波器算法的基础上进行了 h-1<-T,则说明在位置(n,m-1)处的像素值远 改进和简化. 大于(n-1,m-1)及(n+1,m-1)的像素值,所 为了在检出宽度为单个像素的脉冲干扰的同 以认为在位置(n,m-1)处存在一个宽度为1的脉 时,还能抑制具有一定宽度的脉冲干扰及高斯白噪 冲干扰,这时用宽度为3的中值滤波器可将其滤除, 声,首先检测是否存在脉冲型的于扰噪声,若不存在 程序转向对下一像素(即(n+1,m-1)处)的检测. 脉冲型的干扰噪声则直接进行平滑滤波;若存在脉 上述T,为检测阚值
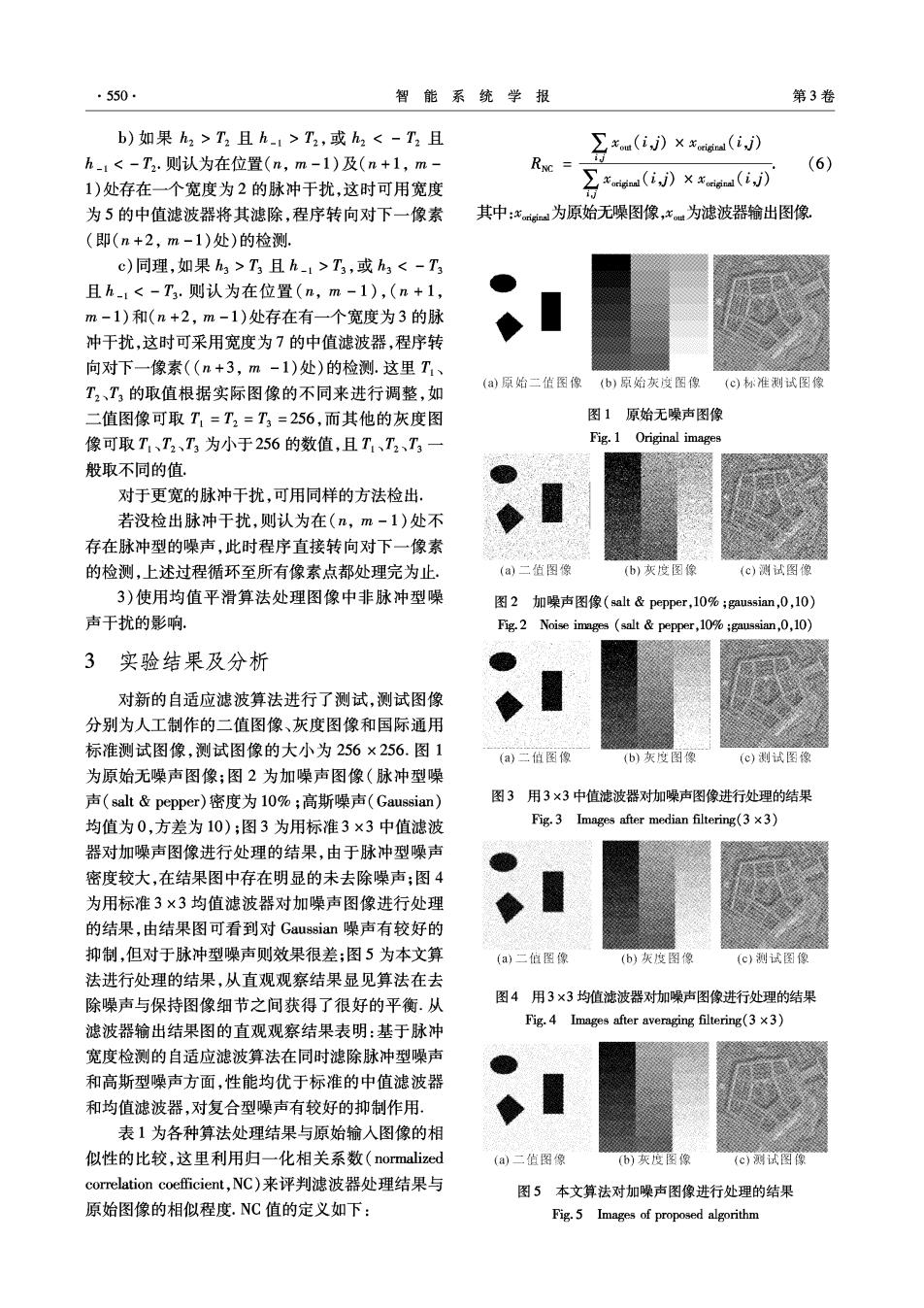
.550. 智能系统学报 第3卷 b)如果h2>T2且h-1>T2,或h2T且h-1>T3,或h3<-T 且h-1<-T3.则认为在位置(n,m-1),(n+1, m-1)和(n+2,m-1)处存在有一个宽度为3的脉 冲干扰,这时可采用宽度为7的中值滤波器,程序转 向对下一像素((n+3,m-1)处)的检测.这里T (a)原始二值图像(b)原始灰度图像(c)标准测试图像 T2、T3的取值根据实际图像的不同来进行调整,如 二值图像可取T1=T2=T3=256,而其他的灰度图 图1原始无噪声图像 像可取T、T2、T3为小于256的数值,且T、T2、T3一 Fig.1 Original images 般取不同的值。 对于更宽的脉冲于忧,可用同样的方法检出, 若没检出脉冲干扰,则认为在(n,m-1)处不 存在脉冲型的噪声,此时程序直接转向对下一像素 的检测,上述过程循环至所有像素点都处理完为止 (a)二值图像 (b)灰度图像 (c)测试图像 3)使用均值平滑算法处理图像中非脉冲型噪 图2加噪声图像(salt&pepper,10%;gaussian,0,10) 声干扰的影响, Fig.2 Noise images (salt pepper,10%;gaussian,,10) 3 实验结果及分析 对新的自适应滤波算法进行了测试,测试图像 分别为人工制作的二值图像、灰度图像和国际通用 标准测试图像,测试图像的大小为256×256.图1 (a)二伯图像 (b)灰度图像 (c)测试图豫 为原始无噪声图像;图2为加噪声图像(脉冲型噪 声(salt&pepper)密度为10%;高斯噪声(Gaussian) 图3用3×3中值滤波器对加噪声图像进行处理的结果 均值为0,方差为10);图3为用标准3×3中值滤波 Fig.3 Images after median filtering(3 x3) 器对加噪声图像进行处理的结果,由于脉冲型噪声 密度较大,在结果图中存在明显的未去除噪声;图4 为用标准3×3均值滤波器对加噪声图像进行处理 的结果,由结果图可看到对Gaussian噪声有较好的 抑制,但对于脉冲型噪声则效果很差;图5为本文算 (a)二位图像 (b)灰度图像 (c)测试图像 法进行处理的结果,从直观观察结果显见算法在去 除噪声与保持图像细节之间获得了很好的平衡.从 图4用3×3均值滤波器对加噪声图像进行处理的结果 Fig.4 Images after averaging filtering(3 x3) 滤波器输出结果图的直观观察结果表明:基于脉冲 宽度检测的自适应滤波算法在同时滤除脉冲型噪声 和高斯型噪声方面,性能均优于标准的中值滤波器 和均值滤波器,对复合型噪声有较好的抑制作用 表1为各种算法处理结果与原始输入图像的相 似性的比较,这里利用归一化相关系数(normalized (a)二值图像 (b)灰度图像 (c)测试图像 correlation coefficient,NC)来评判滤波器处理结果与 图5本文算法对加噪声图像进行处理的结果 原始图像的相似程度.NC值的定义如下: Fig.5 Images of proposed algorithm

第6期 林其伟:采用脉冲宽度检测的自适应滤波算法 551· 表1滤波器处理结果与原图像相似性的比较(NC值)】 Table 1 The normalized comparability between the original image and filtering image(NC) 图像处理方法 二值图像 灰度图像 测试图像 加噪声 0.9834 0.9644 0.9649 3×3中值滤波 0.9960 0.9918 0.9892 3×3均值滤波 0.9983 0.9965 0.9945 本文算法 0.9987 0.9981 0.9962 从表1的定量测试结果数据可以看到本文算法 由表3可见,本文算法在运行速度方面也具有 对二值图像或是灰度图像、自然图像或是人造图像 一定的优势 在滤波处理结果与原图像相似性比较方面也都显示 4 结束语 出其优势,特别对自然图像的处理效果最为明显.由 于进行了噪声类型的判断,可充分利用中值滤波器 本文算法综合利用中值滤波器和均值平滑滤波 和均值滤波器的优势,在各自的特长上发挥其作用. 的优点,在滤除较宽脉冲噪声和白噪声方面比标准的 采用了噪声脉冲宽度的检测,可以较好地抑制噪声 中值滤波器和改进中值滤波器优越,在相应的环境下 密度较大的脉冲干扰,而同时达到较好地保持原图 可得到较好的滤波效果.在空间域中进行处理,比较 像细节的目的. Lin等人提出的算法更简单,更有利于实际应用。 表2为加入密度为10%(D=10%)的椒盐噪声 参考文献: 和均方差为10(σ=10)的高斯噪声后,本文算法与 改进中值滤波5)处理结果的比较,采用信噪比改善 [1]PITAS I,VENETSANOPOULOS A N.Nonlinear mean fil- 因子S作为客观评判标准.信噪比改善因子S定义 ters in image processing[J].IEEE Trans Acoustics,Speech 如下s: and Signal Processing,1986,34(3):573-584. [2]朱菊华,杨新,李俊.一种改进的自适应保细节中值 ∑(xom(i)-xmea(i)2 S=10·lg 滤波算法[J].计算机工程与应用,2001,37(3):93-95. (7) (a(i,》-x(i》)2 ZHU Juhua,YANG Xin,LI Jun.The improved adaptive mi- 行 nutiae preserving median filter [J].Computer Engineering 其中:xaaa为原始无噪图像,xm为滤波器输出图 and Apllications,2001,37(13):93-95. 像,x为滤波器输入图像 [3]孙忠贵,王玲.一个关于脉冲噪声去除的灰度形态学 表2对Lena图滤波效果的比较 模型[J].计算机应用与软件,2006,23(6):31-32 Table 2 The filtering effect of Lena SUN Zhonggui,WANG Ling.A new gray-scale morphologi- 方法 S/dB cal model for elminating pulse noises of images[J].Com 中值滤波 -4.262 puter Applications and Software,2006,23(6):31-32. 改进中值滤波例 -6.018 [4]LIN H M,WILSON A N.Median filters with adaptive length 本文算法 -6.211 [J].IEEE Trans Circuits System,1988,35(6):593-599. [5]张恒,雷志辉,丁晓华.一种改进的中值滤波算法[J]. 从表2可以看出,本文算法在信噪比的改善方 中国图象图形学报,2004,9(4):408-411. 面具有一定的优势 ZHANG Heng,LEI Zhihui,DING Xiaohua.An improved method of median filter[J].Joumal of Image and Graphics, 表3为运行速度的比较,运行环境为Pentium 2004,9(4):408-411. 4.3GHz主频,1GB内存,MATLAB7.0.文献[4]的 作者简介: 运行时间为本机模拟的结果,以具备可比性, 林其伟,男,1957生,副教授.主要 表3运行速度的比较 研究方向为信号与信息处理、智能仪器 Table 3 The operating speed comparison 仪表、智能信息处理、计算机通信与网 方法 运行时间/ms 络安全等.发表学术论文30余篇. Lin算法可 817.2 本文算法 612.4