
第4卷第2期 智能系统学报 Vol 4 Ng 2 2009年4月 CAA I Transactions on Intelligent Systems Apr 2009 基于模糊K-har monic means的谱聚类算法 汪中2,刘贵全2,陈恩红2 (1中国科学技术大学计算机科学与技术学院,安徽合肥230027,2安徽省计算与通讯软件重点实验室,安徽合肥230027) 摘要:谱聚类作为一种有效的方法广泛应用于机器学习.通过分析谱聚类初始化敏感的实质,引入对初值不敏感 的模糊K-hamonic means算法来克服这一缺点,提出一种基于模糊K-hamonic means的谱聚类算法(FKM-SC).与 传统谱聚类算法以及对初值敏感的Kmeans.FCM算法相比,改进算法不仅可以识别有挑战性的人工数据,并且可以 得到稳定的聚类中心和聚类结果,同时提高了聚类的精确度.实验结果表明了该算法的有效性和可行性 关键词:谱聚类;模糊K-hamonic means初始化敏感;聚类中心 中图分类号:IP311文献标识码:A文章编号:1673-4785(2009)02-0095-05 A spectral clusterng a lgor ithm ba sed on fuzzy K-hamm on ic means WANG Zhong2,L U Gui-quan'2,CHEN En-hong' (1.School of Computer Science,University of Science and Technobgy of China,Hefei 230027,China;2 Key Laborabry of Sofware in Computing and Communication,Hefei 230027,China) A bstract:Spectral clustering is an effective method that is widely used in machine leaming After analyzing the es- sence of initialization sensitivity in spectral clustering,the fuzzy K-hamonic means (FKHM)algorithm was consid- ered to conquer spectral clustering's shortcom ings,then an spectral clustering algorithm based on FKHM was de- veloped Compared with the traditional spectral algorithm and the fuzzy cmeans (FCM)algorithm,the suggested algorithm is more sensitive to initial values The suggested algorithm can not only identify challenging artificial da- ta,but also find stable cluster centers and clustering results,considerably mproving clustering precision Experi- ments showed that it is an effective and feasible way to mprove the perfomance of spectral clustering algorithms Keywords:spectral clustering fuzzy K-hamonic means initialization sensitivity,cluster centers 聚类分析是数据挖掘、机器学习、模式识别等众聚类判据在放松了的连续域中的全局最优解.谱聚 多领域的重要工具.它在执行过程中没有任何关于类算法适用于非测度空间,算法与数据点维数无关, 类别的先验知识和假设,因而被称作是一种无监督而仅与数据点个数有关,因而可以避免由特征向量 的学习方法.近年来产生了大量解决该问题的相关的过高维数所造成的奇异性问题.谱聚类算法尽管 算法,现有的基于产生式模型和基于中心的聚类方 在实践中取得了很好的效果,但是算法本身仍存在 法仅在具有凸形结构的数据上有好的效果,且容易 许多值得研究的问题.文献[2]指出当聚类数目大 陷入局部最优 于实际聚类数时,多路谱聚类方法的效果很差; 为了能在任意形状的样本结构上聚类,且收敛 Fischet等提出了依赖于背景的相似性度量方法和尺 于全局最优,谱聚类算法被广泛应用.谱聚类的思想 度参数问题:由于谱方法的计算复杂度相当高, 来源于谱图划分山,是一种流行的高性能计算方 Fow lkes等提出使用Nystrom逼近方法减少求解特 法.该方法基于两点间的相似关系,利用数据的相似征问题的计算复杂度!:针对谱聚类初始化敏感的 矩阵的特征向量进行聚类,通过特征分解可以获得 特点,Ekn等提出使用对初始值不敏感的方法[) 收稿日期:2008-12-16 本文提出一种基于模糊K-hamonic means的谱 基金项目:国家自然科学基金资助项目(60775037):教育部新世纪优 聚类算法,其主要思想是:首先分析不同数据输入顺 秀人才支持计划资助项目(NCET050549). 通信作者:汪中.Emai让wzpb@mail ustc edu cn 序对相似性矩阵、构造矩阵和生成矩阵的影响,得出 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 4卷第 2期 智 能 系 统 学 报 Vol. 4 №. 2 2009年 4月 CAA I Transactions on Intelligent System s Ap r. 2009 基于模糊 K2har monic means的谱聚类算法 汪 中 1, 2 , 刘贵全 1, 2 , 陈恩红 1, 2 (1. 中国科学技术大学 计算机科学与技术学院 ,安徽 合肥 230027; 2.安徽省计算与通讯软件重点实验室 ,安徽 合肥 230027) 摘 要 :谱聚类作为一种有效的方法广泛应用于机器学习. 通过分析谱聚类初始化敏感的实质 ,引入对初值不敏感 的模糊 K2harmonic means算法来克服这一缺点 ,提出一种基于模糊 K2harmonic means的谱聚类算法 ( FKHM2SC). 与 传统谱聚类算法以及对初值敏感的 K2means、FCM算法相比 ,改进算法不仅可以识别有挑战性的人工数据 ,并且可以 得到稳定的聚类中心和聚类结果 ,同时提高了聚类的精确度. 实验结果表明了该算法的有效性和可行性. 关键词 :谱聚类 ;模糊 K2harmonic means;初始化敏感 ;聚类中心 中图分类号 : TP311 文献标识码 : A 文章编号 : 167324785 (2009) 0220095205 A spectral cluster ing algor ithm based on fuzzy K2harmon ic means WANG Zhong 1, 2 , L IU Gui2quan 1, 2 , CHEN En2hong 1, 2 (1. School of Computer Science, University of Science and Technology of China, Hefei 230027, China; 2. Key Laboratory of Software in Computing and Communication, Hefei 230027, China) Abstract:Spectral clustering is an effective method that iswidely used in machine learning. After analyzing the es2 sence of initialization sensitivity in spectral clustering, the fuzzy K2harmonic means (FKHM) algorithm was consid2 ered to conquer spectral clustering’s shortcom ings, then an spectral clustering algorithm based on FKHM was de2 veloped. Compared with the traditional spectral algorithm and the fuzzy c2means (FCM) algorithm, the suggested algorithm is more sensitive to initial values. The suggested algorithm can not only identify challenging artificial da2 ta, but also find stable cluster centers and clustering results, considerably imp roving clustering p recision. Experi2 ments showed that it is an effective and feasible way to imp rove the performance of spectral clustering algorithm s. Keywords: spectral clustering; fuzzy K2harmonic means; initialization sensitivity; cluster centers 收稿日期 : 2008212216. 基金项目 :国家自然科学基金资助项目 (60775037) ;教育部新世纪优 秀人才支持计划资助项目 (NCET20520549). 通信作者 :汪 中. E2mail: wzspb@mail. ustc. edu. cn. 聚类分析是数据挖掘、机器学习、模式识别等众 多领域的重要工具. 它在执行过程中没有任何关于 类别的先验知识和假设 ,因而被称作是一种无监督 的学习方法. 近年来产生了大量解决该问题的相关 算法 ,现有的基于产生式模型和基于中心的聚类方 法仅在具有凸形结构的数据上有好的效果 ,且容易 陷入局部最优. 为了能在任意形状的样本结构上聚类 ,且收敛 于全局最优 ,谱聚类算法被广泛应用. 谱聚类的思想 来源于谱图划分 [ 1 ] ,是一种流行的高性能计算方 法. 该方法基于两点间的相似关系 ,利用数据的相似 矩阵的特征向量进行聚类 ,通过特征分解可以获得 聚类判据在放松了的连续域中的全局最优解. 谱聚 类算法适用于非测度空间 ,算法与数据点维数无关 , 而仅与数据点个数有关 ,因而可以避免由特征向量 的过高维数所造成的奇异性问题. 谱聚类算法尽管 在实践中取得了很好的效果 ,但是算法本身仍存在 许多值得研究的问题. 文献 [ 2 ]指出当聚类数目大 于实际聚类数时 ,多路谱聚类方法的效果很差 ; Fischer等提出了依赖于背景的相似性度量方法和尺 度参数问题 [ 3 ] ;由于谱方法的计算复杂度相当高 , Fowlkes等提出使用 Nystrom 逼近方法减少求解特 征问题的计算复杂度 [ 4 ] ;针对谱聚类初始化敏感的 特点 , Ekin等提出使用对初始值不敏感的方法 [ 5 ] . 本文提出一种基于模糊 K2harmonic means的谱 聚类算法 ,其主要思想是 :首先分析不同数据输入顺 序对相似性矩阵、构造矩阵和生成矩阵的影响 ,得出

·96 智能系统学报 第4卷 谱聚类初始化敏感的实质原因,通过引入模糊K~ 知识易知,矩阵A1经过若干次初等行或者列变换 Hamonic means(FKM)算法来解决对初值敏感的 则可以得到矩阵A2,故矩阵A,和A2相似.同理,当 问题,从而得到更稳定的聚类性能.在人工数据和真 以任意顺序输入得到的相似矩阵A,均与A,相似. 实数据上进行实验模拟,结果表明,FKHM-SC算法 由于矩阵D,为对角矩阵,其主对角元素为相似矩 相对于原有谱聚类算法(SC)和传统的Kmeans 阵A的相应各行元素之和,故矩阵D,和D2相似 (KM)算法和fuzzy Cmeans(FQM)算法在聚类性能 因为L1=Di12A,D12,L2=D21PA2D;1n,且 和稳定性上有了显著的提高 D,、D,为对角矩阵,由上面的相似关系可知矩阵L1 1谱聚类算法的初始化敏感分析 和L,相似,其对应的特征向量x经过若干次初等 变换可以得到特征向量,则生成矩阵Y和Y2亦 谱聚类算法将数据聚类看成是一个无向图的多 相似.故结论成立 路划分问题,由于图划分问题的组合本质,求图划分 判据的最优解是一个NP难题[6).一个有效的求解 2 改进的谱聚类算法 方法是考虑问题的连续放松形式,将原有问题转换 通过定理1可知,不同输入顺序得到的相似矩 为求解矩阵的特征值和特征向量问题,利用这些特 阵A和最终的生成矩阵Y是相似的,故谱聚类算法 征向量构造一个简化了的数据空间,在该空间中的 对初始值敏感的实质在于NW算法从特征向量获 数据的分布结构更加明显,代表性算法有Ng等人 得最终的聚类方法是否对初始化敏感.传统的K- 提出的NW算法I四 means和FOM算法对初始中心敏感I1,对于不同的 NW算法本质上是利用相似矩阵的特征向量 初始值,可能得到不同的聚类结果.在此基础上,通 进行聚类,选取构造矩阵的前K个最大特征值所对 过引入对初值不敏感的模糊K-hamonic means算法 应的特征向量,从而在K维空间中构成与原数据一 来克服这一缺点 一对应的表述,进而在K维空间中利用Kmeansi或 21模糊K-hamonic means算法 其他简单算法进行聚类, 模糊K-hamonic means(FKHM)算法I1是一种 现有的各种谱聚类算法的差异之处在于:1)构 基于中心的聚类算法,将模糊概念应用到M算 造的相似矩阵不同;2)使用的特征向量不同;3)从 法中,应用数据点对不同聚类的隶属度对目标函 特征向量获得最终的聚类方法不同;4)从连续变量 数中的距离测度进行模糊加权.设X=x,|i=1, 放松到离散变量的方法不同.NW算法是基于上述 :n}为n个数据点的集合,C=C|广=1,…k好 的第3种多类实现方法给出的一种简单有效方法, 为k个聚类中心的集合,d,=‖X,-C‖表示为数 由于传统的Kmeans?算法对初始值敏感,故NW算 据对象到聚类中心的距离表示,采用欧式距离表示 法对初值敏感是否归结于最终的聚类方法.下面给 其目标函数为 出谱聚类算法对初值敏感的证明 定理1设数据集S={,},以2种不 (1 同顺序输入得到的相似矩阵为A、A2,对角矩阵为 六wd, D1、D2,构造矩阵为L1、L2,生成矩阵为Y、Y,则A 式中:w,∈[0,1]表示数据对象X,对聚类中心C 和A2相似,D1和D2相似,L,和L2相似,Y和Y2 k 相似 的隶属度,且 ∑"g=l,a≥0为模糊算子.隶属度 证 明设以,,顺序输入得到的相 函数和聚类中心更新公式为 0A12…A1 (1/d) (2) 似矩阵A1 A21 0 A3 ,以,虽,…马逆 … … .ve Anl An2 0 X 序输入得到的相似矩阵 54 0 An(n-1) Anl C,= 3) W可 A(n.Un 0 2 由矩阵 wrdsi)2 A2n 算法描述为:初始化聚类中心,通过式(2)和式 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
谱聚类初始化敏感的实质原因 ,通过引入模糊 K2 Harmonic means(FKHM)算法来解决对初值敏感的 问题 ,从而得到更稳定的聚类性能. 在人工数据和真 实数据上进行实验模拟 ,结果表明 , FKHM2SC算法 相对于原有谱聚类算法 ( SC) 和传统的 K2means (KM)算法和 fuzzy C2means(FCM )算法在聚类性能 和稳定性上有了显著的提高. 1 谱聚类算法的初始化敏感分析 谱聚类算法将数据聚类看成是一个无向图的多 路划分问题 ,由于图划分问题的组合本质 ,求图划分 判据的最优解是一个 NP难题 [ 6 ] . 一个有效的求解 方法是考虑问题的连续放松形式 ,将原有问题转换 为求解矩阵的特征值和特征向量问题 ,利用这些特 征向量构造一个简化了的数据空间 ,在该空间中的 数据的分布结构更加明显 ,代表性算法有 Ng等人 提出的 NJW 算法 [ 7 ] . NJW 算法本质上是利用相似矩阵的特征向量 进行聚类 ,选取构造矩阵的前 K个最大特征值所对 应的特征向量 ,从而在 K维空间中构成与原数据一 一对应的表述 ,进而在 K维空间中利用 K2means或 其他简单算法进行聚类. 现有的各种谱聚类算法的差异之处在于 : 1)构 造的相似矩阵不同 ; 2)使用的特征向量不同 ; 3)从 特征向量获得最终的聚类方法不同 ; 4)从连续变量 放松到离散变量的方法不同. NJW 算法是基于上述 的第 3种多类实现方法给出的一种简单有效方法 , 由于传统的 K2means算法对初始值敏感 ,故 NJW 算 法对初值敏感是否归结于最终的聚类方法. 下面给 出谱聚类算法对初值敏感的证明. 定理 1 设数据集 S = { s1 , …, sn } ,以 2种不 同顺序输入得到的相似矩阵为 A1、A2 ,对角矩阵为 D1、D2 ,构造矩阵为 L1、L2 ,生成矩阵为 Y1、Y2 ,则 A1 和 A2 相似 , D1 和 D2 相似 , L1 和 L2 相似 , Y1 和 Y2 相似. 证 明 设以 s1 , s2 , …, sn 顺序输入得到的相 似矩阵 A1 = 0 A12 … A1n A21 0 … A2n … … … … An1 An2 … 0 ,以 s1 , s2 , …, sn逆 序输入得到的相似矩阵 A2 = 0 An ( n - 1) … An1 A ( n - 1) n 0 … A ( n - 1) 1 … … … … A1n A2n … 0 , 由矩阵 知识易知 ,矩阵 A1 经过若干次初等行或者列变换 则可以得到矩阵 A2 ,故矩阵 A1 和 A2 相似. 同理 ,当 以任意顺序输入得到的相似矩阵 A2 均与 A1 相似. 由于矩阵 D1 为对角矩阵 ,其主对角元素为相似矩 阵 A1 的相应各行元素之和 ,故矩阵 D1 和 D2 相似. 因为 L1 =D - 1 /2 1 /A1D - 1 /2 1 , L2 =D - 1 /2 2 A2D - 1 /2 2 ,且 D1、D2 为对角矩阵 ,由上面的相似关系可知矩阵 L1 和 L2 相似 ,其对应的特征向量 x1 经过若干次初等 变换可以得到特征向量 x2 ,则生成矩阵 Y1 和 Y2 亦 相似. 故结论成立. 2 改进的谱聚类算法 通过定理 1可知 ,不同输入顺序得到的相似矩 阵 A和最终的生成矩阵 Y是相似的 ,故谱聚类算法 对初始值敏感的实质在于 NJW 算法从特征向量获 得最终的聚类方法是否对初始化敏感. 传统的 K2 means和 FCM算法对初始中心敏感 [ 5 ] ,对于不同的 初始值 ,可能得到不同的聚类结果. 在此基础上 ,通 过引入对初值不敏感的模糊 K2harmonic means算法 来克服这一缺点. 2. 1 模糊 K2harmonic means算法 模糊 K2harmonic means(FKHM )算法 [ 8 ]是一种 基于中心的聚类算法 ,将模糊概念应用到 KHM 算 法 [ 9 ]中 ,应用数据点对不同聚类的隶属度对目标函 数中的距离测度进行模糊加权. 设 X = { xi | i = 1, …, n} 为 n个数据点的集合 , C = { Cj | j = 1, …, k} 为 k个聚类中心的集合 , di, j = ‖Xi - Cj‖表示为数 据对象到聚类中心的距离表示 ,采用欧式距离表示. 其目标函数为 EFHKM = ∑ n i =1 k ∑ k j=1 1 w α ij d 2 i, j . (1) 式中 : wij ∈ [ 0, 1 ]表示数据对象 Xi 对聚类中心 Cj 的隶属度 ,且 ∑ k j=1 wij = 1,α≥0为 模糊算子. 隶属度 函数和聚类中心更新公式为 wij = (1 / d 2 i, j ) 1 / (α+1) ∑ k z =1 (1 / d 2 i, z ) 1 / (α+1) , (2) Cj = ∑ n i =1 w α ij ∑ k z =1 ( w α ij d 2 i, j w α iz d 2 i, z ) 2 Xi ∑ n i =1 w α ij ∑ k z =1 ( w α ij d 2 i, j w α iz d 2 i, z ) 2 . (3) 算法描述为 :初始化聚类中心 ,通过式 (2)和式 ·96· 智 能 系 统 学 报 第 4卷

第2期 汪中,等:基于模糊K-hamonic means的谱聚类算法 97· (3)分别计算隶属度和聚类中心,然后进行迭代,直 到最大的迭代次数或者目标函数式(1)稳定为止. 3 该算法的时间复杂度为O(mXnX),其中m为数 据属性的个数. 22基于模糊K-hamonic means的谱聚类算法 (FKHM-SC) 由于传统谱聚类算法对初始值敏感,本文在 NW算法的框架下提出基于模糊K-hamonic means 的谱聚类算法,具体实现步骤如下: -3-2-101234 输入:n个数据点S={,s,聚类数目k 输出:数据点集的划分 (a)three circles-joined聚类结果(o-Q05) 步骤: 100 1)构造相似矩阵A∈R",其中A= 80 ep(-‖s-S2/2o2),i≠广Aa=0其中0是参 4r从年 数 60 868 2构造矩阵L=D1PAD12.其中D是对角矩 40 m米wx物 阵对角元素为D,=1, 20 3)采用Nystrom逼近方法I计算L的前k个特 20 40 60 80100 征值所对应的特征向量x,,,x。重复特征值取 其相互正交的特征向量)构造矩阵 (b)1 ine and balls聚类结果(o=1) X=[x为…X)∈t,规范化矩阵X的行向量, 100 得到矩阵Y=Xg/(∑X)n: 4)将矩阵Y的每行当作空间中一点,采用上 80 述对初值不敏感的FKM算法聚为k类,如果k的 60 第行数据为第类,则原数据s划分到第类 40 由于谱聚类初始化敏感的特点,考虑到传统的 Kmeans和FCM算法依赖于初始k个对象的选择; 20 而FKHM算法通过对数据点到聚类中心的调和平 均进行加权,动态加权对初值不敏感起到重要的作 20 40 60 80100 用,故改进算法在理论上能得到更稳定的聚类性能: (c)squiggles聚类结果(o=1) 利用Nystrom逼近方法求解矩阵的特征值和特征向 100 量减少了计算的复杂度 ++++ 3实验 80 60 3.1人工数据 文献[7给出一些有挑战性的人工数据聚类问题 0 图1分别给出了FKIM-SC在4组人工数据集上的聚 20 类结果图,FKM-SC可以成功地识别这4组有聚类数 据问题,同时给出了相应的核参数σ的值. 102030 4050607080 FKM-SC可以成功地识别上面4组数据,利用 多个特征向量构造了一个简化的数据空间,在该空 (d)blobs and circles聚类结果(o=2) 间中的数据的分布结构更加明显,通过每组数据的 图1FKHM-SC在4组人工数据集上的聚类结果图 特征向量图可以直观地观察数据的分布」 Fig 1 Cluster results of FKHM-SC on four artificial data sets 1994-2009 China Academie Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
(3)分别计算隶属度和聚类中心 ,然后进行迭代 ,直 到最大的迭代次数或者目标函数式 ( 1)稳定为止. 该算法的时间复杂度为 O (m ×n ×k) ,其中 m 为数 据属性的个数. 2. 2 基于模糊 K2harmonic means的谱聚类算法 (FKHM2SC) 由于传统谱聚类算法对初始值敏感 ,本文在 NJW 算法的框架下提出基于模糊 K2harmonic means 的谱聚类算法 ,具体实现步骤如下 : 输入 : n个数据点 S = { s1 , …, sn },聚类数目 k 输出 :数据点集的划分 步骤 : 1) 构 造 相 似 矩 阵 A ∈ R n ×n , 其 中 Aij = exp ( - ‖si - sj‖ 2 /2σ2 ) , i ≠ j, Aii = 0. 其中 σ是参 数; 2)构造矩阵 L =D - 1 /2 AD - 1 /2 . 其中 D 是对角矩 阵 ,对角元素为 Dii = ∑ n j=1 Aij ; 3)采用 Nystrom逼近方法 [ 4 ]计算 L 的前 k个特 征值所对应的特征向量 x1 , x2 , …, xn (重复特征值取 其 相 互 正 交 的 特 征 向 量 ) 构 造 矩 阵 X = [ x1 x2 … xn ] ∈R n×k ,规范化矩阵 X的行向量 , 得到矩阵 Y =Xij / ( ∑j X 2 ij ) 1 /2 ; 4)将矩阵 Y的每行当作 R k空间中一点 ,采用上 述对初值不敏感的 FKHM算法聚为 k类 ,如果 k的 第 i行数据为第 j类 ,则原数据 si 划分到第 j类. 由于谱聚类初始化敏感的特点 ,考虑到传统的 K2means和 FCM算法依赖于初始 k个对象的选择 ; 而 FKHM算法通过对数据点到聚类中心的调和平 均进行加权 ,动态加权对初值不敏感起到重要的作 用 ,故改进算法在理论上能得到更稳定的聚类性能. 利用 Nystrom逼近方法求解矩阵的特征值和特征向 量减少了计算的复杂度. 3 实 验 3. 1 人工数据 文献 [7 ]给出一些有挑战性的人工数据聚类问题. 图 1分别给出了 FKHM2SC在 4组人工数据集上的聚 类结果图 , FKHM2SC可以成功地识别这 4组有聚类数 据问题 ,同时给出了相应的核参数σ的值. FKHM2SC可以成功地识别上面 4组数据 ,利用 多个特征向量构造了一个简化的数据空间 ,在该空 间中的数据的分布结构更加明显 ,通过每组数据的 特征向量图可以直观地观察数据的分布. ( a) three circles2joined聚类结果 (σ = 0. 05 ) ( b) line and balls聚类结果 (σ = 1) ( c) squiggles聚类结果 (σ = 1) ( d) blobs and circles聚类结果 (σ = 2) 图 1 FKHM2SC在 4组人工数据集上的聚类结果图 Fig. 1 Cluster results of FKHM2SC on four artificial data sets 第 2期 汪 中 ,等 :基于模糊 K2harmonic means的谱聚类算法 ·97·
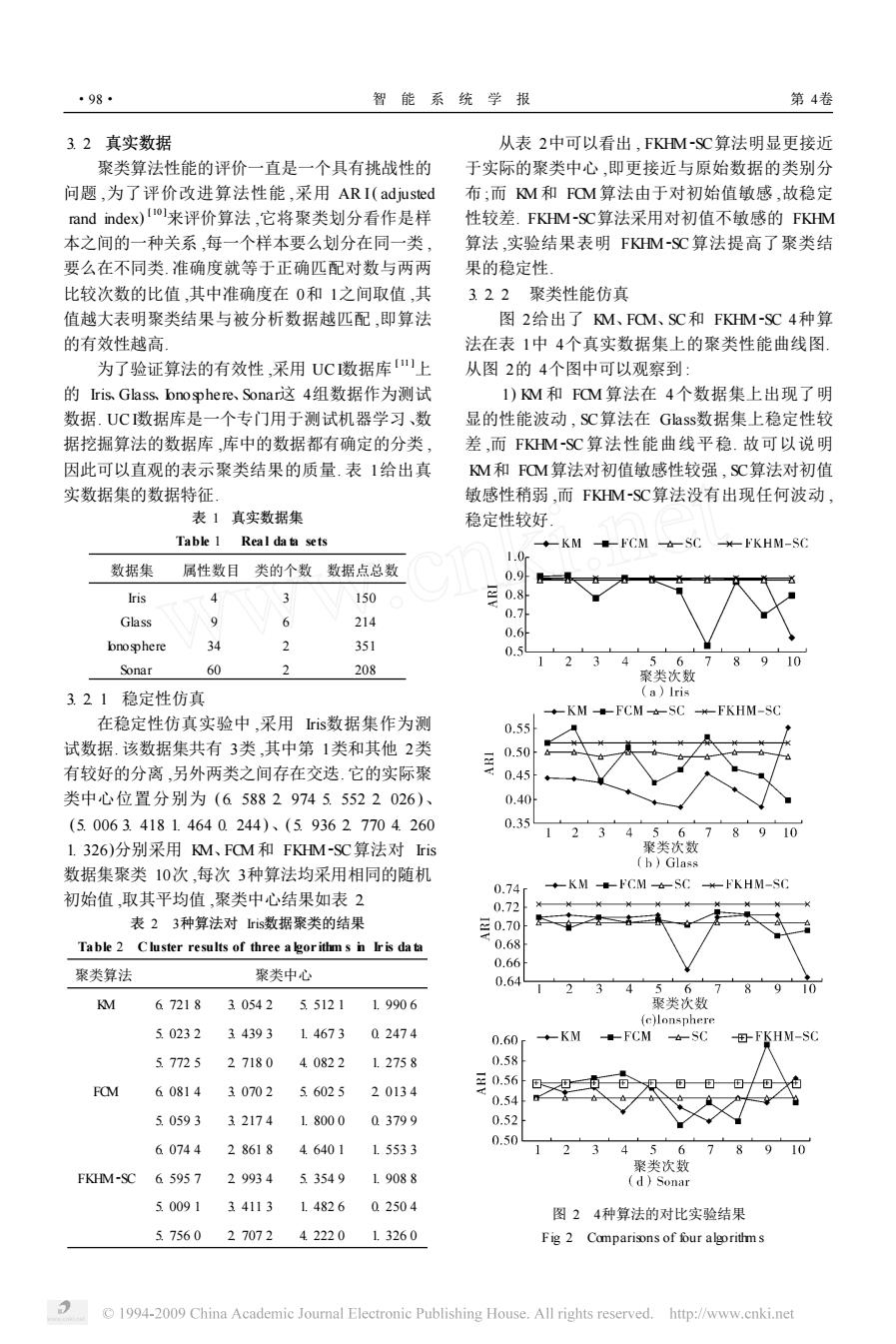
·98* 智能系统学报 第4卷 3.2真实数据 从表2中可以看出,FKM-SC算法明显更接近 聚类算法性能的评价一直是一个具有挑战性的 于实际的聚类中心,即更接近与原始数据的类别分 问题,为了评价改进算法性能,采用ARI(adjusted 布;而M和FQM算法由于对初始值敏感,故稳定 rand index)iol来评价算法,它将聚类划分看作是样 性较差.FKHM-SC算法采用对初值不敏感的FKHM 本之间的一种关系,每一个样本要么划分在同一类, 算法,实验结果表明FIM-SC算法提高了聚类结 要么在不同类.准确度就等于正确匹配对数与两两 果的稳定性。 比较次数的比值,其中准确度在0和1之间取值,其 322聚类性能仿真 值越大表明聚类结果与被分析数据越匹配,即算法 图2给出了M、FQM、SC和FKHM-SC4种算 的有效性越高】 法在表1中4个真实数据集上的聚类性能曲线图, 为了验证算法的有效性,采用UC数据库1上 从图2的4个图中可以观察到: 的ris.Gass、bnosphere.Sonari这4组数据作为测试 1)M和FQM算法在4个数据集上出现了明 数据.UC数据库是一个专门用于测试机器学习、数 显的性能波动,SC算法在Glass数据集上稳定性较 据挖掘算法的数据库,库中的数据都有确定的分类, 差,而FKM-SC算法性能曲线平稳.故可以说明 因此可以直观的表示聚类结果的质量.表1给出真 M和FOM算法对初值敏感性较强,SC算法对初值 实数据集的数据特征」 敏感性稍弱,而FIHM-SC算法没有出现任何波动, 表1真实数据集 稳定性较好 Table 1 Real data sets ◆-KM■-CM-SC-'KHM-SC 1.0r 数据集 属性数目类的个数数据点总数 0.9外 Iris 4 3 150 三0.8 Glass 9 6 0.7 214 0.6 bnosphere 34 2 351 0.5 1 4 56 Sonar 60 2 208 聚类次数 3.21稳定性仿真 (a)lris ◆KM--FCM-SCW-FKHM-SC 在稳定性仿真实验中,采用is数据集作为测 0.55 试数据.该数据集共有3类,其中第1类和其他2类 0.50 有较好的分离,另外两类之间存在交迭.它的实际聚 0.45 类中心位置分别为(6588297455522026)、 0.40 (5.0063.41814640244)、(5.93627704260 0.35 5 6 8 10 1.326)分别采用M、FQM和FKHM-SC算法对ris 聚类次数 (h)Glass 数据集聚类10次,每次3种算法均采用相同的随机 0.74 ◆KM■-FCM女-SC#kKHM-SG 初始值,取其平均值,聚类中心结果如表2 0.72 表23种算法对is数据聚类的结果 三0.70 Table 2 Cluster results of three a lgorithm s n Ir is da ta 0.68 0.66 聚类算法 聚类中心 0.64 6 M 67218 30542 5.5121 1.9906 聚类次数 (c)lonsphere 50232 34393 1.4673 02474 0.60 ◆-KM ■-FCM SC -FKHM-SC 57725 27180 40822 1.2758 0.58 FOM 60814 30702 5.6025 20134 年056 0.54 50593 321741.8000 03799 0.52 0.50 60744 28618 46401 1.5533 4 5 6 7 8 910 聚类次数 FKHM-SC 65957 2993453549 1.9088 (d)Sonar 50091341131.482602504 图24种算法的对比实验结果 5.756027072 42220 1.3260 Fig 2 Comparisons of four algorithms 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
3. 2 真实数据 聚类算法性能的评价一直是一个具有挑战性的 问题 ,为了评价改进算法性能 ,采用 AR I( adjusted rand index) [ 10 ]来评价算法 ,它将聚类划分看作是样 本之间的一种关系 ,每一个样本要么划分在同一类 , 要么在不同类. 准确度就等于正确匹配对数与两两 比较次数的比值 ,其中准确度在 0和 1之间取值 ,其 值越大表明聚类结果与被分析数据越匹配 ,即算法 的有效性越高. 为了验证算法的有效性 ,采用 UC I数据库 [ 11 ]上 的 Iris、Glass、Ionosphere、Sonar这 4组数据作为测试 数据. UC I数据库是一个专门用于测试机器学习、数 据挖掘算法的数据库 ,库中的数据都有确定的分类 , 因此可以直观的表示聚类结果的质量. 表 1给出真 实数据集的数据特征. 表 1 真实数据集 Table 1 Rea l da ta sets 数据集 属性数目 类的个数 数据点总数 Iris 4 3 150 Glass 9 6 214 Ionosphere 34 2 351 Sonar 60 2 208 3. 2. 1 稳定性仿真 在稳定性仿真实验中 ,采用 Iris数据集作为测 试数据. 该数据集共有 3类 ,其中第 1类和其他 2类 有较好的分离 ,另外两类之间存在交迭. 它的实际聚 类中心位置分别为 ( 6. 588 2. 974 5. 552 2. 026 )、 (5. 006 3. 418 1. 464 0. 244 )、( 5. 936 2. 770 4. 260 1. 326)分别采用 KM、FCM和 FKHM2SC算法对 Iris 数据集聚类 10次 ,每次 3种算法均采用相同的随机 初始值 ,取其平均值 ,聚类中心结果如表 2. 表 2 3种算法对 Iris数据聚类的结果 Table 2 C luster results of three a lgor ithm s in Ir is da ta 聚类算法 聚类中心 KM 6. 721 8 3. 054 2 5. 512 1 1. 990 6 5. 023 2 3. 439 3 1. 467 3 0. 247 4 5. 772 5 2. 718 0 4. 082 2 1. 275 8 FCM 6. 081 4 3. 070 2 5. 602 5 2. 013 4 5. 059 3 3. 217 4 1. 800 0 0. 379 9 6. 074 4 2. 861 8 4. 640 1 1. 553 3 FKHM2SC 6. 595 7 2. 993 4 5. 354 9 1. 908 8 5. 009 1 3. 411 3 1. 482 6 0. 250 4 5. 756 0 2. 707 2 4. 222 0 1. 326 0 从表 2中可以看出 , FKHM2SC算法明显更接近 于实际的聚类中心 ,即更接近与原始数据的类别分 布 ;而 KM 和 FCM算法由于对初始值敏感 ,故稳定 性较差. FKHM2SC算法采用对初值不敏感的 FKHM 算法 ,实验结果表明 FKHM2SC算法提高了聚类结 果的稳定性. 3. 2. 2 聚类性能仿真 图 2给出了 KM、FCM、SC和 FKHM2SC 4种算 法在表 1中 4个真实数据集上的聚类性能曲线图. 从图 2的 4个图中可以观察到 : 1) KM 和 FCM 算法在 4个数据集上出现了明 显的性能波动 , SC算法在 Glass数据集上稳定性较 差 ,而 FKHM2SC算法性能曲线平稳. 故可以说明 KM和 FCM算法对初值敏感性较强 , SC算法对初值 敏感性稍弱 ,而 FKHM2SC算法没有出现任何波动 , 稳定性较好. 图 2 4种算法的对比实验结果 Fig. 2 Comparisons of four algorithm s ·98· 智 能 系 统 学 报 第 4卷

第2期 汪中,等:基于模糊K-hamonic means的谱聚类算法 ·99. 2)在4个数据集上,FKHM-SC算法相对于M [7]NG A Y,JORDAN M L,WEISS Y.On spectral clustering 和SC算法在聚类精确度上有显著的提高,且稳定 analysis and an algprithm [C]//Advances in Neural Infr 性较高,即平均聚类性能优于M和C算法,而在 mation Pocessing Systems Cambridge:MI Press,2002: Glass和Sonar数据集上,虽然FQM算法的个别精确 897-856 度高于FKM-SC算法,但是从图中可以看到,FQM [8赵恒,杨万海,张高煜.模糊K-Hamonic Means聚类算 法[J1西安电子科技大学学报,2005,32(4):603606 算法波动性较大,总体平均性能仍然低于FM-SC ZHAO Heng,YANG Wanhai,ZHANG Gaoyu Fuzzy K- 算法.这说明,FHM-SC算法不仅稳定性较好,并且 hamonic means clustering algorithm [J ]Joumal of XDian 取得更高的聚类精确度 University,2005,32(4):603-606 4结束语 [9 ]ZHANG B,HSU M,DA YAL U.K-hamonic means-a data clustering algprithm EB /OL ]2006-01-12 ]htp://hpc 通过分析传统谱聚类算法的对初值敏感的实 isti cnr it/~pameri/datam /articles/HPL-1999-124 pdf 质,提出一种基于FKHM的谱聚类算法(FKHM [10 HANDL J,KNOWLES J.An evolutionary app roach SC).实验表明,FKHM-SC算法在人工数据和真实 multi-objective clustering[J].IEEE Transactons on Evo- 数据上均取得较好的结果.相对于传统的K-means. lutionary Computation,2007,11(1):56-76 FQM和谱聚类算法,该算法不仅具有较高的稳定 作者简介: 汪中,男,1984年生,硕士研究 性,且获得的聚类中心与实际聚类中心更为接近,从 生,主要研究方向为数据挖据、机器学 而聚类性能有了显著的提高.下一步工作将算法应 习. 用到实际问题中 参考文献: [1 ]F IEDLER M A lgebraic connectivity of graphs[M ]Praha: Czechosbovak Mathematical Joumal.1973:298-305 2 ]V ERMA D,MELA M.A comparison of spectral clustering 刘贵全,男,1970年生,副教授,博 algorithm s[R ]University ofW ashingion,2003. 士,主要研究方向为数据挖掘、人工智 [3]F ISCHER L POLAND J.Amp lifying the bbck matrix struc- 能、网络安全等.2003年获安徽省科技 ture for spectral clustering C ]//Proceedings of the 14th 成果三等奖.发表学术论文50余篇. Annual Machine Conference of Belgium and the Nether lands Manno,Switzerland,2005:21-28 [4]FOWLKES C,BELONGIE S,CHUNG F,et al Spectral grouping using the Nystromn method [J].EEE Transactions 陈恩红,男,1968年生,教授,博士 on Pattem Analysis and Machine Intelligence,2007,26 生导师,主要研究方向为数据挖掘与机 (2):217-225 器学习、网络信息处理等.1995年获中 [5]EKN A,PANKANTI S,HAMPAPUR A.Initialization-in- 国科学院院长奖学金优秀奖,1996年获 dependent spectral clustering with applicatons to automatic 中国科学技术大学惠普信息科学青年 video analysis[C]//Proc of IEEE KCASSP.Montreal,Can- 教师奖,2000年获王宽诚有才奖、安徽 ada2004:641-644 省科技进步二等奖,2004年获安徽省科技进步三等奖、中国 [6 ]SH IJ B,MAL IK J.Nomalized cuts and mage segmnentation 科技大学优秀教学成果二等奖,2006年获王宽诚育才奖一 [J ]IEEE Transactions on Pattem Analysis and Machine 等奖.发表学术论文90余篇. Intelligence,2000,22(8):888-905. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
2)在 4个数据集上 , FKHM2SC算法相对于 KM 和 SC算法在聚类精确度上有显著的提高 ,且稳定 性较高 ,即平均聚类性能优于 KM 和 SC算法 ,而在 Glass和 Sonar数据集上 ,虽然 FCM算法的个别精确 度高于 FKHM2SC算法 ,但是从图中可以看到 , FCM 算法波动性较大 ,总体平均性能仍然低于 FKHM2SC 算法. 这说明 , FKHM2SC算法不仅稳定性较好 ,并且 取得更高的聚类精确度. 4 结束语 通过分析传统谱聚类算法的对初值敏感的实 质 ,提出一种基于 FKHM 的谱聚类算法 ( FKHM2 SC). 实验表明 , FKHM2SC算法在人工数据和真实 数据上均取得较好的结果. 相对于传统的 K2means、 FCM和谱聚类算法 ,该算法不仅具有较高的稳定 性 ,且获得的聚类中心与实际聚类中心更为接近 ,从 而聚类性能有了显著的提高. 下一步工作将算法应 用到实际问题中. 参考文献 : [ 1 ] F IEDLER M. A lgebraic connectivity of graphs[M ]. Praha: Czechoslovak Mathematical Journal, 1973: 2982305. [ 2 ]VERMA D, MEILA M. A comparison of spectral clustering algorithm s[R ]. University ofW ashington, 2003. [ 3 ] F ISCHER I, POLAND J. Amp lifying the block matrix struc2 ture for spectral clustering [ C ] / /Proceedings of the 14 th Annual Machine Conference of Belgium and the Nether2 lands. Manno, Switzerland, 2005: 21228. [ 4 ] FOWLKES C, BELONGIE S, CHUNG F, et al. Spectral group ing using the Nystro¨m method [J ]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 26 (2) : 2172225. [ 5 ] EKIN A, PANKANTI S, HAMPAPUR A. Initialization2in2 dependent spectral clustering with app lications to automatic video analysis[C ] / /Proc of IEEE ICASSP. Montreal, Can2 ada, 2004: 6412644. [ 6 ] SH IJ B,MAL IK J. Normalized cuts and image segmentation [J ]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22 (8) : 8882905. [ 7 ]NG A Y, JORDAN M L, W EISS Y. On spectral clustering: analysis and an algorithm [ C ] / /Advances in Neural Infor2 mation Processing System s. Cambridge: M IT Press, 2002: 8972856. [ 8 ]赵 恒 ,杨万海 ,张高煜. 模糊 K2Harmonic Means聚类算 法 [J ]. 西安电子科技大学学报 , 2005, 32 (4) : 6032606. ZHAO Heng, YANG W anhai, ZHANG Gaoyu. Fuzzy K2 harmonic means clustering algorithm [J ]. Journal of XiD ian University, 2005, 32 (4) : 6032606. [ 9 ] ZHANG B, HSU M,DAYAL U. K2harmonic means—a data clustering algorithm [ EB /OL ]. [ 2006201212 ]. http: / /hpc. isti. cnr. it/~palmeri/datam /articles/HPL219992124. pdf. [ 10 ] HANDL J, KNOWLES J. An evolutionary app roach to multi2objective clustering[J ]. IEEE Transactions on Evo2 lutionary Computation, 2007, 11 (1) : 56276. 作者简介 : 汪 中 ,男 , 1984年生 ,硕士研究 生 ,主要研究方向为数据挖掘、机器学 习. 刘贵全 ,男 , 1970年生 ,副教授 ,博 士 ,主要研究方向为数据挖掘、人工智 能、网络安全等. 2003年获安徽省科技 成果三等奖. 发表学术论文 50余篇. 陈恩红 ,男 , 1968年生 ,教授 ,博士 生导师 ,主要研究方向为数据挖掘与机 器学习、网络信息处理等. 1995年获中 国科学院院长奖学金优秀奖 , 1996年获 中国科学技术大学惠普信息科学青年 99· 教师奖 , 2000年获王宽诚育才奖、安徽 省科技进步二等奖 , 2004年获安徽省科技进步三等奖、中国 科技大学优秀教学成果二等奖 , 2006年获王宽诚育才奖一 等奖. 发表学术论文 90余篇. 第 2期 汪 中 ,等 :基于模糊 K2harmonic means的谱聚类算法 ·