
第3卷第6期 智能系统学报 Vol.3 No.6 2008年12月 CAAI Transactions on Intelligent Systems Dec.2008 基于灰度互信息和梯度相似性的 医学图像配准及其加速处理 陈伟卿,李冠华1,欧宗瑛,韩军2 (1.大连理工大学CAD&CG研究所,过宁大连116024;2.大连现代高技术公司,过宁大连116021) 摘要:研究基于归一化互信息的医学图像刚性配准算法,提出改进配准速度和改善配准精度的相应措施.配准处 理包含3项主要计算处理,即空间变换、互信息计算以及优化搜索.针对不同计算处理分别研究了相应加速策略,提 高其计算速度,实现三维体数据的快速配准.并且,针对传统基于互信息测度配准方法未利用图像灰度空间分布信 息,提出将灰度变化梯度相似性与互信息相结合的配准方法,从而进一步提高了配准算法的精度和鲁棒性.实验结 果表明了算法的有效性。 关键词:医学图像配准;互信息:加速方法;梯度相似性 中图分类号:TP791.4文献标识码:A文章编号:1673-4785(2008)06049806 Medical image registration based on grey mutual information and gradient similarity with an accelerated processing method CHEN Wei-qing,LI Guan-hua',OU Zong-ying',HAN Jun2 (1.CAD CG Lab.,Dalian University of Technology,Dalian 116024,China;2.Dalian Modern High-Tech Development Co.,Ltd., Dalian 116021,China) Abstract:This paper presents new methods that have been developed for rigid registration of medical images.These methods are based on normalized mutual information and improve registration speed and precision.The whole regis- tration process includes three main steps:space transformation,mutual information calculation,and optimal search.Some acceleration strategies for fast registration of 3D volume data were investigated.Conventional registra- tion approaches,based on mutual information,neglect the spatial distribution information of images.In view of this drawback,a new method was developed,combining data based on gradient similarity and mutual information.This improves the precision and robustness of the registration algorithm.Experimental results proved the validity of the proposed methods. Keywords:medical image registration;mutual information;acceleration solutions;gradient similarity 各种医学影像设备如计算机断层成像(compu-图像的对应点位置一致,以使两者融合后能够准确 ted tomography,CT)、核磁共振成像(magnetic reso- 地表达相应组织结构.因此,高效、高质量的配准处 nance imaging,MRI)等已在临床治疗中得到广泛应 理是现代医疗图像处理系统的一个重要组成部分. 用,它们依据不同成像原理所提供的图像信息具有 近年来,基于互信息(mutual information,MI)的 互补性,通过信息融合可为临床诊断和治疗带来更 配准方法由于不需要待配准图像的其他有关先验知 加丰富的解剖和功能信息.但在实际应用中遇到的 识,无需人工干预,而且适合多模态医学图像配准, 一个重要问题是多模态医学图像之间的配准问题, 算法具有鲁棒性好、配准精度高等优点,因此得到了 也即是如何通过空间变换使两幅不同成像原理所得 广泛重视.基于互信息的配准方法最早由Wlls 收稿日期:2008-07-02. 等11和Maes等21分别提出,随后得到了广大学者 基金项目:国家863计划资助项目(863-306-ZD13-03-6). 的研究改进,其中Studholme等31提出以归一化互 通信作者:陈伟卿.E-mail:cwqcpx_chen@163.com 信息值作为配准相似度准则,使得配准算法更加具

第6期 陈伟卿,等:基于灰度互信息和梯度相似性的医学图像配准及其加速处理 ·499· 有鲁棒性.然而这种配准方法当前还存在两方面不 示为 足,一是配准速度较慢,特别是当应用于三维图像配 Ismn(A,B)=H(A)+H(B) (4) 准时,由于三维数据包含体素个数巨大,对空间变换 H(A,B) 和互信息计算都带来较大的计算强度;二是仅直接 本文将采用公式(4)所确定的归一化互信息值作为 利用两图像灰度之间的互信息相关性进行配准,其 配准算法的相似度准则。 配准精度有时不够高,特别是当重叠区域较小时,应 基于互信息的配准方法可以视为一个寻优过 考虑增加配准特征.因此,本文针对这两点不足提出 程,其基本思想为通过寻找一组空间变换参数,使得 相应改进,首先采用一系列优化措施改进三维体数 其中一幅图像经过空间变换后与另一幅图像达到空 据的配准速度,然后在互信息计算中引入梯度相关 间一致,此时互信息值达到最大,数学表达为 信息,进一步提高配准算法的精度 T=arg max/(A,T(B)) (5) 1 互信息测度 上式含义表示首先对浮动图像B进行空间变换 T(B),然后计算参考图像A和变换后图像T(B)之 互信息是信息学中的一个重要概念,用来描述 间的归一化互信息值IN,通过优化算法寻找变换 两个系统之间的统计相关性,或一个系统中包含另 矩阵T使得此时的互信息值INw(A,T(B))达到最 一个系统的信息的多少,一般用熵来表示.对于待配 大,也即实现了配准图像A和B的目的. 准的两幅离散图像A和B,其单独熵和联合熵可分 别表示为 2配准算法的加速策略 H(A)=-∑p(a)lbp(a), (1) 基于互信息的配准方法是一个耗时的计算过 sEA 程,尤其对于三维图像的配准,由于数据量较大导致 H(A,B)=-∑∑p(a,b)lbp(a,b). (2) 配准速度很慢,不能适应实际应用的要求.本文对配 其中:P(A)表示图像A的灰度值概率分布,P(A,B) 准过程进行研究,将其分为3个主要计算部分.第1 表示图像A和B的联合概率分布.由公式(1)可知, 部分是浮动图像的空间变换,包括绕3个坐标轴的 熵H(A)反映了图像A中包含信息量的多少,当图 旋转和沿3个坐标轴的平移共6个参数,这也是互 像A中所有体素的灰度值几乎相同时,图像包含了 信息计算过程中耗时最多的一个步骤.第2部分为 较少信息,其直方图分布具有陡峭尖峰,熵值较小; 基于熵的互信息计算,第3部分是优化过程,寻找最 而当图像包含不同数量的多种灰度值时,则反映了 优的空间变换参数.本文分别对3个部分进行分析, 较多信息,其直方图均匀散布,此时熵值较大.由公 并提出相应加速措施 式(2)可知联合熵H(A,B)反映了图像A和B的联 2.1加速空间变换 合直方图的散布状态.同一组织在图像A中形成一 三维图像的刚性空间变换通过矩阵相乘实现,包 个灰度值相近的区域,在图像B中也会形成一个灰 括绕3个坐标的旋转矩阵R,R,和R,以及沿3个坐 度值近似的区域。虽然两幅图像中的灰度值大小并 标轴的平移矩阵T·对于离散图像,每个体素位置 不相同,但当A和B完全配准时,该区域相互重叠, 乘以空间变换矩阵后被变换到新的位置,往往与原有 对应位置的体素灰度值在联合直方图中将形成一个 采样点不相互重合,因此需要进行插值重采样得到新 束状分布,此时联合熵H(A,B)的值较小;而当A和 位置的体素值.三线性插值是经常被采用的插值方 B的对齐度差时,联合直方图将会呈现更加散布的 法,能满足亚像素级的配准要求.本文主要采用3种 状态,联合熵H(A,B)的值也会增大 方法加速空间变换和三线性插值计算过程, 互信息I(A,B)在熵及联合熵的基础上发展而 矩阵相乘是一个相对复杂的数学运算,体数据 来,可以表示为 执行空间变换时,如果对每个体素均执行一次矩阵 I(A.B)=H(A)-H(AI B= 相乘,则将消耗大量的CPU计算能力.由于在刚性 (A)+(B)-(A.B). (3) 变换时,各体素之间的相对位置关系保持不变;因此 式(3)表示图像B中包含图像A的信息量.当两幅 当一个体素点进行空间变换后,其余体素的变换后 图像完全配准时,一幅图像包含另一幅图像的信息 位置可以根据他们之间的相对位置关系来确定,而 量最大,互信息值I(A,B)达到最大.Studholme等3 不必重新乘以变换矩阵,以图1所示的二维刚性变 所提出的归一化互信息(normalized mutual informa- 换为例,A点坐标乘以空间变换矩阵后被变换到 ion,NMI)计算方法对公式(3)进行了相应改进,表 A'(x,y)点位置,B点相对A点的位置为(i,),则

·500· 智能系统学报 第3卷 变换后位置B点的坐标可以表示为 配准速度的提高并无太大贡献. g=x+icos 0-jsin 0, 文献[7-8]中提出,统计联合直方图时所采用的 yw=y isin 0 +jcos 0. 灰度级数对最终配准精度会产生不同程度的影响. 当采用全额的256个灰度级数计算互信息值时,会 其中θ为空间变换的旋转角度.通过相对位置关系 造成最优配准位置的摆动,级数太少又使得图像过 确定其余体素点的变换位置能够简化计算复杂度, 于平滑而转移了配准位置.他们最终提出采用64个 提高空间变换的速度, 灰度级数作为两者的折中,即将待配准两幅图像的 灰度范围从[0,255]缩减到[0,63].本文采用了该 思想将灰度级数缩威为64,这样保证配准精度的同 时也提高了互信息计算的速度。 2.3加速优化过程 基于互信息的配准算法可以视为一个寻优过 程,搜寻最优空间变换参数使两幅图像之间的互信 息值达到最大,因此,优化方法的选择对配准速度和 配准精度都有较大影响.全局搜索方法如模拟退火、 图1二维变换的相对坐标计算 Fig.1 Relative coordinates in 2-D transformation 遗传算法等能够找出全局最优解,但速度很慢;具有 寻优能力较强、收敛速度较快的Powell搜索方法, 亚采样是提高空间变换效率的另一个重要方 该方法在相互正交的方向依次对变换参数进行优 法,已经被广泛采用,文献[45]研究了不同亚采样 化,在每个方向上采用Brent一维搜索方法.该方法 方法对最终配准结果的影响.秦斌杰等6]利用该方 的主要缺点是易受局部极值的影响,得到错误的配 法提出了加速的配准系统设计.亚采样方法降低了 准结果.本文采用粗配准和精配准相结合的方法来 图像分辨率,减小参与运算的体素个数,因此能够较 改进Powell方法,在获得较快配准速度的同时也保 大幅度地提高空间变换速度.但是,亚采样方法在提 证配准精度. 高配准速度的同时也因为降低了图像分辨率而导致 Powell搜索方法的初始值选择是决定搜索结果 配准精度的下降;因此,需要综合考虑配准精度和速 的一个关键因素,当初始值位于最优值附近时,搜索 度两者的相互关系,确定合理的采样系数 方法将很快收敛于该最优值,而当初始值远离最优 由于当前多核处理器的普及,可以采用多线程 值时,则搜索方法很可能会收敛于局部最优值.因此 并行计算的方法加速空间变换和三线性插值过程, 本文首先根据待配准两幅图像的质心进行粗配准, 以充分发挥CPU的计算性能.本文采用双核处理 并将配准结果作为Powell方法的初始值进一步进 器,当执行空间变换时将浮动图像分为2个部分,分 行精确搜索,这样能够加快Powell搜索方法的收敛 别在2个线程中并行运算,包括位置变换和三线性 速度,也能保证搜索得到最优解,设体素灰度值表示 插值,最后再将两个线程的运算结果合并为一个完 为f代x,y,z),(x,y,z)为该体素在体数据中的位置坐 整的体数据,计算与参考图像之间的互信息值.根据 标,则体数据的质心(g.,B,g:)可以通过式(6)计算 本文测试,双线程并行计算能够将空间变换的效率 获得: 提高将近一倍.而且随着当前处理器的发展,三核、 m=∑yf代x,y,), 四核、八核甚至更多核的处理器将越来越普及,因此 Tm100 moio mool 采用并行计算的方法提高空间变换的运行效率将成 gx 8,= ,g:= (6) m0oo mooo m000 为加速配准过程的一个有效方法 分别计算两幅图像的质心,然后将两个质心对 2.2加速互信息计算 齐,则可以求得粗配准结果.因为受图像噪声、数据 浮动图像经空间变换后,需进一步计算与参考 不完备等影响,对齐质心得到的配准结果是不准确 图像之间的互信息值.计算方法为首先统计两幅图 的,是一个粗略的估计值,但该值是接近于最优值 像之间的联合直方图,并根据联合直方图计算边缘 的;因此可以将其作为Powell搜索的初始值,进一 熵和联合熵,最后根据式(4)计算归一化互信息值. 步进行精确搜索。 根据测试,该计算过程所消耗的时间约是空间变换 2.4配准算法流程 所消耗时间的15%,因此该过程的加速计算对最终 综合以上3个方面的加速内容,可以将整个算

第6期 陈伟卿,等:基于灰度互信息和梯度相似性的医学图像配准及其加速处理 ·501· 法流程表示为图2所示的结构.首先对数据进行亚 织在不同模态图像中具有不同的灰度值,对应点的 采样,降低图像分辨率,然后进行粗配准获取初始配 梯度矢量将会指向相同或相反的方向;因此,当两个 准参数.根据初始配准参数对浮动图像进行加速的 梯度矢量之间的夹角为0或π时,均认为它们的方 空间变换和三线性插值,该过程通过双线程执行,然 向相似,为此,引入下面的函数计算对应点对的方向 后统计变换后浮动图像与参考图像之间的联合直方 相似性: 图并计算互信息值.再由Powell优化方法对空间变 (&y)= cos(2ax,)+1 换参数进行调整并判断是否达到最优配准,是则终 2 止循环输出参数,否则按照调整后的空间变换参数 该函数的走势如图3所示. 重新进行计算, 对数据进行亚采样 逃行粗配准获收初始配准参数 加速浮动图像空间变换和三线性插值 图3方向标目相似性函数 Fig.3 Function for gradient directions similarity 统计联合直方图及万.信息值计算 将点对的梯度模值的比值作为该点对的模值相 Powellf优化、调整空问变换参数 似性测度: 6w三 min(I gradx l,I gradyl) N 是否满足 m1gFad,igad,,mar1 grad1,lgad1)≠0, 获取新变换参数 配准要求 max(I gradx1,I grady 1)=a 输出结果 3.2梯度相似性与互信息结合的联合配准测度 图2加速配准算法流程 分别计算待配准图像A和B各对应点对的梯度相 Fig.2 Flowchart of accelerating method for registration 似性,则两幅图像的整体梯度相似性S可表示为 3 结合梯度相似性的互信息方法 S(A,B)=,∑w(a)gy, (s)E(AnB) 由于空间梯度信息也是图像配准时的一个重要 结合归一化互信息计算公式(4),可以得到具有梯 相似特征,而互信息计算并没有考虑这些特征的作 度相似性权重的互信息(gradient similarity mutual 用;因此文献[9-10]在互信息配准算法中引入了梯 information,GSMI)测度,其值为 度、共生矩阵等信息,使得互信息配准的精度和鲁棒 IcsMI =S(A,B)INAL(A,B). 性得到了提高.本文进一步对其进行研究,将两幅图 以GSMI作为配准算法的相似性测度,结合了 像所有对应点的梯度经过组合生成一个梯度相似性 梯度信息和互信息的优点,梯度信息能够有效标识 系数,该系数与互信息相乘作为最终的配准测度. 图像中不同组织之间的边缘特征.对于多模态图像 3.1梯度相似性 配准,尽管不同成像模式会将同一组织成像为不同 图像每个像素点处的梯度包括两方面的信息: 的灰度值,但该器官的边界是确定的,不因成像模式 梯度方向和梯度模值.给定参考图像A中一点x,其 不同而有明显变化,梯度相似性正是对该边界特征 在浮动图像B中的对应点为y,则这组对应点对 的标识.而互信息是一种统计相关性,反映了同一组 (x,y)之间的梯度相似性也包括两方面的内容:方 织在两幅图像中所形成的像素对的重叠情况.因此, 向相似性和模值相似性. 将互信息与梯度信息相结合作为配准测度,将会使 设x点与y点的梯度矢量分别记为gradx和 配准算法更加鲁棒。 grady,则两者之间的夹角可表示为 4实验 gradx·grady =arccos grad gradyl 4.1加速三维配准 其中!·表示模值.由于不同成像技术导致同一组 首先利用第2节所述的加速方法对三维体数据
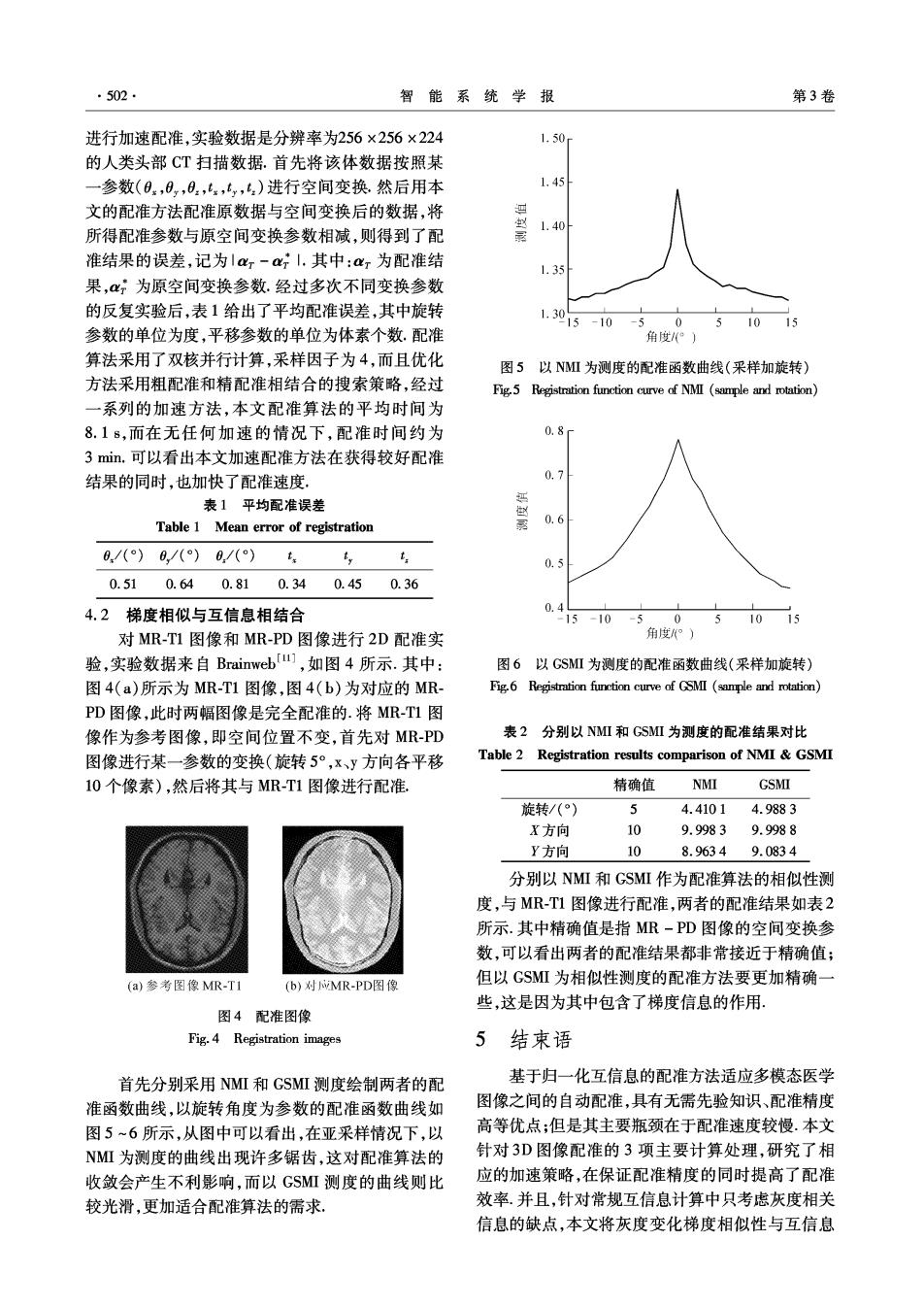
·502. 智能系统学报 第3卷 进行加速配准,实验数据是分辨率为256×256×224 1.50 的人类头部CT扫描数据.首先将该体数据按照某 一参数(0,0,0,,‘,)进行空间变换,然后用本 1.45 文的配准方法配准原数据与空间变换后的数据,将 1.40 所得配准参数与原空间变换参数相减,则得到了配 准结果的误差,记为|ar-rI.其中:r为配准结 1.35 果,α,为原空间变换参数.经过多次不同变换参数 的反复实验后,表1给出了平均配准误差,其中旋转 1.30 15-10-50 51015 参数的单位为度,平移参数的单位为体素个数.配准 角度(°) 算法采用了双核并行计算,采样因子为4,而且优化 图5以NMⅡ为测度的配准函数曲线(采样加旋转) 方法采用粗配准和精配准相结合的搜索策略,经过 Fig5 Registration function curve of NMI (sample and rotation) 一系列的加速方法,本文配准算法的平均时间为 8.1s,而在无任何加速的情况下,配准时间约为 0.8 3min.可以看出本文加速配准方法在获得较好配准 结果的同时,也加快了配准速度. 0.7 表1平均配准误差 Table 1 Mean error of registration 0.6 0./()0,/()0./()t. t: 0.5 0.510.640.810.34 0.450.36 4.2梯度相似与互信息相结合 0.4 -15-10 -50 510i5 对MR-T1图像和MR-PD图像进行2D配准实 角度°) 验,实验数据来自Brainweb,如图4所示.其中: 图6以GSMI为测度的配准函数曲线(采样加旋转) 图4(a)所示为MR-T1图像,图4(b)为对应的MR- Fig.6 Registration function curve of GSMI (sample and rotation) PD图像,此时两幅图像是完全配准的.将MR-T1图 像作为参考图像,即空间位置不变,首先对MR-PD 表2分别以NMI和GSMI为测度的配准结果对比 图像进行某一参数的变换(旋转5°,x、y方向各平移 Table 2 Registration results comparison of NMI GSMI 10个像素),然后将其与MR-T1图像进行配准。 精确值 NMI GSMI 旋转/(°) 4.4101 4.9883 X方向 10 9.9983 9.9988 Y方向 10 8.9634 9.0834 分别以NMI和GSMI作为配准算法的相似性测 度,与MR-T1图像进行配准,两者的配准结果如表2 所示.其中精确值是指MR-PD图像的空间变换参 数,可以看出两者的配准结果都非常接近于精确值; (a)参考图像MR-T1 (b)对MR-PD图像 但以GSMI为相似性测度的配准方法要更加精确一 些,这是因为其中包含了梯度信息的作用. 图4配准图像 Fig.4 Registration images 5结束语 首先分别采用NMI和GSMI测度绘制两者的配 基于归一化互信息的配准方法适应多模态医学 准函数曲线,以旋转角度为参数的配准函数曲线如 图像之间的自动配准,具有无需先验知识、配准精度 图5~6所示,从图中可以看出,在亚采样情况下,以 高等优点;但是其主要瓶颈在于配准速度较慢.本文 NMI为测度的曲线出现许多锯齿,这对配准算法的 针对3D图像配准的3项主要计算处理,研究了相 收敛会产生不利影响,而以GSI测度的曲线则比 应的加速策略,在保证配准精度的同时提高了配准 较光滑,更加适合配准算法的需求。 效率.并且,针对常规互信息计算中只考虑灰度相关 信息的缺点,本文将灰度变化梯度相似性与互信息

第6期 陈伟卿,等:基于灰度互信息和梯度相似性的医学图像配准及其加速处理 ·503· 相结合作为配准算法的相似性测度,从而进一步提 [9]RUECKERT D,CLARKSON M J,HILL D L J,et al.Non- 高了配准算法的精度和鲁棒性。 rigid registration using higher-order mutual information [C]//Proceedings of SPIE Medical Imaging.San Diego, 参考文献: USA,2000:438-447. [1]WELIS I W M,VIOLA P,ATSUMI H,et al.Multi-mo- [10]WANG XX,TIAN J.Image registration based on maximi- dal volume registration by maximization of mutual informa- zation of gradient code mutual information[J].Image Anal tion[J].Medical Image Analysis,1996,1(1):35-51. Stereol,2005,24:1-7 [2]MAES F,COLLIGNON A,VANDERMEULEN D,et al. [11 ]COCOSCO C A,KOLLOKIAN V,KWAN R K S.Brainweb: Multimodality image registraion by maximization of mutual Online interface to a 3D MRI simulated brain database information [J].IEEE Transactions on Medical Imaging, [EB/0L].(2006-06-12)[2008-06-18].htp:/www. 1997,16(2):187-198. bic.mni.megill.ca/brainweb/. [3]STUDHOLME C,HILL D L G,HAWKES D J.An overlap 作者简介: 陈伟卿,女,1976年生,博士研究 invariant entropy measure of 3D medical image aligment [J].Patter Recognition,1999,32(1):71-86. 生,主要研究方向为图像处理分析与理 [4]PLUIM J P W,MAINTZ J B A,VIERGEVER M A.Mutual 解 information matching in multiresolution contexts[J].Image and Vision Computing,2001,19(1/2):45-52. [5]ZHU Y M,COCHOFFS M.Influence of implementation pa- rameters on registration of MR SPECT brain images by maxi- mization of mutual information[J].Journal of Nuclear Med- 李冠华,男,1979年生,博士研究 icine,2002,43(2):160-166. 生,主要研究方向为图像处理与三维可 [6]秦斌杰,庄天戈.三维多模态医学图像配准系统的设计 视化. [J].上海交通大学学报,2003,37(2):228-231. QIN Binjie,ZHUANG Tiange.Multi resolution registration system design for 3D multi-modal medical images[J].Jour- nal of Shanghai Jiaotong University,2003,37(2):228- 231. 欧宗瑛,男,1936年生,教授,博士 [7]WACHOWIAK M P,PETERS T M.High performance med- 生导师,主要研究方向为计算机辅助设 ical image registration using new optimization techniques 计、计算机图像学与图像处理.获省级 [J].IEEE Transactions on Information Technology in Bio- 科技一等奖1项,三等奖2项及参编科 medicine,2006,10(2):344352. 技图书二等奖、教材二等奖各1项.发 [8]WACHOWIAK M P,SMOLIKOVA R,PETERS T M.Mul- 表的学术论文被SCI检索12篇,被E tiresolution biomedical image registration using generalized 检索100余篇, information measures//[C].Proc MICCAI 2003.New York, USA,2003:846853