
第3卷第3期 智能系统学报 Vol 3 Na 3 2008年6月 CAA I Transactions on Intelligent System s Jun 2008 局部搜索的音频数据检索 李应 (福州大学数学与计算机科学学院,福建福州350108) 摘要:根据多媒体音频数据的特点,提出一种适用于快速音频数据检索的局部搜索数据结构,即局部搜索树(bcal search tr心e,LS-tee).在局部搜索树中,分别以音频数据小波变换系数的过零率和平均幅度作为主、次关键码,基于局 部范围对作为索引的其他系数进行组织.其次,基于局部搜索树,提出采用小波包最好基小波塔型算法实现音频数 据检索.最后,把采用局部搜索树的小波包最好基小波塔型算法的搜索和基于小波不同级系数的检索方法相比 较,结果表明,这种方法对音频数据检索的快速和有效性. 关键词:音频数据检索;局部搜索树;小波包最好基;塔型算法 中图分类号:TP391.3,TP31112文献标识码:A文章编号:1673-4785(2008)030259-06 An audio da ta retrieval method ba sed on local search trees LIYing (College ofMathematics and Computer Science,Fuzhou University,Fuzhou 350108,China) Abstract:For fast audio data retrieval,a lcal search tree (LS-k,tree)structure is proposed according o the char- acteristics ofmultmedia audio data In an LS-k tree,the zero-k crossing rate and the average magnitude of the wavelet transfom coefficients in the audio data are taken as main and secondary key codes respectively,and the other coefficients used for the index are organized in the local range On the basis of thisLS-k,tree,an audio data retrieval app roach is presented using the wavelet packet best base and the wavelet pyram idal algorithm.Finally,the research results obtained from the proposed approach are compared with those obtained using the different-k,level wavelet transfom coefficients It is found that the proposed approach is effective and fast for audio data retrieval Keywords:audio data retrieval,bcal search tree (LS-k,tree);wavelet packet best base;pyram idal algorithm 多媒体音频数据,已经成为网络、信息时代信息矩形,而非叶结点包含一组矩形.在R-te中进行插 的重要组成部分.目前,对于基于例子的音频数据分 入一个矩形操作时,遵循原则:结点包含的矩形数n 类、索引、检索、组织和管理方法,己经引起广泛的研 应满足n∈[K/21,K];当插入矩形时,必须使得 究.在文献[1中,Samet对多维数据结构与多媒体 与根结点相关的矩形所需要的扩张最少(以面积计 数据管理中的常用算法进行了全面的描述.其中包 算).当进行一个矩形的搜索操作时,从根结点开 括KDtree点4分树、MX-4分树、R-tree的插入、删 始,根据所查找矩形的坐标,递归地选择子结点,直 除、搜索和范围查询等方法.而R-tree实际上已经成 到找到叶结点为止.与此相对照,在R-tree中删除一 为目前多媒体数据组织和管理的基础,尤其,它对于 个对象,必须避免可能引起的R-tree中的结点“下 在磁盘中存储大量图像数据的情况特别有用2).R- 溢”,确保结点至少包含K2T个矩形 tree结构的大致特点是:每个R-tee有一个值为整 以R-tree为基础,衍生出来的TV-tree,主要根 数K的序.每一个非叶的R-tree结点包含一个矩形 据正被检索的数据,动态和柔性地决定怎样分支的 集合,这个集合最多有K个、至少有「K2个矩形 问题)这种数据结构多用于多媒体文档的搜索。 根结点例外).对于叶结点,每个结点包含一个实 同样衍生于R-tree的贞段树(frame segnent tree)和 R段树(R-Segnent tree or RS-tree)适用于变长度的 收稿日期:2007-1105 基金项目:福建省自然科学基金资助项目(A0510006). 分段.它常用于视频数据的搜索.近年来,又提出 通讯作者:李应.Emai让fi liying@sohu com. 了适用于各种多媒体应用场合的其他空间数据结 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3卷第 3期 智 能 系 统 学 报 Vol. 3 №. 3 2008年 6月 CAA I Transactions on Intelligent System s Jun. 2008 局部搜索的音频数据检索 李 应 (福州大学 数学与计算机科学学院 ,福建 福州 350108) 摘 要 :根据多媒体音频数据的特点 ,提出一种适用于快速音频数据检索的局部搜索数据结构 ,即局部搜索树 ( local search tree,LS2tree). 在局部搜索树中 ,分别以音频数据小波变换系数的过零率和平均幅度作为主、次关键码 ,基于局 部范围对作为索引的其他系数进行组织. 其次 ,基于局部搜索树 ,提出采用小波包最好基小波塔型算法实现音频数 据检索. 最后 ,把采用局部搜索树的小波包最好基 —小波塔型算法的搜索和基于小波不同级系数的检索方法相比 较 ,结果表明 ,这种方法对音频数据检索的快速和有效性. 关键词 :音频数据检索 ;局部搜索树 ;小波包最好基 ;塔型算法 中图分类号 : TP391. 3; TP311. 12 文献标识码 : A 文章编号 : 167324785 (2008) 0320259206 An audio data retr ieval method based on local search trees L I Ying (College ofMathematics and Computer Science, Fuzhou University, Fuzhou 350108, China) Abstract:For fast audio data retrieval, a local search tree (LS2kd tree) structure is p roposed according to the char2 acteristics of multimedia audio data. In an LS2kd tree, the zero2kd crossing rate and the average magnitude of the wavelet transform coefficients in the audio data are taken as main and secondary key codes respectively, and the other coefficients used for the index are organized in the local range. On the basis of thisLS2kd tree, an audio data retrieval app roach is p resented using the wavelet packet best base and the wavelet pyram idal algorithm. Finally, the research results obtained from the p roposed app roach are compared with those obtained using the different2kd level wavelet transform coefficients. It is found that the p roposed app roach is effective and fast for audio data retrieval. Keywords: audio data retrieval; local search tree (LS2kd tree) ; wavelet packet best base; pyram idal algorithm 收稿日期 : 2007211205. 基金项目 :福建省自然科学基金资助项目 (A0510006). 通讯作者 :李 应. E2mail: fj_liying@ sohu. com. 多媒体音频数据 ,已经成为网络、信息时代信息 的重要组成部分. 目前 ,对于基于例子的音频数据分 类、索引、检索、组织和管理方法 ,已经引起广泛的研 究. 在文献 [ 1 ]中 , Samet对多维数据结构与多媒体 数据管理中的常用算法进行了全面的描述. 其中包 括 K2D tree、点 4分树、MX24分树、R2tree的插入、删 除、搜索和范围查询等方法. 而 R2tree实际上已经成 为目前多媒体数据组织和管理的基础 ,尤其 ,它对于 在磁盘中存储大量图像数据的情况特别有用 [ 2 ] . R2 tree结构的大致特点是 :每个 R2tree有一个值为整 数 K的序. 每一个非叶的 R2tree结点包含一个矩形 集合 ,这个集合最多有 K个、至少有 「K/2 ô个矩形 (根结点例外 ). 对于叶结点 ,每个结点包含一个实 矩形 ,而非叶结点包含一组矩形. 在 R2tree中进行插 入一个矩形操作时 ,遵循原则 :结点包含的矩形数 n 应满足 n ∈ [「K/2ô, K ];当插入矩形时 ,必须使得 与根结点相关的矩形所需要的扩张最少 (以面积计 算 ). 当进行一个矩形的搜索操作时 ,从根结点开 始 ,根据所查找矩形的坐标 ,递归地选择子结点 ,直 到找到叶结点为止. 与此相对照 ,在 R2tree中删除一 个对象 ,必须避免可能引起的 R2tree中的结点“下 溢 ”,确保结点至少包含 「K /2ô个矩形. 以 R2tree为基础 ,衍生出来的 TV2tree,主要根 据正被检索的数据 ,动态和柔性地决定怎样分支的 问题 [ 3 ] . 这种数据结构多用于多媒体文档的搜索. 同样衍生于 R2tree的贞段树 ( frame segment tree)和 R2段树 (R2Segment tree or RS2tree)适用于变长度的 分段 [ 1 ] . 它常用于视频数据的搜索. 近年来 ,又提出 了适用于各种多媒体应用场合的其他空间数据结

·260· 智能系统学报 第3卷 构,其中包括:Rtee的分支嫁接算法 A001.wavA002.wav A056.wav A099.wav A100.wav e-tree结构II、RS-tree61、紧凑R-tree7、SS-trees 9 查询数据 产生小波 X-tree-ol、SR-tree、AB-tree2l、LSDh-tree、 多分辨迎近系数 a100…A072a0564级系数 hybrid tree等等.然而,这些多维数据结构主要是 音须数据 %6 多分拆遍近系数 针对多媒体图象数据、视频数据和文档数据的组织 和管理而提出的,它们大都不适用于多媒体音频数 精 a002…a056…a086+ 5级系数 据的组织、管理和搜索.为此,本文针对基于例子和 N3别 基于内容的音频数据检索,以小波包变换和小波多 a002a059 a056 …a010 6级系数 分辨分析为基础提出一种可以高效地组织、管理和 =100 搜索音频数据的局部搜索树(LS-tree),实现音频数 最好基系数 a001a002,a056…a099al00 据检索, 图1用小波最好基与塔型算法检索音频数据过程 1音频数据的检索方法 Fig 1 The process with wavelet packet best base and py- 对于可以检索各种音频数据的索引产生方法 ram idal algorithm retrieval audio data 文献[I5提出了通过短时Fourier?变换和小波变换 数CA6进行预处理,并生成CA6的过零率(Z)和 产生索引的方法.由于音频信号是非平稳信号,而小 平均幅度M).通过这一对参数(Z.,M,),提出并 波变换具有多分辨分析的特点,因此,采用小波变换 建立可以对3个级别的离散小波逼近系数CA6、 产生索引比基于信号统计和基于短时Fourier变换 CA5、CA4进行有效管理的局部搜索索引结构,即 产生索引的方法具有更好的检索精度.对于小波多 LS-tree 分辨率分析,它可以按照不同的尺度因子把H止 bet空间分解为所有小波子空间w,j∈Z)的正交 2关于LS-tree 和,即L)=,.而小波包可以对形,进行进一 21音频数据文件搜索中的问题 步分解,它克服了小波多分辨分解中当时间分辨率 对于一个具有n个音频数据文件的集合,通过 高时频率分辨率低的缺陷,因此具有更好的音频特 对它们相应的6级小波逼近系数CA6进行预处理, 性.对于不同类型的音频信号,它们的频谱差别较 并生成相应的n对参数{(Z,Ma1}:(Za,Man 大,因此,采用小波包来分析具有更为理想的效果. 如图2所示,以过零率(Zeo-crossing rate)为横坐 用小波包变换来分析音频数据,是根据不同的 标、平均幅度(A verage magnitude)为纵坐标,把这n 音频数据选择不同的最好基对音频数据进行分解, 对参数表示在二维空间上 曾经以小波包最好基和小波多分辨分析为基础,用 2.5f 小波包最好基→小波塔型算法检索音频数据.这种 2.0 方法的思想是,把音频数据分解成小波包最佳树结 构系数S和6级、5级、4级等3个级别的离散小波 1.5i 逼近系数CA6、CA5、CA4在检索过程中,首先用SI 1.0 对音频数据进行初步分类:然后,再分别用6级系数 CA6、5级系数CA5和4级系数CA4通过塔形算法 0.5 ”。e 进行检索61,并最后得出结果.这个过程如图1所 0公, 带● 示为了方便分析,取数据集中文件数n=100,且以 0.20.40.60.81.0 过零率 “A+序号表示音频数据文件名). 在图1中,由于音频数据检索的非确定性,检索 图2由过零率(Z4)和平均幅度(M,)组成的向量二 需要对数据集的所有文件进行计算I16).由于CA6、 维空间上的分布 CA5、CA4这3组小波系数大小不等且维数变化较 Fig 2 The distributing of the vectorswhich are consisted of zero-crossing rates and magnitudes 大(维数变化范围10~20000),采用现有的索引结 构很难对这些系数进行有效管理和检索.为了实现 为了提高检索速度和效率,必须把对整个平面 对这类数据的有效管理和搜索,利用时域分析中计 算过零率和平均幅度的方法81,对维数最小的系 的搜索,缩小到局部的搜索.以在数据集中查询按动 快门的声音为例,局部搜索的工作过程下,取按动快 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
构 , 其 中 包 括 : R2tree 的 分 支 嫁 接 算 法 [ 4 ]、 e2tree结构 [ 5 ]、RS2tree [ 6 ]、紧凑 R2tree [ 7 ]、SS2tree [ 8 ]、 X2tree [ 9210 ]、SR2tree [ 11 ]、AB2tree [ 12 ]、LSDh2tree [ 13 ]、 hybrid tree [ 14 ]等等. 然而 ,这些多维数据结构主要是 针对多媒体图象数据、视频数据和文档数据的组织 和管理而提出的 ,它们大都不适用于多媒体音频数 据的组织、管理和搜索. 为此 ,本文针对基于例子和 基于内容的音频数据检索 ,以小波包变换和小波多 分辨分析为基础 ,提出一种可以高效地组织、管理和 搜索音频数据的局部搜索树 (LS2tree) ,实现音频数 据检索. 1 音频数据的检索方法 对于可以检索各种音频数据的索引产生方法 , 文献 [ 15 ]提出了通过短时 Fourier变换和小波变换 产生索引的方法. 由于音频信号是非平稳信号 ,而小 波变换具有多分辨分析的特点 ,因此 ,采用小波变换 产生索引比基于信号统计和基于短时 Fourier变换 产生索引的方法具有更好的检索精度. 对于小波多 分辨率分析 ,它可以按照不同的尺度因子 j把 H il2 bert空间分解为所有小波子空间 wj ( j ∈ Z ) 的正交 和 ,即 L (R ) = Ý j∈Z W j . 而小波包可以对 W j进行进一 步分解 ,它克服了小波多分辨分解中当时间分辨率 高时 ,频率分辨率低的缺陷 ,因此具有更好的音频特 性. 对于不同类型的音频信号 ,它们的频谱差别较 大 ,因此 ,采用小波包来分析具有更为理想的效果. 用小波包变换来分析音频数据 ,是根据不同的 音频数据选择不同的最好基对音频数据进行分解. 曾经以小波包最好基和小波多分辨分析为基础 ,用 小波包最好基 —小波塔型算法检索音频数据. 这种 方法的思想是 ,把音频数据分解成小波包最佳树结 构系数 SI和 6级、5级、4级等 3个级别的离散小波 逼近系数 CA6、CA5、CA4. 在检索过程中 ,首先用 SI 对音频数据进行初步分类 ;然后 ,再分别用 6级系数 CA6、5级系数 CA5和 4级系数 CA4通过塔形算法 进行检索 [ 16 ] ,并最后得出结果. 这个过程如图 1所 示 (为了方便分析 ,取数据集中文件数 n = 100,且以 “A +序号 ”表示音频数据文件名 ). 在图 1中 ,由于音频数据检索的非确定性 ,检索 需要对数据集的所有文件进行计算 [ 16 ] . 由于 CA6、 CA5、CA4这 3组小波系数大小不等且维数变化较 大 (维数变化范围 10~20 000) ,采用现有的索引结 构很难对这些系数进行有效管理和检索. 为了实现 对这类数据的有效管理和搜索 ,利用时域分析中计 算过零率和平均幅度的方法 [ 17218 ] ,对维数最小的系 图 1 用小波最好基与塔型算法检索音频数据过程 Fig. 1 The p rocess with wavelet packet best base and py2 ram idal algorithm retrieval audio data 数 CA6进行预处理 ,并生成 CA6的过零率 ( Zd ) 和 平均幅度 (M d ). 通过这一对参数 ( Zd , M d ) ,提出并 建立可以对 3 个级别的离散小波逼近系数 CA6、 CA5、CA4进行有效管理的局部搜索索引结构 ,即 LS2tree. 2 关于 LS2tree 2. 1 音频数据文件搜索中的问题 对于一个具有 n个音频数据文件的集合 ,通过 对它们相应的 6级小波逼近系数 CA6进行预处理 , 并生成相应的 n对参数 { ( Zd1 , M d 1 ) } …, ( Zdn , M dn ). 如图 2 所示 ,以过零率 ( Zero2crossing rate)为横坐 标、平均幅度 (Average magnitude)为纵坐标 ,把这 n 对参数表示在二维空间上. 图 2 由过零率 ( Zd )和平均幅度 ( M d )组成的向量二 维空间上的分布 Fig. 2 The distributing of the vectorswhich are consisted of zero2crossing rates and magnitudes 为了提高检索速度和效率 ,必须把对整个平面 的搜索 ,缩小到局部的搜索. 以在数据集中查询按动 快门的声音为例 ,局部搜索的工作过程下. 取按动快 ·260· 智 能 系 统 学 报 第 3卷
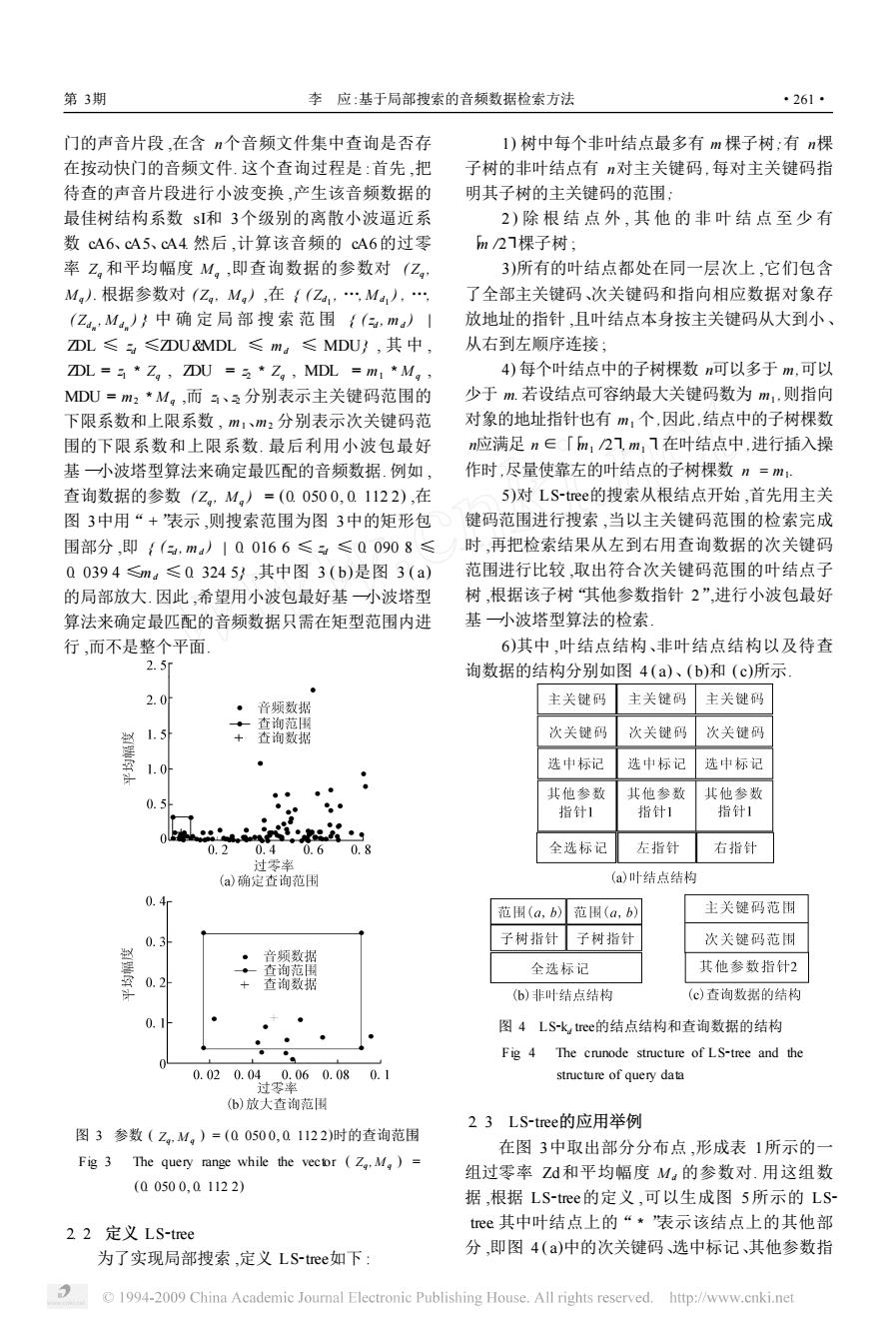
第3期 李应:基于局部搜索的音频数据检索方法 ·261· 门的声音片段,在含n个音频文件集中查询是否存 1)树中每个非叶结点最多有m棵子树:有n棵 在按动快门的音频文件.这个查询过程是:首先,把 子树的非叶结点有n对主关键码,每对主关键码指 待查的声音片段进行小波变换,产生该音频数据的 明其子树的主关键码的范围: 最佳树结构系数$和3个级别的离散小波逼近系 2)除根结点外,其他的非叶结点至少有 数cA6、cA5、44然后,计算该音频的cA6的过零 m21棵子树; 率Z,和平均幅度M,,即查询数据的参数对(Z, 3)所有的叶结点都处在同一层次上,它们包含 Mg人.根据参数对(Zg,Mg),在{(Za,Ma),… 了全部主关键码、次关键码和指向相应数据对象存 (Z.,M,)}中确定局部搜索范围{(,m)1 放地址的指针,且叶结点本身按主关键码从大到小、 DL≤≤DU&MDL≤m,≤MDU},其中, 从右到左顺序连接: ZDL =*Z,ZDU =*Z,MDL =m1 *M 4)每个叶结点中的子树棵数n可以多于m,可以 MDU=m2*M,,而、分别表示主关键码范围的 少于m.若设结点可容纳最大关键码数为m,则指向 下限系数和上限系数,m1、m2分别表示次关键码范 对象的地址指针也有m,个,因此,结点中的子树棵数 围的下限系数和上限系数.最后利用小波包最好 n应满足n∈「m12m,7在叶结点中,进行插入操 基小波塔型算法来确定最匹配的音频数据.例如, 作时,尽量使靠左的叶结点的子树棵数n=m 查询数据的参数(Z,M,)=(0.0500,0.1122),在 5)对LS-tree的搜索从根结点开始,首先用主关 图3中用“+表示,则搜索范围为图3中的矩形包。 键码范围进行搜索,当以主关键码范围的检索完成 围部分,即{(4,ma)100166≤≤00908≤ 时,再把检索结果从左到右用查询数据的次关键码 00394≤m:≤03245},其中图3(b)是图3(a) 范围进行比较,取出符合次关键码范围的叶结点子 的局部放大.因此,希望用小波包最好基小波塔型 树,根据该子树“其他参数指针2”,进行小波包最好 算法来确定最匹配的音频数据只需在矩型范围内进 基小波塔型算法的检索 行,而不是整个平面 6)其中,叶结点结构、非叶结点结构以及待查 2.5r 询数据的结构分别如图4(a)、(b)和(c)所示 2.0 ·音频数据 主关键码 主关键码 主关键码 。查询范围 1.5 +查询数据 次关键码 次关键码 次关键码 1.0 选中标记 选中标记 选中标记 其他参数 其他参数 其他参数 05 指针1 指针1 指针1 0.·s 0.2 0.4 0.6 0.8 全选标记 左指针 右指针 过零率 (a)确定查询范围 (a)叶结点结构 范围(a,b) 范围(a,b) 主关键码范围 0. 子树指针 子树指针 次关键码范围 音频数据 全选标记 其他参数指针2 0.1 查询数据 (b)非叶结点结构 (c)查询数据的结构 图4LS-k tree的结点结构和查询数据的结构 Fig 4 The crunode structure of LS-tree and the 0.020.040.060.080.1 structure of query data 过零率 (6)放大查询范围 23LS-tree的应用举例 图3参数(Z,M,)=(00500,01122)时的查询范围 在图3中取出部分分布点,形成表1所示的一 Fig 3 The query range while the vector (Z.M)= 组过零率Zd和平均幅度M,的参数对.用这组数 (00500,01122) 据,根据LS-tee的定义,可以生成图5所示的LS 22定义LS-tree tree其中叶结点上的“*表示该结点上的其他部 分,即图4(a)中的次关键码、选中标记、其他参数指 为了实现局部搜索,定义LS-tree如下: 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
门的声音片段 ,在含 n个音频文件集中查询是否存 在按动快门的音频文件. 这个查询过程是 :首先 ,把 待查的声音片段进行小波变换 ,产生该音频数据的 最佳树结构系数 sI和 3个级别的离散小波逼近系 数 cA6、cA5、cA4. 然后 ,计算该音频的 cA6的过零 率 Zq 和平均幅度 M q ,即查询数据的参数对 ( Zq , M q ). 根据参数对 ( Zq , M q ) ,在 { ( Zd1 , …, M d1 ) , …, ( Zdn , M dn ) } 中 确 定 局 部 搜 索 范 围 { (zd , md ) | ZDL ≤ zd ≤ZDU&MDL ≤ md ≤ MDU} , 其 中 , ZDL = z1 3 Zq , ZDU = z2 3 Zq , MDL = m1 3 M q , MDU = m2 3 M q ,而 z1、z2 分别表示主关键码范围的 下限系数和上限系数 , m1、m2 分别表示次关键码范 围的下限系数和上限系数. 最后利用小波包最好 基 —小波塔型算法来确定最匹配的音频数据. 例如 , 查询数据的参数 ( Zq , M q ) = (0. 050 0, 0. 112 2) ,在 图 3中用“ + ”表示 ,则搜索范围为图 3中的矩形包 围部分 ,即 { (zd , md ) | 0. 016 6 ≤ zd ≤ 0. 090 8 ≤ 0. 039 4 ≤md ≤ 0. 324 5} ,其中图 3 ( b)是图 3 ( a) 的局部放大. 因此 ,希望用小波包最好基 —小波塔型 算法来确定最匹配的音频数据只需在矩型范围内进 行 ,而不是整个平面. 图 3 参数 ( Zq , M q ) = (0. 050 0, 0. 112 2)时的查询范围 Fig. 3 The query range while the vector ( Zq , M q ) = (0. 050 0, 0. 112 2) 2. 2 定义 LS2tree 为了实现局部搜索 ,定义 LS2tree如下 : 1) 树中每个非叶结点最多有 m 棵子树;有 n棵 子树的非叶结点有 n对主关键码 ,每对主关键码指 明其子树的主关键码的范围; 2 ) 除 根 结 点 外 , 其 他 的 非 叶 结 点 至 少 有 「m /2ô棵子树 ; 3)所有的叶结点都处在同一层次上 ,它们包含 了全部主关键码、次关键码和指向相应数据对象存 放地址的指针 ,且叶结点本身按主关键码从大到小、 从右到左顺序连接 ; 4) 每个叶结点中的子树棵数 n可以多于 m ,可以 少于 m. 若设结点可容纳最大关键码数为 m1 ,则指向 对象的地址指针也有 m1 个,因此 ,结点中的子树棵数 n应满足 n ∈「「m1 /2ô, m1 ô. 在叶结点中,进行插入操 作时,尽量使靠左的叶结点的子树棵数 n = m1 . 5)对 LS2tree的搜索从根结点开始 ,首先用主关 键码范围进行搜索 ,当以主关键码范围的检索完成 时 ,再把检索结果从左到右用查询数据的次关键码 范围进行比较 ,取出符合次关键码范围的叶结点子 树 ,根据该子树“其他参数指针 2”,进行小波包最好 基 —小波塔型算法的检索. 6)其中 ,叶结点结构、非叶结点结构以及待查 询数据的结构分别如图 4 ( a)、( b)和 ( c)所示. 图 4 LS2kd tree的结点结构和查询数据的结构 Fig. 4 The crunode structure of LS2tree and the structure of query data 2. 3 LS2tree的应用举例 在图 3中取出部分分布点 ,形成表 1所示的一 组过零率 Zd和平均幅度 M d 的参数对. 用这组数 据 ,根据 LS2tree的定义 ,可以生成图 5所示的 LS2 tree. 其中叶结点上的“3 ”表示该结点上的其他部 分 ,即图 4 ( a)中的次关键码、选中标记、其他参数指 第 3期 李 应 :基于局部搜索的音频数据检索方法 ·261·

·262 智能系统学报 第3卷 针1等.在图5中,每个关键码的实际值为显示值× 的指针:系数CA5的指针;系数CA4的指针:音频文 10. 件指针.而图4(c)中其他参数指针2”主要包括: 对于本例而言,图4(a)中其他参数指针1”生 查询数据的最佳树结构系数sl系数cA6的指针;,系 要包括:音频数据的最佳树结构系数SI系数CA6 数c45的指针;系数cA4的指针. A(217,1273)1392,1480) B (217,559)(588,1273 (1392,1480 D (217,439)冰457,559) (588,726)冰956,1273) (1392,1480) G 217421T439457556559588622726956111h2731392l480 图5一棵LS-tree Fig 5 A LS-tree 表1一组过零率(Z,)和平均M) 要的范围内,因此这些内容不再进行搜索,只需使相 Table 1 A group of zero-crossng rate and average magn i 应结点D、G和H的“全选标记=TRUE”,同样,也可 tude 以在结点上标上“全选标记=TUE”这样,可以 分布点过零率平均幅度 分布点过零率平均幅度 确定叶结点GH和1中的所有子树是满足 1 0021700114 8 0095600672 00166≤≤0.090的点.再次,确定次关键码搜 2.0072600659 9 0058800107 索的内容.根据表1可以知道,这些点从右到左是: 3 0148000111 10 004390.0276 (0.0726,00659)→(0.0622,01096)→ (0.0588,00107)→(0.0559,0.0588)→ 40139201116 11 0127300129 (0.0556,00251)→(00457,0.0919)- 50045700919 12 0111100231 (00439,00276)→(00421,0.0525)一 60062201096 3 0055600251 (0.0217,01114).最后,用次关键码的范围 70055900588 140042100525 (00394≤m:≤03245)沿着“→方向与子树中 的次关键码进行比较,并把满足次关键码的范围 现在,利用基于例子的方法搜索上述中的一段 Q0394≤m。≤03245的结点选出.它们是: 按动快门声音.查询数据例子的参数同上 (0.0726,00659)→(0.0622,0.1096)一 (Z,M,)=(00500,01122),如果取关键码范围 (0.0559,00588)→(0.0457,0.0919)→ 的下限、上限系数为:=03333、与=18152,m1= (00421,00525)→(0.0217,01114)这样,只 03514、m2=18152(、、m1、m2通过实验确 要取出这些结点中“其他参数指针1所指的其他索 定),那么,主关键码范围是00166≤a≤00908、 引参数,用小波包最好基塔型算法进行检索,进而 次关键码的范围是.因此,以(Z,M,)=Q0500, 减小检索范围,提高检索效率 01122)作为查询数据,将返回符合{(4,ma)1 3搜索结果及不同方法的比较 00166≤4≤00908&00394≤m:≤03245}的参 数对 31基于LS-tree的最好基塔型算法检索的结果 要在图2中,查出符合{(,m4)1,0.0166≤ 在实验中,用LS-tee来管理和组织这些文件, 4≤0.0908&00394≤m:≤03245}的点,首先, 首先为图2所示的100个参数对{(Z,M4, 用主关键码范围(0.0166≤:≤0.0908)从根结点 (Zao,Mam)建立起一棵LS-tree然后,以基于例 A开始搜索.由于在[0.0217,01273]内,所以沿 子的方式对100个音频数据文件用小波包最佳树结 左子树搜索到结点B.其次,确定结果下界.在结点 构系数和小波塔型算法进行检索 B中,由于[0.0217,00559]在00166≤名≤ 通过LS-tee对索引系数的管理,使得需要进行 00908呐,认为结点B的左子树之下的结点在所需 小波包最佳树结构系数和小波塔型算法进行检索的 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
针 1等. 在图 5中 ,每个关键码的实际值为显示值 × 10 4 . 对于本例而言 ,图 4 ( a)中“其他参数指针 1”主 要包括 :音频数据的最佳树结构系数 SI、系数 CA6 的指针 ;系数 CA5的指针 ;系数 CA4的指针 ;音频文 件指针. 而图 4 ( c)中“其他参数指针 2”主要包括 : 查询数据的最佳树结构系数 sI、系数 cA6的指针 ;系 数 cA5的指针 ;系数 cA4的指针. 图 5 一棵 LS2tree Fig. 5 A LS2tree 表 1 一组过零率 ( Zd )和平均 (M d ) Table 1 A group of zero2crossing ra te and average magn i2 tude 分布点 过零率 平均幅度 分布点 过零率 平均幅度 1 0. 021 7 0. 011 4 8 0. 095 6 0. 067 2 2 0. 072 6 0. 065 9 9 0. 058 8 0. 010 7 3 0. 148 0 0. 011 1 10 0. 043 9 0. 027 6 4 0. 139 2 0. 111 6 11 0. 127 3 0. 012 9 5 0. 045 7 0. 091 9 12 0. 111 1 0. 023 1 6 0. 062 2 0. 109 6 13 0. 055 6 0. 025 1 7 0. 055 9 0. 058 8 14 0. 042 1 0. 052 5 现在 ,利用基于例子的方法搜索上述中的一段 按 动 快 门 声 音. 查 询 数 据 例 子 的 参 数 同 上 ( Zq , M q ) = (0. 050 0, 0. 112 2) ,如果取关键码范围 的下限、上限系数为 : z1 = 0. 333 3、z2 = 1. 815 2, m1 = 0. 351 4、m2 = 1. 815 2 ( z1、z2、m1、m2 通过实验确 定 ) ,那么 ,主关键码范围是 0. 016 6≤zd ≤0. 090 8、 次关键码的范围是 . 因此 ,以 ( Zq , M q ) = (0. 050 0, 0. 112 2)作为查询数据 , 将返回符合 { ( zd , md ) | 0. 016 6≤zd ≤0. 090 8&0. 039 4≤md ≤0. 324 5}的参 数对. 要在图 2中 ,查出符合 { ( zd , md ) | , 0. 016 6≤ zd ≤ 0. 090 8&0. 039 4≤md ≤0. 324 5} 的点 ,首先 , 用主关键码范围 (0. 016 6≤ zd ≤0. 090 8)从根结点 A开始搜索. 由于 在 [ 0. 021 7, 0. 127 3 ]内 ,所以沿 左子树搜索到结点 B . 其次 ,确定结果下界. 在结点 B 中 ,由于 [ 0. 021 7, 0. 055 9 ]在 0. 016 6 ≤ zd ≤ 0. 090 8内 ,认为结点 B 的左子树之下的结点在所需 要的范围内 ,因此这些内容不再进行搜索 ,只需使相 应结点 D、G和 H的“全选标记 = TRUE”;同样 ,也可 以在结点 I上标上“全选标记 = TRUE”. 这样 ,可以 确定 叶 结 点 G、H 和 I 中 的 所 有 子 树 是 满 足 0. 016 6≤ zd ≤ 0. 090 8的点. 再次 ,确定次关键码搜 索的内容. 根据表 1可以知道 ,这些点从右到左是 : (0. 072 6, 0. 065 9) → (0. 062 2, 0. 109 6) → (0. 058 8, 0. 010 7) → (0. 055 9, 0. 058 8) → ( 0. 055 6, 0. 025 1) → (0. 045 7, 0. 091 9) → (0. 043 9, 0. 027 6) → (0. 042 1, 0. 052 5) → ( 0. 021 7, 0. 111 4). 最 后 , 用 次 关 键 码 的 范 围 (0. 039 4≤md ≤0. 324 5)沿着“→”方向与子树中 的次关键码进行比较 ,并把满足次关键码的范围 0. 039 4≤md ≤ 0. 324 5 的 结 点 选 出. 它 们 是 : (0. 072 6, 0. 065 9) → (0. 062 2, 0. 109 6) → (0. 055 9, 0. 058 8) → (0. 045 7, 0. 091 9) → ( 0. 042 1, 0. 052 5) → ( 0. 021 7, 0. 111 4 )这样 ,只 要取出这些结点中“其他参数指针 1”所指的其他索 引参数 ,用小波包最好基 —塔型算法进行检索 ,进而 减小检索范围 ,提高检索效率. 3 搜索结果及不同方法的比较 3. 1 基于 LS2tree的最好基 —塔型算法检索的结果 在实验中 ,用 LS2tree来管理和组织这些文件. 首先为图 2所示的 100个参数对 { ( Zd1 , M d1 ) , …, ( Zd100 , M d100 ) }建立起一棵 LS2tree. 然后 ,以基于例 子的方式对 100个音频数据文件用小波包最佳树结 构系数和小波塔型算法进行检索. 通过 LS2tree对索引系数的管理 ,使得需要进行 小波包最佳树结构系数和小波塔型算法进行检索的 ·262· 智 能 系 统 学 报 第 3卷

第3期 李应:基于局部搜索的音频数据检索方法 ·263· 文件范围缩小.也就是说,在经过小波包最佳树结构 系数和小波塔型算法检索之前,首先通过LS-tree进 占用时间比= 该层检索所用单位时间 行搜索,只对这个搜索的结果文件进行小波包最佳 4级小波系数检索所用单位时间 树结构系数的分类」 经过小波包最佳树结构系数的分类,如果只把 表2基于LS-tr©e的小波最佳树塔型算法和不同级小波 塔型算法的第一层检索作为结果,即把查询数据与 系数检索的结果 音频数据的6级小波系数进行比较作检索结果.那 Table 2 Search result w ith wavelet packet best ba se py- ram idal a lgorithm base on LS-tree and different 么要分辩出100个音频数据文件,需要2582次查 level coeff ic ien ts 询数据和音频数据6级小波系数的比较.如果以这 错误文件 数量搜索次数 层比较作为查询结果,那么查询的准确率为71% 如果在第1层检索结果的基础上,再进入第2 第1层 6,9,10,12,13,25,26, 27,37,38,43,45,46,51 层,把塔型算法的第2层检索作为结果,即把查询数 最好基 52,56,59,62,63,66,74, 29 2582 据与音频数据的5级小波系数进行比较作检索结 塔型算法 80,85,87,89,90,94,95 果.在我们的实验中,需要519次查询数据和音频 100 数据5级小波系数的比较.由于5级小波系数的长 2,7,10,12,13,25,26, 度是6级小波的一倍,因此,如果以6级小波比较的 6级 27,34,37,38,45,46,51, 时间衡量,那么增加的比较次数为5192=1038 小波系数 52,56,59,62,63,66,69. 31 10000 次.此时查询的准确率可以达到84%. 74,79,80,85,87,89,90, 与第2层相似,如果再进入第3层比较,在第2 94,95,100 层的基础上需要增加257次查询数据和音频数据的 第2层 2,6,9,12,29,31,34. 4级小波系数比较.这相当于增加2574=1028次 最好基 37,43,51,52,56,66,80, 16 1038 的6级小波系数比较的时间.经过第3层的搜索,准 塔型算法 90,100 确率可以达到94%. 2,12,14,15,18,29,31 3.2不同方法的比较 5级 34,35,37,53,56,63,72 21 20000 对同样的100个音频数据文件用【161中的不同 小波系数 80,88,89,90,92,99,100 级小波系数检索方法进行检索.当用6级粗分辨逼 近小波系数对音频数据集合中的数据进行搜索、并 第3层 6,9,43,52,66,88 把该结果作为最终的搜索结果时,搜索准确率为 最好基 6 1028 69%,并需要进行100Ⅺ100=10000次6级粗分辨 塔型算法 逼近小波系数的相关计算;用5级粗分辨逼近小波 4级 12,13,14,15,21,46,56, 1040000 系数对音频数据集合中的数据进行检索,则准确率 小波系数72,83,90 为79%,需要进行相当于100×1002=20000次6 级粗分辨逼近小波系数的相关计算;用4级粗分辨 从表2和图6(a)中可以看出基于LS-tree的 逼近小波系数对音频数据集合中的数据进行搜索, 最好基塔型算法检索音频数据的有效性,而且,随 准确率为89%,需要进行相当于100×100×4= 着搜索塔型层数的增加,精度也逐渐提高.其检索精 40000次6级粗分辨逼近小波系数的相关计算. 度明显高于不同级小波系数方法.不管用几层塔型 基于LS-tee组织和管理索引系数、用小波包最 算法,从表2和图6(b)可以看出,它所占用的时间 佳树塔型算法的方法和不同级小波粗分辨逼近小 都远低于多级小波系数的方法,而且,随着塔型层数 波系数方法比较结果如表2所示 的增加和搜索精度的提高,花费时间的增加相对较 图6显示了基于LS-tee的最好基塔型算法和 低.也就是说,在需要进行高精度搜索时,基于L$ 不同级小波系数搜索时的检索精度及其花费的时间 tree的最好基塔型算法花费的时间远低于不同级 比率.其中: 小波粗分辨系数搜索算法.在一般情况下,这种方法 可以满足音频数据基于例子的搜索对精度和时间的 检索精度= 检索到的正确文件数 检索文件总数 要求 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
文件范围缩小. 也就是说 ,在经过小波包最佳树结构 系数和小波塔型算法检索之前 ,首先通过 LS2tree进 行搜索 ,只对这个搜索的结果文件进行小波包最佳 树结构系数的分类. 经过小波包最佳树结构系数的分类 ,如果只把 塔型算法的第一层检索作为结果 ,即把查询数据与 音频数据的 6级小波系数进行比较作检索结果. 那 么要分辩出 100个音频数据文件 ,需要 2 582次查 询数据和音频数据 6级小波系数的比较. 如果以这 层比较作为查询结果 ,那么查询的准确率为 71%. 如果在第 1层检索结果的基础上 ,再进入第 2 层 ,把塔型算法的第 2层检索作为结果 ,即把查询数 据与音频数据的 5级小波系数进行比较作检索结 果. 在我们的实验中 ,需要 519次查询数据和音频 数据 5级小波系数的比较. 由于 5级小波系数的长 度是 6级小波的一倍 ,因此 ,如果以 6级小波比较的 时间衡量 ,那么增加的比较次数为 519 ×2 = 1 038 次. 此时查询的准确率可以达到 84%. 与第 2层相似 ,如果再进入第 3层比较 ,在第 2 层的基础上需要增加 257次查询数据和音频数据的 4级小波系数比较. 这相当于增加 257 ×4 = 1 028次 的 6级小波系数比较的时间. 经过第 3层的搜索 ,准 确率可以达到 94%. 3. 2 不同方法的比较 对同样的 100个音频数据文件用 [ 16 ]中的不同 级小波系数检索方法进行检索. 当用 6级粗分辨逼 近小波系数对音频数据集合中的数据进行搜索、并 把该结果作为最终的搜索结果时 ,搜索准确率为 69% ,并需要进行 100 ×100 = 10 000次 6级粗分辨 逼近小波系数的相关计算 ;用 5级粗分辨逼近小波 系数对音频数据集合中的数据进行检索 ,则准确率 为 79% ,需要进行相当于 100 ×100 ×2 = 20 000次 6 级粗分辨逼近小波系数的相关计算 ;用 4级粗分辨 逼近小波系数对音频数据集合中的数据进行搜索 , 准确率为 89% ,需要进行相当于 100 ×100 ×4 = 40 000次 6级粗分辨逼近小波系数的相关计算. 基于 LS2tree组织和管理索引系数、用小波包最 佳树 —塔型算法的方法和不同级小波粗分辨逼近小 波系数方法比较结果如表 2所示. 图 6显示了基于 LS2tree的最好基 2塔型算法和 不同级小波系数搜索时的检索精度及其花费的时间 比率. 其中 : 检索精度 = 检索到的正确文件数 检索文件总数 , 占用时间比 = 该层检索所用单位时间 4级小波系数检索所用单位时间 . 表 2 基于 LS2tree的小波最佳树 —塔型算法和不同级小波 系数检索的结果 Table 2 Search result with wavelet packet best ba se & py2 ram ida l a lgor ithm ba se on LS2tree and d ifferen t level coeffic ien ts 错误文件 数量 搜索次数 第 1层 最好基 塔型算法 6, 9, 10, 12, 13, 25, 26, 27, 37, 38, 43, 45, 46, 51, 52, 56, 59, 62, 63, 66, 74, 80, 85, 87, 89, 90, 94, 95, 100 29 2 582 6级 小波系数 2, 7, 10, 12, 13, 25, 26, 27, 34, 37, 38, 45, 46, 51, 52, 56, 59, 62, 63, 66, 69, 74, 79, 80, 85, 87, 89, 90, 94, 95, 100 31 10 000 第 2层 最好基 塔型算法 2, 6, 9, 12, 29, 31, 34, 37, 43, 51, 52, 56, 66, 80, 90, 100 16 1 038 5级 小波系数 2, 12, 14, 15, 18, 29, 31, 34, 35, 37, 53, 56, 63, 72, 80, 88, 89, 90, 92, 99, 100 21 20 000 第 3层 最好基 塔型算法 6, 9, 43, 52, 66, 88 6 1 028 4级 小波系数 12, 13, 14, 15, 21, 46, 56, 72, 83, 90 10 40 000 从表 2和图 6 ( a) 中可以看出基于 LS2tree的 最好基 2塔型算法检索音频数据的有效性 ,而且 ,随 着搜索塔型层数的增加 ,精度也逐渐提高. 其检索精 度明显高于不同级小波系数方法. 不管用几层塔型 算法 ,从表 2和图 6 ( b)可以看出 ,它所占用的时间 都远低于多级小波系数的方法 ,而且 ,随着塔型层数 的增加和搜索精度的提高 ,花费时间的增加相对较 低. 也就是说 ,在需要进行高精度搜索时 ,基于 LS2 tree的最好基 2塔型算法花费的时间远低于不同级 小波粗分辨系数搜索算法. 在一般情况下 ,这种方法 可以满足音频数据基于例子的搜索对精度和时间的 要求. 第 3期 李 应 :基于局部搜索的音频数据检索方法 ·263·

·264· 智能系统学报 第3卷 [4 ]SCHRECK T,CHEN Z Branch grafting method or R-tree 1.0 ◆基于LS-tree mplementation [J]The Joumal of Systems and Sofwware, 。不同级小波系数 2000.53(1):83-93 0.9 0 [5 SH M K,SR IKANT R,AGRAWAL R High-dimensional sm ilarity poins [J ]IEEE Trans on Knowledge and Data 0.8 0 Engineering,2002,14(1):156-171. [6]PARKD J,HEU S,KM H J.The RS-tree:an efficient da- 古 ta structure for distance browsing queries [J]nfomation Processing Letters,2001,80(2):195-203 0.63 [7]HUANG PW,LN PL,LN H Y.Opti izing storage utili- 4 6 小波级数 zation in R-tree dynam ic index structure for spatial databas- (a)基于LS-tree和不同级小波系统检索的检索精度 es [J ]The Joumal of Systems and Softare,2007,55(3) 291-299 1.0 *基于LS-tree [8 WHIE D A,JA N R Sm ilarity indexing with the SS-tree 口不同级小波级数 0.8 [C]//Proceedings of the Twelfth Intemational Conference on Data Engineering New Orleans,USA:Stanley Y.W. 0.6 Su,1996:516-523 0.4 [9]BERCHTOLD S,KEM D A,KR IEGEL H P The X-tree: an index structure for high-dmensional data [C]//Proc In- 0.2 tl Con on Very Large Databases Bombay,India:VADB, 0 米 1996:28-39 5 6 [10]CA IC,MIRA S K,D NG R Smart wavelet mage cod- 小波级数 ing X-tree approach [C]//Signal Processing 82 [S (b)基于LS-ree和不同级小波系数检索的古用时司比率 1],2002:239-249 图6基于LS-tree不同级小波系数检索的占用时间 [11 ]COLOSSIN G,NASC MENTO M A Benchmarking ac- cess structures for the sm ilarity retrieval of high-dmen- 比率 sonal multmedia data [C]//IEEE Intemational Confer Fig 6 Compare with LS-tree and difference level coef ence Multmedia and Expa New York,USA,2000: 1215-1218 ficient to retrieval audo [12]PRAMAN IK S,LI S,RUAN J.Perfomance analysis of 4 结束语 AB-tree [C]//IEEE Intemational Conference Multmedia and Expa New York,USA,2000:1701-1704 正如前所述,目前,可以适用于各种多媒体数据 [13]HENR CH A The LSDh-tree:an access structure for fea- ture vecors C ]//Data Engineering 14th Intemational 的组织、管理和搜索的空间数据结构很多.这些空间 Conference Orlando,USA,1998:362-369 数据结构一般都是以R-tree为基础提出来的.如,对 [14 ]CHAKRABARTIK,MEHROTRA S The hybrid tree:an index structure for high diensional feature paces[C]// 于图像数据的组织和管理常用R`-tree对于文档数 Data Engineering,15 th Intemational Conference Sydney, 据的组织管理采用TV-tree对于视频数据的管理通 1999:440-447. [15 ]SUBRAMANYA S R Indexing and searching schemes or 常采用帧段树或RS-tee等.但对于多媒体音频数据 audio data in audio/multmedia databases(multmedia da- 的组织管理却鲜有文献.针对这种情况,本文提出并 tabase)[D ]USA:George Washington Univ,1999 定义了LS-tree来组织管理多媒体音频数据.同时, [16 ]L I Y,HOU Y.Search audio data with the wavelet Pyram i dal algprithm [J ]Infomation Processing Letter,2004,91 把这种结构用于以小波包最好基小波塔型算法为 (1):49-55 基础的音频数据检索中.实验结果表明了这种方法 [17]ZHANG T,JA Y K CC Audio content analysis for online audiovisual data segentation and classification [J].IEEE 的有效性和实用性.可以认为,这种索引结构如果能 Trans Speech and Audio Processing.2001,9(4):441- 进一步和音频数据的分段和分类技术相结合,将为 457 实现真正的基于例子和基于内容的多媒体音频数据 [18 ]UMAPATHY K,KR ISHNAN S,RAO R K Audio signal feature extraction and classificaton using bcal discrm inant 检索提供有效的方法和思路, bases [J].EEE Trans Audio,Speech and Language Pro- cessing2006,15(4):1236-1246 参考文献: 作者简介: [1]SAMET H The design and analysis of patial data struc- 李应,男,1964年生,副教授,博 tures[D ]MA,USA:AddisonWesley,1989. 士,主要研究方向为多媒体数据检索和 [2]HJAL TASON G,SAMET H.Ranking in patial databases 信息安全,发表学术论文6篇 [C]//Advances in Spatial Databases-4th Symposium. Berlin,Gemany:SpringerVerlag.1995:83-95 [3]L N K L JAGAD ISH H V,FALOUTSOS C The TV-tree: an index structure for high-dmensional data [J].VLDB Joumal,.1994,3(4):517-542 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 6 基于 LS2tree不同级小波系数检索的占用时间 比率 Fig. 6 Compare with LS2tree and difference level coef2 ficient to retrieval audio 4 结束语 正如前所述 ,目前 ,可以适用于各种多媒体数据 的组织、管理和搜索的空间数据结构很多. 这些空间 数据结构一般都是以 R2tree为基础提出来的. 如 ,对 于图像数据的组织和管理常用 R 3 2tree、对于文档数 据的组织管理采用 TV2tree、对于视频数据的管理通 常采用帧段树或 RS2tree等. 但对于多媒体音频数据 的组织管理却鲜有文献. 针对这种情况 ,本文提出并 定义了 LS2tree来组织管理多媒体音频数据. 同时 , 把这种结构用于以小波包最好基 2小波塔型算法为 基础的音频数据检索中. 实验结果表明了这种方法 的有效性和实用性. 可以认为 ,这种索引结构如果能 进一步和音频数据的分段和分类技术相结合 ,将为 实现真正的基于例子和基于内容的多媒体音频数据 检索提供有效的方法和思路. 参考文献 : [ 1 ] SAMET H. The design and analysis of spatial data struc2 tures[D ]. MA,USA: Addison2W esley, 1989. [ 2 ]HJALTASON G, SAMET H. Ranking in spatial databases [ C ] / /Advances in Spatial Databases—4 th Symposium. Berlin, Germany: Sp ringer2Verlag, 1995: 83295. [ 3 ]L IN K I, JAGAD ISH H V, FALOUTSOS C. The TV2tree: an index structure for high2dimensional data [ J ]. VLDB Journal, 1994, 3 (4) : 5172542. [ 4 ] SCHRECK T, CHEN Z. Branch grafting method for R2tree imp lementation [J ]. The Journal of Systems and Software, 2000, 53 (1) : 83293. [ 5 ] SH IM K, SR IKANT R, AGRAWAL R. H igh2dimensional sim ilarity joins [ J ]. IEEE Trans on Knowledge and Data Engineering, 2002, 14 (1) : 1562171. [ 6 ] PARK D J, HEU S, KIM H J. The RS2tree: an efficient da2 ta structure for distance browsing queries [ J ]. Information Processing Letters, 2001, 80 (2) : 1952203. [ 7 ]HUANG PW , L IN P L, L IN H Y. Op timizing storage utili2 zation in R2tree dynam ic index structure for spatial databas2 es [J ]. The Journal of Systems and Software, 2007, 55 (3) : 2912299. [ 8 ]WH ITE D A, JA IN R. Sim ilarity indexing with the SS2tree [C ] / /Proceedings of the Twelfth International Conference on Data Engineering. New O rleans, USA: Stanley Y. W. Su, 1996: 516 2523. [ 9 ]BERCHTOLD S, KEIM D A, KR IEGEL H P. The X2tree: an index structure for high2dimensional data [C ] / / Proc In2 tl Con on Very Large Databases. Bombay, India: VADB, 1996: 28239. [ 10 ]CA I C, M ITRA S K, D ING R. Smart wavelet image cod2 ing: X2tree app roach [ C ] / / Signal Processing 82. [ S. l. ], 2002: 2392249. [ 11 ] COLOSSI N G, NASCIMENTO M A. Benchmarking ac2 cess structures for the sim ilarity retrieval of high2dimen2 sional multimedia data [ C ] / / IEEE International Confer2 ence Multimedia and Expo. New York, USA, 2000: 121521218. [ 12 ] PRAMAN IK S, L I S, RUAN J. Performance analysis of AB2tree [ C ] / / IEEE International Conference Multimedia and Expo. New York, USA, 2000: 170121704. [ 13 ]HENR ICH A The LSDh2tree: an access structure for fea2 ture vectors [ C ] / /Data Engineering 14 th International Conference. O rlando, USA, 1998: 3622369. [ 14 ]CHAKRABARTI K, MEHROTRA S. The hybrid tree: an index structure for high dimensional feature spaces[ C ] / / Data Engineering, 15 th International Conference. Sydney, 1999: 440 2447. [ 15 ] SUBRAMANYA S R. Indexing and searching schemes for audio data in audio /multimedia databases(multimedia da2 tabase) [D ]. USA: George W ashington Univ, 1999. [ 16 ]L I Y, HOU Y. Search audio data with the wavelet Pyram i2 dal algorithm [J ]. Information ProcessingLetter, 2004, 91 (1) : 49255. [ 17 ] ZHANG T, JAY K C C. Audio content analysis for online audiovisual data segmentation and classification [J ]. IEEE Trans Speech and Audio Processing, 2001, 9 ( 4 ) : 4412 457. [ 18 ]UMAPATHY K, KR ISHNAN S, RAO R K. Audio signal feature extraction and classification using local discriminant bases [J ]. IEEE Trans Audio, Speech and Language Pro2 cessing, 2006, 15 (4) : 123621246. 作者简介 : 李 应 ,男 , 1964年生 ,副教授 ,博 士 ,主要研究方向为多媒体数据检索和 信息安全 ,发表学术论文 6篇. ·264· 智 能 系 统 学 报 第 3卷