
第4卷第1期 智能系统学报 Vol 4 Na 1 2009年2月 CAA I Transactions on Intelligent Systems Feb 2009 直线伺服系统的双目标非脆弱控制器的设计及仿真 黄宜庆1黄友锐,章魁 (1.安徽理工大学电气与信息工程学院,安徽淮南232001,2常州信息职业技术学院电子与电气工程学院,江苏 常州213164) 摘要:针对直线伺服系统中存在的多种不确定性,提出一种双目标非脆弱控制器的控制方法.从系统的区域极点 配置和保性能控制2种控制目标出发,利用M方法推导出鲁棒状态反馈控制器的存在条件,同时考虑直线伺服系 统中,控制器增益存在的加性摄动,设计出的控制器实现了系统2种性能指标的优化.并给出具体的算例说明了设 计方法的可行性,仿真实验结果表明该控制方法具有很强的鲁棒性. 关键词:区域极点配置;保性能控制;直线电机伺服系统;非脆弱控制器 中图分类号:TP13文献标识码:A文章编号:1673-4785(2009)01-0085-06 Design and simula tion of a dua l-object non-fragile controller for a lnear motor servo system HUANG Yi-qing,HUANG You-rui,ZHANG Kui (1.School of Electronic and nomation Engineering.AnhuiUniversity of Science and Technolgy,Huainan 232001,China;2 School of Electonic Engineering.Chang hou College of nomation Technology,Changhou 213164,China) Abstract:A double-object non-fragile robust controller was devebped to solve uncertainties in linear mobr servo systems Starting from to control targets-regional pole placement and guaranteed cost control,the existing condi- tions for robust feedback controllers were enhanced by using the linear matrix inequalities (LM D)approach After considering the additive perturbation of controller gains in a linear motor servo system,the controller was designed and the to perfomance indices opti ized Finally,a numerical smulation proved that the method is robust Keywords:regonal pole placement guaranteed cost control,linear motor servo system;non-fragile controller 在鲁棒控制理论中,闭环系统的极点能保证其 性能下降,经典设计方法在综合考虑跟踪误差、抑制 动态和稳态性能),而保性能控制则能使闭环系 扰动、降低不确定性影响后,保证鲁棒稳定性方面难 统的某个指标小于一个确定的上界.为了使设计后 于做到最优.针对这些缺陷,文章利用LMI(linear 的闭环系统具有更强的鲁棒性,20世纪80年代末 matrix inequality)方法实现了永磁直线伺服系统的 期多目标优化问题得以发展.同时由于控制器本身 双目标非脆弱控制器的设计,综合考虑了系统的区 实现过程当中存在着仪器精度不足、计算误差等因 域极点配置[7和保性能控制【0)2种目标.利用线 素,故而控制器本身可能存在着脆弱性31,因此, 性矩阵不等式的方法推导出双目标非脆弱控制器的 对控制器脆弱性的研究也越来越被重视】 存在条件,将控制器的设计转化为一组可以求解的 永磁直线伺服系统以其精度高、响应快且能消 线性矩阵不等式系统,设计过程中克服了传统方法 除机械运动变换机构带来的不良影响等优点得到广 的保守性,从仿真图可以看出,得到了较好的效果 泛应用和关注61;但采用直接驱动时,外界及自身 1问题的描述 的扰动将无缓冲地作用在电机上,系统对负载扰动、 测量噪声及动子质量变化更为敏感,导致系统伺服 考虑由以下状态方程描述的线性时不变系统: x()=(A+△A)x()+ 收稿日期:200804-28 B:w(0 +B2u(v. 1) 通信作者:黄宜庆.Email yighuang@163.com 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 4卷第 1期 智 能 系 统 学 报 Vol. 4 №. 1 2009年 2月 CAA I Transactions on Intelligent System s Feb. 2009 直线伺服系统的双目标非脆弱控制器的设计及仿真 黄宜庆 1 ,黄友锐 1 ,章 魁 2 (1. 安徽理工大学 电气与信息工程学院 ,安徽 淮南 232001; 2. 常州信息职业技术学院 电子与电气工程学院 , 江苏 常州 213164) 摘 要 :针对直线伺服系统中存在的多种不确定性 ,提出一种双目标非脆弱控制器的控制方法. 从系统的区域极点 配置和保性能控制 2种控制目标出发 ,利用 LM I方法推导出鲁棒状态反馈控制器的存在条件 ,同时考虑直线伺服系 统中 ,控制器增益存在的加性摄动 ,设计出的控制器实现了系统 2种性能指标的优化. 并给出具体的算例说明了设 计方法的可行性 ,仿真实验结果表明该控制方法具有很强的鲁棒性. 关键词 :区域极点配置 ;保性能控制 ;直线电机伺服系统 ;非脆弱控制器 中图分类号 : TP13 文献标识码 : A 文章编号 : 167324785 (2009) 0120085206 Design and simulation of a dual2object non2fragile controller for a linear motor servo system HUANG Yi2qing 1 , HUANG You2rui 1 , ZHANG Kui 2 (1. School of Electronic and Information Engineering, AnhuiUniversity of Science and Technology, Huainan 232001, China; 2. School of Electronic Engineering, Changzhou College of Information Technology, Changzhou 213164, China) Abstract:A double2object non2fragile robust controller was developed to solve uncertainties in linear motor servo system s. Starting from two control targets2regional pole p lacement and guaranteed cost control, the existing condi2 tions for robust feedback controllers were enhanced by using the linear matrix inequalities (LM I) app roach. After considering the additive perturbation of controller gains in a linear motor servo system, the controller was designed and the two performance indices op tim ized. Finally, a numerical simulation p roved that the method is robust. Keywords: regional pole p lacement; guaranteed cost control; linear motor servo system; non2fragile controller 收稿日期 : 2008204228. 通信作者 :黄宜庆. E2mail: yiqhuang@163. com. 在鲁棒控制理论中 ,闭环系统的极点能保证其 动态和稳态性能 [ 1 ] ,而保性能控制 [ 2 ]则能使闭环系 统的某个指标小于一个确定的上界. 为了使设计后 的闭环系统具有更强的鲁棒性 , 20世纪 80年代末 期多目标优化问题得以发展. 同时由于控制器本身 实现过程当中存在着仪器精度不足、计算误差等因 素 ,故而控制器本身可能存在着脆弱性 [ 325 ] ,因此 , 对控制器脆弱性的研究也越来越被重视. 永磁直线伺服系统以其精度高、响应快且能消 除机械运动变换机构带来的不良影响等优点得到广 泛应用和关注 [ 6 ] ;但采用直接驱动时 ,外界及自身 的扰动将无缓冲地作用在电机上 ,系统对负载扰动、 测量噪声及动子质量变化更为敏感 ,导致系统伺服 性能下降. 经典设计方法在综合考虑跟踪误差、抑制 扰动、降低不确定性影响后 ,保证鲁棒稳定性方面难 于做到最优. 针对这些缺陷 ,文章利用 LM I( linear matrix inequality)方法实现了永磁直线伺服系统的 双目标非脆弱控制器的设计 ,综合考虑了系统的区 域极点配置 [ 729 ]和保性能控制 [ 10211 ] 2种目标. 利用线 性矩阵不等式的方法推导出双目标非脆弱控制器的 存在条件 ,将控制器的设计转化为一组可以求解的 线性矩阵不等式系统 ,设计过程中克服了传统方法 的保守性 ,从仿真图可以看出 ,得到了较好的效果. 1 问题的描述 考虑由以下状态方程描述的线性时不变系统 : xÛ( t) = (A + △A ) x ( t) + B1w ( t) +B2 u ( t). (1)

86* 智能系统学报 第4卷 其中:A,B∈R,x()∈R”是系统的状态,u()∈ 阵,H、P是表征控制器摄动的常数矩阵且pP0,e2>0,使得下列不等式成立 性能指标J<J.其中△F=HPE,E是适当维数的矩 E1 Er-X (A +gDX +B2Y E2B2H 0 X (A +gT +YiB: X XF 0 XET 0 0 -EI 0 <0 (6) E2H'B: FX 0 0 0 EXT 0 0 -e21 则系统(1)的非脆弱控制器u()=(F+△F)x() 引理2)对于系统1)和非脆弱控制器(3), 存在且名义控制器增益F=YX 使得二次型性能指标J<J广,当且仅当存在正常数 证明由文献[8中的定理且令△B=0时,便 ,、e,和对称正定矩阵X2、矩阵Y,使下列不等式 可容易地得到此引理,其详细的证明过程略 成立 Π X2FL XET X2 FXI -EI 0 0 0 EXi 0 -EI 0 0 <0. (7) X 0 -Q 0 Y 0 -R 则非脆弱控制器u()=(F+△F)x()的名义控制 定理1对于系统1),若存在非脆弱性控制 器增益F=YX,且二次型性能指标上界J= 器(3)满足性能指标1)、2)当且仅当存在对称正定 trace(X人.其中:Π=(AX2+B2Y,)+(AX2+ 矩阵X和矩阵Y以及正常数e,i=1,2,3,4,使得下 B2 Y)T+E EI +aBE ETB2. 列不等式存在 E E-X (A +qlX +B2 Y 0 E2B,H 0 X (A +gT+YB: ·X XFI XE 0 0 -E1I 0 <0. (8) e2HB: FX 0 -82I 0 0 EX 0 0 -e,1 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
其中 : A, B ∈R n ×n , x ( t) ∈R n 是系统的状态 , u ( t) ∈ R m 是控制输入 , w ( t) ∈R q 是外部扰动输入 , △A、 △B 为参数不确定性 , 满足范数有界 条件. 即 : △A = E1ΣF1 ,且满足 ΣTΣ 0,ε2 > 0,使得下列不等式成立. ε1 E1 E T 1 - rX1 (A + qI) X1 +B2 Y1 0 ε2B2 H 0 X1 (A + qI) T + Y T 1B T 2 - rX1 X1 F T 1 0 X1 E T 0 0 - ε1 I 0 0 ε2 H T B T 2 FX1 0 - ε2 I 0 0 EX T 1 0 0 - ε2 I < 0, (6) 则系统 (1)的非脆弱控制器 u ( t) = ( F + △F ) x ( t) 存在且名义控制器增益 F = Y1 X - 1 1 . 证明 由文献 [ 8 ]中的定理且令 △B = 0时 ,便 可容易地得到此引理 ,其详细的证明过程略. 引理 2 [ 9 ] 对于系统 ( 1)和非脆弱控制器 ( 3) , 使得二次型性能指标 J < J 3 ,当且仅当存在正常数 ε3、ε4 和对称正定矩阵 X2、矩阵 Y2 ,使下列不等式 成立. ∏ X2 F1 X2 E T X2 Y T 2 F T 1 X T 2 - ε3 I 0 0 0 EX T 2 0 - ε4 I 0 0 X T 2 0 0 - Q - 1 0 Y2 0 0 0 - R - 1 < 0, (7) 则非脆弱控制器 u ( t) = ( F + △F ) x ( t)的名义控制 器增益 F = Y2 X - 1 2 , 且二次型性能指标上界 J 3 = trace ( X - 1 2 ). 其中 : ∏ = (AX2 + B2 Y2 ) + (AX2 + B2 Y2 ) T +ε3 E1 E T 1 +ε4B E1 E T 1B T 2 . 定理 1 对于系统 ( 1) ,若存在非脆弱性控制 器 (3)满足性能指标 1) 、2)当且仅当存在对称正定 矩阵 X和矩阵 Y以及正常数εi , i = 1, 2, 3, 4,使得下 列不等式存在. ε1 E1 E T 1 - rX (A + qI) X +B2 Y 0 ε2B2 H 0 X (A + qI) T + Y T B T 2 - rX XF T 1 0 XE T 0 0 - ε1 I 0 0 ε2 H T B T 2 FX 0 - ε2 I 0 0 EX T 0 0 - ε2 I < 0, (8) ·86· 智 能 系 统 学 报 第 4卷
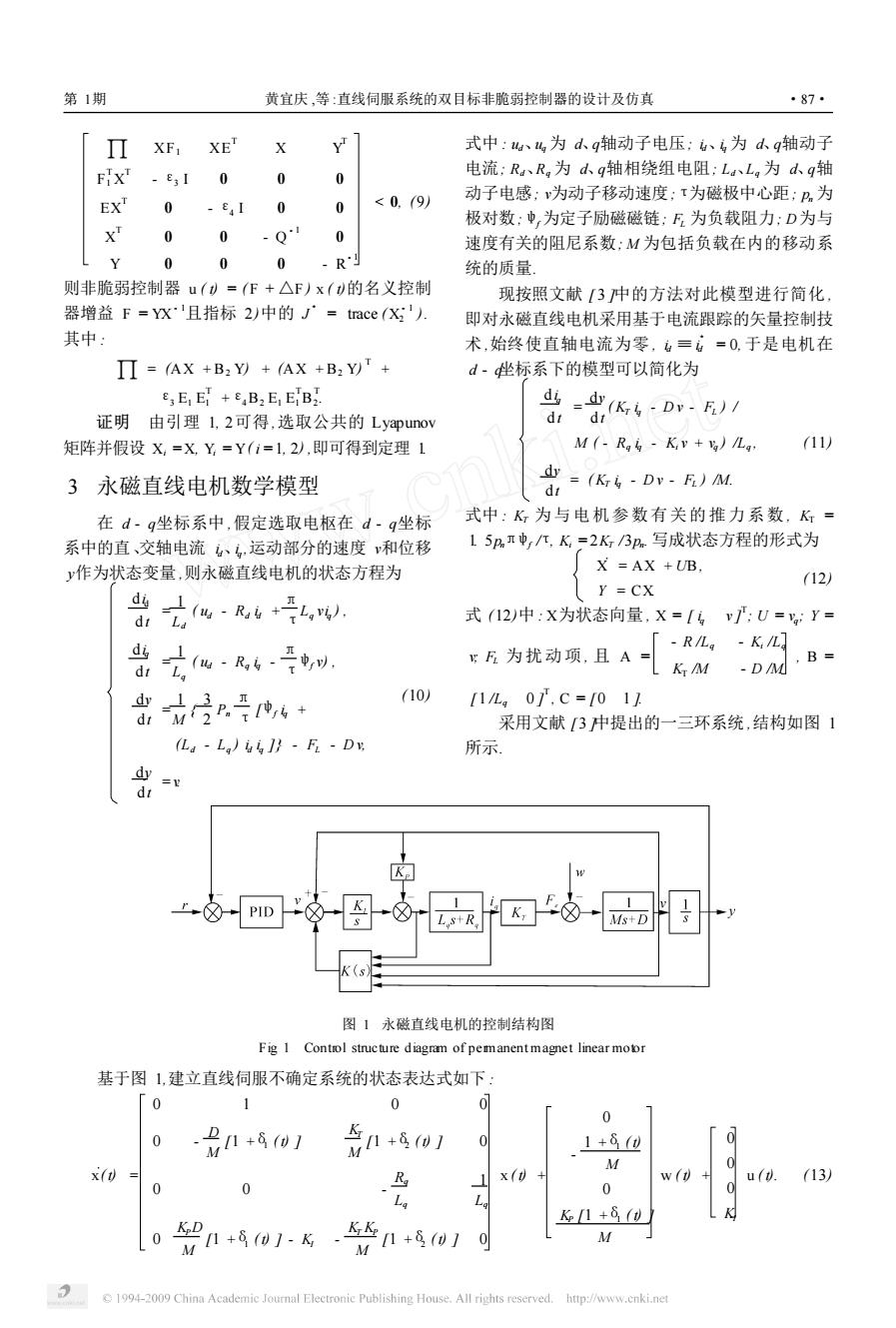
第1期 黄宜庆,等:直线伺服系统的双目标非脆弱控制器的设计及仿真 87 Π XF XET 式中:、弘,为dg轴动子电压;、为dg轴动子 FIXT -e310 0 0 电流:Ra、R,为dq轴相绕组电阻;La、Lg为q轴 EXT 动子电感;v为动子移动速度;τ为磁极中心距;为 0 EI 0 0 <0.(9 极对数;中,为定子励磁磁链;F为负载阻力;D为与 0 0 -Q 速度有关的阻尼系数;M为包括负载在内的移动系 00 0 -R 统的质量, 则非脆弱控制器u()=(F+△F)x()的名义控制 现按照文献[3冲的方法对此模型进行简化 器增益F=X且指标2)中的J'=tace(X'. 即对永磁直线电机采用基于电流跟踪的矢量控制技 其中: 术,始终使直轴电流为零,三右=0,于是电机在 II=(AX +B:Y)+(AX +B2 Y)T+ d-坐标系下的模型可以简化为 E3 EE+B2 E ETB2. 证明由引理1,2可得,选取公共的Lyapunov 马=部K4Dm-E1 dt 矩阵并假设X,-X,Y=Y(i=1,2),即可得到定理1 M(-Rgi Kv+La (11) 3永磁直线电机数学模型 dy (K-Dy-F)M. di 在d-q坐标系中,假定选取电枢在d-q坐标 式中:K,为与电机参数有关的推力系数,K= 系中的直、交轴电流、,运动部分的速度和位移 15Aπ中,/兀,K=2K3n.写成状态方程的形式为 y作为状态变量,则永磁直线电机的状态方程为 X =AX +UB (12) Y=CX 6w-6+私,). dt La 式(12)中:X为状态向量,X=[6v:U=g:Y= -RLg-KL gF为扰动项,且A= KM D/M ,B= 10) d,Mf2B.中,6+ 1/Lg0,c=011 采用文献[3中提出的一三环系统,结构如图1 (La Lo)i 1 F-Dv. 所示。 dy 区a Ms+D (s) 图1永磁直线电机的控制结构图 Fig 1 Control structure diagram of pemanentmagnet linear mobr 基于图1,建立直线伺服不确定系统的状态表达式如下: 0 0 0 0 n501 n01 0 1+8(@ M x()= x()+ w u.(13) 0 0 0 K1+8(w] 号n+5o1-k.5n+o1可 M M C1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
∏ XF1 XE T X Y T F T 1 X T - ε3 I 0 0 0 EX T 0 - ε4 I 0 0 X T 0 0 - Q - 1 0 Y 0 0 0 - R - 1 < 0, (9) 则非脆弱控制器 u ( t) = ( F + △F ) x ( t)的名义控制 器增益 F = YX - 1且指标 2)中的 J 3 = trace ( X - 1 2 ). 其中 : ∏ = (AX +B2 Y) + (AX +B2 Y) T + ε3 E1 E T 1 +ε4B2 E1 E T 1B T 2 . 证明 由引理 1, 2可得,选取公共的 Lyapunov 矩阵并假设 Xi =X, Yi = Y( i =1, 2) ,即可得到定理 1. 3 永磁直线电机数学模型 在 d - q坐标系中 ,假定选取电枢在 d - q坐标 系中的直、交轴电流 id、iq ,运动部分的速度 v和位移 y作为状态变量 ,则永磁直线电机的状态方程为 did dt = 1 Ld ( ud - Rd id + π τ Lq viq ) , diq dt = 1 Lq ( ud - Rq iq - π τ ψf v) , dv dt = 1 M { 3 2 Pn π τ [ψf iq + (Ld - Lq ) id iq ]} - FL - D v, dy dt =v. (10) 式中 : ud、uq 为 d、q轴动子电压; id、iq 为 d、q轴动子 电流; Rd、Rq 为 d、q轴相绕组电阻; Ld、Lq 为 d、q轴 动子电感; v为动子移动速度;τ为磁极中心距; pn 为 极对数;ψf 为定子励磁磁链; FL 为负载阻力; D为与 速度有关的阻尼系数; M 为包括负载在内的移动系 统的质量. 现按照文献 [ 3 ]中的方法对此模型进行简化 , 即对永磁直线电机采用基于电流跟踪的矢量控制技 术 ,始终使直轴电流为零 , id ≡i 3 d = 0, 于是电机在 d - q坐标系下的模型可以简化为 diq dt = dv dt ( KT iq - D v - FL ) / M ( - Rq iq - Ki v + vq ) /Lq , dv dt = ( KT iq - D v - FL ) /M. (11) 式中 : KT 为与电机参数有关的推力系数 , KT = 1. 5pnπψf /τ, Ki = 2KT /3pn . 写成状态方程的形式为 XÛ= AX + UB, Y = CX. (12) 式 (12)中 : X为状态向量 , X = [ iq v ] T ; U = vq ; Y = v; FL 为 扰动项 , 且 A = - R /Lq - Ki /Lq KT /M - D /M , B = [ 1 /Lq 0 ] T , C = [ 0 1 ]. 采用文献 [3 ]中提出的一三环系统 ,结构如图 1 所示. 图 1 永磁直线电机的控制结构图 Fig. 1 Control structure diagram of permanent magnet linear motor 基于图 1,建立直线伺服不确定系统的状态表达式如下 : xÛ(t) = 0 1 0 0 0 - D M [1 +δ1 (t) ] KT M [1 +δ2 (t) ] 0 0 0 - Rq Lq 1 Lq 0 KPD M [1 +δ1 (t) ] - KI - KT KP M [1 +δ2 (t) ] 0 x ( t) + 0 - 1 +δ1 ( t) M 0 KP [1 +δ1 ( t) ] M w ( t) + 0 0 0 KI u ( t). (13) 第 1期 黄宜庆 ,等 :直线伺服系统的双目标非脆弱控制器的设计及仿真 ·87·

·88 智能系统学报 第4卷 式(13)中:8,()、8()为系统模型中DM,1M的 不确定参数摄动;0,>0,·2>0为参数摄动的最大 4数例仿真 值,即满足1⑧()1≤01,16()|≤02,01,02为已 选取文献[3中参数进行仿真,M.=25kgD.= 知常数 12N·s/m,K=25NA,E.=200N,K=50,K= 为充分考虑扰动的影响,式(2)中的w项的系 200,01=025,02=0125,Lg=90mH,R,=12 数固定取为摄动范围内的最大值,则式2可改写 取r=q=1,即要求闭环极点在半径为1,圆心 成系统1)的表达形式, 为(-1,0)的左半平面内,H= 其中: [02020202/,E=Q=l,R=1,P=031 0 1 0 0 利用Matlab中的M工具箱中feap求解决器 0 D K 0 求解线性矩阵不等式(8)和9),结果所得控制器的 M 增益: A R 0 0 F=[07235-7873106542-328611 Lg L 所以双目标非脆弱控制器增益: KpD KiK2 0 K 0 F·=F+△F= M M 07835-7813107142-322611, 0 0 0 闭环系统的二次型性能指标为J°=82642,极点 0 D8() K82(0 0 P.2=-0823502593iP=-13652.P4= M M △A -06914 0 0 0 0.6 0 KD6,() KK8,(0 0 0.5 一考虑控制器的加性摄动 M M 0.4 …不考虑控制器的加性摄动 0 0.3 1+8(少 0.2 0.1 M B1= 0 0 -0.1 K1+8,() -0.2 M -0.3 01 2345678910 由△A=E,∑F1,可得 1/s 0 0 图2直轴电流的状态曲线 0 1 E1= Fig 2 Response of D-axis currenti 0 0 0 -Kp 0.6 K 0.5f 考虑控制器的加性摄动 「8(d 0 0.4 …不考虑控制器的加性摄动 0 0 0.3 8(边 0 0 0.2 0 0.1 0 8(边 0, 0 -0.1 0 012345678910 t/s DO 0 0 图3交轴电流马的状态曲线 K02 0 0 Fig 3 Response of D-axis currenti, 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
式 (13)中 :δ1 ( t)、δ2 ( t)为系统模型中 D /M , 1 /M 的 不确定参数摄动;σ1 > 0,σ2 > 0为参数摄动的最大 值 ,即满足 |δ1 ( t) | ≤σ1 , |δ2 ( t) | ≤σ2 , σ1 ,σ2 为已 知常数. 为充分考虑扰动的影响 ,式 ( 2)中的 w 项的系 数固定取为摄动范围内的最大值 ,则式 ( 2)可改写 成系统 (1)的表达形式. 其中 : A = 0 1 0 0 0 - D M KT M 0 0 0 - Rq Lq 1 Lq 0 KPD M - KI - KT KP M 0 , △A = 0 0 0 0 0 - D M δ1 ( t) KT M δ2 ( t) 0 0 0 0 0 0 KPD M δ1 ( t) - KP KT M δ2 ( t) 0 , B1 = 0 - 1 +δ1 ( t) M 0 KP [1 +δ1 ( t) ] M . 由 △A = E1ΣF1 ,可得 E1 = 0 0 0 0 1 1 0 0 0 0 - KP - KP , Σ = δ1 ( t) σ1 0 0 0 δ1 ( t) σ1 0 0 0 δ2 ( t) σ2 , F1 = 0 0 0 0 0 - Dσ1 M 0 0 0 0 KTσ2 M 0 . 4 数例仿真 选取文献 [3 ]中参数进行仿真 , M e = 25 kg, De = 1. 2N·s/m, KTe = 25 N /A, FL e = 200 N, KP = 50, KI = 200,σ1 = 0. 25,σ2 = 0. 125, Lq = 9. 0 mH, Rq = 1. 2. 取 r = q = 1,即要求闭环极点在半径为 1,圆心 为 ( - 1, 0 ) 的 左 半 平 面 内 , H = [ 0. 2 0. 2 0. 2 0. 2 ], E =Q = I4 , R = 1, P = 0. 3 I. 利用 Matlab中的 LM I工具箱中 feasp求解决器 求解线性矩阵不等式 (8)和 (9) ,结果所得控制器的 增益 : F = [0. 723 5 - 7. 873 1 0. 654 2 - 3. 286 1 ]. 所以双目标非脆弱控制器增益 : F 3 = F + △F = [0. 783 5 - 7. 813 1 0. 714 2 - 3. 226 1 ], 闭环系统的二次型性能指标为 J 3 = 8. 264 2,极点 P1, 2 = - 0. 823 5 ±0. 259 3 i, P3 = - 1. 365 2, P4 = - 0. 691 4. 图 2 直轴电流 id 的状态曲线 Fig. 2 Response of D2axis current id 图 3 交轴电流 iq的状态曲线 Fig. 3 Response of D2axis current iq ·88· 智 能 系 统 学 报 第 4卷
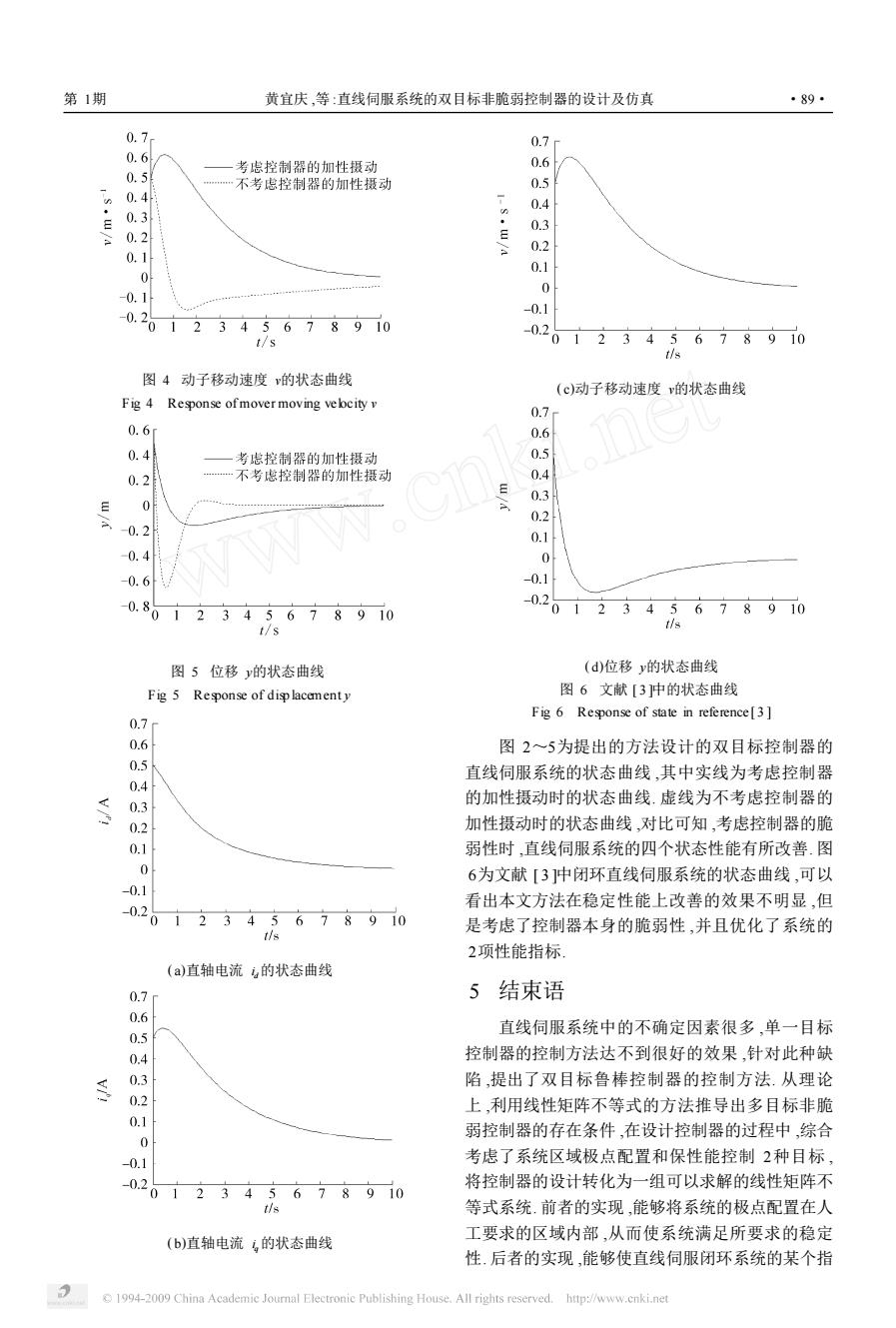
第1期 黄宜庆,等:直线伺服系统的双目标非脆弱控制器的设计及仿真 89 0.7 0.7 0.6 考虑控制器的加性摄动 0.6 0.5 …不考虑控制器的加性摄动 0.5 0.4 0.4 0.3 0.2 s.W/A 0.3 0.2 0.1 0.1 -0.1 0 -0.1 -0.2 01 2345678910 t/s -0.2012345678910 t/s 图4动子移动速度的状态曲线 (c)动子移动速度v的状态曲线 Fig 4 Response ofmover moving vebcity v 0.7 0.6 0.6 0.4 考虑控制器的加性摄动 0.5 0.2 不考虑控制器的加性摄动 0.4 0.3 0 0.2 0.2 0.1 -0.4 0.6 -0.1 0.8 -0.2 12345678910 012345678910 t/s 图5位移y的状态曲线 (d)位移yv的状态曲线 Fig 5 Response of disp lacementy 图6文献[3中的状态曲线 Fig 6 Response of state in reference[3] 0.7r 0.6 图2~5为提出的方法设计的双目标控制器的 0.5 直线伺服系统的状态曲线,其中实线为考虑控制器 0.4 0.3 的加性摄动时的状态曲线,虚线为不考虑控制器的 0.2 加性摄动时的状态曲线,对比可知,考虑控制器的脆 弱性时,直线伺服系统的四个状态性能有所改善.图 0 6为文献【3]中闭环直线伺服系统的状态曲线,可以 -0.1 0.2 看出本文方法在稳定性能上改善的效果不明显,但 012345678910 是考虑了控制器本身的脆弱性,并且优化了系统的 t/s 2项性能指标 (a)直轴电流的状态曲线 0.7 5结束语 0.6 0.5 直线伺服系统中的不确定因素很多,单一目标 0.4 控制器的控制方法达不到很好的效果,针对此种缺 0.3 陷,提出了双目标鲁棒控制器的控制方法.从理论 0.2 上,利用线性矩阵不等式的方法推导出多目标非脆 0.1 弱控制器的存在条件,在设计控制器的过程中,综合 0 -0.1 考虑了系统区域极点配置和保性能控制2种目标, 0.201 将控制器的设计转化为一组可以求解的线性矩阵不 2345678910 t/s 等式系统.前者的实现,能够将系统的极点配置在人 工要求的区域内部,从而使系统满足所要求的稳定 (b)直轴电流的状态曲线 性.后者的实现,能够使直线伺服闭环系统的某个指 1994-2009 China Academie Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 4 动子移动速度 v的状态曲线 Fig. 4 Response of mover moving velocity v 图 5 位移 y的状态曲线 Fig. 5 Response of disp lacement y ( a)直轴电流 id 的状态曲线 ( b)直轴电流 iq的状态曲线 ( c)动子移动速度 v的状态曲线 ( d)位移 y的状态曲线 图 6 文献 [ 3 ]中的状态曲线 Fig. 6 Response of state in reference[ 3 ] 图 2~5为提出的方法设计的双目标控制器的 直线伺服系统的状态曲线 ,其中实线为考虑控制器 的加性摄动时的状态曲线. 虚线为不考虑控制器的 加性摄动时的状态曲线 ,对比可知 ,考虑控制器的脆 弱性时 ,直线伺服系统的四个状态性能有所改善. 图 6为文献 [ 3 ]中闭环直线伺服系统的状态曲线 ,可以 看出本文方法在稳定性能上改善的效果不明显 ,但 是考虑了控制器本身的脆弱性 ,并且优化了系统的 2项性能指标. 5 结束语 直线伺服系统中的不确定因素很多 ,单一目标 控制器的控制方法达不到很好的效果 ,针对此种缺 陷 ,提出了双目标鲁棒控制器的控制方法. 从理论 上 ,利用线性矩阵不等式的方法推导出多目标非脆 弱控制器的存在条件 ,在设计控制器的过程中 ,综合 考虑了系统区域极点配置和保性能控制 2种目标 , 将控制器的设计转化为一组可以求解的线性矩阵不 等式系统. 前者的实现 ,能够将系统的极点配置在人 工要求的区域内部 ,从而使系统满足所要求的稳定 性. 后者的实现 ,能够使直线伺服闭环系统的某个指 第 1期 黄宜庆 ,等 :直线伺服系统的双目标非脆弱控制器的设计及仿真 ·89·

·90· 智能系统学报 第4卷 标小于一个确定的上界,具有现实应用意义.同时进 chno bgy,2000,22(5):396-399 一步考虑了控制器本身存在的脆弱性,此种控制方 [7偷立.鲁棒控制线性矩阵不等式处理方法M] 法在直线伺服系统的控制中具有广泛的应用前景 北京:清华大学出版社,2002 最后给出具体的数例进行仿真,从仿真结果可以看 [8谢立,王国强,刘济林.圆盘区域极点约束鲁棒非脆弱 出,设计的控制器改善了系统的稳定性并且闭环系 控制[J]传感技术学报,2006,19(2):486-490 XIE Li,WANG Guoqiang,L U Jilin Robust non-fragile 统都达到了所要求的2个性能指标 control with pole constraint in a circular disk[J]Chinese 参考文献: Joumal of Sensors and Actuators,2006,19(2):486-490. [9]史忠科,吴方向,王蓓,等.鲁棒控制理论[M1北京 [1]ZHOU Xianfeng,JANGWen The pole placement of a sin- 国防工业出版社,2003 gular system with delay [J ]Math,2007,22 (3):384- [10]XUE Anke,SUN Youxian On the robustness of quadratic 387. guaranteed cost control or parameter uncertain systems [2]YU Li,CHU Jian An LM I approach to guaranteed cost [J]Contol Theory and App lications,2000,17(6):941- control of linear uncertain tme-delay system s[J.Automat- 944 ic,1999,35(6):1155-1159 [11 ]L IEN C H,LEONDES C T Guaranteed cost observer [3陈一秀,王永初.直线伺服系统的鲁棒保性能控制研究 based controls for a class of uncertain neutral tme-delay [J]中国电机工程学报,2006,26(24):174-178 systams [J ]Optm ization Theory and Applications, CHEN Yixiu,WANG Yongchu Study on robust guaranteed 2005,11(6):137-156 cost control for linear moor servo system [J]Proceedings 作者简介: of the CSEE (Chinese Society for Electrical Engineering), 黄宜庆,男,1983年生,硕士研究 2006,26(24):174-178 生,主要研究方向为智能控制和鲁棒控 [4侏国听,郭庆鼎.永磁直线伺服系统H鲁棒控制的综 制理论 合与分析[J]电机与控制学报,2006,10(1):13. ZHU Guoxin,GO Qingding Synthesis and analysis ofo bust control or pemanent magnet linear servo system [J ] 黄友锐,男,1971年生,教授,硕士 Electric Machines and Contol,2006,10(1):1-3 生导师,电气与信息工程学院院长.主 [5 FAMULARO D,DORATO P Robust non-fragile LQ con- 要研究方向为智能控制和运动控制理 toller the static state feedback case [J]Int J Control, 论,发表学术论文38篇, 2000,73(2):159-165 [6傅建国,郭庆鼎,唐光谱.直线永磁同步伺服电机H鲁 棒位置控制器设计[J]沈阳工业大学学报,2000,22 章魁,男,1981年生,助教,主要 (5):396-399 研究方向为智能控制理论 FU Jianguo,GO Q ingding.TANG Guangpu Robust posi- tion controller design for linear pemanent magnet syncho- nous servo motor[J].Joumal of Shenyang University of Te- 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
标小于一个确定的上界 ,具有现实应用意义. 同时进 一步考虑了控制器本身存在的脆弱性 ,此种控制方 法在直线伺服系统的控制中具有广泛的应用前景. 最后 ,给出具体的数例进行仿真 ,从仿真结果可以看 出 ,设计的控制器改善了系统的稳定性并且闭环系 统都达到了所要求的 2个性能指标. 参考文献 : [ 1 ] ZHOU Xianfeng, J IANGW en. The pole p lacement of a sin2 gular system with delay [ J ]. Math, 2007, 22 ( 3 ) : 3842 387. [ 2 ] YU L i, CHU Jian. An LM I app roach to guaranteed cost control of linear uncertain time2delay systems[J ]. Automat2 ic, 1999, 35 (6) : 115521159. [ 3 ]陈一秀 , 王永初. 直线伺服系统的鲁棒保性能控制研究 [J ]. 中国电机工程学报 , 2006, 26 (24) : 1742178. CHEN Yixiu, WANG Yongchu. Study on robust guaranteed cost control for linear motor servo system [J ]. Proceedings of the CSEE (Chinese Society for Electrical Engineering) , 2006, 26 (24) : 1742178. [ 4 ]朱国昕 , 郭庆鼎. 永磁直线伺服系统 H∞鲁棒控制的综 合与分析 [J ]. 电机与控制学报 , 2006, 10 (1) : 123. ZHU Guoxin, GUO Q ingding. Synthesis and analysis of ro2 bust control for permanent magnet linear servo system [J ]. Electric Machines and Control, 2006, 10 (1) : 123. [ 5 ] FAMULARO D, DORATO P. Robust non2fragile LQ con2 troller the static state feedback case [ J ]. Int J Control, 2000, 73 (2) : 1592165. [ 6 ]傅建国 ,郭庆鼎 ,唐光谱. 直线永磁同步伺服电机 H∞鲁 棒位置控制器设计 [ J ]. 沈阳工业大学学报 , 2000, 22 (5) : 3962399. FU Jianguo, GUO Q ingding, TANG Guangpu. Robust posi2 tion controller design for linear permanent magnet synchro2 nous servo motor[J ]. Journal of Shenyang University of Te2 chnology, 2000, 22 (5) : 3962399. [ 7 ]俞 立. 鲁棒控制 ———线性矩阵不等式处理方法 [M ]. 北京 :清华大学出版社 , 2002. [ 8 ]谢 立 ,王国强 ,刘济林. 圆盘区域极点约束鲁棒非脆弱 控制 [J ]. 传感技术学报 , 2006, 19 (2) : 4862490. X IE L i, WANG Guoqiang, L IU Jilin. Robust non2fragile control with pole constraint in a circular disk [J ]. Chinese Journal of Sensors and Actuators, 2006, 19 (2) : 4862490. [ 9 ]史忠科 ,吴方向 ,王 蓓 ,等. 鲁棒控制理论 [M ]. 北京 : 国防工业出版社 , 2003. [ 10 ]XUE Anke, SUN Youxian. On the robustness of quadratic guaranteed cost control for parameter uncertain system s [ J ]. Control Theory and App lications, 2000, 17 (6) : 9412 944. [ 11 ]L IEN C H, LEONDES C T. Guaranteed cost observer2 based controls for a class of uncertain neutral time2delay system s [ J ]. Op tim ization Theory and App lications, 2005, 11 (6) : 1372156. 作者简介 : 黄宜庆 ,男 , 1983 年生 ,硕士研究 生 ,主要研究方向为智能控制和鲁棒控 制理论. 黄友锐 ,男 , 1971年生 ,教授 ,硕士 生导师 ,电气与信息工程学院院长. 主 要研究方向为智能控制和运动控制理 论 ,发表学术论文 38篇. 章 魁 ,男 , 1981年生 ,助教 ,主要 研究方向为智能控制理论. ·90· 智 能 系 统 学 报 第 4卷