
第3卷第6期 智能系统学报 Vol.3 No.6 2008年12月 CAAI Transactions on Intelligent Systems Dec.2008 最佳鉴别矢量集在无监督模式下的扩展 曹苏群2,王士同,陈晓峰,邓赵红 (1.江南大学信息学院,江苏无锡214122:2.淮阴工学院机械系,江苏淮安223001) 摘要:基于Fisher准则函数的最佳鉴别矢量集是一种重要的有监督特征提取方法,在模式识别领域有着重要的影 响.提出一种将最佳鉴别矢量集扩展到无监督模式下的方法,其基本思想是通过定义的模糊Fisher准则函数将Fish- 线性判别扩展成一种半模糊聚类算法,通过该算法求得最佳鉴别矢量和模糊散布矩阵,进而构造出最佳鉴别矢量 集.实验表明,在聚类有效性、分类准确率均优于无监督模式下常用的主成分分析特征提取算法. 关键词:最佳鉴别矢量集;无监督模式;Fisher准则;半模糊聚类 中图分类号:TP181文献标识码:A文章编号:1673-4785(2008)060511-12 Extending the optimal set of discriminant vectors for an unsupervised pattern CAO Su-qun'2,WANG Shi-tong',CHEN Xiao-feng',DENG Zhao-hong (1.School of Information,Jiangnan University,Wuxi 214122,China;2.Department of Mechanical Engineering,Huaiyin Institute of Technology,Huaian 223001,China) Abstract:The optimal set of discriminant vectors,based on the Fisher criterion function,is an important supervised feature extraction method and has great influence in the area of pattern recognition.In this paper,an extension of the optimal set of discriminant vectors in unsupervised patterns is presented.The basic idea is to extend Fisher line- ar discriminants to a novel semi-fuzzy clustering algorithm through a predefined fuzzy Fisher criterion function.With the proposed algorithm,an optimal discriminant vector and fuzzy scatter matrixes can be figured out and then an un- supervised optimal set of discriminant vectors can be obtained.Experimental results for real datasets,testing cluste- ring validity and correct classification recognition rates,demonstrated that this method is superior to the principal component analysis feature extraction algorithm in unsupervised patterns. Keywords:optimal set of discriminant vectors;unsupervised pattern;Fisher criterion;semi-fuzzy clustering 在模式识别领域中,Fisher线性判别方法应别矢量计算公式,实现了高维特征空间向低维空 用广泛,其基本思想是在Fisher准则函数取极值条间的投影转换.Jin和Yang等在文献[5]中给出了 件下,求得一个最佳鉴别方向,然后将模式高维特征 较Duchene和Leclercq更为简单的最佳鉴别矢量计 向量投影到该最佳鉴别方向上,构成一维鉴别特征 算公式并提出了具有统计不相关性的最佳鉴别矢量 空间,进而在此一维空间完成模式鉴别分析.Sam- 集.此后,文献[6-11]对此进行了进一步探讨.由于 mon在1970年发展了Fisher线性判别方法,提出了 在无监督模式下,通常无法使用Fisher线性判别方 最佳鉴别平面技术[],将它用于解决两类问题,实 法求解最佳鉴别矢量,因此所有这些最佳鉴别矢量 现了高维特征空间向二维空间的投影转换.Foly和 集计算方法均只适用于样本类别信息已知情况下. Sammon进一步对两类问题提出了最佳鉴别矢量 本文提出一种将最佳鉴别矢量集扩展到无监督 集3].Duchene和Leclercq给出了多类问题的最佳鉴 模式下的方法,其基本思想是:通过给出模糊Fisher 准则函数定义,实现Fisher线性判别在无监督模式 收稿日期:2008-05-12. 下的扩展,进而求得无监督模式下基于模糊Fisher 基金项目:教育部优秀人才支持计划资助项目(NCET-040496):教 育部重点科学研究资助项目(105087). 准则的最佳鉴别矢量,在此基础上参照传统最佳鉴 通信作者:曹苏群.mail:caosuqun@126.com. 别矢量集计算方法完成其在无监督模式下的扩展

·512. 智能系统学报 第3卷 按照文献[12]中对无监督情况下的特征降维方法 其中:入为Lagrange乘子,o,即该广义特征方程中 的分类,从本质上讲,本文提出的方法属于聚类后降 最大的特征值对应的特征向量.对于两类问题,可以 维34],即通过聚类得到样本类别信息,从而将有 求得w1=S(m1-m2).通过Y=wX,实现模式X 监督特征降维方法引人无监督模式. 由d维向1维的投影转换. 若已求出k(k≥1)个最佳鉴别矢量w1,w2,…, 1最佳鉴别矢量集 w4,第个最佳鉴别矢量wk+1是在满足下列正交条 设X包含N个d维样本x1,x2,…,xw,可用d× 件下的使得式(1)取得最大值的向量: N矩阵表示,模式类别有c个,各类别样本数分别为 w+10=0,i=1,2,…,k (3) N(i=1,2,…,c),N,+N2+…+N。=N.定义模式 由文献[5]知,ω+1是下列广义特征方程中最大的 类间散布矩阵S。和类内散布矩阵S。分别为 特征值对应的特征向量: =含0m-m-, PSO+=AS.@k+ (4) 其中P=I-D(DSD)-DS,这里记D= S.=名名(5-m)4识 c Ni [w2…0]. 求出的r(r≤d)个最佳鉴别矢量w1,2,…,w, 式中:x表示属于第i类的样本,m:(i=1,2,…,c) 构成最佳鉴别矢量集,通过 是第类样本的均值向量,x是总体样本的均值向 量. 定义Fisher准则函数为 Y= w J(w)= wSw a'S.0. (1) 实现模式X由d维向r维的投影转换。 使J(ω)取得极大值的矢量ω,称为最佳鉴别 综上所述,可以用下图表示Fisher准则函数、最 矢量,此时,样本在ω1方向投影将具有最大类间散 佳鉴别矢量、最佳鉴别平面和最佳鉴别矢量集的求 布和最小类内散布.使用Lagrange乘子法求解知, 解关系。 当S非奇异时,有 S6w1=入Snw1: (2) 散布师阵S。,S 最伴鉴别矢量w,(d维→1维) S0,=S0, 00,=0(1,2,,r1) Fisher准划函数 max (J.) 最佳鉴别矢苹集w,o,,w,(d雌→) J(o)-_o'So PS@=S.0 oSo 图1 Fisher准则函数及最佳鉴别矢量、最佳鉴别矢量集求解关系 Fig.1 Relationships between Fisher criterion function and optimal set of discriminant vectors 2无监督模式下最佳鉴别矢量集 5-名25-g-) 2.1模糊Fisher准则函数 模糊类间散布矩阵记为S 参照Wu等在文献[15]中模糊散布矩阵定义, S师=】 9(m-到(m-到 (6) 将模糊理论引入Fisher判别方法, 在样本空间,定义模糊类内散布矩阵记为S, 式中:x为所有样本均值向量,m:为第i类样本均值 向量,c为类别数,N为样本总数,u为j样本属于第

第6期 曹苏群,等:最佳鉴别矢量集在无监督模式下的扩展 ·513· i类的隶属度,4e[0,1]且公g=1,m为模糊指数 函数: 且m>1,一般可取2, J。= wSBω S加-wSω (8) 设y=ωx,在该投影空间,定义各类样本均值 2.2基于模糊Fisher准则的算法 向量记为m,有 使用Lagrange乘子法求解J取得极大值时,取 m:w'm (7) w,m:和g的值. 定义模糊类内散布矩阵记为S, 3.-名-成0G- 定义Lagrange函数为 L=wSBw-λwSw+ 's-o'm.)(o'x,-o'm)!- 名(名- (9) wS W 式中:入和入G=1,2,…,n)为Lagrange乘子. 将L分别对w,m:及4求偏导数,并令偏导数 模糊类间散布矩阵记为S· 为零,经附录A求解步骤可求得 =名(m-)(m- Spo =ASkew, (10) 含2w属到aw属-o到r m= (11) oTSBω 月41- 定义模糊Fisher准则(fuzzy Fisher criterion) (w(出-m)g-)w-o(m-(m-到w)六 4g= (12) A(w(5-m,)(丐-m,)w-w(m,-)(m.-到o) 解式(10)为求一般矩阵SS%的本征值问题,取A 1.0 0.9 最优鉴州矢是方向线 为该矩阵的最大特征值,而ω为对应的特征向量. 0.8 在模糊聚类中,通常限定g∈[0,1];因此,对 青马便分区 0.7 式(12)给出如下限定条件,若 06 w'(x-m)(x-m:)w≤ 0.5 0.4 o(%-(m-到o, 。二8品 分界我。8 (13) 0.3 0.2 则:山g=1,且对所有≠i,有=0.也就是说,当该 0.1 条件满足时,样本点x将完全隶属于第i类,即在此 0 0.20.4x0.60.81.0 范围内采用硬划分.根据此条件几何意义知:将样本 点、聚类中心以及所有样本中心向ω方向投影,若 图2FFC聚类硬划分区示意图 样本投影点与聚类中心投影点欧氏距离小于或等于 Fig.2 Fuzzy Fisher criterion based clustering hard partition regions 聚类中心投影点与所有样本中心投影点间欧氏距离 1)使用K-means算法初始化隶属矩阵U以及 的上,则对该点采用硬划分可以使用图2,对此作 聚类中心m:; 出直观解释 2)使用式(5)、(6)分别计算S和SB,根据式 图中:“口”为第1类样本点,“O”为第2类样 (10)求得广义特征方程的最大特征值入,并取w为 本点,样本点中带“·”标记的为满足式(13)而采用 属于入的模为1的特征向量; 硬划分的点,将这些点按虚线方向向最佳鉴别矢量 3)使用式(8)计算模糊Fisher准则函数Jc,若 方向线投影 它相对上次准则函数数值的改变量小于某个给定阈 根据求解结果,本算法描述如下: 值或迭代次数超过设定次数,则算法停止;

.514 智能系统学报 第3卷 4)使用式(12)、(11)分别计算新的隶属矩阵U 其中P=I-DT(DSD)1DS,这里记D= 以及聚类中心m:,返回步骤2) [w,w2…]. 2.3无监督模式下最佳鉴别矢量集 求出的r(r≤d)个最佳鉴别矢量w1,2,…,w 通过上述算法,由式(10)求得最佳鉴别矢量, 构成最佳鉴别矢量集,同样通过 设为ω1,并根据求得的隶属矩阵U和聚类中心m, 由式(5)和(6)求得S和Sb 「w 若已求出(k≥1)个最佳鉴别矢量w1,w2,…, Y= X wk,第k+1个最佳鉴别矢量wk+1是在满足下列正 交条件下的使得式(1)取得最大值的向量 @r w+1w:=0,i=1,2,…,k 实现模式X由d维向r维的投影转换, 参照式(4)知,k+1是下列广义特征方程中最大的 综上所述,对照图1,可以用图3表示最佳鉴别 特征值对应的特征向量: PSp@k-1=ASωk+Ir 矢量集在无监督模式下的扩展方法, 最佳鉴别矢w,(d维→1维) 模糊散i矩阵SS S@=1S.0 w'u=0(1=1,2,,r-1) 模糊Fisher准同函数: max (Je) 最件鉴别矢址集0,:,0,(维→r维) J(w)= oSw PS.@.=AS m. 0s0 图3模糊Fisher准则函数及最佳鉴别矢量、最佳鉴别矢量集求解关系 Fig.3 Relationships between fuzzy Fisher criterion function and unsupervised optimal set of discriminant vectors 名的约当指数(Rand index,RI)I7]作为聚类有效性 3 实验结果及其分析 评价指标 采用UCI16中is,Wdc等4个数据集作为实 RI具体解释如下:定义P,P2分别为原数据集 验数据,这4个数据集基本信息如表1所示, D的类别标记和变换后数据集聚类划分结果,通过 表1实验所用数据集的基本信息 公式 Table 1 Basic information of experimental dataset 数据集 类别数样本数特征数 R(P,P:)=nx(n-1)/2 a +b Iris 3 150 4 来计算这两种划分的一致性.其中:a表示D中任意 Pima indians diabetes 2 768 两个样本d:、d在P、P2中同属于一类的个数;b表 Wine 3 178 13 示d:、d,都不属于同一类的个数;n表示数据集D的 Wdbe 2 569 30 样本个数.显然,I的范围为[0,1],只有在P、P2 3.1聚类有效性 完全一致的情况下,I值为1.I统计的值越小,两 使用FCM和K-means算法分别对使用主成分 种划分差距越大.为了保证比较的准确性和公平性, 分析(principal component analysis,PCA)、最佳鉴别 两种算法分别进行100次,计算测得的R肛均值,并 矢量集(optimal set of discriminant vectors,OSDV)和 绘制FCM和K-means分别对降维数据进行聚类所 无监督最佳鉴别矢量集(unsupervised optimal set of 得RI值和特征维数曲线图以及分别采用PCA,OS discriminant vectors,UOSDV)降维后的数据进行聚 DV和UOSDV降维后2维数据散布图如图4~7和 类,将聚类结果与原数据集类别标记相比较,通过著 表2~5所示
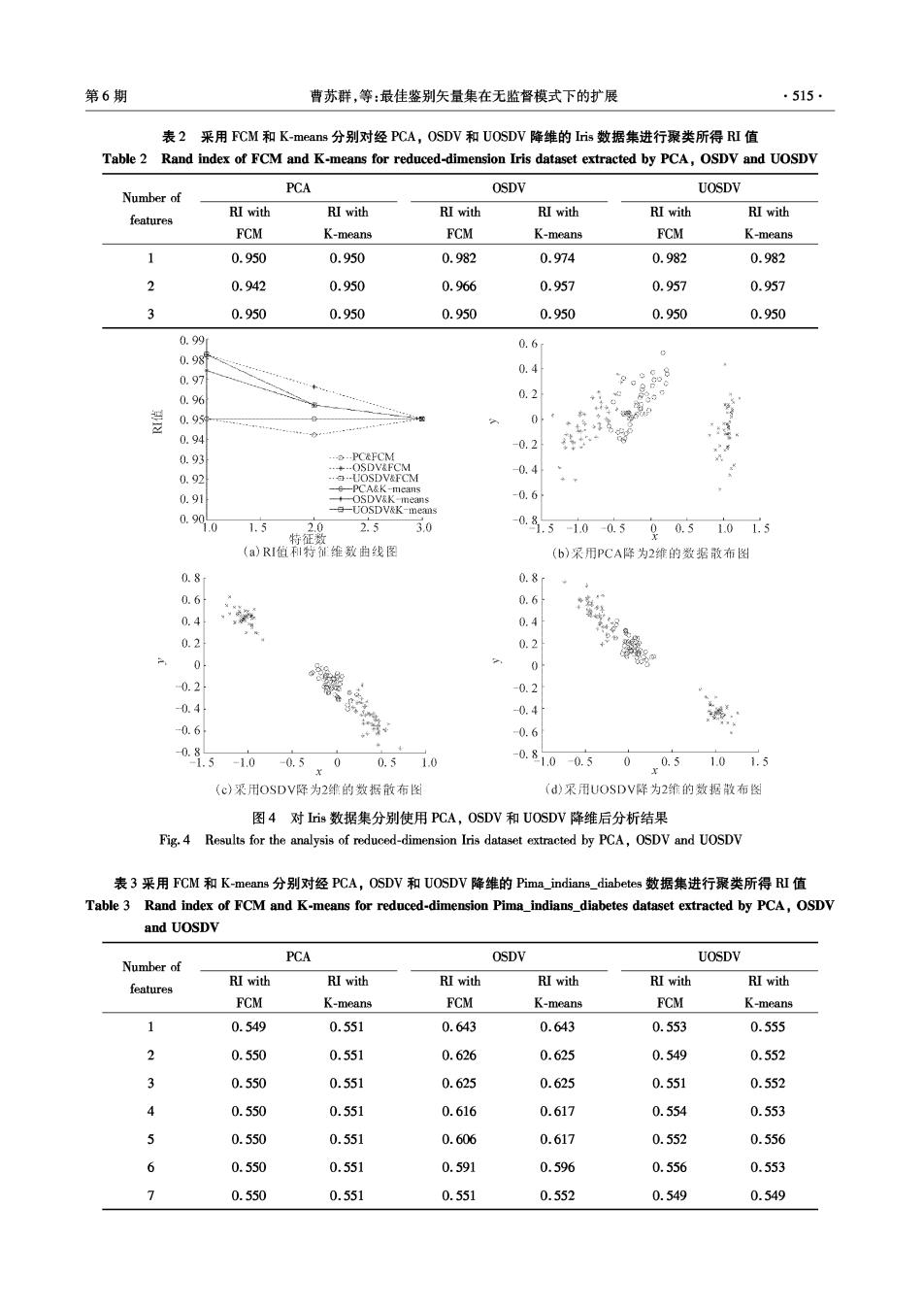
第6期 曹苏群,等:最佳鉴别矢量集在无监督模式下的扩展 ·515· 表2采用FCM和K-means分别对经PCA,OSDV和UOSDV降维的Inis数据集进行聚类所得RI值 Table 2 Rand index of FCM and K-means for reduced-dimension Iris dataset extracted by PCA,OSDV and UOSDV PCA OSDV UOSDV Number of RI with RI with RI with features RI with RI with RI with FCM K-means FCM K-means FCM K-means 1 0.950 0.950 0.982 0.974 0.982 0.982 2 0.942 0.950 0.966 0.957 0.957 0.957 3 0.950 0.950 0.950 0.950 0.950 0.950 0.99 0.6 0.981 0.4 0.97 0.96 0.2 0.95 0 0.94 0.2 0.93 PC&FCM -0.4 0.92 0.91 OSDV&K eans 0.6 0.9 1.0 1.5 2.5 3.0 特征数 -0.8.510-0.5 90.51015 (a)RI但I符征维数曲线图 (b)采用PCA降为2维的数据散布图 0.8 0.8r 0.6 0.6 4 0.4 0.4 0.2 0.2 0 0 0.2 -0.2 0.4 -0.4 -0.6 0.6 0.8 1.5 -1.0 -0.5 0 0.51.0 0.810 -0.5 0 r05 1.01.5 (c)采用OSDV降为2维的数据散布图 (d)采用JOSDV降为2维的数据散布图 图4对Iis数据集分别使用PCA,OSDV和UOSDV降维后分析结果 Fig.4 Results for the analysis of reduced-dimension Iris dataset extracted by PCA,OSDV and UOSDV 表3采用FCM和K-means分别对经PCA,OSDV和UOSDV降维的Pima_indians_.diabetes数据集进行聚类所得RI值 Table 3 Rand index of FCM and K-means for reduced-dimension Pima_indians diabetes dataset extracted by PCA,OSDV and UOSDV PCA OSDV UOSDV Number of RI with RI with RI with RI with RI with RI with features FCM K-means FCM K-means FCM K-means 1 0.549 0.551 0.643 0.643 0.553 0.555 2 0.550 0.551 0.626 0.625 0.549 0.552 3 0.550 0.551 0.625 0.625 0.551 0.552 4 0.550 0.551 0.616 0.617 0.554 0.553 5 0.550 0.551 0.606 0.617 0.552 0.556 6 0.550 0.551 0.591 0.596 0.556 0.553 1 0.550 0.551 0.551 0.552 0.549 0.549
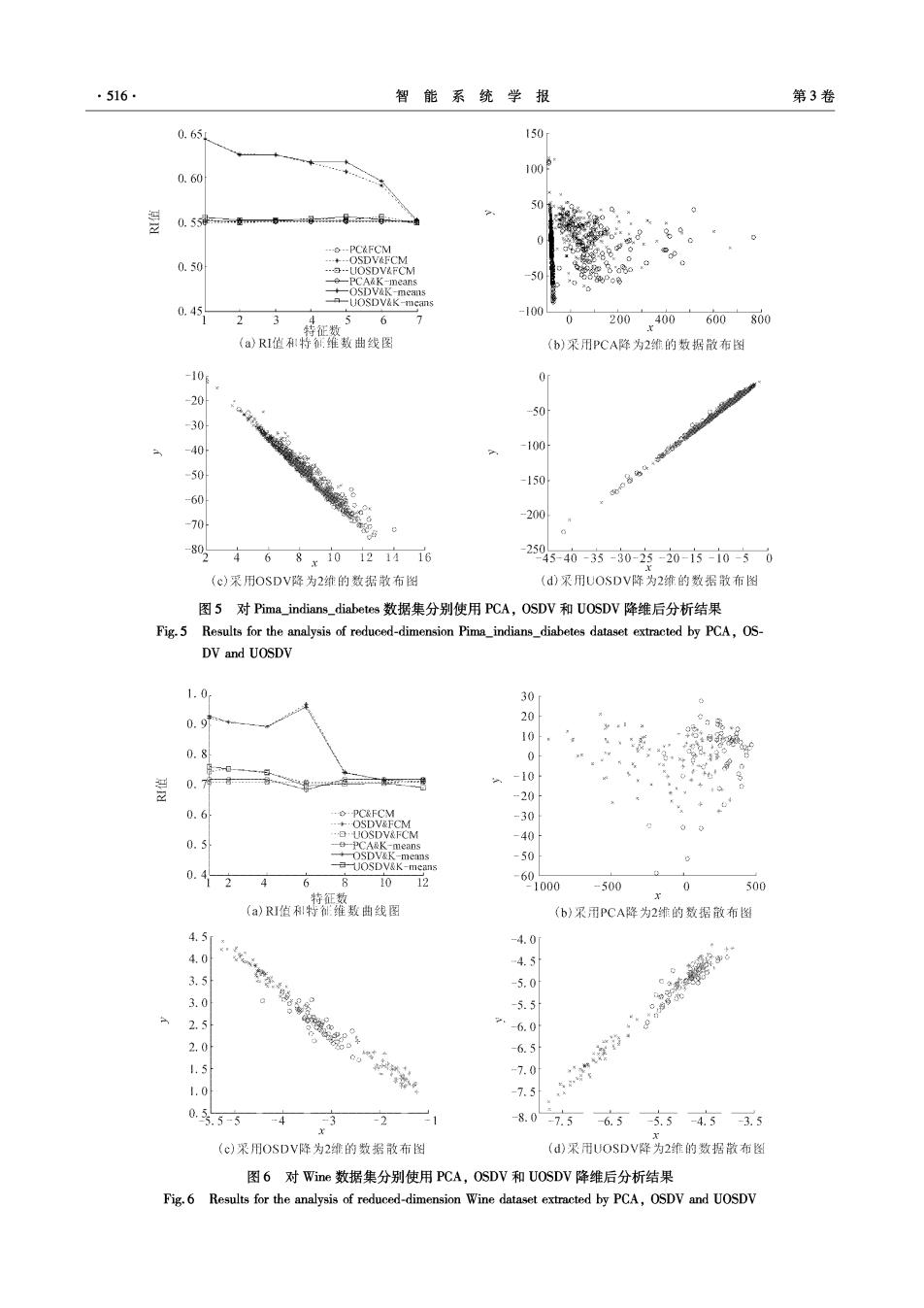
516 智能系统学报 第3卷 0.65 150 0.60 100 50 0.55禄… ----PC&FCM 0.50 a.0gD 50 -OSDV& means means 0.45 -UOSDV&K-means -100 2 3 567 200400600800 (a)RI值:特征维数曲线图 (b)采用PCA降为2维的数据散布图 -10e 0 -20 0 -30 -40 -100 50 -150 60 70 -200 0% 4 68x10121416 25045-40-3-80-320-1市-1050 (c)采用OSDV降为2维的数据散布图 (d)采用UOSDV降为2维的数据散布图 图5对Pima_indians_.diabetes数据集分别使用PCA,OSDV和UOSDV降维后分析结果 Fig.5 Results for the analysis of reduced-dimension Pima_indians_diabetes dataset extracted by PCA,OS- DV and UOSDV 1.0 30 0.9 10 0.8 0 0.7 -10 -20 0.6 PC&FCM -+·OSDV&FCM -30 ·UOSDV&FCM -40 0.5 台PCA&K-means 988"e % 0.4 2 6 10 12 60 000 -500 0 500 特征数 (a)RI值和特维数曲线图 (b)采用PCA降为2维的数据散布图 4.5m -4.0 4.0 -4.5 3.5 -5.0 3.0 -5.5 2.5 -6.0 2.0 -6.5 1.5 -7.0 1.0 -7.5 0.5.5-5 -4 3 -21 8.0-7.56.5-5.5-4.53.5 (c)采用OSDV降为2绯的数据散布图 (d)采用UOSDV降为2维的数据散布图 图6对Wie数据集分别使用PCA,OSDV和UOSDV降维后分析结果 Fig.6 Results for the analysis of reduced-dimension Wine dataset extracted by PCA,OSDV and UOSDV

第6期 曹苏群,等:最佳鉴别矢量集在无监督模式下的扩展 517 表4采用FCM和K-means分别对经PCA,OSDV和UOSDV降维的Wine数据集进行聚类所得RI值 Table 4 Rand index of FCM and K-means for reduced-dimension Wine dataset extracted by PCA,OSDV PCA OSDV UOSDV Number of features RI with RI with RI with RI with RI with RI with FCM K-means FCM K-means FCM K-means 1 0.711 0.719 0.924 0.931 0.745 0.761 2 0.711 0.719 0.910 0.910 0.754 0.754 4 0.711 0.719 0.896 0.896 0.742 0.744 6 0.711 0.685 0.969 0.961 0.707 0.698 8 0.711 0.719 0.744 0.741 0.704 0.704 10 0.711 0.719 0.715 0.717 0.707 0.707 12 0.711 0.719 0.712 0.719 0.714 0.692 800 0.90 600 0.85 400 0.80 200 0 0.70 .PC&FCM -200-9 0.65 +…OSDV&FCM …b-UOSDV&FCM -400- -e-PCA&K-means 0.60 车08*em -600 0.55 -800 5 10 15 20 25 4000-3000-2000-1000 01000 特征数 (a)RI俏和特征维数出线图 (b)采用PCA降为2维的数据散布图 0.18 -0.02 0.16 -0.04 0.14 -0.06 0.12 .-0.08 0.10 0.10 0.08 0.06 0.0%.17 -0.150.130.110.090.0 0.2 -0.10-0.080.06 -0.04 (c)采用OSDV降为2维的致据散布图 (d)采用UOSDV降为2维的数据做图 图7对Wdc数据集分别使用PCA,OSDV和UOSDV降维后分析结果 Fig.7 Results for the analysis of reduced-dimension Wdbe dataset extracted by PCA,OSDV and UOSDV 表5采用FCM和K-means分别对经PCA,OSDV和UOSDV降维的Wdbc数据集进行聚类所得RI值 Table 5 Rand index of FCM and K-means for reduced-dimension Wdbc dataset extracted by PCA,OSDV and UOSDV PCA OSDV UOSDV Number of RI with features RI with RI with RI with RI with RI with FCM K-means FCM K-means FCM K-means 1 0.750 0.750 0.935 0.932 0.863 0.863
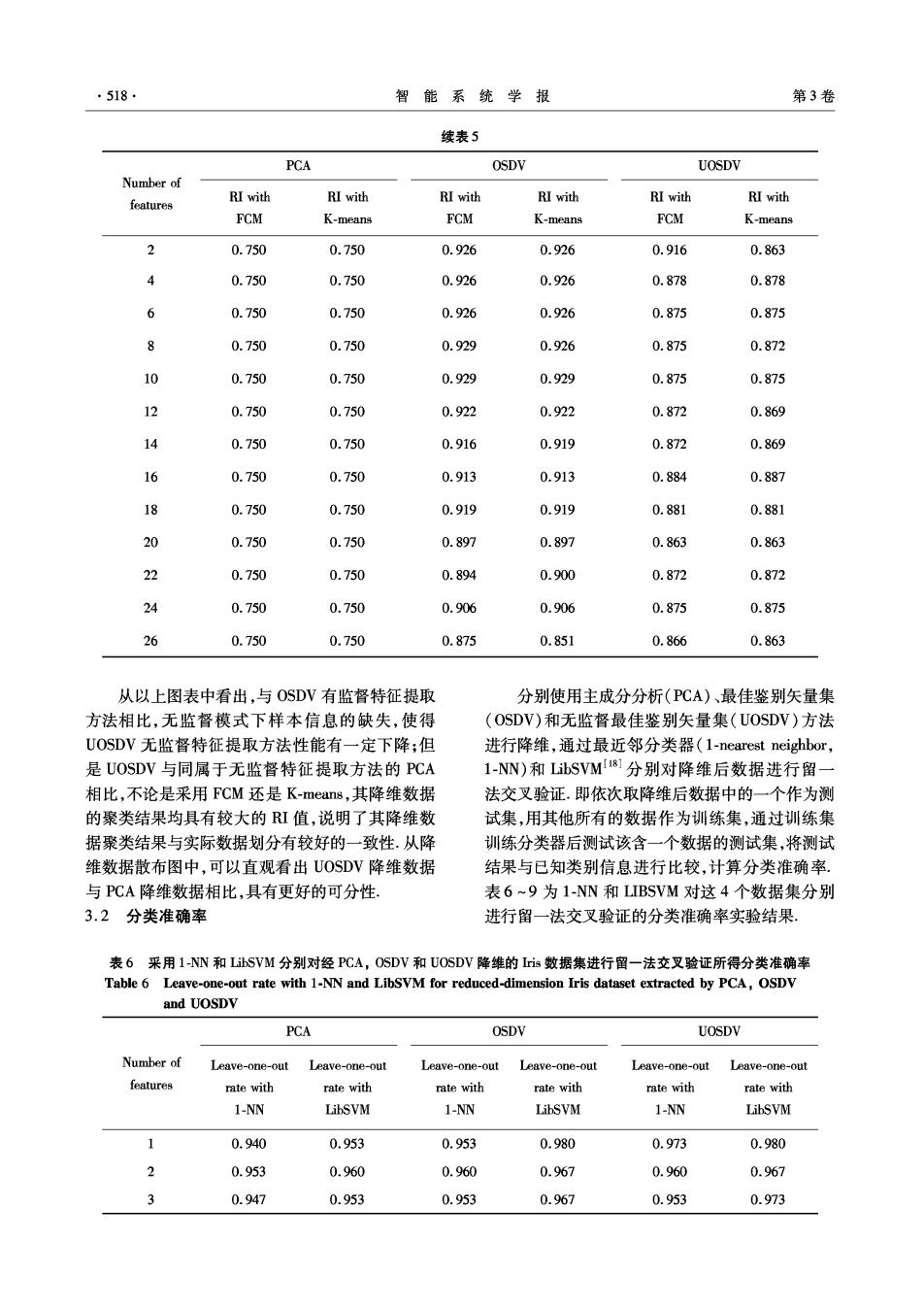
·518. 智能系统学报 第3卷 续表5 PCA OSDV UOSDV Number of RI with RI with RI with RI with RI with features RI with FCM K-means FCM K-means FCM K-means 2 0.750 0.750 0.926 0.926 0.916 0.863 4 0.750 0.750 0.926 0.926 0.878 0.878 6 0.750 0.750 0.926 0.926 0.875 0.875 8 0.750 0.750 0.929 0.926 0.875 0.872 10 0.750 0.750 0.929 0.929 0.875 0.875 12 0.750 0.750 0.922 0.922 0.872 0.869 14 0.750 0.750 0.916 0.919 0.872 0.869 16 0.750 0.750 0.913 0.913 0.884 0.887 18 0.750 0.750 0.919 0.919 0.881 0.881 20 0.750 0.750 0.897 0.897 0.863 0.863 22 0.750 0.750 0.894 0.900 0.872 0.872 24 0.750 0.750 0.906 0.906 0.875 0.875 26 0.750 0.750 0.875 0.851 0.866 0.863 从以上图表中看出,与OSDV有监督特征提取 分别使用主成分分析(PCA)、最佳鉴别矢量集 方法相比,无监督模式下样本信息的缺失,使得 (OSDV)和无监督最佳鉴别矢量集(UOSDV)方法 UOSDV无监督特征提取方法性能有一定下降;但 进行降维,通过最近邻分类器(1-nearest neighbor, 是UOSDV与同属于无监督特征提取方法的PCA 1-NN)和LibSVM81分别对降维后数据进行留 相比,不论是采用FCM还是K-means,其降维数据 法交叉验证.即依次取降维后数据中的一个作为测 的聚类结果均具有较大的I值,说明了其降维数 试集,用其他所有的数据作为训练集,通过训练集 据聚类结果与实际数据划分有较好的一致性.从降 训练分类器后测试该含一个数据的测试集,将测试 维数据散布图中,可以直观看出UOSDV降维数据 结果与已知类别信息进行比较,计算分类准确率. 与P℃A降维数据相比,具有更好的可分性。 表6~9为1-NN和LIBSVM对这4个数据集分别 3.2分类准确率 进行留一法交叉验证的分类淮确率实验结果, 表6采用1-NN和LibSVM分别对经PCA,OSDV和UOSDV降维的is数据集进行留一法交叉验证所得分类准确率 Table 6 Leave-one-out rate with 1-NN and LibSVM for reduced-dimension Iris dataset extracted by PCA,OSDV and UOSDV PCA OSDV UOSDV Number of Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out features rate with rate with rate with rate with rate with rate with 1-NN LibSVM 1-NN LibSVM 1-NN LibSVM 1 0.940 0.953 0.953 0.980 0.973 0.980 2 0.953 0.960 0.960 0.967 0.960 0.967 3 0.947 0.953 0.953 0.967 0.953 0.973
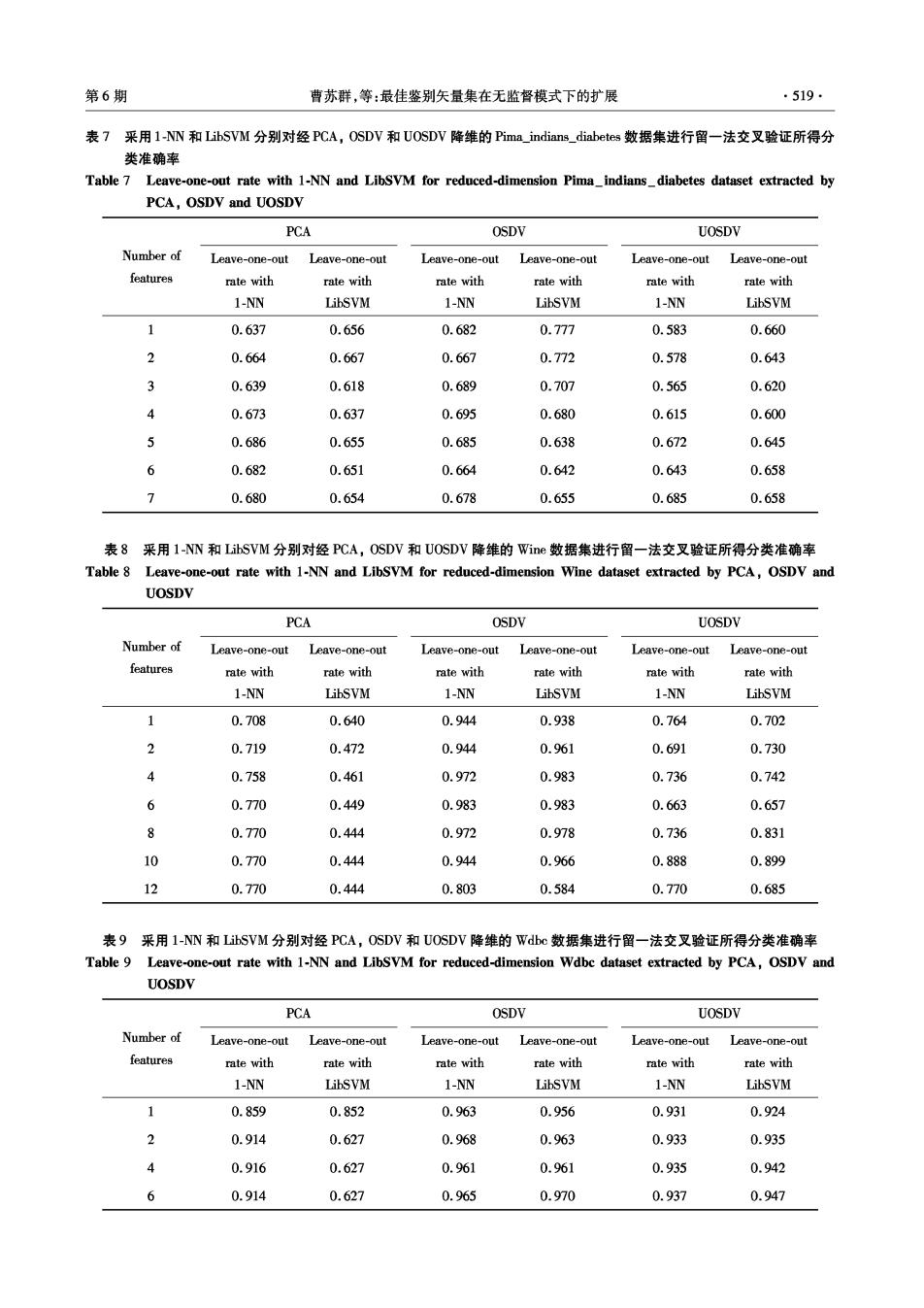
第6期 曹苏群,等:最佳鉴别矢量集在无监督模式下的扩展 519 表7采用l-NN和LibSVM分别对经PCA,OSDV和UOSDV降维的Pima_indians._diabetes数据集进行留一法交叉验证所得分 类准确率 Table 7 Leave-one-out rate with 1-NN and LibSVM for reduced-dimension Pima indians diabetes dataset extracted by PCA,OSDV and UOSDV PCA OSDV UOSDV Number of Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out features rate with rate with rate with rate with rate with rate with 1-NN LibSVM 1-NN LibSVM 1-NN LibSVM 1 0.637 0.656 0.682 0.777 0.583 0.660 2 0.664 0.667 0.667 0.772 0.578 0.643 3 0.639 0.618 0.689 0.707 0.565 0.620 0.673 0.637 0.695 0.680 0.615 0.600 5 0.686 0.655 0.685 0.638 0.672 0.645 6 0.682 0.651 0.664 0.642 0.643 0.658 0.680 0.654 0.678 0.655 0.685 0.658 表8采用l-NN和LibSVM分别对经PCA,OSDV和UOSDV降维的Wine数据集进行留一法交叉验证所得分类准确率 Table 8 Leave-one-out rate with 1-NN and LibSVM for reduced-dimension Wine dataset extracted by PCA,OSDV and UOSDV PCA OSDV UOSDV Number of Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out features rate with rate with rate with rate with rate with rate with 1-NN LibSVM 1-NN LibSVM 1-NN LibSVM 1 0.708 0.640 0.944 0.938 0.764 0.702 2 0.719 0.472 0.944 0.961 0.691 0.730 4 0.758 0.461 0.972 0.983 0.736 0.742 6 0.770 0.449 0.983 0.983 0.663 0.657 8 0.770 0.444 0.972 0.978 0.736 0.831 10 0.770 0.444 0.944 0.966 0.888 0.899 12 0.770 0.444 0.803 0.584 0.770 0.685 表9采用1-NN和LibSVM分别对经PCA,OSDV和UOSDV降维的Wdc数据集进行留一法交叉验证所得分类准确率 Table 9 Leave-one-out rate with 1-NN and LibSVM for reduced-dimension Wdbc dataset extracted by PCA,OSDV and UOSDV PCA OSDV UOSDV Number of Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out features rate with rate with rate with rate with rate with rate with 1-NN LibSVM 1-NN LibSVM 1-NN LibSVM 1 0.859 0.852 0.963 0.956 0.931 0.924 2 0.914 0.627 0.968 0.963 0.933 0.935 4 0.916 0.627 0.961 0.961 0.935 0.942 6 0.914 0.627 0.965 0.970 0.937 0.947
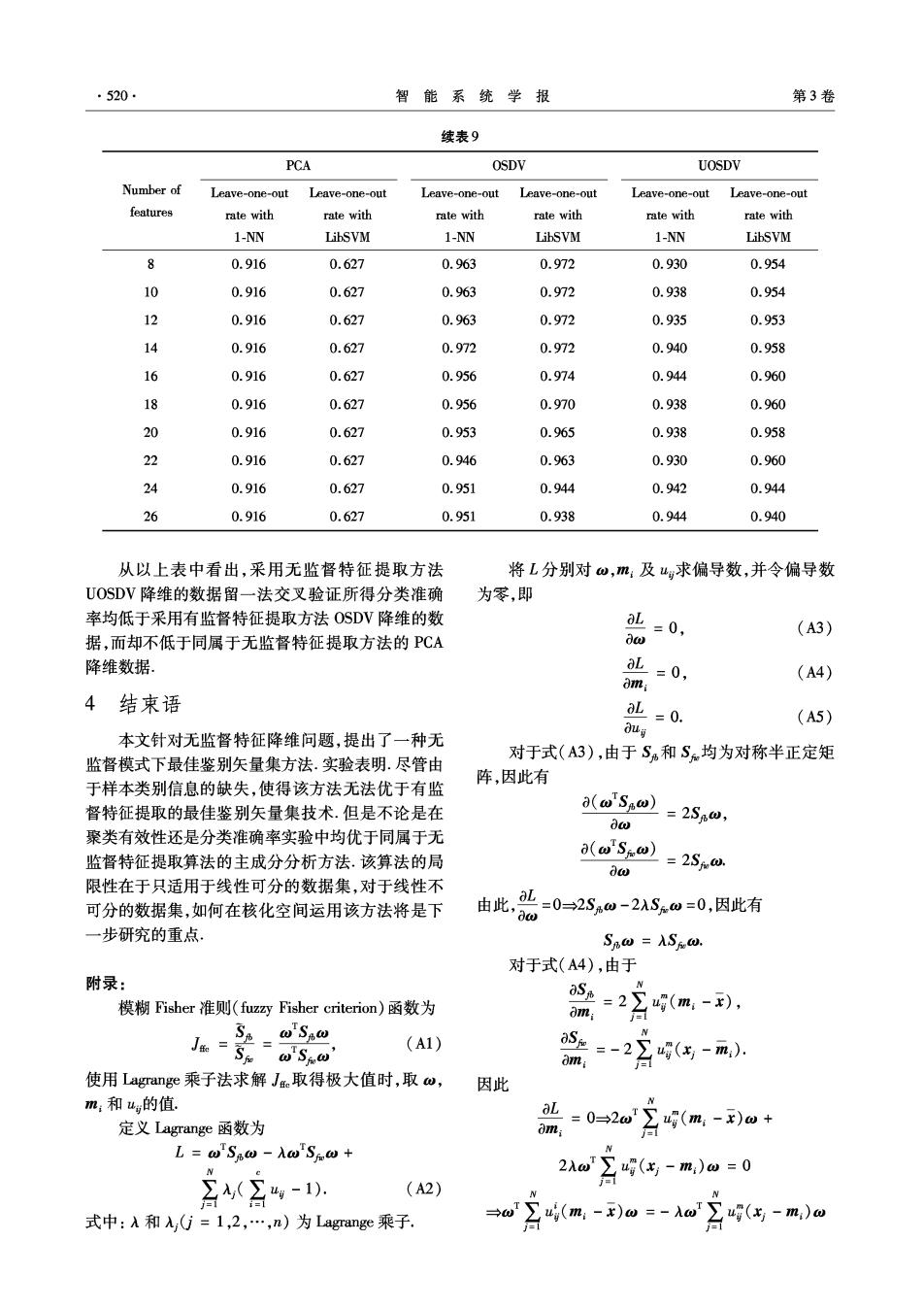
·520· 智能系统学报 第3卷 续表9 PCA OSDV UOSDV Number of Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out Leave-one-out features rate with rate with rate with rate with rate with rate with 1-NN LibSVM 1-NN LibSVM 1-NN LibSVM 8 0.916 0.627 0.963 0.972 0.930 0.954 10 0.916 0.627 0.963 0.972 0.938 0.954 12 0.916 0.627 0.963 0.972 0.935 0.953 14 0.916 0.627 0.972 0.972 0.940 0.958 16 0.916 0.627 0.956 0.974 0.944 0.960 18 0.916 0.627 0.956 0.970 0.938 0.960 20 0.916 0.627 0.953 0.965 0.938 0.958 22 0.916 0.627 0.946 0.963 0.930 0.960 24 0.916 0.627 0.951 0.944 0.942 0.944 26 0.916 0.627 0.951 0.938 0.944 0.940 从以上表中看出,采用无监督特征提取方法 将L分别对ω,m:及g求偏导数,并令偏导数 UOSDV降维的数据留一法交叉验证所得分类准确 为零,即 率均低于采用有监督特征提取方法OSDV降维的数 aL-0, (A3) 据,而却不低于同属于无监督特征提取方法的PCA dw 降维数据 L=0, (A4) omi 4结束语 L=0. (A5) 本文针对无监督特征降维问题,提出了一种无 dug 对于式(A3),由于S和S均为对称半正定矩 监督模式下最佳鉴别矢量集方法.实验表明.尽管由 于样本类别信息的缺失,使得该方法无法优于有监 阵,因此有 督特征提取的最佳鉴别矢量集技术.但是不论是在 a(wSaw) =2S6ω, dw 聚类有效性还是分类准确率实验中均优于同属于无 a(wSw) 监督特征提取算法的主成分分析方法.该算法的局 aw =2Sw. 限性在于只适用于线性可分的数据集,对于线性不 可分的数据集,如何在核化空间运用该方法将是下 由此,=0=2S%0-2ASw=0,因此有 一步研究的重点。 SBω=ASw, 对于式(A4),由于 附录: 模糊Fisher准则(fuz四Fisher criterion)函数为 S2=2∑g(m,-), om: 1 SA'So N Ja-5fS0 (A1) aS=-2∑(-m,) om: 使用Lagrange乘子法求解Je取得极大值时,取w, 因此 m:和u的值 定义Lagrange函数为 =0-2w月9(,-)m+ 0m: L=wSBw-AwSω+ 2入 T∑g(x-m)ω=0 公-. (A2) 台1 式中:入和入yG=1,2,…,n)为Lagrange乘子. →w(m-w=-w4(与-m)