
第3卷第5期 智能系统学报 Vol 3 Na 5 2008年10月 CAA I Transactions on Intelligent Systems 0ct2008 局部测地距离估计的Hessian局部线性嵌入 文贵华,江丽君2,文军 (1华南理工大学计算机科学与工程学院,广东广州510641;2华南理工大学电子材料科学与工程系,广东广州 510641,3湖北民族学院理学院,湖北恩施445000) 摘要:为处理极度弯曲的数据流形,提出了基于局部测地距离估计的Hessian局部线性嵌入算法,算法采用Hessian局 部线性嵌入(HLLE)的概念框架,采用局部估计的测地距离而不是欧氏距离来确定每个点的邻域,从而减少数据流形弯 曲对邻域选择的影响.算法可认为是全局和局部方法的综合,在性能上不仅比HLE显著提高,有更强的鲁棒性,而且时 间增加不明显.标准数据集上的实验结果验证了所提方法的有效性. 关键词:流形学习;Hessian变换;局部线性嵌入;测地距离 中图分类号:1P391文献标识码:A文章编号:1673-4785(2008)050429-07 Usng locally estinated geodesic distances to i prove Hessian local linear em beddng WEN Gui-hua',JNG Li-jun,WEN Jun' (1.SchoolofComputer Science and Engineering.South China University of Technolgy,Guangzhou 510641,China,2 Deparment of Electronic Material Science and Engineering.South China University of Technology,Gunaghou 510641,China;3.School ofMathe- matical Science,Hubei Insitute for Natonalities,Enshi 445000.China) Abstract:To deal with highly curved data manifolds,the Hessian locally linear embedding(HLLE)algorithm was modified based on a bcally estmated geodesic distance It used the general conceptual framework of HLLE to guar- antee correct setting of local isometry to an open connected subset It empbys the bcally estmated geodesic dis- tance instead of the Euclidean distance to detem ine the neighborhood of any point,so that it reduces the disbrting influence of curvature of the data manifold on detem ining the neighborhood This approach can be regarded as the integration of a bcalmethod and a glbalmethod,so that it has better peromance and stability than HILLE,with only a slight increase in computational tie Experments conducted on benchmark data sets verified etficoncy of the proposed app roach Keywords:maniold leaming Hessian transfomation;bcally linear embedding geodesic distance 很多高维数据如遥感、气候等常常分布于较低 多改进算法.LE在降维嵌入过程中保持局部的几 维的流形上,自从国际著名期刊《Science》在2000 何结构不变,并能避免局部极小,最终获得一个全 年发表2种最有代表性的方法OMAP和LLE2)局的低维嵌入系统,效果也很好.目前发展的改进算 以来,寻找描述这样低维流形的参数空间就成为最 法包括利用拉普拉斯(Lap lac ian)B1、赫森(Hessian) 近的研究热点.ISOMAP在降维过程中通过计算点 变换改进的算法HE,、利用数据分类信息改进 对之间的测地距离,并采用MDS方法来获取全局最 的监督LLEI、增量式LLE6、利用Fisher改进的 优的几何结构,获得了较好的效果,目前已发展了很 LE)、以及利用PCA改进的鲁棒性LLE⑧等.性能 上,HLLE是对LE的较大改进,它在某些情况下超 收稿日期:2007-11-25 基金项目:广东省科技攻关资助项目(2007B030803006):湖北省科 越了ISOMAP的能力.ISOMA P的基本假设是全局 技攻关资助项目(2005A4101C17), 通信作者:文贵华.Emai止crghwen@(scut edu cn 等距映射和凸的参数空间,这在很多情况下难以满 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3卷第 5期 智 能 系 统 学 报 Vol. 3 №. 5 2008年 10月 CAA I Transactions on Intelligent System s Oct. 2008 局部测地距离估计的 Hessian局部线性嵌入 文贵华 1 , 江丽君 2 , 文 军 3 (1. 华南理工大学 计算机科学与工程学院 , 广东 广州 510641; 2. 华南理工大学 电子材料科学与工程系 ,广东 广州 510641; 3. 湖北民族学院 理学院 ,湖北 恩施 445000) 摘 要 :为处理极度弯曲的数据流形 ,提出了基于局部测地距离估计的 Hessian局部线性嵌入算法. 算法采用 Hessian局 部线性嵌入 (HLLE)的概念框架 ,采用局部估计的测地距离而不是欧氏距离来确定每个点的邻域 ,从而减少数据流形弯 曲对邻域选择的影响. 算法可认为是全局和局部方法的综合 ,在性能上不仅比 HLLE显著提高 ,有更强的鲁棒性 ,而且时 间增加不明显. 标准数据集上的实验结果验证了所提方法的有效性. 关键词 :流形学习 ; Hessian变换 ;局部线性嵌入 ; 测地距离 中图分类号 : TP391 文献标识码 : A 文章编号 : 167324785 (2008) 0520429207 Using locally estimated geodesic distances to improve Hessian local linear embedding W EN Gui2hua 1 , J IANG L i2jun 2 , W EN Jun 3 ( 1. School of Computer Science and Engineering, South China University of Technology, Guangzhou 510641, China; 2. Department of Electronic Material Science and Engineering, South China University of Technology, Gunagzhou 510641, China; 3. School ofMathe2 matical Science, Hubei Insitute for Nationalities, Enshi 445000, China) Abstract: To dealwith highly curved data manifolds, the Hessian locally linear embedding (HLLE) algorithm was modified based on a locally estimated geodesic distance. It used the general concep tual framework of HLLE to guar2 antee correct setting of local isometry to an open connected subset. It emp loys the locally estimated geodesic dis2 tance instead of the Euclidean distance to determ ine the neighborhood of any point, so that it reduces the distorting influence of curvature of the data manifold on determ ining the neighborhood. This app roach can be regarded as the integration of a local method and a global method, so that it has better performance and stability than HLLE, with only a slight increase in computational time. Experiments conducted on benchmark data sets verified etficioncy of the p roposed app roach. Keywords:manifold learning; Hessian transformation; locally linear embedding; geodesic distance 收稿日期 : 2007211225. 基金项目 :广东省科技攻关资助项目 ( 2007B030803006) ; 湖北省科 技攻关资助项目 (2005AA101C17) 1 通信作者 :文贵华. E2mail: crghwen@ scut. edu. cn. 很多高维数据如遥感、气候等常常分布于较低 维的流形上 ,自从国际著名期刊《Science》在 2000 年发表 2种最有代表性的方法 ISOMAP [ 1 ]和 LLE [ 2 ] 以来 ,寻找描述这样低维流形的参数空间就成为最 近的研究热点. ISOMAP在降维过程中通过计算点 对之间的测地距离 ,并采用 MDS方法来获取全局最 优的几何结构 ,获得了较好的效果 ,目前已发展了很 多改进算法. LLE在降维嵌入过程中保持局部的几 何结构不变 , 并能避免局部极小 ,最终获得一个全 局的低维嵌入系统 ,效果也很好. 目前发展的改进算 法包括利用拉普拉斯 (Lap lacian) [ 3 ]、赫森 (Hessian) 变换改进的算法 HLLE [ 4 ]、利用数据分类信息改进 的监督 LLE [ 5 ]、增量式 LLE [ 6 ]、利用 Fisher改进的 LLE [ 7 ]、以及利用 PCA改进的鲁棒性 LLE [ 8 ]等. 性能 上 , HLLE是对 LLE的较大改进 ,它在某些情况下超 越了 ISOMAP的能力. ISOMAP的基本假设是全局 等距映射和凸的参数空间 ,这在很多情况下难以满

·430· 智能系统学报 第3卷 足.而LLE只要求局部等距映射和开的连通参数 距离,方法是假定当两点非常近时,测地距离等于欧 空间,因而应用范围更宽.但是LE需要保持邻域 氏距离,而对较远的点对之间的测地距离则根据近 的线性化,当数据流形比较弯曲时,难以满足,不可 邻点之间测地距离的累加实现.当观察数据集足够 避免地面临短路问题,因此需要邻域优化.目前有3 密集且内在的参数空间是凸的,则SOMAP能够成 类与邻域相关的工作,第1类是构造连通的邻域 功地获得参数空间.ISOMAP面临的问题是,在很多 图9-):第2类采用新的测度来选择邻域点1-51,例 情况下参数空间并不是凸的,此时它得不到正确的 如监督LE利用分类信息构造新的测度)],但需要 结果 分类信息,替代策略是采用自动聚类确定分类信 HLLE采用局部线性方法实现流形学习.它只 息)同时图代数还可以用来定义新的测度并优化 要求局部等距映射的子集是开的且连通,而不必是 邻域14-s1,以及利用测地距离确定邻域1,11等:第3 凸的.其理论依据来源于流形切空间上的Hessian 类是研究邻域的大小问题,包括如何选择合适的邻 变换.假定流形MCR”是光滑的,其任意点m∈M 域大小61,以及适用于非均匀分布流形的邻域大小 都有切空间TM),在此空间引入欧氏空间的内积 自适应确定算法1.本文的工作属于第2类,采用 就可以建立局部坐标系统,且有原点O∈TmM).设 局部估计的测地距离来确定邻域,以减少流形弯曲 Nm是m∈M的邻域,对任意m'∈Nm都有惟一的 对邻域选择的影响.此前华南理工大学曾采用测地 最近点v'∈T.M)使得映射m'→v是光滑的,因此 距离来确定HLE的邻域Is1,Claudio Varini采用测 Nm具有局部坐标系统,记为(n,m.设 地距离来确定LE的邻域),但它们都需要计算 F:M→R在m附近是C2光滑的,G:U→R,UCR是 所有点对之间的测地距离,然后用于确定邻域,增加 零点O的一个邻域.令g(x)=f(m),因m'x是 的时间复杂度太高,接近OW).为此本文改变策 光滑的,g是C光滑的,则f的Hessian变换为 略,只估计每个点与其局部区域内的点之间的测地 距离,并用之确定HLE的邻域,不仅增加的时间不 m,=是是§ Cx:C g(x)Ix-0 明显,而且效果仍然很好.最后的实验表明此改进算 二次型HD=m)d定义了fM一 法在降维性能上比ISOMA P、HLLE和LLE都有效, 更适合于处理弯曲的数据流形 R在M上的平均弯曲率,其中‖·I2是Frobenius 范数.可以证明若参数空间⊙CR是开的连通子 1 Hessian局部线性嵌入 集,则H(f)有一个(d+1)维的零空间(null pace), 假定有一个参数空间⊙CR和一个光滑映射 参数空间能够通过计算此零空间的一个合适的基坐 中:⊙→R",其中嵌入空间R”满足n>d,则称M= 标来发现,这就是HLE的核心.由此可以发现:1) 中©)为流形.流形学习的目的是根据观察数据确 框架上HLLE与LE和LE一致,不同的是用Hes 定参数空间⊙CR ISOMAP采用等距嵌入(isomet- sian变换取代了LE的Lap lacian算子,而LLE是LE ric embedding)和等角嵌入(conomal embedding) 理论框架下的一种经验实现;2)HLE需要对每个 来实现流形学习.其基本假设是:1)等距,即测地距 数据点计算n次偏导数,当观察数据的维非常高 离在等距嵌入映射下是不变的,流形上任意点之间 时,计算量不小:3)每个点的切空间要求其邻域是 的测地距离在等距嵌入变换下获得的欧氏空间中仍 线性的,当邻域高度弯曲时,极易面临短路威胁,这 然保持G(x以=Ia-B‖,x∈M,y∈M,a∈O,B∈O; 是HLLE需要克服的另一个主要问题 2凸性,即参数空间⊙CR是凸的.对任意a,B∈⊙, 线段{(1-)a+B11∈0,1)仍然属于⊙ 2改进算法 SOMA P算法利用等距嵌入的这种不变性,在 HLLE对极度弯曲的数据流形难以得到正确的 没有任何关于观察数据测度知识的基础上构造测地 结果,原因是被当作线性化的局部区域实际上包含 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
足. 而 HLLE只要求局部等距映射和开的连通参数 空间 ,因而应用范围更宽. 但是 HLLE需要保持邻域 的线性化 ,当数据流形比较弯曲时 ,难以满足 ,不可 避免地面临短路问题 ,因此需要邻域优化. 目前有 3 类与邻域相关的工作 ,第 1 类是构造连通的邻域 图 [ 9210 ] ;第 2类采用新的测度来选择邻域点 [ 11215 ] ,例 如监督 LLE利用分类信息构造新的测度 [ 5 ] ,但需要 分类信息 ,替代策略是采用自动聚类确定分类信 息 [ 13 ] . 同时图代数还可以用来定义新的测度并优化 邻域 [ 14215 ] ,以及利用测地距离确定邻域 [ 11, 18 ]等 ;第 3 类是研究邻域的大小问题 ,包括如何选择合适的邻 域大小 [ 16 ] ,以及适用于非均匀分布流形的邻域大小 自适应确定算法 [ 17 ] . 本文的工作属于第 2类 ,采用 局部估计的测地距离来确定邻域 ,以减少流形弯曲 对邻域选择的影响. 此前华南理工大学曾采用测地 距离来确定 HLLE的邻域 [ 18 ] , Claudio Varini采用测 地距离来确定 LLE的邻域 [ 11 ] , 但它们都需要计算 所有点对之间的测地距离 ,然后用于确定邻域 ,增加 的时间复杂度太高 ,接近 O (N 3 ). 为此本文改变策 略 ,只估计每个点与其局部区域内的点之间的测地 距离 ,并用之确定 HLLE的邻域 ,不仅增加的时间不 明显 ,而且效果仍然很好. 最后的实验表明此改进算 法在降维性能上比 ISOMAP、HLLE和 LLE都有效 , 更适合于处理弯曲的数据流形. 1 Hessian局部线性嵌入 假定有一个参数空间 Θ d,则称 M = φ(Θ)为流形. 流形学习的目的是根据观察数据确 定参数空间 Θ< R d . ISOMAP采用等距嵌入 ( isomet2 ric embedding) 和等角嵌入 ( conformal embedding) 来实现流形学习. 其基本假设是 : 1)等距 ,即测地距 离在等距嵌入映射下是不变的 ,流形上任意点之间 的测地距离在等距嵌入变换下获得的欧氏空间中仍 然保持 G ( x, y) =‖α-β‖, x∈M, y∈M,α∈Θ,β∈Θ; 2)凸性,即参数空间Θ< R d 是凸的. 对任意 α,β∈Θ, 线段 { (1 - t)α+βt | t∈(0, 1) }仍然属于 Θ. ISOMAP算法利用等距嵌入的这种不变性 ,在 没有任何关于观察数据测度知识的基础上构造测地 距离 ,方法是假定当两点非常近时 ,测地距离等于欧 氏距离 ,而对较远的点对之间的测地距离则根据近 邻点之间测地距离的累加实现. 当观察数据集足够 密集且内在的参数空间是凸的 ,则 ISOMAP能够成 功地获得参数空间. ISOMAP面临的问题是 ,在很多 情况下参数空间并不是凸的 ,此时它得不到正确的 结果. HLLE采用局部线性方法实现流形学习. 它只 要求局部等距映射的子集是开的且连通 ,而不必是 凸的. 其理论依据来源于流形切空间上的 Hessian 变换. 假定流形 M < R n 是光滑的 ,其任意点 m ∈M 都有切空间 Tm (M ) ,在此空间引入欧氏空间的内积 就可以建立局部坐标系统 ,且有原点 O∈Tm (M ). 设 Nm 是 m ∈M 的邻域 , 对任意 m ′∈Nm 都有惟一的 最近点 v′∈Tm (M )使得映射 m ′→v′是光滑的 ,因此 Nm 具有局部坐标系统 ,记为 x1 ( tan, m ) , …, x ( tan, m ) d . 设 F:M →R在 m 附近是 C 2 光滑的 , G: U→R, U < R d 是 零点 O 的一个邻域. 令 g ( x) = f (m ′) ,因 m ′→x是 光滑的 , g是 C 2 光滑的 ,则 f的 Hessian变换为 (H tan f (m ) ) i, j = 5 5xi 5 5xj g ( x) | x =0 . 二次型 H ( f) = M∫‖H tan f (m ) ‖ 2 F dm 定义了 f:M → R在 M 上的平均弯曲率 ,其中 ‖·‖ 2 F 是 Frobenius 范数. 可以证明若参数空间 Θ < R d 是开的连通子 集 ,则 H ( f)有一个 ( d + 1)维的零空间 ( null space) , 参数空间能够通过计算此零空间的一个合适的基坐 标来发现 ,这就是 HLLE的核心. 由此可以发现 : 1) 框架上 HLLE与 LE和 LLE一致 ,不同的是用 Hes2 sian变换取代了 LE的 Lap lacian算子 ,而 LLE是 LE 理论框架下的一种经验实现 ; 2) HLLE需要对每个 数据点计算 n ×n次偏导数 ,当观察数据的维非常高 时 ,计算量不小; 3)每个点的切空间要求其邻域是 线性的 ,当邻域高度弯曲时 ,极易面临短路威胁 ,这 是 HLLE需要克服的另一个主要问题. 2 改进算法 HLLE对极度弯曲的数据流形难以得到正确的 结果 ,原因是被当作线性化的局部区域实际上包含 ·430· 智 能 系 统 学 报 第 3卷

第5期 文贵华,等:局部测地距离估计的Hessian局部线性嵌入 ·431 了很多弯曲的曲面,从而容易导致短路问题如图1 ②利用所有t迭代计算所有的d(x,x)= 所示,HLE采用欧氏距离确定点x的5邻域就导 mind d (x.x),d (x.x)+d (xx) 致短路问题,其邻域为虚线园内的点,点的类别分别 这样计算测地距离的时间复杂度近似为 为{square,square,square,circle,circle},这显然发 Ox3),复杂度太高.从图1可以看出,用测地距 生了短路现象,因为类别为square的点并不是点x 离确定x点的邻域,不必要计算x到所有点的测地 在流形上的最近邻,由此确定的邻域扭曲了数据真 距离,只需要计算x附近的点就可以了.具体方法是 实的邻域结构,进而产生不正确的低维嵌入,尤其对 首先确定局部区域大小L,然后以x为中心,选择其 稀疏或含噪音的数据集更是如此.相反,用测地距离 L个最近邻点构成该点的局部区域,进而在此局部 确定的邻域则为虚曲线内的点,点的类别为{circle,. 区域内估计x到其他L个点之间的测地距离.最后 circle,circle,circle,.circle},这是正确的结果.因此 根据估计的测地距离来选择最小的k个最近邻作为 只要测地距离的估计是正确的,那么确定的邻域就 点x的邻域,由此形成的邻域可显著减少短路边,如 能导致正确的低维嵌入 图2所示,其中k=12,L=mXk=512,而用于计 算测地距离的邻域大小k=6图2(a)的样本是从 Swiss roll surface随机采样600个点,但叠加了均值 为0和方差为Q3的高斯噪音后的含噪音数据集 图2(b)是利用Euclidean距离确定的邻域图,其中 明显出现了短路边,它们将靠得很近的2个不同曲 面连接了起来,而图2(c)是用局部估计的测地距离 确定的邻域,其中没有任何短路边出现,这说明了利 用局部估计的测地距离改进HLLE将取得更好的嵌 入结果.将据此改进的HLE记为GHLE,以区 别于利用全局估计的测地距离改进的HLLE,记为 图1欧氏距离和测地距离确定的不同邻域 GA-HLLE为保持算法的清晰性,给出完整的G Fig 1 Different neighborhoods using Euclidean distance HLE算法如下: and geodesic distance 10 以前采用ISOMA P计算测地距离的方法计算输 入数据之间的测地距离,并用之确定每个数据点的 01050-5 2010010 x-20100-10 邻域,然后用HLE方法计算每个点的低维嵌 入1,ISOMA P计算测地距离主要包括2步: (a)噪音数据集 (b)Euclidean (c)局部估计 1)根据观察数据x和邻域大小k构造邻域权重 图2利用Euclidean距离和局部估计的 图G=少,E.V对应于X中的观察数据,E为连接 测地距离确定的不同邻域图 2点的边的集合,(x,)∈E若x,是x的k最近邻, Fig 2 D ifferent neighborhood graph susing Euclidean x,与y之间的距离为殴氏距离dG(x, distance and bcally estmated geodesic distance 2)通过求G上任意两点之间的最短距离来估 算法CL-HLEE算法(X,kk,dm): 计流形上所有点对之间的测地距离d(x,x) /*输入中X是高维观察数据,k是用于确定切 ①初始化 空间的局部邻域大小,d是低维参数空间的维数,而 dE(x,,ifx,)∈E k是用于估计测地距离的邻域大小,m确定局部区 de (x.x) else 域的参数.输出是低维参数空间W*/ 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
了很多弯曲的曲面 ,从而容易导致短路问题. 如图 1 所示 , HLLE采用欧氏距离确定点 x的 52邻域就导 致短路问题 ,其邻域为虚线园内的点 ,点的类别分别 为 { square, square, square, circle, circle} ,这显然发 生了短路现象 ,因为类别为 square的点并不是点 x 在流形上的最近邻 ,由此确定的邻域扭曲了数据真 实的邻域结构 ,进而产生不正确的低维嵌入 ,尤其对 稀疏或含噪音的数据集更是如此. 相反 ,用测地距离 确定的邻域则为虚曲线内的点 ,点的类别为 { circle, circle, circle, circle, circle} ,这是正确的结果. 因此 只要测地距离的估计是正确的 ,那么确定的邻域就 能导致正确的低维嵌入. 图 1 欧氏距离和测地距离确定的不同邻域 Fig. 1 D ifferent neighborhoods using Euclidean distance and geodesic distance 以前采用 ISOMAP计算测地距离的方法计算输 入数据之间的测地距离 ,并用之确定每个数据点的 邻域 , 然后用 HLLE 方法计算每个 点的低 维嵌 入 [ 15 ] , ISOMAP计算测地距离主要包括 2步 : 1)根据观察数据 x和邻域大小 k构造邻域权重 图 G = (V, E). V 对应于 X中的观察数据 , E为连接 2点的边的集合 , ( xi , xj ) ∈E若 xi 是 xj的 k最近邻 , xi 与 xj之间的距离为殴氏距离 dG ( xi , xj ). 2)通过求 G上任意两点之间的最短距离来估 计流形上所有点对之间的测地距离 dG ( xi , xj ). ①初始化 dG ( xi , xj ) = dE ( xi , xj ) , if( xi , xj ) ∈ E, ∞, else. ②利用所有 t, 迭代计算所有的 dG ( xi , xj ) = m in{ dG ( xi , xj ) , dG ( xi , xt ) + dG ( xt , xj ) }. 这样 计 算 测 地 距 离 的 时 间 复 杂 度 近 似 为 O ( | x | 3 ) ,复杂度太高. 从图 1可以看出 ,用测地距 离确定 x点的邻域 ,不必要计算 x到所有点的测地 距离 ,只需要计算 x附近的点就可以了. 具体方法是 首先确定局部区域大小 L,然后以 x为中心 ,选择其 L个最近邻点构成该点的局部区域 ,进而在此局部 区域内估计 x到其他 L 个点之间的测地距离. 最后 根据估计的测地距离来选择最小的 k个最近邻作为 点 x的邻域 ,由此形成的邻域可显著减少短路边 ,如 图 2所示 ,其中 k = 12, L =m ×k = 5 ×12,而用于计 算测地距离的邻域大小 kg = 6. 图 2 ( a)的样本是从 Swiss roll surface随机采样 600个点 ,但叠加了均值 为 0和方差为 0. 3的高斯噪音后的含噪音数据集 , 图 2 ( b)是利用 Euclidean距离确定的邻域图 ,其中 明显出现了短路边 ,它们将靠得很近的 2个不同曲 面连接了起来 ,而图 2 ( c)是用局部估计的测地距离 确定的邻域 ,其中没有任何短路边出现 ,这说明了利 用局部估计的测地距离改进 HLLE将取得更好的嵌 入结果. 将据此改进的 HLLE记为 GL2HLLE,以区 别于利用全局估计的测地距离改进的 HLLE,记为 GA2HLLE. 为保持算法的清晰性 ,给出完整的 GL2 HLLE算法如下 : ( a)噪音数据集 ( b) Euclidean ( c)局部估计 图 2利用 Euclidean距离和局部估计的 测地距离确定的不同邻域图 Fig. 2 D ifferent neighborhood graph susing Euclidean distance and locally estimated geodesic distance 算 法 GL2HLEE算法 (X, k, kg , d, m ) : /3 输入中 X是高维观察数据 , k是用于确定切 空间的局部邻域大小 , d是低维参数空间的维数 ,而 kg 是用于估计测地距离的邻域大小 , m 确定局部区 域的参数. 输出是低维参数空间 W 3 / 第 5期 文贵华 ,等 :局部测地距离估计的 Hessian局部线性嵌入 ·431·

·432· 智能系统学报 第3卷 1)首先计算每个点的mXk个最近邻构成该 LLE、ISOMAP及其许多改进算法都采用的标准测试 点的局部区域,然后以k为邻域大小估计x到局部 数据,包括Swiss roll surface、S-cuve、3 D clusters、To- 区域内.其他任意点之间的测地距离,然后根据估计 oidal Helix和Twin Peaks,.在每个数据集上均采样 的测地距离来选择最小的k个最近邻作为点x的邻 600个点构造实验数据. 域,并将每个点的邻域表达为中心化的行向量k 31性能分析 矩阵M; GHLE等5种方法在几种标准数据集上的 2)采用奇异值分解每个邻域矩阵M',将其正 运行结果如图3~7所示.图3中的实验数据是采用 交向量V的前d个分量作为其切空间: HLE的方法从Swiss roll surface.上采样一个数据规 3)求切空间的Hessian矩阵.当d=2时,根据 模为600个点的长方形但从其中心移去一个小的长 切空间中的点形成如下矩阵X=[1V,.1V,2 方形而形成的非凸数据集,这也是HLE实验中采 N.)2N.22)N.1.2)1,其中V.1 用的实验数据.不难发现在采样的这个数据集上 表示切空间中所有点的第一维的值,对d>2采用相 LLE和HLE不能够完美地将数据嵌入在二维空 同的方法创建1+d+d(d+1)2列的矩阵,然后用 间.ISOMAP将去除的区域强烈膨胀,并扭曲其余的 Gram-Schm idti正交化x'产生新的正交矩阵又,将其 数据点.而GA-HLLE和GHLE能够较完美地将 转置后取最后的d(d+l)/2列构成Hessian矩阵H'; 数据嵌入在二维空间,其中心移去的一个小长方形 少首先构造二次型H,=∑∑(H),H)山, 也能在嵌入的二维空间中正确体现,因此在这个数 对H进行特征分析,获取其d+1个最小特征值对 据集上GLHLLE能够解决ISOMAP等其他方法不 应的d+1维子空间,第1个特征值0对应于常函 能解决的问题.同时在剩余的4个数据集上,GL 数,接下来的d个特征向量就构成d维空间,对其选 HLE和GA-HLLE都胜过HLE和LLE,而G 择一个正交基,变换就可获得要恢复的参数空 HLLE和GA-HLLE的效果无明显区别.在有的数据 间w. 集如图5上它们的性能略差于SOMA P,而在另外 算法GL-HLLE中的1)利用局部估计的测地距 一些数据集如图3和图7上它们的性能则优于SO- 离确定每个点的邻域,余下的步骤与HLLE相同,因 MAP因此从整体性能上GL-HLLE和GA-HLLE是 此复杂的数学推导和更详细的算法描述见HLLE原 相对较好的方法,特别是它们都比LE好 文.GHLE增加了估计局部测地距离的时间 10 ON),N=X|,但与HLLE一样都只需要N个k 稀疏的特征问题计算,而ISOMAP需要一个NW 20 -50 密集的特征问题求解.如果N很大时,显然G 105-50 -40-200204060 HLE比ISOMAP有优越性,而从后面的实验结果 (a)原始数据 (b)LLE (c)ISOMAP 看,GL-HLLE的降维性能比HLLE、ISOMAP和LLE 0.10 0.05 0.05 都要好 0.05 y 3实验分析 -0.05 实验比较GL-HLLE与GA-HLLE、HLE、LLE -0.0500.05-0.0500.05 -0.0500.05 和SOMA方法的性能和时间复杂度.几种方法均采 (d)HLLE (e)GA-HILE (f)GL-HLLE 用Matlab编程实现,其中HLE、LLE和ISOMAP采 图3几种算法在数据集wiss roll surface.上的结果 用原作者提供的Matlab代码,GA-HLLE和G Fig 3 Embedding results of the compared app roaches HLLE由作者编程实现.实验中的参数设置为线性 on Swiss roll surface data 重构的邻域k=12,局部区域大小为5水,而估计 测地距离的邻域参数取6实验数据采用HLLE 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
1) 首先计算每个点的 m ×k个最近邻构成该 点的局部区域 ,然后以 kg 为邻域大小估计 x到局部 区域内. 其他任意点之间的测地距离 ,然后根据估计 的测地距离来选择最小的 k个最近邻作为点 x的邻 域 ,并将每个点的邻域表达为中心化的行向量 k ×n 矩阵 M i ; 2) 采用奇异值分解每个邻域矩阵 M i ,将其正 交向量 V的前 d个分量作为其切空间; 3) 求切空间的 Hessian矩阵. 当 d = 2时 ,根据 切空间中的点形成如下矩阵 X i = [ 1 V·, 1 V·, 2 (V·, 1 ) 2 (V·, 2 2 ) (V·, 1 ×V·, 2 ) ],其中 V·, 1 表示切空间中所有点的第一维的值 ,对 d > 2采用相 同的方法创建 1 + d + d ( d + 1) /2列的矩阵 ,然后用 Gram2Schm idt正交化 X i 产生新的正交矩阵 X i ,将其 转置后取最后的 d ( d +1) /2列构成 Hessian矩阵 H i ; 4) 首先构造二次型 Hij = 6l 6r ( (H l ) r, i (H l ) r, j ), 对 H 进行特征分析 ,获取其 d + 1个最小特征值对 应的 d + 1维子空间 ,第 1个特征值 0对应于常函 数 ,接下来的 d个特征向量就构成 d维空间 ,对其选 择一个正交基 , 变换就可获得要恢复的参数空 间 W. 算法 GL2HLLE中的 1)利用局部估计的测地距 离确定每个点的邻域 ,余下的步骤与 HLLE相同 ,因 此复杂的数学推导和更详细的算法描述见 HLLE原 文 [ 4 ] . GL2HLLE增加了估计局部测地距离的时间 O (N ) , N = |X | ,但与 HLLE一样都只需要 N 个 k ×k 稀疏的特征问题计算 ,而 ISOMAP需要一个 N ×N 密集的特征问题求解. 如果 N 很大时 , 显然 GL2 HLLE比 ISOMAP有优越性 ,而从后面的实验结果 看 , GL2HLLE的降维性能比 HLLE、ISOMAP和 LLE 都要好. 3 实验分析 实验比较 GL2HLLE与 GA2HLLE、HLLE、LLE 和 ISOMA方法的性能和时间复杂度. 几种方法均采 用 Matlab编程实现 ,其中 HLLE、LLE和 ISOMAP采 用原作者 提 供 的 Matlab 代 码 , GA2HLLE 和 GL2 HLLE由作者编程实现. 实验中的参数设置为线性 重构的邻域 k = 12,局部区域大小为 5 ×k, 而估计 测地距离的邻域参数取 6. 实验数据采用 HLLE、 LLE、ISOMAP及其许多改进算法都采用的标准测试 数据 ,包括 Swiss roll surface、S2curve、3D clusters、To2 roidal Helix和 Twin Peaks,在每个数据集上均采样 600个点构造实验数据. 3. 1 性能分析 GL2HLLE等 5种方法在几种标准数据集上的 运行结果如图 3~7所示. 图 3中的实验数据是采用 HLLE的方法从 Swiss roll surface上采样一个数据规 模为 600个点的长方形但从其中心移去一个小的长 方形而形成的非凸数据集 ,这也是 HLLE实验中采 用的实验数据 [ 4 ] . 不难发现在采样的这个数据集上 LLE和 HLLE不能够完美地将数据嵌入在二维空 间. ISOMAP将去除的区域强烈膨胀 ,并扭曲其余的 数据点. 而 GA2HLLE和 GL2HLLE能够较完美地将 数据嵌入在二维空间 ,其中心移去的一个小长方形 也能在嵌入的二维空间中正确体现 ,因此在这个数 据集上 GL2HLLE能够解决 ISOMAP等其他方法不 能解决的问题. 同时在剩余的 4 个数据集上 , GL2 HLLE和 GA2HLLE 都胜过 HLLE 和 LLE, 而 GL2 HLLE和 GA2HLLE的效果无明显区别. 在有的数据 集如图 5上它们的性能略差于 ISOMAP,而在另外 一些数据集如图 3和图 7上它们的性能则优于 ISO2 MAP. 因此从整体性能上 GL2HLLE和 GA2HLLE是 相对较好的方法 ,特别是它们都比 HLLE好. 图 3几种算法在数据集 Swiss roll surface上的结果 Fig. 3 Embedding results of the compared app roaches on Swiss roll surface data ·432· 智 能 系 统 学 报 第 3卷

第5期 文贵华,等:局部测地距离估计的Hessian局部线性嵌入 ·433· 0.5 -0.05 -1012 0 5 4234 -101 44-202 (a)原始数据 (b)LLE (c)ISOMAP (a)原始数据 (b)LLE (c)ISOMAP 0.05 0.05 其0.05 0.05 0.05 0.02 30 0 -0.05 0.05 -0.05 0 0.02 +4°-0.05 -0.04 -0.10-0.050 -0.0500.05 -0.0500.05 0.05Cr -0.06 -0.0500.05 -0.0200.020.04-0.0500.05 (d)HLLE (e)GA-HLLE (n)GL-HLLE (d)HLLE (e)GA-HLLE (f)GL-HLLE 图4几种算法在数据集S-cuve上的结果 图6几种算法在数据集3 D clusters上的结果 Fig 4 Embedding results of the compared appoaches Fig 6 Embedding results of the compared appoaches on S-curve data on 3D clusters data 102-2 0.5 -15 -101 -10010 x0.5050 -1012 -10 1 (a)原始数据 (b)LLE (c)ISOMAP (a)原始数据 (b)LLE (c)ISOMAP 0.05 0.05 0.05 0 0.05 0.05 0.05 -0.05 -0.05 -0.05 -0.10 -0.0500.05 -0.0500.05 -0.0500.05 -0.05 -0.05 -0.05 (d)HLLE (e)GA-HLLE (GL-HLLE -0.0500.05 -0.0500.05 -0.0500.05 (d)HLLE (e)GA-HLLE (f)GL-HLLE 图5几种算法在数据集Tomoidal Helix上的结果 Fig 3 Embedding results of the compared app roaches on 图7几种算法在数据集win Peaks.上的结果 Toroidal Helix data Fig 7 Embedding results of the compared app roaches on Twin Peaks data 3.2局部区域参数的选择 1500、2000、2500个点的5类规模的数据样本,每 相对于GA-HLLE,GL-HLLE引入了确定局部 类规模的样本随机采样5次,记录LE HLLE、SO 区域的参数m,与估计测地距离的局部区域大小L MAP、GA-HLLE和G-HLLE5种方法分别运行这5 的关系是L=m从其中k为用于线性重构造的邻 个样本的平均时间作为该规模的时间,则5种方法 域.幸运的是m的取值一般小于10图8的结果表 在5类规模数据上的平均时间如表1所示.不难发 明m=3时GHLE在几个数据集上均己经取得 现,GHLE和HLE的运行时间很接近,但是GA 较好的效果,m>3时增加的效果不明显,这说明m HLE的运行时间显著高于GL-HLLE,是几种方法 取很小的值就可获得满意的效果,这样m参数的选 中运行最慢的,这说明从嵌入性能上GLE和 取就非常容易,同时在局部区域L内估计测地距离 也自然只需要少量的时间. GA-HLLE相当,但在时间上GL-HLLE却有显著优 33运行时间比较 势,特别是它在嵌入性能上比HLE有显著优越,但 从Swiss Roll Surface上依次采样500、1000、 时间只有很细微的增加 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 4几种算法在数据集 S2curve上的结果 Fig. 4 Embedding results of the compared app roaches on S2curve data 图 5几种算法在数据集 Toroidal Helix上的结果 Fig. 3 Embedding results of the compared app roaches on Toroidal Helix data 3. 2 局部区域参数的选择 相对于 GA2HLLE, GL2HLLE引入了确定局部 区域的参数 m ,与估计测地距离的局部区域大小 L 的关系是 L =m ×k,其中 k为用于线性重构造的邻 域. 幸运的是 m 的取值一般小于 10. 图 8的结果表 明 m = 3时 GL2HLLE在几个数据集上均已经取得 较好的效果 , m > 3时增加的效果不明显 ,这说明 m 取很小的值就可获得满意的效果 ,这样 m 参数的选 取就非常容易 ,同时在局部区域 L 内估计测地距离 也自然只需要少量的时间. 3. 3 运行时间比较 从 Swiss Roll Surface上依次采样 500、1 000、 图 6几种算法在数据集 3D clusters上的结果 Fig. 6 Embedding results of the compared app roaches on 3D clusters data 图 7几种算法在数据集 Twin Peaks上的结果 Fig. 7 Embedding results of the compared app roaches on Twin Peaks data 1 500、2 000、2 500个点的 5类规模的数据样本 ,每 类规模的样本随机采样 5次 ,记录 LLE、HLLE、ISO2 MAP、GA2HLLE和 GL2HLLE5种方法分别运行这 5 个样本的平均时间作为该规模的时间 ,则 5种方法 在 5类规模数据上的平均时间如表 1所示. 不难发 现 , GL2HLLE和 HLLE的运行时间很接近 ,但是 GA2 HLLE的运行时间显著高于 GL2HLLE,是几种方法 中运行最慢的 ,这说明从嵌入性能上 GL2HLLE和 GA2HLLE相当 ,但在时间上 GL2HLLE却有显著优 势 ,特别是它在嵌入性能上比 HLLE有显著优越 ,但 时间只有很细微的增加. 第 5期 文贵华 ,等 :局部测地距离估计的 Hessian局部线性嵌入 ·433·
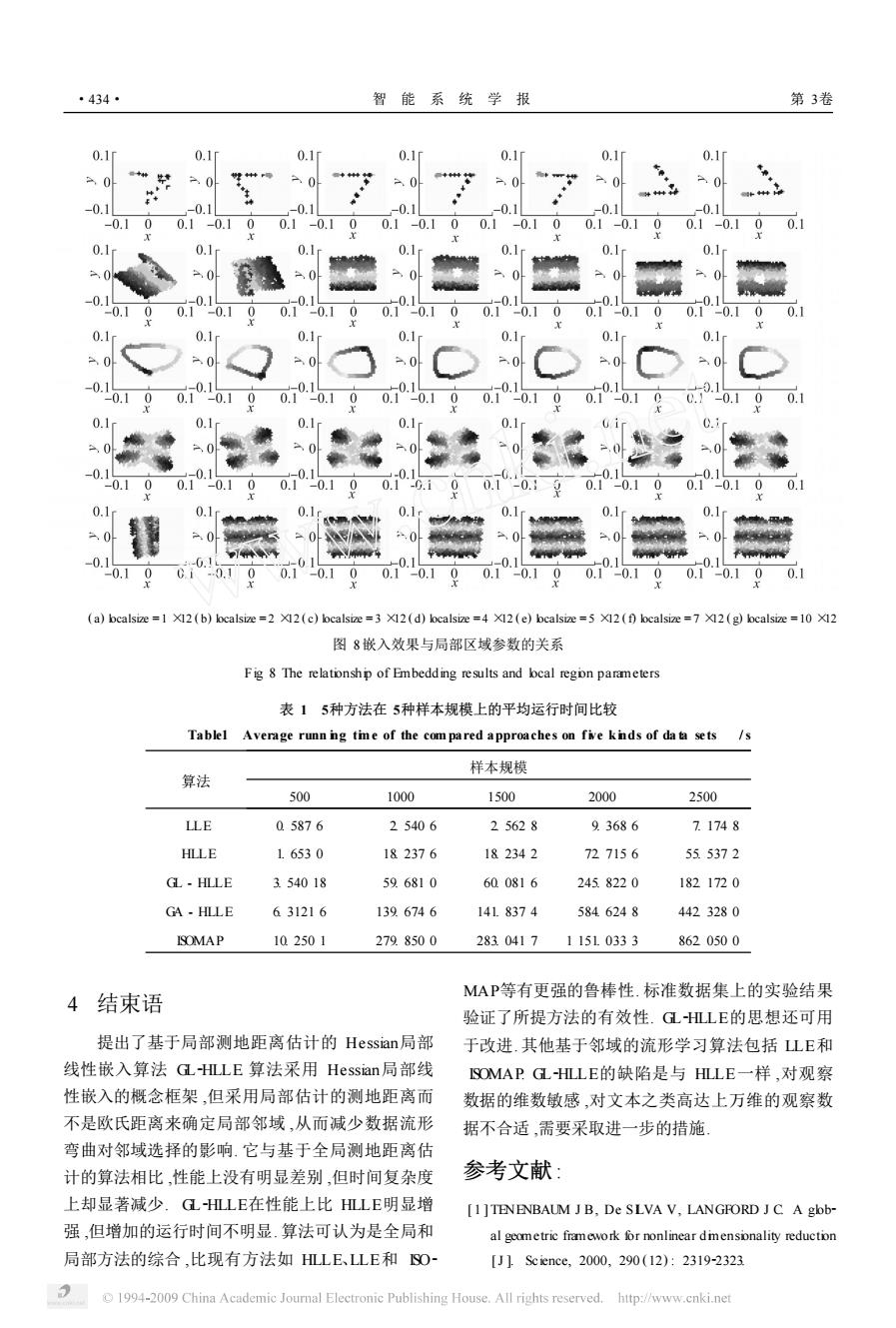
·434· 智能系统学报 第3卷 0.1 0.1 0.11 0.1 0.1 0.1 0.1 0 20 >0 .0 0 m0 0 -0.1 0.1 0.1 -0.1 -0.1 -0.1 -0.1 0 0.1 -0.1 0.1-010 0.1-0.100.1-0.100.1-0.100.1-0.100.1 0.1 0.1 0.1 0 -0. -0.11 1 0.1 -0.10 0.10.190.1-0.100.-0.100.10.100.-0100.-0.100.1 0.1 0.1m 0.1 0.1 0.1r 0.1 0 0 0 0 -0. -0.1 -0.1 -0.1 -0.19 -0.1 -0.1 -0.100.1-0.100.1-0.100.1-0.100.1-0.100.1-0.100.-0.100.1 0. 0.1 0.1 0.1 0.i 0 1 0 0.1 0.1 0.1 0.1 0.1 0.1 0 0 0.1 0.1 -0.1 0.1-0.1 0 0.1 -0.10 0.1 -0.10 0.1 -0.10 0.1 (a)bcalsize =1 X12 (b)localsize =2 X12(c)localsize =3 X12(d)localsize =4 X12(e)bcalsize =5 X12 (f)localsize =7 X12(g)localsize =10 X12 图8嵌入效果与局部区域参数的关系 Fig 8 The relationship of Embedding results and bcal regon parameters 表15种方法在5种样本规模上的平均运行时间比较 Tablel Average runn ng tme of the com pared approaches on five knds of data sets /s 样本规模 算法 500 1000 1500 2000 2500 LLE 05876 25406 25628 9.3686 71748 HLLE 1.6530 182376 182342 727156 55.5372 GL-HLLE 3.54018 596810 600816 2458220 1821720 GA-HLLE 631216 1396746 141.8374 5846248 4423280 ISOMAP 102501 2798500 2830417 11510333 8620500 MAP等有更强的鲁棒性.标准数据集上的实验结果 4结束语 验证了所提方法的有效性.GL-HLLE的思想还可用 提出了基于局部测地距离估计的Hessian局部 于改进.其他基于邻域的流形学习算法包括LE和 线性嵌入算法GL-HLLE算法采用Hessian局部线 ISOMAP GL-HLLE的缺陷是与HLLE一样,对观察 性嵌入的概念框架,但采用局部估计的测地距离而 数据的维数敏感,对文本之类高达上万维的观察数 不是欧氏距离来确定局部邻域,从而减少数据流形 据不合适,需要采取进一步的措施 弯曲对邻域选择的影响.它与基于全局测地距离估 计的算法相比,性能上没有明显差别,但时间复杂度 参考文献: 上却显著减少.GHLE在性能上比HⅢLE明显增 [1]TENENBAUM J B,De SLVA V,LANGFORD J C A glb- 强,但增加的运行时间不明显.算法可认为是全局和 al geometric framework for nonlinear dmensonality reduction 局部方法的综合,比现有方法如HLE、LLE和SO [J].Science,2000,290(12):2319-2323 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
( a) localsize = 1 ×12 ( b) localsize = 2 ×12 ( c) localsize = 3 ×12 ( d) localsize = 4 ×12 ( e) localsize = 5 ×12 ( f) localsize = 7 ×12 ( g) localsize = 10 ×12 图 8嵌入效果与局部区域参数的关系 Fig. 8 The relationship of Embedding results and local region parameters 表 1 5种方法在 5种样本规模上的平均运行时间比较 Table1 Average runn ing tim e of the com pared approaches on five k inds of da ta sets /s 算法 样本规模 500 1000 1500 2000 2500 LLE 0. 587 6 2. 540 6 2. 562 8 9. 368 6 7. 174 8 HLLE 1. 653 0 18. 237 6 18. 234 2 72. 715 6 55. 537 2 GL - HLLE 3. 540 18 59. 681 0 60. 081 6 245. 822 0 182. 172 0 GA - HLLE 6. 3121 6 139. 674 6 141. 837 4 584. 624 8 442. 328 0 ISOMAP 10. 250 1 279. 850 0 283. 041 7 1 151. 033 3 862. 050 0 4 结束语 提出了基于局部测地距离估计的 Hessian局部 线性嵌入算法 GL2HLLE. 算法采用 Hessian局部线 性嵌入的概念框架 ,但采用局部估计的测地距离而 不是欧氏距离来确定局部邻域 ,从而减少数据流形 弯曲对邻域选择的影响. 它与基于全局测地距离估 计的算法相比 ,性能上没有明显差别 ,但时间复杂度 上却显著减少. GL2HLLE在性能上比 HLLE明显增 强 ,但增加的运行时间不明显. 算法可认为是全局和 局部方法的综合 ,比现有方法如 HLLE、LLE和 ISO2 MAP等有更强的鲁棒性. 标准数据集上的实验结果 验证了所提方法的有效性. GL2HLLE的思想还可用 于改进. 其他基于邻域的流形学习算法包括 LLE和 ISOMAP. GL2HLLE的缺陷是与 HLLE一样 ,对观察 数据的维数敏感 ,对文本之类高达上万维的观察数 据不合适 ,需要采取进一步的措施. 参考文献 : [ 1 ]TENENBAUM J B, De SILVA V, LANGFORD J C. A glob2 al geometric framework for nonlinear dimensionality reduction [J ]. Science, 2000, 290 (12) : 231922323. ·434· 智 能 系 统 学 报 第 3卷

第5期 文贵华,等:局部测地距离估计的Hessian局部线性嵌入 ·435· [2]ROW EIS S T,SAUL L K Nonlinear dmensionality reduc- bedd ing based on opti ization of neighborhood [J].Joumal tion by locally linear embedding [J]Science,2000,290 of System Smulaton,2007,19(13):3119-3122 (12):2319-2323 [15 ]W EN Guihua,J ANGLijun,NIGEL R S Using graph al [3 ]BELKN M,NIYOGI P Laplacian eigermaps for dmen- gebra to optm ize neighborhood for Isometric mapping sionality reduction and data representation[J Neural Com- [C]//20th Intemational Joint Conference on Artificial In- puting.2003,15(6):1373-1396 telligence DCA 1-07).India,2007:2398-2403. [4]DONOHO D L,GR MES C Hessian eigermaps locally [16]SAMKO O,MARSHALL A D,ROSN PL Selection of linear emnbedding,techniques for high-dmensional data[J]. the optmal parameter value for the Isomap algorithm [J ] PNAS.2003,100(10):591-596 Pattem Recognition Letters.2006,27(9):968-979 [5 ]De R DDER D,KOUROPTEVA O,OKUN O,et al Super [17文贵华,江丽君,文军.邻域参数动态变化的局部线性 vised bcally linear embedding[C]//Artificial Neural Net 嵌入[J]软件学报,2008,19(7):1666-1673 works and Neural Infomation Processing Istanbul,Turkey: WEN Guihua,J ANGLijun,WEN Jun Dynam ically deter Springer,,2003:333-341. m ining neighborhood parameter for locally linear embedding [6]KOUROPTEVA O,OKUN O,PIETIKA NEN M.Incremen- [J1.Joumal of Sofare,2008.19(7):1666-1673 tal locally linear embedding[J ]Pattem Recognition,2005, [18 ]W EN Guihua,J ANG Lijun Gbbalizing bcal neighbor 38(10):1764-1767. hood for bcally linear embedding [C]//Proceedings of [7]De R DDER D,LOOGM,RENDERSM JT Local fisher 2006 IEEE Intemational Conference on System,Man and embedding[C]//Proceedings of the 17th Intemational Con- Cybemetics Taibei,China,2006:3491-3496 ference on Pattem Recognition S I ]2004:295-298. [19]De R DDER D,LOOGM,RENDERS M J T Local fisher [8 ]CHANG Hong.YENG Dityan Robust bcally linear embed- embedding [C]//Proceedings of the 17th Intemational ding[J].Pattem Recognition,2000,39(6):1053-1065. Conference on Pattem Recognition Cambridge,UK, [9]YANGL.Building k-connected neighborhood graphs for iso- 2004:295298 metric data embedding[J].EEE Transactions on Pattem A- [20 ]HONG Chang,YEUND Yang Robust locally linear em- nalysis and Machine Intelligence,2006,28(5):827-831. bedding[J ]Pattem Recognition,2003,39(6):1053- [10]YANG L Building connected neighborhood graphs for 1065 cally linear embedding[C]//18 th Intemational Conference 作者简介: on Pattem Recognition Hong Kong,China,2006:1680- 文贵华,男,1968年生,主要研究方向 1683 为创新计算、认知几何、机器学习与数据挖 [11 ]VAR NI C,DEGENHARD A,NATTKEMPER T W. SOLLE:LLE with geodesic distance[J].Neurocomputing. 2006,69(15):1768-1771 [12王和勇,郑杰,姚正安,李磊.基于聚类和改进距离 的LE方法在数据降维中的应用[J]计算机研究与发 江丽君,女,1971年生,主要研究方向 展,2006.43(8):1485-1490 为机器学习与图形CAD WANG Heyong,ZHENG Jie,YAO Zhengan,LILei Ap- plication of diension reduction on using mproved LLE based on clustering[J].Joumal of Computer Research and Development,.2006,43(8):1485-1490 文军,男,1964年生,主要研究方向 [13]WEN Guihua,JANG Lijun,WEN Jun,NIGEL R S 为创新计算与应用。 Clustering-based nonlinear dmensionality reduction on manifold [C ]//Lecture Notes in Artificial Intelligence (LNA D).Springer,2006:444-453. [14文贵华江丽君,文军.基于邻域优化的局部线性嵌入 [J]系统仿真学报,2007,19(13):3119-3122 WEN Guihua,JANGLijun,WEN Jun Locally linear em- 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
[ 2 ]ROW EIS S T, SAUL L K. Nonlinear dimensionality reduc2 tion by locally linear embedding [ J ]. Science, 2000, 290 (12) : 231922323. [ 3 ]BELKIN M, N IYOGI P. Lap lacian eigenmap s for dimen2 sionality reduction and data rep resentation [J ]. Neural Com2 puting, 2003, 15 (6) : 137321396. [ 4 ] DONOHO D L, GR IMES C. Hessian eigenmap s: locally linear embedding, techniques for high2dimensional data[J ]. PNAS, 2003, 100 (10) : 5912596. [ 5 ]De R IDDER D, KOUROPTEVA O, OKUN O, et al. Super2 vised locally linear embedding [ C ] / /A rtificial Neural Net2 works and Neural Information Processing. Istanbul, Turkey: Sp ringer, 2003: 3332341. [ 6 ] KOUROPTEVA O, OKUN O, P IETIKA INEN M. Incremen2 tal locally linear embedding[J ]. Pattern Recognition, 2005, 38 (10) : 1764217671 [ 7 ]De R IDDER D, LOOGM, REINDERSM J T. Local fisher embedding[C ] / /Proceedings of the 17 th International Con2 ference on Pattern Recognition. [ S. l. ], 2004: 29522981 [ 8 ]CHANG Hong, YENG D ityan. Robust locally linear embed2 ding[J ]. Pattern Recognition, 2000, 39 (6) : 105321065. [ 9 ] YANG L. Building k2connected neighborhood graphs for iso2 metric data embedding[J ]. IEEE Transactions on Pattern A2 nalysis and Machine Intelligence, 2006, 28 (5) : 8272831. [ 10 ]YANG L. Building connected neighborhood graphs for lo2 cally linear embedding[ C ] / /18 th International Conference on Pattern Recognition. Hong Kong, China, 2006: 16802 1683. [ 11 ] VAR IN I C, DEGENHARD A, NATTKEMPER T W. ISOLLE: LLE with geodesic distance[J ]. Neurocomputing, 2006, 69 (15) : 176821771. [ 12 ]王和勇 ,郑 杰 ,姚正安 ,李 磊. 基于聚类和改进距离 的 LLE方法在数据降维中的应用 [J ]. 计算机研究与发 展 , 2006, 43 (8) : 148521490. WANG Heyong, ZHENG Jie, YAO Zhengan, L ILei. Ap2 p lication of dimension reduction on using imp roved LLE based on clustering[J ]. Journal of Computer Research and Development, 2006, 43 (8) : 148521490. [ 13 ]W EN Guihua, J IANG L ijun, W EN Jun, N IGEL R S. Clustering2based nonlinear dimensionality reduction on manifold [ C ] / /Lecture Notes in A rtificial Intelligence (LNA I). Sp ringer, 2006: 4442453. [ 14 ]文贵华、江丽君 ,文 军. 基于邻域优化的局部线性嵌入 [J ]. 系统仿真学报 , 2007, 19 (13) : 311923122. W EN Guihua, J IANG L ijun, W EN Jun. Locally linear em2 bedding based on op tim ization of neighborhood [J ]. Journal of System Simulation, 2007, 19 (13) : 311923122. [ 15 ]W EN Guihua, J IANGL ijun , N IGEL R S. U sing graph al2 gebra to op timize neighborhood for Isometric mapp ing [C ] / /20 th International Joint Conference on A rtificial In2 telligence ( IJCA I207). India, 2007: 239822403. [ 16 ] SAMKO O, MARSHALL A D, ROSIN P L. Selection of the op timal parameter value for the Isomap algorithm [J ]. Pattern Recognition Letters, 2006, 27 (9) : 9682979. [ 17 ]文贵华 ,江丽君 ,文 军. 邻域参数动态变化的局部线性 嵌入 [J ]. 软件学报 , 2008, 19 (7) : 166621673. W EN Guihua, J IANG L ijun, W EN Jun. Dynam ically deter2 m ining neighborhood parameter for locally linear embedding [J ]. Journal of Software, 2008, 19 (7) : 166621673. [ 18 ]W EN Guihua, J IANG L ijun. Globalizing local neighbor2 hood for locally linear embedding [ C ] / /Proceedings of 2006 IEEE International Conference on System, Man and Cybernetics. Taibei, China, 2006: 349123496. [ 19 ]De R IDDER D,LOOG M, REINDERS M J T. Local fisher embedding [ C ] / /Proceedings of the 17 th International Conference on Pattern Recognition. Cambridge, UK, 2004: 2952298. [ 20 ] HONG Chang, YEUND Yang. Robust locally linear em2 bedding[ J ]. Pattern Recognition, 2003, 39 ( 6 ) : 10532 1065. 作者简介 : 文贵华 , 男 , 1968年生 ,主要研究方向 为创新计算、认知几何、机器学习与数据挖 掘. 江丽君 , 女 , 1971年生 ,主要研究方向 为机器学习与图形 CAD. 文 军 , 男 , 1964年生 ,主要研究方向 为创新计算与应用. 第 5期 文贵华 ,等 :局部测地距离估计的 Hessian局部线性嵌入 ·435·