
第3卷第5期 智能系统学报 Vol 3 Na 5 2008年10月 CAA I Transactions on Intelligent Systems Oct 2008 免疫克隆算法调节参数的非线性控制器设计 黄忠报,李士勇 (哈尔滨工业大学控制科学与工程系,黑龙江哈尔滨150001) 摘要:以模糊神经网络(N)为基础,结合误差线性反馈构造了一种新型的非线性控制器.非线性控制器的设计 难点在于参数的确定问题,用传统的算法对控制器参数寻优时容易陷入局部收敛,难于取得可靠的参数,因此提出 一种改进的免疫克隆选择算法,用于确定非线性控制器的最优参数.倒立摆的仿真实验表明改进的免疫克隆算法在 控制器参数寻优中取得良好的效果,所设计的控制器具有很强的非线性适应能力, 关键词:改进的免疫克隆选择算法,非线性控制器;参数寻优 中图分类号:TP273文献标识码:A文章编号:1673-4785(2008)05040808 A nonlnear con troller design usng an mmune clonal selection a lgor ithm HUANG Zhong-bao,L I Shi-yong (Deparment of Contol Science and Engineering.Harbin Institute of Technolgy,Harbin 150001,China) Abstract:A nonlinear controller based on a fuzzy neural netork(FNN)and linear error feedback was construc- ted But the difficulty in nonlinear controller design lies in identification of the parameters being controlled Optmi zation of the parameters may lead to a bcal convergence if traditional methods are used,resulting in unreliable op- eration We therefore developed a modified mmune clonal selection algorithm (m-SA)to opti ize parameters of the nonlinear controller A smulation with an inverted pendulum demonstrated that the m-CSA effectively optmi zes controller parameters and the design has strong nonlinear adaptive ability Keywords:m-CSA;nonlinear controller,parameter opti ization 模糊神经网络(NN)以其很强的非线性适应 变量不断远离所要求目标点的情况,其误差反馈到 能力,近年来在控制器设计中得到广泛的应用,是模 输入端时会超出控制器所能承受的范围,引起运算 糊理论同神经网络相结合的产物,集学习、联想、识 出现爆炸的情况.而采用遗传算法等传统的智能 别、自适应及模糊信息处理于一体.能解决传统PD算法容易引起过早收敛的问题,不能很好地确定控 控制器对于迟滞性非线性对象的控制显得无能为力 制器的参数.因此本文从两方面设计新型的非线性 的问题.但是以N为基础的控制器设计最关键的 控制器:一方面,把控制对像的误差状态变量e作为 问题是参数的确定.随着控制状态变量的增加,所用 模糊神经网络的输入端,把反映控制对象误差变化 到的模糊规则和神经元也成倍地增多,这给控制器 的状态变量通过线性反馈作为补偿与模糊神经网 的参数寻优造成极大的困难.传统的误差反向训练 络的输出量相加,最后作为控制器的输出,另一方 方法容易陷入局部收敛,而且还依赖于初始值, 面,提出一种改进的免疫克隆算法,用于优化所改进 有时会出现训练退化的现象,使得控制对象的状态 的非线性控制器。 基于生物免疫系统的自学习、自适应2等智能 收稿日期:2008-03-21 特性,近年来相继出现了许多新颖的免疫算法,如启 基金项目:因家自然科学基金资助项目(60773065). 通信作者:黄忠报.Emai止hazhba@l63cam 发式自适应免疫克隆算法1.生物免疫系统蕴含耐 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3卷第 5期 智 能 系 统 学 报 Vol. 3 №. 5 2008年 10月 CAA I Transactions on Intelligent System s Oct. 2008 免疫克隆算法调节参数的非线性控制器设计 黄忠报 , 李士勇 (哈尔滨工业大学 控制科学与工程系 ,黑龙江 哈尔滨 150001) 摘 要 :以模糊神经网络 ( FNN)为基础 ,结合误差线性反馈构造了一种新型的非线性控制器. 非线性控制器的设计 难点在于参数的确定问题 ,用传统的算法对控制器参数寻优时容易陷入局部收敛 ,难于取得可靠的参数 ,因此提出 一种改进的免疫克隆选择算法 ,用于确定非线性控制器的最优参数. 倒立摆的仿真实验表明改进的免疫克隆算法在 控制器参数寻优中取得良好的效果 ,所设计的控制器具有很强的非线性适应能力. 关键词 :改进的免疫克隆选择算法 ;非线性控制器 ;参数寻优 中图分类号 : TP273 文献标识码 : A 文章编号 : 167324785 (2008) 0520408208 A nonlinear controller design using an immune clonal selection algor ithm HUANG Zhong2bao, L I Shi2yong (Department of Control Science and Engineering, Harbin Institute of Technology, Harbin 150001, China) Abstract:A nonlinear controller based on a fuzzy neural network (FNN ) and linear error feedback was construc2 ted. But the difficulty in nonlinear controller design lies in identification of the parameters being controlled. Op tim i2 zation of the parameters may lead to a local convergence if traditionalmethods are used, resulting in unreliable op2 eration. We therefore developed a modified immune clonal selection algorithm (m2ICSA) to op tim ize parameters of the nonlinear controller. A simulation with an inverted pendulum demonstrated that the m2ICSA effectively op tim i2 zes controller parameters and the design has strong nonlinear adap tive ability. Keywords:m2ICSA; nonlinear controller; parameter op tim ization 收稿日期 : 2008203221. 基金项目 :国家自然科学基金资助项目 (60773065). 通信作者 :黄忠报. E2mail: hazhba@163. com. 模糊神经网络 (FNN)以其很强的非线性适应 能力 ,近年来在控制器设计中得到广泛的应用 ,是模 糊理论同神经网络相结合的产物 ,集学习、联想、识 别、自适应及模糊信息处理于一体. 能解决传统 PID 控制器对于迟滞性非线性对象的控制显得无能为力 的问题. 但是以 FNN为基础的控制器设计最关键的 问题是参数的确定. 随着控制状态变量的增加 ,所用 到的模糊规则和神经元也成倍地增多 ,这给控制器 的参数寻优造成极大的困难. 传统的误差反向训练 方法 [ 1 ]容易陷入局部收敛 ,而且还依赖于初始值 , 有时会出现训练退化的现象 ,使得控制对象的状态 变量不断远离所要求目标点的情况 ,其误差反馈到 输入端时会超出控制器所能承受的范围 ,引起运算 出现“爆炸 ”的情况. 而采用遗传算法等传统的智能 算法容易引起过早收敛的问题 ,不能很好地确定控 制器的参数. 因此本文从两方面设计新型的非线性 控制器 :一方面 ,把控制对像的误差状态变量 e作为 模糊神经网络的输入端 ,把反映控制对象误差变化 的状态变量 eÛ通过线性反馈作为补偿与模糊神经网 络的输出量相加 ,最后作为控制器的输出 ;另一方 面 ,提出一种改进的免疫克隆算法 ,用于优化所改进 的非线性控制器. 基于生物免疫系统的自学习、自适应 [ 2 ]等智能 特性 ,近年来相继出现了许多新颖的免疫算法 ,如启 发式自适应免疫克隆算法 [ 3 ] . 生物免疫系统蕴含耐

第5期 黄忠报,等:免疫克隆算法调节参数的非线性控制器设计 ·409· 受性、免疫记忆、分布式并行处理、自组织、自学习、 个子个体;当前群体倛样本总数为m)即A,=X, 自适应和鲁棒性等强大的信息处理能力,可为工程 X2,Xm,克隆算子为 领域提供各种富有成效的智能计算和方法.免疫克 9 =g(X,.m)Int(m- A1X))片 1) 隆选择算法来源于传统的生物免疫克隆原理,由 ∑A1X De Castro!51在此基础上于2000年将克隆选择原理 引入到免疫算法中,用于求函数极值取得很好的效 式中:nt(·)表示上取整函数,由此当前抗体扩增 果,此外,还将其应用到数据挖掘中.文献[8]利 为五,=(瓦,2,…元,X,则群体A,的 用Parzen窗估计法来计算抗体的熵并作为选择抗 数量扩增为n1=∑9,这样可以保证每个抗体在 体的依据,进而提出了一种新型的免疫进化算法.但 克隆阶段不被除掉,有利于保持个体的多样性 是,这些算法在计算抗体的熵作为抗体选择的评价 2)高频变异成熟操作.为了提高抗体局部搜索 值时都没有结合抗体的适应度.,本文把抗体熵与适 能力,文献I0在De Castro提出的免疫克隆选择算 应度加权作为抗体选择的评价值,同时采取高斯变 法基础上,对抗体的每个基因分量施加了变异算子 异策略使抗体成熟,提出了一种改进的免疫克隆选 kk=exp(-f)(1+Gauss(0,1))/10,f为抗体的 择算法(modified mmune clonal seletion algorithm,m- 适应度,Gauss0.l)为随机高斯算子.其采取的操作 CS4),并在此基础上对设计的新型非线性控制器 方法是:对于每个抗体的分量,首先在其正负方向分 参数寻优 别对称地施加该变异算子,扩展出2个相应的子抗 1改进的免疫克隆选择算法 体,这样每个n维抗体扩出2n个子个体;然后选出 该子群中的最优个体,用于估算其确定的超立方体 基于抗体克隆选择机理,采用克隆选择算子的 的最好顶点.该方法在电磁场参数优化问题中取得 算法统称为免疫克隆选择计算1.为免疫克隆选择 良好的效果 算法建立一个统一的描述,首先把抗原、抗体分别对 由于在实际应用中抗体的适应度可能会很 应要解决的问题和候选解,将抗体亲合力的计算作 大,使得变异算子趋向于0,影响进一步的有效搜 为寻找最优解的依据:然后模拟淋巴细胞再生过程, 索.因此本文引入反余切函数,使施加的变异算子为 对抗体进行克隆操作,扩增出新的个体,同时模拟抗 体的成熟过程,对候选解进行高频变异操作,在其局 kI =exp(-arctan(AD).(1 Gauss(0.1)2 2) 部搜索空间中选择亲合力最大的抗体;最后根据免 式中:A为抗体的亲合力,对应于.为了进一步对 疫系统的正负反馈调节机制,如果抗体的浓度超过 一定的阈值,就进行抑制,保持抗体的浓度平衡.可 克隆后的群体A,进行变异成熟操作,按如下方法进 以把克隆选择算法分为以下4个步骤: 行操作:对于原抗体群A,的个体X,如果按步骤1) 1)克隆操作.根据文献[9的方法,对每个抗体 所求得的相应克隆算子4,=1,按照文献[10的方 施加克隆算子,使其扩增裂变成为若干子抗体,扩增 法如上文说明对其进行高频变异成熟操作:如果 的数量取决于抗体的适应度亲合力)和当前抗体 克隆算子9,≥2,先从X,的克隆体中选一抗体 群的总数,如下所述: X,(1≤≤4,)按照文献10的方法进行高频变异操 记向量X=(x,,x的优化问题为P,即 作,余下的9,~1个克隆子抗体分别对其所有的基 maxf(x),x∈Xf(x)对应的抗体适应度设为AI(x) 因分量都施加式(2)所示的变异算子 在一些条件下需要把f(x)转化为相应的亲合度, 需要说明的是,X(1≤≤4,)施加变异算子1 以便对抗体评价值进行估算,例如出现f(x)<0时, 以后,得到的变异个体,可能会超出搜索空间的 一般地,通过AI(x)=ep(arctan(f(x)),将其映射 范围.De Castro提出的免疫克隆选择算法中在这问 题上直接用原来的抗体取代X,为了进一步提高 到区间Ip(-2,ep2)1由此当前初始群体 局搜索能力,当出现超出搜索空间的变异个体时,本 A,的个体X,通过施加克隆算子q,后分别扩增出q, 文对变异算子k作如下的修正: 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
受性、免疫记忆、分布式并行处理、自组织、自学习、 自适应和鲁棒性等强大的信息处理能力 ,可为工程 领域提供各种富有成效的智能计算和方法. 免疫克 隆选择算法来源于传统的生物免疫克隆原理 [ 4 ] ,由 De Castro [ 526 ]在此基础上于 2000年将克隆选择原理 引入到免疫算法中 ,用于求函数极值取得很好的效 果 ,此外 ,还将其应用到数据挖掘 [ 7 ]中. 文献 [ 8 ]利 用 Parzen窗估计法来计算抗体的熵并作为选择抗 体的依据 ,进而提出了一种新型的免疫进化算法. 但 是 ,这些算法在计算抗体的熵作为抗体选择的评价 值时都没有结合抗体的适应度. 本文把抗体熵与适 应度加权作为抗体选择的评价值 ,同时采取高斯变 异策略使抗体成熟 ,提出了一种改进的免疫克隆选 择算法 (modified immune clonal seletion algorithm,m2 ICSA) ,并在此基础上对设计的新型非线性控制器 参数寻优. 1 改进的免疫克隆选择算法 基于抗体克隆选择机理 ,采用克隆选择算子的 算法统称为免疫克隆选择计算 [ 9 ] . 为免疫克隆选择 算法建立一个统一的描述 ,首先把抗原、抗体分别对 应要解决的问题和候选解 ,将抗体亲合力的计算作 为寻找最优解的依据 ;然后模拟淋巴细胞再生过程 , 对抗体进行克隆操作 ,扩增出新的个体 ,同时模拟抗 体的成熟过程 ,对候选解进行高频变异操作 ,在其局 部搜索空间中选择亲合力最大的抗体 ;最后根据免 疫系统的正负反馈调节机制 ,如果抗体的浓度超过 一定的阈值 ,就进行抑制 ,保持抗体的浓度平衡. 可 以把克隆选择算法分为以下 4个步骤 : 1)克隆操作. 根据文献 [ 9 ]的方法 ,对每个抗体 施加克隆算子 ,使其扩增裂变成为若干子抗体 ,扩增 的数量取决于抗体的适应度 (亲合力 )和当前抗体 群的总数 ,如下所述 : 记向量 X = ( x1 , x2 , …, xm )的优化问题为 P,即 max f ( x) , x∈X. f ( x)对应的抗体适应度设为 A I( x) (在一些条件下需要把 f ( x)转化为相应的亲合度 , 以便对抗体评价值进行估算 ,例如出现 f ( x) < 0时 , 一般地 ,通过 A I( x) = exp ( arctan ( f ( x) ) ) ,将其映射 到区间 [ exp ( - π 2 ) , exp ( π 2 ) ]. 由此当前初始群体 At的个体 Xi 通过施加克隆算子 qi 后分别扩增出 qi 个子个体;当前群体 (其样本总数为 m )即 At = { X1 , X2 , …, Xm },克隆算子 [ 9 ]为 qi = g (Xi , m ) = Int(m · A I(Xi ) ∑ m j=1 A I(Xj ) ). (1) 式中 : Int( ·)表示上取整函数 ,由此当前抗体扩增 为 A t = { X 11 , X 12 , …, X 1q i , X 2 , …, X m qm },则群体 At 的 数量扩增为 n t = ∑ m i =1 qi ,这样可以保证每个抗体在 克隆阶段不被除掉 ,有利于保持个体的多样性. 2)高频变异成熟操作. 为了提高抗体局部搜索 能力 ,文献 [10 ]在 De Castro提出的免疫克隆选择算 法基础上 ,对抗体的每个基因分量施加了变异算子 k, k = exp ( - f 3 ) ( 1 + Gauss( 0, 1) ) /10, f 3 为抗体的 适应度 , Gauss(0, 1)为随机高斯算子. 其采取的操作 方法是 :对于每个抗体的分量 ,首先在其正负方向分 别对称地施加该变异算子 ,扩展出 2个相应的子抗 体 ,这样每个 n维抗体扩出 2n个子个体;然后选出 该子群中的最优个体 ,用于估算其确定的超立方体 的最好顶点. 该方法在电磁场参数优化问题中取得 良好的效果. 由于在实际应用中抗体的适应度 f 3 可能会很 大 ,使得变异算子趋向于 0,影响进一步的有效搜 索. 因此本文引入反余切函数 ,使施加的变异算子为 k l =exp ( - a rctan (A I) ) ·(1 + Gauss(0, 1) ) /2. (2) 式中 : A I为抗体的亲合力 ,对应于 f 3 . 为了进一步对 克隆后的群体 A t 进行变异成熟操作 ,按如下方法进 行操作 :对于原抗体群 At的个体 Xi ,如果按步骤 1) 所求得的相应克隆算子 qi = 1,按照文献 [ 10 ]的方 法 (如上文说明 )对其进行高频变异成熟操作;如果 克隆算子 qi ≥2, 先从 Xi 的克隆体中选一抗体 X ij (1≤j≤qi )按照文献 [ 10 ]的方法进行高频变异操 作 ,余下的 qi - 1个克隆子抗体分别对其所有的基 因分量都施加式 (2)所示的变异算子. 需要说明的是 , X ij ( 1≤j≤qi )施加变异算子 k l 以后 ,得到的变异个体 X ′ij可能会超出搜索空间的 范围. De Castro提出的免疫克隆选择算法中在这问 题上直接用原来的抗体取代 X ′ij . 为了进一步提高 局搜索能力 ,当出现超出搜索空间的变异个体时 ,本 文对变异算子 k l作如下的修正 : 第 5期 黄忠报 ,等 :免疫克隆算法调节参数的非线性控制器设计 ·409·

·410· 智能系统学报 第3卷 记抗体X=(x,2,,x)的基因分量x的搜 性的估算方法,然而它是基于抗体基因型空间的,不 索范围为[a,b,则修正的变异算子k1在正方向上 适合实数编码的算法,文献[8利用Parzen窗估计 取为 法来计算抗体的熵并以此作为选择抗体的依据.这 kl =(b x,)exp(-arctan(A D)rand 3) 是估算实数编码空间的抗体分布的一种重要方法, 负方向的修正变异算子k取为 本文参考该方法对抗体的评价值进行估算, kI =(a,-x,)exp(-arctan(A 1))rand (4) 从空间几何的角度考虑,当个体均匀分布于搜 式中:and为f0,1的随机变量.由此抗体X,得到 索空间时最有利于进行全局搜索.当群体中的大部 相应的2n+q,个变异子个体.最后由X,及其2n+q, 分抗体聚集在一个局部空间,而少数的个体远离它 个子抗体组成的子群体选择亲合力较大的9:个抗 们,那么这些孤立的个体更能有利于搜索更优个体 体进入下一代,由此得到X,的成熟抗体群,记为B。应当保留下来进入下一代.根据Parn窗估计法得 3)更新记忆抗体从成熟后的群体B,取出亲合出的概率密度函数特点,孤立的个体相应的概率密 力较大的N。一般取10一20,并且满足N。4W。(No为初 式中:核函数中采用多变量的高斯函数,表示为 始抗体的数量)时免疫系统开始对抗体进行抑制, 1 φu 并且骨髓又产生新的N,/51([·表示上取整符 2m)1∑ ep.u'∑w 号)个新抗体 7) 抑制抗体的过程实质上是克隆选择过程:保留 式中:T为转置操作,∑为协方差矩阵,取为对角 一些个体进入下一代,清除一些评价值过低的抗体. 矩阵,按照文献[8的方法,其对角元素表示为抗体 确定好抗体的评价值才能对抗体进行有效地选择, 相应的基因分量的方差即 便以搜索潜在的更优个体.传统的克隆选择算法只 0,-a数、4a起 (8) 是按照抗体亲合力的大小作为抗体选择的标准,这 IUI 不利于保持抗体的多样性,进而影响到进一步搜索 式中:4ma和mm分别表示群体中的抗体在第基因 潜在最优解的可能性.为此应该对抗体的评价值作 分量的最大值和最小值.如果0,=0,取0,=104 新的定义.根据免疫学正负反馈的浓度调节机制,适 不同于文献[8的抗体评价值估算法,本文作 应度低而浓度又高的抗体繁殖应该受到抑制,同时 如下的评价值估算: 应该激励那些有助于杀灭抗原而浓度又比较低的抗 1(u,)=1-P(u,)+w arctan(A I(u,)).(9) 体,使抗体不断优化.信息熵1-是反映抗体多样 式中:w为抗体亲合力的影响权值,一般取Q05~ 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
记抗体 X = ( x1 , x2 , …, xm )的基因分量 xi 的搜 索范围为 [ ai , bi ],则修正的变异算子 kl在正方向上 取为 k l = ( bi - xi ) exp ( - a rctan (A I) ) rand. (3) 负方向的修正变异算子 k l取为 k l = ( ai - xi ) exp ( - a rctan (A I) ) rand. (4) 式中 : rand为 [ 0, 1 ]的随机变量. 由此抗体 Xi 得到 相应的 2n + qi 个变异子个体. 最后由 Xi 及其 2n + qi 个子抗体组成的子群体选择亲合力较大的 qi 个抗 体进入下一代 ,由此得到 Xi 的成熟抗体群 ,记为 B t . 3)更新记忆抗体. 从成熟后的群体 B t 取出亲合 力较大的 Nc (一般取 10~20,并且满足 Nc 4N0 (N0 为初 始抗体的数量 )时免疫系统开始对抗体进行抑制 , 并且骨髓又产生新的 [Nt /5 ] ( [ · ]表示上取整符 号 )个新抗体. 抑制抗体的过程实质上是克隆选择过程 :保留 一些个体进入下一代 ,清除一些评价值过低的抗体. 确定好抗体的评价值才能对抗体进行有效地选择 , 便以搜索潜在的更优个体. 传统的克隆选择算法只 是按照抗体亲合力的大小作为抗体选择的标准 ,这 不利于保持抗体的多样性 ,进而影响到进一步搜索 潜在最优解的可能性. 为此应该对抗体的评价值作 新的定义. 根据免疫学正负反馈的浓度调节机制 ,适 应度低而浓度又高的抗体繁殖应该受到抑制 ,同时 应该激励那些有助于杀灭抗原而浓度又比较低的抗 体 ,使抗体不断优化. 信息熵 [ 11213 ]是反映抗体多样 性的估算方法 ,然而它是基于抗体基因型空间的 ,不 适合实数编码的算法 ,文献 [ 8 ]利用 Parzen窗估计 法来计算抗体的熵并以此作为选择抗体的依据. 这 是估算实数编码空间的抗体分布的一种重要方法 , 本文参考该方法对抗体的评价值进行估算. 从空间几何的角度考虑 ,当个体均匀分布于搜 索空间时最有利于进行全局搜索. 当群体中的大部 分抗体聚集在一个局部空间 ,而少数的个体远离它 们 ,那么这些孤立的个体更能有利于搜索更优个体 , 应当保留下来进入下一代. 根据 Parzen窗估计法得 出的概率密度函数特点 ,孤立的个体相应的概率密 度就比较小. 如果它的适应度较高就更应当被选择 , 并在由其构成的局部空间生成更多的抗体便以进一 步搜索更优抗体 ,因此赋予它的评价值就应当比较 高;相反 ,概率密度比较大 (它的浓度大 )而适应度 低的抗体 ,就应当被抑制 ,被新的抗体所取代 ,使抗 体朝着有利于搜索潜在更优抗体的方向进化. 因此 抗体的选择评价值应当是 Parzen窗估计概率密度 的减函数 ,是适应度的增函数. 确定方法如下 : 对于抗体群 U = { ui | i = 1, 2, …, | U | }. (5) 式中 : ui ∈R n , |U |表示种群总数 ,抗体的第 j个基因 分量 ui, j∈[ aj , bj ],根据 Parzen窗估计法 ,抗体 u的 局部空间概率密度估计值为 p^ ( u ) = 1 | U | ∑u i φ( u - ui ). (6) 式中 :核函数 φ采用多变量的高斯函数 ,表示为 φ( u ) = 1 (2π) n 2 | ∑| 1 2 exp ( - 1 2 u T ∑ - 1 u ). (7) 式中 : T为转置操作 , ∑为协方差矩阵 ,取为对角 矩阵 ,按照文献 [ 8 ]的方法 ,其对角元素表示为抗体 相应的基因分量的方差即 σj = ujmax - ujm in | U | . (8) 式中 : ujmax和 ujm in分别表示群体中的抗体在第 j基因 分量的最大值和最小值. 如果 σj = 0,取 σj = 10 - 4 . 不同于文献 [ 8 ]的抗体评价值估算法 ,本文作 如下的评价值估算 : I( ui ) = 1 - P^ ( ui ) +w 3 arc tan (A I( ui ) ). (9) 式中 : w 为抗体亲合力的影响权值 ,一般取 0. 05~ ·410· 智 能 系 统 学 报 第 3卷
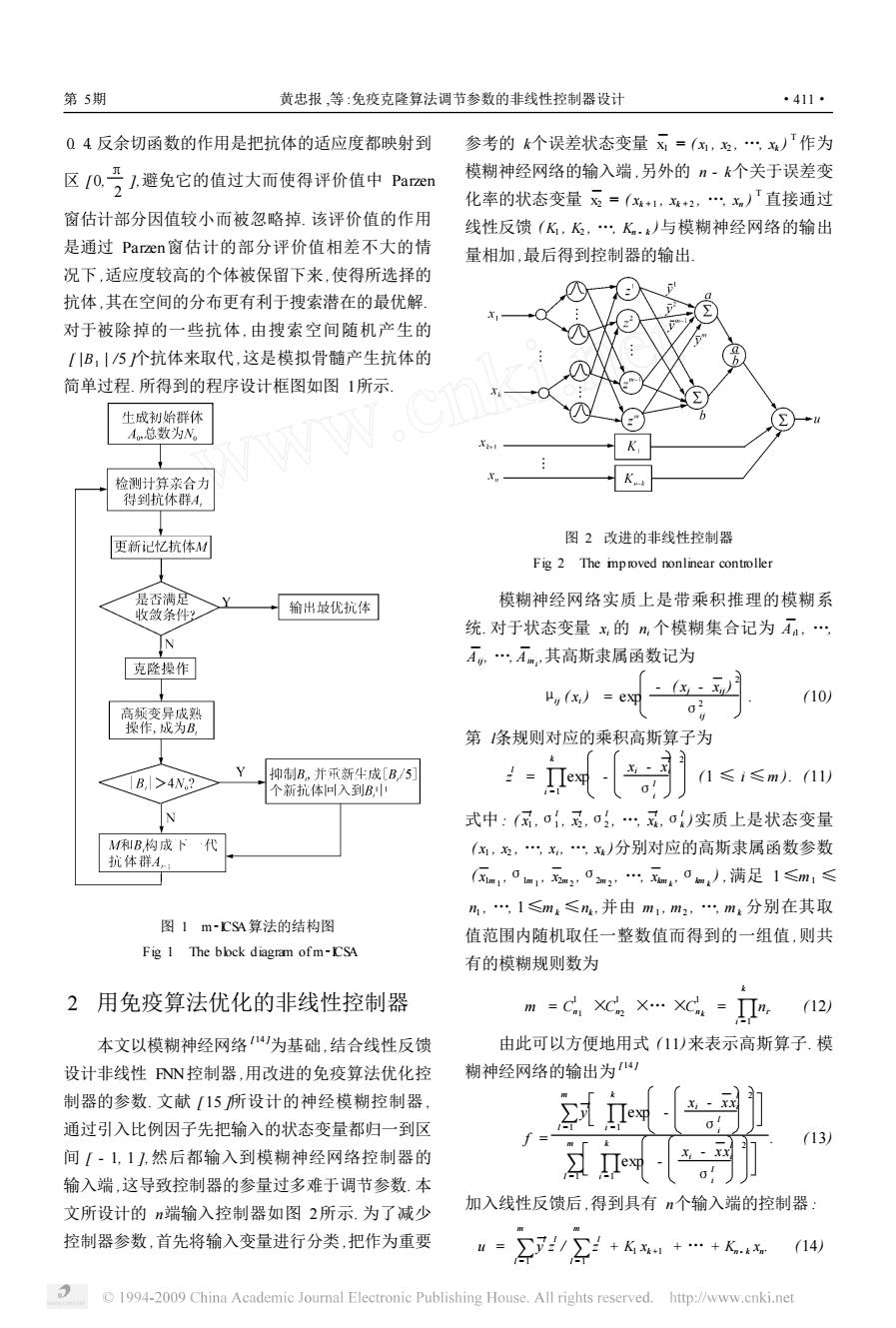
第5期 黄忠报,等:免疫克隆算法调节参数的非线性控制器设计 411 Q4反余切函数的作用是把抗体的适应度都映射到 参考的k个误差状态变量=(,,,)「作为 区021,避免它的值过大而使得评价值中Pan 模糊神经网络的输入端,另外的n~k个关于误差变 化率的状态变量=(xk+,+2,x)「直接通过 窗估计部分因值较小而被忽略掉.该评价值的作用 线性反馈(K,,K.与模糊神经网络的输出 是通过Parzen窗估计的部分评价值相差不大的情 量相加,最后得到控制器的输出 况下,适应度较高的个体被保留下来,使得所选择的 抗体,其在空间的分布更有利于搜索潜在的最优解。 对于被除掉的一些抗体,由搜索空间随机产生的 [IB,1/5个抗体来取代,这是模拟骨髓产生抗体的 简单过程.所得到的程序设计框图如图1所示 生成初始群休 A,总数为N。 检测计算亲合力 K 得到抗休群A, 更新记忆抗体M 图2改进的非线性控制器 Fig 2 The mproved nonlinear controller 是否满定 输出歧优抗体 模糊神经网络实质上是带乘积推理的模糊系 收敛条件2 统.对于状态变量x的m,个模糊集合记为瓦, N A,Am,其高斯隶属函数记为 克隆操作 μg(x)=ex (xi-xi (10) 高频变异成熟 操作,成为B 第条规则对应的乘积高斯算子为 B,|>4N2 抑制B,并币新生成[B,/5 (1≤i≤m).(11) 个新抗体回入到B N 式中:属,,,o,,)实质上是状态变量 M和B构成下 代 (:,五,,分别对应的高斯隶属函数参数 抗体群A (不m1,0m1,五m2,0m2,片4,0m:,满足1≤m1≤ h,:1≤mg≤n,并由m1,m2,”m分别在其取 图1m-℃SA算法的结构图 值范围内随机取任一整数值而得到的一组值,则共 Fig 1 The bbck diagram ofm-CSA 有的模糊规则数为 2用免疫算法优化的非线性控制器 m=CCnX…C=n, (12 本文以模糊神经网络为基础,结合线性反馈 由此可以方便地用式(11)来表示高斯算子.模 设计非线性NN控制器,用改进的免疫算法优化控 糊神经网络的输出为 制器的参数.文献「15所设计的神经模糊控制器, 通过引入比例因子先把输入的状态变量都归一到区 13 间[-1,1),然后都输入到模糊神经网络控制器的 e X-xx 输入端,这导致控制器的参量过多难于调节参数.本 文所设计的n端输入控制器如图2所示.为了减少 加入线性反馈后,得到具有n个输入端的控制器: 控制器参数,首先将输入变量进行分类,把作为重要 = +Kk1+…+Kn.kn(14) 1994-2009 China Academic Journal Electronie Publishing House.All rights reserved. http://www.cnki.net
0. 4. 反余切函数的作用是把抗体的适应度都映射到 区 [0, π 2 ],避免它的值过大而使得评价值中 Parzen 窗估计部分因值较小而被忽略掉. 该评价值的作用 是通过 Parzen窗估计的部分评价值相差不大的情 况下 ,适应度较高的个体被保留下来 ,使得所选择的 抗体 ,其在空间的分布更有利于搜索潜在的最优解. 对于被除掉的一些抗体 , 由搜索空间随机产生的 [ |B1 | /5 ]个抗体来取代 ,这是模拟骨髓产生抗体的 简单过程. 所得到的程序设计框图如图 1所示. 图 1 m2ICSA算法的结构图 Fig. 1 The block diagram of m2ICSA 2 用免疫算法优化的非线性控制器 本文以模糊神经网络 [ 14 ]为基础 ,结合线性反馈 设计非线性 FNN控制器 ,用改进的免疫算法优化控 制器的参数. 文献 [ 15 ]所设计的神经模糊控制器 , 通过引入比例因子先把输入的状态变量都归一到区 间 [ - 1, 1 ],然后都输入到模糊神经网络控制器的 输入端 ,这导致控制器的参量过多难于调节参数. 本 文所设计的 n端输入控制器如图 2所示. 为了减少 控制器参数 ,首先将输入变量进行分类 ,把作为重要 参考的 k个误差状态变量 x1 = ( x1 , x2 , …, xk ) T作为 模糊神经网络的输入端 ,另外的 n - k个关于误差变 化率的状态变量 x2 = ( xk + 1 , xk + 2 , …, xn ) T 直接通过 线性反馈 ( K1 , K2 , …, Kn - k )与模糊神经网络的输出 量相加 ,最后得到控制器的输出. 图 2 改进的非线性控制器 Fig. 2 The imp roved nonlinear controller 模糊神经网络实质上是带乘积推理的模糊系 统. 对于状态变量 xi 的 ni 个模糊集合记为 A i1 , …, A ij , …, A in i ,其高斯隶属函数记为 μij ( xi ) = exp - ( xj - xij ) 2 σ2 ij . (10) 第 l条规则对应的乘积高斯算子为 z l = ∏ k i =1 exp - xi - x l i σl i 2 (1 ≤ i ≤m ). (11) 式中 : ( x l 1 ,σl 1 , x l 2 ,σl 2 , …, x l k ,σl k )实质上是状态变量 ( x1 , x2 , …, xi , …, xk )分别对应的高斯隶属函数参数 ( x1m 1 ,σ1m 1 , x2m 2 ,σ2m 2 , …, xkm k ,σkm k ) ,满足 1≤m1 ≤ n1 , …, 1≤mk ≤nk ,并由 m1 , m2 , …, mk 分别在其取 值范围内随机取任一整数值而得到的一组值 ,则共 有的模糊规则数为 m = C 1 n1 ×C 1 n2 ×… ×C 1 nk = ∏ k i =1 ni . (12) 由此可以方便地用式 ( 11)来表示高斯算子. 模 糊神经网络的输出为 [ 14 ] f = ∑ m l =1 y l ∏ k i =1 exp - xi - xx l i σl i 2 ∑ m l =1 ∏ k i =1 exp - xi - xx l i σl i 2 . (13) 加入线性反馈后 ,得到具有 n个输入端的控制器 : u = ∑ m l =1 y l z l /∑ m l =1 z l + K1 xk +1 + … + Kn - k xn . (14) 第 5期 黄忠报 ,等 :免疫克隆算法调节参数的非线性控制器设计 ·411·

·412· 智能系统学报 第3卷 设控制器作为模糊神经网络输入端的状态变量 行高频变异成熟操作,生成抗体群B。 为x=(,,),它的每个变量x,对应的模糊 7)对于群体B,若满足|B,I>4Wo,按第1节的 集合数n,是一定的.用改进的免疫算法优化这些参 4)步对抗体进行浓度调节,使得抗体群B,的总数 数时,抗原对应要优化的问题,B细胞产生的抗体及 N,=I1B,I/41,并重新生成d=[1B,|/5个新抗体 其亲合力分别对应控制器参数的解空间及评价参数 加入到群体B,中 的指标函数.根据第1节所给出的改进算法,参数寻 8)由记忆抗体群M和B,生成下一代的群体 优的步骤如下: A+1,使1=1+1,转入2),进行循环操作 1)生成抗体.由于抗体基因较多,采用二进制 3 仿真分析 编码,转换计算开销大,所以采用实数编码.首先随 机产生N。个抗体,组成初始群体Ao对应于式(10) 基于模糊神经网络,本文所设计的非线性控制 ~(14)所要确定的参数,抗体可以表示为序列(, 器不需要量化输入状态变量,和传统的模糊控制器 01,,01,a,0,,0,习,, 结构不完全相同,还将误差变化率的状态变量线性 ,K,,K.,编码长度为 反馈到输入端,如图2所示.倒立摆是典型的非线性 1=2++大 控制对象,本文用新型控制器对其控制,进行仿真实 (15) 验,以便说明设计的控制器在非线性对象控制中的 2检测及计算抗体亲合力.为了使控制对象的 有效性.倒立摆的动力学方程为 状态尽快回到平衡位置,同时希望控制器的输出尽 M+m)m”+m lcos(0)6=-br+m府sin0)+u 可能小,本文采取如下所示的二次型性能指标: m lcos()+(I+mf)=-+m lgsin(0). J=x(DQx(0+uRu(v)dt (16) 式中:u为控制量作用在小车上的力),x为小车位 0 移,0为摆杆与垂直方向的夹角,g=98m/S为重力 优化的结果就是要使J→mm由于有些抗体使 加速度.倒立摆模型的其他参数为:小车质量M= 得系统的状态越来越偏离平衡位置,使得 王趋 1096kg摆杆质量m=0109kg小车的摩擦系数 向无穷小,由式14计算得到的u为无穷大,这给 b=01Nm·s;摆杆轴心到质心的长度1= 计算评价值造成很大的困难,因此本文先对群体检 025m摆杆惯量1=00034kg·m2:摆杆摩擦阻力 矩系数f=000218kg·m/3.易知该倒立摆有4个 测,如果在计算抗体指标值过程中出现∑<δ6 状态变量:小车的位移x摆杆角度日,小车速度x,摆 为很小的一个正常数,一般取105),清除掉该抗 杆角速度日控制的目标是使单级倒立摆从某一初 体.这是模拟抗体自然死亡的简单过程.对于满足检 始状态能回到平衡位置0,0,0.0): 测条件的抗体计算其亲合力: 不同于文献15控制器的设计方法,本文直接 4/=-1 把小车位移和摆杆角度(x,)作为模糊神经网络的 (17) a+J 输入端,把小车速度和摆杆角速度(x)作为误差变 式中:a为一个很小的正数,保证分母不为零.由此, 化率,通过线性反馈给控制量1设小车位移和摆杆 得到符合检测要求的群体A,记其种群数为N 角度各有“正”、“零”、“负”3个模糊语言值,形成 3)更新记忆抗体.根据第1节的第3)步的方法 条模糊规则.假设小车位移正模糊集、零模糊集、负 取N.=12,更新记忆抗体M 模糊集高斯型隶属函数参数为(1,01),(2 4)判断收敛条件.若连续20代记忆抗体适应度的 o12,(,03;相应地,摆杆角度各模糊集参量为 平均值不变即满足收敛条件,输出相应的最优参数,停 (1,021),2,02,(,03人为表示方便,以x 止搜索:若不满足收敛条件转入5)继续搜索 x分别表示小车位移和摆杆角度的模糊语言值,以 5)克隆操作.按第1节的1)步骤的方法,求抗 y表示控制器输出的模糊语言值.由此模糊控制器 体的克隆算子9 的规则可以表示为:if x and:heny的形式,每条 6)变异成熟操作.由第1节的2)步骤对抗体进 规则对应如下的高斯算子: 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
设控制器作为模糊神经网络输入端的状态变量 为 x = ( x1 , x2 , …, xk ) T ,它的每个变量 xi 对应的模糊 集合数 ni 是一定的. 用改进的免疫算法优化这些参 数时 ,抗原对应要优化的问题 , B 细胞产生的抗体及 其亲合力分别对应控制器参数的解空间及评价参数 的指标函数. 根据第 1节所给出的改进算法 ,参数寻 优的步骤如下 : 1)生成抗体. 由于抗体基因较多 ,采用二进制 编码 ,转换计算开销大 ,所以采用实数编码. 首先随 机产生 N0 个抗体 ,组成初始群体 A0 . 对应于式 ( 10) ~(14)所要确定的参数 ,抗体可以表示为序列 ( x11 , σ11 , …, x1n1 ,σ1n1 , …, xi1 ,σi1 , …, xknk ,σknk , y l , …, y l , y m , K1 , K2 , …, Kn - k ) ,编码长度为 n l = 2∑ k i =1 ni + ∏ k i =1 ni + n - k. (15) 2)检测及计算抗体亲合力. 为了使控制对象的 状态尽快回到平衡位置 ,同时希望控制器的输出尽 可能小 ,本文采取如下所示的二次型性能指标 : J = ∫ ∞ 0 ( x T ( t) Q x ( t) + u T Ru ( t) ) dt. (16) 优化的结果就是要使 J→m in. 由于有些抗体使 得系统的状态越来越偏离平衡位置 ,使得 ∑ m i =1 z i 趋 向无穷小 ,由式 ( 14)计算得到的 u为无穷大 ,这给 计算评价值造成很大的困难 ,因此本文先对群体检 测 ,如果在计算抗体指标值过程中出现 ∑ m i =1 z i 4N0 ,按第 1节的 4)步对抗体进行浓度调节 ,使得抗体群 B t 的总数 Nt = [ |B t | /4 ],并重新生成 d = [ |B t | /5 ]个新抗体 加入到群体 B t 中. 8)由记忆抗体群 M 和 B t 生成下一代的群体 At + 1 ,使 t = t + 1,转入 2) ,进行循环操作. 3 仿真分析 基于模糊神经网络 ,本文所设计的非线性控制 器不需要量化输入状态变量 ,和传统的模糊控制器 结构不完全相同 ,还将误差变化率的状态变量线性 反馈到输入端 ,如图 2所示. 倒立摆是典型的非线性 控制对象 ,本文用新型控制器对其控制 ,进行仿真实 验 ,以便说明设计的控制器在非线性对象控制中的 有效性. 倒立摆的动力学方程为 (M +m )m¨+m lcos(θ)θ¨= - bxÛ+mθlÛ 2 sin (θ) + u m lx¨cos(θ) + ( I + m l 2 )θ¨= - θfÛ+ m lgsin (θ). 式中 : u为控制量 (作用在小车上的力 ) , x为小车位 移 ,θ为摆杆与垂直方向的夹角 , g = 9. 8m /s 2 为重力 加速度. 倒立摆模型的其他参数为 :小车质量 M = 1. 096 kg;摆杆质量 m = 0. 109 kg;小车的摩擦系数 b = 0. 1 N /m · s - 1 ; 摆杆轴心到质心的长度 l = 0. 25 m;摆杆惯量 I = 0. 003 4 kg·m 2 ;摆杆摩擦阻力 矩系数 f = 0. 002 18 kg·m /s 2 . 易知该倒立摆有 4个 状态变量 :小车的位移 x,摆杆角度θ,小车速度 xÛ,摆 杆角速度 θÛ. 控制的目标是使单级倒立摆从某一初 始状态能回到平衡位置 (0, 0, 0, 0). 不同于文献 [15 ]控制器的设计方法 ,本文直接 把小车位移和摆杆角度 ( x,θ)作为模糊神经网络的 输入端 ,把小车速度和摆杆角速度 ( xÛ)作为误差变 化率 ,通过线性反馈给控制量 u. 设小车位移和摆杆 角度各有“正 ”、“零 ”、“负 ”3个模糊语言值 , 形成 条模糊规则. 假设小车位移正模糊集、零模糊集、负 模糊集高斯型隶属函数参数为 ( x11 , σ11 ) , ( x12 , σ12 ) , ( x13 ,σ13 ) ;相应地 ,摆杆角度各模糊集参量为 ( x21 ,σ21 ) , ( x22 ,σ22 ) , ( x23 ,σ23 ). 为表示方便 ,以 x1、 x2 分别表示小车位移和摆杆角度的模糊语言值 ,以 y表示控制器输出的模糊语言值. 由此模糊控制器 的规则可以表示为 : if x1 and x2 then y的形式 ,每条 规则对应如下的高斯算子 : ·412· 智 能 系 统 学 报 第 3卷

第5期 黄忠报,等:免疫克隆算法调节参数的非线性控制器设计 ·413· =e冲 (x-2 0-) 方,了,,人.把表示小车位移和倒立摆模糊语言 “正”、“零”、“负的中心调节范围分别限定在区间 exp x-2 0-五 [02.2了[-03,03人[-2,-021,其方差调节 o 02 区间分别为[05,2041[04,21(寸, 3=e州 x-五2 0. ,k,)的调节区间分别为[20,400了[-80 80、[-400.0/、[10.200/、[-20,20入[-400 =e州 x-2)2 0-月 20/、10,100人-100,100人[-400,01[10 601、10,601取倒立摆的初始状态为(06.05.0 3=ex x-五22 0.2 0),二次型性能指标参数为:Q=diag10,1,0,0) o12 O2 R=001,按式16)和(17)计算抗体的评价值 =e冲 x-22 0. 运用m-CS4算法优化这些参数时,取初始群 体总数N。=30,常数N。=12.权值w=02.搜索的 }=e x-3)2 0-) 最大次数设为en=50搜索最优参数过程如图3 x-五s2 0- 所示.为了对比,本文还将所改进的免疫克隆选择算 =ex 0B3 O2 法和文献[I0提出的改进型m-A Net免疫算法做对 比,分别独立运行30次,得到表2和图3所示的对 =e对 x-五2 . 6 比情况.最终得到控制器参数如表1所示.其中小车 9 速度和摆杆角速度的反馈系数分别为k=37328. =237409.将确定最优参数后的控制器控制不 9 +kx 18) 同初始状态的倒立摆系统,得到如下图4至图6所 示的各响应曲线, 所要求的参数序列为(,01,2,·12,, 0B,.0,2,02,,02,方,,,,克, 表1改进的非线性控制器最优参数 Table 1 Optial parameters of the in proved nonlnear controller 推理规则 ,语言值 中心 方差 ,语言值 中心 方差 身中心 正 11340 06367 正 07462 09091 3441750 2 正 11340 06367 0 00285 05643 -28098 正 11340 06367 .13215 08977 -2059399 0 00591 03620 正 07462 09091 1649429 J 0 00591 03620 0 00285 05643 17961 6 0 00591 03620 负 .13215 08977 .2492808 > 负 .04521 08611 正 07462 09091 357714 负 -04521 08611 0 00285 05643 -554351 9 负 -04521 08611 负 .13215 08977 .3740226 注:口y表示小车位移摆杆角度控制器输出对应的隶属函数 表2 m-A Net和m-CSA的性能对比 Table 2 The performance com par ison in m-A Net and m-CSA 算法 最大计算函数次数最小计算函数次数 平均最优值 方差 N1/N2/N3 获得最优解的次数 mANet 2520 1846 01920 514X03 46/2330 30 m-CSA 1564 985 02041 135X03 25/1518 30 注:N1N2N3表示获得最优解时需要迭代的最大次数平均次数最小次数 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
z 1 = exp ( x - x11 ) 2 σ2 11 - (θ- x21 ) 2 σ2 21 , z 2 = exp ( x - x11 ) 2 σ2 11 - (θ- x22 ) 2 σ2 22 , z 3 = exp ( x - x11 ) 2 σ2 11 - (θ- x23 ) 2 σ2 23 , z 4 = exp ( x - x12 ) 2 σ2 12 - (θ- x21 ) 2 σ2 21 , z 5 = exp ( x - x12 ) 2 σ2 12 - (θ- x22 ) 2 σ2 22 , z 6 = exp ( x - x12 ) 2 σ2 12 - (θ- x23 ) 2 σ2 23 , z 7 = exp ( x - x13 ) 2 σ2 13 - (θ- x21 ) 2 σ2 21 , z 8 = exp ( x - x13 ) 2 σ2 13 - (θ- x22 ) 2 σ2 22 , z 9 = exp ( x - x13 ) 2 σ2 13 - (θ- x23 ) 2 σ2 23 , u = ∑ 9 i =1 z i y i ∑ 9 i =1 z i + k1 xÛ+ k2θÛ. (18) 所要求的参数序列为 ( x11 ,σ11 , x12 ,σ12 , x13 , σ13 , x21 ,σ21 , x22 ,σ22 , x23 ,σ23 , y 1 , y 2 , y 3 , y 4 , y 5 , y 6 , y 7 , y 8 , y 9 , k1 , k2 ). 把表示小车位移和倒立摆模糊语言 “正 ”、“零 ”、“负 ”的中心调节范围分别限定在区间 [ 0. 2, 2 ]、[ - 0. 3, 0. 3 ]、[ - 2, - 0. 2 ],其方差调节 区间分别为 [ 0. 5, 2 ]、[ 0. 4, 1 ]、[ 0. 4, 2 ]. ( y 1 , y 2 , …, y 9 , k1 , k2 )的调节区间分别为 [ 20, 400 ]、[ - 80, 80 ]、[ - 400, 0 ]、[ 10, 200 ]、[ - 20, 20 ]、[ - 400, 20 ]、[ 10, 100 ]、[ - 100, 100 ]、[ - 400, 0 ]、[ 10, 60 ]、[10, 60 ]. 取倒立摆的初始状态为 (0. 6, 0. 5, 0. 0) ,二次型性能指标参数为 : Q = diag ( 10, 1, 0, 0) , R = 0. 01,按式 (16)和 (17)计算抗体的评价值. 运用 m2ICSA 算法优化这些参数时 ,取初始群 体总数 N0 = 30,常数 Nc = 12,权值 w = 0. 2,搜索的 最大次数设为 gen = 50. 搜索最优参数过程如图 3 所示. 为了对比 ,本文还将所改进的免疫克隆选择算 法和文献 [ 10 ]提出的改进型 m2A iNet免疫算法做对 比 ,分别独立运行 30次 ,得到表 2和图 3所示的对 比情况. 最终得到控制器参数如表 1所示. 其中小车 速度和摆杆角速度的反馈系数分别为 k1 = 37. 328, k2 = 23. 740 9 . 将确定最优参数后的控制器控制不 同初始状态的倒立摆系统 ,得到如下图 4至图 6所 示的各响应曲线. 表 1 改进的非线性控制器最优参数 Table 1 O ptima l param eters of the im proved non linear con troller 推理规则 x1 语言值 x1f中心 x1f方差 x2 语言值 x2f中心 x2f方差 yf 中心 1 正 1. 134 0 0. 636 7 正 0. 746 2 0. 909 1 344. 175 0 2 正 1. 134 0 0. 636 7 0 0. 028 5 0. 564 3 - 2. 809 8 3 正 1. 134 0 0. 636 7 负 - 1. 321 5 0. 897 7 - 205. 939 9 4 0 0. 059 1 0. 362 0 正 0. 746 2 0. 909 1 164. 942 9 5 0 0. 059 1 0. 362 0 0 0. 028 5 0. 564 3 1. 796 1 6 0 0. 059 1 0. 362 0 负 - 1. 321 5 0. 897 7 - 249. 280 8 7 负 - 0. 452 1 0. 861 1 正 0. 746 2 0. 909 1 35. 771 4 8 负 - 0. 452 1 0. 861 1 0 0. 028 5 0. 564 3 - 55. 435 1 9 负 - 0. 452 1 0. 861 1 负 - 1. 321 5 0. 897 7 - 374. 022 6 注 : x1f、x2f、yf 表示小车位移、摆杆角度、控制器输出对应的隶属函数 表 2 m2A iNet和 m2ICSA的性能对比 Table 2 The performance com par ison in m 2A iNet and m 2ICSA 算法 最大计算函数次数 最小计算函数次数 平均最优值 方差 N1 /N2 /N3 获得最优解的次数 m2A INet 2 520 1 846 0. 192 0 5. 14 ×10 - 3 46 /23 /30 30 m2ICSA 1 564 985 0. 204 1 1. 35 ×10 - 3 25 /15 /18 30 注 :N1 /N2 /N3表示获得最优解时需要迭代的最大次数 /平均次数 /最小次数 第 5期 黄忠报 ,等 :免疫克隆算法调节参数的非线性控制器设计 ·413·
·414 智能系统学报 第3卷 0.22 0.6 0.20 HHHHHHHHHHHHHHH 0.4 0.18 0.2 初始状态(-0.5,0.4,0.0) 0.16 0 +一m-1CSA 02 0.14 ··m-AiNet 0.4 0.1 23456 0 10 20 30 40 50 t/s 迭代次数 (6)摆杆角度的响应曲线 50 图3控制器参数寻优过程 Fig 3 The permance of controller's parameter optm izaton 初始状态(0.5,-0.4,0.0) -50 -100 1.0 1500 2 3 456 I/s 0.5 (c)控制器的输出曲线 初始状态(0.65,0.7,0.0) 图5初始状态(065,07,00)的响应曲线 0.50 Fig 5 The response curve when the initial 0.511.522.533.6 t/s state is(-05,-04,00) (a)小车位移的响应曲线 1.5 0.2 1.0 0. 初始状态(0.65,0.7,0.0) 0.5 初始状态(0.1,-0.2,0.0) -0.1 0.2 0.500.511.522.533.6 0 0.511.522.533.6 t/s t/s (6)摆植角度的响应线 (a)小车位移的响应曲线 0.2 200 0. 初始状态(0.1,0.2,0.0) 100 初始状态(0.65,0.7,0.0) 100 0.1 200 0 0.5 1 1.522.533.6 0.2 t/s 0 0.511.522.533.6 (c)控制器的输H曲线 tis (6)摆朴角度的响应曲线 图4初始状态(065,07,00)的响应曲线 0 Fig 4 The response curve when the initial state is(0 65, 初始状念(0.1,0.2,0.0) 07,00) -10 0.4 -20 0.2 0 -30 初始状态(-0.5,0.4,0.0) 0 0.2 0.511.522.533.6 0.4 (c)控制器的输出曲线 0.6 0.8 图6初始状态(01,-02,00)的响应曲线 -1.0 0 2 3 456 Fig 6 The response curve when the initial state is(0 1, t/s -02,00) (a)摆植角角度的响应曲线 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
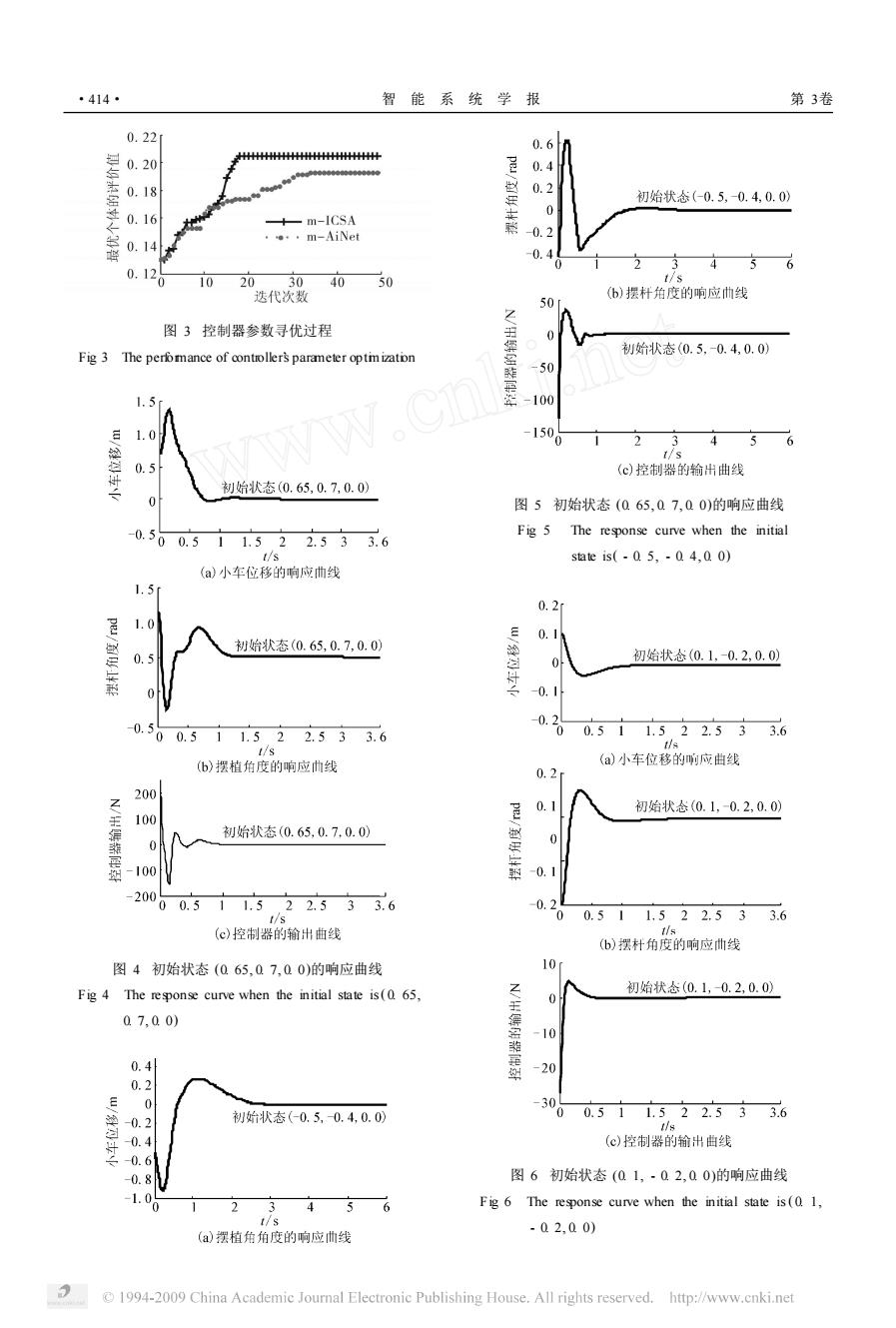
图 3 控制器参数寻优过程 Fig. 3 The performance of controller’s parameter optimization 图 4 初始状态 (0. 65, 0. 7, 0. 0)的响应曲线 Fig. 4 The response curve when the initial state is( 0. 65, 0. 7, 0. 0) 图 5 初始状态 (0. 65, 0. 7, 0. 0)的响应曲线 Fig. 5 The response curve when the initial state is( - 0. 5, - 0. 4, 0. 0) 图 6 初始状态 (0. 1, - 0. 2, 0. 0)的响应曲线 Fig. 6 The response curve when the initial state is( 0. 1, - 0. 2, 0. 0) ·414· 智 能 系 统 学 报 第 3卷

第5期 黄忠报,等:免疫克隆算法调节参数的非线性控制器设计 ·415- 由仿真图可知,将误差变化率做线性补偿的模 tic appoach [M Sydney,kdea Group Publishing.Univ 糊神经网络控制器,用改进的免疫克隆选择算法进 New South Wales,2001:24-70. 行参数寻优取得很好的效果,该控制器能够控制不 [8 ]TAN K C,GOH K,MAMUN AA.An evolutionary artifi- 同状态的倒立摆这样典型的非线性控制对象,非线 cial mmune system ormultiobjective optm ization [J].Eu- ropean Joumal of Operational Research,2008,187:371- 性适应能力强,可以作为非线性智能控制器的一种 392 设计方法。 [9焦李成,杜海峰,刘芳,等.免疫优化计算、学习与识 4结束语 别M]北京:科学出版社,2006:6162 [10 ]CAMPELO F,GU MARAES F G,KGARASHIH,et al A 本文通改进抗体的变异操作,并采取抗体熵函 modified mmune netork algorithm formultmodal electro 数和适应度加权的方法,在对抗体进行抑制操作时 magnetic problem s[J].IEEE Transactions on Magnetics, 将其作为抗体选择的评价值,从而提出了改进的免 2006,42(4):1111-1114 [11 ]FUKUDA T,MORI K,TSUKAMA M.Artificial imune 疫克隆算法,由图3可知该算法在所设计的非线性 systems and their app lications[M [S L ]Spring-Ver 控制器参数寻优过程中比m-A Net免疫算法Io1具 ag1999:210-229. 有更明显的优势;此外,本文基于模糊神经网络,结 [12 ]CHUN J S,JUNG H K HAHN S Y.A study on compari- 合误差线性反馈,将误差的变化率作为补偿输入到 son ofoptm izaton perfomances be teen mmune algprithm 控制器的另外输入端最后将它们相加,设计了一种 and other heuristic algorithm [J ]IEEE Transactions on 新型的非线性控制器;倒立摆的仿真实验表明,确定 Magnetics,1998,34(5):2972-2975 最优参数后,控制器具有很强的非线性适应能力.而 [13]CUIX,L IM,FANG T Study of population diversity of 且不需要量化输入的状态变量,调节参数较容易,可 multi-objective evolutionary algorithm based on mmune and entropy principles[C]//Proceedings of the 2001 Con- 以作为非线性控制器设计的参考方法, gress on Evolutionary Computation Seoul,South Korea, 参考文献 2001:1316-1321 [14正立新.模糊系统与模糊控制教程[M).北京:清华大 [1 ]WANG Lixin Design and analysis of fuzzy identifiers of 学出版社,2003:133-134 nonlinear dynam ic systems[J]IEEE Transactions on Au- [15 ]O X Q,LIS Y The chaos artificial mmune algorithm tomatic Control,1995,40(1):11-23. and its app lication to RBF neuro-fuzzy controller design [2李涛.计算机免疫学[M)北京:电子工业出版社, [C]//IEEE Intematonal Conference on System,Man and 2004:39-40 Cybemetics Washingion,DC,USA,2003:2809-2814. [3胡江强,郭晨,李铁山.启发式自适应免疫克隆算法 作者简介 [J]哈尔滨工程大学学报,2007,28(1):15 黄忠报,男,1981年生,硕士研究 HU Jianggiang,GO Chen,L I Tieshan Heuristic adaptive 生,主要研究方向为人工免疫智能算 mmune clne algorithm [J].Joumal of Harbin Engineering 法非线性控制, University,2007,28(1):1-5. [4 ]BURNET F M.The clonal selection theory of acquired m- munity M ]Cambridge,UK:Cambridge Univ Press, 1959:45-140. [5 ]De CASTRO L N,TMM S J.An artificial imune netork 李士勇,男,1943年生,教授,博士生 for multiodal function opti ization C ]/Proceedings of 导师,中国自动化学会智能自动化专业委 the 2002 Congress on Evolutionary Computation Honol- 员会委员,针算机测量与控制编委.主 ulu,HL USA,2002:699-704 要研究领域为模糊控制、神经控制、智能 [6 ]De CASTRO L N,Von ZUBEN FJ.Leaming and optim iza- 控制、智能优化算法、非线性科学与复杂 tion using the clonal selecting princple[J]IEEE Transac- 性科学等.在国内外发表学术论文120余 tions on Evolutionary Computaton,2002,6(3):239-251. 篇编著教材与专著共5部。 [7]De CASTRO LN,VON ZUBEN F J.Data m ining a heuris 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
由仿真图可知 ,将误差变化率做线性补偿的模 糊神经网络控制器 ,用改进的免疫克隆选择算法进 行参数寻优取得很好的效果 ,该控制器能够控制不 同状态的倒立摆这样典型的非线性控制对象 ,非线 性适应能力强 ,可以作为非线性智能控制器的一种 设计方法. 4 结束语 本文通改进抗体的变异操作 ,并采取抗体熵函 数和适应度加权的方法 ,在对抗体进行抑制操作时 将其作为抗体选择的评价值 ,从而提出了改进的免 疫克隆算法 ,由图 3可知该算法在所设计的非线性 控制器参数寻优过程中比 m2A iNet免疫算法 [ 10 ]具 有更明显的优势 ;此外 ,本文基于模糊神经网络 ,结 合误差线性反馈 ,将误差的变化率作为补偿输入到 控制器的另外输入端最后将它们相加 ,设计了一种 新型的非线性控制器 ;倒立摆的仿真实验表明 ,确定 最优参数后 ,控制器具有很强的非线性适应能力. 而 且不需要量化输入的状态变量 ,调节参数较容易 ,可 以作为非线性控制器设计的参考方法. 参考文献 : [ 1 ]WANG L ixin. Design and analysis of fuzzy identifiers of nonlinear dynamic system s[J ]. IEEE Transactions on Au2 tomatic Control, 1995, 40 (1) : 11223. [ 2 ]李 涛. 计算机免疫学 [M ]. 北京 :电子工业出版社 , 2004: 39240. [ 3 ]胡江强 ,郭 晨 ,李铁山. 启发式自适应免疫克隆算法 [J ]. 哈尔滨工程大学学报 , 2007, 28 (1) : 125. HU Jiangqiang, GUO Chen, L I Tieshan. Heuristic adap tive immune clone algorithm [J ]. Journal of Harbin Engineering University, 2007, 28 (1) : 125. [ 4 ]BURNET F M. The clonal selection theory of acquired im2 munity [ M ]. Cambridge, UK: Cambridge Univ Press, 1959: 452140 . [ 5 ]De CASTRO L N, TIMM IS J. An artificial immune network for multimodal function op tim ization [ C ] / / Proceedings of the 2002 Congress on Evolutionary Computation. Honol2 ulu, H I, USA, 2002: 6992704. [ 6 ]De CASTRO L N, Von ZUBEN F J. Learning and op tim iza2 tion using the clonal selecting p rincip le[J ]. IEEE Transac2 tions on Evolutionary Computation, 2002, 6 (3) : 2392251. [ 7 ]De CASTRO LN,VON ZUBEN F J. Data mining: a heuris2 tic app roach [M ]. Sydney, Idea Group Publishing, Univ New South W ales, 2001: 24270. [ 8 ] TAN K C, GOH K, MAMUN A A. An evolutionary artifi2 cial immune system formultiobjective op timization [J ]. Eu2 ropean Journal of Operational Research, 2008, 187: 3712 392. [ 9 ]焦李成 , 杜海峰 , 刘 芳 ,等. 免疫优化计算、学习与识 别 [M ]. 北京 : 科学出版社 , 2006: 61262. [ 10 ]CAMPELO F, GU IMARAES F G, IGARASH I H, et al. A modified immune network algorithm formultimodal electro2 magnetic p roblems[J ]. IEEE Transactions on Magnetics, 2006, 42 (4) : 111121114. [ 11 ] FUKUDA T, MOR I K, TSUKIAMA M. A rtificial immune systems and their app lications[M ]. [ S. L. ], Sp ring2Ver2 lag, 1999: 2102229. [ 12 ]CHUN J S, JUNG H K. HAHN S Y. A study on compari2 son of op timization performances between immune algorithm and other heuristic algorithm [ J ]. IEEE Transactions on Magnetics, 1998, 34 (5) : 297222975. [ 13 ]CU I X, L IM, FANG T. Study of population diversity of multi2objective evolutionary algorithm based on immune and entropy p rincip les[C ] / /Proceedings of the 2001 Con2 gress on Evolutionary Computation. Seoul, South Korea, 2001: 131621321. [ 14 ]王立新. 模糊系统与模糊控制教程 [M ]. 北京 :清华大 学出版社 , 2003: 1332134. [ 15 ] ZUO X Q, L I S Y. The chaos artificial immune algorithm and its app lication to RBF neuro2fuzzy controller design [C ] / / IEEE International Conference on System, Man and Cybernetics. W ashington, DC, USA, 2003: 280922814. 作者简介 : 黄忠报 ,男 , 1981 年生 ,硕士研究 生 ,主要研究方向为人工免疫智能算 法、非线性控制. 李士勇 ,男 , 1943年生 ,教授 ,博士生 导师 ,中国自动化学会智能自动化专业委 员会委员 ,《计算机测量与控制 》编委. 主 要研究领域为模糊控制、神经控制、智能 控制、智能优化算法、非线性科学与复杂 性科学等.在国内外发表学术论文 120余 篇 ,编著教材与专著共 5部. 第 5期 黄忠报 ,等 :免疫克隆算法调节参数的非线性控制器设计 ·415·