
第3卷第1期 智能系统学报 Vol.3 N2 1 2008年2月 CAAI Transactions on Intelligent Systems Fcb.2008 线性不确定离散时滞系统的鲁棒非脆弱H控制 吴珠,刘国栋 (江南大学通信与控制工程学院,江苏无锡214122) 摘要:基于线性矩阵不等式(LM⑩方法,研究了线性不确定离散时滞系统的鲁棒非脆弱H状态反馈控制器的设 计问题.系统的不确定项参数和控制器的增益变化都是时变的且满足线性分式形式的范数有界.考虑了控制器增益 存在加性和乘性摄动的2种情形,以LM1形式给出了非脆弱H控制器存在的充分条件,保证了闭环系统的鲁棒稳 定性和一定的H衰减水平.实例表明了该设计方法的有效性 关键词:不确定系统;时滞;非脆弱;鲁棒H控制;线性矩阵不等式 中图分类号:TP13文献标识码:A文章编号:16734785(2008)01-006605 Robust and non-fragile H control for linear discrete-time systems with time-delay and uncerta inties WU Zhu,LIU Guo-dong (College of Communication and Control Engineering,Jiangnan University,Wuxi 214122,China) Abstract:This paper deals with the problem of robust and non-fragile Hcontrol via state feedback for lin- ear discrete-time systems with time-delay and normbounded parametric uncertainties by using a method of linear matrix inequality (LMD).Both the gain perturbations of the controller and the uncertain terms of the system are time-varying and normbounded with linear fractional form.Moreover,the gain perturbations of the controller are considered to be either additive or multiplicative.Sufficient conditions for the exist- ence of a robust and nomfragile controller are given in terms of LMI,so the resulting closed-loop system is robustly stable and attains a certain H attenuation level.A numerical example is provided to demonstrate the effectiveness of the method. Key words uncertain system;time-delay;nomfragile;robust Hcontrol;linear matrix inequalities 在各类工业系统中,模型的不确定性和时滞现象 和乘性增益摄动的H控制问题.文中将在此框架下作 是普遍存在的,对这类系统的分析和综合问题一直是 进一步扩展,研究不确定离散时滞系统的鲁棒非脆弱 控制理论和控制工程领域中的研究热点,鲁棒H控制 H控制问题. 问题就是其中之一3).但所设计的控制器都要求是准 确实现的,而实际上,由于数字器件的有限字长、模数 1问题描述 转换的精度等原因,使得控制器存在着一定的不确定 考虑如下一类不确定离散时滞系统: 性,从而造成闭环系统的性能下降甚至稳定性破坏.因 xk+1=(A+△A)xW+(A+△A)x(k- 此,近年来非脆弱控制问题引起了人们的关注!.对 d+(B1+△Bw(W+(B2+△B2)u, 线性连续系统,文献[5]利用Riccati不等式方法设计了 z(W=(C+△Cx(+(Ca+△Ca)x(k-d山+ 非脆弱H-控制器,文献[6]则运用了LM1的方法,文 (D+△Dw(付+(D2+△D2)u(, 献7]设计了非线性时滞系统的非脆弱保成本控制器。 x付=0,k<0,x0)=x0. (1) 对线性离散系统,文献[8]研究了控制器参数具有加性 式中:x(k)∈R”是状态变量,u()∈R"是控制输 收稿日期:2007-01-25. 入,w(付∈R”是外部扰动输入,且w∈L2I0,∞, 通讯作者:吴珠.Email:jstianlan@126.com z(材∈R是被调输出,A、Aa、B1、B2、C、Ca、D1、D2 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
第 3 卷第 1 期 智 能 系 统 学 报 Vol. 3 №. 1 2008 年 2 月 CAA I Transactions on Intelligent Systems Feb. 2008 线性不确定离散时滞系统的鲁棒非脆弱 H ∞控制 吴 珠 ,刘国栋 (江南大学 通信与控制工程学院 ,江苏 无锡 214122) 摘 要 :基于线性矩阵不等式(LMI) 方法 ,研究了线性不确定离散时滞系统的鲁棒非脆弱 H ∞状态反馈控制器的设 计问题. 系统的不确定项参数和控制器的增益变化都是时变的且满足线性分式形式的范数有界. 考虑了控制器增益 存在加性和乘性摄动的 2 种情形 ,以 LMI 形式给出了非脆弱 H ∞控制器存在的充分条件 ,保证了闭环系统的鲁棒稳 定性和一定的 H ∞衰减水平. 实例表明了该设计方法的有效性. 关键词 :不确定系统 ;时滞 ;非脆弱 ;鲁棒 H ∞控制 ;线性矩阵不等式 中图分类号 : TP13 文献标识码 :A 文章编号 :167324785 (2008) 0120066205 Robust and non2fragile H∞ control for linear discrete2time systems with time2delay and uncertainties WU Zhu , L IU Guo2dong (College of Communication and Control Engineering , Jiangnan University , Wuxi 214122 , China) Abstract :This paper deals wit h t he problem of robust and non2fragile H ∞ control via state feedback for lin2 ear discrete2time systems wit h time2delay and norm2bounded parametric uncertainties by using a met hod of linear matrix inequality (LMI) . Both t he gain perturbations of t he controller and t he uncertain terms of t he system are time2varying and norm2bounded with linear fractional form. Moreover , t he gain perturbations of t he controller are considered to be either additive or multiplicative. Sufficient conditions for t he exist2 ence of a robust and non2fragile controller are given in terms of LMI , so the resulting closed2loop system is robustly stable and attains a certain H ∞ attenuation level. A numerical example is provided to demonstrate t he effectiveness of t he met hod. Keywords :uncertain system ; time2delay ; non2fragile ; robust H ∞ control ; linear matrix inequalities 收稿日期 :2007201225. 通讯作者 :吴 珠. E2mail :jstianlan @126. com. 在各类工业系统中 ,模型的不确定性和时滞现象 是普遍存在的 ,对这类系统的分析和综合问题一直是 控制理论和控制工程领域中的研究热点 ,鲁棒 H∞控制 问题就是其中之一[123] . 但所设计的控制器都要求是准 确实现的 ,而实际上 ,由于数字器件的有限字长、模数 转换的精度等原因 ,使得控制器存在着一定的不确定 性 ,从而造成闭环系统的性能下降甚至稳定性破坏. 因 此 ,近年来非脆弱控制问题引起了人们的关注[428] . 对 线性连续系统 ,文献[5]利用 Riccati 不等式方法设计了 非脆弱 H∞控制器 ,文献[6]则运用了 LMI 的方法 , 文 献[7]设计了非线性时滞系统的非脆弱保成本控制器. 对线性离散系统 ,文献[8]研究了控制器参数具有加性 和乘性增益摄动的 H∞控制问题.文中将在此框架下作 进一步扩展 ,研究不确定离散时滞系统的鲁棒非脆弱 H∞控制问题. 1 问题描述 考虑如下一类不确定离散时滞系统 : x( k + 1) = (A +ΔA) x( k) + ( Ad +ΔAd ) x( k - d) + (B1 +ΔB1 ) w( k) + (B2 +ΔB2 ) u( k) , z( k) = ( C +ΔC) x( k) + ( Cd +ΔCd ) x( k - d) + ( D1 +ΔD1 ) w( k) + ( D2 +ΔD2 ) u( k) , x( k) = 0 , k < 0 , x(0) = x0 . (1) 式中 : x ( k) ∈R n 是状态变量 , u ( k) ∈R m 是控制输 入 ,w( k) ∈R p 是外部扰动输入 ,且 w ∈L2 [ 0 , ∞) , z( k) ∈R q 是被调输出 , A、Ad 、B1 、B2 、C、Cd 、D1 、D2 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第1期 吴珠,等:线性不确定离散时滞系统的鲁棒非脆弱H控制 *67* 是适当维常数矩阵,d是系统状态滞后时间,△A、 文中的目的是:设计系统1)的状态反馈控制器 △A△B1、△B2、△C、△Ca、△D1、△D2为不确定实值 2),使得闭环系统(5)对所有满足F(E,(≤ 矩阵函数,它们表示了系统中随时间变化的参数不 的F(k)(1=1,2,3)是渐近稳定的且满足 确定性」 lz(材20是预先给定的常数 为不失一般性,假定系统的参数不确定性具有 在给出主要结论之前,先给出下列引理 如下形式: 引理1)取M、H、E和J为合适维数的实矩 [△A△AG△B△B2 阵,且M=M,则以下条件等价: L△C△C.△D,△D 1)M+HAE+E△TH0,使得 /EEEE. M 式中:H(i=1,2)、E(i=1,2,3,4)为具有适当维数 AHT 0,闭环系统(5)渐近 u(W=(K+△KWx(W 2) 稳定且满足Iz(付20存在状 z(k)=Ckx(k)+Cakx(k-d)+Dkw(k). 态反馈控制器(2),其控制器增益摄动△K满足式 (5) 3),使得闭环系统5)渐近稳定且满足川z()20(i=1,2),对 Ax=(A+△AW+(B+△B2)(K+△, 称正定矩阵X和Y,矩阵W,使得 AK=Ad+△Ad,Bx=B1+△B1, 「 华明 <0. 7) Cx=(C+△C+(D2+△D)(K+△KN, CaK=Ca+△Ca,Dx=D1+△D1. 式中: -X 0 -Y 0 0-21 AX+B2W AY Bi -X 职= CX+D2W CaY DI 0 -1 X 0 0 0 0 -Y ★ ★ 0 0 0 入HFAH LE X+EW EY Es 0 0 0 AJ -入 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
是适当维常数矩阵 , d 是系统状态滞后时间 , ΔA、 ΔAd 、ΔB1 、ΔB2 、ΔC、ΔCd 、ΔD1 、ΔD2 为不确定实值 矩阵函数 ,它们表示了系统中随时间变化的参数不 确定性. 为不失一般性 ,假定系统的参数不确定性具有 如下形式 : ΔA ΔAd ΔB1 ΔB2 ΔC ΔCd ΔD1 ΔD2 = H1 H2 F1 ( k) ( I - J 1 F1 ( k) ) - 1 · [ E1 E2 E3 E4 ]. 式中 : Hi ( i = 1 ,2) 、Ei ( i = 1 ,2 ,3 ,4) 为具有适当维数 的已知实矩阵 ,且 F1 ( k) 为时变扰动矩阵 ,Lebasgue 可测并且满足 : F T 1 ( k) F1 ( k) ≤I. 考虑到状态反馈控制器本身含有不确性 : u( k) = ( K +ΔK) x( k) . (2) 式中 : K∈R m ×n为控制器增益矩阵 ,ΔK为增益的摄 动. 考虑如下 2 种形式的控制器增益摄动 : 1) 加法式摄动 ΔK = H3 F2 ( k) ( I - J 2 F2 ( k) ) - 1 E5 , F T 2 ( k) F2 ( k) ≤I. (3) 2) 乘法式摄动 ΔK = H4 F3 ( k) ( I - J 3 F3 ( k) ) - 1 E6 K, F T 3 ( k) F3 ( k) ≤I. (4) 式中 : Hi ( i = 3 ,4) 、Ei ( i = 5 ,6) 为具有适当维数的已 知实矩阵 , Fi ( k) ( i = 2 , 3) 为 Lebasgue 可测的时变 扰动矩阵并且满足 : F T i ( k) Fi ( k) ≤I. 将控制器(2) 代入系统(1) 得到闭环系统 : x( k + 1) = AK x ( k) + AdK x ( k - d) + Bkw ( k) , z( k) = CK x ( k) + CdK x ( k - d) + DKw ( k) . (5) 式中 : AK = ( A +ΔA) + (B2 +ΔB2 ) ( K+ΔK) , AdK = Ad +ΔAd ,BK = B1 +ΔB1 , CK = ( C +ΔC) + ( D2 +ΔD2 ) ( K+ΔK) , CdK = Cd +ΔCd , DK = D1 +ΔD1 . 文中的目的是 :设计系统(1) 的状态反馈控制器 (2) ,使得闭环系统(5) 对所有满足 F T i ( k) Fi ( k) ≤I 的 F ( k ) ( i = 1 , 2 , 3 ) 是 渐 近 稳 定 的 且 满 足 ‖z( k) ‖2 0 是预先给定的常数. 在给出主要结论之前 ,先给出下列引理. 引理 1 [9 ] 取 M、H、E 和 J 为合适维数的实矩 阵 ,且 M = M T ,则以下条件等价 : 1) M + HΔE + E TΔT H T 0 ,使得 M 3 3 λH T - λI 3 E λJ - λI 0 ,闭环系统(5) 渐近 稳定且满足 ‖z( k) ‖2 0 存在状 态反馈控制器 (2) ,其控制器增益摄动ΔK满足式 (3) ,使得闭环系统(5) 渐近稳定且满足 ‖z ( k) ‖2 0 ( i = 1 , 2) ,对 称正定矩阵 X和 Y,矩阵 W ,使得 Ψ1 ΨT 2 Ψ2 Ψ3 < 0. (7) 式中 : Ψ1 = - X 3 3 3 3 3 3 3 0 - Y 3 3 3 3 3 3 0 0 - γ2 I 3 3 3 3 3 AX + B2W Ad Y B1 - X 3 3 3 3 CX + D2W Cd Y D1 0 - I 3 3 3 X 0 0 0 0 - Y 3 3 0 0 0 λ1 H T 1 λ1 H T 2 0 - λ1 I 3 E1 X + E4W E2 Y E3 0 0 0 λ1 J 1 - λ1 I , 第 1 期 吴 珠 ,等 :线性不确定离散时滞系统的鲁棒非脆弱 H ∞控制 · 76 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·68· 智能系统学报 第3卷 000AB2出)T(D2h)T00飞(Eh)9 E5X00 0 0 00 0 此时,控制器(2)中的反馈增益为K=WX·1 证明由引理1),式6)等价于 -P+Q 0 -Q 0 0-21 ★ ★ A+B2(K+△ Ad B1 -P* 0(i=1,2),对 D和左乘sT,并令X=p1,Y=Q',W=KX,即可 称正定矩阵X和Y,矩阵w,使得式8)成立.此时, 得式7) 控制器2)中的增益为:K=wX1 定理2对系统(1)和给定的常数Y>0,存在状 中 <0 态反馈控制器2),其控制器增益摄动△K满足式 (8) (4),使得闭环系统(5)渐近稳定且满足‖z(2< 式中:功=叫 000(B2 Ha)(D2 Ha)T 00(Ea H) 4= L EsW 00 0 0 00 0J 「-14J 3= 证明同定理1的证明. 「0.30. 「10 注:若不考虑控制器(2)中的增益摄动(公K= B1=-0.30.4,B2=42 0),即为标准的鲁棒H状态反馈控制器,那么定理 L-0.50. L15 1中的式7)和定理2中的式(8)就退化为 0.21 0.6 「0.50.20.1 c= 玛<0. 9 10.31.c-0 0.40.2 「0.50110 3仿真实例 D002D01 将系统(1)的参数矩阵取为 并设矩阵f∈R33,H=diag0.1,0.1,0.1), 「10.701 0.40.1 07 「0.10 01 h=000. ,E=diag1,1.5,1), A=0.320.8,Aa= 00.20 L-0.20-1 L O 0.10.2 E=diag0.4,0.2,0.2), 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved htp://www.cnki.net
Ψ2 = 0 0 0 λ2 (B2 H3 ) T λ2 ( D2 H3 ) T 0 0 λ2 ( E4 H3 ) T E5 X 0 0 0 0 0 0 0 , Ψ3 = - λ2 I λ2 J T 2 λ2 J 2 - λ2 I . 此时 ,控制器(2) 中的反馈增益为 K= WX - 1 . 证明 由引理(1) ,式(6) 等价于 - P + Q 3 3 3 3 3 3 0 - Q 3 3 3 3 3 0 0 - γ2 I 3 3 3 3 A + B2 ( K +ΔK) Ad B1 - P - 1 3 3 3 C + D2 ( K +ΔK) Cd D1 0 - I 3 3 0 0 0 λ1 H T 1 λ1 H T 2 - λ1 I 3 E1 + E4 ( K +ΔK) E2 E3 0 0 λ1 J 1 - λ1 I 0 ,存在状 态反馈控制器 (2) ,其控制器增益摄动ΔK满足式 (4) ,使得闭环系统(5) 渐近稳定且满足 ‖z( k) ‖2 0 ( i = 1 , 2) ,对 称正定矩阵 X和 Y,矩阵 W ,使得式 (8) 成立. 此时 , 控制器(2) 中的增益为 : K= WX - 1 . Φ1 ΦT 2 Φ2 Φ3 < 0. (8) 式中 :Φ1 =Ψ1 , Φ2 = 0 0 0 λ2 (B2 H4 ) T λ2 ( D2 H4 ) T 0 0 λ2 ( E4 H4 ) T E6W 0 0 0 0 0 0 0 , Φ3 = - λ2 I λ2 J T 3 λ2 J 3 - λ2 I . 证明 同定理 1 的证明. 注 :若不考虑控制器 (2) 中的增益摄动 (ΔK = 0) ,即为标准的鲁棒 H ∞状态反馈控制器 ,那么定理 1 中的式(7) 和定理 2 中的式(8) 就退化为 Ψ1 < 0. (9) 3 仿真实例 将系统(1) 的参数矩阵取为 A = 1 0. 7 0 0. 3 2 0. 8 - 0. 2 0 - 1 , Ad = 0. 4 0. 1 0 0 0. 2 0 0 0. 1 0. 2 , B1 = 0. 3 0. 2 - 0. 3 0. 4 - 0. 5 0. 1 ,B2 = 1 0 4 2 1 5 , C = 0. 2 1 0. 6 1 0. 3 1 , Cd = 0. 5 0. 2 0. 1 0 0. 4 0. 2 , D1 = 0. 5 0 0 0. 2 , D2 = 1 0 0 1 . 并设矩阵 F1 ∈R 3 ×3 , H1 = diag (0. 1 ,0. 1 ,0. 1) , H2 = 0. 1 0 0 0 0 0. 1 , E1 = diag (1 ,1. 5 ,1) , E2 = diag (0. 4 ,0. 2 ,0. 2) , · 86 · 智 能 系 统 学 报 第 3 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
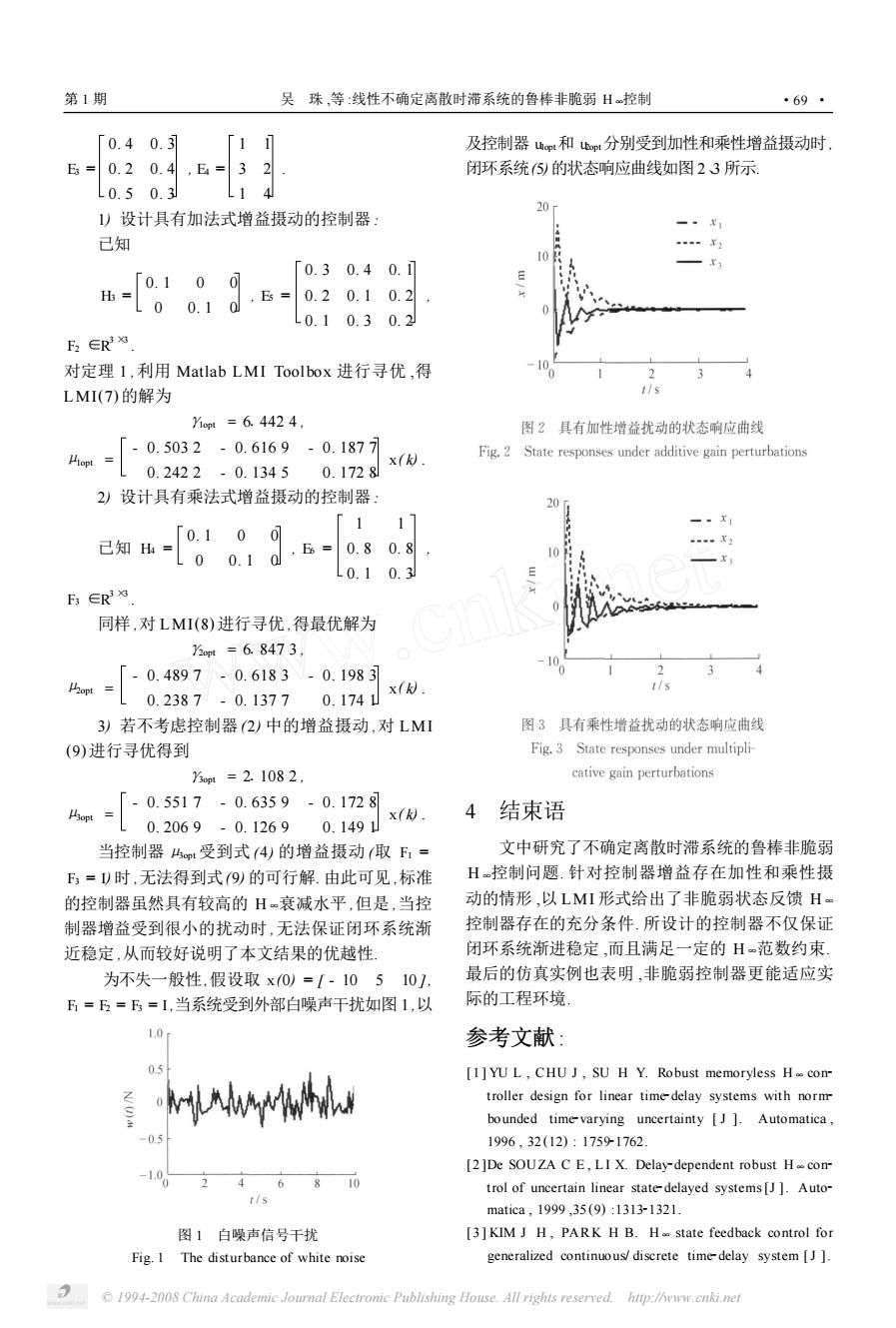
第1期 吴珠,等:线性不确定离散时滞系统的鲁棒非脆弱H控制 ·69· 「0.40.3 1 及控制器p和p分别受到加性和乘性增益摄动时, E3=0.20.4 ,E4=3 2 闭环系统(⑤)的状态响应曲线如图23所示」 L0.50.3到 20 )设计具有加法式增益摄动的控制器: 一。x 己知 07 「0.30.40.1 0.1 0 h=00.10 Es=0.20.10.2 L0.10.30.2 0 E2∈R3为 对定理1,利用Matlab LMI Toolbox进行寻优,得 2 3 LMI(7)的解为 1/s Yiopt 6.442 4. 图2具有加性增益扰动的状态响应曲线 -0.5032-0.6169-0.1877 x() Fig.2 State responses under additive gain perturbations 0.2422-0.1345 0.1728 2)设计具有乘法式增益摄动的控制器: 20 1 7 0 己知= 0.10 00.1a,=0.80.8 10 0.10.3 B∈R3为 P9 同样,对LMI(8)进行寻优,得最优解为 t=6.8473 -10 -0.4897-0.6183-0.1983 0 2 3 x( 1/s 0.2387-0.13770.174 3)若不考虑控制器(2)中的增益摄动,对LMI 图3具有乘性增益扰动的状态响应曲线 (9)进行寻优得到 Fig.3 State responses under multipli- gt=2.1082 cative gain perturbations 「-0.5517-0.6359-0.1728 x(. 4 结束语 0.2069-0.12690.1491 当控制器p受到式4)的增益摄动(取F,= 文中研究了不确定离散时滞系统的鲁棒非脆弱 =)时,无法得到式9)的可行解.由此可见,标准 H一控制问题.针对控制器增益存在加性和乘性摄 的控制器虽然具有较高的H~衰减水平,但是,当控 动的情形,以LMI形式给出了非脆弱状态反馈H一 制器增益受到很小的扰动时,无法保证闭环系统渐 控制器存在的充分条件.所设计的控制器不仅保证 近稳定,从而较好说明了本文结果的优越性, 闭环系统渐进稳定,而且满足一定的H一范数约束 为不失一般性,假设取x0)=[-10510], 最后的仿真实例也表明,非脆弱控制器更能适应实 五=F=F=1,当系统受到外部白噪声千扰如图1,以 际的工程环境 1.0 参考文献: 0.5 [1]YU L,CHU J,SU H Y.Robust memoryless H.con h1wh troller design for linear time-delay systems with norm bounded time-varying uncertainty [J ]Automatica, 0.3 1996,32(12):17591762. [2]De SOUZA C E,LI X.Delay-dependent robust Hcon -1.0 6810 trol of uncertain linear state-delayed systems [J].Auto- 1/s matica,1999,35(9):1313-1321. 图1白噪声信号干扰 [3]KIM J H,PARK H B.H-state feedback control for Fig.I The disturbance of white noise generalized continuous/discrete time-delay system [J]. 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
E3 = 0. 4 0. 3 0. 2 0. 4 0. 5 0. 3 , E4 = 1 1 3 2 1 4 . 1) 设计具有加法式增益摄动的控制器 : 已知 H3 = 0. 1 0 0 0 0. 1 0 , E5 = 0. 3 0. 4 0. 1 0. 2 0. 1 0. 2 0. 1 0. 3 0. 2 , F2 ∈R 3 ×3 . 对定理 1 ,利用 Matlab LMI Toolbox 进行寻优 ,得 LMI(7) 的解为 γ1opt = 61442 4 , μ1opt = - 0. 503 2 - 0. 616 9 - 0. 187 7 0. 242 2 - 0. 134 5 0. 172 8 x( k) . 2) 设计具有乘法式增益摄动的控制器 : 已知 H4 = 0. 1 0 0 0 0. 1 0 , E6 = 1 1 0. 8 0. 8 0. 1 0. 3 , F3 ∈R 3 ×3 . 同样 ,对 LMI(8) 进行寻优 ,得最优解为 γ2opt = 61847 3 , μ2opt = - 0. 489 7 - 0. 618 3 - 0. 198 3 0. 238 7 - 0. 137 7 0. 174 1 x( k) . 3) 若不考虑控制器 (2) 中的增益摄动 ,对 LMI (9) 进行寻优得到 γ3opt = 21108 2 , μ3opt = - 0. 551 7 - 0. 635 9 - 0. 172 8 0. 206 9 - 0. 126 9 0. 149 1 x( k) . 当控制器μ3opt 受到式 (4) 的增益摄动 (取 F1 = F3 = I) 时 ,无法得到式(9) 的可行解. 由此可见 ,标准 的控制器虽然具有较高的 H ∞衰减水平 ,但是 ,当控 制器增益受到很小的扰动时 ,无法保证闭环系统渐 近稳定 ,从而较好说明了本文结果的优越性. 图 1 白噪声信号干扰 Fig. 1 The disturbance of white noise 为不失一般性,假设取 x(0) = [ - 10 5 10 ], F1 = F2 = F3 = I ,当系统受到外部白噪声干扰如图 1 ,以 及控制器 u1opt和 u2opt分别受到加性和乘性增益摄动时, 闭环系统(5)的状态响应曲线如图 2、3 所示. 4 结束语 文中研究了不确定离散时滞系统的鲁棒非脆弱 H ∞控制问题. 针对控制器增益存在加性和乘性摄 动的情形 ,以 LMI 形式给出了非脆弱状态反馈 H ∞ 控制器存在的充分条件. 所设计的控制器不仅保证 闭环系统渐进稳定 ,而且满足一定的 H ∞范数约束. 最后的仿真实例也表明 ,非脆弱控制器更能适应实 际的工程环境. 参考文献 : [1 ] YU L , CHU J , SU H Y. Robust memoryless H ∞ con2 troller design for linear time2delay systems with norm2 bounded time2varying uncertainty [ J ]. Automatica , 1996 , 32 (12) : 175921762. [ 2 ]De SOUZA C E , L I X. Delay2dependent robust H ∞ con2 trol of uncertain linear state2delayed systems[J ]. Auto2 matica , 1999 ,35 (9) :131321321. [3 ] KIM J H , PAR K H B. H ∞ state feedback control for generalized continuous/ discrete time2delay system [J ]. 第 1 期 吴 珠 ,等 :线性不确定离散时滞系统的鲁棒非脆弱 H ∞控制 · 96 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·70· 智能系统学报 第3卷 Automatica,1999,35(8):1443-1451 Hcontrol for discrete-time uncertain linear systems[J]. [4]KEEL L H,BHATTACHARYYA S P.Robust,fragile Control Engineering of China,2005,12(4):335-338. or optimal[J ]IEEE Trans Automatica Control,1997,42 [9]XIE L.Output feedback Ho control of systems with pa- (8):10981105. rameter uncertainty[J ]Int J Control,1996,63(4):741- [5]YANG G H,WANGJ L.Nomfragile H control for 750. linear systems with multiplicative controller gain varia- 作者简介 tions[0].Automatica,2001,37(5):727-737. 吴珠,女,1983年生,硕士研究生 [6]王武,杨富文.具有控制器增益变化的不确定时滞系统 主要研究方向为基于LMI的线性时滞系统 的鲁棒H控制[J].自动化学报,2002,28(6):1043 的鲁棒控制. 1046. WANG Wu,YANG Fuwen.Robust Hoo control for line- ar time-delay uncetain systems with controller gain varia- tions[J ]Acta Automatica Sinica,2002,28(6):1043- 1046. 刘国栋,男,1950年生,教授,硕士生 [7]XIE N,TAN GG Y.Delay-dependent nonfragile guaram 导师,主要研究方向为智能控制理论及应 teed cost control for nonlinear time-delay systems [J ] 用机器人控制系统等.发表学术论文20余 Nonlinear Analysis,2006,64(9):2084-2097. 篇 [8]王武,杨富文.不确定离散系统的鲁棒非脆弱H控制 [J].控制工程,2005,12(4):335338. WANG Wu,YANG Fuwen.Robust and nomrfragile 第3届粗糙集与知识技术国际学术会议 The 3rd International Conference on Rough Sets and Kno wledge Technology Since the introduction of rough sets in 1982 by Professor Zdzislaw Pawlak,we have witnessed great advances in both theory and applications.Rough set theory is closely related to knowledge technology in a variety of forms such as knowledge discovery,approximate reasoning,intelligent and multiagent system design,knowledge intensive computations.The cutting-edge knowledge technologies have great impact on learning,pattern recognition,machine intelligence and automation of acquisition,transformation,commu- nication,exploration and exploitation of knowledge.A principal thrust of such technologies is the utiliza- tion of methodologies that facilitate knowledge processing.To present the state-of-the-art scientific re- sults,encourage academic and industrial interaction,and promote collaborative research in rough sets and knowledge technology worldwide,the 3rd International Conference on Rough Sets and Knowledge Tech- nology will be held in Chengdu,China,May 17-19,2008. Topics (included,but are not limited to): Computing Theory and Paradigms Knowledge Technology Intelligent Information Processing Intelligent Control More information at http:/sist.switu.edu.cn/imc/itw06/rskt2008/ 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
Automatica ,1999 ,35 (8) :144321451. [4 ] KEEL L H ,B HA TTACHAR YYA S P. Robust ,fragile or optimal[J ]. IEEE Trans Automatica Control ,1997 ,42 (8) : 109821105. [5 ] YAN G G H , WAN G J L. Non2fragile H ∞ control for linear systems with multiplicative controller gain varia2 tions[J ]. Automatica ,2001 ,37 (5) :7272737. [6 ]王 武 ,杨富文. 具有控制器增益变化的不确定时滞系统 的鲁棒 H ∞控制 [J ]. 自动化学报 , 2002 , 28 ( 6) : 10432 1046. WAN G Wu , YAN G Fuwen. Robust H ∞ control for line2 ar time2delay uncetain systems with controller gain varia2 tions[J ]. Acta Automatica Sinica , 2002 , 28 ( 6) : 10432 1046. [7 ]XIE N , TAN G G Y. Delay2dependent nonfragile guaran2 teed cost control for nonlinear time2delay systems [J ]. Nonlinear Analysis , 2006 , 64 (9) : 208422097. [8 ]王 武 ,杨富文. 不确定离散系统的鲁棒非脆弱 H ∞控制 [J ]. 控制工程 ,2005 ,12 (4) :3352338. WAN G Wu , YAN G Fuwen. Robust and non2fragile H ∞ control for discrete2time uncertain linear systems[J ]. Control Engineering of China ,2005 ,12 (4) :3352338. [9 ]XIE L. Output feedback H ∞ control of systems with pa2 rameter uncertainty[J ]. Int J Control ,1996 ,63 (4) :7412 750. 作者简介 : 吴 珠 , 女 , 1983 年生 , 硕士研究生 , 主要研究方向为基于 LMI 的线性时滞系统 的鲁棒控制. 刘国栋 , 男 , 1950 年生 , 教授 , 硕士生 导师 , 主要研究方向为智能控制理论及应 用、机器人控制系统等. 发表学术论文 20 余 篇. 第 3 届粗糙集与知识技术国际学术会议 The 3rd International Conference on Rough Sets and Knowledge Technology Since t he introduction of rough sets in 1982 by Professor Zdzislaw Pawlak , we have wit nessed great advances in bot h t heory and applications. Rough set theory is closely related to knowledge technology in a variety of forms such as knowledge discovery , approximate reasoning , intelligent and multiagent system design , knowledge intensive comp utations . The cutting2edge knowledge technologies have great impact on learning , pattern recognition , machine intelligence and automation of acquisition , transformation , commu2 nication , exploration and exploitation of knowledge. A p rincipal t hrust of such technologies is the utiliza2 tion of met hodologies t hat facilitate knowledge processing. To present t he state2of2t he2art scientific re2 sults , encourage academic and industrial interaction , and promote collaborative research in rough sets and knowledge technology worldwide , t he 3rd International Conference on Rough Sets and Knowledge Tech2 nology will be held in Chengdu , China , May 17219 , 2008 . Topics (included , but are not limited to) : Comp uting Theory and Paradigms Knowledge Technology Intelligent Information Processing Intelligent Control More information at http :/ / sist. swjt u. edu. cn/ imc/ itw06/ rskt2008/ . · 07 · 智 能 系 统 学 报 第 3 卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net