
第3卷第1期 智能系统学报 Vol.3 Ne 1 2008年2月 CAAI Transactions on Intelligent Systems Fcb.2008 基于粒子群算法的MIMO CDMA 平坦衰落信道均衡器 王兆伟,肖扬,刘湘黔 (北京交通大学信息科学研究所,北京100044) 摘要:粒子群优化算法是一类有效的随机全局优化技术,它利用粒子种群搜索解空间,每个粒子表示一个被优化 问题的潜在解,通过粒子间的相互作用发现复杂空间中的最优区域.MMO系统在不增加带宽的前提下,成倍地提 高通信系统的容量和频谱利用率,而复杂的传播信道使接收信号产生SL基于粒子群优化算法的MMO信道均衡 器应用于MIMO CDMA系统能有效抑制平坦衰落、信道间干扰以及背景噪声干扰.仿真结果证明其误码率性能明 显优于传统均衡器,收敛速度快于基于GA的均衡器且更易于实现. 关键词:码分多址:均衡器:多输入多输出平坦衰落信道:粒子群优化算法:参考信号 中图分类号:TN911.5:TP18文献标识码:A文章编号:16734785(2008)01-003805 Application of particle swarm optimization in MIMO CDMA flat fa ding channel equalizers WANG Zhao-wei,XIAO Yang,LIU Xiang qian (Institute of Information Science,Beijing Jiaotong University,Beijing 100044,China) Abstract:Particle swarm optimization(PSO)algorithms are efficient in stochastic global optimization.PSO algorithms use a particle population to search for the solution space,in which each particle represents a so- lution to the problem to be optimized,and finds optimal regions in complex searching spaces through the interaction of individuals in the population.The MIMO scheme can multiply the channel capacity of wire- less communication several times without increased bandwidth,but the complex channels produce inter- symbol interference (ISD)in received signals.We studied a PSO MIMO channel equalizer in an MIMO CD- MA system that is not sensitive to the coherency of channels,flat fading,or noise.Simulations show that the bit-error rate (BER)performance of the proposed PSO MIMO channel equalizer is better than that of conventional adaptive equalizers,converges faster than GA-based equalizers,and is easier to implement. Key words:CDMA;channel equalizer;MIMO flat fading channel;PSO;reference signals 1995年J.Kennedy和R.C.Eberhart受到鸟到全局最优.经过众多学者10余年的研究,已被广 群觅食的启发,于是提出了粒子群算法(particle泛应用于解决多个领域的优化问题,如自适应滤波 swarm optimization,PSO)l,该算法是一种进化计 器2)、无线通信中的多用户检测]等方面 算技术,与传统的优化算法相比,PS0不受优化函 多输入多输出(multiple input&multiple out- 数结构影响,且不计算优化梯度,能在非线性多峰的 put,MIMO)系统是近年来无线通信领域的一个热 复杂解空间内搜索真正解,同时能处理参数空间变 门课题.它在不增加带宽的前提下,成倍地提高通信 化的优化问题,基本不受解空间峰数和维数的限制, 系统的容量和频谱利用率6).其实现方式是在发射 与同是进化算法的遗传算法相比较,PSO能更快达 端和接收端都使用多个天线,而不是传统的单天线: 无线通信信号传播路径非常复杂,且受信道间干扰, 收稿日期:2007-0518. 通讯作者:王兆伟.E-mail:05120357@bjtu.edu.cn. 导致传输信号畸变,产生接收符号间干扰(IS).自 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved htp://www.cnki.net
第 3 卷第 1 期 智 能 系 统 学 报 Vol. 3 №. 1 2008 年 2 月 CAA I Transactions on Intelligent Systems Feb. 2008 基于粒子群算法的 MIMO CDMA 平坦衰落信道均衡器 王兆伟 ,肖 扬 ,刘湘黔 (北京交通大学 信息科学研究所 ,北京 100044) 摘 要 :粒子群优化算法是一类有效的随机全局优化技术 ,它利用粒子种群搜索解空间 ,每个粒子表示一个被优化 问题的潜在解 ,通过粒子间的相互作用发现复杂空间中的最优区域. MIMO 系统在不增加带宽的前提下 ,成倍地提 高通信系统的容量和频谱利用率 ,而复杂的传播信道使接收信号产生 ISI. 基于粒子群优化算法的 MIMO 信道均衡 器应用于 MIMO CDMA 系统能有效抑制平坦衰落、信道间干扰以及背景噪声干扰. 仿真结果证明其误码率性能明 显优于传统均衡器 ,收敛速度快于基于 GA 的均衡器且更易于实现. 关键词 :码分多址 ;均衡器 ;多输入多输出平坦衰落信道 ;粒子群优化算法 ;参考信号 中图分类号 : TN911. 5 ; TP18 文献标识码 :A 文章编号 :167324785 (2008) 0120038205 Application of particle swarm optimization in MIMO CDMA flat fading channel equalizers WAN G Zhao2wei , XIAO Yang , L IU Xiang2qian (Institute of Information Science , Beijing Jiaotong University , Beijing 100044 ,China) Abstract :Particle swarm optimization (PSO) algorit hms are efficient in stochastic global optimization. PSO algorit hms use a particle pop ulation to search for the solution space , in which each particle represents a so2 lution to t he problem to be optimized , and finds optimal regions in complex searching spaces t hrough t he interaction of individuals in t he pop ulation. The MIMO scheme can multiply t he channel capacity of wire2 less communication several times wit hout increased bandwidt h , but t he complex channels p roduce inter2 symbol interference (ISI) in received signals. We st udied a PSO MIMO channel equalizer in an MIMO CD2 MA system t hat is not sensitive to t he coherency of channels , flat fading , or noise. Simulations show t hat t he bit2error rate (BER) performance of t he proposed PSO MIMO channel equalizer is better t han t hat of conventional adaptive equalizers , converges faster t han GA2based equalizers , and is easier to implement. Keywords :CDMA ;channel equalizer ;MIMO flat fading channel ;PSO ;reference signals 收稿日期 :2007205218. 通讯作者 :王兆伟. E2mail :05120357 @bjt u. edu. cn. 1995 年 J . Kennedy 和 R. C. Eberhart 受到鸟 群觅食的启发 ,于是提出了粒子群算法 (particle swarm optimization ,PSO) [1 ] ,该算法是一种进化计 算技术 ,与传统的优化算法相比 ,PSO 不受优化函 数结构影响 ,且不计算优化梯度 ,能在非线性多峰的 复杂解空间内搜索真正解 ,同时能处理参数空间变 化的优化问题 ,基本不受解空间峰数和维数的限制 , 与同是进化算法的遗传算法相比较 ,PSO 能更快达 到全局最优. 经过众多学者 10 余年的研究 ,已被广 泛应用于解决多个领域的优化问题 ,如自适应滤波 器[2 ] 、无线通信中的多用户检测[324 ]等方面. 多输入多输出(multiple inp ut & multiple out2 p ut , MIMO) 系统是近年来无线通信领域的一个热 门课题. 它在不增加带宽的前提下 ,成倍地提高通信 系统的容量和频谱利用率[526 ] . 其实现方式是在发射 端和接收端都使用多个天线 ,而不是传统的单天线. 无线通信信号传播路径非常复杂 ,且受信道间干扰 , 导致传输信号畸变 ,产生接收符号间干扰 ( ISI) . 自 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第1期 王兆伟,等:基于粒子群算法的MIMO CDMA平坦衰落信道均衡器 ·39 适应均衡器技术能有效地消除码间干扰,传统方法 s和s,则s=bcW,s=bcW,cw为PX1 是首先由信道估计器估计出信道矩阵H,然后由 归一化扩频序列.同一MS的天线使用相同的扩 H滤波恢复发送数据序列,而此方法误码率性能 频码 差.文献8提出在估计出信道矩阵后,利用H1恢 序列sW和s经过OPSK调制后发送到平 复信号,提高了误码率性能,然而使用这种方法的前 坦衰落信道,由BS接收,接收序列经过QPSK接收 提是必须保证H为非奇异矩阵.文中提出基于粒子 机后等价如下式 群算法的信道均衡器,采用粒子群优化算法,由参考 r「hh「s「n 信号估计出均衡参数,然后构造信道均衡器.在平坦 L=Lh+n 衰落信道的情况下能够替代传统均衡器,而且大大 式中:h,i,∈1,2}表示发射机天线到接收机天 提高了误码率性能,同时,与同是进化算法的遗传算 线j的信道参数,服从瑞利分布.n”,j∈{1,2}表示 法(GA)相比,能更快地收敛,辨识出均衡参数, 接收机天线j接收到的噪声,服从CN0,1)零均值 1 系统模型 复高斯白噪声)分布 如图3所示,接收序列⑧和为均衡器输 DS-CDMA系统是多用户共享信道6,1),因此 入.首先,PS0均衡器利用MS端发射的参考序列 文中的MMO技术应用于DS-CDMA系统,最大限 「g 度地利用信道带宽并使系统具有良好的适应性.现 辨识出均衡矩阵G= ,然后对数据序列 L 有MMO技术主要应用于无线通信系统的下链路, 进行均衡: 而文中考虑CDMA系统的上链路,利用MIMO技 术提高基站性能 sgn(ReG (2 为简便,设计的MIMO CDMA系统利用2个 式中:sgn()为符号函数 天线MS(mobile station)发射信号,利用2个天线 第k个MS的发射序列为 BS(base station)接收信号,其上链路信道如图1所 y®=cwHz 示.其中MS的发射机采用图2所示模型,上链路的 以®=cwHW (3 并行序列分别通过MS的天线1和天线2发射 天线1 天线1 天线1 OPSK c(k) MS BS 调制 PSO 解打 发射机 接收机 BS 接收机 天线2 h 天线2 OPSK c(k) 调制 解 天线2 图1MMO上链路信道 Fig.1 The MIMO CDMA communication system 图3 MIMO BS接收机示意图 天线 c(k) OPSK Fig 3 Block diagram of the MIMO BS receiver 扩频 调制 MS 设不同MS扩频序列的互相关函数为R= 发射机 天线2 c(k) (几)x×x,其中=c°(0c”(),n为扩频码长 OPSK 扩频 调制 度,K为CDMA系统中MS数量,互相关矩阵R为 Toeplitz矩阵 图2 MIMO MS发射机示意图 Fig.2 Block diagram of the MIMO MS transmitter 2基于粒子群算法的MMO信道均 多个MS中,第k个MS的数据序列{b"}分为 衡器 2个子序列{b}和{b冫.这2个子序列经过线性 基本的PS0包括一个由多个粒子(个体)组成 扩频,通过2个天线分别发射出去,发射序列表示为 的群体,每个粒子代表了问题的一个可能解,并用一 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
适应均衡器技术能有效地消除码间干扰 ,传统方法 是首先由信道估计器估计出信道矩阵 H [7 ] ,然后由 H T 滤波恢复发送数据序列 ,而此方法误码率性能 差. 文献[8 ]提出在估计出信道矩阵后 ,利用 H - 1 恢 复信号 ,提高了误码率性能 ,然而使用这种方法的前 提是必须保证 H 为非奇异矩阵. 文中提出基于粒子 群算法的信道均衡器 ,采用粒子群优化算法 ,由参考 信号估计出均衡参数 ,然后构造信道均衡器. 在平坦 衰落信道的情况下能够替代传统均衡器 ,而且大大 提高了误码率性能 ,同时 ,与同是进化算法的遗传算 法( GA) 相比 ,能更快地收敛 ,辨识出均衡参数. 1 系统模型 DS2CDMA 系统是多用户共享信道[6 ,9211 ] ,因此 文中的 MIMO 技术应用于 DS2CDMA 系统 ,最大限 度地利用信道带宽并使系统具有良好的适应性. 现 有 MIMO 技术主要应用于无线通信系统的下链路 , 而文中考虑 CDMA 系统的上链路 ,利用 MIMO 技 术提高基站性能. 为简便 ,设计的 MIMO CDMA 系统利用 2 个 天线 MS(mobile station) 发射信号 ,利用 2 个天线 BS(base station) 接收信号 ,其上链路信道如图 1 所 示. 其中 MS 的发射机采用图 2 所示模型 ,上链路的 并行序列分别通过 MS 的天线 1 和天线 2 发射. 多个 MS 中 ,第 k 个 MS 的数据序列{ b ( k) }分为 2 个子序列{ b ( k) 1 } 和{ b ( k) 2 } . 这 2 个子序列经过线性 扩频 ,通过 2 个天线分别发射出去 ,发射序列表示为 s ( k) 1 和 s ( k) 2 ,则 s ( k) 1 = b ( k) 1 c ( k) ,s ( k) 2 = b ( k) 2 c ( k) , c ( k) 为 P ×1 归一化扩频序列. 同一 MS 的天线使用相同的扩 频码. 序列 s ( k) 1 和 s ( k) 2 经过 OPSK调制[12 ]后发送到平 坦衰落信道 ,由 BS 接收 ,接收序列经过 QPSK 接收 机后等价如下式 : r ( k) 1 r ( k) 2 = h ( k) 11 h ( k) 21 h ( k) 12 h ( k) 22 s ( k) 1 s ( k) 2 + n ( k) 1 n ( k) 2 . (1) 式中 : h ( k) ij , i , j ∈{ 1 , 2} 表示发射机天线到接收机天 线 j 的信道参数 ,服从瑞利分布. n ( k) j , j ∈{ 1 ,2}表示 接收机天线 j 接收到的噪声 ,服从 CN (0 ,1) (零均值 复高斯白噪声) 分布. 如图 3 所示 ,接收序列 r ( k) 1 和 r ( k) 2 为均衡器输 入. 首先 ,PSO 均衡器利用 MS 端发射的参考序列 辨识出均衡矩阵 G = g ( k) 11 g ( k) 21 g ( k) 12 g ( k) 22 ,然后对数据序列 进行均衡 : z ( k) 1 z ( k) 2 = sgn (Re{ G r ( k) 1 r ( k) 2 }) . (2) 式中 :sgn ( ·) 为符号函数. 第 k 个 MS 的发射序列为 y ( k) 1 = c ( k) H z ( k) 1 , y ( k) 2 = c ( k) H z ( k) 2 . (3) 图 3 MIMO BS 接收机示意图 Fig13 Block diagram of the MIMO BS receiver 设不同 MS 扩频序列的互相关函数为 R = (ηij ) K×K ,其中ηij = ∑ n l = 1 c ( i) ( l) c ( j) ( l) , n 为扩频码长 度 , K 为 CDMA 系统中 MS 数量 ,互相关矩阵 R 为 Toeplitz 矩阵. 2 基于粒子群算法的 MIMO 信道均 衡器 基本的 PSO 包括一个由多个粒子 (个体) 组成 的群体 ,每个粒子代表了问题的一个可能解 ,并用一 第 1 期 王兆伟 ,等 :基于粒子群算法的 MIMO CDMA 平坦衰落信道均衡器 ·39 · © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·40· 智能系统学报 第3卷 个适应度函数对解的优劣进行评估.在迭代过程中」 这些粒子利用自己的历史经验和相互交流的信息随 forj=0to4-1(文中的X有4个参数) 机地以一定的速度在解空间移动,直至达到最优解 或近似解,).PSO和GA相似,但PS0的参数和 w()=w(t(1-)+an(d(p西-x(t-)+ 操作算子都少得多,鲁棒性强,收敛速度在一般情况 a2()(pe-y(t-1)) 7) 下更快 保证 vg()∈l-vaax,max] (8) 信道均衡器首先要估计出均衡器矩阵.考虑式 xg(1)=xg(t-1)+vy(1) 9) 2)模型,在一帧内,1g}(i,j=2)可以视为常数,需 保证 xy()∈[-xma,xma] (10) 要确定的参数g共有4个.显而易见,性能越好的 均衡滤波模型,其滤波输出信号(滤波器响应)与参 if f(x()<f(P.) 考信号的差值愈小,因此将均衡矩阵估计问题转化 P=Xi(t) 成一个使均衡器响应与参考信号差值最小的优化问 if f(Pi)<f (Pbea) 题.文中根据最小均方误差准则,利用粒子群算法估 Pbest P 计出矩阵G.MS端每个天线发射的一帧信号包括 Mbit参考序列和Nbit数据序列 选取如下形式的适应函数: 式中:w()为惯性权重:a、a为进化因子,是固定常 4) 数,一般在0~2取值;n、n为相互独立的随机数, 服从U(0,1)分布;式(7)和式(9)为粒子搜索过程 式中:f:为粒子i的适应值,其中Jm=sum(sm-am2 式(8)和式(10)用来确保粒子在搜索空间范围内移 sm=[m得,s3为第m个参考序列,am为第i个粒子第 动 gg门「r m个信号输出,am=Re ,其中 3)迭代结束,全局最优位置P即为均衡矩阵 的值,即G=P.然后根据式2)和式(3),可以由 为接收到的第m个信号向量,由式2)可知 数据信号的信道响应恢复出数据信号 与传统的均衡器算法比较,文中提出利用基于 zm=sgn(am.全局最优适应函数值为 粒子群算法均衡器,主要考虑到在粒子群算法在求 foes =minfi (5) 解过程中:)有多个搜索方向,不受解初始值限制, 需要估计的参数为4个,从而确定粒子的搜索 多个粒子每次迭代都随机运动保证算法有多个搜索 空间为二维矩阵X=[xa ,相应的粒子搜索 方向,传统算法(如LMS算法)是只有一个搜索方 向且受限于初始值的选择;2)考虑解所经历的最好 速度V,= 局部和全局最优位置P,、Pe 位置和全局最好位置,而传统算法是不考虑解所经 历的最好位置.这使得粒子群算法辨识的信道比传 均为相同结构的矩阵,于是有如下的信道均衡算法: 统算法辨识的信道更逼近实际信道,能获得比传统 )初始随机设定粒子群个体数量、最大迭 算法构造的均衡器更好的误码率性能, 代次数tx,随机产生每个粒子的位置和速度 与GA算法比较,通常GA要经过选择、交叉和 V,根据式4)计算每个粒子的适应值,将每个粒子 变异3个过程,而P$0只有变异过程,参数和操作 的当前位置作为其局部最好位置,P,根据式(5)计 算子少,易于硬件实现.在每一代计算后,保留种群 算f,适应值最小的粒子的位置作为全局最优位 最优解的同时,保留每个个体的历史最优解,然后随 置Pet; 机选取进化方向,如此能够在新的一代中同时保留 2)搜索过程如下: 全局和局部最优解,使P$0有趋势地随机进化,收 for 1=1 to fmax 敛速度更快 w()=0.9-(1-1)0.5/1max 6) 3 仿真结果 for i=0 to(npop-1) 设CDMA上链路系统每个用户分别用2根天 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
个适应度函数对解的优劣进行评估. 在迭代过程中 , 这些粒子利用自己的历史经验和相互交流的信息随 机地以一定的速度在解空间移动 ,直至达到最优解 或近似解[1 ,13 ] . PSO 和 GA 相似 ,但 PSO 的参数和 操作算子都少得多 ,鲁棒性强 ,收敛速度在一般情况 下更快. 信道均衡器首先要估计出均衡器矩阵. 考虑式 (2) 模型 ,在一帧内 ,{ gij} ( i , j = 2) 可以视为常数 ,需 要确定的参数 gij 共有 4 个. 显而易见 ,性能越好的 均衡滤波模型 ,其滤波输出信号 (滤波器响应) 与参 考信号的差值愈小 ,因此将均衡矩阵估计问题转化 成一个使均衡器响应与参考信号差值最小的优化问 题. 文中根据最小均方误差准则 ,利用粒子群算法估 计出矩阵 G. MS 端每个天线发射的一帧信号包括 M bit 参考序列和 N bit 数据序列. 选取如下形式的适应函数 : f i = 1 M ∑ M m = 1 J m . (4) 式中:f i 为粒子 i 的适应值,其中 J m = sum(sm - ^aim ) 2 , sm = [m ( k) m1 ,s ( k) m2 ]为第 m 个参考序列,^aim为第 i 个粒子第 m 个 信 号 输 出, ^aim = Re g ( k) 11 g ( k) 21 g ( k) 12 g ( k) 22 r ( k) m1 r ( k) m2 , 其 中 r ( k) m1 r ( k) m2 为接收到的第 m 个信号向量 ,由式 ( 2) 可知 zm = sgn ( ^am ) . 全局最优适应函数值为 f best = min{ f i} . (5) 需要估计的参数为 4 个 ,从而确定粒子的搜索 空间为二维矩阵 Xi = xi0 xi1 xi3 xi4 ,相应的粒子搜索 速度 Vi = vi0 vi1 vi3 vi4 ,局部和全局最优位置 Pi 、Pbest 均为相同结构的矩阵 ,于是有如下的信道均衡算法 : 1) 初始随机设定粒子群个体数量 npop 、最大迭 代次数 tmax , 随机产生每个粒子的位置 Xi 和速度 Vi ,根据式(4) 计算每个粒子的适应值 ,将每个粒子 的当前位置作为其局部最好位置 , Pi 根据式 (5) 计 算 f best ,适应值最小的粒子的位置作为全局最优位 置 Pbest ; 2) 搜索过程如下 : for t = 1 to tmax { w ( t) = 019 - ( t - 1) ×015/ tmax (6) for i = 0 to ( npop - 1) { for j = 0 to 4 - 1 (文中的 X有 4 个参数) { vij (t) = w(t) vij (t - 1) + c1 r1 j (t) ( pij - xij (t - 1) ) + c2 r2 j ( t) ( pbest j - xij ( t - 1) ) (7) 保证 vij ( t) ∈[ - vmax , vmax ] (8) xij ( t) = xij ( t - 1) + vij ( t) (9) 保证 xij ( t) ∈[ - xmax , xmax ] (10) } if f ( Xi ( t) ) < f ( Pi) Pi = Xi ( t) if f ( Pi) < f ( Pbest) Pbest = Pi } } 式中 :w ( t) 为惯性权重; c1 、c2 为进化因子 ,是固定常 数 ,一般在 0~2 取值; r1 、r2 为相互独立的随机数 , 服从 U (0 ,1) 分布;式 (7) 和式(9) 为粒子搜索过程 , 式(8) 和式(10) 用来确保粒子在搜索空间范围内移 动. 3) 迭代结束 ,全局最优位置 Pbest 即为均衡矩阵 的值 ,即 G = Pbest . 然后根据式 (2) 和式 (3) ,可以由 数据信号的信道响应恢复出数据信号. 与传统的均衡器算法比较 ,文中提出利用基于 粒子群算法均衡器 ,主要考虑到在粒子群算法在求 解过程中 :1) 有多个搜索方向 ,不受解初始值限制 , 多个粒子每次迭代都随机运动保证算法有多个搜索 方向 , 传统算法 (如 LMS 算法) 是只有一个搜索方 向且受限于初始值的选择 ;2) 考虑解所经历的最好 位置和全局最好位置 , 而传统算法是不考虑解所经 历的最好位置. 这使得粒子群算法辨识的信道比传 统算法辨识的信道更逼近实际信道 ,能获得比传统 算法构造的均衡器更好的误码率性能. 与 GA 算法比较 ,通常 GA 要经过选择、交叉和 变异 3 个过程 ,而 PSO 只有变异过程 ,参数和操作 算子少 ,易于硬件实现. 在每一代计算后 ,保留种群 最优解的同时 ,保留每个个体的历史最优解 ,然后随 机选取进化方向 ,如此能够在新的一代中同时保留 全局和局部最优解 ,使 PSO 有趋势地随机进化 ,收 敛速度更快. 3 仿真结果 设 CDMA 上链路系统每个用户分别用 2 根天 ·40 · 智 能 系 统 学 报 第 3 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
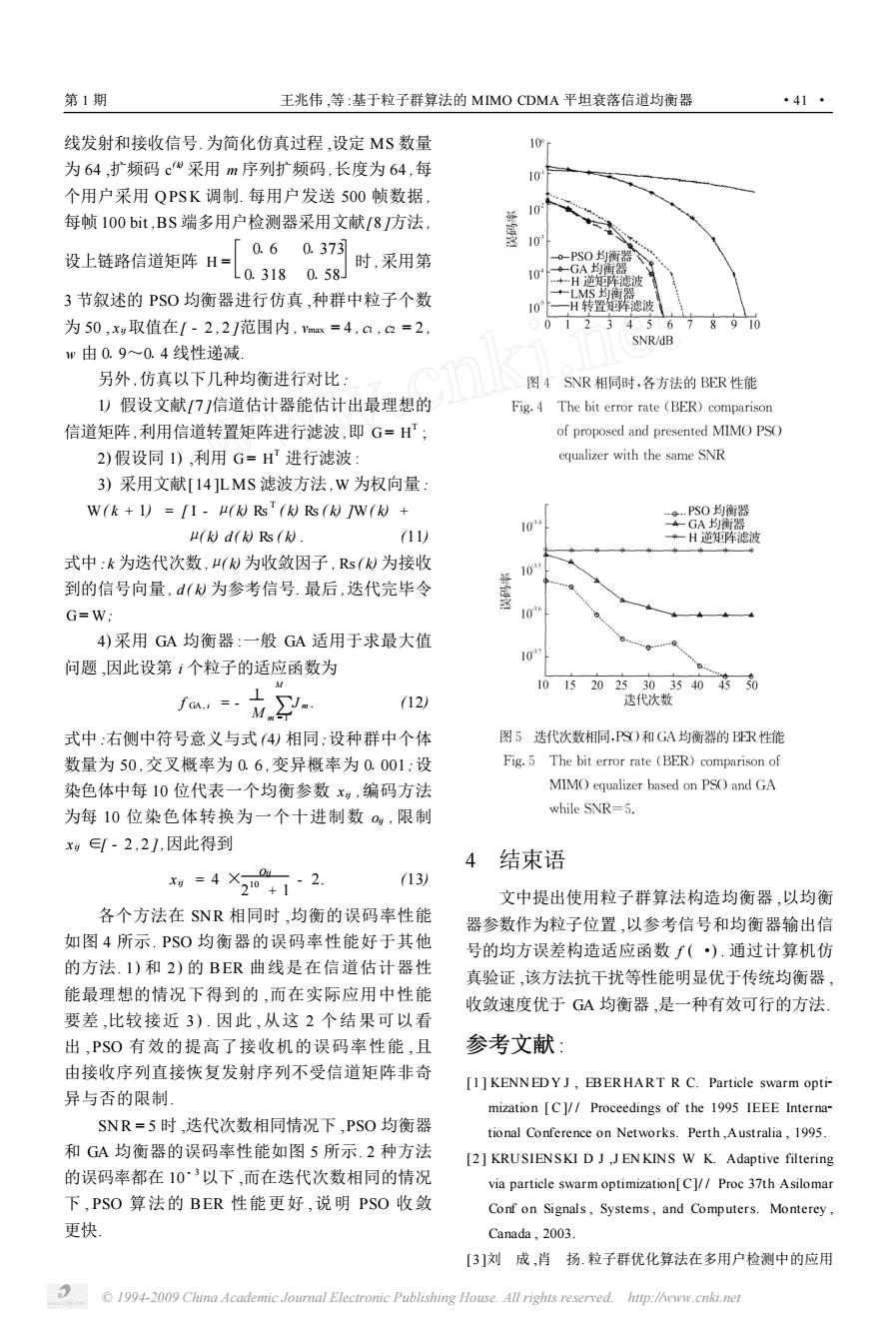
第1期 王兆伟,等:基于粒子群算法的MIMO CDMA平坦衰落信道均衡器 ·41· 线发射和接收信号.为简化仿真过程,设定MS数量 10 为64,扩频码cW采用m序列扩频码,长度为64,每 I10 个用户采用QPSK调制.每用户发送500帧数据, 每帧100bit,BS端多用户检测器采用文献[8方法, 「0.60.373 10 设上链路信道矩阵H= 时,采用第 o-PS0均海器 L0.3180.58」 10 H逆矩阵滤波 3节叙述的PS0均衡器进行仿真,种群中粒子个数 LMS均衡器 10 H转置定阵滤波 为50,xy取值在[-2,21范围内,mx=4,a,a=2, 2345678910 SNR/dB w由0.9~0.4线性递减 另外,仿真以下几种均衡进行对比: 图4SNR相同时,各方法的BER性能 1)假设文献[7/信道估计器能估计出最理想的 Fig.4 The bit error rate (BER)comparison 信道矩阵,利用信道转置矩阵进行滤波,即G=H; of proposed and presented MIMO PSO 2)假设同1),利用G=H进行滤波: equalizer with the same SNR 3)采用文献[14]LMS滤波方法,W为权向量: W(k+1)=[I-H(k)Rs(k)Rs(k)w(k)+ 。-PS0均衡器 μ(d(Rs(月 10 GA均衡器 11) ◆一H逆矩阵滤波 式中:k为迭代次数,(为收敛因子,Rs()为接收 10 到的信号向量,d(材为参考信号.最后,迭代完毕令 G=W: 4 4)采用GA均衡器:一般GA适用于求最大值 10 问题,因此设第1个粒子的适应函数为 fa 101520253035404550 12) 迭代次数 式中:右侧中符号意义与式4)相同:设种群中个体 图5迭代次数相同,PS)和GA均衡器的BR性能 数量为50,交叉概率为0.6,变异概率为0.001;设 Fig.5 The bit error rate (BER)comparison of 染色体中每10位代表一个均衡参数x),编码方法 MIMO equalizer based on PSO and GA 为每10位染色体转换为一个十进制数0,限制 while SNR=5. xg∈[-2,21,因此得到 4 结束语 刘=4X2+12 (13) 文中提出使用粒子群算法构造均衡器,以均衡 各个方法在SNR相同时,均衡的误码率性能 器参数作为粒子位置,以参考信号和均衡器输出信 如图4所示.PSO均衡器的误码率性能好于其他 号的均方误差构造适应函数∫(·).通过计算机仿 的方法.1)和2)的BER曲线是在信道估计器性 真验证,该方法抗干扰等性能明显优于传统均衡器, 能最理想的情况下得到的,而在实际应用中性能 收敛速度优于GA均衡器,是一种有效可行的方法, 要差,比较接近3).因此,从这2个结果可以看 出,PSO有效的提高了接收机的误码率性能,且 参考文献: 由接收序列直接恢复发射序列不受信道矩阵非奇 [1]KENN EDYJ,EBERHART R C.Particle swarm opti- 异与否的限制, mization [C]//Proceedings of the 1995 IEEE Interna- SNR=5时,迭代次数相同情况下,PSO均衡器 tional Conference on Networks.Perth,Australia,1995. 和GA均衡器的误码率性能如图5所示.2种方法 [2]KRUSIENSKI D J ,J EN KINS W K.Adaptive filtering 的误码率都在10·3以下,而在迭代次数相同的情况 via particle swarm optimization[C//Proc 37th Asilomar 下,PSO算法的BER性能更好,说明PSO收敛 Conf on Signals,Systems,and Computers.Monterey, 更快」 Canada,2003. [3]刘成,肖扬.粒子群优化算法在多用户检测中的应用 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
线发射和接收信号. 为简化仿真过程 ,设定 MS 数量 为 64 ,扩频码 c ( k) 采用 m 序列扩频码 ,长度为 64 ,每 个用户采用 Q PSK 调制. 每用户发送 500 帧数据 , 每帧 100 bit ,BS 端多用户检测器采用文献[8 ]方法 , 设上链路信道矩阵 H = 016 01373 01318 0158 时 ,采用第 3 节叙述的 PSO 均衡器进行仿真 ,种群中粒子个数 为 50 , xij取值在[ - 2 , 2 ]范围内 , vmax = 4 , c1 , c2 = 2 , w 由 019~014 线性递减. 另外 ,仿真以下几种均衡进行对比 : 1) 假设文献[7 ]信道估计器能估计出最理想的 信道矩阵 ,利用信道转置矩阵进行滤波 ,即 G = H T ; 2) 假设同 1) ,利用 G = H T 进行滤波 : 3) 采用文献[ 14 ]LMS 滤波方法 ,W 为权向量 : W( k + 1) = [ I - μ( k) Rs T ( k) Rs ( k) ]W( k) + μ( k) d ( k) Rs ( k) . (11) 式中 : k 为迭代次数 ,μ( k) 为收敛因子 , Rs( k) 为接收 到的信号向量 , d ( k) 为参考信号. 最后 ,迭代完毕令 G = W; 4) 采用 GA 均衡器 :一般 GA 适用于求最大值 问题 ,因此设第 i 个粒子的适应函数为 f GA , i = - 1 M ∑ M m = 1 J m . (12) 式中 :右侧中符号意义与式 (4) 相同;设种群中个体 数量为 50 ,交叉概率为 016 ,变异概率为 01001 ;设 染色体中每 10 位代表一个均衡参数 xij ,编码方法 为每 10 位染色体转换为一个十进制数 oij , 限制 xij ∈[ - 2 ,2 ] ,因此得到 xij = 4 × oij 2 10 + 1 - 2. (13) 各个方法在 SNR 相同时 ,均衡的误码率性能 如图 4 所示. PSO 均衡器的误码率性能好于其他 的方法. 1) 和 2) 的 BER 曲线是在信道估计器性 能最理想的情况下得到的 ,而在实际应用中性能 要差 ,比较接近 3 ) . 因此 ,从这 2 个结果可以看 出 ,PSO 有效的提高了接收机的误码率性能 ,且 由接收序列直接恢复发射序列不受信道矩阵非奇 异与否的限制. SNR = 5 时 ,迭代次数相同情况下 ,PSO 均衡器 和 GA 均衡器的误码率性能如图 5 所示. 2 种方法 的误码率都在 10 - 3以下 ,而在迭代次数相同的情况 下 ,PSO 算法的 BER 性能更好 ,说明 PSO 收敛 更快. 4 结束语 文中提出使用粒子群算法构造均衡器 ,以均衡 器参数作为粒子位置 ,以参考信号和均衡器输出信 号的均方误差构造适应函数 f ( ·) . 通过计算机仿 真验证 ,该方法抗干扰等性能明显优于传统均衡器 , 收敛速度优于 GA 均衡器 ,是一种有效可行的方法. 参考文献 : [1 ] KENNED Y J , EBERHART R C. Particle swarm opti2 mization [ C]/ / Proceedings of the 1995 IEEE Interna2 tional Conference on Networks. Perth ,Australia , 1995. [2 ] KRUSIENSKI D J ,J EN KINS W K. Adaptive filtering via particle swarm optimization[C]/ / Proc 37th Asilomar Conf on Signals , Systems , and Computers. Monterey , Canada , 2003. [3 ]刘 成 ,肖 扬. 粒子群优化算法在多用户检测中的应用 第 1 期 王兆伟 ,等 :基于粒子群算法的 MIMO CDMA 平坦衰落信道均衡器 ·41 · © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·42· 智能系统学报 第3卷 [J].中国铁道科学,2006,27(4):129132. [12]ZHENG K,WANG W B.Analysis and optimization of LIU Cheng,XIAO Yang.Particle swarm optimization in pilot-channel-assisted QPSK for DSCDMA systems multiuser detection[J].China Railway Science,2006,27 [J ]IEEE Transactions on Communications,1998,46 (4):129132 (9):1122-1124. [4]GUO Z Q,XIAO Y.MIMO system multiuser detection [13]SHI Y,EBERHART R C.A modified particle swarm based on particle swarm optimization algorithm C]// optimizer [C]//Proceedings of the 1998 IEEE World Proc 2006 8th International Conference on Signal Pro- Congress on Computational Intelligence.Alaska,USA, cessing.Guilin,2006. 1998. [5]TELA TAR I E.Capacity of multr-antenna Gaussian [14]肖扬,宋明艳.变频长自适应数字滤波器的稳定条件 channels[J ]European Trans on Telecomm,1999,10 [U].通信学报,2001,22(10):8892. (6):585-595. XIAO Yang,SONG Mingyan.Stability conditions of [6]FOCHINI GJ,GANS MJ.On limits of wireless com- variable step-size adaptive digital filter [J].Journal on munications in a fading environment when using multiple Communications,2001,22(10):88-92. antennas[J].Wireless Personal Communications,1998, 作者简介: 6(3):311-335. 王兆伟,男,1982生,博士研究生,主要 [7]CHEN W,XIAO Y,ZHAO Y.The algorithm imple- 研究方向为通信网体系结构、无线信道均衡、 ment of WCDMA channel estimation[C]//7th Interna 智能优化算法, tional Conference on Signal Processing Proceedings.Bei- jing,2004. [8]XIAO Y.L EE M H.MIMO multiuser detection for CD- MA systems[C]//2006 8th International Conference on Signal Processing.Guilin,2006. 肖扬,男,1955年生,教授,博士生导 [9]SHIU D S,FOSCHINI GJ,GANS MJ.Fading correla 师,主要研究方向为时空处理、多维系统理论 tion and its effect on the capacity of multielement antenna 与应用、多维信息处理.发表论文100余篇, systems[J ]IEEE Trans Commun,2000,48(3):502- 其中被SCI、EI、ISTP检索80余篇 513 [10]CHOI RL,LETAIEF KB,MURCH R D.MIMO CD- MA antenna systems [C]//2000 IEEE International 刘湘黔,男,1971年生,副教授,硕士生 Conference on Communications(ICC 2000).New Orle- 导师,主要研究方向为网络控制、鲁棒控制 ans,USA,2000. 等 [11]XIAO Y,LEE M H.Low complexity MIMO-LDPC CDMA systems over multipath channels [J ]IEICE Transactions on Communications,2006,E89-B (5): 1713-1717. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.hup://www.cnki.net
[J ]. 中国铁道科学 ,2006 ,27 (4) :1292132. L IU Cheng , XIAO Yang. Particle swarm optimization in multiuser detection[J ]. China Railway Science , 2006 ,27 (4) : 1292132. [4 ] GUO Z Q , XIAO Y. MIMO system multiuser detection based on particle swarm optimization algorithm [ C ]/ / Proc 2006 8th International Conference on Signal Pro2 cessing. Guilin , 2006. [5 ] TELA TAR I E. Capacity of multi2antenna Gaussian channels[J ]. European Trans on Telecomm , 1999 , 10 (6) : 5852595. [6 ] FOCHINI G J , GANS M J. On limits of wireless com2 munications in a fading environment when using multiple antennas[J ]. Wireless Personal Communications , 1998 , 6 (3) : 3112335. [7 ] CHEN W , XIAO Y , ZHAO Y. The algorithm imple2 ment of WCDMA channel estimation [ C]/ / 7th Interna2 tional Conference on Signal Processing Proceedings. Bei2 jing ,2004. [8 ]XIAO Y,L EE M H. MIMO multiuser detection for CD2 MA systems[ C]/ / 2006 8th International Conference on Signal Processing. Guilin , 2006. [ 9 ]SHIU D S , FOSCHINI GJ , GANS M J. Fading correla2 tion and its effect on the capacity of multielement antenna systems[J ]. IEEE Trans Commun , 2000 , 48 (3) : 5022 513. [ 10 ]CHOI R L , L ETAIEF K B ,MURCH R D. MIMO CD2 MA antenna systems [ C ]/ / 2000 IEEE International Conference on Communications( ICC 2000) . New Orle2 ans ,USA , 2000. [11 ] XIAO Y , L EE M H. Low complexity MIMO2LDPC CDMA systems over multipath channels [J ]. IEICE Transactions on Communications , 2006 , E892B ( 5 ) : 171321717. [12 ]ZHEN G K ,WAN G W B. Analysis and optimization of pilot2channel2assisted QPSK for DS2CDMA systems [J ]. IEEE Transactions on Communications , 1998 , 46 (9) :112221124. [13 ]SHI Y , EBERHART R C. A modified particle swarm optimizer [ C]/ / Proceedings of the 1998 IEEE World Congress on Computational Intelligence. Alaska ,USA , 1998. [14 ]肖 扬 ,宋明艳. 变频长自适应数字滤波器的稳定条件 [J ]. 通信学报 ,2001 ,22 (10) :88292. XIAO Yang , SON G Mingyan. Stability conditions of variable step2size adaptive digital filter [J ]. Journal on Communications , 2001 , 22 (10) : 88292. 作者简介 : 王兆伟 ,男 ,1982 生 ,博士研究生 ,主要 研究方向为通信网体系结构、无线信道均衡、 智能优化算法. 肖 扬 ,男 ,1955 年生 ,教授 , 博士生导 师 ,主要研究方向为时空处理、多维系统理论 与应用、多维信息处理. 发表论文 100 余篇 , 其中被 SCI、EI、ISTP 检索 80 余篇. 刘湘黔 ,男 ,1971 年生 ,副教授 ,硕士生 导师 ,主要研究方向为网络控制、鲁棒控制 等. ·42 · 智 能 系 统 学 报 第 3 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net