
第3卷第2期 智能系统学报 Vol.3№2 2008年4月 CAAI Transactions on Intelligent Systems Apr.2008 动态影响图模型研究 俞奎2,王浩2姚宏亮2 (1.常州纺织服装职业技术学院,江苏常州213164;2.合肥工业大学计算机与信息学院,安徽合肥230009) 摘要:部分可观察马尔可夫决策过程在策略空间和状态空间上的计算复杂性,使求解其一个最优策略成为NP hard难题.为此,提出一种动态影响图模型来建模不确定环境下的Agent动态决策问题.动态影响图模型以有向无 环图表示系统变量之间的复杂关系.首先,动态影响图利用动态贝叶斯网络表示转移模型和观察模型以简化系统的 状态空间:其次,效用函数以效用结点的形式清晰地表示出来,从而简化系统效用函数的表示;最后,通过决策结点 表示系统的行为来简化系统的策略空间.通过实例从3个方面和POMDP模型进行了比较研究的结果表明,动态影 响图模型为大型的POMDP问题提供了一种简明的表示方式,最后在Ro bocup环境初步验证了该模型. 关键词:动态贝叶斯网络;影响图,马尔可夫决策过程;部分可观察马尔可夫决策过程,动态影响图 中图分类号:TP181文献标识码:A文章编号:1673-4785(2008)02-015908 A dynamic influence diagram for dyna mic decision processes YU Kui'2,WANG Hao2,YAO Hong-liang' (1.Department of Computer Science,Institute of Textile and Garment of Changzhou,Changzhou 213164,China;2.School of Computer and Information,Hefei University of Technology,Hefei 230009,China) Abstract:Computational complexities in strategy space and state space make the partially observable Mark- ov decision process(POMDP)an NP-hard problem.Therefore,in this paper,a dynamic influence diagram is proposed to model the decisionmaking problem with a single agent,in which a directed acyclic diagram is used to express the complex relationships between systematic variables.Firstly,a dynamic Bayesian net- work is used to represent the transition and observation models so as to reduce the state space of the sys- tem.Secondly,in order to reduce the representational complexity of the utility function,it is expressed in terms of utility nodes.Finally,the actions of the system are represented with decision nodes to simplify the strategy space.The dynamic influence diagram is compared with the POMDP using these three as- pects.Our research indicates that a dynamic influence diagram provides a simple way to express POMDP problems.Experiments in the Robocup environment verified the effectiveness of the proposed model. Key words:dynamic Bayesian networks;influence diagrams;Markov decision process;partially observable Markov decision process;dynamic influence diagram 动态决策问题是人工智能领域研究的中心问题 POMDP通过从环境中获得的观察来感知环境的状 之一.马尔可夫决策过程I(Markov decision 态.因此POMDP更适合不确定情形下动态决策问 process,MDP)和部分可观察马尔可夫决策过程I 题的建模.求解POMDP的算法通常是把POMDP (partially observable Markov decision process, 转换为一个连续状态下的MDP求解.Kaelbling等 POMDP)是研究动态决策问题的有效模型.MDP 人给出了求解POMDP的精确求解算法1,由于信 所假设的是Aget能够确切获知环境的状态. 度状态MDP(belief MDP)是一个连续状态的模型, 策略空间和状态空间的复杂性呈指数级增长,算法 收稿日期:2007-0620. 基金项目:国家自然科学基金资助项目(60575023,60705015);安徽 实际上不可行.因此许多研究者提出了POMDP的 省自然科学基金资助项目(070412064). 近似求解算法).实际上对于离散的POMDP,求 通讯作者:俞奎.Email:ykui713@hotmail.com 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3 卷第 2 期 智 能 系 统 学 报 Vol. 3 №. 2 2008 年 4 月 CAA I Transactions on Intelligent Systems Apr. 2008 动态影响图模型研究 俞 奎1 ,2 ,王 浩2 ,姚宏亮2 (1. 常州纺织服装职业技术学院 ,江苏 常州 213164 ;2. 合肥工业大学 计算机与信息学院 ,安徽 合肥 230009) 摘 要 :部分可观察马尔可夫决策过程在策略空间和状态空间上的计算复杂性 ,使求解其一个最优策略成为 NP2 hard 难题. 为此 ,提出一种动态影响图模型来建模不确定环境下的 Agent 动态决策问题. 动态影响图模型以有向无 环图表示系统变量之间的复杂关系. 首先 ,动态影响图利用动态贝叶斯网络表示转移模型和观察模型以简化系统的 状态空间 ;其次 ,效用函数以效用结点的形式清晰地表示出来 ,从而简化系统效用函数的表示 ;最后 ,通过决策结点 表示系统的行为来简化系统的策略空间. 通过实例从 3 个方面和 POMDP 模型进行了比较 ,研究的结果表明 ,动态影 响图模型为大型的 POMDP 问题提供了一种简明的表示方式 ,最后在 Robocup 环境初步验证了该模型. 关键词 :动态贝叶斯网络 ; 影响图 ; 马尔可夫决策过程 ; 部分可观察马尔可夫决策过程 ; 动态影响图 中图分类号 : TP181 文献标识码 :A 文章编号 :167324785 (2008) 0220159208 A dynamic influence diagram for dynamic decision processes YU Kui 1 ,2 , WAN G Hao 2 , YAO Hong2liang 2 (1. Department of Computer Science , Institute of Textile and Garment of Changzhou , Changzhou 213164 , China ;2. School of Computer and Information , Hefei University of Technology , Hefei 230009 , China) Abstract :Comp utational complexities in strategy space and state space make t he partially observable Mark2 ov decision process (POMDP) an N P2hard problem. Therefore , in t his paper , a dynamic influence diagram is propo sed to model t he decision2making problem wit h a single agent , in which a directed acyclic diagram is used to express t he complex relationship s between systematic variables. Firstly , a dynamic Bayesian net2 work is used to represent the transition and observation models so as to reduce t he state space of the sys2 tem. Secondly , in order to reduce t he representational complexity of t he utility f unction , it is exp ressed in terms of utility nodes. Finally , t he actions of the system are represented wit h decision nodes to simplify t he strategy space. The dynamic influence diagram is compared wit h t he POMDP using these t hree as2 pects. Our research indicates t hat a dynamic influence diagram provides a simple way to exp ress POMDP problems. Experiments in the Robocup environment verified t he effectiveness of t he proposed model. Keywords :dynamic Bayesian networks; influence diagrams ; Markov decision process; partially observable Markov decision process ; dynamic influence diagram 收稿日期 :2007206220. 基金项目 :国家自然科学基金资助项目 (60575023 ,60705015) ;安徽 省自然科学基金资助项目(070412064) . 通讯作者 :俞 奎. E2mail :ykui713 @hotmail. com. 动态决策问题是人工智能领域研究的中心问题 之一. 马 尔 可 夫 决 策 过 程[1 ] ( Markov decision process , MDP) 和部分可观察马尔可夫决策过程[ 2 ] ( partially observable Markov decision process , POMDP) 是研究动态决策问题的有效模型. MDP 所假设的是 Agent 能够确切获知环境的状态. POMDP 通过从环境中获得的观察来感知环境的状 态. 因此 POMDP 更适合不确定情形下动态决策问 题的建模. 求解 POMDP 的算法通常是把 POMDP 转换为一个连续状态下的 MDP 求解. Kaelbling 等 人给出了求解 POMDP 的精确求解算法[3 ] ,由于信 度状态 MDP(belief MDP) 是一个连续状态的模型 , 策略空间和状态空间的复杂性呈指数级增长 ,算法 实际上不可行. 因此许多研究者提出了 POMDP 的 近似求解算法[425 ] . 实际上对于离散的 POMDP ,求

·160· 智能系统学报 第3卷 解一个最优策略是PSPACE-complete难题l;求解 状态s采用a动作使环境状态转移到s的概率 &optimal策略是NP-hard难题).状态空间、值函 MDP模型所假设的是Agent能够确切获知环境的 数和策略表示的复杂性是造成求解POMDP问题 状态 的主要难点」 POMDP不要求Agent事先了解身处环境的状 本文在动态贝叶斯网络和影响图的基础上提出 态,而是通过从环境中获得的观察来感知环境的状 一种动态影响图(dynamic influence diagram,DD) 态.POMDP模型的定义如下: 模型来建模不确定环境下的Agent动态决策问题, POMDP由六元组R(s,a b(s) 络的另一种扩展模型,影响图可以同贝叶斯网络一 由于POMDP问题最优策略学习转变为“信度 样,表示多变量之间的复杂关系:另外,由于其结合 状态MDP”(belief MDP)最优策略的学习,造成一 了效用理论,因而比贝叶斯网络更适合处理Agent 个严重的问题就是由于其状态空间是连续的,值函 决策.它虽然在贝叶斯网络基础上结合了效用理论, 数、策略表示和状态空间的复杂性使求解POMDP 但不易表示和处理动态的决策问题 是一个NP-hard难题, DD将DBN简洁的表示动态领域知识的能力 因此针对状态空间和值函数表示的复杂性, 和影响图具有的决策能力有机地结合起来,使DD Boutilier和Poole把因式MDP扩展应用到POM 从状态空间、值函数的表示和策略空间3个方面降 DP模型中,提出了因式POMDP(factored POM- 低了求解动态决策问题的复杂性 DP)I.因式POMDP利用动态贝叶斯网络来表示 1)DBN表示DD的转移模型和观察模型.DD 转移模型和观察模型,用决策树或代数决策图来表 利用DBN蕴涵的条件独立性和稀疏性简化系统的 示转移概率和值函数.由于POMDP模型的值函数 状态空间; 是分段线性凸函数,随着状态空间的增长,表示值函 2)效用函数用效用结点的形式清晰地表示出 数的决策树或代数决策树的数目会指数级的增长」 来,简化系统的效用函数的表示; 因此,因式POMDP仍然不能有效处理大型的 3)DD中的决策结点表示系统的行为,一个决 POMDP的最优决策问题 策节点只和少数几个状态变量相联系,简化系统的 在Boutilier等人研究的基础上,把动态贝叶斯 策略空间 网络和影响图结合,提出动态影响图(dynamic in 研究表明DD为大型的POMDP问题提供了 fluence diagram,DD)模型来建模不确定环境下的 一种简明的表示方式 Agent动态决策问题,以解决复杂情况下的动态决 1 POMDP模型 策问题 MDP是表示和处理单个Agent动态决策问题 2动态影响图模型 的主要模型.MDP由四元组定义,S 2.1动态影响图模型的表示 是一个环境状态集,A表示系统行为集合,奖赏函数 动态影响图可以定义成一个二元组,其中B,表示t时刻的影响图,B。=(E,Vs), R(s,a,s)为系统在状态s采用a动作使环境状态 其中E,表示连接B,和B1的有向边,Vs表示E: 转移到s获得的瞬时奖赏值,记T(s,a,s)为系统在 所连接的顶点的集合.动态影响图结点集合V= 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
解一个最优策略是 PSPACE2complete 难题[6 ] ;求解 ε2optimal 策略是 NP2hard 难题[7 ] . 状态空间、值函 数和策略表示的复杂性是造成求解 POMDP 问题 的主要难点. 本文在动态贝叶斯网络和影响图的基础上提出 一种动态影响图(dynamic influence diagram , DID) 模型来建模不确定环境下的 Agent 动态决策问题 , 以解决 POMDP 模型不能有效求解复杂的动态决 策问题. DID 是一个有向无环图 ,用 DBN 表示转移 模型和观察模型 ,用效用节点表示效用函数 ,决策节 点表示系统的行为 ,这样 DID 利用图模型蕴涵的条 件独立性简洁表示了系统中变量之间的复杂关系. 动态 贝 叶 斯 网 络[8 ] ( dynamic bayesian net2 works , DBN) 是贝叶斯网络的一种扩展模型 ,是对 具有随机过程性质的不确定性问题进行建模的一种 有力的工具. 由于 DBN 没有决策节点 ,DBN 不易处 理 Agent 的决策问题. 影响图[9 ] (influence diagrams , ID) 是贝叶斯网 络的另一种扩展模型 ,影响图可以同贝叶斯网络一 样 ,表示多变量之间的复杂关系 ;另外 ,由于其结合 了效用理论 ,因而比贝叶斯网络更适合处理 Agent 决策. 它虽然在贝叶斯网络基础上结合了效用理论 , 但不易表示和处理动态的决策问题. DID 将 DBN 简洁的表示动态领域知识的能力 和影响图具有的决策能力有机地结合起来 ,使 DID 从状态空间、值函数的表示和策略空间 3 个方面降 低了求解动态决策问题的复杂性. 1) DBN 表示 DID 的转移模型和观察模型. DID 利用 DBN 蕴涵的条件独立性和稀疏性简化系统的 状态空间 ; 2) 效用函数用效用结点的形式清晰地表示出 来 ,简化系统的效用函数的表示 ; 3) DID 中的决策结点表示系统的行为 ,一个决 策节点只和少数几个状态变量相联系 ,简化系统的 策略空间. 研究表明 DID 为大型的 POMDP 问题提供了 一种简明的表示方式. 1 POMDP 模型 MDP 是表示和处理单个 Agent 动态决策问题 的主要模型. MDP 由四元组 定义 , S 是一个环境状态集 , A 表示系统行为集合 ,奖赏函数 R : S ×A →R 和状态转移函数 T : S ×A →PD ( S) . 记 R (s, a , s′) 为系统在状态 s 采用 a 动作使环境状态 转移到 s′获得的瞬时奖赏值;记 T (s, a ,s′) 为系统在 状态 s 采用 a 动作使环境状态转移到 s′的概率. MDP 模型所假设的是 Agent 能够确切获知环境的 状态. POMDP 不要求 Agent 事先了解身处环境的状 态 ,而是通过从环境中获得的观察来感知环境的状 态. POMDP 模型的定义如下[2 ] : POMDP 由六元组 定义. 其中 :1) S :环境状态的有限集合; 2) A :动作的有限 集合;3) T : S ×A →П( S) ;其中 П( S) 为状态的分 布 ,在某一状态 s 执行动作 a 后 ,下一个状态 s′的概 率分布 ,一般用 T (s, a , s′) 表示; 4) R : S 3 A →R;报 酬函数 ,表示在状态 s 执行动作 a 所能获得的报酬 , 也用 R (s, a) 表示;5) Z :观察的有限集合 ,即系统可 以感知的世界状态集合; 6) O : S 3 A →П( Z) ;其中 П( Z) 为观察的分布. 观察函数 ,表示系统在采取动 作 a 转移到状态 s′时 ,观察函数 О确定其在可能观 察上的概率分布 ,记为 O(s′, a , o) . p ( b, a) = s∑∈S R (s, a) b(s) . 由于 POMDP 问题最优策略学习转变为“信度 状态 MDP”( belief MDP) 最优策略的学习 ,造成一 个严重的问题就是由于其状态空间是连续的 ,值函 数、策略表示和状态空间的复杂性使求解 POMDP 是一个 NP2hard 难题. 因此针对状态空间和值函数表示的复杂性 , Boutilier 和 Poole 把因式 MDP 扩展应用到 POM2 DP 模型中 ,提出了因式 POMDP (factored POM2 DP) [10 ] . 因式 POMDP 利用动态贝叶斯网络来表示 转移模型和观察模型 ,用决策树或代数决策图来表 示转移概率和值函数. 由于 POMDP 模型的值函数 是分段线性凸函数 ,随着状态空间的增长 ,表示值函 数的决策树或代数决策树的数目会指数级的增长. 因此 , 因式 POMDP 仍然不能有 效处理大 型的 POMDP 的最优决策问题. 在 Boutilier 等人研究的基础上 ,把动态贝叶斯 网络和影响图结合 ,提出动态影响图 ( dynamic in2 fluence diagram , DID) 模型来建模不确定环境下的 Agent 动态决策问题 ,以解决复杂情况下的动态决 策问题. 2 动态影响图模型 2. 1 动态影响图模型的表示 动态影响 图 可以定 义成一个 二元组 ,其中 Bt 表示 t 时刻的影响图 , Bts = ( Et ,V ts ) , 其中 Er 表示连接 B t 和 B t - 1 的有向边 , V ts 表示 Et 所连接的顶点的集合. 动态影响图结点集合 V = · 061 · 智 能 系 统 学 报 第 3 卷

第2期 俞奎,等:动态影响图模型研究 ·161· (D,X,O,U,其中D表示决策变量集,X表示随机 响图中假定Parents(O,)sX',即执行每个行动后 变量集,O表示X所对应的观察值变量集,U表示 可观察变量的取值依赖于系统状态变量,同时假定 效用结点集.设在1时刻系统的状态随机变量集为 可观察变量没有孩子结点.则给定决策规则。动态 X=(X,X,,X,状态对应的观察随机变量集 影响图的观察模型为P6(O),是变量x在 为O=(O,O2,,O),决策结点变量集为D= Parents(o)中的取值 fD1,D2,Dm},每个决策结点有一个与行为集对 令elt是动态影响图在t时刻可观察变量O的 应的效用结点集为U=U,U,Um}.一个DD模 一组取值,为到t时刻可观察变量的所有可能取 型有结构策略模型概率模型和效用模型3个部分构 值,x[1]为XItJ的取值,在给定决策规则8时,则 成 随机变量、观察值变量和决策变量在1时刻的联合 概率分布表示为 PBX,E,DW=PXX1,D夏 PO.1XW夏P(D pa(D.》 式中:X,是Agent的状态变量集,O,是观察值的变 量集 图1单个Agent3个时间片的动态影响图 定义3效用模型在动态影响图中用一个效 Fig.I Three time slices DID for a single Agent 用结点山,表示1时刻状态的效用值.每个效用结点 定义1结构策略模型设A=(8,…)是 U,有一个和父结点集P。(U)相联系的局部效用函 1时刻Agent的一个决策规则集,结构策略模型为t 数U,(P.(U).由于效用函数具有时分性,在DD 时刻的每个决策结点D,确定一个局部决策规则6, 里每个时间片包含一个回报结点,则各个局部效用 G是D,的父结点集Pa(D)和行为选择之间的一个 和为 映射: 6:papy→0n, (1) U(X.D)= SU(P.(U)) 3) 式中:Q%rD,表示决策结点D,的父结点集可能的取 每个效用结点和一个局部效用函数相联系,一 值空间,QD,表示决策结点D,可能的行为空间.一 个效用结点U,的效用函数可表示为 个决策规范?是为t时刻的决策集中每个决策结点 U(P(U))=f(X,.=wix++wixi. 分配一个决策规则 式中:P(U)=1X,X}是效用结点U,父结点 定义2概率模型给定决策规则时决策结点 集;权重w:对应一个变量X,∈P(U),其表示X, 看成随机结点,给定1时刻的决策规则6,决策结点 对效用结点U,影响的度量 D,的条件概率为 则对于给定策略规范4时,时刻1的期望效用为 1,6Pa(D)=d; EU(0)= Ps (D:Pa(D))= 2 (x0) 、0,其他 (40 式中:d表示为Agent行为集合中的一个行为. 2.2 动态影响图模型的性质 在动态影响图中,转移模型和观察模型可以 定理1动态影响图中,给定决策规则。时 表示为一个DBN,系统状态被一组随机变量X= Ps(x[t+1八e1+1],d)的信度更新与POMDP中 {X,:,,Xm}表示,每个X在有限值域Dom 相同决策规则下的b(s)是等价的 (X)中取一定的值.每个变量X,的取值定义了系 证明令在t时刻DD执行给定决策规则8, 统的一个状态.令X,是当前时间片的变量,X,是 得到观察et+1时,Ps,(x[t+11elt+1],d)的信 下一个时间片的变量.X!的父结点集为Parents 度更新如下: (X)三(X,D).每个结点X,!有一个条件概率表 1)预测 Pa(Parents(X)).给定决策规则G,转移概率 Ps(x[t+1]1e2,d42)= P6(x1x,d表示为 SP(xIt +1]xIt]dz,e2)P(xIt]e2,d2)= Px'Ix,d=ΠP6xIaW 式中:h是变量x和d在Parents,(X)中的取值. ()d) 可观察变量集0={0,O,,O},在动态影 (5) 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
( D , X , O ,U) ,其中 D 表示决策变量集 , X 表示随机 变量集 , O 表示 X 所对应的观察值变量集 , U 表示 效用结点集. 设在 t 时刻系统的状态随机变量集为 X = { X1 , X2 , …, Xn } ,状态对应的观察随机变量集 为O = ( O1 , O2 , …, On ) , 决策结点变量集为 D = { D1 , D2 , …, Dn } ,每个决策结点有一个与行为集对 应的效用结点集为 U = {U1 ,U2 , …,Um }. 一个 DID 模 型有结构策略模型、概率模型和效用模型 3 个部分构 成. 图 1 单个 Agent 3 个时间片的动态影响图 Fig. 1 Three time slices DID for a single Agent 定义 1 结构策略模型 设Λt = (δi t , …,δM t ) 是 t 时刻 Agent 的一个决策规则集 ,结构策略模型为 t 时刻的每个决策结点 D t 确定一个局部决策规则δt , δt 是 D t 的父结点集 Pa ( Dt) 和行为选择之间的一个 映射 : δt ∶ΩPa ( Dt ) →ΩDt . (1) 式中 :ΩPa ( Dt ) 表示决策结点 Dt 的父结点集可能的取 值空间 ,ΩDt 表示决策结点 D t 可能的行为空间. 一 个决策规范σt 是为 t 时刻的决策集中每个决策结点 分配一个决策规则. 定义 2 概率模型 给定决策规则时决策结点 看成随机结点 ,给定 t 时刻的决策规则δt ,决策结点 Dt 的条件概率为 Pδt ( Dt | Pa ( Dt) ) = 1 ,δt ( Pa ( Dt) ) = dj ; 0 ,其他. (2) 式中 : dj 表示为 Agent 行为集合中的一个行为. 在动态影响图中 , 转移模型和观察模型可以 表示为一个 DBN ,系统状态被一组随机变量 X = { X1 , X2 , …, Xn } 表示 , 每个 Xi 在有限值域 Dom ( Xi) 中取一定的值. 每个变量 Xi 的取值定义了系 统的一个状态. 令 Xi 是当前时间片的变量 , X′i 是 下一个时间片的变量. X′i 的父结点集为 Parents ( X′i ) Α ( X , D) . 每个结点 X′i 有一个条件概率表 Pa ( X′i | Parents( X′i ) ) . 给定决策规则δt ,转移概率 Pδt ( x′| x , d) 表示为 Pδt ( x′| x , d) = ∏i Pδt ( x′i | ui) . 式中 : ui 是变量 x 和 d 在 Parentδt ( X′) 中的取值. 可观察变量集 O = { O1 , O2 , …, On } ,在动态影 响图中假定 Parents ( Oi) Α X′,即执行每个行动后 可观察变量的取值依赖于系统状态变量 ,同时假定 可观察变量没有孩子结点. 则给定决策规则δt 动态 影响图的观察模型为 Pδt ( Oi | u′i ) , u′i 是变量 x′在 Parents( O′i ) 中的取值. 令 e[ t]是动态影响图在 t 时刻可观察变量 O 的 一组取值 , e1 :t为到 t 时刻可观察变量的所有可能取 值 , x [ t]为 X [ t]的取值 ,在给定决策规则δt 时 , 则 随机变量、观察值变量和决策变量在 t 时刻的联合 概率分布表示为 Pσt ( Xt , Et , Dt) = Xt∏∈Xt P ( Xt | Xt- 1 , Dt- 1 ) Xt∏∈Xt P( Ot | Xt) Dt∏∈Dt Pδk t ( Dt- 1 | pa ( Dt- 1 ) ) . 式中 : Xt 是 Agent 的状态变量集 , Ot 是观察值的变 量集. 定义 3 效用模型 在动态影响图中用一个效 用结点 Ut 表示 t 时刻状态的效用值. 每个效用结点 Ut ,有一个和父结点集 Pa (Ut) 相联系的局部效用函 数 Ut ( Pa (Ut) . 由于效用函数具有时分性 , 在 DID 里每个时间片包含一个回报结点 ,则各个局部效用 和为 U ( X , D) = ∑ m t = 1 Ut ( Pa (Ut) ) . (3) 每个效用结点和一个局部效用函数相联系 ,一 个效用结点 Ut 的效用函数可表示为 Ut ( Pa (Ut) ) = f t ( X 1 t , …, X n t ) = w 1 t X 1 t + …+ w n t X n t . 式中 : Pa (Ut) = { X 1 t , …, X n t }是效用结点 Ut 父结点 集;权重 w i t 对应一个变量 X t ∈Pa (Ut) ,其表示 Xt 对效用结点 Ut 影响的度量. 则对于给定策略规范σt 时,时刻 t 的期望效用为 EU (σt) = ∑Xt Pσt ( Xt , Ot , Dt) U t∑∈U t ( Pa (Ut) ) . (4) 2. 2 动态影响图模型的性质 定理 1 动态影响图中 ,给定决策规则δt 时 , Pδt ( x[ t + 1 ]| e[ t + 1 ] , dt) 的信度更新与 POMDP 中 相同决策规则下的 b’(s’) 是等价的. 证明 令在 t 时刻 DID 执行给定决策规则δt , 得到观察 e[ t + 1 ]时 , Pδt ( x[ t + 1 ]| e[ t + 1 ] , dt) 的信 度更新如下 : 1) 预测 Pδt ( x [ t + 1 ] | e12 , d12 ) = x∑ [ t] P( x[ t + 1 ] | x[ t] d2 , e12 ) P( x[ t] | e12 , d12 ) = ∑ [ t] P( x[ t + 1 ] | x[ t] , d2 ) P( x [ t] | e1 , dt- 1 ) . (5) 第 2 期 俞 奎 ,等 :动态影响图模型研究 · 161 ·

·162· 智能系统学报 第3卷 2)更新 U P5(x[t+1]e1+1],d)= P(xIt+1]en,eft+1].di)= aP(et+1]1x[t+1])ez)P(x[t+1],e2,dk)= U(X,Y,☑=U1(X,)+U1Y,☑ op(elt+1]x[t+11)P(xIt+1].en2,d)= 图2一个影响图效用结点的分解 oP(elt+1]1 xft+11) Fig.2 The separability of utility node ∑P(xt+1]小xt]le2,d42. 6) 图1.DD可以近似为一个影响图的多步决策问题的 扩展,因此DD中的效用结点也具有累加可分性 式中:是归一化因子,P(e1+1八x1+1)为观察 定理3给定一个DD的初始决策规范4和 模型,式6)中的求和式中,第1个因子是转移模型, 初始效用函数U。(Xo,D),则t=1时的4和 第2因子则是当前状态分布.由式(5)和6)可以用 U1(X,D)在时间上具有不变性 任何的DBN推理算法求解计算P(x[t+IIe[t+ 证明由式(1)和式(6)可知,1=1时的4和 1),d,这样就可以利用DBN强大的概率推理能力 U1(X,D)完全依赖于B,和Bs的结构,又因为 进行信度更新计算 DD的B,和Bs结构具有时间不变性,因而1=1时 在POMDP模型中,假定在当前状态s下执行 的4和U1(X,D)在时间上也具有不变性.而1=0 行动a,得到观察o,则到达状态s的信度b'(s)为 时的④和U(Xo,D)是和时间无关的,需要事先给 b'(s)=P.(s'1o,a,= 定,证毕 OP(o s',a,b P(s'l a,b= 3 模型比较 3P.(ol s'a p.(s'l a.b.9 P(s1 a.b= DD以有向无环图简洁地表示系统中变量之间 00(s'.a.(s.a.s)b(s (7) 复杂的关系.本节从知识表示与状态空间、模型的值 式中:0(s',a,o是观察模型,T(s,a,s)转移模型: 函数的表示模型推理能力3个方面把DD模型和 b(s是系统的当前状态.显然与式6)是等价的.但 POMDP模型进行比较 3.1知识表示与状态空间 将复杂系统的状态分解成一些组成变量,利用DBN POMDP模型通过列举系统可能所有的状态为 中条件独立性和稀疏性简化系统的状态空间数.因 此式6)和7)不仅是等价的,而且式6)利用条件独 其建模,存储每个状态的转移概率和其回报函数值. DD利用图模型中蕴涵的条件独立性来分解联合概 立性指数级地降低了式(7)的参数个数和状态空间 数,证毕 率分布,降低知识表示和获取的复杂性.DD将复杂 系统的状态分解成一些组成变量,以简洁的图模型 定义4效用函数的时分性(time-separability) 是指一个状态序列的效用是状态序列里的每个状态 表示了系统中主要的变量,清晰地描述了系统变量 之间的关系,利用DBN蕴涵的条件独立性和稀疏 的效用的和.累加可分性(additive separability)指 一个效用函数可分解为一组效用函数之和 性,转移模型和观察模型的全联合分布可分解成若 干个局部的概率分布表示,同时网络的拓扑结构表 定理2动态影响图中的效用结点具有时分性 和累加可分性 明如何从局部的概率分布获得全联合分布,大大简 证明在DD中,效用函数是由效用结点清晰 化了系统的状态空间」 的表达,每个时间步中的效用函数是条件独立的,如 例如一个感冒病人的症状可以用2个变量来描 图1,在1+2时间步的效用是前面每个时间步获得 述:headaches和temperature,令X={H(head 的期望回报累加和,这与POMDP中的回报函数具 aches),T(temperature)),H=(yes,no),T=(nor- 有时分性是一致的 mal,slightly high,high).则2个时间片中变量H 在文献[11]中,Tatman和Shachter证明了在 和T是相互独立的,即P(T,|T.1,H.1)= 影响图的多步决策问题中效用结点的累加可分离 P(T引T.).这样在DD只需要4+9=13个转移 性,如图2. 概率参数,而POMDP需要55=25个转移概率参 数,假设行为的状态空间为1. 由于DD每个时间片其实就是一个影响图,如 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
2) 更新 Pδt ( x [ t + 1 ] | e[ t + 1 ] , dt) = P( x[ t + 1 ] | e12 , e[ t + 1 ] , dt) = 5 P( e[ t + 1 ] | x[ t + 1 ]) e12 ) P( x[ t + 1 ] , e12 , d2 ) = 5 P( e[ t + 1 ] | x [ t + 1 ]) P( x [ t + 1 ] , e12 , d2 ) = 5 P( e[ t + 1 ] | x[ t + 1 ]) x∑[ t] P( x [ t + 1 ] | x [ t] | e12 , d12 . (6) 式中 :а是归一化因子 , P( e[ t + 1 ]| x [ t + 1 ]) 为观察 模型 ,式(6) 中的求和式中 ,第 1 个因子是转移模型 , 第 2 因子则是当前状态分布. 由式(5) 和 (6) 可以用 任何的 DBN 推理算法求解计算 P( x [ t + 1 ]| e[ t + 1 ] , dt) ,这样就可以利用 DBN 强大的概率推理能力 进行信度更新计算. 在 POMDP 模型中 ,假定在当前状态 s 下执行 行动 a ,得到观察 o,则到达状态 s′的信度 b′(s′) 为 b′(s′) = Pr (s′| o , a , b) = 5 Pr ( o | s′, a , b) Pr (s′| a , b) = 5 Pr ( o | s′, a) t∑∈S Pr (s′| a , b,s) Pr (s | a , b) = 5O(s′, a , o) t∑∈S T (s, a ,s′) b(s) . (7) 式中 :O (s′, a , o) 是观察模型 , T (s, a , s′) 转移模型; b(s) 是系统的当前状态. 显然与式 (6) 是等价的. 但 将复杂系统的状态分解成一些组成变量 ,利用 DBN 中条件独立性和稀疏性简化系统的状态空间数. 因 此式(6) 和(7) 不仅是等价的 ,而且式(6) 利用条件独 立性指数级地降低了式 (7) 的参数个数和状态空间 数 ,证毕. 定义 4 效用函数的时分性(time2separability) 是指一个状态序列的效用是状态序列里的每个状态 的效用的和. 累加可分性 (additive separability) 指 一个效用函数可分解为一组效用函数之和. 定理 2 动态影响图中的效用结点具有时分性 和累加可分性. 证明 在 DID 中 ,效用函数是由效用结点清晰 的表达 ,每个时间步中的效用函数是条件独立的 ,如 图 1 ,在 t + 2 时间步的效用是前面每个时间步获得 的期望回报累加和. 这与 POMDP 中的回报函数具 有时分性是一致的. 在文献[ 11 ]中 , Tatman 和 Shachter 证明了在 影响图的多步决策问题中效用结点的累加可分离 性 ,如图 2. 由于 DID 每个时间片其实就是一个影响图 ,如 U ( X , Y , Z) = U1 ( X , Y) + U1 ( Y , Z) 图 2 一个影响图效用结点的分解 Fig. 2 The separability of utility node 图 1. DID 可以近似为一个影响图的多步决策问题的 扩展 ,因此 DID 中的效用结点也具有累加可分性. 定理 3 给定一个 DID 的初始决策规范σ0 和 初始效用函数 Uo ( X0 , D0 ) , 则 t = 1 时的 σ1 和 U1 ( X1 , D1 ) 在时间上具有不变性. 证明 由式 (1) 和式 ( 6) 可知 , t = 1 时的σ1 和 U1 ( X′1 , D1 ) 完全依赖于 Bt 和 B ts 的结构 , 又因为 DID 的 Bt 和 B ts结构具有时间不变性 ,因而 t = 1 时 的σ1 和 U1 ( X1 , D1 ) 在时间上也具有不变性. 而 t = 0 时的σ0 和 Uo ( X0 , D0 ) 是和时间无关的 ,需要事先给 定 ,证毕. 3 模型比较 DID 以有向无环图简洁地表示系统中变量之间 复杂的关系. 本节从知识表示与状态空间、模型的值 函数的表示、模型推理能力 3 个方面把 DID 模型和 POMDP 模型进行比较. 3. 1 知识表示与状态空间 POMDP 模型通过列举系统可能所有的状态为 其建模 ,存储每个状态的转移概率和其回报函数值. DID 利用图模型中蕴涵的条件独立性来分解联合概 率分布 ,降低知识表示和获取的复杂性. DID 将复杂 系统的状态分解成一些组成变量 ,以简洁的图模型 表示了系统中主要的变量 ,清晰地描述了系统变量 之间的关系. 利用 DBN 蕴涵的条件独立性和稀疏 性 ,转移模型和观察模型的全联合分布可分解成若 干个局部的概率分布表示 ,同时网络的拓扑结构表 明如何从局部的概率分布获得全联合分布 ,大大简 化了系统的状态空间. 例如一个感冒病人的症状可以用 2 个变量来描 述 :headaches 和 temperat ure , 令 X = { H ( head2 aches) , T (temperat ure) } , H = (yes ,no) , T = (nor2 mal , slightly high , high) . 则 2 个时间片中变量 H 和 T 是 相 互 独 立 的 , 即 P ( Ti | Ti - 1 , Hi - 1 ) = P( Ti | Ti - 1 ) . 这样在 DID 只需要 4 + 9 = 13 个转移 概率参数 ,而 POMDP 需要 5 ×5 = 25 个转移概率参 数 ,假设行为的状态空间为 1. · 261 · 智 能 系 统 学 报 第 3 卷

第2期 俞奎,等:动态影响图模型研究 ·163* 般情况下,假设状态空间2,可用M个状态 MDP,因此其状态空间是连续的,POMDP的最优 变量表示,每个变量至多有S个状态和N个父结 值函数用分段线性凸函数表示,线性分段凸函数由 点.则利用条件独立性联合概率分布可用 一组a向量表示,如图4 O(M(S)参数,否则需要O(S“)个参数.假设M= 10,S=3,N=4,需要810个参数而不是5904900 个参数.下面考虑一个复杂一点的例子,如图3 D R 图42个状态的POMDP模型的值函数V: Fig.4 Value function VI'of POMDP for two states HC HC 根据定义,信状态度MDP模型是一个具有连 WC WC 续状态空间的模型,精确求解算法的复杂度非常高, COBS 以至于求解状态、动作和观察的集合元素超过10的 + 问题都非常困难6.一个重要的原因就是用来表示 最优值函数的线性分段凸函数,这种表示形式的复 图3一个动态影响图 杂度随着迭代的进行,增长得也非常得快.表示第 Fig.3 A example of DID i+l步值函数的a向量集的大小会在一步迭代后就 图3是一个动态影响图的例子,如果顾客想要 达到指数量级0(419),这一步更新所需的 咖啡(want coffee,WC),并得到了咖啡(has coffee, 计算复杂度是0(0A川S219),其中I表示 HC机器人得到奖赏(reward,R),否则得到惩罚. 第1步值向量的数目,|9表示状态空间.如果假设 机器人如果在下雨(rain,R)的情况下穿过街道去 初始的值函数是线性的,那么经过次迭代后,第1 买咖啡(get coffee,GetC)的话,可能被淋湿(wet, 次值函数对应的向量集大小是0(44,即使 W),除非带伞(umbrella,U),当然机器人可以完成 对于简单的有限阶POMDP问题,求解最优策略的 其他的任务,详见文献[2].这里是一个简化的向前 时间复杂度也是PSPACE-hard问题.无限阶的问 看一步的动态影响图,图中只标出了时间片之间变 题求解则可能是不可计算的.一种解决办法是求解 量的关系.OBs是一组可观察变量,D,是决策(行 与最优解差距小于某个特定精度的近似解,但有时 为)结点.该例子有5个布尔型的状态变量:R、U、 即使是这样都是不可计算的).因此,大量的研究 W、HC、WC和一个决策变量D,U为效用结点,假 重点被放在寻找近似解的算法研究上,实际上求解 设1OBs=2,A=2 optimal策略也是NP-hard难题, 在图3中,S=2=32,10=2,|A=2,则 在DD中效用函数以效用结点的形式清晰地 POMDP模型需要的转移概率参数为S凶S× 表达出来,对于离散的DD模型,其变量的状态空 |4川=2048,观察模型需要的概率参数为1O1× 间仍然是离散的,避免了用分段线性凸函数表示效 |SA=128,这样使POMDP只适合处理小规 用函数.DD中的效用节点并不依赖所有的变量,通 模的问题.在DD模型中P(R',U',W,HC,WC个 常只由一部分变量决定.如图3,影响效用结点是 R.U.W.HC.WC.D)=P(RR)P(UU)P(W W、WC、HC,而与其他节点无关.这样大大简化了 R,U,W,D)P(HC1HCP(WCWC).这样就把 效用函数表示的复杂性,但其复杂性会随着其父节 整个系统变量的全联合分布转变成局部的概率分布 点的个数的增加而指数级的增加.但幸运的是由于 表示,图3中所需的转移概率参数转换为5个局部 父节点的个数总是有限的,又由定理2可知,效用函 概率表示,只需要40个参数,因此DD大大简化了 数的累加可分性可进一步分离效用函数,使每个效 系统的状态空间 用结点依赖于更小的一组状态和行为变量,如图5 3.2模型的值函数表示 在POMDP中,值函数被转化为与每个状态转 由于求解POMDP问题的算法通常把POMDP 移相联系的效用值.更改值函数可能需要对所有的 转换为一个连续状态下的MDP求解,即信度状态 转移和状态的回报函数重新构造.在DD中效用函 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
一般情况下 ,假设状态空间 Ωx 可用 M 个状态 变量表示 ,每个变量至多有 S 个状态和 N 个父结 点. 则 利 用 条 件 独 立 性 联 合 概 率 分 布 可 用 O( M ( S N ) ) 参数 ,否则需要 O( S M ) 个参数. 假设 M = 10 , S = 3 , N = 4 ,需要 810 个参数而不是 5 904 900 个参数. 下面考虑一个复杂一点的例子 ,如图 3. 图 3 一个动态影响图 Fig. 3 A example of DID 图 3 是一个动态影响图的例子. 如果顾客想要 咖啡(want coffee , W C) ,并得到了咖啡(has coffee , H C) 机器人得到奖赏 (reward , R) ,否则得到惩罚. 机器人如果在下雨 (rain , R) 的情况下穿过街道去 买咖啡 (get coffee , GetC) 的话 ,可能被淋湿 (wet , W ) ,除非带伞(umbrella , U) ,当然机器人可以完成 其他的任务 ,详见文献[ 2 ]. 这里是一个简化的向前 看一步的动态影响图 ,图中只标出了时间片之间变 量的关系. OBs 是一组可观察变量 , Dt 是决策 (行 为) 结点. 该例子有 5 个布尔型的状态变量 : R、U 、 W 、H C、W C 和一个决策变量 D , U 为效用结点 ,假 设| OBs| = 2 ,| A| = 2. 在图 3 中 ,| S | = 2 5 = 32 ,| O| = 2 , | A | = 2 ,则 POMDP 模型需要的转移概率参数为| S | ×| S | × | A| = 2 048 ,观察模型需要的概率参数为| O| × | S| ×| A| = 128 , 这样使 POMDP 只适合处理小规 模的问题. 在 DID 模型中 P( R′,U′, W′, H C′, W C′| R ,U , W , H C, W C , Dt) = P( R′| R) P(U′| U) P( W′| R ,U , W , Dt) P( H C′| H C) P ( W C| W C′) . 这样就把 整个系统变量的全联合分布转变成局部的概率分布 表示 ,图 3 中所需的转移概率参数转换为 5 个局部 概率表示 ,只需要 40 个参数 ,因此 DID 大大简化了 系统的状态空间. 3. 2 模型的值函数表示 由于求解 POMDP 问题的算法通常把 POMDP 转换为一个连续状态下的 MDP 求解 ,即信度状态 MDP ,因此其状态空间是连续的 ,POMDP 的最优 值函数用分段线性凸函数表示 ,线性分段凸函数由 一组 a 向量表示 ,如图 4. 图 4 2 个状态的 POMDP 模型的值函数 V 3 1 Fig. 4 Value function V 3 1 of POMDP for two states 根据定义 ,信状态度 MDP 模型是一个具有连 续状态空间的模型 ,精确求解算法的复杂度非常高 , 以至于求解状态、动作和观察的集合元素超过 10 的 问题都非常困难[ 6 ] . 一个重要的原因就是用来表示 最优值函数的线性分段凸函数 ,这种表示形式的复 杂度随着迭代的进行 ,增长得也非常得快. 表示第 i + 1步值函数的 a 向量集的大小会在一步迭代后就 达到指数量级 O (| A | | Гi | | Ω| ) ,这一步更新所需的 计算复杂度是 O( (| A| | S| 2 | Гi | | Ω| ) ,其中| Гi | 表示 第 i 步值向量的数目 , | Ω| 表示状态空间. 如果假设 初始的值函数是线性的 ,那么经过 i 次迭代后 ,第 i 次值函数对应的向量集大小是 O (| A | | Ω| i - 1 ,即 使 对 于简单的有限阶 POMDP 问题 ,求解最优策略的 时间复杂度也是 PSPACE2hard 问题. 无限阶的问 题求解则可能是不可计算的. 一种解决办法是求解 与最优解差距小于某个特定精度的近似解 ,但有时 即使是这样都是不可计算的[7 ] . 因此 ,大量的研究 重点被放在寻找近似解的算法研究上 ,实际上求解 ε2optimal 策略也是 NP2hard 难题. 在 DID 中效用函数以效用结点的形式清晰地 表达出来 ,对于离散的 DID 模型 ,其变量的状态空 间仍然是离散的 ,避免了用分段线性凸函数表示效 用函数. DID 中的效用节点并不依赖所有的变量 ,通 常只由一部分变量决定. 如图 3 ,影响效用结点是 W 、W C、H C ,而与其他节点无关. 这样大大简化了 效用函数表示的复杂性 ,但其复杂性会随着其父节 点的个数的增加而指数级的增加. 但幸运的是由于 父节点的个数总是有限的 ,又由定理 2 可知 ,效用函 数的累加可分性可进一步分离效用函数 ,使每个效 用结点依赖于更小的一组状态和行为变量 ,如图 5. 在 POMDP 中 ,值函数被转化为与每个状态转 移相联系的效用值. 更改值函数可能需要对所有的 转移和状态的回报函数重新构造. 在 DID 中效用函 第 2 期 俞 奎 ,等 :动态影响图模型研究 · 361 ·
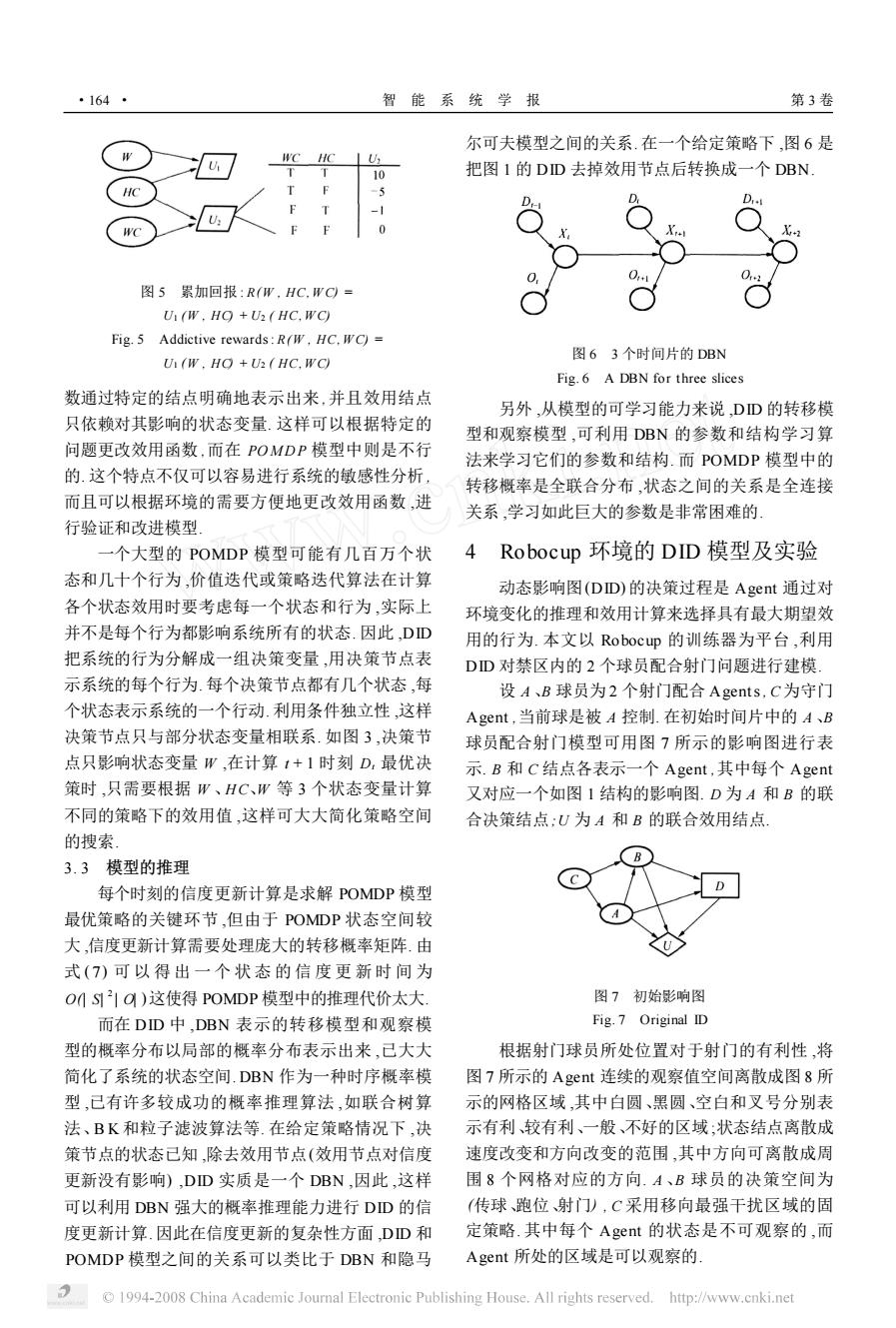
·164- 智能系统学报 第3卷 尔可夫模型之间的关系.在一个给定策略下,图6是 WC HC 10 把图I的DD去掉效用节点后转换成一个DBN 图5累加回报:R(W,HC.WC= U(W.HO +U(HC.WC) Fig.5 Addictive rewards:R(W,HC.WC)= 图63个时间片的DBN U(W.HO +U2(HC.WC) Fig.6 A DBN for three slices 数通过特定的结点明确地表示出来,并且效用结点 另外,从模型的可学习能力来说,DD的转移模 只依赖对其影响的状态变量.这样可以根据特定的 型和观察模型,可利用DBN的参数和结构学习算 问题更改效用函数,而在POMDP模型中则是不行 法来学习它们的参数和结构.而POMDP模型中的 的.这个特点不仅可以容易进行系统的敏感性分析, 转移概率是全联合分布,状态之间的关系是全连接 而且可以根据环境的需要方便地更改效用函数,进 关系,学习如此巨大的参数是非常困难的」 行验证和改进模型 一个大型的POMDP模型可能有几百万个状 4 Robocup环境的DID模型及实验 态和几十个行为,价值迭代或策略迭代算法在计算 动态影响图(DD)的决策过程是Agent通过对 各个状态效用时要考虑每一个状态和行为,实际上 环境变化的推理和效用计算来选择具有最大期望效 并不是每个行为都影响系统所有的状态.因此,DD 用的行为.本文以Robocup的训练器为平台,利用 把系统的行为分解成一组决策变量,用决策节点表 DD对禁区内的2个球员配合射门问题进行建模: 示系统的每个行为.每个决策节点都有几个状态,每 设A、B球员为2个射门配合Agents,C为守门 个状态表示系统的一个行动.利用条件独立性,这样 Agent,当前球是被A控制.在初始时间片中的A、B 决策节点只与部分状态变量相联系.如图3,决策节 球员配合射门模型可用图7所示的影响图进行表 点只影响状态变量W,在计算1+1时刻D,最优决 示.B和C结点各表示一个Agent,其中每个Agent 策时,只需要根据W、HC、W等3个状态变量计算 又对应一个如图1结构的影响图.D为A和B的联 不同的策略下的效用值,这样可大大简化策略空间 合决策结点:U为A和B的联合效用结点 的搜索。 3.3模型的推理 每个时刻的信度更新计算是求解POMDP模型 最优策略的关键环节,但由于POMDP状态空间较 大,信度更新计算需要处理庞大的转移概率矩阵.由 式(7)可以得出一个状态的信度更新时间为 OMS21O)这使得POMDP模型中的推理代价太大. 图7初始影响图 而在DD中.DBN表示的转移模型和观察模 Fig.7 Original ID 型的概率分布以局部的概率分布表示出来,己大大 根据射门球员所处位置对于射门的有利性,将 简化了系统的状态空间.DBN作为一种时序概率模 图7所示的Agent连续的观察值空间离散成图8所 型,已有许多较成功的概率推理算法,如联合树算 示的网格区域,其中白圆、黑圆、空白和叉号分别表 法、BK和粒子滤波算法等.在给定策略情况下,决 示有利较有利、一般、不好的区域;状态结点离散成 策节点的状态已知,除去效用节点(效用节点对信度 速度改变和方向改变的范围,其中方向可离散成周 更新没有影响),DD实质是一个DBN,因此,这样 围8个网格对应的方向.A、B球员的决策空间为 可以利用DBN强大的概率推理能力进行DD的信 (传球、跑位射门),C采用移向最强干扰区域的固 度更新计算.因此在信度更新的复杂性方面,DD和 定策略.其中每个Aget的状态是不可观察的,而 POMDP模型之间的关系可以类比于DBN和隐马 Agent所处的区域是可以观察的 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 5 累加回报 : R(W , HC, W C) = U1 (W , HC) + U2 ( HC, W C) Fig. 5 Addictive rewards: R(W , HC, W C) = U1 (W , HC) + U2 ( HC, W C) 数通过特定的结点明确地表示出来 ,并且效用结点 只依赖对其影响的状态变量. 这样可以根据特定的 问题更改效用函数 ,而在 POMD P 模型中则是不行 的. 这个特点不仅可以容易进行系统的敏感性分析 , 而且可以根据环境的需要方便地更改效用函数 ,进 行验证和改进模型. 一个大型的 POMDP 模型可能有几百万个状 态和几十个行为 ,价值迭代或策略迭代算法在计算 各个状态效用时要考虑每一个状态和行为 ,实际上 并不是每个行为都影响系统所有的状态. 因此 ,DID 把系统的行为分解成一组决策变量 ,用决策节点表 示系统的每个行为. 每个决策节点都有几个状态 ,每 个状态表示系统的一个行动. 利用条件独立性 ,这样 决策节点只与部分状态变量相联系. 如图 3 ,决策节 点只影响状态变量 W ,在计算 t + 1 时刻 Dt 最优决 策时 ,只需要根据 W 、H C、W 等 3 个状态变量计算 不同的策略下的效用值 ,这样可大大简化策略空间 的搜索. 3. 3 模型的推理 每个时刻的信度更新计算是求解 POMDP 模型 最优策略的关键环节 ,但由于 POMDP 状态空间较 大 ,信度更新计算需要处理庞大的转移概率矩阵. 由 式 ( 7) 可 以 得 出 一 个 状 态 的 信 度 更 新 时 间 为 O(| S| 2 | O| )这使得 POMDP 模型中的推理代价太大. 而在 DID 中 ,DBN 表示的转移模型和观察模 型的概率分布以局部的概率分布表示出来 ,已大大 简化了系统的状态空间. DBN 作为一种时序概率模 型 ,已有许多较成功的概率推理算法 ,如联合树算 法、B K 和粒子滤波算法等. 在给定策略情况下 ,决 策节点的状态已知 ,除去效用节点(效用节点对信度 更新没有影响) ,DID 实质是一个 DBN ,因此 ,这样 可以利用 DBN 强大的概率推理能力进行 DID 的信 度更新计算. 因此在信度更新的复杂性方面 ,DID 和 POMDP 模型之间的关系可以类比于 DBN 和隐马 尔可夫模型之间的关系. 在一个给定策略下 ,图 6 是 把图 1 的 DID 去掉效用节点后转换成一个 DBN. 图 6 3 个时间片的 DBN Fig. 6 A DBN for three slices 另外 ,从模型的可学习能力来说 ,DID 的转移模 型和观察模型 ,可利用 DBN 的参数和结构学习算 法来学习它们的参数和结构. 而 POMDP 模型中的 转移概率是全联合分布 ,状态之间的关系是全连接 关系 ,学习如此巨大的参数是非常困难的. 4 Robocup 环境的 DID 模型及实验 动态影响图(DID) 的决策过程是 Agent 通过对 环境变化的推理和效用计算来选择具有最大期望效 用的行为. 本文以 Robocup 的训练器为平台 ,利用 DID 对禁区内的 2 个球员配合射门问题进行建模. 设 A 、B 球员为 2 个射门配合 Agents, C为守门 Agent ,当前球是被 A 控制. 在初始时间片中的 A 、B 球员配合射门模型可用图 7 所示的影响图进行表 示. B 和 C 结点各表示一个 Agent ,其中每个 Agent 又对应一个如图 1 结构的影响图. D 为 A 和 B 的联 合决策结点;U 为 A 和 B 的联合效用结点. 图 7 初始影响图 Fig. 7 Original ID 根据射门球员所处位置对于射门的有利性 ,将 图 7 所示的 Agent 连续的观察值空间离散成图 8 所 示的网格区域 ,其中白圆、黑圆、空白和叉号分别表 示有利、较有利、一般、不好的区域 ;状态结点离散成 速度改变和方向改变的范围 ,其中方向可离散成周 围 8 个网格对应的方向. A 、B 球员的决策空间为 (传球、跑位、射门) , C 采用移向最强干扰区域的固 定策略. 其中每个 Agent 的状态是不可观察的 ,而 Agent 所处的区域是可以观察的. · 461 · 智 能 系 统 学 报 第 3 卷
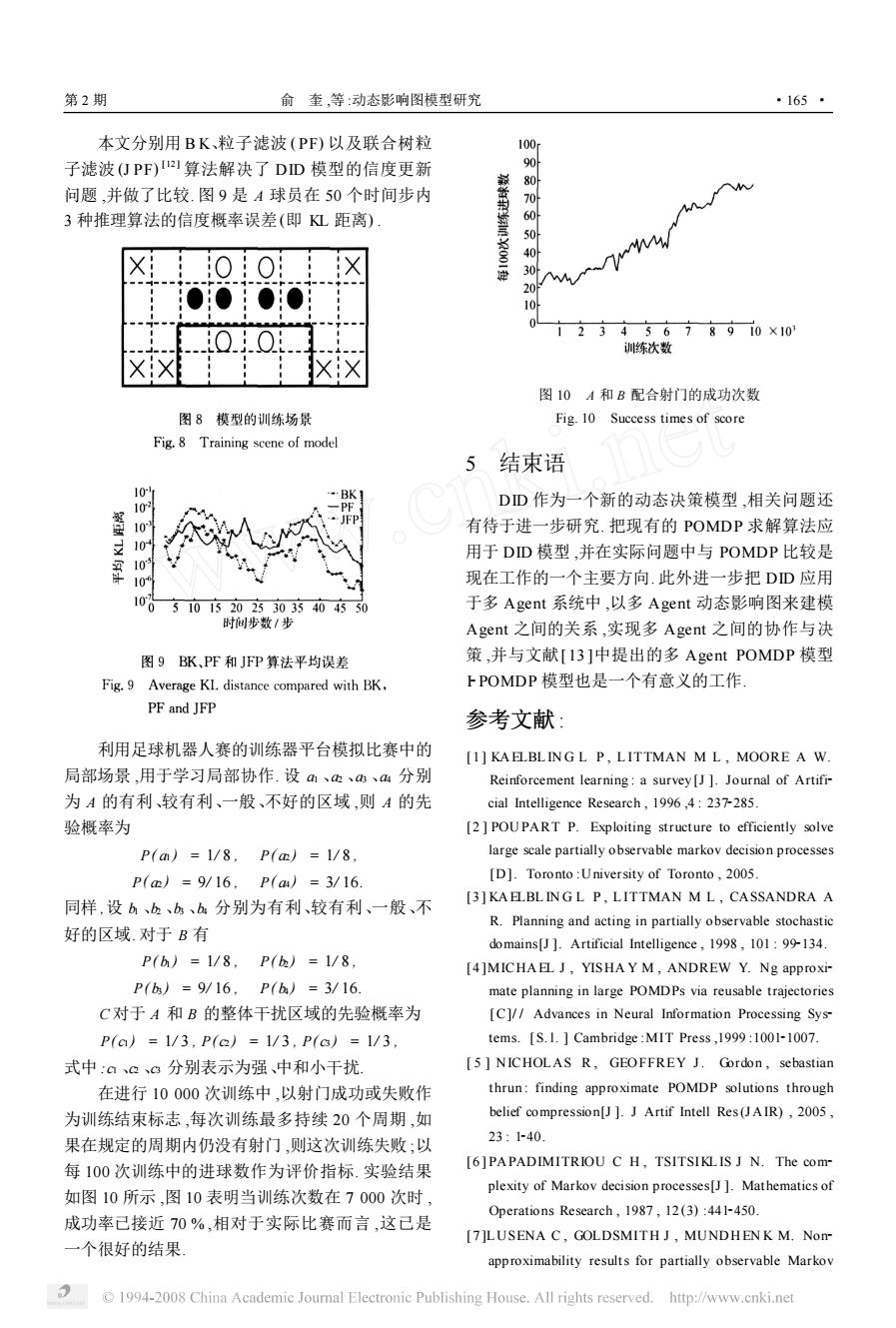
第2期 俞奎,等:动态影响图模型研究 ·165· 本文分别用BK、粒子滤波(PF)以及联合树粒 100 子滤波(仃PF)2算法解决了DD模型的信度更新 问题,并做了比较.图9是A球员在50个时间步内 3种推理算法的信度概率误差(即L距离) 40 M 30 20 00 10 0..0 2345678910×10 训练次数 图10A和B配合射门的成功次数 图8模型的训练场景 Fig.10 Success times of score Fig.8 Training scene of model 5结束语 0 BK】 10 DD作为一个新的动态决策模型,相关问题还 有待于进一步研究.把现有的POMDP求解算法应 10 用于DD模型,并在实际问题中与POMDP比较是 109 现在工作的一个主要方向.此外进一步把DD应用 100 5101520233035404550 于多Agent系统中,以多Agent动态影响图来建模 时间步数/步 Agent之间的关系,实现多Agent之间的协作与决 图9BK、PF和JFP算法平均误差 策,并与文献[I3]中提出的多Agent POMDP模型 Fig.9 Average KL distance compared with BK, FPOMDP模型也是一个有意义的工作 PF and JFP 参考文献: 利用足球机器人赛的训练器平台模拟比赛中的 [1]KAELBLINGL P,LITTMAN M L,MOORE A W 局部场景,用于学习局部协作.设m、、、4分别 Reinforcement learning:a survey [J ]Journal of Artifi- 为A的有利、较有利、一般、不好的区域,则A的先 cial Intelligence Research,1996,4:237-285. 验概率为 [2]POUPART P.Exploiting structure to efficiently solve P(am)=1/8,P(m)=1/8, large scale partially observable markov decision processes P(m)=9/16,P(aa)=3/16 [D].Toronto:University of Toronto,2005. [3]KA ELBLINGL P,LITTMAN M L,CASSANDRA A 同样,设b、b、bs、b分别为有利、较有利、一般、不 R.Planning and acting in partially observable stochastic 好的区域.对于B有 domains[J ]Artificial Intelligence,1998,101:99-134. P(h)=1/8,P()=1/8, [4]MICHAEL J,YISHA Y M,ANDREW Y.Ng approxi- P(b)=9/16,P(h)=3/16 mate planning in large POMDPs via reusable trajectories C对于A和B的整体干扰区域的先验概率为 [C]//Advances in Neural Information Processing Sys- P(ca)=1/3,P(a)=1/3,P(c6)=1/3 tems.[S.1.Cambridge:MIT Press,1999:1001-1007. 式中:a。3分别表示为强、中和小千扰 [5 NICHOLAS R,GEOFFREY J.Gordon,sebastian 在进行10000次训练中,以射门成功或失败作 thrun:finding approximate POMDP solutions through 为训练结束标志,每次训练最多持续20个周期,如 belief compression[J ]J Artif Intell Res(JAIR),2005, 果在规定的周期内仍没有射门,则这次训练失败;以 23:1-40. 每100次训练中的进球数作为评价指标.实验结果 [6]PAPADIMITRIOU C H,TSITSIKLIS J N.The com- plexity of Markov decision processes[J ]Mathematics of 如图10所示,图10表明当训练次数在7000次时, Operations Research,1987,12(3):441-450. 成功率己接近70%,相对于实际比赛而言,这己是 [7]LUSENA C,GOLDSMITH J,MUNDHENK M.Nom 一个很好的结果 approximability results for partially observable Markov 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
本文分别用 B K、粒子滤波 (PF) 以及联合树粒 子滤波 (J PF) [12 ] 算法解决了 DID 模型的信度更新 问题 ,并做了比较. 图 9 是 A 球员在 50 个时间步内 3 种推理算法的信度概率误差(即 KL 距离) . 利用足球机器人赛的训练器平台模拟比赛中的 局部场景 ,用于学习局部协作. 设 a1 、a2 、a3 、a4 分别 为 A 的有利、较有利、一般、不好的区域 ,则 A 的先 验概率为 P( a1 ) = 1/ 8 , P( a2 ) = 1/ 8 , P( a2 ) = 9/ 16 , P( a4 ) = 3/ 16. 同样 ,设 b1 、b2 、b3 、b4 分别为有利、较有利、一般、不 好的区域. 对于 B 有 P( b1 ) = 1/ 8 , P( b2 ) = 1/ 8 , P( b3 ) = 9/ 16 , P( b4 ) = 3/ 16. C 对于 A 和 B 的整体干扰区域的先验概率为 P( c1 ) = 1/ 3 , P( c2 ) = 1/ 3 , P( c3 ) = 1/ 3 , 式中 :c1 、c2 、c3 分别表示为强、中和小干扰. 在进行 10 000 次训练中 ,以射门成功或失败作 为训练结束标志 ,每次训练最多持续 20 个周期 ,如 果在规定的周期内仍没有射门 ,则这次训练失败 ;以 每 100 次训练中的进球数作为评价指标. 实验结果 如图 10 所示 ,图 10 表明当训练次数在 7 000 次时 , 成功率已接近 70 % ,相对于实际比赛而言 ,这已是 一个很好的结果. 图 10 A 和 B 配合射门的成功次数 Fig. 10 Success times of score 5 结束语 DID 作为一个新的动态决策模型 ,相关问题还 有待于进一步研究. 把现有的 POMDP 求解算法应 用于 DID 模型 ,并在实际问题中与 POMDP 比较是 现在工作的一个主要方向. 此外进一步把 DID 应用 于多 Agent 系统中 ,以多 Agent 动态影响图来建模 Agent 之间的关系 ,实现多 Agent 之间的协作与决 策 ,并与文献[ 13 ]中提出的多 Agent POMDP 模型 I2POMDP 模型也是一个有意义的工作. 参考文献 : [1 ] KA ELBL IN G L P , L ITTMAN M L , MOORE A W. Reinforcement learning : a survey[J ]. Journal of Artifi2 cial Intelligence Research , 1996 ,4 : 2372285. [2 ] POUPART P. Exploiting structure to efficiently solve large scale partially observable markov decision processes [D]. Toronto :University of Toronto , 2005. [3 ] KA ELBL IN G L P , L ITTMAN M L , CASSANDRA A R. Planning and acting in partially observable stochastic domains[J ]. Artificial Intelligence , 1998 , 101 : 992134. [4 ]MICHA EL J , YISHA Y M , ANDREW Y. Ng approxi2 mate planning in large POMDPs via reusable trajectories [C]/ / Advances in Neural Information Processing Sys2 tems. [ S. l. ] Cambridge :MIT Press ,1999 :100121007. [ 5 ] NICHOLAS R , GEOFFREY J. Gordon , sebastian thrun : finding approximate POMDP solutions through belief compression[J ]. J Artif Intell Res(J AIR) , 2005 , 23 : 1240. [6 ] PAPADIMITRIOU C H , TSITSIKL IS J N. The com2 plexity of Markov decision processes[J ]. Mathematics of Operations Research , 1987 , 12 (3) :4412450. [7 ]LUSENA C , GOLDSMITH J , MUNDHEN K M. Non2 approximability results for partially observable Markov 第 2 期 俞 奎 ,等 :动态影响图模型研究 · 561 ·

·166· 智能系统学报 第3卷 decision processes [J ]Journal of Artificial Intelligence 作者简介: Research,2001,14:83-103. 俞奎,男,1979年生,硕士研究生, [8]DEAN T,KANAZAWA K.Probabilistic temporal rea 主要研究方向为贝叶斯网络建模与推理、 soning [C]//National Conference on Artificial Intelli- Agent技术,发表学术论文7篇」 gence.Washington:AAAI Press,1988,524-528. [9]RONALD A,HOWARD,JAMES E.Readings on the principles and applications of decision analysis [M].[S. 1.]Strategic Decision Group,1984. [10]BOUTILIER C,DEAN T,HANKS S.Decisiontheo- 王浩,男,1962年生,教授,博士, retic planning:structural assumptions and computation 合肥工业大学计算机与信息学院副院长, al leverage [J ]Journal of Artificial Intelligence Re- 主要研究方向为人工智能、数据挖掘、面 search,1999,11:1-94. 向对象技术等,中国自动化学会机器人竞 [11JOSEPH A,TATMAN,ROSS D,et al.Dynamic pro- 赛工作委员会委员、安徽省高校中青年骨 gramming and influence diagrams[J].IEEE Transations 干教师.先后参加国家自然科学基金、国 on Systems,Man,and Cybernetics,1990,20(2):365- 家教委博士点基金等10多项课题研究, 379. 获安徽省科技进步三等奖2项.目前主持 [12 ]BRENDA N G.Avi Pfeffer,Factored Particles for 国家自然科学基金和安徽省自然科学基 Scalable Monitoring[C]//Uncertainty in Artificial In 金等多项课题, telligence Morgan Kaufmann.San Francisco,USA, 2002:370377. 姚宏亮,男,1972年生,副教授,博士, [13]PRASHANT D,PIOTR G.A particle filtering based 主要研究方向为贝叶斯网络、Agent技术, approach to approximating interactive POMDPs[C]//P 发表学术论文10余篇。 National Conference on Artificial Intelligence,Menlo Park.AAAI Press2005:969-974. 2008中国智能系统工程学术大会 2008 Conference on Intelligent systems Engineering 21世纪将是智能科学突飞猛进的世纪,将是智能系统工程大放异彩的世纪.智能系统工程化、工程系统 智能化将是人工智能走向社会、走向应用、走向成功的必由之路,将是人类科学开发智能、科学利用智能的必 由之路.当前,智能系统工程相关研究和应用呈现出方兴未艾的发展势头,研究队伍迅速扩大,研究领域急速 拓展,一大批研究项目得到国家自然科学基金和国家科技攻关计划的支持,带动着信息科学向更高层次发展 智能系统工程是人工智能的重要发展领域,为了推动和展示智能系统工程领域的研究进展,交流总结近 年来智能系统工程领域的最新成果,中国人工智能学会智能系统工程专业委员会将于2008年在西南石油大 学(中国-成都)组织召开中国智能系统工程学术大会,会议的主题是“智能系统工程的新发展”.本次会议将 围绕智能系统工程特色创新成果进行交流与展示.征文范围(但不限于):1)理论创新;2)技术创新,3)应用 创新;4)学科创新」 全文截稿日期:2008610. 会议开始日期:2008101」 会议网站:http:/dxy.swpu.edu.cn/ReadNews.asp NewsID=5l5 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
decision processes[J ]. Journal of Artificial Intelligence Research , 2001 , 14 :832103. [8 ]DEAN T , KANAZAWA K. Probabilistic temporal rea2 soning [ C ]/ / National Conference on Artificial Intelli2 gence. Washington :AAAI Press , 1988 , 5242528. [9 ]RONALD A , HOWARD , J AMES E. Readings on the principles and applications of decision analysis [ M]. [ S. l. ] : Strategic Decision Group , 1984. [10 ]BOU TIL IER C , DEAN T , HAN KS S. Decision2theo2 retic planning : structural assumptions and computation2 al leverage [J ]. Journal of Artificial Intelligence Re2 search , 1999 , 11 :1294. [11 ]JOSEPH A , TA TMAN , ROSS D , et al. Dynamic pro2 gramming and influence diagrams[J ]. IEEE Transations on Systems , Man , and Cybernetics , 1990 , 20 (2) :3652 379. [12 ] BRENDA N G. Avi Pfeffer , Factored Particles for Scalable Monitoring [ C]/ / Uncertainty in Artificial In2 telligence Morgan Kaufmann. San Francisco , USA , 2002 :3702377. [13 ] PRASHAN T D , PIO TR G. A particle filtering based approach to approximating interactive POMDPs[C]/ / P National Conference on Artificial Intelligence , Menlo Park. AAAI Press ,2005 :9692974. 作者简介 : 俞 奎 ,男 ,1979 年生 ,硕士研究生 , 主要研究方向为贝叶斯网络建模与推理、 Agent 技术 ,发表学术论文 7 篇. 王 浩 , 男 , 1962 年生 , 教授 ,博士 , 合肥工业大学计算机与信息学院副院长 , 主要研究方向为人工智能、数据挖掘、面 向对象技术等 ,中国自动化学会机器人竞 赛工作委员会委员、安徽省高校中青年骨 干教师. 先后参加国家自然科学基金、国 家教委博士点基金等 10 多项课题研究 , 获安徽省科技进步三等奖 2 项. 目前主持 国家自然科学基金和安徽省自然科学基 金等多项课题. 姚宏亮 ,男 ,1972 年生 ,副教授 ,博士 , 主要研究方向为贝叶斯网络、Agent 技术 , 发表学术论文 10 余篇. 2008 中国智能系统工程学术大会 2008 Conference on Intelligent systems Engineering 21 世纪将是智能科学突飞猛进的世纪 ,将是智能系统工程大放异彩的世纪. 智能系统工程化、工程系统 智能化将是人工智能走向社会、走向应用、走向成功的必由之路 ,将是人类科学开发智能、科学利用智能的必 由之路. 当前 ,智能系统工程相关研究和应用呈现出方兴未艾的发展势头 ,研究队伍迅速扩大 ,研究领域急速 拓展 ,一大批研究项目得到国家自然科学基金和国家科技攻关计划的支持 ,带动着信息科学向更高层次发展. 智能系统工程是人工智能的重要发展领域 ,为了推动和展示智能系统工程领域的研究进展 ,交流总结近 年来智能系统工程领域的最新成果 ,中国人工智能学会智能系统工程专业委员会将于 2008 年在西南石油大 学(中国 - 成都) 组织召开中国智能系统工程学术大会 ,会议的主题是“智能系统工程的新发展”. 本次会议将 围绕智能系统工程特色创新成果进行交流与展示. 征文范围(但不限于) : 1) 理论创新 ;2) 技术创新 ;3) 应用 创新 ;4) 学科创新. 全文截稿日期 : 200826210. 会议开始日期 : 200821021. 会议网站 : http :/ / dxy. swp u. edu. cn/ ReadNews. asp NewsID = 515. · 661 · 智 能 系 统 学 报 第 3 卷