
第3卷第2期 智能系统学报 Vol.3№2 2008年4月 CAAI Transactions on Intelligent Systems Apr.2008 复杂网络上的群体决策 王龙,伏锋,陈小杰,王靖,武斌,楚天广,谢广明 (北京大学工学院,北京100871) 摘要:主要论述了复杂网络上群体决策的研究现状和最新进展.首先介绍了观点动力学研究中的几种基本模型, 即Isig模型、投票者模型、多数决定模型和有界自信模型等.其次以这些模型为基础,讨论了小世界、无标度等复杂 网络上观点动力学的研究结果,然后指出了观点动力学与语言游戏、一致性和耦合振子同步问题的联系,接着给出 了笔者在观点动力学方面所做的一些相关工作,最后指出了复杂网络上群体决策的未来发展方向和一些可能的应 用前景. 关键词:复杂网络:群体决策:观点动力学:自组织行为:复杂性科学:多智能体系统:群体行为:语言游戏 中图分类号:TP18文献标识码:A文章编号:16734785(2008)02009514 Collective decision-making over complex net works WANG Long,FU Feng,CHEN Xiaojie,WANG Jing,WU Bin,CHU Tiarr guang,XIE Guang ming (College of Engineering,Peking University,Beijing 100871,China) Abstract:In this paper,current theories and recent developments in collective decisionmaking over com- plex networks are discussed.First,several basic models in opinion dynamics are introduced,including the Ising model,the voter model,the majority rule model,the bounded confidence model,etc.Then,based upon these models,some recent findings about opinion dynamics over complex networks such as small- world and scale-free networks are discussed.Connections between opinion dynamics,language games, consensus,and synchronization of coupled oscillators are analyzed.Some original work on opinion dynam- ics is also presented.Finally possible future research directions and applications for collective decision making in complex networks are given. Key words :complex networks;collective decisionmaking;opinion dynamics;self-organization;complexity science;multi-Agent systems;collective behaviors;consensus;language games 观点动力学(opinion dynamics)主要研究社会 注.近年来,由于复杂性科学研究的兴起,在不同学 经济系统中由于个体之间决策的影响与外界公共信 科的交叉和融合之下,出现了经济物理学(econo 息的影响,人群中对某些特定事件或事物所持的不 physics))2l、社会物理学(soci1 ophysics)1,1、人工社 同观点的形成(formation)和演化(evolution)等现 会221等新兴研究领域,其研究范畴都包括了观点 象,并包括观点的一致性(consensus)与多样性(di- 动力学纵观观点动力学的发展,可以看出它在政治 versity)保持等问题).数十年来,观点动力学在社 事务2]、电子商务2]、市场营销、专家决策系 会学1、心理学61、政治科学川、经济学8)、物理 统03,]等方面都得到了成功的应用和发展,从而 学1、系统科学0201等不同学科中得到了广泛的关 加深了人们对观点的形成和演化的认识,同时也引 起了不同学科背景的研究人员的兴趣 收稿日期:2007-0712. 观点是个体对某事物或问题所持的看法或选 基金项目:国家自然科学基金资助项目(60674050,60528007);国家 “973”资助项目(2002CB312200);国家“863”资助项目 择.为研究方便,观点可以简化为一个二值选择(bi (2006AA04Z258);“十一五”计划资助项目 (A2120061303). nary choice),分别用+1和-1表示,如支持(+1) 通讯作者:王龙.E-mail:longwang@pku.edu.cn. 或反对(-1)某个候选人或某种行为.更一般地,可 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3 卷第 2 期 智 能 系 统 学 报 Vol. 3 №. 2 2008 年 4 月 CAA I Transactions on Intelligent Systems Apr. 2008 复杂网络上的群体决策 王 龙 ,伏 锋 ,陈小杰 ,王 靖 ,武 斌 ,楚天广 ,谢广明 (北京大学 工学院 ,北京 100871) 摘 要 :主要论述了复杂网络上群体决策的研究现状和最新进展. 首先介绍了观点动力学研究中的几种基本模型 , 即 Ising 模型、投票者模型、多数决定模型和有界自信模型等. 其次以这些模型为基础 ,讨论了小世界、无标度等复杂 网络上观点动力学的研究结果 ,然后指出了观点动力学与语言游戏、一致性和耦合振子同步问题的联系 ,接着给出 了笔者在观点动力学方面所做的一些相关工作 ,最后指出了复杂网络上群体决策的未来发展方向和一些可能的应 用前景. 关键词 :复杂网络 ;群体决策 ;观点动力学 ;自组织行为 ;复杂性科学 ;多智能体系统 ;群体行为 ;语言游戏 中图分类号 : TP18 文献标识码 :A 文章编号 :167324785 (2008) 0220095214 Collective decision2making over complex networks WANG Long , FU Feng , CHEN Xiao2jie , WANG Jing , WU Bin , CHU Tian2guang , XIE Guang2ming (College of Engineering , Peking University , Beijing 100871 , China) Abstract :In t his paper , current t heories and recent developments in collective decision2making over com2 plex networks are discussed. First , several basic models in opinion dynamics are introduced , including t he Ising model , t he voter model , t he majority rule model , t he bounded confidence model , etc. Then , based upon t hese models , some recent findings about opinion dynamics over complex networks such as small2 world and scale2free networks are discussed. Connections between opinion dynamics , language games , consensus , and synchronization of coupled oscillators are analyzed. Some original work on opinion dynam2 ics is also presented. Finally possible f ut ure research directions and applications for collective decision2 making in complex networks are given. Keywords :complex networks; collective decision2making ; opinion dynamics; self2organization ; complexity science ; multi2Agent systems; collective behaviors; consensus ; language games 收稿日期 :2007207212. 基金项目 :国家自然科学基金资助项目 (60674050 ,60528007) ;国家 “973”资助项目 ( 2002CB312200) ; 国家“863”资助项目 ( 2006AA04Z258 ) ; “ 十 一 五 ” 计 划 资 助 项 目 (A2120061303) . 通讯作者 :王 龙. E2mail :longwang @pku. edu. cn. 观点动力学 (opinion dynamics) 主要研究社会 经济系统中由于个体之间决策的影响与外界公共信 息的影响 ,人群中对某些特定事件或事物所持的不 同观点的形成 (formation) 和演化 (evolution) 等现 象 ,并包括观点的一致性 (consensus) 与多样性 (di2 versity) 保持等问题[124 ] . 数十年来 ,观点动力学在社 会学[5 ] 、心理学[6 ] 、政治科学[7 ] 、经济学[8 ] 、物理 学[9 ] 、系统科学[10220 ] 等不同学科中得到了广泛的关 注. 近年来 ,由于复杂性科学研究的兴起 ,在不同学 科的交叉和融合之下 ,出现了经济物理学 ( econo2 p hysics) [ 21 ] 、社会物理学 (sociop hysics) [1 ,3 ] 、人工社 会[22223 ]等新兴研究领域 ,其研究范畴都包括了观点 动力学. 纵观观点动力学的发展 ,可以看出它在政治 事务[24 ] 、电 子 商 务[25 ] 、市 场 营 销、专 家 决 策 系 统[10213 ,19 ]等方面都得到了成功的应用和发展 ,从而 加深了人们对观点的形成和演化的认识 ,同时也引 起了不同学科背景的研究人员的兴趣. 观点是个体对某事物或问题所持的看法或选 择. 为研究方便 ,观点可以简化为一个二值选择 (bi2 nary choice) ,分别用 + 1 和 - 1 表示 ,如支持 ( + 1) 或反对( - 1) 某个候选人或某种行为. 更一般地 , 可

·96 智能系统学报 第3卷 以映射为介于一段区间内的任一实数,如对某一使 熟的模型和研究方法,从而可以促进这些领域的相 用商品的满意度评价,从“很坏”到“很好”,就可以用 互融合和发展 闭区间[0,1]来描述.实际上,由于人们所产生的观 1 基本模型 点值并不是严格精确的,因此可以将个体的观点值 模糊化,用之间[0,Q]的实数表示个体的观点值.给 l.1 Ising模型与Gauber动力学(Gauber dynam 定初始时刻观点在人群中的分布,就可以根据某种 ics) 个体观点更新规则来考察群体中的观点演化.目前, 在观点动力学研究中,Ising模型是最基本的也 关于观点演化的模型有很多,如Ising模型、投票者 是应用最广泛的模型9,4s).Ising模型最初用于 模型(voter model)、多数决定模型(majority model) 相变研究中,后来随着复杂性科学的发展,由于其机 和有界自信模型(bounded confidence model)等,且 理简单且具有丰富的动力学行为,能有效地模拟二 大多数工作都可归到以上几类模型.这些模型一般 值观点的演化,因此被广泛地应用于观点动力学的 假设个体观点的更新受到周围环境中其他个体决策 研究中,假设一个群体由N个个体(类似统计物理 (或社会群体选择趋势)的影响.为了描述个体之间 学中的自旋(spin)组成,个体具有二值的观点: 的复杂社会(影响)关系近年来蓬勃发展的复杂网 a()=1,i=1,…,N(类似于自旋的方向).如在 络理论为其提供了方便而系统的框架:网络中的顶 金融市场中的决策:“+1”对应于“买”,“.1”对应于 点表示个体,边表示个体之间的相互作用关系260) “卖”.个体1的观点更新受周围邻居和整个社会趋 可以知道,社会关系网络具有小世界和无标度等特 势的影响类似于自旋的方向选择受局部自旋相互 性,有的还具有社团结构(community structure).著 作用和外在场的影响):g(1+1)以概率p:()取 名的Watts-Strogatz(WS)小世界网络模型s)和 +1,1-p:()取-1: Barabasi-Albert(BA)无标度网络模型就是对真 p(t)= 实社会网络可行有效的刻画,在一定程度上能反映 1+e始 真实社会网络的特征.因此,与在全连通图或多维规 N 则格子上研究观点动力学相比,以及达到一致的时 五W=w太,0+hrW 间跟系统大小的标度关系等:也关注不同观点之间 Ka表示Boltzmann常数,T表示个体决策中的随 的竞争关系,考察是否存在不同观点的共存态,不同 机因素,包括噪声、决策错误等(对应于绝对温度) 网络拓扑对群体观点演化的影响等.另一方面,观点 1,()的右端第1项表示个体周围邻居的影响(局部 和网络拓扑的共同演化是当前研究中的一个热点问 场),a表示其作用强度,第2项表示整个社会趋势 题.事实上,社会网络是持续动态演化的,个体将根 的影响(外场),即系统平均观点r()(系统反馈)对 据与邻居观点相互作用的结果进行连接的调整,同 个体决策的影响,:表示系统反馈对个体决策作用 时调整后的网络连接也影响群体的观点演化 g().另外 个体之间观点的表达是建立在共同语言基础上 的大小程度.r1定义为r)=上之 Ni-1 的.与观点动力学的研究类似,语言的演化(evolu~ ()、几()分别表示个体与周围邻居和系统反馈的 tion of language)是研究语音、语义、语法等表达方 确信程度,一般取为介于(-1,1)之间的非相关 式一致性的涌现行为(emergent behavior)B).近 (noncorrelated)随机噪声.以上介绍的Ising模型所 几年来出现的命名游戏(naming game)是一类简化 演化的过程也称为Glauber动力学.为了模型简单 的语言演化模型0),这些研究方向和内容属于广 和方便处理,一般假设kaT=1,特殊地,若考虑T= 义的观点动力学,与观点动力学有着紧密的联系.同 0,则个体观点更新的过程由一个随机的过程变成了 时应该指出:近年来系统控制界的热点问题,如多智 确定性的更新过程,称为零温度Glauber动力学 能体系统的一致性问题(consensus problem),其模 (zero-temperature Glauber dynamics).(t+ 型和方法与观点动力学有相似之处4*4,.而且物理 1)=sign1,若1,=0,则个体随机选择+1或-1.上 界、非线性科学界、动力系统界等长期研究的同步问 sing模型一般用于观点是二值的情形,如果观点是 题,也与观点动力学有着千丝万缕的联系05].因 连续的或离散多值的,就需要用其他模型来刻画观 此,观点动力学的研究可以借鉴这些领域内比较成 点的演化了 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
以映射为介于一段区间内的任一实数 ,如对某一使 用商品的满意度评价 ,从“很坏”到“很好”,就可以用 闭区间[ 0 ,1 ]来描述. 实际上 ,由于人们所产生的观 点值并不是严格精确的 ,因此可以将个体的观点值 模糊化 ,用之间[0 ,Q ]的实数表示个体的观点值. 给 定初始时刻观点在人群中的分布 ,就可以根据某种 个体观点更新规则来考察群体中的观点演化. 目前 , 关于观点演化的模型有很多 ,如 Ising 模型、投票者 模型(voter model) 、多数决定模型(majority model) 和有界自信模型 ( bounded confidence model) 等 ,且 大多数工作都可归到以上几类模型. 这些模型一般 假设个体观点的更新受到周围环境中其他个体决策 (或社会群体选择趋势) 的影响. 为了描述个体之间 的复杂社会(影响) 关系 ,近年来蓬勃发展的复杂网 络理论为其提供了方便而系统的框架 :网络中的顶 点表示个体 ,边表示个体之间的相互作用关系[ 26230 ] . 可以知道 ,社会关系网络具有小世界和无标度等特 性 ,有的还具有社团结构(community structure) . 著 名的 Watts2Strogatz ( WS) 小世界网络模型[31 ] 和 Barabasi2Albert (BA) 无标度网络模型[ 32 ]就是对真 实社会网络可行有效的刻画 ,在一定程度上能反映 真实社会网络的特征. 因此 ,与在全连通图或多维规 则格子上研究观点动力学相比 ,以及达到一致的时 间跟系统大小的标度关系等 ;也关注不同观点之间 的竞争关系 ,考察是否存在不同观点的共存态 ,不同 网络拓扑对群体观点演化的影响等. 另一方面 ,观点 和网络拓扑的共同演化是当前研究中的一个热点问 题. 事实上 ,社会网络是持续动态演化的 ,个体将根 据与邻居观点相互作用的结果进行连接的调整 ,同 时调整后的网络连接也影响群体的观点演化. 个体之间观点的表达是建立在共同语言基础上 的. 与观点动力学的研究类似 ,语言的演化 (evolu2 tion of language) 是研究语音、语义、语法等表达方 式一致性的涌现行为 (emergent behavior) [33239 ] . 近 几年来出现的命名游戏( naming game) 是一类简化 的语言演化模型[ 40247 ] . 这些研究方向和内容属于广 义的观点动力学 ,与观点动力学有着紧密的联系. 同 时应该指出 :近年来系统控制界的热点问题 ,如多智 能体系统的一致性问题 (consensus problem) ,其模 型和方法与观点动力学有相似之处[48249 ] . 而且物理 界、非线性科学界、动力系统界等长期研究的同步问 题 ,也与观点动力学有着千丝万缕的联系[50253 ] . 因 此 ,观点动力学的研究可以借鉴这些领域内比较成 熟的模型和研究方法 ,从而可以促进这些领域的相 互融合和发展. 1 基本模型 1. 1 Ising 模型与 Glauber 动力学 ( Glauber dynam2 ics) 在观点动力学研究中 ,Ising 模型是最基本的也 是应用最广泛的模型[1 ,9 ,54258 ] . Ising 模型最初用于 相变研究中 ,后来随着复杂性科学的发展 ,由于其机 理简单且具有丰富的动力学行为 ,能有效地模拟二 值观点的演化 ,因此被广泛地应用于观点动力学的 研究中. 假设一个群体由 N 个个体 (类似统计物理 学中的自旋 (spin) ) 组成 ,个体具有二值的观点 : σi ( t) = ±1 , i = 1 , …, N (类似于自旋的方向) . 如在 金融市场中的决策“: + 1”对应于“买”“, - 1”对应于 “卖”. 个体 i 的观点更新受周围邻居和整个社会趋 势的影响(类似于自旋的方向选择受局部自旋相互 作用和外在场的影响) :σi ( t + 1) 以概率 pi ( t) 取 + 1 ,1 - pi ( t) 取 - 1 : pi ( t) = 1 1 + e - 2 I i (t) KB T , Ii ( t) = aξ( t) 1 Ni ∑ N j = 1 σj ( t) + hηi i ( t) r( t) . KB 表示 Boltzmann 常数 , T 表示个体决策中的随 机因素 ,包括噪声、决策错误等 (对应于绝对温度) , Ii ( t) 的右端第 1 项表示个体周围邻居的影响 (局部 场) , a 表示其作用强度 ,第 2 项表示整个社会趋势 的影响(外场) ,即系统平均观点 r( t) (系统反馈) 对 个体决策的影响 , hi 表示系统反馈对个体决策作用 的大小程度. r( t) 定义为 r( t) = 1 N Σ N j = 1 σj ( t) . 另外 , ξ( t) 、ηi ( t) 分别表示个体与周围邻居和系统反馈的 确信程度 , 一般取为介于 ( - 1 , 1) 之间的非相关 (noncorrelated) 随机噪声. 以上介绍的 Ising 模型所 演化的过程也称为 Glauber 动力学. 为了模型简单 和方便处理 ,一般假设 kB T = 1. 特殊地 ,若考虑 T = 0 ,则个体观点更新的过程由一个随机的过程变成了 确定性的更新过程 , 称为零温度 Glauber 动力学 (zero2temperat ure Glauber dynamics) . 此时σi ( t + 1) = sign Ii ,若 Ii = 0 ,则个体随机选择 + 1 或 - 1. I2 sing 模型一般用于观点是二值的情形 ,如果观点是 连续的或离散多值的 ,就需要用其他模型来刻画观 点的演化了. ·96 · 智 能 系 统 学 报 第 3 卷

第2期 王龙,等:复杂网络上的群体决策 ·97· 1.2投票者模型(voter model) 投票者模型是观点动力学研究中比较简单的一 种模型s96].假设个体观点受到周围邻居的影响,并 14 且更新时从周围邻居中随机选择一个邻居的观点, 取代自己的观点(见图1).由于在投票者模型中很 容易写出系统不同状态之间的转移概率,因此许多 问题可以进行解析分析,这是此模型的一个优点 图3多数决定投票模型示意图 Fig.3 Schematic graph of majority voter model 点的相互作用与演化2221.设x()为个体i的观点 图1投票者模型示意图 值,i=1,,N.在1时刻,向量x(t)=(x1() Fig.I Schematic graph of voter model x2(),,xx())的元素由各个个体的观点值组成, 在图1中,个体1从周围邻居中随机选取一个 称之为背景(profile).模型假设2个个体之间的观 邻居j,用j的观点+1取代自己原先的观点-1. 点差异在某一个界之内时,他们之间的观点才有相 1.3多数决定模型(majority rule model,MR) 互影响,即影响i的观点的个体集合为 多数决定模型刻画个体决策时充分利用周围邻 1i,x(0)=1≤j≤N(0-y1≤, 居的信息,观点更新时选取数目占优的那个观 式中:G表示个体i的自信强度(confidence level) 点2-641.一般地,从系统中选取奇数个个体(如G 由此,个体1下一时刻的观点取为 个),被选中个体的观点全部更新为G个个体中较 多个体持有的观点(见图2).一般网络上多数决定 x+V=.xI,e0: 式中|表示集合元素个数.式(1)可以写成如下 模型的更新过程为:随机选取一个节点,节点下一时 形式: 刻选取某观点的概率正比于周围邻居所持此观点的 x(t+1)=A(t,x(t))x() 总数目.这种更新规则又叫做多数决定投票模型 式中:A(1,x(W)={a画},是一个行和为1的随机矩 (majority voter model),见图3.实际上,MR模型在 阵.对于j1(i,x(),a则=0;对于j∈1(i,x() 理论上一般很难解析,但是由于模型更符合实际,也 a叫=|1(i,x()川1.这是关于有界自信的线性模 得到了很好的研究」 型.还有其他有界自信的非线性模型,参见文献 651,这里不再赘述 2复杂网络上的观点动力学 一般地,在复杂网络上的各种动力学研究中,网 图2多数决定模型示意图 络的节点表示个体,节点之间的边表示个体之间的 Fig.2 Schematic graph of majority rule model 相互作用和影响.个体就是通过这样的相互作用并 在图2中,在个体i和其邻居(共5人)中,选择 且按照一定的演化规则来更新自身的状态、属性.复 -1的有3人,占多数,因此i及其邻居下一时刻观 杂网络上的观点动力学即是在这种框架下来研究系 点依据多数原则取为-1.在图3中,个体i的邻居 统观点的形成、传播和一致性等问题的.复杂网络上 中1/4选择+1,3/4选择-1,因此下一时刻i以1/ 的观点动力学主要分为两方面:一方面是研究静态 4概率选择+1,以314概率选择.1。 网络上的观点动力学问题:另一方面是关注网络拓 l.4有界自信模型(bounded confidence model) 扑和观点动力学的共同演化问题 更为现实一些,在某些情况下,观点并不是二值 首先讨论静态网络上基于投票者模型的一些相 的,如前文所叙,观点可以映射为一段区间内的任一 关结论.在异质网络网络中大部分节点的邻居数目 实数,此时有界自信模型就可以用来描述群体中观 存在差异,甚至成幂律分布)上,Sood等人16o研究 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
1. 2 投票者模型(voter model) 投票者模型是观点动力学研究中比较简单的一 种模型[59261 ] . 假设个体观点受到周围邻居的影响 ,并 且更新时从周围邻居中随机选择一个邻居的观点 , 取代自己的观点 (见图 1) . 由于在投票者模型中很 容易写出系统不同状态之间的转移概率 ,因此许多 问题可以进行解析分析 ,这是此模型的一个优点. 图 1 投票者模型示意图 Fig. 1 Schematic graph of voter model 在图 1 中 ,个体 i 从周围邻居中随机选取一个 邻居 j ,用 j 的观点 + 1 取代自己原先的观点 - 1. 1. 3 多数决定模型( maj orit y rule model , M R) 多数决定模型刻画个体决策时充分利用周围邻 居的信息 , 观点更新时选取数目占优的那个观 点[62264 ] . 一般地 , 从系统中选取奇数个个体 (如 G 个) ,被选中个体的观点全部更新为 G 个个体中较 多个体持有的观点 (见图 2) . 一般网络上多数决定 模型的更新过程为 :随机选取一个节点 ,节点下一时 刻选取某观点的概率正比于周围邻居所持此观点的 总数目. 这种更新规则又叫做多数决定投票模型 (majority voter model) ,见图 3. 实际上 ,MR 模型在 理论上一般很难解析 ,但是由于模型更符合实际 ,也 得到了很好的研究. 图 2 多数决定模型示意图 Fig. 2 Schematic graph of majority rule model 在图 2 中 ,在个体 i 和其邻居(共 5 人) 中 ,选择 - 1 的有 3 人 ,占多数 ,因此 i 及其邻居下一时刻观 点依据多数原则取为 - 1. 在图 3 中 ,个体 i 的邻居 中 1/ 4 选择 + 1 ,3/ 4 选择 - 1 ,因此下一时刻 i 以 1/ 4 概率选择 + 1 ,以 3/ 4 概率选择 - 1. 1. 4 有界自信模型(bounded confidence model) 更为现实一些 ,在某些情况下 ,观点并不是二值 的 ,如前文所叙 ,观点可以映射为一段区间内的任一 实数 ,此时有界自信模型就可以用来描述群体中观 图 3 多数决定投票模型示意图 Fig. 3 Schematic graph of majority voter model 点的相互作用与演化[22223 ] . 设 xi ( t) 为个体 i 的观点 值 , i = 1 , …, N . 在 t 时刻 , 向量 x ( t) = ( x1 ( t) , x2 ( t) , …, x N ( t) ) 的元素由各个个体的观点值组成 , 称之为背景 (profile) . 模型假设 2 个个体之间的观 点差异在某一个界之内时 ,他们之间的观点才有相 互影响 ,即影响 i 的观点的个体集合为 I(i , x (t)) = 1 ≤j ≤N ≤| xi (t) - xj ( y) | ≤εi , 式中 :εi 表示个体 i 的自信强度 (confidence level) . 由此 ,个体 i 下一时刻的观点取为 xi ( t + 1) =| I( i , x ( t) ) | - 1 j ∈I(∑i , x ( t) ) x j ( t) . (1) 式中 :| ·| 表示集合元素个数. 式 (1) 可以写成如下 形式 : x ( t + 1) = A( t , x ( t) ) x( t) . 式中 :A( t , x( t) ) = { aij} ,是一个行和为 1 的随机矩 阵. 对于 j I ( i , x( t) ) , aij = 0 ;对于 j ∈I ( i , x ( t) ) , aij = | I ( i , x ( t) ) | - 1 . 这是关于有界自信的线性模 型. 还有其他有界自信的非线性模型 , 参见文献 [65 ] ,这里不再赘述. 2 复杂网络上的观点动力学 一般地 ,在复杂网络上的各种动力学研究中 ,网 络的节点表示个体 ,节点之间的边表示个体之间的 相互作用和影响. 个体就是通过这样的相互作用并 且按照一定的演化规则来更新自身的状态、属性. 复 杂网络上的观点动力学即是在这种框架下来研究系 统观点的形成、传播和一致性等问题的. 复杂网络上 的观点动力学主要分为两方面 :一方面是研究静态 网络上的观点动力学问题;另一方面是关注网络拓 扑和观点动力学的共同演化问题. 首先讨论静态网络上基于投票者模型的一些相 关结论. 在异质网络(网络中大部分节点的邻居数目 存在差异 ,甚至成幂律分布) 上 , Sood 等人[ 60 ] 研究 第 2 期 王 龙 ,等 :复杂网络上的群体决策 ·97 ·

·98 智能系统学报 第3卷 了基于二值观点的投票者模型.通过运用平均场方 相同观点的节点聚在一起成条形的现象.Li等) 法对模型进行理论分析,发现系统能够达到一致状 通过数值仿真研究了在空间方格上随机加边对收敛 态(即所有个体持有相同的观点),并且收敛的平均 时间的影响,发现随机加边可以缩短网络的平均最 时间Tx的量级为N/b,其中N为个体的数目, 短路径,从而使得收敛时间变短.Lambiotte!7用平 表示网络度分布的k阶矩(k th moment).当网 均场方法分析了二分网络(dichotomous networks, 络的度分布为幂律分布时,指数v>3时Tw量级为 即网络只由2种度不同的节点组成)上的观点动力 N,指数v=3时Tx量级为N/InN;指数2<v<3 学行为,发现度的差异性对系统中不同观点共存状 时,Tw的量级为N2w.”,指数v=2时Tw量级 态到观点一致状态的转变是有影响的,并且系统呈 为AnN)2:指数v<2时Tw量级为O(1);指数v< 现出非均分现象,说明系统观点的一致性与其网络 2时Tx量级为0(1).另外,对于节点度相关或不 连通性有很大关系.进一步地,他们研究了带有社团 相关的网络,这些理论分析和仿真结果都吻合得比 结构的网络上的多数决定模型,讨论了网络上观点 较好.而在方格网络上,Krapivsky等66-6)发现系统 呈现的不同状态与社团网络结构的关系63,! 收敛时间与其维度有关.当维度是1时,其收敛到一 基于Ising模型,Bartolozzi等s研究了无标度 致状态的时间量级为N2;维度是2时,其收敛到一 网络上的观点动力学.初始时刻+1和·1两种观点 致状态的时间量级为NInN;当维度大于2时,收敛 随机均匀地分布在网络的节点上,并且令kaT=1. 可以发现随着强度α的不断增大,系统平均观点r 时间减少到N.这些结果表明,在异质网络上的投 对应于时间序列在零值附近的波动强度会越来越 票者模型中,系统能较快到达一致状态.进一步地, 大,从而使系统到达不了一致状态,并且r对应于时 文献[68]研究了分形方格网络上的投票者模型,发 间序列的所有值概率分布函数近似为高斯分布,而 现网络上观点状态的无序性(观点不同的节点对占 所有节点对的比值)是时间的幂律函数.Castellano 且对应于其他不同的参数这种分布依然存在.进一 等6发现在个体数目相同的情况下,小世界网络上 步地,Jung等s简化了上述模型,定义l,()为 M 的系统收敛时间比规则网络上的要短,其收敛时间 1:()=∑9().与文献[541相反的是,他们发现 量级为N.并且,当个体数目趋向无穷大时,小世界 系统平均观点r可以收敛到+1或者-1,并且BA 网络上不能表现出观点的完全有序性,因为小世界 网络上的系统收敛时间比其他网络的要短 网络上的长程连接能够抑制观点的有序化.另外,文 基于有界自信模型251,文献[74]研究了增长 献[61]发现引入少量的“狂热者”(即永远不改变自 的无标度网络上的观点动力学.初始时刻,每个个体 己观点的个体)将会阻碍系统到达一致状态,并且能 都赋给一个(0,1)之间的观点值.在观点演化过程 使这种不同观点共存的状态保持稳定.文献[70]在 中,随机选取个体1及它的一个邻居j,计算他们的 平均磁场守恒的条件下研究BA网络上的投票者模 观点值差异6,=g-g,当差异值满足|8,|<e时, 型,发现点对演化(link-update,以网络上的边为研 个体观点值做相应调整:a=q-δ,且g,=g- 究对象)时,磁场守恒,系统的收敛时间量级为N: δ,,其中£为差异极限,u(0<u<0.5)为收敛参 单点演化(node-update,以网络上的节点为研究对 数,表示改变观点值的强度.仿真结果表明系统观点 象)时,平均磁场在网络上不守恒.如果偏好性地进 动力学依赖于参数£,它决定了观点最终分布的峰 行单点演化,则可以使其平均磁场守恒 值:而个体数目N和收敛参数u只影响系统的收敛 基于多数决定模型,Krapivsky等61研究了方 时间和最终观点的分布范围:另外,无论在固定的无 格上二值观点的传播动力学,发现系统中群体观点 标度网络上还是在增长的无标度网络上,这些结果 达到一致状态的收敛时间量级为lnN,其中N为 均成立.Krause Deffuant等人提出了几类改进的有 个体的数目,并且收敛时间随着方格网络维度的增 界自信模型,即Krause-Hegselmann(KH)模型和 大而减少,当维度大于4的时候,有可能出现一个临 Weisbuch-Deffuant模型(WD)2223】.文献[76]在 界维度使得收敛时间与个体数目N无关.进一步 KH模型的基础上,研究发现,在BA网络上存在一 地,Chen等I研究了有限维空间方格上的观点动 个比较小的自信值使得扰动传播行为发生变化 力学,发现系统能最终达到一致状态.有趣的是,在 并且存在一个临界值£,当自信值大于临界值时,初 系统达到一致状态的过程中,在方格网络上出现了 始的扰动可以传播到其他所有节点.并且网络的平 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
了基于二值观点的投票者模型. 通过运用平均场方 法对模型进行理论分析 ,发现系统能够达到一致状 态(即所有个体持有相同的观点) ,并且收敛的平均 时间 TN 的量级为 N u 2 1 / u2 ,其中 N 为个体的数目 , uk 表示网络度分布的 k 阶矩 ( k th moment) . 当网 络的度分布为幂律分布时 ,指数 v > 3 时 TN 量级为 N ,指数 v = 3 时 TN 量级为 N / ln N ;指数 2 < v < 3 时 , TN 的量级为 N (2 v - 4) / ( v - 1) ,指数 v = 2 时 TN 量级 为(ln N) 2 ;指数 v < 2 时 TN 量级为 O (1) ;指数 v < 2 时 TN 量级为 O (1) . 另外 ,对于节点度相关或不 相关的网络 ,这些理论分析和仿真结果都吻合得比 较好. 而在方格网络上 , Krapivsky 等[66267 ]发现系统 收敛时间与其维度有关. 当维度是 1 时 ,其收敛到一 致状态的时间量级为 N 2 ;维度是 2 时 ,其收敛到一 致状态的时间量级为 Nln N ;当维度大于 2 时 ,收敛 时间减少到 N . 这些结果表明 ,在异质网络上的投 票者模型中 ,系统能较快到达一致状态. 进一步地 , 文献[ 68 ]研究了分形方格网络上的投票者模型 ,发 现网络上观点状态的无序性 (观点不同的节点对占 所有节点对的比值) 是时间的幂律函数. Castellano 等[69 ]发现在个体数目相同的情况下 ,小世界网络上 的系统收敛时间比规则网络上的要短 ,其收敛时间 量级为 N . 并且 ,当个体数目趋向无穷大时 ,小世界 网络上不能表现出观点的完全有序性 ,因为小世界 网络上的长程连接能够抑制观点的有序化. 另外 ,文 献[ 61 ]发现引入少量的“狂热者”(即永远不改变自 己观点的个体) 将会阻碍系统到达一致状态 ,并且能 使这种不同观点共存的状态保持稳定. 文献[ 70 ]在 平均磁场守恒的条件下研究 BA 网络上的投票者模 型 ,发现点对演化 (link2update ,以网络上的边为研 究对象) 时 ,磁场守恒 ,系统的收敛时间量级为 N ; 单点演化 ( node2update ,以网络上的节点为研究对 象) 时 ,平均磁场在网络上不守恒. 如果偏好性地进 行单点演化 ,则可以使其平均磁场守恒. 基于多数决定模型 , Krapivsky 等[64 ] 研究了方 格上二值观点的传播动力学 ,发现系统中群体观点 达到一致状态的收敛时间量级为 ln N ,其中 N 为 个体的数目 ,并且收敛时间随着方格网络维度的增 大而减少 ,当维度大于 4 的时候 ,有可能出现一个临 界维度使得收敛时间与个体数目 N 无关. 进一步 地 ,Chen 等[62 ] 研究了有限维空间方格上的观点动 力学 ,发现系统能最终达到一致状态. 有趣的是 ,在 系统达到一致状态的过程中 ,在方格网络上出现了 相同观点的节点聚在一起成条形的现象. Li 等[71 ] 通过数值仿真研究了在空间方格上随机加边对收敛 时间的影响 ,发现随机加边可以缩短网络的平均最 短路径 ,从而使得收敛时间变短. Lambiotte [72 ]用平 均场方法分析了二分网络 (dichotomous networks , 即网络只由 2 种度不同的节点组成) 上的观点动力 学行为 ,发现度的差异性对系统中不同观点共存状 态到观点一致状态的转变是有影响的 ,并且系统呈 现出非均分现象 ,说明系统观点的一致性与其网络 连通性有很大关系. 进一步地 ,他们研究了带有社团 结构的网络上的多数决定模型 , 讨论了网络上观点 呈现的不同状态与社团网络结构的关系[63 ,73 ] . 基于 Ising 模型 ,Bartolozzi 等[ 54 ]研究了无标度 网络上的观点动力学. 初始时刻 + 1 和 - 1 两种观点 随机均匀地分布在网络的节点上 ,并且令 kB T = 1. 可以发现随着强度 a 的不断增大 ,系统平均观点 r 对应于时间序列在零值附近的波动强度会越来越 大 ,从而使系统到达不了一致状态 ,并且 r 对应于时 间序列的所有值概率分布函数近似为高斯分布 ,而 且对应于其他不同的参数这种分布依然存在. 进一 步地 ,J ung 等[ 55 ] 简化了上述模型 , 定义 Ii ( t) 为 Ii ( t) = ∑ M j =1 σj ( t) . 与文献[54 ]相反的是 ,他们发现 系统平均观点 r 可以收敛到 + 1 或者 - 1 ,并且 BA 网络上的系统收敛时间比其他网络的要短. 基于有界自信模型 [22 ,75 ] ,文献[ 74 ]研究了增长 的无标度网络上的观点动力学. 初始时刻 ,每个个体 都赋给一个 (0 ,1) 之间的观点值. 在观点演化过程 中 ,随机选取个体 i 及它的一个邻居 j ,计算他们的 观点值差异δij =σi - σj ,当差异值满足|δij | <ε时 , 个体观点值做相应调整 :σi =σi - uδij 且σj =σj - uδij ,其中ε为差异极限 , u (0 < u < 0. 5) 为收敛参 数 ,表示改变观点值的强度. 仿真结果表明系统观点 动力学依赖于参数ε,它决定了观点最终分布的峰 值;而个体数目 N 和收敛参数 u 只影响系统的收敛 时间和最终观点的分布范围;另外 ,无论在固定的无 标度网络上还是在增长的无标度网络上 ,这些结果 均成立. Krause、Deff uant 等人提出了几类改进的有 界自信模型 ,即 Krause2Hegselmann ( KH) 模型和 Weisbuch2Deff uant 模型 ( WD) [22223 ] . 文献 [ 76 ] 在 KH 模型的基础上 ,研究发现 ,在 BA 网络上存在一 个比较小的自信值εd 使得扰动传播行为发生变化 , 并且存在一个临界值εs ,当自信值大于临界值时 ,初 始的扰动可以传播到其他所有节点. 并且网络的平 ·98 · 智 能 系 统 学 报 第 3 卷

第2期 王龙,等:复杂网络上的群体决策 ·99· 均度和初始扰动的个体数目的改变对以上结果的影 到了更多地分析9则,目前,关于这方面的研究比较为 响比较小.文献[77]发现在KH和WD模型上,向 大家所关注,相信它将是今后研究的一个重点方向 量维度的增加对一致状态的收敛有促进作用 3相关的群体决策问题 除了采用以上常用模型来研究网络上的观点动 力学问题,还可以采用其他模型,如Galam和Szna 3.1语言游戏(language games) jd等人为研究观点动力学提出的相关模型58,7s). 语言演化过程的研究,如词汇、语法的发展等, 其实这些模型和上述几类模型有着非常密切的关 吸引了国际上众多学者的研究兴趣).个体观点 系其中有些模型就是在这些模型的基础上加以改 的表达是基于语言的,因此语言的演化研究也可以 进得到的.除了用这些模型来研究复杂网络上的观 看作是一类广义的观点演化过程.这里,将简单介绍 点动力学,噪声、非线性作用、记忆效应等机制也可 语言游戏中关于语法演化(evolution of grammar) 以加以考虑65,28).借助这些机制,再结合以上模 的一个基本模型31,并指出它与上文所介绍的观点 型,复杂网络上的观点动力学将成为复杂网络动力 动力学模型的联系 学中一个新的热点 考虑一个异质人群中的语言演化动力学问题, 另一方面,观点动力学与网络拓扑的共同演化 假设语法G,其中含有n个候选语法,G,G, 问题也得到了关注和研究.网络拓扑不同对观点传 G.每一个语法都有各自的构成规则.定义参数 播是有影响的,而不同个体之间的观点相互影响也 表示一个句子同时符合语法G,和G的概率,即语 可以反作用于网络拓扑.在社会系统中,研究系统观 法G,和G相通的程度,其中0≤,且aa=1 点收敛的模型大致分为2种:一种是个体对事物观 由a构成的矩阵A表示这n个语法之间两两相通 点的形成是受邻居观点影响的:另外一种是对事物 的程度.假设一个使用语法G,的个体和一个使用语 持相同(近)观点的个体比较容易成为邻居.Nw~ 法G,的个体交流的收益是F(G,G)=(a+ man等ss结合以上实际情形,通过一个概率参数 a)/2,显然F(G,G)=1.设x,为使用语法G,的 中来控制这2种演化过程的相互影响程度,进而提 个体占群体的比例,那么每个使用语法G,的个体的 出了一种考察网络拓扑和个体观点相互作用的模 型.他们发现,改变这个参数,系统平衡时的状态可 平均收益可以表示为f:=∑xF(G,G).假设一 以由不同观点共存的状态转化到绝大多数个体持相 个后代在使用语法G,的语言环境里学习,但最终说 同观点的状态.另外,G1等81也提出了一种观点 的却是使用语法G的语言的概率是Q,.根据复制 传播和网络拓扑共同演化的模型,其规则如下:初始 突变方程(replicator-mutator equation),可以得到 网络拓扑为N个节点组成的全连通图:观点+1, 该模型的人口动力学方程为 -1随机等比例地分布在网络上.在演化过程中,每 =,1=1,…m 2) 次从网络中随机选取一节点对(节点之间相互连 接),如果选取的节点对的状态相同,进行下一步演 式中:=∑f,∑:=1.可以看出,式2有很 化,否则,即当选取的节点对之间的观点不同时,节 多稳定的和不稳定的平衡点.而当Qg=0时,这个 点对中的一个节点以概率p1改变自己的状态,即采 系统存在i个非对称的稳定平衡点x:=1,x=0() 用另一个节点的状态来保证节点对之间的观点相 ≠).当Q,比较大时,惟一的稳定平衡点是在所有 同,或者节点对以概率1-p保持观点不变,在这种 语法的使用者比例x,几乎相等的点处取得.因此当 情况下,两节点之间的边再以概率2断开.按照这 Qg=0,j≠i时,系统会收敛到全局一致的语法 样的演化规则,网络会演化成为由互不连通的社团 (universal grammar)).式(2)可以看成一个非线性 组成,社团内部的个体保持相同的观点,而社团之间 耦合的观点动力学模型,并且最终能达到一致.此 个体的观点不同,从而形成了不同观点有效分离的 外,引起物理界研究人员兴趣的命名游戏(naming 有趣现象.相应地,Rosvall等人采用个体之间交流 game)1o1,也可以看成一类广义的观点动力学.由 反馈的规则研究了系统中拓扑结构和信息之间的自 此,观点演化的研究可以借鉴语言演化中的一些模 组织现象s8)进一步地,通过运用统计物理的方法, 型,并且可以运用演化博弈论的相关理论,从而可以 观点动力学与网络拓扑的共同演化问题在理论上得 进一步地促进观点动力学的发展 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
均度和初始扰动的个体数目的改变对以上结果的影 响比较小. 文献[77 ]发现在 KH 和 WD 模型上 ,向 量维度的增加对一致状态的收敛有促进作用. 除了采用以上常用模型来研究网络上的观点动 力学问题 ,还可以采用其他模型 ,如 Galam 和 Szna2 jd 等人为研究观点动力学提出的相关模型[58 ,78281 ] . 其实这些模型和上述几类模型有着非常密切的关 系 ,其中有些模型就是在这些模型的基础上加以改 进得到的. 除了用这些模型来研究复杂网络上的观 点动力学 ,噪声、非线性作用、记忆效应等机制也可 以加以考虑[ 65 ,82284 ] . 借助这些机制 ,再结合以上模 型 ,复杂网络上的观点动力学将成为复杂网络动力 学中一个新的热点. 另一方面 ,观点动力学与网络拓扑的共同演化 问题也得到了关注和研究. 网络拓扑不同对观点传 播是有影响的 ,而不同个体之间的观点相互影响也 可以反作用于网络拓扑. 在社会系统中 ,研究系统观 点收敛的模型大致分为 2 种 :一种是个体对事物观 点的形成是受邻居观点影响的 ;另外一种是对事物 持相同 (近) 观点的个体比较容易成为邻居. New2 man 等[85 ]结合以上实际情形 ,通过一个概率参数 <来控制这 2 种演化过程的相互影响程度 ,进而提 出了一种考察网络拓扑和个体观点相互作用的模 型. 他们发现 ,改变这个参数 ,系统平衡时的状态可 以由不同观点共存的状态转化到绝大多数个体持相 同观点的状态. 另外 , Gil 等[ 86287 ] 也提出了一种观点 传播和网络拓扑共同演化的模型 ,其规则如下 :初始 网络拓扑为 N 个节点组成的全连通图;观点 + 1 , - 1随机等比例地分布在网络上. 在演化过程中 ,每 次从网络中随机选取一节点对 (节点之间相互连 接) ,如果选取的节点对的状态相同 ,进行下一步演 化;否则 ,即当选取的节点对之间的观点不同时 ,节 点对中的一个节点以概率 p1 改变自己的状态 ,即采 用另一个节点的状态来保证节点对之间的观点相 同;或者节点对以概率 1 - p1 保持观点不变 ,在这种 情况下 ,两节点之间的边再以概率 p2 断开. 按照这 样的演化规则 ,网络会演化成为由互不连通的社团 组成 ,社团内部的个体保持相同的观点 ,而社团之间 个体的观点不同 ,从而形成了不同观点有效分离的 有趣现象. 相应地 , Rosvall 等人采用个体之间交流 反馈的规则研究了系统中拓扑结构和信息之间的自 组织现象[88 ] . 进一步地 ,通过运用统计物理的方法 , 观点动力学与网络拓扑的共同演化问题在理论上得 到了更多地分析[89294] .目前 ,关于这方面的研究比较为 大家所关注 ,相信它将是今后研究的一个重点方向. 3 相关的群体决策问题 3. 1 语言游戏(language games) 语言演化过程的研究 ,如词汇、语法的发展等 , 吸引了国际上众多学者的研究兴趣[33239 ] . 个体观点 的表达是基于语言的 ,因此语言的演化研究也可以 看作是一类广义的观点演化过程. 这里 ,将简单介绍 语言游戏中关于语法演化 (evolution of grammar) 的一个基本模型[35 ] ,并指出它与上文所介绍的观点 动力学模型的联系. 考虑一个异质人群中的语言演化动力学问题. 假设语法 G, 其中含有 n 个候选语法 , G1 , G2 , …, Gn . 每一个语法都有各自的构成规则. 定义参数 aij 表示一个句子同时符合语法 Gi 和 Gj 的概率 ,即语 法 Gi 和 Gj 相通的程度 ,其中 0 ≤aij ≤1 ,且 aii = 1. 由 aij构成的矩阵 A 表示这 n 个语法之间两两相通 的程度. 假设一个使用语法 Gi 的个体和一个使用语 法 Gj 的个体交流的收益是 F ( Gi , Gj ) = ( aij + aji) / 2 ,显然 F( Gi , Gi) = 1. 设 xi 为使用语法 Gi 的 个体占群体的比例 ,那么每个使用语法 Gi 的个体的 平均收益可以表示为 f i = ∑ j x j F ( Gi , Gj) . 假设一 个后代在使用语法 Gi 的语言环境里学习 ,但最终说 的却是使用语法 Gj 的语言的概率是 Qij . 根据复制 突变方程 (replicator2mutator equation) ,可以得到 该模型的人口动力学方程为 x . i = ∑ n j =1 x j f jQji - <x i , i = 1 , …, n. (2) 式中 :< = ∑i x i f i , ∑i x i = 1. 可以看出 ,式(2) 有很 多稳定的和不稳定的平衡点. 而当 Qij = 0 时 ,这个 系统存在 i 个非对称的稳定平衡点 x i = 1 , x j = 0 ( j ≠i) . 当 Qij 比较大时 ,惟一的稳定平衡点是在所有 语法的使用者比例 xi 几乎相等的点处取得. 因此当 Qij = 0 , j ≠i 时 , 系统会收敛到全局一致的语法 (universal grammar) . 式 (2) 可以看成一个非线性 耦合的观点动力学模型 ,并且最终能达到一致. 此 外 ,引起物理界研究人员兴趣的命名游戏 (naming game) [40247 ] ,也可以看成一类广义的观点动力学. 由 此 ,观点演化的研究可以借鉴语言演化中的一些模 型 ,并且可以运用演化博弈论的相关理论 ,从而可以 进一步地促进观点动力学的发展. 第 2 期 王 龙 ,等 :复杂网络上的群体决策 ·99 ·

·100 智能系统学报 第3卷 3.2一致性和同步问题 始时刻+1的比例为p,采用BA无标度网络,取节 一致性问题是近年来国际控制界兴起的一个研 点数N=1000,平均度k=4,然后设定其观点动力 究热点问题.从物理的角度考察这一问题可追溯到 学演化规则.基于Ising模型及文献[70],首先定义 1995年发表在Physical Review Letters上的相变模 1(0=∑(0 型,即Vicsek模型).一致性问题关注一群通过局 个体i在下一时刻采取+1的概率为p,(),采取 部作用(与最近邻居的信息交互)的个体能否在某些 物理状态(速度、角度等)上达到一致4).设个体相 -1的概率为1-p:(),其中 1 互作用的拓扑关系图为G=(V,E,其中V=1,2, p:(0=1+e20 N},E={(i,j)∈X:aoy,A={ag}为图 这里所有个体的状态采用同步更新规则,用系统平 G的邻接矩阵.个体i的邻居集合为N,且N,= 均观点来衡量观点传播的情况.所有的数据点对应 {j∈:a判}.个体i的状态x,(在平均一致性协 于100次运行结果的平均值」 议(average-consensus)下的动态方程为 研究了在这3种初始观点分布情况下,系统达 x()=ay(x()-x,() 到稳态时系统平均观点对p的变化情况,如图4所 示.可以看出,对C2,即初始时+1占据度较大的 也可写成向量方程:x=-Lx,其中x=(x1,, xw),L为图G的拉氏矩阵(Laplacian matrix).当拓 节点,在初始比例p比较小的时候,能够使系统达 扑关系图是连通图时,系统中的个体状态渐近收敛 到全是+1的一致状态,而对C_3,即初始时-1占 据度较大的节点,当系统能够达到+1的一致状态 到所有个体初态的平均值.这个线性耦合模型与观 点动力学中的有界自信模型很相似,关注的角度都 时,初始比例p比其他2种分布情况的初始比例要 是系统能否达到一致.本质上来说,有界自信模型所 高一些.相应地,在这种情况下,系统比较容易到达 研究的内容可以看成离散的一致性问题.因此,把2 -1的一致状态.而对C_1,由于初始时刻观点+1 个问题结合起来考虑,特别是利用控制理论中的反 和-1都是随机均匀地分布在网络的节点上,当p0.5时,系统达到稳态时,系统平均观点接近 方面,观点动力学中聚类分离现象(polarization, +1.通过以上比较,可以看出,在无标度网络上,初 fragmentation),即不同观点的个体聚集到一起,也 始观点的分布情况能够影响观点的传播行为.尤其 可以借鉴一致性问题中的分群现象来研究 是初始时,相同观点占据度大的节点并且连接在一 值得一提的是,比一致性问题更悠久,在化学工 起,形成一个聚集类(cluster),是有利于此种观点在 程、非线性科学、物理学等领域中得到广泛而深入研 网络上传播的.进一步地,在上述结论的基础上,研 究的耦合振子同步问题,可以为观点动力学的研究, 究节点度的非线性作用对观点传播的影响.在上述 特别是个体观点之间存在非线性相互作用时,提供 模型的基础上,重新定义: 一定的研究思路505) 1w=k万o山 (3) 4群体决策中的一致性行为 式中:k、分别表示个体i和j的邻居数目节点i 4.1初始观点分布情况和节点度的非线性作用对 和j的度).在这里,由于C1中+1和-1随机均匀 观点传播的影响 地分布在网络上的节点上,在这种情况下比较难观 首先考察在无标度网络上,不同初始观点分布 察到节点度的非线性作用对同一观点的传播作用, 情况和节点度的非线性作用对二值观点传播的影 所以在这里只研究C2和C3的情况.可以想象, 响.一般地,在考察复杂网络上的观点动力学时,初 当初始的某种观点聚集到度比较大的节点上时, 始条件大都设定为+1和·1等比例随机地分布在 a>0是有利于这种观点在网络上传播的.如图5所 网络的顶点上.在这里,考察无标度网络上3种初始 示,可以发现,在C_2中,a越大越有利于观点+1 观点分布情况对观点动力学的影响:1)+1和-1随 的传播.相反地,如图6所示,在C3中,a越大越有 机分布(C_1);2)+1占据网络中度较大的节点 利于观点·1的传播.研究结果说明了在无标度网 (C2);3)-1占据网络中度较大的节点(C_3).初 络上不同的初始观点分布情况对观点的传播是有影 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
3. 2 一致性和同步问题 一致性问题是近年来国际控制界兴起的一个研 究热点问题. 从物理的角度考察这一问题可追溯到 1995 年发表在 Physical Review Letters 上的相变模 型 ,即 Vicsek 模型[95 ] . 一致性问题关注一群通过局 部作用(与最近邻居的信息交互) 的个体能否在某些 物理状态(速度、角度等) 上达到一致[48249 ] . 设个体相 互作用的拓扑关系图为 G = (V , E) ,其中 V = { 1 , 2 , …, N} , E = { ( i , j) ∈V ×V : aij ≠0} , A = { aij } 为图 G的邻接矩阵. 个体 i 的邻居集合为 N i , 且 Ni = { j ∈V : aij ≠0} . 个体 i 的状态 x i ( t) 在平均一致性协 议(average2consensus) 下的动态方程为 x . ( t) = j ∑∈N i aij ( x j ( t) - xi ( t) ) . 也可写成向量方程 : x . = - L x ,其中 x = ( x1 , x2 , …, x N ) ,L 为图 G 的拉氏矩阵(Laplacian matrix) . 当拓 扑关系图是连通图时 ,系统中的个体状态渐近收敛 到所有个体初态的平均值. 这个线性耦合模型与观 点动力学中的有界自信模型很相似 ,关注的角度都 是系统能否达到一致. 本质上来说 ,有界自信模型所 研究的内容可以看成离散的一致性问题. 因此 ,把 2 个问题结合起来考虑 ,特别是利用控制理论中的反 馈原理 ,为观点动力学设计可能的一致性协议 ,研究 实现到达一致性的数学条件是十分有意义的. 另一 方面 ,观点动力学中聚类分离现象 (polarization , fragmentation) ,即不同观点的个体聚集到一起 ,也 可以借鉴一致性问题中的分群现象来研究. 值得一提的是 ,比一致性问题更悠久 ,在化学工 程、非线性科学、物理学等领域中得到广泛而深入研 究的耦合振子同步问题 ,可以为观点动力学的研究 , 特别是个体观点之间存在非线性相互作用时 ,提供 一定的研究思路[ 50253 ] . 4 群体决策中的一致性行为 4. 1 初始观点分布情况和节点度的非线性作用对 观点传播的影响 首先考察在无标度网络上 ,不同初始观点分布 情况和节点度的非线性作用对二值观点传播的影 响. 一般地 ,在考察复杂网络上的观点动力学时 ,初 始条件大都设定为 + 1 和 - 1 等比例随机地分布在 网络的顶点上. 在这里 ,考察无标度网络上 3 种初始 观点分布情况对观点动力学的影响 :1) + 1 和 - 1 随 机分布 (C_ 1) ; 2) + 1 占据网络中度较大的节点 (C_2) ;3) - 1 占据网络中度较大的节点 (C_3) . 初 始时刻 + 1 的比例为 p . 采用 BA 无标度网络 ,取节 点数 N = 1 000 ,平均度 k = 4 ,然后设定其观点动力 学演化规则. 基于 Ising 模型及文献[70 ] ,首先定义 Ii ( t) = ∑ j σj ( t) , 个体 i 在下一时刻采取 + 1 的概率为 pi ( t) ,采取 - 1的概率为 1 - pi ( t) ,其中 pi ( t) = 1 1 + e - 2 I i ( t) . 这里所有个体的状态采用同步更新规则 ,用系统平 均观点来衡量观点传播的情况. 所有的数据点对应 于 100 次运行结果的平均值. 研究了在这 3 种初始观点分布情况下 ,系统达 到稳态时系统平均观点对 p 的变化情况 ,如图 4 所 示. 可以看出 ,对 C_2 ,即初始时 + 1 占据度较大的 节点 ,在初始比例 p 比较小的时候 ,能够使系统达 到全是 + 1 的一致状态 , 而对 C_3 ,即初始时 - 1 占 据度较大的节点 ,当系统能够达到 + 1 的一致状态 时 ,初始比例 p 比其他 2 种分布情况的初始比例要 高一些. 相应地 ,在这种情况下 ,系统比较容易到达 - 1 的一致状态. 而对 C_1 ,由于初始时刻观点 + 1 和 - 1都是随机均匀地分布在网络的节点上 ,当 p 0. 5 时 ,系统达到稳态时 ,系统平均观点接近 + 1. 通过以上比较 ,可以看出 ,在无标度网络上 ,初 始观点的分布情况能够影响观点的传播行为. 尤其 是初始时 ,相同观点占据度大的节点并且连接在一 起 ,形成一个聚集类(cluster) ,是有利于此种观点在 网络上传播的. 进一步地 ,在上述结论的基础上 ,研 究节点度的非线性作用对观点传播的影响. 在上述 模型的基础上 ,重新定义 : Ii ( t) = ki ∑ j k ασj j ( t) ∑ j k α j . (3) 式中 : ki 、kj 分别表示个体 i 和 j 的邻居数目(节点 i 和 j 的度) . 在这里 ,由于 C_1 中 + 1 和 - 1 随机均匀 地分布在网络上的节点上 ,在这种情况下比较难观 察到节点度的非线性作用对同一观点的传播作用 , 所以在这里只研究 C_2 和 C_3 的情况. 可以想象 , 当初始的某种观点聚集到度比较大的节点上时 , α> 0是有利于这种观点在网络上传播的. 如图 5 所 示 ,可以发现 ,在 C_2 中 ,α越大越有利于观点 + 1 的传播. 相反地 ,如图 6 所示 ,在 C_3 中 ,α越大越有 利于观点 - 1 的传播. 研究结果说明了在无标度网 络上不同的初始观点分布情况对观点的传播是有影 ·100 · 智 能 系 统 学 报 第 3 卷

第2期 王龙,等:复杂网络上的群体决策 ·101- 响的,另外在初始观点分布的情况下考虑节点度的 对自己当前观点持不肯定态度.假设这2种个体随 非线性作用,可以看到它对观点传播有比较明显的 机均匀地分布在网络的节点上,并且其比例分别为 作用 f和1·∫(在演化过程中,个体的属性不改变).初 始时刻观点+1和·1等比例随机地分布在均匀随 1.01 机网络上(网络节点N=1000,平均度k=4).在共 0.5 同演化过程中,个体A以概率p断开与自己不同观 -3 点的一个邻居的连接,然后从自己邻居的邻居中选 择一个和自己观点相同的个体连接上(保证网络中 -0.5 边的数目不变),否则以1·p的概率不断开连接 而是采取邻居的观点来更新自己的状态:个体B则 0.20.40.60.81.012 总是采取邻居的观点来更新自己的状态.在这里采 图4对应于不同初始观点分布,系统平均观点 用异步更新的规则,仿真结果对应于100次实现取 对参数p的变化情况 平均,即10次初始网络拓扑实现对应于10次不同 Fig.4 The mean opinion as a function of for 的初始条件分布.有趣的是,可以发现当系统中这2 different initial distributions for +1 and-1 种属性的个体都存在,且比例相差不多时,系统达到 1.2r 稳态时网络拓扑会表现出异质网络的特征,即网络 0.8 的度分布具有幂律的性质,如图7所示.而在这个演 0.4 化过程中,网络会演化为由相互不连接的社团结构 (社团内部个体的观点相同)组成,并且群体中大部 ◆a=0 a= 分个体主要分布在2个大的社团内部.如图8所示, -0.4 当∫比较小时,群体中所有个体的观点最终能够达 -0.8 到一致,并且都分布在一个社团里面:而当f比较 120 0.2 0.4p0.6 0.81.01.2 大时,群体中所有个体的观点最终不能达到一致,但 图5在C2下,对应于不同参数a,系统平均观点 主要分布在两个大的社团(社团之间不连接)里面 对参数p的变化情况 而且社团之间的个体观点不一致5-).这些结果在 Fig.5 The mean opinion as a function of p for different 一定程度上揭示了社会中观点传播的一些现象, values of a in the case of C 2 0.1 -p-0.6.f0.5 1.2[ 0.01 0.8 。 slope=-2.81 0.4 是1E3 1E-4 -0.4H 1E-5H -0.8 100 主丰丰本丰本 02 04p0.608102 图7当p=0.6和f=0.5时,系统达到稳态时 网络的度分布情况 图6在C3下,对应于不同参数α,系统平均观点 Fig.7 The degree-distribution of the network in 对参数P的变化情况 steady state with p=0.6 and f=0.5 Fig.6 The mean opinion as a function of p for different values of a in the case of C3 1.0 4.2观点和网络拓扑的共同演化 0.8 现实世界中群体内部的大部分个体都表现出不 均一性(inhomogeneity).在这里,主要考察群体属 0.6 -p0.6 =0.8 性的不均一性如何影响基于网络拓扑和观点传播的 0. 共同演化动力学行为.设定在群体中有2种属性的 0.20.40.60.81.0.2 个体,个体A对自己当前观点持肯定态度,个体B (a)不同p时,MN的值 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
响的 ,另外在初始观点分布的情况下考虑节点度的 非线性作用 ,可以看到它对观点传播有比较明显的 作用. 4. 2 观点和网络拓扑的共同演化 现实世界中群体内部的大部分个体都表现出不 均一性(inhomogeneity) . 在这里 ,主要考察群体属 性的不均一性如何影响基于网络拓扑和观点传播的 共同演化动力学行为. 设定在群体中有 2 种属性的 个体 ,个体 A 对自己当前观点持肯定态度 ,个体 B 对自己当前观点持不肯定态度. 假设这 2 种个体随 机均匀地分布在网络的节点上 ,并且其比例分别为 f 和 1 - f (在演化过程中 ,个体的属性不改变) . 初 始时刻观点 + 1 和 - 1 等比例随机地分布在均匀随 机网络上(网络节点 N = 1 000 ,平均度 k = 4) . 在共 同演化过程中 ,个体 A 以概率 p 断开与自己不同观 点的一个邻居的连接 ,然后从自己邻居的邻居中选 择一个和自己观点相同的个体连接上 (保证网络中 边的数目不变) ,否则以 1 - p 的概率不断开连接 , 而是采取邻居的观点来更新自己的状态;个体 B 则 总是采取邻居的观点来更新自己的状态. 在这里采 用异步更新的规则 ,仿真结果对应于 100 次实现取 平均 ,即 10 次初始网络拓扑实现对应于 10 次不同 的初始条件分布. 有趣的是 ,可以发现当系统中这 2 种属性的个体都存在 ,且比例相差不多时 ,系统达到 稳态时网络拓扑会表现出异质网络的特征 ,即网络 的度分布具有幂律的性质 ,如图 7 所示. 而在这个演 化过程中 ,网络会演化为由相互不连接的社团结构 (社团内部个体的观点相同) 组成 ,并且群体中大部 分个体主要分布在 2 个大的社团内部. 如图 8 所示 , 当 f 比较小时 ,群体中所有个体的观点最终能够达 到一致 ,并且都分布在一个社团里面;而当 f 比较 大时 ,群体中所有个体的观点最终不能达到一致 ,但 主要分布在两个大的社团 (社团之间不连接) 里面 , 而且社团之间的个体观点不一致[85287 ] . 这些结果在 一定程度上揭示了社会中观点传播的一些现象. 第 2 期 王 龙 ,等 :复杂网络上的群体决策 ·101 ·

·102· 智能系统学报 第3卷 自己观点相同的邻居的邻居,最终的观点数目将会 05 减少.这些结果表明,观点更新和调整邻居的共同演 0.4 03 -p0.4 化是维持观点多样性的一种可能的机制.本文研究 。-p0.6 02 -P0.8 的结果对于保护人类独有的一些文化、语言和宗教 01 具有启示意义 4.3加权环上命名游戏中的一致性现象 0.20.40.60.81.01.2 命名游戏为研究词语的形成提供了有效的平 (b)不同p时,N的值 台.命名游戏是一个二人博弈.二人对同一物体进行 图8对应于不同的p时,图(a)中的N1/N和图(b)中的 命名,双方对命名物体有各自的词汇库.博弈时, N2/N对参数∫的变化情况 个为言者(speaker),另一个为听者(hearer),每次言 Fig.8 The ratios N/N (a).N2/N (b)as a function 者从自己的词汇库中按一定规则选择一个词告知听 of f for different values of p 者,听者作出相应判断并更新自己的词汇库.命名游 戏就是在这样的框架下来研究词语形成的机制.在 1.0 这里,建立了比较符合实际的命名游戏模型,并考察 0.8 了该模型在加权环上的演化情况.设每个个体对待 0. 命名物体都有相同的2个词汇,且对这2个词汇都 有一定的确定性(用这种确定性来表示个体的状 0.4 31 态).具体地,用x=(xa,x2来表示个体i的状态 02 式中:xa,x2分别表示个体i对词汇1和2的确定 性程度.初始时刻,n个个体分布在一个加权环上, 0.2 0.40.60.8 10 并且有一定的初始状态.在演化过程中,当1是听 D 者,j是言者时,i与j博弈一次:j此时保持状态不 图9观点效目在参收空回<p,5,上的变化情况 变)会选择自己确定性程度较大的词告之i使之状 Fig 9 The final nutr of opinions in the parameter space ( 态发生改变,同时个体1也会部分保留自己之前的 在图9中,参数取值为N=1000,k=10,G= 状态,因此个体i之后的状态为 50.为了刻画人类社会中多种观点并存的现象,基于 (x()=x(+(1-)eargmaxf xn(1)x(0. 偏好多数(majority-preference,MP)与回避少数 式中:e=1,0),a=0,1),而u∈0,11表示个体 (minority-avoidance,MA)2条原则,提出了动态演 对当前状态的自信程度(保留程度),且当max{x, 化网络上的观点动力学模型.初始时刻,每个个体随 2,xa=x,有argmax{x1,x2,xm/=i.由于 机地持有G种观点中的一个,并且随机地分布在具 在博弈时,个体1会与所有的邻居分别博弈,而且其 有N个顶点,M条边的规则随机网络上.在每一时 对邻居的相信程度也不太一致,所以个体ⅰ下一时 间步长,随机选取一个个体,按照MP和MA规则 刻的最终状态是所有邻居对其博弈作用的加权之 进行观点更新或调整邻居」 和可以表示为 I)MP:以p的概率进行观点更新.个体i接受 x:(t+1)=∑wn$(x() 其邻居中多数个体(数日最多)所持的观点; iENT 2)MA:以1-p的概率进行邻居调整.个体 式中:N()表示个体i的所有邻居,参数wn(网络上 断开一条与持有个体数目最少观点的邻居的边,并 节点j对节点1的连接权值)表示个体1对其邻居j 以中的概率随机重连到与其持有相同观点的邻居的 的相信程度,可以用来表示个体j对个体i状态的 邻居,或以1·中的概率随机选取除最近邻居之外的 影响程度.在本文的模型中,当1=0时,i的状态变 个体连上.重复以上步骤,直到每个个体的观点都与 为eargmax{x(t),x2g},表示个体i完全相信j,或i 其邻居中最多数观点一致.称此状态为“一致性”状 没有自信:而当=1时,i的状态不发生变化,表示 态.相关的仿真结果见图9.可以发现随着p值的增 个体1完全自信,此时演化不能进行.因此只研究 加,系统中存在一个从多数观点并存到单一观点状 u∈0,11的情形,并且系统采用同步更新规则.可 态的相变.另外,参数中也影响着观点多样性,尤其 以证明,当初始时刻所有个体都对同一个词有更高 是在相变点附近.也就是说,若个体倾向于重连到与 的确定性且u∈0,1时,则不论个体对其2个邻居 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
在图 9 中 ,参数取值为 N = 1 000 , k = 10 , G = 50. 为了刻画人类社会中多种观点并存的现象 ,基于 偏好多数 ( majority2preference , MP) 与回避少数 (minority2avoidance ,MA) 2 条原则 ,提出了动态演 化网络上的观点动力学模型. 初始时刻 ,每个个体随 机地持有 G种观点中的一个 ,并且随机地分布在具 有 N 个顶点 , M 条边的规则随机网络上. 在每一时 间步长 ,随机选取一个个体 ,按照 MP 和 MA 规则 进行观点更新或调整邻居. 1) MP:以 p 的概率进行观点更新. 个体 i 接受 其邻居中多数个体(数目最多) 所持的观点 ; 2) MA :以 1 - p 的概率进行邻居调整. 个体 i 断开一条与持有个体数目最少观点的邻居的边 ,并 以 <的概率随机重连到与其持有相同观点的邻居的 邻居 ,或以 1 - <的概率随机选取除最近邻居之外的 个体连上. 重复以上步骤 ,直到每个个体的观点都与 其邻居中最多数观点一致. 称此状态为“一致性”状 态. 相关的仿真结果见图 9. 可以发现随着 p 值的增 加 ,系统中存在一个从多数观点并存到单一观点状 态的相变. 另外 ,参数 <也影响着观点多样性 ,尤其 是在相变点附近. 也就是说 ,若个体倾向于重连到与 自己观点相同的邻居的邻居 ,最终的观点数目将会 减少. 这些结果表明 ,观点更新和调整邻居的共同演 化是维持观点多样性的一种可能的机制. 本文研究 的结果对于保护人类独有的一些文化、语言和宗教 具有启示意义. 4. 3 加权环上命名游戏中的一致性现象 命名游戏为研究词语的形成提供了有效的平 台. 命名游戏是一个二人博弈. 二人对同一物体进行 命名 ,双方对命名物体有各自的词汇库. 博弈时 ,一 个为言者(speaker) ,另一个为听者(hearer) ,每次言 者从自己的词汇库中按一定规则选择一个词告知听 者 ,听者作出相应判断并更新自己的词汇库. 命名游 戏就是在这样的框架下来研究词语形成的机制. 在 这里 ,建立了比较符合实际的命名游戏模型 ,并考察 了该模型在加权环上的演化情况. 设每个个体对待 命名物体都有相同的 2 个词汇 ,且对这 2 个词汇都 有一定的确定性 (用这种确定性来表示个体的状 态) . 具体地 ,用 xi = ( xi1 , xi2 ) 来表示个体 i 的状态. 式中 : xi1 , xi2分别表示个体 i 对词汇 1 和 2 的确定 性程度. 初始时刻 , n 个个体分布在一个加权环上 , 并且有一定的初始状态. 在演化过程中 , 当 i 是听 者 , j 是言者时 , i 与 j 博弈一次 : j (此时保持状态不 变) 会选择自己确定性程度较大的词告之 i 使之状 态发生改变 ,同时个体 i 也会部分保留自己之前的 状态 ,因此个体 i 之后的状态为 <j ( xi ( t) ) = μx i ( t) + (1 - μ) eargmax { x j1 ( t) , x j2 ( t) } . 式中 :e1 = (1 ,0) , e2 = (0 , 1) ,而 u ∈[0 , 1 ]表示个体 对当前状态的自信程度 (保留程度) ,且当 max{ x1 , x2 , …, x n } = xi ,有 argmax{ x1 , x2 , …, x n } = i . 由于 在博弈时 ,个体 i 会与所有的邻居分别博弈 ,而且其 对邻居的相信程度也不太一致 ,所以个体 i 下一时 刻的最终状态是所有邻居对其博弈作用的加权之 和 ,可以表示为 xi ( t + 1) = j ∈∑N ( i) wji <j ( xi ( t) ) . 式中 : N ( i) 表示个体 i 的所有邻居 ,参数 wji (网络上 节点 j 对节点 i 的连接权值) 表示个体 i 对其邻居 j 的相信程度 ,可以用来表示个体 j 对个体 i 状态的 影响程度. 在本文的模型中 ,当 u = 0 时 , i 的状态变 为 eargmax { x j1 ( t) , x j2 ( t) } ,表示个体 i 完全相信 j ,或 i 没有自信;而当 u = 1 时 , i 的状态不发生变化 ,表示 个体 i 完全自信 ,此时演化不能进行. 因此只研究 u ∈[0 ,1 ]的情形 ,并且系统采用同步更新规则. 可 以证明 ,当初始时刻所有个体都对同一个词有更高 的确定性且 u ∈[0 ,1 ]时 ,则不论个体对其 2 个邻居 ·102 · 智 能 系 统 学 报 第 3 卷

第2期 王龙,等:复杂网络上的群体决策 ·103· 的信任程度如何分配,当时间足够长时,所有个体都 矩阵,矩阵元素,表示社团i中的个体和社团j中 会对起初那个确定性较高的词有几乎100%的确定 的个体进行博弈的概率这种定义类似于文献[97] 性,即 中的接触概率).由社团结构的定义,可以得到矩阵 l,x:(0→eam4saeo1,1→oo 需要满足以下几点: 特别地,当群体中只有2个个体时,得到了一个 有趣的结论:不论2个博弈者初始状态如何,存在 1)4=1,0≤w≤1: 0w(i≠j》 信则达成一致是必然的.但此时为达到一致所需要 在这里,只考虑2种策略(A和B)的博弈演化 的时间可能会更长 情况,设博弈收益矩阵 为了叙述更一般的结论(n>2),先引入一个概 念:加权环的关键对.如果w.+1>w+2,且w+1.> [:9 w.1.,则称(i,i+1)是加权环的一个关键对.可以 式中:参数a、c分别表示与策略A博弈时,A、B的 看出,关键对之间有较强的互相学习的倾向.按照关 收益:参数b、d分别表示与策略B博弈时,A、B的 键对的个数可以将加权环的全体做等价分类,记B 收益.设x,表示第i个社团中使用A策略个体的比 为没有关键对的加权环的全体,A,为只有1个关键 例,表示使用B策略个体的比例,则该系统的状 对的加权环的全体,A2为有2个或2个以上关键对 态可以用向量(x1,2,x来表示,且第i个社团 的加权环的全体 中的A策略和B策略的收益分别为 当加权环中W∈A1,并记(i,i+1)为惟一的关 键对,记a=,里a,引x·a|,6八一 ,mi,利xa·}j=ami1xa~xal},6= f=cwx+d∑gy |w1-w+1l,若a6>b,则存在0u时,x:()e,x+1()e, 相应地,带有社团结构的复制动力学方程可以写成 1→∞,进而可以证明,x1()e,t→c∞ x:=x:(f-f), 对于只有一个关键对的加权环,只要关键对能 y.=y(fa-f) 在有限时间内对同一个词有更大的确定性,则系统 式中:f,=xf:+yfm.注意到x,+y=1,因此可 最终会达到一致.进一步可以发现,如果W∈A2,且 以简化为 任意一组关键对都分别满足相应a6>b的条件, 则群体会有局部一致现象出现,即每个个体都会在 dx=x(1x)1(a-b-c+d]wx+ dt 有限时间内只对一个词汇有更强的确定性,并且局 (b-d. (4) 部相邻个体会对同一词汇有更强的确定性.这些结 在方程(4)所描述的带有社团结构的系统中,如 果也许能在一定程度上揭示社会生活中方言形成的 果所有社团的状态最终都趋于一个相同的值,那么 内在机理, 就说该系统达到了一致 4.4社团网络上策略演化的一致性 当n=2时,即该系统只包含2个社团,可以发 基于3.2中的内容,在这里通过复制动力学来 现如果收益矩阵中的参数满足3个条件1)a>c且 研究群体策略演化的一致性问题.实际上,群体策略 b>d;2)ad;3)ac且 上,尤其是在具有社团结构的网络上却考虑得比较 b<d时,系统存在不惟一的吸收态,它们的吸引盆 少在这里,研究了具有社团结构的网络上策略演化 由方程(4)的内部平衡点(x`,x)来决定,其中 的一致性问题,重点研究了网络中各个社团状态达 x`=(b-d/(a-b-c+d,如果系统的初始状态 到一致的条件.所谓社团结构,就是内部连接概率大 位于吸收态0,0)和(1,1)的吸引盆中,那么此时系 于外部连接概率的一种空间构形.考虑在一个混合 统仍然可以达到一致:如果系统的初始状态落在吸 均匀的、无限的人口中,一共有n个大小基本相等的 收态0,)或者1.0)的吸引盆中,那么此时2个社 社团.定义矩阵W为网络中各社团之间的连接概率 团最终达到完全相反的2个状态(一个社团内部个 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
的信任程度如何分配 ,当时间足够长时 ,所有个体都 会对起初那个确定性较高的词有几乎 100 %的确定 性 ,即 Π1 , xi ( t) →eargmax{ x i1 (0) , x i2 (0) } , t → ∞. 特别地 ,当群体中只有 2 个个体时 ,得到了一个 有趣的结论 :不论 2 个博弈者初始状态如何 ,存在 0 2) ,先引入一个概 念 : 加权环的关键对. 如果 wi , i + 1 > wi + 2 , i且 w i + 1 , i > wi - 1 , i ,则称 ( i , i + 1) 是加权环的一个关键对. 可以 看出 ,关键对之间有较强的互相学习的倾向. 按照关 键对的个数可以将加权环的全体做等价分类 ,记 B 为没有关键对的加权环的全体 , A1 为只有 1 个关键 对的加权环的全体 , A2 为有 2 个或 2 个以上关键对 的加权环的全体. 当加权环中 W ∈A1 ,并记 ( i , i + 1) 为惟一的关 键对 , 记 a 3 = max s ∈{ i , i + 1} { | x x1 - x x2 | } , b 3 = min s ∈{ i , i + 1} {| xs1 - xs2 | } , j = argmin s ∈{ i , i + 1} { | xs1 - xs2 | } ,δ= | wj - 1 , j - wj + 1 , j | ,若 a 3δ> b 3 ,则存在 0 u 3 时 , xi ( t) →es , xi + 1 ( t) →es , t →∞ ,进而可以证明 , x1 ( t) →es , t → ∞. 对于只有一个关键对的加权环 ,只要关键对能 在有限时间内对同一个词有更大的确定性 ,则系统 最终会达到一致. 进一步可以发现 ,如果 W ∈A2 ,且 任意一组关键对都分别满足相应 a 3δ> b 3 的条件 , 则群体会有局部一致现象出现 ,即每个个体都会在 有限时间内只对一个词汇有更强的确定性 ,并且局 部相邻个体会对同一词汇有更强的确定性. 这些结 果也许能在一定程度上揭示社会生活中方言形成的 内在机理. 4. 4 社团网络上策略演化的一致性 基于 3. 2 中的内容 ,在这里通过复制动力学来 研究群体策略演化的一致性问题. 实际上 ,群体策略 演化的一致性问题在混合均匀的网络上已得到了比 较深入的研究[96 ] ,但是在具有其他拓扑结构的网络 上 ,尤其是在具有社团结构的网络上却考虑得比较 少. 在这里 ,研究了具有社团结构的网络上策略演化 的一致性问题 ,重点研究了网络中各个社团状态达 到一致的条件. 所谓社团结构 ,就是内部连接概率大 于外部连接概率的一种空间构形. 考虑在一个混合 均匀的、无限的人口中 ,一共有 n 个大小基本相等的 社团. 定义矩阵 W 为网络中各社团之间的连接概率 矩阵 ,矩阵元素 wij表示社团 i 中的个体和社团 j 中 的个体进行博弈的概率 (这种定义类似于文献[97 ] 中的接触概率) . 由社团结构的定义 ,可以得到矩阵 需要满足以下几点 : 1) ∑ n j =1 ωij = 1 ,0 ≤wij ≤1 ; 2) wij = wji ; 3) wii > wij ( i ≠j) . 在这里 ,只考虑 2 种策略( A 和 B ) 的博弈演化 情况 ,设博弈收益矩阵为 a b c d . 式中 :参数 a、c 分别表示与策略 A 博弈时 , A 、B 的 收益;参数 b、d 分别表示与策略 B 博弈时 , A 、B 的 收益. 设 xi 表示第 i 个社团中使用 A 策略个体的比 例 , yi 表示使用 B 策略个体的比例 ,则该系统的状 态可以用向量( x1 , x2 , …, x n ) 来表示 ,且第 i 个社团 中的 A 策略和 B 策略的收益分别为 f Ai = a ∑ n j = 1 wij x j + b ∑ n j =1 wij y j , f Bi = c ∑ n j =1 wij x j + d ∑ n j =1 wij y j . 相应地 ,带有社团结构的复制动力学方程可以写成 x . i = xi ( f Ai - f i) , y . i = yi ( f Bi - f i) . 式中 : f i = xi f Ai + yi f Bi . 注意到 xi + yi = 1 ,因此可 以简化为 d xi dt = xi (1 - xi) [ ( a - b - c + d) ] ∑ n j = 1 wij x j + ( b - d) . (4) 在方程(4) 所描述的带有社团结构的系统中 ,如 果所有社团的状态最终都趋于一个相同的值 ,那么 就说该系统达到了一致. 当 n = 2 时 ,即该系统只包含 2 个社团 ,可以发 现如果收益矩阵中的参数满足 3 个条件 1) a > c 且 b > d ;2) a d; 3) a c 且 b < d 时 ,系统存在不惟一的吸收态 ,它们的吸引盆 由方程 ( 4) 的内部平衡点 ( x 3 , x 3 ) 来决定 , 其中 x 3 = ( b - d) / ( a - b - c + d) . 如果系统的初始状态 位于吸收态(0 ,0) 和(1 ,1) 的吸引盆中 ,那么此时系 统仍然可以达到一致;如果系统的初始状态落在吸 收态(0 ,1) 或者 (1 , 0) 的吸引盆中 ,那么此时 2 个社 团最终达到完全相反的 2 个状态 (一个社团内部个 第 2 期 王 龙 ,等 :复杂网络上的群体决策 ·103 ·
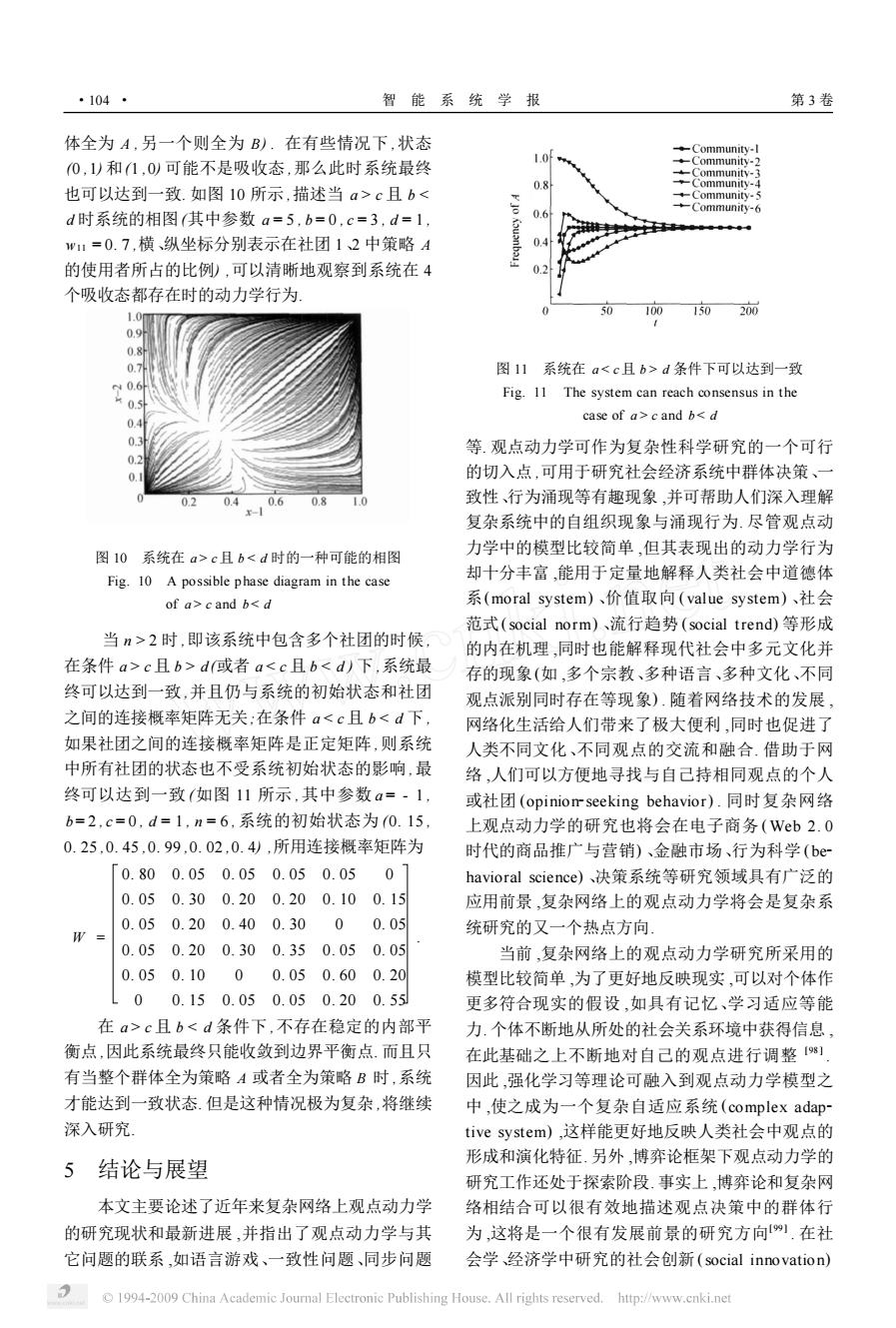
·104· 智能系统学报 第3卷 体全为A,另一个则全为B).在有些情况下,状态 ◆-ommunitv. 0,)和1,0)可能不是吸收态,那么此时系统最终 1.0 -Community-2 Community-3 -Community-4 也可以达到一致.如图10所示,描述当a>c且bd条件下可以达到一致 40. Fig.11 The system can reach consensus in the case of a>c and bc且bcand b2时,即该系统中包含多个社团的时候, 的内在机理,同时也能解释现代社会中多元文化并 在条件a>c且b>d或者ac且b<d条件下,不存在稳定的内部平 力.个体不断地从所处的社会关系环境中获得信息 衡点,因此系统最终只能收敛到边界平衡点.而且只 在此基础之上不断地对自己的观点进行调整劉 有当整个群体全为策略A或者全为策略B时,系统 因此,强化学习等理论可融入到观点动力学模型之 才能达到一致状态.但是这种情况极为复杂,将继续 中,使之成为一个复杂自适应系统(complex adap- 深入研究 tive system),这样能更好地反映人类社会中观点的 形成和演化特征.另外,博弈论框架下观点动力学的 5结论与展望 研究工作还处于探索阶段.事实上,博弈论和复杂网 本文主要论述了近年来复杂网络上观点动力学 络相结合可以很有效地描述观点决策中的群体行 的研究现状和最新进展,并指出了观点动力学与其 为,这将是一个很有发展前景的研究方向).在社 它问题的联系,如语言游戏、一致性问题、同步问题 会学、经济学中研究的社会创新(social innovation) 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
体全为 A ,另一个则全为 B) . 在有些情况下 ,状态 (0 ,1) 和(1 ,0) 可能不是吸收态 ,那么此时系统最终 也可以达到一致. 如图 10 所示 ,描述当 a > c 且 b c 且 b c and b 2 时 ,即该系统中包含多个社团的时候 , 在条件 a > c 且 b > d (或者 a c 且 b d 条件下可以达到一致 Fig. 11 The system can reach consensus in the case of a > c and b < d 等. 观点动力学可作为复杂性科学研究的一个可行 的切入点 ,可用于研究社会经济系统中群体决策、一 致性、行为涌现等有趣现象 ,并可帮助人们深入理解 复杂系统中的自组织现象与涌现行为. 尽管观点动 力学中的模型比较简单 ,但其表现出的动力学行为 却十分丰富 ,能用于定量地解释人类社会中道德体 系(moral system) 、价值取向 ( value system) 、社会 范式(social norm) 、流行趋势 (social trend) 等形成 的内在机理 ,同时也能解释现代社会中多元文化并 存的现象(如 ,多个宗教、多种语言、多种文化、不同 观点派别同时存在等现象) . 随着网络技术的发展 , 网络化生活给人们带来了极大便利 ,同时也促进了 人类不同文化、不同观点的交流和融合. 借助于网 络 ,人们可以方便地寻找与自己持相同观点的个人 或社团 (opinion2seeking behavior) . 同时复杂网络 上观点动力学的研究也将会在电子商务 ( Web 2. 0 时代的商品推广与营销) 、金融市场、行为科学 ( be2 havioral science) 、决策系统等研究领域具有广泛的 应用前景 ,复杂网络上的观点动力学将会是复杂系 统研究的又一个热点方向. 当前 ,复杂网络上的观点动力学研究所采用的 模型比较简单 ,为了更好地反映现实 ,可以对个体作 更多符合现实的假设 ,如具有记忆、学习适应等能 力. 个体不断地从所处的社会关系环境中获得信息 , 在此基础之上不断地对自己的观点进行调整 [98 ] . 因此 ,强化学习等理论可融入到观点动力学模型之 中 ,使之成为一个复杂自适应系统 (complex adap2 tive system) ,这样能更好地反映人类社会中观点的 形成和演化特征. 另外 ,博弈论框架下观点动力学的 研究工作还处于探索阶段. 事实上 ,博弈论和复杂网 络相结合可以很有效地描述观点决策中的群体行 为 ,这将是一个很有发展前景的研究方向[99 ] . 在社 会学、经济学中研究的社会创新 (social innovation) ·104 · 智 能 系 统 学 报 第 3 卷