
第3卷第1期 智能系统学报 Vol.3 Ng 1 2008年2月 CAAI Transactions on Intelligent Systems Fcb.2008 π型隶属函数的典型模糊控制器的解析结构 张香燕,张乃尧 (清华大学自动化系,北京100084) 摘要:研究了一种新型的典型模糊控制器,它的输入隶属函数采用π型样条函数,具有二阶逼近特性,而一般典型 模糊控制器采用的三角形隶属函数只具有一阶逼近特性,因此研究这种新型的模糊控制器具有重要的意义.文章首 先给出了该类典型模糊控制器的定义,推导了它的解析表达式,证明了该类典型模糊控制器可以等效为一个全局的 二维继电器和一个局部的非线性PD控制器之和.在此基础上,给出了其极限特性和非线性特性 关键词:典型模糊控制器;型隶属函数;解析结构 中图分类号:TP273文献标识码:A文章编号:1673-4785(2008)01-0031-07 Analytical structure of a classic fuzzy controller with membership functions ZHAN G Xiangyan,ZHAN G Nai-yao (Department of Automation,Tsinghua University,Beijing 100084,China) Abstract:A new classic fuzzy controller with membership functions is proposed.The function,a spline function with two-order approximation,has been widely used in approximation theory.Since fuzzy con- trollers with triangular membership functions are only universal approximators with only first-order ap- proximation accuracy,it is very valuable to study the property of fuzzy controllers with membership func- tions.In this paper,we define the new fuzzy controller,deduce its output expression and prove that the controller is equivalent to an integration of a two-dimensional multilevel relay and a local nonlinear PD con- troller.On this basis,we finally analyze the limiting and nonlinear properties of the controller. Key words :classic fuzzy controller;membership function;analytical structure 自从1972年Zadeh教授提出模糊控制的基本 非线性PI控制器,之后很多学者对此进行了深入扩 原理以来,由于模糊控制器的不确定性以及结构的 展研究4】,也得到了一类TS模糊控制器的解析 复杂性,使得它的研究一般采用黑箱方法,这与经典结构.模糊控制器与线性PWPD控制器的解析结构 控制理论中广泛采用的基于解析分析的技术方法大关系,说明了它们之间的增益关系,为模糊控制系统 有不同,不能对系统特性和性能进行有效的数学分的稳定性设计提供了方案2).然而,在目前已有的 析.为了对模糊控制器的结构进行深入的研究,从 研究成果中,为了简化模糊控制器的解析表达式推 1989年开始,应浩教授等开创了采用解析分析方法 导,隶属函数一般采用三角形隶属函数.但由于三角 研究模糊控制器的结构这一新的研究方向,并取得 形函数自身的一些缺点,当其用于函数逼近时有时 了诸多重要的研究成果),这也引起了国内外学者 不能达到预期的良好效果,.李洪兴教授指出模糊 的关注).Ying)最先证明了2个线性输入模糊 控制器的本质是一类插值器],因此模糊控制器的 集,4个模糊规则,Zadeh模糊逻辑AND和OR操 性能与各个变量的隶属函数形状有着密切的关系: 作的重心解模糊器的最简单Mamdani模糊控制是 Koskolis1也同样指出模糊规则的输入变量的隶属函 收稿日期:2007-0622. 数形状直接影响着模糊系统对于连续函数的逼近能 基金项目:国家自然科学基金资助项目(60474024);教育部博士点专 项基金资助项目(20040003106). 力.因此寻求一类特殊的能够替代三角形隶属函数 通讯作者:张香燕.Eail:zhangxiangyan0(3@mals.tsirghua.edu.cn 的函数具有重要的意义.在纯数学逼近理论,神经网 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
第 3 卷第 1 期 智 能 系 统 学 报 Vol. 3 №. 1 2008 年 2 月 CAA I Transactions on Intelligent Systems Feb. 2008 π型隶属函数的典型模糊控制器的解析结构 张香燕 ,张乃尧 (清华大学 自动化系 ,北京 100084) 摘 要 :研究了一种新型的典型模糊控制器 ,它的输入隶属函数采用π型样条函数 ,具有二阶逼近特性 ,而一般典型 模糊控制器采用的三角形隶属函数只具有一阶逼近特性 ,因此研究这种新型的模糊控制器具有重要的意义. 文章首 先给出了该类典型模糊控制器的定义 ,推导了它的解析表达式 ,证明了该类典型模糊控制器可以等效为一个全局的 二维继电器和一个局部的非线性 PD 控制器之和. 在此基础上 ,给出了其极限特性和非线性特性. 关键词 :典型模糊控制器 ;型隶属函数 ;解析结构 中图分类号 : TP273 文献标识码 :A 文章编号 :167324785 (2008) 0120031207 Analytical structure of a classic fuzzy controller with πmembership functions ZHAN G Xiang2yan , ZHAN G Nai2yao (Department of Automation , Tsinghua University , Beijing 100084 , China) Abstract :A new classic f uzzy controller withπmembership f unctions is proposed. Theπf unction , a spline f unction wit h two2order approximation , has been widely used in approximation t heory. Since f uzzy con2 trollers with triangular membership f unctions are only universal approximators wit h only first2order ap2 proximation accuracy , it is very valuable to st udy t he property of f uzzy controllers wit h membership f unc2 tions. In this paper , we define t he new f uzzy controller , deduce its outp ut expression and prove that t he controller is equivalent to an integration of a two2dimensional multilevel relay and a local nonlinear PD con2 troller. On t his basis , we finally analyze t he limiting and nonlinear properties of t he controller. Keywords :classic f uzzy controller ; πmembership f unction ; analytical struct ure 收稿日期 :2007206222. 基金项目 :国家自然科学基金资助项目(60474024) ;教育部博士点专 项基金资助项目(20040003106) . 通讯作者 :张香燕. E2mail :zhangxiangyan03 @mails. tsirghua. edu. cn. 自从 1972 年 Zadeh 教授提出模糊控制的基本 原理以来 ,由于模糊控制器的不确定性以及结构的 复杂性 ,使得它的研究一般采用黑箱方法 ,这与经典 控制理论中广泛采用的基于解析分析的技术方法大 有不同 ,不能对系统特性和性能进行有效的数学分 析. 为了对模糊控制器的结构进行深入的研究 ,从 1989 年开始 ,应浩教授等开创了采用解析分析方法 研究模糊控制器的结构这一新的研究方向 ,并取得 了诸多重要的研究成果[226 ] ,这也引起了国内外学者 的关注[7213 ] . Ying [ 3 ]最先证明了 2 个线性输入模糊 集 ,4 个模糊规则 ,Zadeh 模糊逻辑 AND 和 OR 操 作的重心解模糊器的最简单 Mamdani 模糊控制是 非线性 PI 控制器 ,之后很多学者对此进行了深入扩 展研究[ 4211 ] ,也得到了一类 T2S 模糊控制器的解析 结构. 模糊控制器与线性 PI/ PD 控制器的解析结构 关系 ,说明了它们之间的增益关系 ,为模糊控制系统 的稳定性设计提供了方案[12213 ] . 然而 ,在目前已有的 研究成果中 ,为了简化模糊控制器的解析表达式推 导 ,隶属函数一般采用三角形隶属函数. 但由于三角 形函数自身的一些缺点 ,当其用于函数逼近时有时 不能达到预期的良好效果[14 ] . 李洪兴教授指出模糊 控制器的本质是一类插值器[ 15 ] ,因此模糊控制器的 性能与各个变量的隶属函数形状有着密切的关系. Kosko [15 ]也同样指出模糊规则的输入变量的隶属函 数形状直接影响着模糊系统对于连续函数的逼近能 力. 因此寻求一类特殊的能够替代三角形隶属函数 的函数具有重要的意义. 在纯数学逼近理论 ,神经网 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
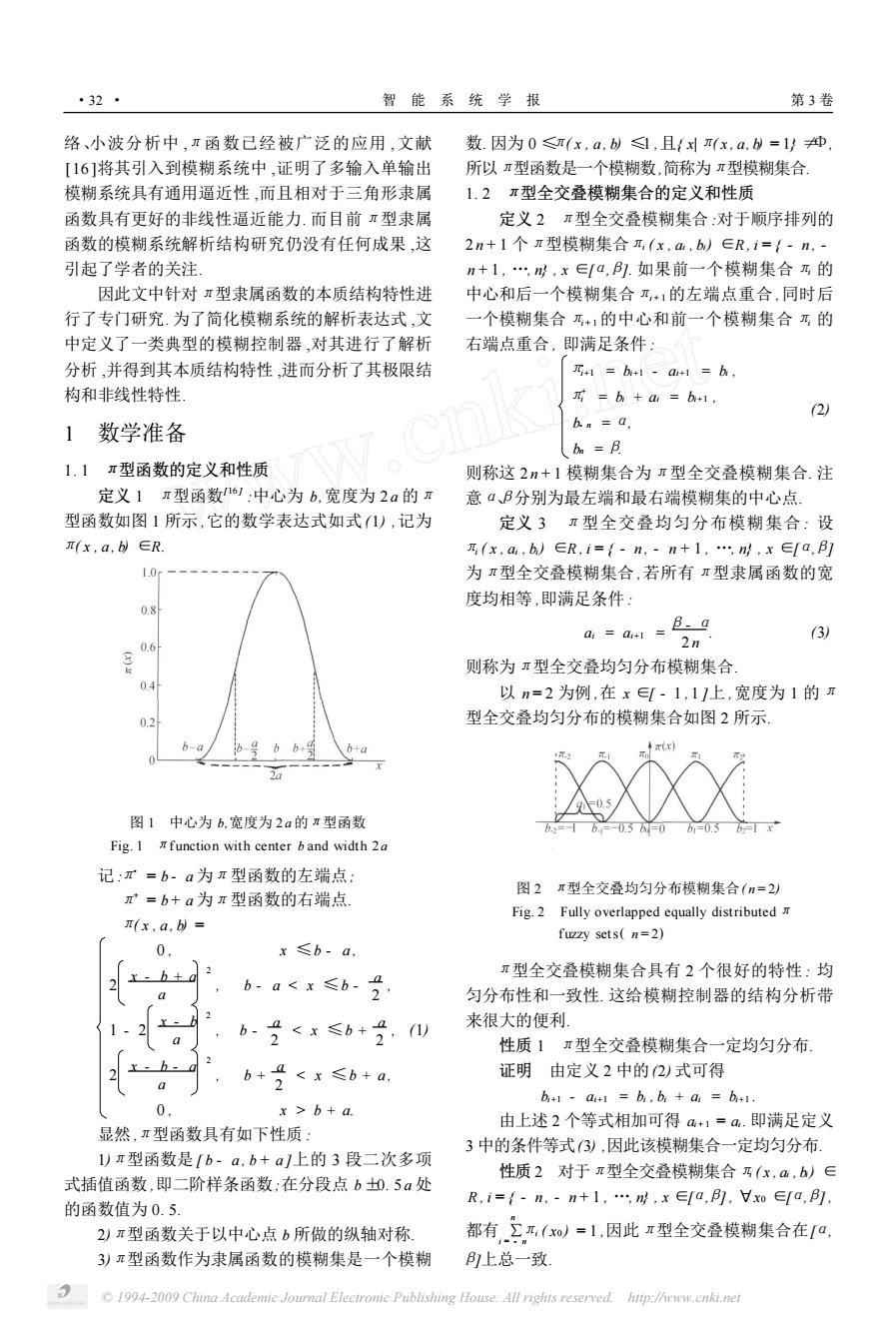
·32 智能系统学报 第3卷 络、小波分析中,Ⅱ函数已经被广泛的应用,文献 数.因为0≤π(x,a,bl,且{刘(x,a,b=1}绅 [16]将其引入到模糊系统中,证明了多输入单输出 所以π型函数是一个模糊数,简称为π型模糊集合 模糊系统具有通用逼近性,而且相对于三角形隶属 1.2π型全交叠模糊集合的定义和性质 函数具有更好的非线性逼近能力.而目前π型隶属 定义2π型全交叠模糊集合:对于顺序排列的 函数的模糊系统解析结构研究仍没有任何成果,这 2n+1个π型模糊集合元(x,a,b)∈R,i={-n,- 引起了学者的关注 n+1,,m,x∈[a,.如果前一个模糊集合乃的 因此文中针对π型隶属函数的本质结构特性进 中心和后一个模糊集合+1的左端点重合,同时后 行了专门研究.为了简化模糊系统的解析表达式,文 一个模糊集合乃+1的中心和前一个模糊集合乃的 中定义了一类典型的模糊控制器,对其进行了解析 右端点重合,即满足条件 分析,并得到其本质结构特性,进而分析了其极限结 r+1=b+l-a+1=b, 构和非线性特性 =b+a b1, 2) 1数学准备 b.n a ba=月 1.1π型函数的定义和性质 则称这2n+1模糊集合为π型全交叠模糊集合.注 定义1π型函数61:中心为b,宽度为2a的π 意aB分别为最左端和最右端模糊集的中心点. 型函数如图1所示,它的数学表达式如式1),记为 定义3π型全交叠均匀分布模糊集合:设 r(x,a,b∈R 可(x,a,b)∈R,i=f-n,-n+1,n,x∈fa,] 1.0 为π型全交叠模糊集合,若所有π型隶属函数的宽 度均相等,即满足条件: 0.8 B.a a:=a+1= 3) 0.6 2n 则称为π型全交叠均匀分布模糊集合 0.4 以n=2为例,在x∈[-1,11上,宽度为1的π 0.2 型全交叠均匀分布的模糊集合如图2所示。 h+a 年元 2a 图1中心为b,宽度为2a的π型函数 03 Fig.I function with center b and width 2a 记:r=b-a为π型函数的左端点, π=b+a为π型函数的右端点 图2π型全交叠均匀分布模糊集合(n=2) Fig.2 Fully overlapped equally distributed (x,a,= fuzzy sets(n=2) 0 x≤b-a, π型全交叠模糊集合具有2个很好的特性:均 b-a<x≤b- 2 匀分布性和一致性.这给模糊控制器的结构分析带 a b-2 <x≤b+1 a 来很大的便利 21 1) 性质1π型全交叠模糊集合一定均匀分布. b+0 <x≤b+a 证明由定义2中的2)式可得 b+1-a+1=b,ba+a=b+1. 0 x b+a. 由上述2个等式相加可得a+1=a.即满足定义 显然,π型函数具有如下性质: 3中的条件等式3),因此该模糊集合一定均匀分布. 1)π型函数是[b-a,b+a]上的3段二次多项 性质2对于π型全交叠模糊集合乃(x,a,b)∈ 式插值函数,即二阶样条函数:在分段点b0.5a处 R,i={-n,-n+1,,n,x∈Ia,1,Vxo∈a,] 的函数值为0.5. 2)π型函数关于以中心点b所做的纵轴对称 都有,工严,(o)=1,因此r型全交叠模糊集合在a, 3)π型函数作为隶属函数的模糊集是一个模糊 上总一致 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
络、小波分析中 ,π函数已经被广泛的应用 ,文献 [16 ]将其引入到模糊系统中 ,证明了多输入单输出 模糊系统具有通用逼近性 ,而且相对于三角形隶属 函数具有更好的非线性逼近能力. 而目前π型隶属 函数的模糊系统解析结构研究仍没有任何成果 ,这 引起了学者的关注. 因此文中针对π型隶属函数的本质结构特性进 行了专门研究. 为了简化模糊系统的解析表达式 ,文 中定义了一类典型的模糊控制器 ,对其进行了解析 分析 ,并得到其本质结构特性 ,进而分析了其极限结 构和非线性特性. 1 数学准备 1. 1 π型函数的定义和性质 定义 1 π型函数[16 ] :中心为 b,宽度为 2 a 的π 型函数如图 1 所示 ,它的数学表达式如式 (1) ,记为 π( x , a , b) ∈R. 图 1 中心为 b,宽度为 2 a 的π型函数 Fig. 1 πfunction with center b and width 2 a 记 :π- = b - a 为π型函数的左端点; π+ = b + a 为π型函数的右端点. π( x , a , b) = 0 , x ≤b - a , 2 x - b + a a 2 , b - a b + a. (1) 显然 ,π型函数具有如下性质 : 1)π型函数是[ b - a , b + a ]上的 3 段二次多项 式插值函数 ,即二阶样条函数;在分段点 b±0. 5 a 处 的函数值为 0. 5. 2)π型函数关于以中心点 b 所做的纵轴对称. 3)π型函数作为隶属函数的模糊集是一个模糊 数. 因为 0 ≤π( x , a , b) ≤1 ,且{ x|π( x , a, b) = 1} ≠Φ, 所以π型函数是一个模糊数,简称为π型模糊集合. 1. 2 π型全交叠模糊集合的定义和性质 定义 2 π型全交叠模糊集合 :对于顺序排列的 2 n + 1 个π型模糊集合πi ( x , ai , bi) ∈R , i = { - n , - n + 1 , …, n} , x ∈[α,β]. 如果前一个模糊集合πi 的 中心和后一个模糊集合πi + 1 的左端点重合 ,同时后 一个模糊集合πi + 1 的中心和前一个模糊集合πi 的 右端点重合 , 即满足条件 : π- i+1 = bi+1 - ai+1 = bi , π+ i = bi + ai = bi+1 , b- n =α, bn =β. (2) 则称这 2 n + 1 模糊集合为π型全交叠模糊集合. 注 意α、β分别为最左端和最右端模糊集的中心点. 定义 3 π型全交叠均匀分布模糊集合 : 设 πi ( x , ai , bi) ∈R , i = { - n , - n + 1 , …, n} , x ∈[α,β] 为π型全交叠模糊集合 ,若所有π型隶属函数的宽 度均相等 ,即满足条件 : ai = ai+1 = β- α 2 n . (3) 则称为π型全交叠均匀分布模糊集合. 以 n = 2 为例 ,在 x ∈[ - 1 , 1 ]上 ,宽度为 1 的π 型全交叠均匀分布的模糊集合如图 2 所示. 图 2 π型全交叠均匀分布模糊集合( n = 2) Fig. 2 Fully overlapped equally distributedπ fuzzy sets( n = 2) π型全交叠模糊集合具有 2 个很好的特性 : 均 匀分布性和一致性. 这给模糊控制器的结构分析带 来很大的便利. 性质 1 π型全交叠模糊集合一定均匀分布. 证明 由定义 2 中的(2) 式可得 bi+1 - ai+1 = bi , bi + ai = bi+1 . 由上述 2 个等式相加可得 ai + 1 = ai . 即满足定义 3 中的条件等式(3) ,因此该模糊集合一定均匀分布. 性质 2 对于π型全交叠模糊集合πi ( x , ai , bi) ∈ R , i = { - n , - n + 1 , …, n} , x ∈[α,β] , Πx0 ∈[α,β] , 都有 ∑ n i = - n πi ( x0 ) = 1 ,因此π型全交叠模糊集合在[α, β]上总一致. ·32 · 智 能 系 统 学 报 第 3 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第1期 张香燕,等:π型隶属函数的典型模糊控制器的解析结构 ·33 证明因为0∈(a,],不妨设x0∈(b,b+1], e'=Ger, t∈(-n,-n+1,n-1],在此区间只有乃、r+1 r =Grrt, (4) 的值不为0,即亚,=0(i≠,且i≠+1).由π函数的 u=Guu'. 定义和性质,亚、乃+1在交叉点的函数值为亚(b+ 式中:e`,r`,u∈-1,1] 0.5a=乃+1(b+1-0.5+1)=0.5,因此[b,b+1] 设采用π型隶属函数的典型模糊控制器,其设 可分为2段[b,b+0.5am和[br+0.5a,b+i1.由于 计参数如下: π型函数的对称性,只需证明前一区间即可 1)输入和输出变量的模糊集及隶属函数. x0∈b,b,+0.5a1,由定义1可得 正规化的输入变量e`、r采用全交叠均匀分布 π,(xo)+π+1(x0)= 的π型隶属函数,如图4(a)所示.正规化的输出变 12- 量u采用均匀分布的单点隶属函数,如图4(b)所 示.设e°、r分别定义2n+1个模糊集合,其中n个 a a+1 由性质(1)可得a+1=a,b+1=+a,将其代 为正,n个为负,1个为零,分别为(p=-n,刊 入上式得 和厉(g=-n,…W,模糊集合的中心分别为= π(xo)+乃1(x0)= pn和b品=gn,宽度分别为2d和2d,相邻模糊集 中心之间的距离分别为a=d2=l/n输出u定义 1-2b2 4n+1个模糊集合,用U:(z=-2n,2W表示,U a: 所以,兀(xo)+元+1(xo)+ 1-1.i.t+1 可(x0)=1,即 的中心为8=2n相邻模糊子集中心之间的距离为 之元(xo)=1 s=2n 2 采用π型隶属函数的典型模糊控制 器定义 研究的典型模糊控制器为两输入一输出模糊系 统f:UCRΨCR,其中U=UXU2CR为输入 (a)全交叠均匀分布的π型输人隶属函数 空间,VCR为输出空间,模糊控制系统的结构如图 3所示 ↑4) 6 5, 模 被 G 控 控 对 .dw+13+2+6100102m-102r10m 象 器 (b)均匀分布的单点输出隶属函数 图4模糊控制器的输入输出隶属函数 Fig.4 The membership functions of the input 图3模糊控制系统的结构图 variables and the output variable for the Fig.3 The structure of the fuzzy control system defined fuzzy controller 2)模糊控制规则 其中,单输入单输出(SISO)被控对象的输入为 山,输出为y,参考输入为s,1为离散时间变量,T 这里采用线性控制规则,也就是输出模糊子集 的下标与输入模糊子集的下标成线性关系.这里输 为采样周期.设模糊控制器的2个输入分别为误差 出模糊子集的下标为输入模糊子集下标的和,即:= e和误差的差分r,输出为山,即 p+q. er =S:-yr, R If e'is and r'is.Then u'is U:. r=△e=e-e.1. 引入比例因子G、G,、G.使输入输出变量正规 (p=-n,nq=-n,…,n;z=-2n,…2 化,即 3)模糊推理方法 采用Sum-Product模糊推理方法 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
证明 因为 x0 ∈[α,β] ,不妨设 x0 ∈[ bt , bt + 1 ] , t ∈[ - n , - n + 1 , …, n - 1 ] ,在此区间只有πt 、πt + 1 的值不为 0 ,即πi = 0 ( i ≠t ,且 i ≠t + 1) . 由π函数的 定义和性质 ,πt 、πt + 1 在交叉点的函数值为πt ( bt + 0. 5 at) =πt + 1 ( bt + 1 - 0. 5 at + 1 ) = 0. 5 ,因此[ bt , bt + 1 ] 可分为 2 段[ bt , bt + 0. 5 at ]和[ bt + 0. 5 at , bt + 1 ]. 由于 π型函数的对称性 , 只需证明前一区间即可. Πx0 ∈[ bt , bt + 0. 5 at ] ,由定义 1 可得 πt ( x0 ) +πt+1 ( x0 ) = 1 - 2 x - bt at 2 + 2 x - bt+1 + at+1 at + 1 2 . 由性质 (1) 可得 at + 1 = at , bt + 1 = bt + at ,将其代 入上式得 πt ( x0 ) +πt+1 ( x0 ) = 1 - 2 x0 - bt at 2 + 2 x0 - bt - at + at at 2 = 1. 所以 ,πt ( x0 ) +πt + 1 ( x0 ) + ∑ N i = 1 , i ≠t , t + 1 πi ( x0 ) = 1 , 即 ∑ N i = 1 πi ( x0 ) = 1. 2 采用π型隶属函数的典型模糊控制 器定义 研究的典型模糊控制器为两输入一输出模糊系 统 f :U < R 2 →V < R ,其中 U = U1 ×U2 < R 2 为输入 空间 ,V < R 为输出空间 ,模糊控制系统的结构如图 3 所示. 图 3 模糊控制系统的结构图 Fig. 3 The structure of the fuzzy control system 其中 ,单输入单输出(SISO) 被控对象的输入为 ut ,输出为 yt ,参考输入为 st , t 为离散时间变量 , T 为采样周期. 设模糊控制器的 2 个输入分别为误差 et 和误差的差分 rt ,输出为 ut ,即 et = st - yt , rt = Δet = et - et- 1 . 引入比例因子 Ge 、Gr 、Gu 使输入输出变量正规 化 ,即 e 3 = Geet , r 3 = Gr rt , ut = Gu u 3 . (4) 式中 :e 3 , r 3 , u 3 ∈[ - 1 ,1 ]. 设采用π型隶属函数的典型模糊控制器 ,其设 计参数如下 : 1) 输入和输出变量的模糊集及隶属函数. 正规化的输入变量 e 3 、r 3 采用全交叠均匀分布 的π型隶属函数 ,如图 4 (a) 所示. 正规化的输出变 量 u 3 采用均匀分布的单点隶属函数 ,如图 4 ( b) 所 示. 设 e 3 、r 3 分别定义 2 n + 1 个模糊集合 ,其中 n 个 为正 , n 个为负 ,1 个为零 ,分别为π1 p ( p = - n , …, n) 和π2 q ( q = - n , …, n) ,模糊集合的中心分别为b 1 p = p/ n和 b 2 q = q/ n ,宽度分别为 2 a 1 和 2 a 2 ,相邻模糊集 中心之间的距离分别为 a 1 = a 2 = 1/ n. 输出 u 3 定义 4 n + 1 个模糊集合 ,用 U z ( z = - 2 n , …,2 n) 表示 , U z 的中心为δz = z 2 n ,相邻模糊子集中心之间的距离为 s = 1 2 n . 图 4 模糊控制器的输入输出隶属函数 Fig. 4 The membership functions of the input variables and the output variable for the defined fuzzy controller 2) 模糊控制规则 这里采用线性控制规则 ,也就是输出模糊子集 的下标与输入模糊子集的下标成线性关系. 这里输 出模糊子集的下标为输入模糊子集下标的和 ,即z = p + q. Rpq :If e 3 isπ1 p and r 3 isπ2 q , Then u 3 is U z . ( p = - n , …, n; q = - n , …, n; z = - 2 n , …,2 n) 3) 模糊推理方法 采用 Sum2Product 模糊推理方法. 第 1 期 张香燕 ,等 :π型隶属函数的典型模糊控制器的解析结构 ·33 · © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·34… 智能系统学报 第3卷 Sum:x1Ox2⊙…⊙x,= 根据π型典型模糊控制器的解析表达式,研究 min1,x+x2, 了它的结构特性,极限特性和非线性特性,总结成下 Product:xx2x=x1x2x 面3个定理 4)解模糊方法 定理1(π型典型模糊控制器的结构定理)π 由性质2和π型隶属函数的性质可知,任意几 型典型模糊控制器可以等效为一个全局的二维继电 个规则的激活度之和必然小于等于1,所以Sum 器和一个局部的非线性PD控制器之和 Product中的有界和可以用普通和代替,因此采用 证明根据上面推导出的典型模糊控制器的解 重心法解模糊可得模糊控制器的输出为 析表达式6)式分为2部分,即 u°=(p,g+(e',r), 7) ∑πpe)r,(r)(p+s 5) P(p.q)pg 8) 2n πn(e)乃r) P.9-n e',r)=e+4 (9 2n 3π型典型模糊控制器的解析表达式 式中:(p,的作用是全局性的,只与e、r所在 及结构分析 的小区间在整个输入空间中的位置有关,因此是一 为不失一般性,设e∈[,+1I,r'∈[, 个全局的二维继电器.而中(e`,r)与严p1(e`)和 +11,p∈-n,5n-1,q∈{-n,…n-1}.在此 g+1(r)有关,由于采用均匀分布的隶属函数,各个 区域只有4条模糊规则被激活,即 模糊集合的宽度相同,乃p+1(e`)和+1(r)只与e If e'is and r'is,Then u'=(p+q)s; 和r相对于模糊集合中心点的距离相关,即与e'、 If e'is and r'is.Then u=(p+q+1)s: r在小区间内的相对位置有关,所以,虫(e°,r)的 fe'iso+and r'is元,Then u`=(p+q+l)s: 作用是局部性的,且是一个非线性的PD控制器. If e'is and r'is.Then u=(p+q+2)s: 以n=2为例,中(p,和u`的控制曲面分别 由5)式得 如图5和图6所示. ,·=之rne),(r)(p+4s ∑πp(e)(r) P.9-. 卫卫,Ln++工,Lp+q+1 刀prg+Tp+g刀g+元n兀g+1+刀+g兀g+1 ,卫Lp+g+1g+卫卫p+q+2s 05 刀prg+Tp+1Tg+πprg+1+兀p+1兀g+1 分母=几g刀p+刀p+1乃g+prp+1+兀n1g+1= 图5:(pg)的控制曲面图 (πp+刀p+1几+(πp+几p+)几g+1= Fig.5 Control surface of (p.q) 刀g+πg+1=1, 分子=乃,πg(p+gs+,1元(p+9+1)s+ πnπg1(p+q+1)s+元m+11(p+q+2s= (π,刀g+1元g+兀nrg+1+刀n1g+1)(p+s+ -0.5 -10 (πp+1元+πprg+1+2刀p+1πg+1)s= 0 0.5 0 (p+4s+(1+乃s=p土9+L+亚4 0. -0.5 2n 2n 因此,可得 图64”的控制曲面图 u=P,tg+L+山 Fig.6 Control surface of u 6) 2n 2n 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved hup://www.cnki.net
Sum : x1 © x2 © …© x r = min{ 1 , x1 + x2 …+ x r} , Product : x1 ·x2 …x r = x1 x2 …x r . 4) 解模糊方法 由性质 2 和π型隶属函数的性质可知 ,任意几 个规则的激活度之和必然小于等于 1 ,所以 Sum2 Product 中的有界和可以用普通和代替 ,因此采用 重心法解模糊可得模糊控制器的输出为 u 3 ∑ n p , q= - n πp ( e 3 )πq ( r 3 ) ( p + q) s ∑ n p , q= n πp ( e 3 )πq ( r 3 ) . (5) 3 π型典型模糊控制器的解析表达式 及结构分析 为不失一般性 , 设 e 3 ∈[ b 1 p , b 1 p + 1 ] , r 3 ∈[ b 2 q , b 2 p + 1 ] , p ∈{ - n , …, n - 1} , q ∈{ - n , …, n - 1} . 在此 区域只有 4 条模糊规则被激活 ,即 If e 3 isπ1 p and r 3 isπ2 q , Then u 3 = ( p + q) s; If e 3 isπ1 p and r 3 isπ2 q+ 1 , Then u 3 = ( p + q + 1) s; If e 3 isπ1 p + 1 and r 3 isπ2 q , Then u 3 = ( p + q + 1) s; If e 3 isπ1 p + 1 and r 3 isπ2 q+ 1 , Then u 3 = ( p + q + 2) s; 由(5) 式得 u 3 = ∑ n p , q= - n πp ( e 3 )πq ( r 3 ) ( p + q) s ∑ n p , q= - n πp ( e 3 )πq ( r 3 ) = πpπq ( p + q) s +πp+1πq ( p + q + 1) s πpπq +πp+qπq +πpπq+1 +πp+qπq+1 + πpπq+1 ( p + q + 1) s +πp+1πq+1 ( p + q + 2) s πpπq +πp+1πq +πpπq+1 +πp+1πq+1 , 分母 = πqπp +πp+1πq +πpπp+1 +πp+1πq+1 = (πp +πp+1 )πq + (πp +πp+1 )πq+1 = πq +πq+1 = 1 , 分子 = πpπq ( p + q) s +πp+1πq ( p + q + 1) s + πpπq+1 ( p + q + 1) s +πp+1πq+1 ( p + q + 2) s = (πpπq +πp+1πq +πpπq+1 +πp+1πq+1 ) ( p + q) s + (πp+1πq +πpπq+1 + 2πp+1πq+1 ) s = ( p + q) s + (πp+1 +πq+1 ) s = p + q 2 n + πp+1 +πq+1 2 n . 因此 ,可得 u 3 = p + q 2 n + πp+1 +πq+1 2 n . (6) 根据π型典型模糊控制器的解析表达式 ,研究 了它的结构特性 ,极限特性和非线性特性 ,总结成下 面 3 个定理. 定理 1 (π型典型模糊控制器的结构定理) π 型典型模糊控制器可以等效为一个全局的二维继电 器和一个局部的非线性 PD 控制器之和. 证明 根据上面推导出的典型模糊控制器的解 析表达式(6) 式分为 2 部分 ,即 u 3 = ΦG ( p , q) +ΦL ( e 3 , r 3 ) , (7) ΦG ( p , q) = p + q 2 n , (8) ΦL ( e 3 , r 3 ) = πp+1 ( e 3 ) +πq+1 ( r 3 ) 2 n . (9) 式中 :ΦG ( p , q) 的作用是全局性的 ,只与 e 3 、r 3 所在 的小区间在整个输入空间中的位置有关 ,因此是一 个全局的二维继电器. 而ΦL ( e 3 , r 3 ) 与πp + 1 ( e 3 ) 和 πq+ 1 ( r 3 ) 有关 ,由于采用均匀分布的隶属函数 ,各个 模糊集合的宽度相同 ,πp + 1 ( e 3 ) 和πq+ 1 ( r 3 ) 只与 e 3 和 r 3 相对于模糊集合中心点的距离相关 ,即与 e 3 、 r 3 在小区间内的相对位置有关 ,所以 ,ΦL ( e 3 , r 3 ) 的 作用是局部性的 , 且是一个非线性的 PD 控制器. 以 n = 2 为例 ,ΦG ( p , q) 和 u 3 的控制曲面分别 如图 5 和图 6 所示. ·34 · 智 能 系 统 学 报 第 3 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第1期 张香燕,等:π型隶属函数的典型模糊控制器的解析结构 ·35 注释1当典型模糊控制器的输出为△山,= 器的解析表达式,得到了该模糊控制器可以等效为 h-h.1时,π型典型模糊控制器可以等效为一个全 一个全局的二维继电器和一个局部的非线性PD控 局的二维继电器和一个局部的非线性PI控制器之 制器之和的结论:并且研究了其极限特性和非线性 和,即: 特性,得出了其非线性度只与输入变量的模糊集合 △u=P,9++山= 个数有关,模糊集合个数越多,非线性度越小的结 2n 2n 论.由于π型隶属函数具有二阶逼近性能,而且π (p,+(e`,r) 型全交叠模糊集合具有均匀分布性和一致性,这给 定理2(π型典型模糊控制器的极限定理)对 模糊控制器的结构分析带来了很大的便利,也为π 于π型典型模糊控制器,当2个输入变量的模糊集 型隶属函数的典型模糊控制器的稳定性设计奠定了 个数趋向无穷时,全局的二维继电器趋近于线性 基础.然而三角形隶属函数的模糊控制器具有简单 PD控制器,而局部的非线性控制器将会消失,即: “=g(p,g+(e,r), 易于实现的优点,因此在π型隶属函数的控制器设 计中,如何平衡控制器的逼近性和设计的简单性值 (p.-lim(p.e+r) 得进一步的深入研究, (e`,r)=lim(e`,r)=0. 附录 证明篇幅较长,见附录 定理2的证明. 注释2由定理2可知,当2个输入变量的模 1)(p,部分的证明, 糊集个数n趋向无穷时,π型典型模糊控制器的输 由(p,的定义和式8)可得: 出等效于一个线性PD控制器,其比例和微分放大 系数分别为k=寸,k贴=过 e(p,g=imp,g=lim”2 因为e∈[,g11,r∈[6,61I:即e`∈ 定义3模糊控制器的非线性度P定义为 1$I p= [天r子所以当m-时。 Im+l m e片r丹代入上式可得 定理3(π型典型模糊控制器的非线性定理) π 型典型模糊控制器的非线性度为1/m p.=m2=e+r. 证明因为 2)(e‘,r)部分的证明 1克L 由(e°,r)的定义和式9)可得: p= |9nx|+川x|一n (e',r')lim 「亚e)+r⊥ 2n 141=-max2n 2n n q-·M,“1 又因为 因为4片 n」 ,当n |9s|=。,max 卫(e+卫r⊥ 时。r即p之 n'2n' p-. 2n g-··“1 丨生L nr'.q 所以p=1典+川Ln 由π型隶属函数的定义,可得 注释3由定理3可知,π型典型模糊控制器的 非线性度只与输入变量定义的模糊集合的个数n有 当e+别时, 关,n越大,非线性度越小.当输入空间进行无穷划 e)=1.2x2 分,也就是每个子区域足够小时,π型典型模糊控制 器收敛为一个线性D控制器,其非线性度也逐渐 1.2n e-n/n =1-2(e-pl2 趋于0. 当e 卫+L时, 4结束语 2n'n e)=2 x-bo-a 文章推导了具有π型隶属函数的典型模糊控制 a 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.nei
注释 1 当典型模糊控制器的输出为Δut = ut - ut - 1时 ,π型典型模糊控制器可以等效为一个全 局的二维继电器和一个局部的非线性 PI 控制器之 和 ,即 : Δu 3 = p + q 2 n + πp+1 +πq+1 2 n = ΦG ( p , q) +ΦL ( e 3 , r 3 ) . 定理 2 (π型典型模糊控制器的极限定理) 对 于π型典型模糊控制器 ,当 2 个输入变量的模糊集 个数趋向无穷时 , 全局的二维继电器趋近于线性 PD 控制器 ,而局部的非线性控制器将会消失 ,即 : u 3 n→∞ = Φ∞ G ( p , q) +Φ∞ L ( e 3 , r 3 ) , Φ∞ G ( p , q) = limn→∞ ΦG ( p , q) = 1 2 ( e 3 + r 3 ) , Φ∞ L ( e 3 , r 3 ) = limn→∞ Φ∞ L ( e 3 , r 3 ) = 0. 证明篇幅较长 ,见附录. 注释 2 由定理 2 可知 ,当 2 个输入变量的模 糊集个数 n 趋向无穷时 ,π型典型模糊控制器的输 出等效于一个线性 PD 控制器 ,其比例和微分放大 系数分别为 K ∞ P = 1 2 , K ∞ D = 1 2 . 定义 3 模糊控制器的非线性度ρ定义为[6 ] ρ = | <Lmax | | <Lmax | +| <Gmax | . 定理 3 (π型典型模糊控制器的非线性定理) π 型典型模糊控制器的非线性度为 1/ n. 证明 因为 ρ = | <Lmax | | <Lmax | +| <Gmax | = 1 n . | <Lmax | = max p = - n, …, n- 1 q= - n, …, n- 1 p + q 2 n = 2 ( n + 1) 2 n = n - 1 n , 又因为 | <Lmax | = max p = - n 1 , …, n 1 - 1 q= - n 2 , …, n 2 - 1 πp+1 ( e 3 ) +πq ( r 3 ) 2 n = 1 n , 所以 ,ρ= | <Lmax | | <Lmax | + | <Gmax | = 1 n . 注释 3 由定理 3 可知 ,π型典型模糊控制器的 非线性度只与输入变量定义的模糊集合的个数 n 有 关 , n 越大 ,非线性度越小. 当输入空间进行无穷划 分 ,也就是每个子区域足够小时 ,π型典型模糊控制 器收敛为一个线性 PD 控制器 ,其非线性度也逐渐 趋于 0. 4 结束语 文章推导了具有π型隶属函数的典型模糊控制 器的解析表达式 ,得到了该模糊控制器可以等效为 一个全局的二维继电器和一个局部的非线性 PD 控 制器之和的结论; 并且研究了其极限特性和非线性 特性 , 得出了其非线性度只与输入变量的模糊集合 个数有关 ,模糊集合个数越多 , 非线性度越小的结 论. 由于π型隶属函数具有二阶逼近性能 ,而且π 型全交叠模糊集合具有均匀分布性和一致性 , 这给 模糊控制器的结构分析带来了很大的便利 ,也为π 型隶属函数的典型模糊控制器的稳定性设计奠定了 基础. 然而三角形隶属函数的模糊控制器具有简单 易于实现的优点 ,因此在π型隶属函数的控制器设 计中 ,如何平衡控制器的逼近性和设计的简单性值 得进一步的深入研究. 附录 定理 2 的证明. 1)Φ∞ G ( p , q) 部分的证明. 由Φ∞ G ( p , q) 的定义和式(8) 可得 : Φ∞ G ( p , q) = limn →∞ ΦG ( p , q) = limn→∞ p + q 2 n . 因为 e 3 ∈[ b 1 p , b 1 p + 1 ] , r 3 ∈[ b 2 q , b 2 q+ 1 ]; 即 e 3 ∈ p n , p + 1 n , r 3 ∈ q n , q + 1 n , 所以 , 当 n →∞时 , e 3 → p n , r 3 → q n ,代入上式可得 : Φ∞ G ( p , q) = limn →∞ p + q 2 n = 1 2 ( e 3 + r 3 ) . 2)Φ∞ L ( e 3 , r 3 ) 部分的证明. 由Φ∞ L ( e 3 , r 3 ) 的定义和式(9) 可得 : Φ∞ L ( e 3 , r 3 ) = limn →∞ πp+1 ( e 3 ) +πq+1 ( r 3 ) 2 n . 因为 e 3 ∈ p n , p + 1 n , r 3 ∈ q n , q + 1 n ,当 n → ∞时 , e 3 → p n , 1 2 n , r 3 → q n , 1 2 n , 即 ne 3 - p → 1 2 , nr 3 - q → 1 2 . 由π型隶属函数的定义 ,可得 当 e 3 ∈ p n , p n + 1 2 n 时 , πp ( e 3 ) = 1 - 2 x - b 1 p a1 2 = 1 - 2 e 3 - p/ n 1/ n 2 = 1 - 2 ( ne 3 - p) 2 ; 当 e 3 ∈ p n + 1 2 n , p n + 1 n 时 , πp ( e 3 ) = 2 x - b 1 p - a1 a1 2 = 第 1 期 张香燕 ,等 :π型隶属函数的典型模糊控制器的解析结构 ·35 · © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·36· 智能系统学报 第3卷 e'.pin-v 综上,可得e和r的隶属度函数如表1、2所 1/n =2(e·-p-1)2 示.并将表12中的值代入式3)中,可得到(P 同理可得,(r)的分段隶属度函数 ,如表3所示 并且由定理1可知 rp(e)+刀p1(e)=1,几g(r)+几g1(r)=1. 表1输入e在区间骨骨+日 n 上的隶属函数值,(e),+1(e) Table 1 The value of)and(c)for c' (e') +e") 。+ 1-2(e'.p2 2(e'.p2 。++ 2n'n n 2(me'-p-)2 1.2(me'.p-1)2 表2 箱入“在区间骨丹+日 上的隶属函数值(r),”+1(r) +日 P Table 2 The value of(r)and (r)for r' in L nn (r) πg+1(r`) 1-2(nr-g2 2(nr'-g2 4+1.4+1 L n 2n'n 2(mr-9-102 1-2(r'-g-2 下面针对表格3中的4种情况分别讨论: 第1种情况: 因此0≤e·p寸.0≤r·g寸可得0≤ (p.q)lim(p.= 2(e-p2+2(nrq2≤1.所以,(p,q= e··p2+m·-2 1im4(p,g=0. lim 又因为+动r+为 表3。卡+日,片+区城内的控制曲面(0 Table 3 r e r' 日4.4+1 r 4+4+1 L n'n 2n Ln 2n'nn 。 e'.p2±m'.2 1+2e'.p2.2m'.g-1)2 2n 1.2e·.ps12+2r'.2 L.ne'.p-12.m'.g-2 n 2n n 第2种情况: lim 1±2e·.p2.2r·g-12 2n (p.q)lim(p.q= 又因为e:+r+n+ 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.nei
2 e 3 - p/ n - 1/ n 1/ n 2 = 2 ( ne 3 - p - 1) 2 . 同理可得πq ( r 3 ) 的分段隶属度函数. 并且由定理 1 可知 πp ( e 3 ) +πp+1 ( e 3 ) = 1 ,πq ( r 3 ) +πq+1 ( r 3 ) = 1. 综上 ,可得 e 3 和 r 3 的隶属度函数如表 1、2 所 示. 并将表 1、2 中的值代入式(3) 中 ,可得到ΦL ( p , q) ,如表 3 所示. 表 1 输入 e 3 在区间 p n , p n + 1 n 上的隶属函数值πp ( e 3 ) ,πp + 1 ( e 3 ) Table 1 The value of πp ( e 3 ) andπp + 1 ( e 3 ) for e 3 in p n , p n + 1 n πp ( e 3 ) πp + 1 ( e 3 ) e 3 ∈ p n , p n + 1 2 n 1 - 2 ( ne 3 - p) 2 2 ( ne 3 - p) 2 e 3 ∈ p n + 1 2 n , p n + 1 n 2 ( ne 3 - p - 1) 2 1 - 2 ( ne 3 - p - 1) 2 表 2 输入 r 3 在区间 q n , q n + 1 n 上的隶属函数值πq ( r 3 ) ,πq + 1 ( r 3 ) Table 2 The value of πq ( r 3 ) andπq + 1 ( r 3 ) for r 3 in q n , q n + 1 n πq ( r 3 ) πq+ 1 ( r 3 ) r 3 ∈ q n , q n + 1 2 n 1 - 2 ( nr 3 - q) 2 2 ( nr 3 - q) 2 r 3 ∈ q n + 1 2 n , q n + 1 n 2 ( nr 3 - q - 1) 2 1 - 2 ( nr 3 - q - 1) 2 下面针对表格 3 中的 4 种情况分别讨论 : 第 1 种情况 : Φ∞ L ( p , q) = limn→∞ ΦL ( p , q) = limn→∞ ( ne 3 - p) 2 + ( nr 3 - q) 2 n , 又因为 e 3 ∈ p n , p n + 1 2 n , r 3 ∈ q n , q n + 1 2 n , 因此 0 ≤ne 3 - p ≤ 1 2 ,0 ≤nr 3 - q ≤ 1 2 可得 0 ≤ 2 ( ne 3 - p) 2 + 2 ( nr 3 - q) 2 ≤1. 所以 ,Φ∞ L ( p , q) = limn→∞ Φ∞ L ( p , q) = 0. 表 3 e 3 ∈ p n , p n + 1 n , r 3 ∈ q n , q n + 1 n 区域内的控制曲面ΦL ( p , q) Table 3 The value of ΦL ( p , q) for e 3 in p n , p n + 1 n and r 3 in q n , q n + 1 n e 3 r 3 r 3 ∈ q n , q n + 1 2 n r 3 ∈ q n + 1 2 n , q n + 1 n e 3 ∈ p n , p n + 1 2 n ( ne 3 - p) 2 + ( nr 3 - q) 2 n 1 + 2 ( ne 3 - p) 2 - 2 ( nr 3 - q - 1) 2 2 n e 3 ∈ p n + 1 2 n , p n + 1 n 1 - 2 ( ne 3 - p - 1) 2 + 2 ( nr 3 - q) 2 2 n 1 - ( ne 3 - p - 1) 2 - ( nr 3 - q - 1) 2 n 第 2 种情况 : Φ∞ L ( p , q) = limn→∞ ΦL ( p , q) = limn →∞ 1 + 2 ( ne 3 - p) 2 - 2 ( nr 3 - q - 1) 2 2 n , 又因为 e 3 ∈ p n , p n + 1 2 n , r 3 ∈ q n + 1 2 n , q n + 1 n , ·36 · 智 能 系 统 学 报 第 3 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第1期 张香燕,等:π型隶属函数的典型模糊控制器的解析结构 ·37 因此,0≤ne°-p≤,-≤r-g-1≤0,得 shaped membership functions[J].Science in China(Se- ≤2,·2 ries E),2000,43(3):263274 之+2ep2.21m92≤所以, [9]FAN X Z,ZHANG N Y,Li N.Structure analysis of typical fuzzy controllers with unequally spaced fuzzy sets h(p,=lim4(p,=0. for input and output variables [J ]Chinese Journal of E- 第3种情况: lectronics,2001,10(3):326-331. 同理,·分≤e'·p10.0≤r:g≤寸 [10]DU X Y,ZHANGN Y,YU N.Structure analysis and function evaluation of a kind of fuzzy PID controllers 因此.支92ep-)+21arg2≤受 [J].Chinese Journal of Electronics,2004,13(4):654- 659. 所以,(p,g=lim(p,g=0. [11]DU X Y,ZHANG N Y.Structure analysis of MISO 第4种情况, typical fuzzy controllers [J].Advances in System Sci- 同理支≤ep-1①,之≤r.g ence and Applications,2004,4(2):169-174. [12]李少远,田永青.模糊控制器的结构化分析及系统化设 1.因此12-2(ne-p-1)2-2(nr-g 计方法[U1.控制与决策,2001,16(4):435438. 1)2.所以,(p,=lim攻(p,=0. LI Shaoyuan,TIAN Yongqing.Structure analysis and 综合以上4种情况可得(p,g=Iim(p, systematic design of typical fuzzy controllers [J ]Con- trol and Decision,2001.16(4):435-438. y=0. [13]HU B G,MANN G K I,GOSINE R G.New method- 参考文献: ology for analytical and optimal design of fuzzy PID con trollers [J ]IEEE Transactions on Fuzzy Systems, [1]王立新.模糊系统与模糊控制教程[M].王迎军,译.北 1999,7(5):521-539. 京:清华大学出版社,2003. [2]SIL ER W,YING H.Fuzzy control theory:the linear [14]MITA IM S,KOSKO B.The shape of fuzzy sets in a- case [J ]Fuzzy Sets and Systems,1989,33(2):275- daptive function approximation [J].IEEE Transactions 290. on Fuzzy Systems,2004,9(4):637-656. [3]YING H,SIL ER W,BUCKL EYJ J.Fuzzy control the- [15]李洪兴.模糊控制的插值机理[U].中国科学(E辑), ory:a nonlinear case [J].Automatica,1990,26(3): 1998,28(3):259267 513-520. LI Hongxing.Interpolation mechanism of fuzzy control [4]YIN G H.The simplest fuzzy controllers using different [J ]Science in China(Series E),1998,28(3):259- methods are different nonlinear proportional-integral con 267 trollers with variable gains [J].Automatica,1993,29: [16]HASSINE R,KARRA Y F.Approximation properties 1579-1589. of piecewise parabolic functions fuzzy logic systems [J]. [5]YIN G H.A nonlinear fuzzy controller with linear control Fuzzy Sets and Systems,2006,157:501-515. rules is the sum of a global two-dimensional multilevel 作者简介: relay and a local nonlinear proportional-integral control- 张香燕,女,1982年生,博士研究生,主 ler[J].Automatica,1993,29(2):499505. 要研究方向为模糊系统与分层模糊系统,在 [6]YING H.Fuzzy control and modeling:analytical founda- 国内外期刊和会议上共发表文章5篇」 tions applications M].New York:IEEE Press, 2000. [7]LI N,ZHANG N Y,JIN K Y.Structure analysis of typical fuzzy controllers with unevenly distributed input 张乃尧,男,1946年生,教授,博士生导 membership functions[J].Journal of Tsinghua Universi- 师,主要研究方向为模糊控制理论及应用、 ty,2000,40(1):120123. 机器人足球、音乐情感识别等.已发表论文 [8]曾珂,张乃尧,徐文立.采用伪梯形隶属函数的一类 100余篇,其中被SCI检索10余篇,EI检索 模糊控制器的结构分析卫].中国科学(E),2000,30(4): 30余篇. 320-330. ZEN G Ke,ZHAN G Naiyao,XU Wenli.Structure anal- ysis of a class of fuzzy controllers using pseudo trapezoid 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved http://www.cnki.net
因此 ,0 ≤ne 3 - p ≤ 1 2 , - 1 2 ≤nr 3 - q - 1 ≤0 , 得 1 2 ≤1 + 2 ( ne 3 - p) 2 - 2 ( nr 3 - q - 1) 2 ≤ 3 2 . 所以 , Φ∞ L ( p , q) = limn→∞ Φ∞ L ( p , q) = 0. 第 3 种情况 : 同理 , - 1 2 ≤ne 3 - p - 1 ≤0 , 0 ≤nr 3 - q ≤ 1 2 , 因此 , 1 2 ≤1 - 2 ( ne 3 - p - 1) 2 + 2 ( nr 3 - q) 2 ≤ 3 2 . 所以 ,Φ∞ L ( p , q) = limn →∞ Φ∞ L ( p , q) = 0. 第 4 种情况 , 同理 , - 1 2 ≤ne 3 - p - 1 ≤0 , - 1 2 ≤nr 3 - q - 1 ≤0. 因此 1 ≤2 - 2 ( ne 3 - p - 1) 2 - 2 ( nr 3 - q - 1) 2 ≤2. 所以 ,Φ∞ L ( p , q) = limn→∞ Ф∞ L ( p , q) = 0. 综合以上 4 种情况可得Φ∞ L ( p , q) = limn→∞ Φ∞ L ( p , q) = 0. 参考文献 : [1 ]王立新. 模糊系统与模糊控制教程[ M ]. 王迎军 ,译. 北 京 : 清华大学出版社 , 2003. [2 ] SIL ER W , YIN G H. Fuzzy control theory : the linear case [J ]. Fuzzy Sets and Systems , 1989 , 33 (2) : 2752 290. [3 ] YIN G H , SIL ER W , BUCKL EYJ J. Fuzzy control the2 ory : a nonlinear case [J ]. Automatica , 1990 , 26 ( 3) : 5132520. [4 ] YIN G H. The simplest fuzzy controllers using different methods are different nonlinear proportional2integral con2 trollers with variable gains [J ]. Automatica , 1993 , 29 : 157921589. [ 5 ] YIN G H. A nonlinear fuzzy controller with linear control rules is the sum of a global two2dimensional multilevel relay and a local nonlinear proportional 2integral control2 ler [J ]. Automatica , 1993 , 29 (2) : 4992505. [6 ] YIN G H. Fuzzy control and modeling : analytical founda2 tions & applications [ M ]. New York : IEEE Press , 2000. [7 ]L I N , ZHAN G N Y, J IN K Y. Structure analysis of typical fuzzy controllers with unevenly distributed input membership functions[J ]. Journal of Tsinghua Universi2 ty , 2000 , 40 (1) :1202123. [8 ]曾 珂 , 张乃尧 , 徐文立. 采用伪梯形隶属函数的一类 模糊控制器的结构分析[J ]. 中国科学( E) , 2000 , 30 (4) : 3202330. ZEN G Ke , ZHAN G Naiyao , XU Wenli. Structure anal2 ysis of a class of fuzzy controllers using pseudo trapezoid shaped membership functions[J ]. Science in China ( Se2 ries E) , 2000 , 43 (3) : 2632274. [9 ] FAN X Z , ZHAN G N Y , Li N. Structure analysis of typical fuzzy controllers with unequally spaced fuzzy sets for input and output variables [J ]. Chinese Journal of E2 lectronics , 2001 , 10 (3) : 3262331. [ 10 ]DU X Y , ZHAN G N Y , YU N. Structure analysis and function evaluation of a kind of fuzzy PID controllers [J ]. Chinese Journal of Electronics , 2004 , 13 (4) : 6542 659. [11 ] DU X Y , ZHAN G N Y. Structure analysis of MISO typical fuzzy controllers [J ]. Advances in System Sci2 ence and Applications , 2004 , 4 (2) : 1692174. [ 12 ]李少远 , 田永青. 模糊控制器的结构化分析及系统化设 计方法[J ]. 控制与决策 , 2001 , 16 (4) : 4352438. L I Shaoyuan , TIAN Yongqing. Structure analysis and systematic design of typical fuzzy controllers [J ]. Con2 trol and Decision , 2001 , 16 (4) :4352438. [13 ] HU B G, MANN G K I , GOSIN E R G. New method2 ology for analytical and optimal design of fuzzy PID con2 trollers [J ]. IEEE Transactions on Fuzzy Systems , 1999 , 7 (5) : 5212539. [14 ]MITAIM S , KOSKO B. The shape of fuzzy sets in a2 daptive function approximation [J ]. IEEE Transactions on Fuzzy Systems , 2004 , 9 (4) : 6372656. [15 ]李洪兴. 模糊控制的插值机理[J ]. 中国科学 ( E 辑) , 1998 , 28 (3) : 2592267. L I Hongxing. Interpolation mechanism of fuzzy control [J ]. Science in China ( Series E) , 1998 , 28 (3) : 2592 267. [16 ] HASSIN E R , KARRA Y F. Approximation properties of piecewise parabolic functions fuzzy logic systems [J ]. Fuzzy Sets and Systems , 2006 ,157 : 5012515. 作者简介 : 张香燕 ,女 ,1982 年生 ,博士研究生 ,主 要研究方向为模糊系统与分层模糊系统 ,在 国内外期刊和会议上共发表文章 5 篇. 张乃尧 ,男 ,1946 年生 ,教授 ,博士生导 师 ,主要研究方向为模糊控制理论及应用、 机器人足球、音乐情感识别等. 已发表论文 100 余篇 ,其中被 SCI 检索 10 余篇 ,EI 检索 30 余篇. 第 1 期 张香燕 ,等 :π型隶属函数的典型模糊控制器的解析结构 ·37 · © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net