
第3卷第1期 智能系统学报 Vol.3№1 2008年2月 CAAI Transactions on Intelligent Systems Fcb.2008 多边形序列的最短路径算法 李发捷,KL ETTE Reinhard (1.格罗宁根大学数学与计算科学学院,荷兰格罗宁根9700:2.奥克兰大学计算机科学系,新西兰奥克兰1142) 摘要:给定平面上一个含k个简单多边形的序列及一个起点p和一个终点q,近似地计算一条最短路径使得它开 始于P点,然后按指定的次序访问每个多边形,最后终止于q点.如果多边形是两两不相交且是非凸的,那么此问题 至今还没有算法解.应用一种R算法,给出复杂性为x(9·O(W的一种近似算法,这里n是给定多边形的顶点总数, 函数x(g定义为L。与L的差与e的商,其中Lo是初始路径长度,L是最优路径长度,e是计算精确度.给定的R算 法稍作修改也能用来近似地解决3个NP完全或NP困难的三维欧几里德最短路径问题(ESP).它们的复杂性均为 k(9·O(利,这里k是含有所给定的障碍物的堆的层数. 关键词:算法;最短路径;旅游多边形;部件切割;q矩形 中图分类号:TP202+7文献标识码:A文章编号:1673-4785(2008)01-0023-08 Shortest path algorithms for sequences of polygons LI Fa-jie',KL ETTE Reinhard2 (1.Institute for Mathematics and Computing Science,University of Groningen P.O.Box 800,9700 AV Groningen,The Nether- lands;2.Computer Science Department,The University of Auckland Private Bag 92019,Auckland 1142,New Zealand) Abstract:Given a sequence of k simple polygons in a plane,and a start point p,a target point q.We ap- proximately compute a shortest path that starts at p,then visit each of the polygons in the specified order, and finally end at g.So far no solution is known if the polygons are disjoint with each other and nomcon- vex.By applying a rubberband algorithm,we give an approximate algorithm with time complexity in K(O(n,where n is the total number of vertices of the given polygons,and function K(is the differ- ence between Lo and L over e,where Lo is the length of the initial path,and L is the true (i.e.,optimum) path length.The given rubberband algorithm can also be applied to solve approximately three NP-complete or NPhard 3D Euclidean shortest path (ESP)problems in K((,where k is the number of layers in a stack which contains the defined obstacles. Key words:rubberband algorithm;shortest paths;touring polygons;parts cutting;qrectangles 1问题的提出 本文报告R算法的一些应用.R算法最初由文 献[1]提出,然后文献[2]加以详细研究.在详细说 1.1旅游多边形问题 明R算法之前,首先描述2个紧密相关的问题,旅 回忆文献[3所引入的一些概念和符号.该文首 游多边形问题和部件切割问题,文中将给出它们的 次提出旅游多边形问题.假设π是一个平面,它可以 近似解.本文第2节介绍R算法的基本原理和一些 表示成R.考虑多边形P,Cπ,这里i=1,2,k及 应用时应注意的问题,第3节举例说明它关于旅游 两点p,g∈刀假如pm=p及p+1=q,p:∈R2,此处 多边形问题和q矩形问题的应用,第4节结束 i=1,2,k,p以p,pi,pm,p,q)表示路径ppmp 全文 …paq CRi.假如p(p,q〉表示路径p(p,p1,p, 收稿日期:2007-0616. pk,q〉不会引起混淆,p,∈P,满足p,是aP,∩p(p 通讯作者:李发捷.上mail:F.li@rug.nl. p〉上的沿着路径第一点(aP,表示P,的边界,以下 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3 卷第 1 期 智 能 系 统 学 报 Vol. 3 №. 1 2008 年 2 月 CAA I Transactions on Intelligent Systems Feb. 2008 多边形序列的最短路径算法 李发捷1 , KL ETTE Reinhard 2 (1. 格罗宁根大学 数学与计算科学学院 ,荷兰 格罗宁根 9700 ;2. 奥克兰大学 计算机科学系 ,新西兰 奥克兰 1142) 摘 要 :给定平面上一个含 k 个简单多边形的序列及一个起点 p 和一个终点 q ,近似地计算一条最短路径使得它开 始于 p 点 ,然后按指定的次序访问每个多边形 ,最后终止于 q点. 如果多边形是两两不相交且是非凸的 ,那么此问题 至今还没有算法解. 应用一种 R 算法 ,给出复杂性为κ(ε) ·O( n) 的一种近似算法 ,这里 n 是给定多边形的顶点总数 , 函数κ(ε) 定义为 L0 与 L 的差与ε的商 ,其中 L0 是初始路径长度 , L 是最优路径长度 ,ε是计算精确度. 给定的 R 算 法稍作修改也能用来近似地解决 3 个 NP 完全或 NP 困难的三维欧几里德最短路径问题 ( ESP) . 它们的复杂性均为 κ(ε) ·O( k) ,这里 k 是含有所给定的障碍物的堆的层数. 关键词 :R 算法 ;最短路径 ;旅游多边形 ;部件切割 ;q 矩形 中图分类号 : TP202 + 7 文献标识码 :A 文章编号 :167324785 (2008) 0120023208 Shortest path algorithms for sequences of polygons L I Fa2jie 1 , KL ETTE Reinhard 2 (1. Institute for Mathematics and Computing Science , University of Groningen P. O. Box 800 ,9700 AV Groningen ,The Nether2 lands; 2. Computer Science Department , The University of Auckland Private Bag 92019 , Auckland 1142 , New Zealand) Abstract :Given a sequence of k simple polygons in a plane , and a start point p , a target point q. We ap2 proximately comp ute a shortest pat h that starts at p , t hen visit each of t he polygons in t he specified order , and finally end at q. So far no solution is known if t he polygons are disjoint wit h each ot her and non2con2 vex. By applying a rubberband algorit hm , we give an approximate algorit hm with time complexity in κ(ε) ·O( n) , where n is t he total number of vertices of t he given polygons , and f unctionκ(ε) is the differ2 ence between L0 and L overε, where L0 is the length of t he initial pat h , and L is the true (i. e. , optimum) path lengt h. The given rubberband algorithm can also be applied to solve app roximately t hree N P2complete or NP2hard 3D Euclidean shortest pat h ( ESP) problems inκ(ε) ·O( k) , where k is t he number of layers in a stack which contains the defined obstacles. Keywords :rubberband algorit hm ;shortest pat hs ; touring polygons ; parts cutting ; q2rectangles 收稿日期 :2007206216. 通讯作者 :李发捷. E2mail : F. li @rug. nl. 本文报告 R 算法的一些应用. R 算法最初由文 献[ 1 ]提出 ,然后文献[ 2 ]加以详细研究. 在详细说 明 R 算法之前 ,首先描述 2 个紧密相关的问题 ,旅 游多边形问题和部件切割问题 ,文中将给出它们的 近似解. 本文第 2 节介绍 R 算法的基本原理和一些 应用时应注意的问题 ,第 3 节举例说明它关于旅游 多边形问题和 q 矩形问题的应用 , 第 4 节结束 全文. 1 问题的提出 111 旅游多边形问题 回忆文献[3 ]所引入的一些概念和符号. 该文首 次提出旅游多边形问题. 假设π是一个平面 ,它可以 表示成 R 2 . 考虑多边形 Pi <π,这里 i = 1 ,2 , …, k 及 两点 p , g ∈π. 假如 p0 = p 及 p k + 1 = q , pi ∈R 2 ,此处 i = 1 ,2 , …, k ,ρ〈p , p1 , p2 , …, pk , q〉表示路径 p p1 p2 …pkq < R 2 . 假如ρ〈p , q〉表示路径ρ〈p , p1 , p2 , …, pk , q〉不会引起混淆 , pi ∈Pi 满足 p i 是 9 Pi ∩ρ〈p , pi〉上的沿着路径第一点( 9 Pi 表示 Pi 的边界 ,以下

·24 智能系统学报 第3卷 同),那么说路径p(p,q〉访问P于p,点,此处i= 1,2,…k 无约束TPP问题定义如下: 在平面上如何寻找出一条欧几里德最短路径 Pp,p,p,p,q〉,使得它按给定次序(i=1,2, 付访问每个多边形P 假定对于任意i,j∈1,2,…k,0P∩8P= 0,而且每个P,都是凸的,文献37讨论这类特别情 形并且给出复杂性为O(kdog(W))的算法解.这 图1说明文献[4]中简化的PTSP(假定这里多边形 里n是平面π上所有多边形P,的顶点总数,1=1, 按照给定次序访问) 2,…k Fig 1 Illustration for the simplified P TSP in Ref.[4]where 根据他们的结果,文献3指出,“一个最能引起 polygons are assumed to be given in a particular order 兴趣的公开的问题是确定两两不相交的非凸的简单 多边形的TPP复杂性” 法,进而按启发式方法解决这个简化了的P 本文3.1节的算法2针对这个问题给出一个复 TSP.但它没有给出这个方法的复杂性分析的证明: 杂性为x(g·O(m的一种近似算法,这里n是给定 作为文献[4]的工作的后续工作,文献[11]证明了一 所有多边形的顶点总数,£是精确度 个进一步简化了的PTSP(即文献[11]只考虑凸多 1.2部件切割问题 边形,且这些多边形按照给定次序访问)是多项式时 在各种各样的加工工业上,例如制衣、制窗、机 间可解的(见图2).如果再加上一个条件:起点是给 械加工等,常常需要从大片的纸、布料玻璃金属上 定的(见图3),那么称他们能解决这个问题,算法的 面切割出很多的部件假如以简单多边形为模型). 复杂性是O(kdog(/)).这里n是平面上所有多 受到这些应用的启发,文献[4提出3种切割模式: 边形的顶点总数,aPCT,i=1,2,,k )连续切割问题:切割工具访问每个对象(例如 简单多边形正好一次.切割刀具可以从对象的边缘 上任意一点开始,但在移动到下一对象前必须切割 完整个对象.因此,那个对象的进入点和离开点必须 是同一点. 2)端点切割问题:进入和退出每个对象的某个 预先规定的边沿点.但可以切割每个对象成为几个 部分.也就是说,它可以重复地访问一个对象 图2说明文献[11]中进一步简化的P-TSP 3)间歇切割问题:这是最一般的情形.每个对象 (假定这里多边形全是凸的) 可以被切割成为几个部分而且进入和离开点没有受 Fig.2 Illustration for the further simplified 到限制. P-TSP in Ref.11]also assuming convex polygons 文献[4]集中考虑每个对象都是一个简单多边 形的连续切割问题.他们称这个问题为模板切割旅 行售货员问题(PTSP).它是著名的旅行售货员问 题(TSP)的推广例 PTSP可进一步推广到广义的TSP (GTSP)).如果每个多边形都退化成一个单一顶 点,那么PTSP就变成TSP,是己知NP困难的 由此可知PTSP也是NP困难的 图3说明文献[3]中的PTSP(假定这里给定起点s) PTSP的困难使得文献[4]添加上一个条件来 Fig.3 Illustration for the P-TSP as considered 考虑这个问题:假定所有多边形都按一个给定的次 in Ref.[3].now also with a given start point s 序访问(见图1),于是基于一种拉格朗日放松方 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
同) ,那么说路径ρ〈p , q〉访问 Pi 于 p i 点 ,此处 i = 1 ,2 , …, k. 无约束 TPP 问题定义如下 : 在平面上如何寻找出一条欧几里德最短路径 ρ〈p , p1 , p2 , …, pk , q〉,使得它按给定次序 ( i = 1 , 2 , …, k) 访问每个多边形 Pi . 假定对于任意 i , j ∈{ 1 , 2 , …, k} , 9 Pi ∩9 Pj = ª,而且每个 Pi 都是凸的 ,文献[3 ]讨论这类特别情 形并且给出复杂性为 O ( knlog ( n/ k) ) 的算法解. 这 里 n 是平面π上所有多边形 Pi 的顶点总数 , i = 1 , 2 , …, k. 根据他们的结果 ,文献[3 ]指出“, 一个最能引起 兴趣的公开的问题是确定两两不相交的非凸的简单 多边形的 TPP 复杂性”. 本文 311 节的算法 2 针对这个问题给出一个复 杂性为κ(ε) ·O( n) 的一种近似算法 ,这里 n 是给定 所有多边形的顶点总数 ,ε是精确度. 112 部件切割问题 在各种各样的加工工业上 ,例如制衣、制窗、机 械加工等 ,常常需要从大片的纸、布料、玻璃、金属上 面切割出很多的部件 (假如以简单多边形为模型) . 受到这些应用的启发 ,文献[4 ]提出 3 种切割模式 : 1) 连续切割问题 :切割工具访问每个对象(例如 简单多边形) 正好一次. 切割刀具可以从对象的边缘 上任意一点开始 ,但在移动到下一对象前必须切割 完整个对象. 因此 ,那个对象的进入点和离开点必须 是同一点. 2) 端点切割问题 :进入和退出每个对象的某个 预先规定的边沿点. 但可以切割每个对象成为几个 部分. 也就是说 ,它可以重复地访问一个对象. 3) 间歇切割问题 :这是最一般的情形. 每个对象 可以被切割成为几个部分而且进入和离开点没有受 到限制. 文献[4 ]集中考虑每个对象都是一个简单多边 形的连续切割问题. 他们称这个问题为模板切割旅 行售货员问题 (P2TSP) . 它是著名的旅行售货员问 题( TSP) 的推广[5 ] . P2TSP 可 进 一 步 推 广 到 广 义 的 TSP ( GTSP) [627 ] . 如果每个多边形都退化成一个单一顶 点 ,那么 P2TSP 就变成 TSP ,是已知 N P 困难的[8 ] . 由此可知 P2TSP 也是 NP 困难的. P2TSP 的困难使得文献[4 ]添加上一个条件来 考虑这个问题 :假定所有多边形都按一个给定的次 序访问 (见图 1) ,于是基于一种拉格朗日放松方 图 1 说明文献[4 ]中简化的 P2TSP(假定这里多边形 按照给定次序访问) Fig11 Illustration for the simplified P2TSP in Ref. [4] where polygons are assumed to be given in a particular order 法[9210 ] ,进而按启发式方法解决这个简化了的 P2 TSP. 但它没有给出这个方法的复杂性分析的证明. 作为文献[ 4 ]的工作的后续工作 ,文献[11 ]证明了一 个进一步简化了的 P2TSP(即文献[ 11 ]只考虑凸多 边形 ,且这些多边形按照给定次序访问) 是多项式时 间可解的(见图 2) . 如果再加上一个条件 :起点是给 定的(见图 3) ,那么称他们能解决这个问题 ,算法的 复杂性是 O( knlog ( n/ k) ) . 这里 n 是平面上所有多 边形的顶点总数 , 9 Pi <π, i = 1 ,2 , …, k. ·24 · 智 能 系 统 学 报 第 3 卷

第1期 李发捷,等:多边形序列的最短路径算法 ·25 同的端点的情形.例如,假设算法1的输入为下列的 2 R算法 数据: 利用以下一个非常简单的二维例子来说明R s1=p,2=pp,4=0,0),=(2,4),9= 算法的基本思想.考虑无约束TPP的一个退化情 3,0),p=1,0,及q=2,0(见图5). 形:每个多边形都收缩成一条单一的直线段(见图 4).以下的算法是R算法的简化了的版本(“弧版 本”.它可以说明原始的R算法的基本原理 图5说明2个脚步元素可能含有相同的端点 Fig,5 Illustration for identical endpoints of steps 作为初始,假设pm和m分别是s和”的中 图4TSP的退化情形,k=3 点.也就是说,p1=(1,2)和p2=(2.5,2).这样就得 Fig 4 Degenerate case of the TPP,for k=3 到初始多边线路即包含于多边形边界的一条路径) 算法1 p=〈p,pm,pm,q的长是5.5616.算法1找到近似的 1)Lete=10~o(选定精确度) 最短路径是P=〈p,p1,p2,q〉,p1=(0.3646, 2)计算初始路径p=〈p,p,pm,p,q〉的长 0.7291),p2=(2.8636,0.5455),它的长是 度h. 4.4944(见表1) 3)Let g=p and i=1. 4)while i£,令h=h,转到3 p=.在这种情形下,算法1的4)中的②步的输 否则,停止 出将是错误的:所计算的路径p=〈p,p,p2,q〉, 步骤1)的精确度参数ε可以选定给定计算机 p1=和p2=.它的长是8.1231.(文献[2J的 所能保证的最大可能的数量精确度, 引理16,看到在这个例子里,p1≠m,p) 在本文的其余的部分称{,2,sx为R算 称这个初始例子的情形为应用R算法时出现 法的脚步集,而每个5是R算法的一个脚步元素 的一条退化路径.它可能出现在算法的初始化或算 在一个脚步集当中,可能出现2个脚步元素具有相 法后面的重复迭代中间.一般地说,它是定义成为初 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
2 R 算法 利用以下一个非常简单的二维例子来说明 R 算法的基本思想. 考虑无约束 TPP 的一个退化情 形 :每个多边形都收缩成一条单一的直线段 (见图 4) . 以下的算法是 R 算法的简化了的版本 “( 弧版 本”) . 它可以说明原始的 R 算法的基本原理. 图 4 TSP 的退化情形 , k = 3 Fig14 Degenerate case of the TPP ,for k = 3 算法 1 1) Letε= 10 - 10 (选定精确度) . 2) 计算初始路径ρ=〈p , p1 , p2 , …, pk , q〉的长 度 l1 . 3) Let q1 = p and i = 1. 4) while i ε,令 l1 = l2 ,转到 3) . 否则 ,停止. 步骤 1) 的精确度参数ε可以选定给定计算机 所能保证的最大可能的数量精确度. 在本文的其余的部分称 { s1 ,s2 , …,sk } 为 R 算 法的脚步集 ,而每个 si 是 R 算法的一个脚步元素. 在一个脚步集当中 ,可能出现 2 个脚步元素具有相 同的端点的情形. 例如 ,假设算法 1 的输入为下列的 数据 : s1 = q1 q2 ,s2 = q2 q3 , q1 = (0 ,0) , q2 = (2 , 4) , q3 = (3 ,0) , p = (1 ,0) ,及 q = (2 ,0) (见图 5) . 图 5 说明 2 个脚步元素可能含有相同的端点 Fig15 Illustration for identical endpoints of step s 作为初始 ,假设 p1 和 p2 分别是 s1 和 s2 的中 点. 也就是说 , p1 = (1 ,2) 和 p2 = (215 ,2) . 这样就得 到初始多边线路(即包含于多边形边界的一条路径) ρ=〈p , p1 , p2 , q〉的长是 51561 6. 算法 1 找到近似的 最短路径是ρ=〈 p , p′1 , p′2 , q〉, p′1 = ( 01364 6 , 01729 1 ) , p′2 = ( 21863 6 , 01545 5 ) , 它 的 长 是 41494 4 (见表 1) . 表 1 初始由图 5 说明的重复数 I 和结果δs ( p1 = (1 ,2) 和 p2 = ( 215 ,2)作为初始点) Table 1 Numbor I of iterations and resultingδs for the initialization illustrated by Fig15 ( with p1 = ( 1 ,2) and p2 = ( 215 ,2) as initialization points) I δ 1 - 01890 0 2 - 01175 2 3 - 01001 9 4 - 11293 5e - 005 5 - 81443 5e - 008 6 - 51493 0e - 010 7 - 31574 0e - 012 现在假定一个不同的初始点的输入 ,使得 p1 = p2 = q2 . 在这种情形下 ,算法 1 的 4) 中的 ②步的输 出将是错误的 :所计算的路径ρ=〈p , p′1 , p′2 , q〉, p′1 = q2 和 p′2 = q2 . 它的长是 81123 1. (文献[2 ]的 引理 16 ,看到在这个例子里 , p1 ≠p0 , p2 ) . 称这个初始例子的情形为应用 R 算法时出现 的一条退化路径. 它可能出现在算法的初始化或算 法后面的重复迭代中间. 一般地说 ,它是定义成为初 第 1 期 李发捷 ,等 :多边形序列的最短路径算法 ·25 ·
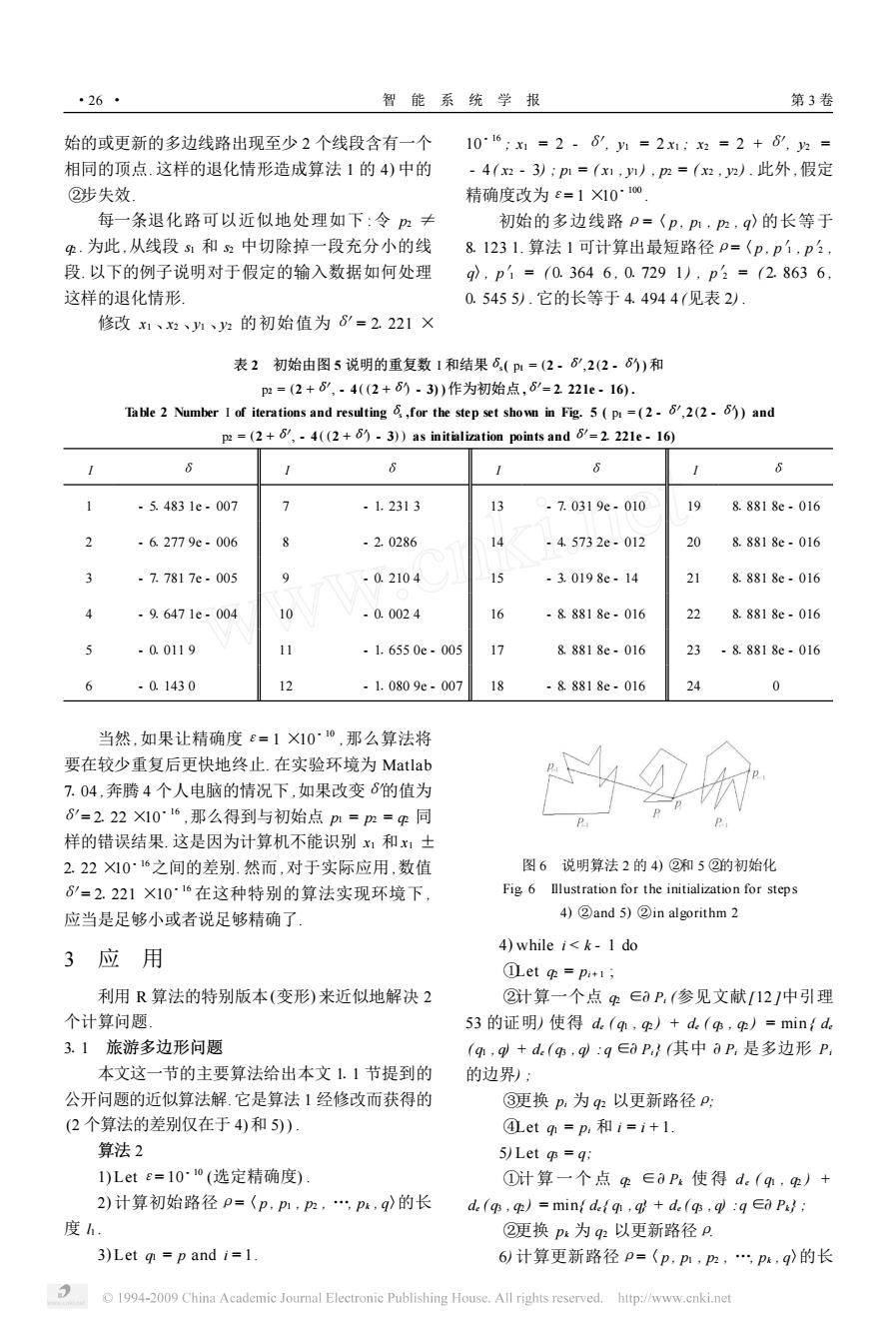
·26· 智能系统学报 第3卷 始的或更新的多边线路出现至少2个线段含有一个 106;x1=2-6,M=2x1;x2=2+8,2= 相同的顶点.这样的退化情形造成算法1的4)中的 -4(x2-3);pm1=(x1,n),p=(x2,2).此外,假定 ②步失效」 精确度改为e=1X101oo」 每一条退化路可以近似地处理如下:令历≠ 初始的多边线路p=〈p,p,m,g〉的长等于 .为此,从线段和2中切除掉一段充分小的线 8.1231.算法1可计算出最短路径p=〈p,p1,p?, 段.以下的例子说明对于假定的输入数据如何处理 q,p1=(0.3646,0.7291),p2=(2.8636, 这样的退化情形 0.5455).它的长等于4.4944(见表2). 修改x1、2、h、2的初始值为6=2.221× 表2初始由图5说明的重复数1和结果6,(p=(2.6',2(2·6)和 2=(2+6”,-4(2+6)-3)作为初始点,6-2221e-16. Table 2 Number I of iterations and resulting ,for the step set shown in Fig.5(p=(2-6,2(2)and p2 =(2+6,-4((2+6)-3))as initialization points and 6/=2 22le-16) 6 6 -5.4831e-007 7 -1.2313 13 .7.0319e-010 g 8.8818e-016 2 -6.2779e-006 8 -2.0286 14 -45732e.012 20 8.8818e-016 3 -7.7817e-005 9 -0.2104 -3.0198e-14 21 8.8818e-016 4 -9.6471e.004 10 -0.0024 16 -8.8818e-016 22 8.8818e-016 -0.0119 11 -1.6550e-005 8.8818e-016 2 -8.8818e-016 -0.1430 12 -1.0809e-007 18 -8.8818e-016 24 0 当然,如果让精确度£=1X10~°,那么算法将 要在较少重复后更快地终止.在实验环境为Matlab 7.04,奔腾4个人电脑的情况下,如果改变6的值为 8=2.22X1016,那么得到与初始点pm=pm=p同 样的错误结果.这是因为计算机不能识别x1和x1士 2.221016之间的差别.然而,对于实际应用,数值 图6说明算法2的4)②和5②的初始化 8=2.221×10~16在这种特别的算法实现环境下, Fig 6 lllustration for the initialization for steps 应当是足够小或者说足够精确了. 4)②and5)②in algorithm2 4)while i<k-1 do 3应用 ①etp=pi+1; 利用R算法的特别版本(变形)来近似地解决2 ②计算一个点∈0P(参见文献121中引理 个计算问题 53的证明)使得d.(q,)+d.(,)=min{de 3.1旅游多边形问题 (m,g+d.(,q:q∈P}(其中aP,是多边形P 本文这一节的主要算法给出本文1.1节提到的 的边界): 公开问题的近似算法解.它是算法1经修改而获得的 ③更换p,为q2以更新路径P: (2个算法的差别仅在于4)和5) ④etqm=p,和i=i+1. 算法2 5)Let gs=q: 1)Letc=10~io(选定精确度) ①计算一个点∈aP使得d.(,)+ 2)计算初始路径p=〈p,pm,pm,,p,q〉的长 de(s q)=mint de(n,q+d.(s.q :qep 度h. ②更换p:为q以更新路径P. 3)Let g=p and i=1. 6)计算更新路径p=〈p,pP,p,p,q的长 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
始的或更新的多边线路出现至少 2 个线段含有一个 相同的顶点. 这样的退化情形造成算法 1 的 4) 中的 ②步失效. 每一条退化路可以近似地处理如下 :令 p2 ≠ q2 . 为此 ,从线段 s1 和 s2 中切除掉一段充分小的线 段. 以下的例子说明对于假定的输入数据如何处理 这样的退化情形. 修改 x1 、x2 、y1 、y2 的初始值为δ′= 21221 × 10 - 16 ; x1 = 2 - δ′, y1 = 2 x1 ; x2 = 2 + δ′, y2 = - 4 ( x2 - 3) ; p1 = ( x1 , y1 ) , p2 = ( x2 , y2 ) . 此外 ,假定 精确度改为ε= 1 ×10 - 100 . 初始的多边线路ρ=〈 p , p1 , p2 , q〉的长等于 81123 1. 算法 1 可计算出最短路径ρ=〈p , p′1 , p′2 , q〉, p′1 = ( 01364 6 , 01729 1 ) , p′2 = ( 21863 6 , 01545 5) . 它的长等于 41494 4 (见表 2) . 表 2 初始由图 5 说明的重复数 I 和结果δs( p1 = (2 - δ′,2 (2 - δ′) ) 和 p2 = (2 +δ′, - 4 ( (2 +δ′) - 3) )作为初始点 ,δ′= 21221e - 16) . Table 2 Number I of iterations and resultingδs ,for the step set shown in Fig. 5 ( p1 = ( 2 - δ′,2 (2 - δ′) ) and p2 = (2 +δ′, - 4 ( (2 +δ′) - 3) ) as initialization points andδ′= 21221e - 16) I δ I δ I δ I δ 1 - 51483 1e - 007 7 - 11231 3 13 - 71031 9e - 010 19 81881 8e - 016 2 - 61277 9e - 006 8 - 210286 14 - 41573 2e - 012 20 81881 8e - 016 3 - 71781 7e - 005 9 - 01210 4 15 - 31019 8e - 14 21 81881 8e - 016 4 - 91647 1e - 004 10 - 01002 4 16 - 81881 8e - 016 22 81881 8e - 016 5 - 01011 9 11 - 11655 0e - 005 17 81881 8e - 016 23 - 81881 8e - 016 6 - 01143 0 12 - 11080 9e - 007 18 - 81881 8e - 016 24 0 当然 ,如果让精确度ε= 1 ×10 - 10 ,那么算法将 要在较少重复后更快地终止. 在实验环境为 Matlab 7104 ,奔腾 4 个人电脑的情况下 ,如果改变δ′的值为 δ′= 2122 ×10 - 16 ,那么得到与初始点 p1 = p2 = q2 同 样的错误结果. 这是因为计算机不能识别 x1 和 x1 ± 2122 ×10 - 16之间的差别. 然而 ,对于实际应用 ,数值 δ′= 21221 ×10 - 16 在这种特别的算法实现环境下 , 应当是足够小或者说足够精确了. 3 应 用 利用 R 算法的特别版本(变形) 来近似地解决 2 个计算问题. 311 旅游多边形问题 本文这一节的主要算法给出本文 111 节提到的 公开问题的近似算法解.它是算法 1 经修改而获得的 (2 个算法的差别仅在于 4)和 5)) . 算法 2 1) Letε= 10 - 10 (选定精确度) . 2) 计算初始路径ρ=〈p , p1 , p2 , …, pk , q〉的长 度 l1 . 3) Let q1 = p and i = 1. 图 6 说明算法 2 的 4) ②和 5 ②的初始化 Fig16 Illustration for the initialization for step s 4) ②and 5) ②in algorithm 2 4) while i < k - 1 do ①Let q2 = pi + 1 ; ②计算一个点 q2 ∈9 Pi (参见文献[12 ]中引理 53 的证明) 使得 de ( q1 , q2 ) + de ( q3 , q2 ) = min { de ( q1 , q) + de ( q3 , q) : q ∈9 Pi} (其中 9 Pi 是多边形 Pi 的边界) ; ③更换 pi 为 q2 以更新路径ρ; ④Let q1 = pi 和 i = i + 1. 5) Let q3 = q; ①计算一个点 q2 ∈9 Pk 使得 de ( q1 , q2 ) + de ( q3 , q2 ) = min{ de { q1 , q} + de ( q3 , q) :q ∈9 Pk } ; ②更换 pk 为 q2 以更新路径ρ. 6) 计算更新路径ρ=〈p , p1 , p2 , …, pk , q〉的长 ·26 · 智 能 系 统 学 报 第 3 卷

第1期 李发捷,等:多边形序列的最短路径算法 ·27· 度h 7)Let 6=h-k. 8如果6>e,令h=b,返回3). 否则,停止 算法2的输入例子见图7.图8显示一些测量 的时间用以说明算法的时间复杂性(正确性和时间 复杂性的证明见文献[2).解旅游问题动物园看护 人问题约束TPP问题和看守人路线问题的算法都 可以由修改算法2而获得) 图9说明子程序1 Fig 9 Illustration for procedure 1 4)Letq=minf,4}(点的坐标按字典排列次 序比较大小) 5)输出q 如果存在i,j∈1,2,…k使得i≠,0P,n aP+1≠O,那么修改算法2如下:假设pm=p, p+I=q,P6=p,而且P+1=q(算法2与算法3的 图7算法2的输入例子 差别仅在4)中的①和5)中的①.假设P=fp,p1。 Fig.7 Input example for algorithm 2 ph,pk,p时 .0 算法3 0.8 1)Letc=10~0(选定精确度) 0.6 2)计算初始路径p=〈p,pm,pm,p,q〉的长 0.4 度h. 0.2 3)Let g=p and i=1. 4)while i<k-1 do 13151719×10 X ①如果(p:=p.1且p,≠p+)或(p,≠p.1且 图8算法2的运行时间 p,=P+或(p:=P.1且p=p+1),那么应用子程 Fig.8 Measured run times for algorithm 2 序1计算一点p,使得p:卡p.且p,≠p+1 ②Letp=pi+1: 以下的子程序用以处理退化路出现的情形.当 ③计算一个点∈aP(参见文献21中引理53 应用算法3(它是算法2的一个变形)于无约束TPP 的证明)使得d.(,)+d.(,)=min{d(, 时,因为所有的多边形未必都有两两不相交的,有必 q)+d.(,9):q∈8P}其中a卫是多边形P,的 要处理这样情况 边界.): 子程序1 ④更换p,为q2以更新路径P: 输入:一点p和2个多边形B和P使得p2∈ ⑤etqm=p:和i=i+1. aP∩8B(见图9). 5)①如果(pk=pk.1且pk卡pk+1)或(p:卡pk.1 输出:一点q∈aP使得d.(g,p≤e而且q 且pk=pk+)或(P=pk.1且p:=pk+),那么应用子 0P2 程序1计算一点P:使得pk卡p.1且p:≠pk+1: 1)Let£=10~0(选定精确度); ②etp=q 2)寻找一点e∈EP)使得p∈e1∩a,此处 ③计算一个点∈P:使得d:(,p)+ j=1,2: d.(.)=min d.(aq)d.(gs g):qp 3)Let er=q.假设p和年分别是线段mp ④更换p:为92以更新路径P 和qpp上的两点(见图9)使得d。(g,p)≤e而且 6)计算更新路径p=〈p,pm,pm,pk,q〉的长 9乃,此处j=1,2; 边h. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
度 l2 . 7) Letδ= l1 - l2 . 8) 如果δ>ε,令 l1 = l2 ,返回 3) . 否则 ,停止. 算法 2 的输入例子见图 7. 图 8 显示一些测量 的时间用以说明算法的时间复杂性 (正确性和时间 复杂性的证明见文献[2 ]) . 解旅游问题、动物园看护 人问题、约束 TPP 问题和看守人路线问题的算法都 可以由修改算法 2 而获得[2 ] ) . 以下的子程序用以处理退化路出现的情形. 当 应用算法 3 (它是算法 2 的一个变形) 于无约束 TPP 时 ,因为所有的多边形未必都有两两不相交的 ,有必 要处理这样情况. 子程序 1 输入 :一点 p 和 2 个多边形 P1 和 P2 使得 p2 ∈ 9 P1 ∩9 P2 (见图 9) . 输出 :一点 q ∈9 P1 使得 de ( q , p) ≤ε而且 q 9 P2 . 1) Letε= 10 - 10 (选定精确度) ; 2) 寻找一点 ej ∈E ( Pj ) 使得 p ∈e1 ∩e2 , 此处 j = 1 ,2 ; 3) Let e1 = q1 q2 . 假设 q3 和 q4 分别是线段 q1 p 和 q2 p 上的两点 (见图 9) 使得 de ( qj , p) ≤ε而且 qj ≠9 P2 ,此处 j = 1 ,2 ; 图 9 说明子程序 1 Fig19 Illustration for procedure 1 4) Let q = min{ q3 , q4 } (点的坐标按字典排列次 序比较大小) . 5) 输出 q. 如果存在 i , j ∈{ 1 , 2 , …, k} 使得 i ≠j , 9 Pi ∩ 9 Pi + 1 ≠ ª, 那么修改算法 2 如下 : 假设 p0 = p , pk + 1 = q , P0 = p ,而且 Pk + 1 = q (算法 2 与算法 3 的 差别仅在 4) 中的 ①和 5) 中的 ①) . 假设 P = { p , p1 , p2 , …, pk , p} . 算法 3 1) Letε= 10 - 10 (选定精确度) . 2) 计算初始路径ρ=〈p , p1 , p2 , …, pk , q〉的长 度 l1 . 3) Let q1 = p and i = 1. 4) while i < k - 1 do ①如果 ( pi = pi - 1 且 pi ≠pi + 1 ) 或 ( pi ≠pi - 1 且 pi = pi + 1 ) 或( pi = pi - 1 且 pi = pi + 1 ) ,那么应用子程 序 1 计算一点 pi 使得 p i ≠pi - 1且 pi ≠pi + 1 ; ②Let q3 = pi + 1 ; ③计算一个点 q2 ∈9 Pi (参见文献[2 ]中引理 53 的证明) 使得 de ( q1 , q2 ) + de ( q3 , q2 ) = min{ de ( q1 , q′) + de ( q3 , q′) :q′∈9 Pi} (其中 9 Pi 是多边形 Pi 的 边界. ) ; ④更换 pi 为 q2 以更新路径ρ; ⑤Let q1 = pi 和 i = i + 1. 5) ①如果 ( pk = pk - 1 且 pk ≠pk + 1 ) 或 ( pk ≠pk - 1 且 pk = pk + 1 ) 或( pk = pk - 1且 pk = pk + 1 ) ,那么应用子 程序 1 计算一点 pk 使得 p k ≠pk - 1且 pk ≠pk + 1 ; ②Let q3 = q; ③计算一个点 q2 ∈9 Pk 使得 de ( q1 , q2 ) + de ( q3 , q2 ) = min { de ( q1 q) + de ( q3 q) :q ∈9 Pk } ; ④更换 pk 为 q2 以更新路径ρ. 6) 计算更新路径ρ=〈p , p1 , p2 , …, pk , q〉的长 边 l2 . 第 1 期 李发捷 ,等 :多边形序列的最短路径算法 ·27 ·

·28· 智能系统学报 第3卷 7)Letδ=h-h. 这一段应用算法2有效地解2个特殊的ESP 8)如果6>c,令h=h,转3) 问题.还指出了,这两问题的“补问题”是NP困难的 否则,停止 或NP完全的 文献2J的11.5节应用这个算法证明在所有简 关键多边形的概念的推广:假定Ⅱ是一个简单 单多边形是未必两两不相交和非凸的情形下,TPP 连通可能无界)的多面体,而且允许关键多边形是 可以有复杂性为多项式时间的近似算法解: 无界的.例如,一个广义关键多边形可以有一个顶点 定理1I无约束TPP存在复杂性为 在无穷远,或它可以是一个关键多边形的补 x(g·O(W的一种近似算法,这里n是给定多边形 使用文献12所引入的一些概念,假设(x0,, 的顶点总数 0)是三维空间中的一个点, 根据以下定理,寻找这个问题的精确解是NP S=f(x,y,:m≤xx0且y1>0. 个单位球的紧的多面体区域),表示为Ⅱ假设Ⅱ的 Sm={(x,y,o):-∞<x<∞Λ地≤y≤n: 边集是E,顶点集是V={m,2,…m S,={(x,y,:0≤x≤m八∞<y< 对于p∈Ⅱ,假设。是经过p而且平行于xoy 假设S(S)称为一个水平垂直)条, 面的平面,π。∩是有限个简单多边形组成的集合. S4=f(x,y,):m≤x<∞∧0≤y≤n}: 单个点看作是一个退化多边形.假设P是一个由P S%=x,y,):-∞<x≤∧b≤y≤n} 和π决定的这类简单多边形 S=f(x,y,):m≤x≤nΛw≤y<g; 任何简单多边形P是π。∩的一个连通部分, Sn=(x,y,0):0≤x≤1Λ∞<y≤b} 称为的相对于p的一个关键多边形 按照它们的几何形状,注意到 任何顶点p决定有限个关键多边形集.考虑任 S[S,S,S4]在(+x,+以[(-x,+以,(-x 何顶点p只确定一个关键多边形而且它是凸的情 -以,(+x,-y以]方向上是无界的:s[s1在 形:一个简单多面体是一个一型简单多面体当且仅 土x[y]方向上是无界的:s[Si Sy S]在+x 当任何顶点恰好确定一个凸关键多边形(图10 [-x,+y,-y方向上是无界的. ().一个简单多面体是一个二型简单多面体当且 S:、Sa、S,、S,和S,是轴对准矩形(见图11),这 仅当任何顶点恰好确定一个关键多边形(图10 里i=1,2,3,4,j=1,2.如果S中每个矩形在4个方 (b创) 向-x、+x、~y或+y中至少一个方向上是无界 的,轴对准矩形的堆(一个两两平行但不相交的轴对 准矩形的集合)S称为类似地形的 例1假设是一个简单多面体满足每个广义 关键多边形是轴对准矩形.假设p、q∈Ⅲ满足p:< ,Vg={v:p:<:<g且v白},这里V是的顶 点集.由文献2]的定理27可知,包含于中p和q a)一型简单多面体 (b)二型简单多面体 中间的欧几里德最短路径可以以复杂性 x(g·O(V)来近似计算.因此,这种特别的情形 图10简单多面体 的E$P问题可以有效地近似解决.然而,如果修改 Fig 10 Polyhedron 使得每个广义关键多边形是一个轴对准矩形的 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
7) Letδ= l1 - l2 . 8) 如果δ>ε,令 l1 = l2 ,转 3) . 否则 ,停止. 文献[2 ]的 1115 节应用这个算法证明在所有简 单多边形是未必两两不相交和非凸的情形下 , TPP 可以有复杂性为多项式时间的近似算法解 : 定理 1 [2 ] 无 约 束 TPP 存 在 复 杂 性 为 κ(ε) ·O( n) 的一种近似算法 ,这里 n 是给定多边形 的顶点总数. 根据以下定理 ,寻找这个问题的精确解是 NP 困难的 : 定理 2 [3 ] 对于任何 Minkowski 距离 Lp ( p ≥1) , 如果多边形 Pi 是非凸的,且它们的边与 x 轴成 0°、45° 或 90°,那么旅游多边形问题( TPP)是 NP 困难的. 312 q 矩形 对于放置于笛卡尔直角坐标系 x y z 中的三维 欧几里德空间中一个简单多面体 (即一个同胚于一 个单位球的紧的多面体区域) ,表示为 Ⅱ. 假设 Ⅱ的 边集是 E,顶点集是 V = { v1 , v2 , …, vn } . 对于 p ∈Ⅱ,假设πp 是经过 p 而且平行于 x oy 面的平面 ,πp ∩Ⅱ是有限个简单多边形组成的集合. 单个点看作是一个退化多边形. 假设 P 是一个由 p 和π决定的这类简单多边形. 任何简单多边形 P 是πp ∩Ⅱ的一个连通部分 , 称为 Ⅱ的相对于 p 的一个关键多边形. 任何顶点 p 决定有限个关键多边形集. 考虑任 何顶点 p 只确定一个关键多边形而且它是凸的情 形 :一个简单多面体是一个一型简单多面体当且仅 当任何顶点恰好确定一个凸关键多边形 (图 10 ( a) ) . 一个简单多面体是一个二型简单多面体当且 仅当任何顶点恰好确定一个关键多边形 (图 10 ( b) ) . 图 10 简单多面体 Fig110 Polyhedron 这一段应用算法 2 有效地解 2 个特殊的 ESP 问题. 还指出了 ,这两问题的“补问题”是 NP 困难的 或 NP 完全的. 关键多边形的概念的推广 :假定 Ⅱ是一个简单 连通(可能无界) 的多面体 ,而且允许关键多边形是 无界的. 例如 ,一个广义关键多边形可以有一个顶点 在无穷远 ,或它可以是一个关键多边形的补. 使用文献[12 ]所引入的一些概念 ,假设( x0 , y0 , z0 ) 是三维空间中的一个点 , S1 = { ( x , y ,z0 ) :x0 ≤x x0 且 y1 > y0 . Sh = { ( x , y ,z0 ) : - ∞< x < ∞∧y0 ≤y ≤y1 }; Sv = { ( x , y ,z0 ) :x0 ≤x ≤x1 ∧- ∞ < y < ∞}. 假设 S h ( S v ) 称为一个水平(垂直) 条 , Sh 1 = { ( x , y ,z0 ) :x0 ≤x < ∞∧y0 ≤y ≤y1 } ; Sh 2 = { ( x , y ,z0 ) : - ∞< x ≤x1 ∧y0 ≤y ≤y1 }; Sv 1 = { ( x , y ,z0 ) :x0 ≤x ≤x1 ∧y0 ≤y < ∞} ; Sv 2 = { ( x , y ,z0 ) :x0 ≤x ≤x1 ∧- ∞< y ≤y0 }. 按照它们的几何形状 ,注意到 S1 [ S2 , S3 , S4 ]在( + x , + y) [ ( - x , + y) , ( - x , - y) , ( + x , - y ) ] 方 向 上 是 无 界 的; sh [ sv ] 在 ±x [ ±y ]方向上是无界的; sh 1 [ sh 2 sv 1 sv 2 ] 在 + x [ - x , + y , - y ]方向上是无界的. S i 、S h 、S v 、S h j 和 S v j 是轴对准矩形(见图 11) ,这 里 i = 1 ,2 ,3 ,4 , j = 1 ,2. 如果 S 中每个矩形在 4 个方 向 - x、+ x、- y 或 + y 中至少一个方向上是无界 的 ,轴对准矩形的堆(一个两两平行但不相交的轴对 准矩形的集合) S 称为类似地形的. 例 1 假设 Ⅱ是一个简单多面体满足每个广义 关键多边形是轴对准矩形. 假设 p、q ∈Ⅱ满足 pz < qz ,V pq = { v : pz < vz < qz 且 v ∈V } ,这里 V 是 Ⅱ的顶 点集. 由文献[2 ]的定理 27 可知 ,包含于 Ⅱ中 p 和 q 中间 的 欧 几 里 德 最 短 路 径 可 以 以 复 杂 性 κ(ε) ·O(| V pq | ) 来近似计算. 因此 ,这种特别的情形 的 ESP 问题可以有效地近似解决. 然而 ,如果修改 Ⅱ使得每个广义关键多边形是一个轴对准矩形的 ·28 · 智 能 系 统 学 报 第 3 卷

第1期 李发捷,等:多边形序列的最短路径算法 ·29· 以有效地近似解决(见图12) 0.12 (, (Xi.W.Zo) 0.10 0.08 20.06 (x%) 0.04 0.02 10141822×10 图11轴对准矩形 Fig 11 Axis-aligned rectangles 图12算法2应用于q矩形的补的运行时间 补,那么根据定理3,寻找包含于Ⅱ中p和g中间的 Fig 12 Ilustration of measured run time for algorithm 2 欧几里德最短路径是NP完全的, applied to the complements of qrectangles. 定理32)判定是否存在一个长最多L的,回 例4修改例2如下(也只是稍微修改例2当 避以轴对准矩形堆为障碍物的,轴一对准矩形堆中 中的D:假设Ⅱ是一个单连通多面体满足每个关键 的欧几里德最短路径是NP完全的.如果所有轴对 多边形是一个三角形的补.由文献[21的定理32可 准矩形是一或三型q矩形,那么此问题在这种特别 知,包含于中p和q中间的欧几里德最短路径可 的情形下也是NP完全的 以以复杂性K(9·OAVm)来近似计算 例2修改例1当中的Ⅱ:假设Ⅱ是一个简单 例5假设S是k个水平或垂直条的堆.包含 多面体满足每个广义关键多边形是一个三角形.由 于S中的欧几里德最短路径可以以复杂性x(©·O 文献2的定理27可知,包含于Ⅱ中p和g中间的 (付近似计算.根据定理5,寻找该问题的精确解是 欧几里德最短路径可以以复杂性x(9·O(V网) NP完全的 定理52,判定是否存在一个长最多为L的 来近似计算.因此,这种特别的情形的ESP问题可 以有效地近似解决.然而,如果修改使得每个广义 回避以水平或垂直条的堆为障碍物的,欧几里德最 短路径是NP完全的 关键多边形是一个三角形的补,那么根据定理4,寻 例6假设S是k个类似地形的,轴对准矩形 找包含于中p和g中间的欧几里德最短路径是 的堆,包含于S中的欧几里德最短路径可以以复杂 NP完全的: 定理4)判定是否存在一个长最多为L的, 性x(9·O(从来近似计算.根据定理6,寻找该问题 的精确解的最好的己知算法的复杂性是O(k): 回避以三角形堆为障碍物的,欧几里德最短路径是 定理621假设S是k个地形的,轴对准矩形 NP困难的 的堆,S中的欧几里德最短路径可以以复杂性O() 在本文以下的3.3节的例3和例4,近似地解 来计算 决这2个非常困难的问题 例6说明了一个最好的已知算法的复杂性是 3.33个NP完全或NP困难问题 O(k)的精确解问题却可以以复杂性x(g·O(付来 正如本文3.2节一样,再次推广关键多边形的 近似计算(精确度参数ε可以选定给定计算机所能 概念,同样允许无界的多边形.现在应用推广的算法 保证的最大可能的数量精确度)」 2近似地解决本文3.2节所提到的困难问题, 例3修改例1如下:假设Ⅱ是一个单连通多 4结束语 面体,满足每个关键多边形是一个轴对准矩形的补 本文首先详细介绍一个简单版本的R算法作 假设p,q∈满足p:<华,这里V是的顶点集.由 为引导这个算法逼近的基本思想.然后从一个实例, 文献2的定理32可知,包含于Ⅱ中p和g中间的 而且给出一个一般的程序来解释如何处理退化路 欧几里德最短路径可以以复杂性x()·O(V网) 径.最后文章报告当应用R算法的几个版本时的结 来近似计算.因此,这种特别的情形的ESP问题可 果.实例说明R算法定义了一个广阔的可应用的算 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 11 轴对准矩形 Fig111 Axis2aligned rectangles 补 ,那么根据定理 3 ,寻找包含于 Ⅱ中 p 和 q 中间的 欧几里德最短路径是 N P 完全的. 定理 3 [12 ] 判定是否存在一个长最多 L 的 ,回 避以轴对准矩形堆为障碍物的 ,轴一对准矩形堆中 的欧几里德最短路径是 N P 完全的. 如果所有轴对 准矩形是一或三型 q 矩形 ,那么此问题在这种特别 的情形下也是 NP 完全的. 例 2 修改例 1 当中的 Ⅱ:假设 Ⅱ是一个简单 多面体满足每个广义关键多边形是一个三角形. 由 文献[2 ]的定理 27 可知 ,包含于 Ⅱ中 p 和 q 中间的 欧几里德最短路径可以以复杂性κ(ε) ·O (| V pq | ) 来近似计算. 因此 ,这种特别的情形的 ESP 问题可 以有效地近似解决. 然而 ,如果修改 Ⅱ使得每个广义 关键多边形是一个三角形的补 ,那么根据定理 4 ,寻 找包含于 Ⅱ中 p 和 q 中间的欧几里德最短路径是 NP 完全的 : 定理 4 [13 ] 判定是否存在一个长最多为 L 的 , 回避以三角形堆为障碍物的 ,欧几里德最短路径是 NP 困难的. 在本文以下的 313 节的例 3 和例 4 ,近似地解 决这 2 个非常困难的问题. 313 3 个 N P 完全或 N P 困难问题 正如本文 312 节一样 ,再次推广关键多边形的 概念 ,同样允许无界的多边形. 现在应用推广的算法 2 近似地解决本文 312 节所提到的困难问题. 例 3 修改例 1 如下 :假设 Ⅱ是一个单连通多 面体 ,满足每个关键多边形是一个轴对准矩形的补. 假设 p , q ∈Ⅱ满足 pz < qz ,这里 V 是 Ⅱ的顶点集. 由 文献[2 ]的定理 32 可知 ,包含于 Ⅱ中 p 和 q 中间的 欧几里德最短路径可以以复杂性κ(ε) ·O (| V pq | ) 来近似计算. 因此 ,这种特别的情形的 ESP 问题可 以有效地近似解决(见图 12) . 图 12 算法 2 应用于 q 矩形的补的运行时间 Fig112 Illustration of measured run time for algorithm 2 applied to the complements of q2rectangles. 例 4 修改例 2 如下 (也只是稍微修改例 2 当 中的 Ⅱ) :假设 Ⅱ是一个单连通多面体满足每个关键 多边形是一个三角形的补. 由文献[2 ]的定理 32 可 知 ,包含于 Ⅱ中 p 和 q 中间的欧几里德最短路径可 以以复杂性κ(ε) ·O(| V pq | ) 来近似计算. 例 5 假设 S 是 k 个水平或垂直条的堆. 包含 于 S 中的欧几里德最短路径可以以复杂性κ(ε) ·O ( k) 近似计算. 根据定理 5 ,寻找该问题的精确解是 NP 完全的. 定理 5 [12 ] 判定是否存在一个长最多为 L 的 , 回避以水平或垂直条的堆为障碍物的 ,欧几里德最 短路径是 N P 完全的. 例 6 假设 S 是 k 个类似地形的 ,轴对准矩形 的堆 ,包含于 S 中的欧几里德最短路径可以以复杂 性κ(ε) ·O( k) 来近似计算. 根据定理 6 ,寻找该问题 的精确解的最好的已知算法的复杂性是 O( k 4 ) : 定理 6 [12 ] 假设 S 是 k 个地形的 ,轴对准矩形 的堆 , S 中的欧几里德最短路径可以以复杂性O ( k 4 ) 来计算. 例 6 说明了一个最好的已知算法的复杂性是 O( k 4 ) 的精确解问题却可以以复杂性κ(ε) ·O( k) 来 近似计算(精确度参数ε可以选定给定计算机所能 保证的最大可能的数量精确度) . 4 结束语 本文首先详细介绍一个简单版本的 R 算法作 为引导这个算法逼近的基本思想. 然后从一个实例 , 而且给出一个一般的程序来解释如何处理退化路 径. 最后文章报告当应用 R 算法的几个版本时的结 果. 实例说明 R 算法定义了一个广阔的可应用的算 第 1 期 李发捷 ,等 :多边形序列的最短路径算法 ·29 ·

·30· 智能系统学报 第3卷 法种类而且均以x线性的复杂性近似地解决几个困 [12]MITCHELL J S B,SHARIR M.New results on shor- 难的几何问题 test paths in three dimensions[C]//Proc SCG Brook- lyn.New York,2004. 参考文献: [13]CANN YJ,REIF J H.New lower bound techniques for [1 ]BULOW T,KL ETTE R.Digital curves in 3D space and a robot motion planning problems[C]//Proc IEEE Conf Foundations Computer Science.Los Angeles,USA, linear-time length estimation algorithm [J ]IEEE Trans 1987. Pattern Analysis Machine Intelligence,2002,24(7):962 作者简介: -970. 李发捷,男,1965年生,博士,荷兰格罗 [2]LIF,KL ETTE R.Exact and approximate algorithms for 宁根大学博士后,主要研究方向为数字几何、 the calculation of shortest paths [R].IMA Minneapolis 计算几何、天文数据的计算机视觉分析,发表 2006.www.ima.umn.edu/preprints/oct2006. 论文10余篇. [3]DROR M,EFRAT A,LUBIW A,et al.Touring a se- quence of polygons[C]//ProcSTOC.San Diego,USA, 2003. [4]HOEFT J,PALEHAR U S.Heuristics for the platecut- KL ETTE Reinhard,男,1950年生,博 ting traveling salesman problem [J ]IIE Transactions, 士,教授,主要研究方向为并行计算、图像处 1997,29(9):719.731. 理、计算机视觉、数字几何、计算几何,发表论 (5]LAWLER E,L ENSTRA J,RINNOOY K A,et al.The 文250多篇,出版专著8部,编辑专著21部」 traveling salesman problem [M].New York:John Wiley KL ETTE Reinhard教授担任“IEEE and Sons,1985. Trans.PAMl”(Associate Editor),“CAAl [6]LAPORTE G,MERCURE H,NOBERT Y.Generalized Transactions on Intelligent Systems(智能系 traveling salesman problem through n clusters [J].Dis- 统学报)”(Member of Editorial Board),“Springers Computa crete Applied Mathematics,1987,18(2):185-197. tional Imaging and Vision"(Editor),"International Journal of [7]NOON C E.BEAN J C.An ecient transformation of the Computer Vision"(Member of Editorial Board),"Machine generalized traveling salesman problem [J ]INFOR, GRAPHICS &VISION"(Member of Advisory Board),"Op- 1993,31:39.44. to-Electronics Review"(Member of Editorial Advisory [8 GAREY M R,GRA HAM R L,JOHNSON D S.Some Board)等期刊的编辑或委员.是以下因际学术会议的主要发 NP-complete geometric problems[C]//Proc ACM Sym- 起人:CAIP conferences(International Conference on Com pos Theory Computing.Hershey,USA,1976. puter Analysis of Images and Patterns)(Member of Steering [9]GEOFFRION A M.Lagrangean relaxation and its uses in Committee).是28场国际学术会议(在智利、德国、新西兰、 integer programming [J ]Mathematical Programming 台湾等地)的主席或副主席.是2005年DAGM奖获得者之 Study,1974(2):28-114. 一曾应邀在阿根廷、中国、印度、意大利新西兰、台湾和美国 [10]GUIGNARD M,KIM S.Lagrangean decomposition: 等地国际学术会议作报告.在德国柏林技术大学、德因哥廷根 amodel yielding stronger Lagrangean bounds[J ]Math- 大学和新西兰奥克兰大学已指导培养14名博士和100多名 ematical Programming,1987,31(3):271-274 硕士 [11 ]DROR M.Polygon plate-cutting with a given order[J IIE Transactions,1999,31(3):271-274. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.enki.net
法种类而且均以κ线性的复杂性近似地解决几个困 难的几何问题. 参考文献 : [1 ]BULOW T , KL ETTE R. Digital curves in 3D space and a linear2time length estimation algorithm [J ]. IEEE Trans Pattern Analysis Machine Intelligence , 2002 ,24 (7) :962 - 970. [2 ]L I F , KL ETTE R. Exact and approximate algorithms for the calculation of shortest paths [ R ]. IMA Minneapolis 2006. www. ima. umn. edu/ preprints/ oct2006. [3 ] DROR M , EFRA T A ,LUBIW A , et al. Touring a se2 quence of polygons[ C ]/ / ProcSTOC. San Diego , USA , 2003. [4 ] HOEFT J , PAL EHAR U S. Heuristics for the platecut2 ting traveling salesman problem [J ]. IIE Transactions , 1997 ,29 (9) :719 - 731. [5 ]LAWL ER E ,L ENSTRA J , RINNOO Y K A , et al. The traveling salesman problem [ M ]. New York :John Wiley and Sons , 1985. [6 ]LAPORTE G, MERCURE H , NOBERT Y. Generalized traveling salesman problem through n clusters[J ]. Dis2 crete Applied Mathematics , 1987 ,18 (2) :185 - 197. [7 ]NOON C E ,BEAN J C. An e2cient transformation of the generalized traveling salesman problem [ J ]. INFOR , 1993 ,31 :39 - 44. [ 8 ] GAREY M R , GRA HAM R L ,JO HNSON D S. Some NP2complete geometric problems[ C]/ / Proc ACM Sym2 pos Theory Computing. Hershey ,USA ,1976. [ 9 ] GEOFFRION A M. Lagrangean relaxation and its uses in integer programming [ J ]. Mathematical Programming Study ,1974 (2) :28 - 114. [10 ] GU IGNARD M , KIM S. Lagrangean decomposition : amodel yielding stronger Lagrangean bounds[J ]. Math2 ematical Programming , 1987 ,31 (3) :271 - 274. [11 ]DROR M. Polygon plate2cutting with a given order[J ]. IIE Transactions , 1999 ,31 (3) :271 - 274. [12 ] MITCHELL J S B ,SHARIR M. New results on shor2 test paths in three dimensions[ C]/ / Proc SCG Brook2 lyn. New York ,2004. [13 ]CANN Y J ,REIF J H. New lower bound techniques for robot motion planning problems[ C]/ / Proc IEEE Conf Foundations Computer Science. Los Angeles , USA , 1987. 作者简介 : 李发捷 ,男 ,1965 年生 ,博士 ,荷兰格罗 宁根大学博士后 ,主要研究方向为数字几何、 计算几何、天文数据的计算机视觉分析 ,发表 论文 10 余篇. KL ETTE Reinhard , 男 , 1950 年 生 , 博 士 ,教授 ,主要研究方向为并行计算、图像处 理、计算机视觉、数字几何、计算几何 ,发表论 文 250 多篇 ,出版专著 8 部 ,编辑专著 21 部. KL ETTE Reinhard 教 授 担 任“IEEE Trans. PAMI”( Associate Editor ) ,“CAAI Transactions on Intelligent Systems (智能系 统学报) ”(Member of Editorial Board) “, Springers Computa2 tional Imaging and Vision”( Editor) “, International Journal of Computer Vision”( Member of Editorial Board) “, Machine GRAPHICS &VISION”(Member of Advisory Board) “, Op2 to2Electronics Review ”( Member of Editorial Advisory Board) 等期刊的编辑或委员. 是以下国际学术会议的主要发 起人 : CAIP conferences ( International Conference on Com2 puter Analysis of Images and Patterns) (Member of Steering Committee) . 是 28 场国际学术会议 (在智利、德国、新西兰、 台湾等地) 的主席或副主席. 是 2005 年 DA GM 奖获得者之 一. 曾应邀在阿根廷、中国、印度、意大利、新西兰、台湾和美国 等地国际学术会议作报告. 在德国柏林技术大学、德国哥廷根 大学和新西兰奥克兰大学已指导培养 14 名博士和 100 多名 硕士. ·30 · 智 能 系 统 学 报 第 3 卷