正在加载图片...
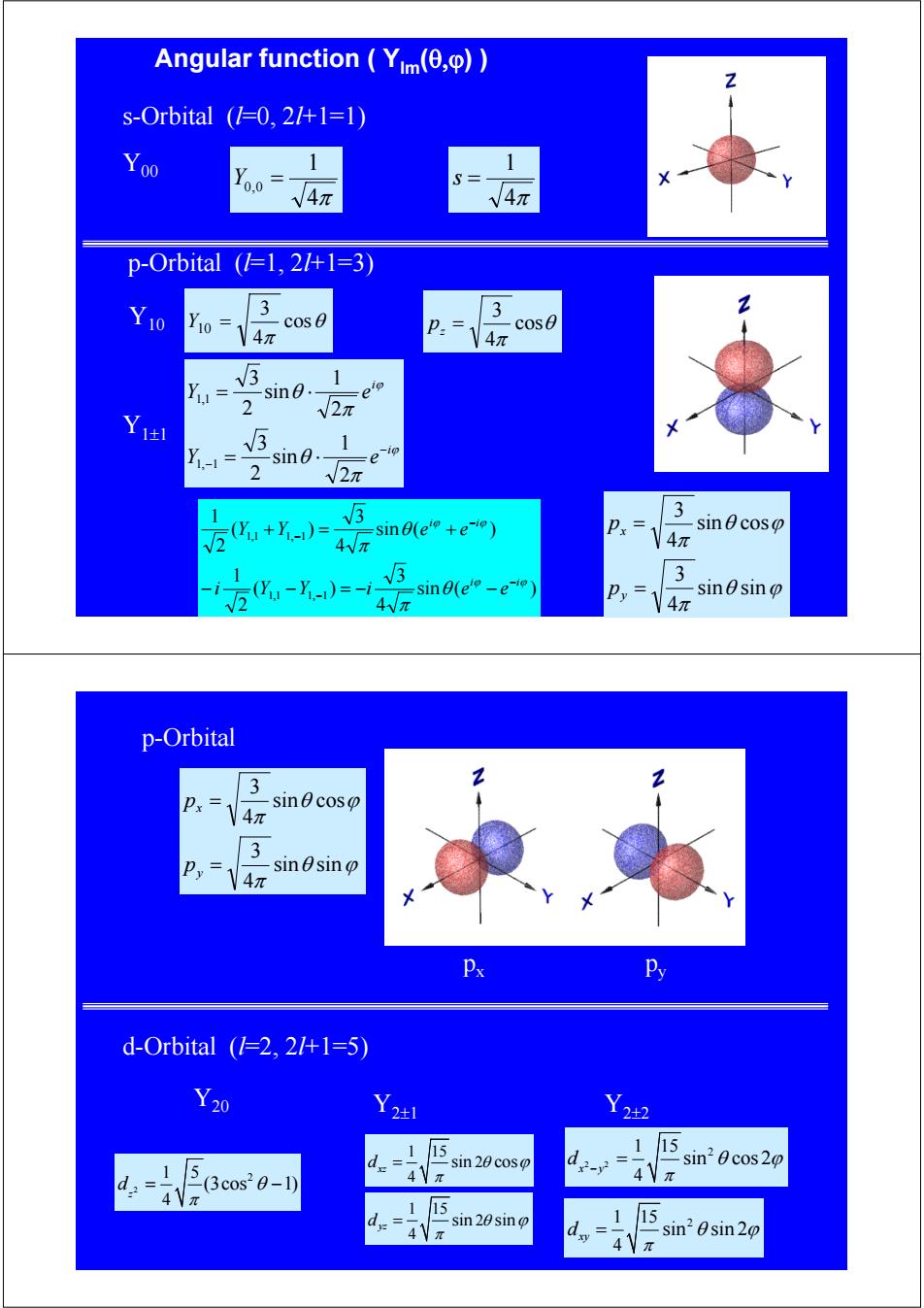
Angular function Yim(,p)) s-Orbital (1=0,21+1=1) Yoo Y 0 S= V4π √4π p-Orbital(1=1,21+1=3) 3 Y10 cos0 3 14π P.= c0s0 -Sin._ 1 Yu= 2元 5 1 Y-1= sin._ 2 2元 3 (Y+Y-) 4V元sn6(ee+ee) 卫x= sinθcosp 4π 3 -2 y-y-i)=- =sine(e-e-i) py sinsin 4π 4π p-Orbital 3 14 sinθcosp 3 Py sinsino 4π Px Py d-Orbital (1=2,21+1=5) Y20 Y22 1 15 1 15 sin 20 cos in20cos2 d 1 (3cos20-1) 4Vπ d2-y= 4Vπ 4V 1 15 sin 20sino 1 15 41 d sin20sin20 4VπAngular function ( Ylm(θ,ϕ) ) s-Orbital (l=0, 2l+1=1) Y00 4π 1 Y0,0 = 4π 1 s = θ ϕ π θ ϕ π sin sin 4 3 sin cos 4 3 = = y x p p p-Orbital (l=1, 2l+1=3) θ π cos 4 3 pz = ϕ ϕ π θ π θ i i Y e Y e − − = ⋅ = ⋅ 2 1 sin 2 3 2 1 sin 2 3 1, 1 1,1 Y1±1 sin ( ) 4 3 ( ) 2 1 sin ( ) 4 3 ( ) 2 1 1,1 1, 1 1,1 1, 1 ϕ ϕ ϕ ϕ θ π θ π i i i i i Y Y i e e Y Y e e − − − − − − = − − + = + θ π cos 4 3 Y10 Y10 = p-Orbital px py Y2±2 d-Orbital (l=2, 2l+1=5) Y2±1 Y20 2 1 5 2 4 (3cos 1) z d π = − θ 1 15 2 4 sin cos xz d θ π = ϕ 1 15 2 4 sin sin yz d θ π = ϕ 2 2 1 15 2 4 sin cos 2 x y d π θ ϕ − = 1 15 2 4 dxy sin sin 2 π = θ ϕ θ ϕ π θ ϕ π sin sin 4 3 sin cos 4 3 = = y x p p