
Chapter 2 Atomic structure 2.1 The Schrodinger equation and its solution for one-electron atoms 2.1.1 The Schrodinger equation The Hamiltonian Operator of one-electron atoms H atom,He+and Li2+ =in+元+ne= 2mn n 2m。 V:+P-
Chapter 2 Atomic structure 2.1 The Schrödinger equation and its solution for one-electron atoms 2.1.1 The Schrödinger equation The Hamiltonian Operator of one-electron atoms H atom, He+ and Li2+ e n e e n n n e n e V m m H = T +T +V − = − ∇ − ∇ + − ˆ 2 2 ˆ ˆ ˆ ˆ 2 2 2 2 h h e N
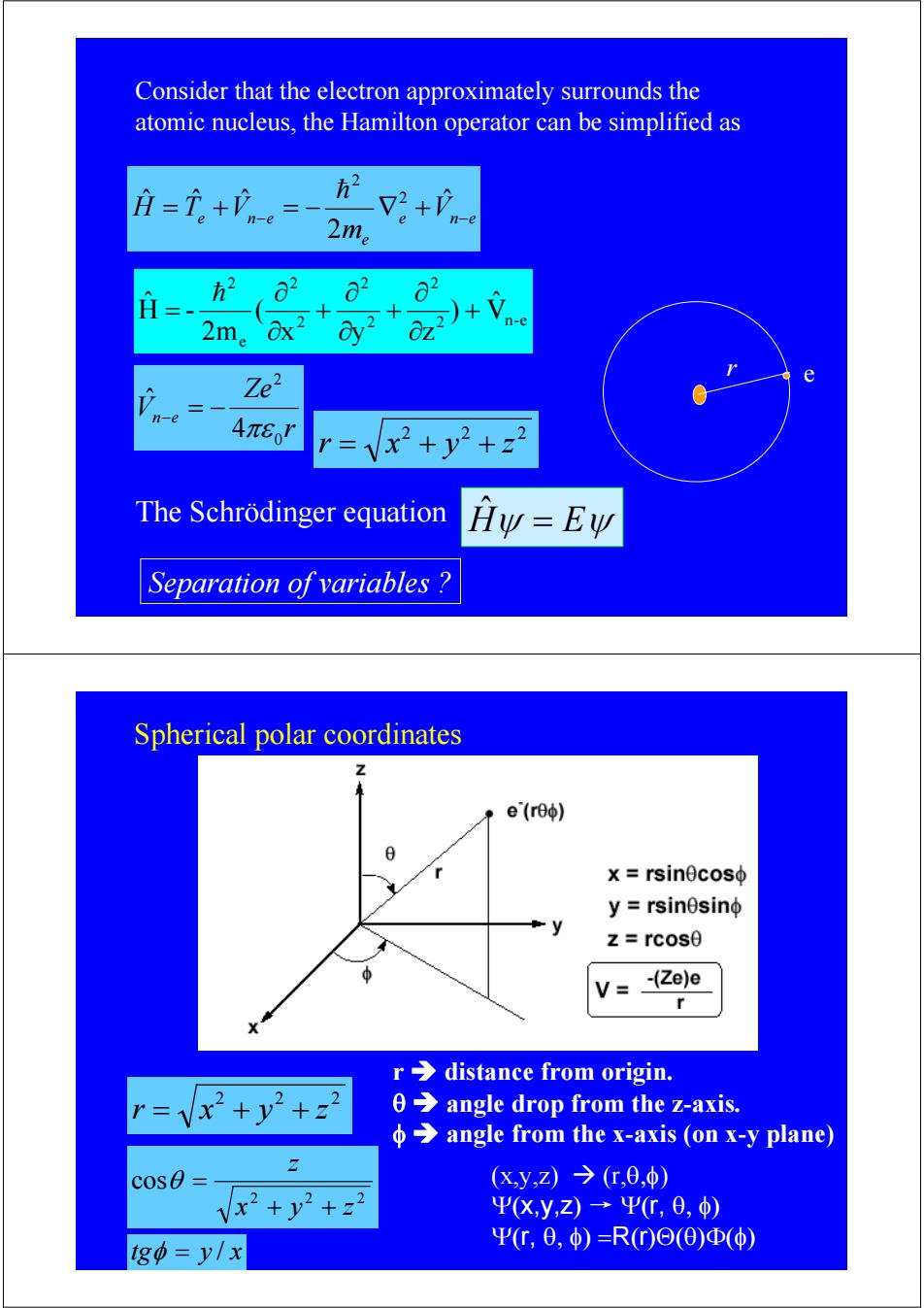
Consider that the electron approximately surrounds the atomic nucleus,the Hamilton operator can be simplified as =i。+n= 2+心 2m。 o2 62 2m。 2)+Vn-e OZ Ze2 e n-e 4πer r=Vx2+y2+z2 The Schrodinger equation Hy=Ew Separation of variables Spherical polar coordinates Z e(re) x rsinecoso y=rsinesinφ z=rcos0 V=_ (Ze)e r r>distance from origin. =Vx+y2+z2 0 angle drop from the z-axis. angle from the x-axis (on x-y plane) cos0= (x,y,Z)→(,0,φ) Vx2+y2+22 ΨX,y,z)→Ψr,6,) g中=y/x Ψr,0,φ)=R(r)Θ(Θ)Φ(φ)
e n e e e n e V m H = T +V − = − ∇ + − ˆ 2 ˆ ˆ ˆ 2 2 h r Ze Vn e 0 2 4 ˆ πε − = − Consider that the electron approximately surrounds the atomic nucleus, the Hamilton operator can be simplified as r e 2 2 2 r = x + y + z 2 n-e 2 2 2 2 2 e 2 Vˆ ) x y z ( 2m H - ˆ + ∂ ∂ + ∂ ∂ + ∂ ∂ = h Separation of variables ? The Schrödinger equation Hˆψ = Eψ Spherical polar coordinates 2 2 2 r = x + y + z (x,y,z) Æ (r,θ,φ) Ψ(x,y,z) → Ψ(r, θ, φ) Ψ(r, θ, φ) =R(r)Θ(θ)Φ(φ) r Î distance from origin. θ Î angle drop from the z-axis. φ Î angle from the x-axis (on x-y plane) 2 2 2 cos x y z z + + θ = tgφ = y / x

Spherical polar coordinates ar、aa0、op、a +( + Ox Ox op sine coso- cosecoso a sinΦ 0 r 00 rsine00 a 0 cos0sinφ a coso a sinsin 的 a a0 rsine dd sine 02 =Cos0. or a0 D2 1 1 (S11n7○ 1 o2 r2 ar Or r2 sine d0 a0' r2sin20062 Ze2 n-e (4πE)r The Schrodinger equation 1 1 a Ze2 (sin 十 ay8π2m(E+ )w=0 or r2sin 00 ae r2sin20862 h2 4π8' 2.1.2 The solution --separation of variables Substitute P(r,0,Φ)=R(r)⊙(O)Φ(φ)into the equation 1 )+7sin0 1 a 1 y8πm(E+ Or sn0c%+7sn900伊 Ze2 )w=0 a0 π8I and multiply with r2 R(r)Θ(0)Φ(φ) 1 1 (sin 1 )+ R(r)ar (0)sine a0 a0 ao0+8(E+4 ()sin20 02 h2 e2r2=0 1 0 2aR(r)、, 8m(E AnEo ze 1 R(r)or Or h2 er=o0)sino o0 (sin) 1 aΦ() + a01 Φ()sin20ap2
Spherical polar coordinates () ( ) ( ) r x xr x xp θ φ θ ∂ ∂∂ ∂ ∂ ∂ ∂ =+ + ∂ ∂∂ ∂∂ ∂∂ cos cos sin sin cos rr rsin θ φ φ θ φ θ θ φ ∂ ∂ ∂ =+ − ∂ ∂∂ cos sin cos sin sin y rr rsin θ φ φ θ φ θ θ φ ∂ ∂ ∂∂ = + ⋅+ ⋅ ∂ ∂ ∂∂ θ θ θ ∂ ∂ − ⋅ ∂ ∂ = ∂ ∂ z r r sin cos 2 2 2 2 2 2 2 2 sin 1 (sin ) sin 1 ( ) 1 θ θ φ θ θ θ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ ∇ = r r r r r r 2 0 (4 ) n e Ze V πε r − = − The Schrödinger equation 2 2 2 2 2 2 22 2 2 0 11 1 8 ( ) (sin ) ( ) 0 sin sin 4 me Ze r E rr r r r h r ψ ψψ π θ ψ θ θ θ θ φ πε ∂∂ ∂ ∂ ∂ + + + += ∂∂ ∂ ∂ ∂ 2.1.2 The solution --- separation of variables Substitute Ψ(r, θ, φ) =R(r)Θ(θ)Φ(φ) into the equation 2 2 2 2 2 2 22 2 2 0 11 1 8 ( ) (sin ) ( ) 0 sin sin 4 me Ze r E rr r r r h r ψ ψψ π θ ψ θ θ θ θ φ πε ∂∂ ∂ ∂ ∂ + + + += ∂∂ ∂ ∂ ∂ and multiply with ( ) ( ) ( ) 2 R r Θ θ Φ φ r ) 0 4 ( ( ) 8 ( )sin 1 ) ( ) (sin ( )sin 1 ) ( ) ( ( ) 1 2 0 2 2 2 2 2 2 2 + + = ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ + ∂ ∂ ∂ ∂ r r ze E h m r R r r R r r e πε π φ φ θ φ θ θ θ θ θ θ ] ( ) ( )sin 1 ) ( ) (sin ( )sin 1 ) [ 4 ( 8 ) ( ) ( ( ) 1 2 2 2 2 0 2 2 2 2 φ φ θ φ θ θ θ πε θ θ θ π ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ + + = − ∂ ∂ ∂ ∂ r r ze E h m r R r r R r r e

1 8(rOR(r)+8'm (E+e e)r2=[ 10 (sin8(0、 aΦ(p) R(r) 4πEJ (0)sine a0 a0 Φ()sin20ap2 1(r) ze- let 8πm(E+ )r2=B R(r)Or h2 Radial part,R eq. 4πE1 1 a (sin() 1 a2D() =-B Angular part ⊙(0)sin0aa a0 Φ()sin20ap2 multiplied sin20 sine (sin 1 ()=-Bsin20 ⊙(0)a 60 Φ()ab2 sine o (sin() +Bsin20=- 1 aΦ() ⊙()a8 a0 ()ap2 sin0 let (sin() +Bsin20=m2 Θ(0)a a0 p©eq. 1 ∂Φ() 三-ml DΦ Φ()a2 eq. a.Φ(b)equation d2Φ(p) dd +m2Φ()=0 Its complex form: Φ=Aetilml№,letm=±ml,Φ=Aem Normalization 2 ΦΦdΦ-=4eme地=l 1 A= V2π 1 m -cosm+- -sin mo V2元 √2 2 Φm(φ)=Φm(p+2π The values of m must be eim(+2r)=eimp.em2r m=0,±1,±2, =1 m magnetic quantum cos2mπ+isin2mn=1 number
β πε π + + = ∂ ∂ ∂ ∂ 2 0 2 2 2 2 ) 4 ( 8 ) ( ) ( ( ) 1 r r ze E h m r R r r R r r let e ] ( ) ( )sin 1 ) ( ) (sin ( )sin 1 ) [ 4 ( 8 ) ( ) ( ( ) 1 2 2 2 2 0 2 2 2 2 φ φ θ φ θ θ θ πε θ θ θ π ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ + + = − ∂ ∂ ∂ ∂ r r ze E h m r R r r R r r e f Angular part f Radial part, R eq. β φ φ θ φ θ θ θ θ θ θ = − ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ 2 2 2 ( ) ( )sin 1 ) ( ) (sin ( )sin 1 β θ φ φ θ φ θ θ θ θ θ θ 2 2 2 2 sin ( ) ( ) 1 ) ( ) (sin ( ) sin sin = − ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ multiplied 2 2 2 ( ) ( ) 1 ) sin ( ) (sin ( ) sin φ φ φ β θ θ θ θ θ θ θ ∂ ∂ Φ Φ + = − ∂ ∂Θ ∂ ∂ Θ 2 2 ) sin ( ) (sin ( ) sin let + = m ∂ ∂Θ ∂ ∂ Θ β θ θ θ θ θ θ θ 2 2 2 ( ) ( ) 1 = −m ∂ ∂ Φ Φ φ φ φ fΘ eq. fΦ eq. a. Φ(φ) equation Its complex form: Φ =Ae±i|m|φ , let m= ±|m|, Φ =Aeim φ ( ) 0 ( ) 2 2 2 + Φ = Φ φ φ φ m d d 1 2 2 0 2 0 * Φ Φ Φ = Φ = − ∫ ∫ d A e e d Normalization im im m m φ φ π π Φ (φ) = Φ (φ + 2π ) m m The values of m must be m = 0,±1,±2,⋅⋅⋅⋅⋅⋅ m : magnetic quantum number 2π 1 A = φ π φ π π φ m i e m im m sin 2 cos 2 1 2 1 Φ = = + imφ im(φ 2π ) imφ im2π e = e = e ⋅e + cos 2 sin 2 1 1 2 + = = π π π m i m eim

complex function Φn=Aemo (m=0,±1,±2,…) Usually,real functions are used,which are deduced from the complex function according to the assumption of the linear combination of these states Aeo=Acosmo+iAsinmo -m=Ae mo=Acosmo-iAsin mo ④D1=Φm+①-m=2Ac0smp=Bcosmp Φ2=Φm-Φm=2 iAsin mo=B'sinmo m normalization condition 1 (2 (Bcosmo)2dΦ=B2π=1 Φ Jo ΦΦdΦ= cosmo B sinmo Table The solution ofΦ(φ)equation m complex form real form 1 1 0 Φ0=1 2元 D022r 1 ①1= cos √2π Vπ 1 Φ1= e ip Φ= 1 sin √2元 Vπ 1 1 2 Φ2= cos20 √2π Φ= Vπ -2= Φ -sin 20 √2π Vπ
ϕ ϕ ϕ ϕ iA m B m A m B m m m m m 2 sin 'sin 2 cos cos 2 1 Φ = Φ − Φ = = Φ = Φ + Φ = = − − Usually, real functions are used, which are deduced from the complex function according to the assumption of the linear combination of these states . complex function Φ = Ae (m = 0,±1,±2,⋅⋅⋅⋅⋅⋅) im m ϕ ϕ ϕ ϕ ϕ ϕ ϕ Ae A m iA m Ae A m iA m im m im m cos sin cos sin Φ = = − Φ = = + − − π ϕ π π π 1 ( cos ) 1 2 2 2 0 1 * 1 2 0 = Φ Φ Φ = Φ = = ∫ ∫ B d B m d B normalization condition ϕ π ϕ π m m sin 1 cos 1 2 1 Φ = Φ = Table The solution of Φ(φ) equation ϕ π π ϕ π π ϕ π π ϕ π π π π ϕ ϕ ϕ ϕ sin 2 1 2 1 2 cos 2 1 2 1 2 sin 1 2 1 1 cos 1 2 1 1 2 1 2 1 0 sin 2 2 2 cos 2 2 2 sin 1 1 cos 1 1 0 0 − Φ = Φ = Φ = Φ = − Φ = Φ = Φ = Φ = Φ = Φ = ± − − ± ± − − ± i i i i e e e e m complex form real form

b.⊙o)equation sinθa ©(0)a0 (sine (+Bsin=m a0 When B=1(/+1),=0,1,2,3,......(0)is a well behaved function, 1:angular momentum quantum number necessary condition:>m hence,l=0,1,2,3…s,p,dfg,h…) m=0.1,0n1,2,-1,0,1,2).… Examples of⊙(o): 1 m Θ(8) 0 0 店 1 0 6 2 cos0 ±1 -sin0 2 2 0 v1 4 (3c0s20-1) ±1 15 sinθcos0 ±2 15 V4 sin20
b. Θ(θ) equation When β=l(l+1), l =0,1,2,3,…… Θ(θ) is a well behaved function, l : angular momentum quantum number necessary condition: l ≥ |m| hence, l = 0, 1, 2, 3,…(s,p,d,f,g,h…) m=0,(-1,0,1),(-2,-1,0,1,2)…… 2 2 ) sin ( ) (sin ( ) sin + = m ∂ ∂Θ ∂ ∂ Θ β θ θ θ θ θ θ θ Examples of Θ(θ): l m 0 0 1 0 ±1 2 0 ±1 ±2 Θ(θ ) θ2 sin 4 15 2 1 cosθ 2 6 sinθ 2 3 (3cos 1) 4 10 2 θ − sinθ cosθ 2 15

c.Solution of R equation 1 dR(r) 8πme(E+ e R(r)dr Or 3 )r2=B 4π6J Solution R(r)=N·ep2L2H n+1(p) 2Z p=2ar= 4πEh2 nao ao =0.529 me2 ao is called Bohr radius n--1 2(p)=-I) {n+10}2 k=0 (n-1-1-k)(21+1+k)Ik necessary condition:n /+1 hence,n 1,2,3,...... n: Principal quantum number 1=0,1,2 Zh2 E= 8元2na 8π2ma R is called Rydberg constant with the value of 13.6 eV Example: 3/2 n=1,=0 R0=2 e-pl2 do n=2,1=0 3/2 1 Z R20 (2-p)ep/2 2W2 ao
c. Solution of R equation β πε π + + = ∂ ∂ 2 0 2 2 2 2 ) 4 ( 8 ) ( ) ( ( ) 1 r r ze E h m r dR r r R r dr e Solution /2 2 1 () ( ) l Rr N e Ln l ρ ρ − + = ⋅ + 0 2 2 Z r r na ρ α = = 1 2 21 1 0 {( )!} ( ) ( 1) ( 1 )!(2 1 )! ! n l lk k m l k n l L nl k l kk ρ ρ − − + + + = + = − −−− ++ ∑ a0 is called Bohr radius o 2 2 0 0 0.529 A 4 = = m e a e πε h necessary condition: n ≥ l+1 hence, n = 1, 2, 3,…… l = 0, 1, 2, …… n: Principal quantum number 22 2 2 2 2 22 2 2 2 2 0 0 ( ) 8 8 Z h hZ Z E R π π mn a ma n n =− =− ⋅ =− R is called Rydberg constant with the value of 13.6 eV n=1, l=0 Example: 3/2 / 2 10 0 2 Z R e a −ρ ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ n=2, l=0 / 2 3/ 2 0 20 (2 ) 2 2 1 ρ ρ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = e a Z R

Some wavefunctions of hydrogen atom and hydrogen-like ions TABLE 14.4 Normalized Hydrogenlike Wave Functions K shell n=1,1=0,m=0 )-图)。 )e-zian Lshell n=2,1=0,m=0 )-(”6- )c-mm n=2,1✉1,m=0 0-z原”系enos0 ao n=2,1=1,m=±1 yp=}ean如9m6 do o-左佰 e-Zr2a0 sinsin do The functions here are real linear combinations of the m+I and m:=-1 wave functions (see p.640). Ψ(,0,φ)=R)⊙(⊙)Φ() 2.2 The physical significance of quantum number
Some wavefunctions of hydrogen atom and hydrogen-like ions Ψ(r, θ, φ) =R(r)Θ(θ)Φ(φ) 2.2 The physical significance of quantum number

2.2.1 The allowed values of quantum numbers Quantum Numbers m 010+1010+1Λ -2-10+1+2 -2-10+1+2 -3-2-10+1+2+3 Problem:What values of the azimuthal (1)and magnetic (m)quantum numbers are allowed for a principal quantum number(n)of 4?How many orbitals are allowed for n=4? Solution:The 1 values go from 0 to (n-1),and for n=3 they are: 1 =0,1,2,3.The values for m go from-1 to zero to +l For1=0,m1=0 1=1,m=-1,0,+1 1=2,m1=-2,-1,0,+1,+2 1=3,m1=-3,-2,-1,0,+1,+2,+3 There are 16 mr values,so there are 16 orbitals for n=4! The total number of orbitals for a given value of n is n2
Quantum Numbers n l ml 1 2 3 4 0 0 1 0 1 2 0 1 2 3 0 0 -1 0 +1 0 -1 0 +1 0 -1 0 +1 -2 -1 0 +1 +2 -2 -1 0 +1 +2 -3 -2 -1 0 +1 +2 +3 2.2.1 The allowed values of quantum numbers Problem: What values of the azimuthal (l) and magnetic (m) quantum numbers are allowed for a principal quantum number (n) of 4? How many orbitals are allowed for n=4? Solution: The l values go from 0 to (n-1), and for n=3 they are: l = 0,1,2,3. The values for m go from -l to zero to +l For l = 0, ml = 0 l = 1, ml = -1, 0, +1 l = 2, ml = -2, -1, 0, +1, +2 l = 3, ml = -3, -2, -1, 0, +1, +2, +3 There are 16 mL values, so there are 16 orbitals for n=4! • The total number of orbitals for a given value of n is n2

2.2.2 The principal quantum number,n .Also called the"energy"quantum number,indicates the approximate distance from the nucleus. Denotes the electron energy shells around the atom,and is derived directly from the Schrodinger equation. 。The higher the value of“n”,the greater the energy of the orbital. Positive integer values of n=1,2,3,etc. Example:Energy states of a H atom. 1 n principal En=-13.6 En -R n=1,2,3..∞ n n=1 ground state R=13.6eV E1=-13.6eV n 2 first excited state n 3 second excited state E2=-3.40eV Principle Quantum Energy. E3=-1.51eV Numher Continuum ev 0 n=5 -0.54 n=4 VVYV业 -0.85 E4=-0.85eV n=3- tvvve Brackett Paschen series -1.51 series n=2 YY业业 -3.39 E5=-0.54eV Balmer senes A=950A A=973A A=1026A A-1216A 业业业业" Convergence limit n"1 -13.6 Lyman series E。=0eV
2.2.2 The principal quantum number, n •Also called the “energy “ quantum number, indicates the approximate distance from the nucleus . • Denotes the electron energy shells around the atom, and is derived directly from the Schrodinger equation. • The higher the value of “n” , the greater the energy of the orbital. • Positive integer values of n = 1 , 2 , 3 , etc. n = principal n = 1, 2, 3 …∞ n = 1 : ground state n = 2 : first excited state n = 3 : second excited state En n = − ⎛ ⎝ ⎜ ⎜ ⎞ ⎠ ⎟ ⎟ 13 6 1 2 . E1 = -13.6 eV E2 = -3.40 eV E3 = -1.51 eV E4 = -0.85 eV E5 = -0.54 eV • • • E∞ = 0 eV Example: Energy states of a H atom. 2 n 2 Z E R n = − R = 13.6 eV