
Chapter 8 The structures and properties of metals and alloys 8.1 The metallic bond and the general properties of metals 8.1.1 The "free-electron"model of the metallic bond The Schrodinger equation for the "free electrons"is V2y+[8π2m]/h2]Evw=0 V=0 Er=5.04*10-19 J or 3.15eV (for Na) Experimental value 3.2 eV 8.1.2 The band theory of solids Considering the electrons in metals moving in a periodic potential field of the metal atoms,the Schrodinger equation is (-h2/[8π2m]72+V)w=Ey Insulator: Metal: Semiconductor: Empty band Thermally Conduction band excited electrons Band gap Eg≥5eV “Bandgap' Eg<3eV Empty states: Filled band Valence band "holes'” Partially filled bands ---conduction bands
Chapter 8 The structures and properties of metals and alloys 8.1 The metallic bond and the general properties of metals 8.1.1 The “free-electron” model of the metallic bond The Schrödinger equation for the “free electrons” is ∇2ψ + [8π2m]/h2]Eψ=0 EF = 5.04*10-19 J or 3.15eV (for Na) Experimental value 3.2 eV V=0 8.1.2 The band theory of solids Considering the electrons in metals moving in a periodic potential field of the metal atoms, the Schrodinger equation is (-h2/[8π2m] ∇2+ V) ψ = Eψ Band gap Partially filled bands ---- conduction bands Eg≥5eV Eg<3eV Empty band Filled band
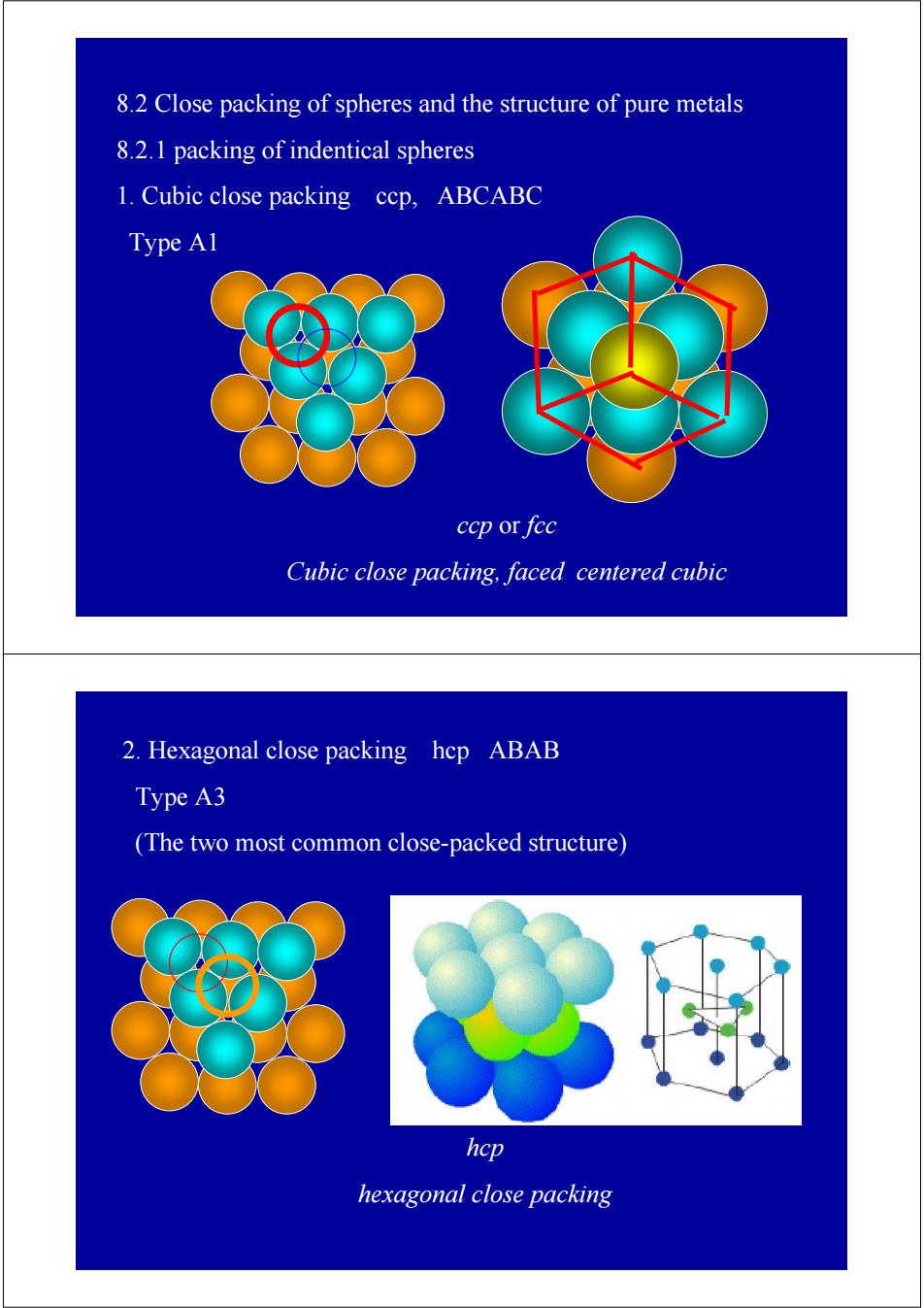
8.2 Close packing of spheres and the structure of pure metals 8.2.1 packing of indentical spheres 1.Cubic close packing ccp,ABCABC Type A1 ccp or fcc Cubic close packing,faced centered cubic 2.Hexagonal close packing hcp ABAB Type A3 (The two most common close-packed structure) 多胶 hcp hexagonal close packing
8.2 Close packing of spheres and the structure of pure metals 8.2.1 packing of indentical spheres 1. Cubic close packing ccp, ABCABC Type A1 ccp or fcc Cubic close packing, faced centered cubic 2. Hexagonal close packing hcp ABAB Type A3 (The two most common close-packed structure) hcp hexagonal close packing
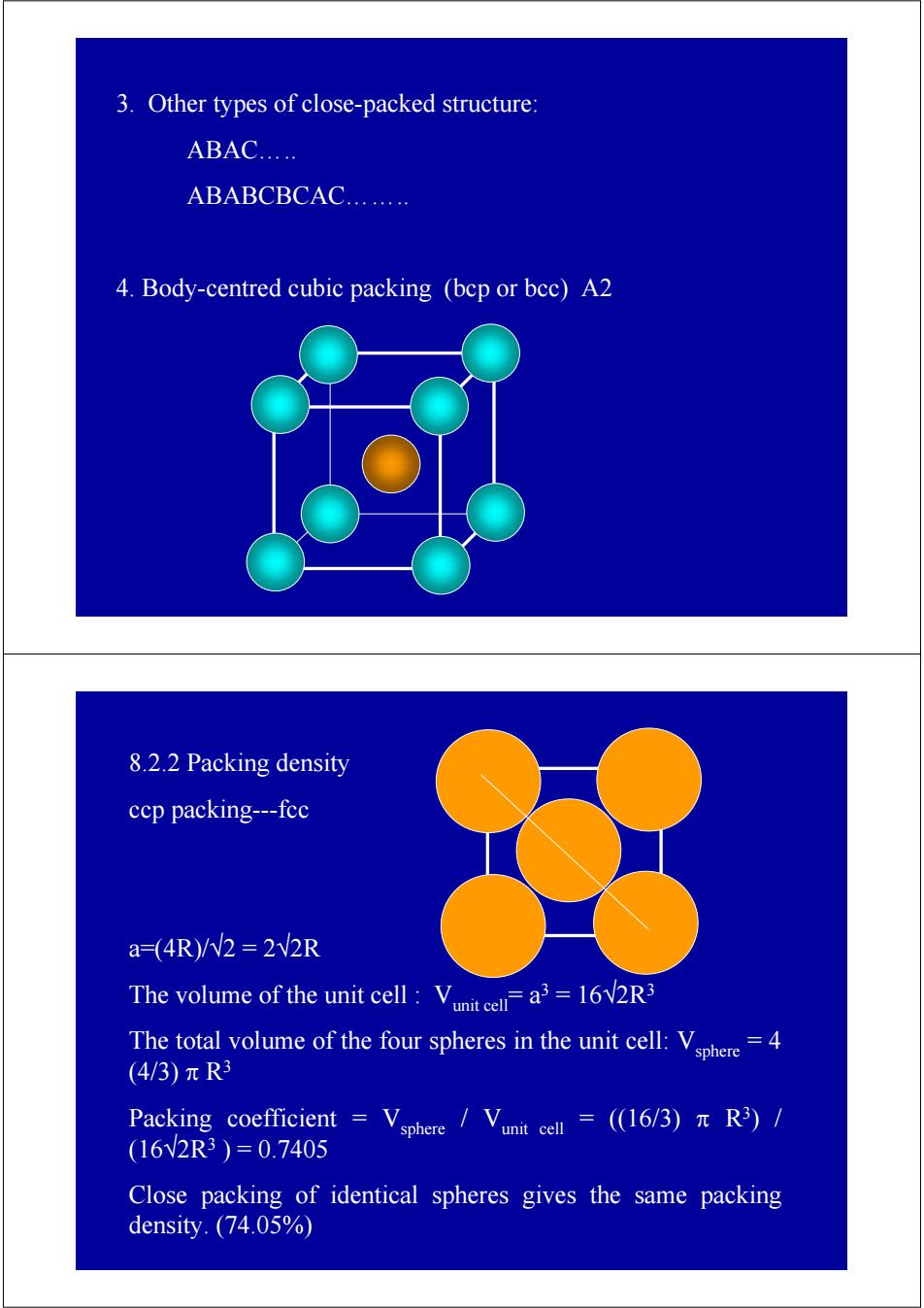
3.Other types of close-packed structure: ABAC..… ABABCBCAC........ 4.Body-centred cubic packing (bep or bec)A2 8.2.2 Packing density ccp packing---fcc a=(4R)/W2=2V2R The volume of the unit cell:Va=16V2R3 The total volume of the four spheres in the unit cell:Vhere=4 (4/3)πR3 Packing coefficient Vsphere ,/Vunit cell=(16/3)πR)/ (16V2R3)=0.7405 Close packing of identical spheres gives the same packing density.(74.05%)
3. Other types of close-packed structure: ABAC….. ABABCBCAC…….. 4. Body-centred cubic packing (bcp or bcc) A2 8.2.2 Packing density ccp packing---fcc a=(4R)/√2 = 2√2R The volume of the unit cell : Vunit cell= a3 = 16√2R3 The total volume of the four spheres in the unit cell: Vsphere = 4 (4/3) π R3 Packing coefficient = Vsphere / Vunit cell = ((16/3) π R3) / (16√2R3 ) = 0.7405 Close packing of identical spheres gives the same packing density. (74.05%)
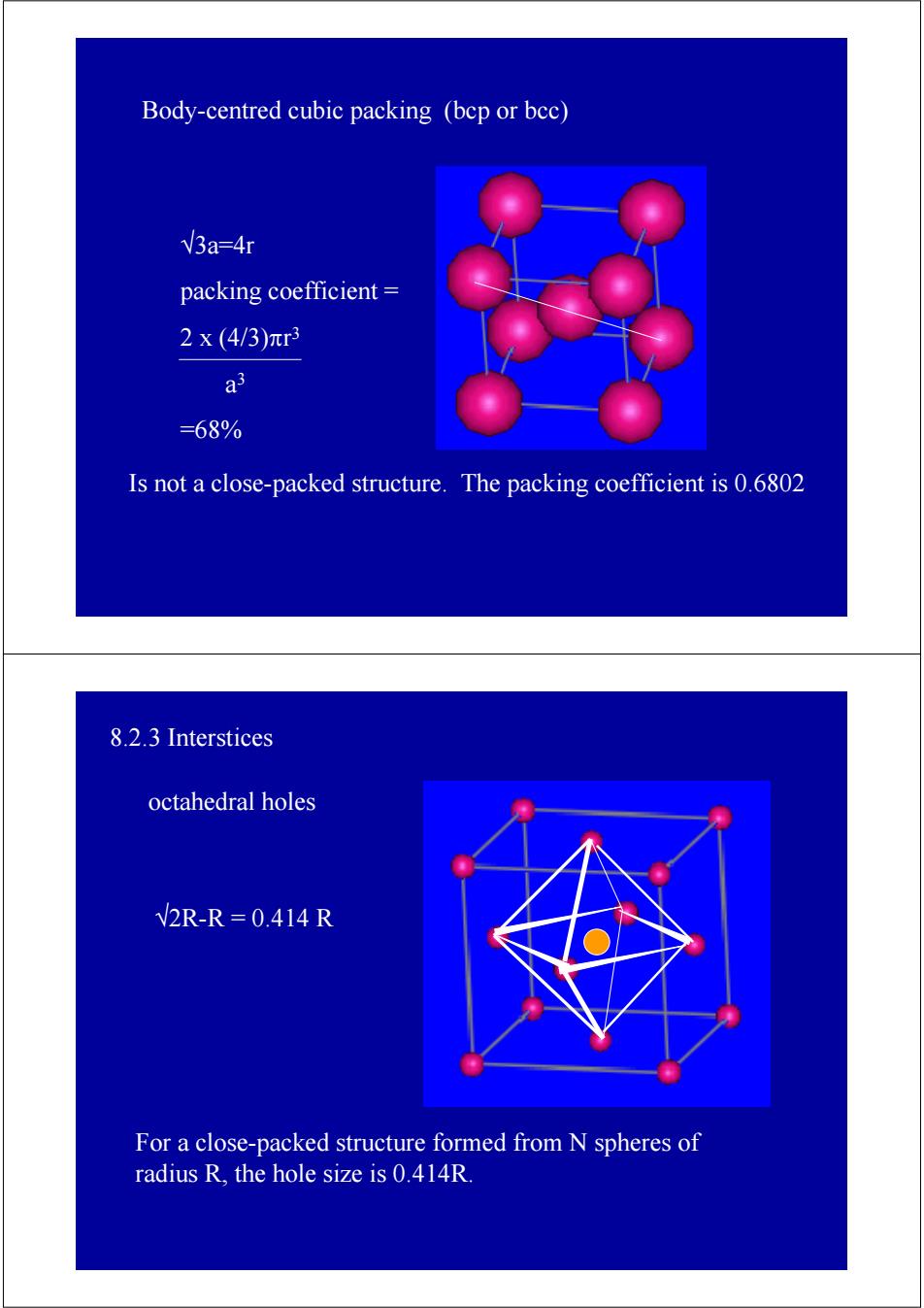
Body-centred cubic packing (bcp or bec) V3a-4r packing coefficient 2x(4/3)πr3 a =68% Is not a close-packed structure.The packing coefficient is 0.6802 8.2.3 Interstices octahedral holes V2R-R=0.414R For a close-packed structure formed from N spheres of radius R,the hole size is 0.414R
Body-centred cubic packing (bcp or bcc) Is not a close-packed structure. The packing coefficient is 0.6802 √3a=4r packing coefficient = 2 x (4/3)πr3 a3 =68% 8.2.3 Interstices For a close-packed structure formed from N spheres of radius R, the hole size is 0.414R. octahedral holes √2R-R = 0.414 R
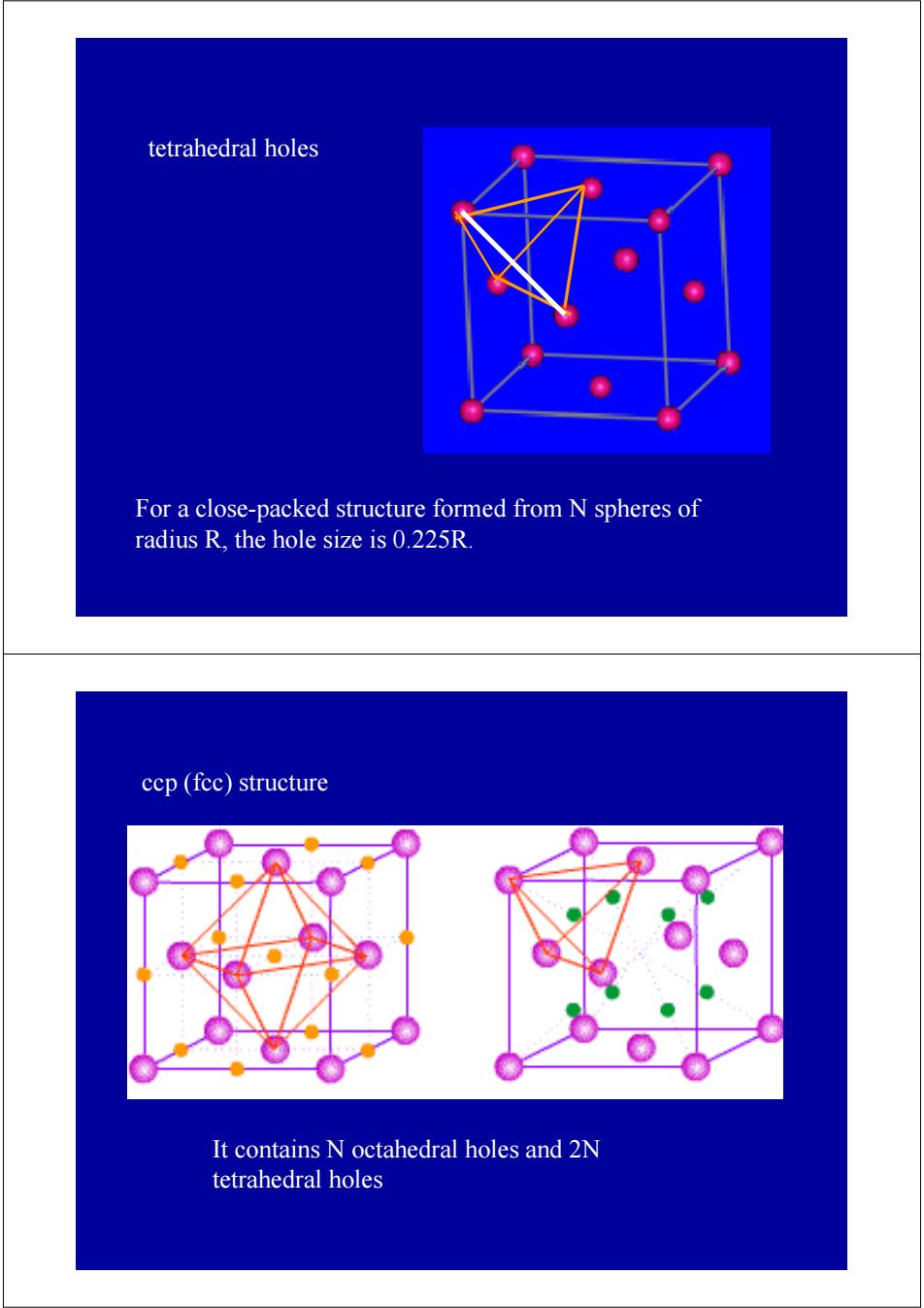
tetrahedral holes For a close-packed structure formed from N spheres of radius R,the hole size is 0.225R. ccp(fec)structure It contains N octahedral holes and 2N tetrahedral holes
For a close-packed structure formed from N spheres of radius R, the hole size is 0.225R. tetrahedral holes It contains N octahedral holes and 2N tetrahedral holes ccp (fcc) structure

hep structure Interstices in bcp structure There are 3 octahedral holes The holes are not regular octahedra but are compressed. r/R=0.154 There are 6 tetrahedral holes and 12 trigonal holes
hcp structure Interstices in bcp structure There are 3 octahedral holes. The holes are not regular octahedra but are compressed. r/R = 0.154 There are 6 tetrahedral holes and 12 trigonal holes

8.2.4 A structural survey of pure metals A1,A2,A3 A4 The diamond structure) H He Li Be B C N Ne Na Mg St P C Ar K Ca Se Ti Cr Mn Fe Ni Cu Zn Ga Ge As Se Br Kr Rb Sr Zr Nb Mo Ru Rh Pd Ag Cd In Sn Sb Te J Cs Be La Hr Ta Re Os Pt Au Hg Pb Bi Po At Rn Fr Ra Ac CePr Nd PmSmEu Gd To Dy Ho Er Tu Yh Lu Th Pa U Np Pu AmCmBk Cr E TmMd bcp fee hcp
8.2.4 A structural survey of pure metals A1, A2, A3 A4 ( The diamond structure) bcp fcc hcp

The number of electrons in the s and p orbital affects the type of structure: When the average number ofs and p electrons for each atoms is small,type A2 is preferred Na Ne]3s! is large Al is preferred Al 3s23pl is intermediate value,A3 is preferred Mg 3s2 8.2.5 Atomic radii of metals (1)Within a family,the atomic radius increases as the atomic number increases (2)Within the same period,the atomic radius decreases as the atomic number increases (3)For transition metals within the same period,the atomic radius first decreases steadily and then increase slightly (4)“lanthanide contraction”effect
The number of electrons in the s and p orbital affects the type of structure: When the average number of s and p electrons for each atoms is small, type A2 is preferred Na [Ne]3s1 is large A1 is preferred Al 3s23p1 is intermediate value, A3 is preferred Mg 3s2 8.2.5 Atomic radii of metals (1) Within a family, the atomic radius increases as the atomic number increases. (2) Within the same period, the atomic radius decreases as the atomic number increases (3) For transition metals within the same period, the atomic radius first decreases steadily and then increase slightly. (4) “lanthanide contraction” effect

8.3 The structures and properties of alloys Alloy is the product of two and more metal Alloys may be divided into three major categories: Metallic solid solution Metallic compounds Metallic interstitial compounds 8.3.1 The structure of metallic solid solutions The structure of a bimetallic solid solution is usually similar to the metals except that fraction of the atoms of one metal is statistically substituted by the atoms of another metal The tendency to form a solid solution depends on (1)The positions in the periodic table and the similarity in chemical as well as physical properties. (2)the similarity in atomic radii (3)the structural type of the pure metals. ccp:Cu,Ag,Au,Ni,B-Co,Y-Fe,Pt,Ir,Rh,Pd bcp:a-Fe,V,Cr bcp:Mo,W
8.3 The structures and properties of alloys Alloy is the product of two and more metal. Alloys may be divided into three major categories: Metallic solid solution Metallic compounds Metallic interstitial compounds 8.3.1 The structure of metallic solid solutions • The structure of a bimetallic solid solution is usually similar to the metals except that fraction of the atoms of one metal is statistically substituted by the atoms of another metal. • The tendency to form a solid solution depends on : (1) The positions in the periodic table and the similarity in chemical as well as physical properties. (2) the similarity in atomic radii (3) the structural type of the pure metals. ccp: Cu, Ag, Au, Ni, β-Co, γ-Fe, Pt, Ir, Rh, Pd bcp: α-Fe, V, Cr bcp: Mo, W

8.3.2 The structure of metallic compounds The stoichiometric phase 1.The structure of the alloy MgCu, Cu ●Mg 2.The structure of the alloy CaCus Many alloys which act as reservoirs for hydrogen such as LaNi5,LaCo5 and CeCo5 have 6 the same structure as CaCu5. (c) Ca ●Cu
8.3.2 The structure of metallic compounds The stoichiometric phase 1. The structure of the alloy MgCu2 2. The structure of the alloy CaCu5 Many alloys which act as reservoirs for hydrogen such as LaNi5, LaCo5 and CeCo5 have the same structure as CaCu5