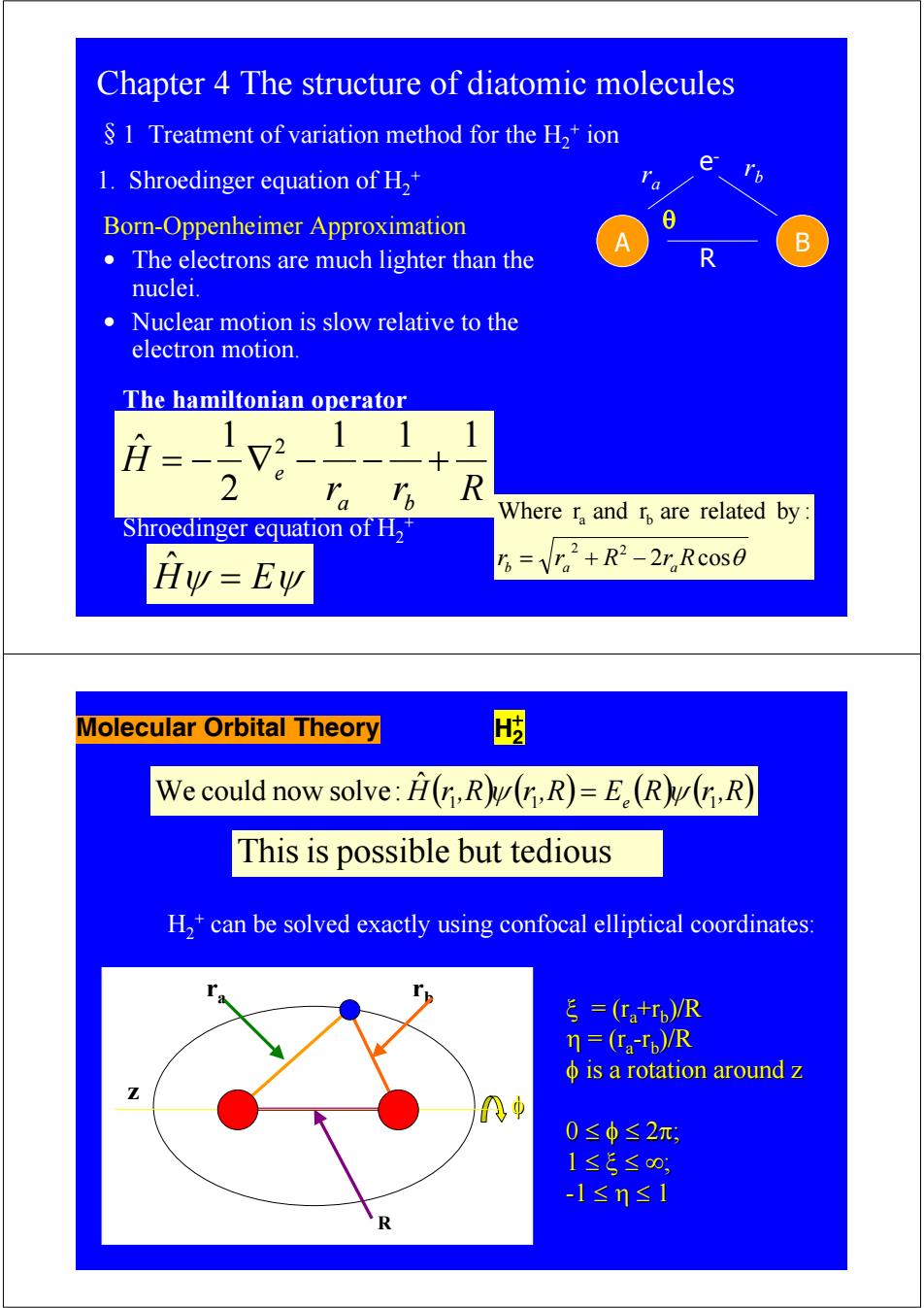
Chapter 4 The structure of diatomic molecules S 1 Treatment of variation method for the H,+ion e 1.Shroedinger equation of H2+ Born-Oppenheimer Approximation 8 B The electrons are much lighter than the nuclei. Nuclear motion is slow relative to the electron motion. The hamiltonian operator 1 1 H 2 、R Where r,and r are related by: Shroedinger equation of H2 Hy=Ew B=V2+R2-2,Rc0s0 Molecular Orbital Theory We could now solve:H(r,R(n,R)=E.(R(r,R) This is possible but tedious H,*can be solved exactly using confocal elliptical coordinates: ξ=(tr,)R n=(ra-Tp)/R φis a rotation around z 0≤φ≤2π, 1≤5≤0, -1≤n≤1 R
Chapter 4 The structure of diatomic molecules §1 Treatment of variation method for the H2 + ion 1. Shroedinger equation of H2 + A B e- r r b a R Born-Oppenheimer Approximation • The electrons are much lighter than the nuclei. • Nuclear motion is slow relative to the electron motion. r r R H a b e 1 1 1 2 1 ˆ 2 = − ∇ − − + The hamiltonian operator 2 cosθ Where r and r are related by : 2 2 a b rb = ra + R − raR θ Hˆψ = Eψ Shroedinger equation of H2 + Molecular Orbital Theory H2 + We could now solve: Hˆ ( )( ) r 1,R ψ r 1,R = Ee (R)( ) ψ r 1,R Thisis possible but tedious H2 + can be solved exactly using confocal elliptical coordinates: ra rb z ξ = (ra +rb)/R η = (ra-rb)/R φ is a rotation around z is a rotation around z 0 ≤ φ ≤ 2π; 1 ≤ ξ ≤ ∞; -1 ≤ η ≤ 1 R φ

Ψe1e=F(5,n)(2元y12eim where m-=0,±l,±2,±3, The associated quantum number is A.>orbital angular momentum 入=m Each electronic level with m 40 is doubly degenerate,i.e.+m,-m atoms:e=0,1.2....and the atomic orbitals are called:s,p,d,etc diatomics:入=0,l,2,.and the molecular orbitals are:o,π,δ,etc 入 letter Vece=F(5,n)(2元-12 eim 入 3 入=ml letter G 元 a e b f (a3
ψelec = F(ξ,η) (2π)-1/2 eimφ where m=0, ±1, ±2, ±3, letter λ σ 0 π 1 δ 2 φ 3 γ 4 The associated quantum number is λ. Æ orbital angular momentum λ =|m| Each electronic level with m ≠0 is doubly degenerate, i.e. + |m|,-|m| atoms: l = 0,1,2,... and the atomic orbitals are called: s,p,d, etc. diatomics: λ = 0,1,2, ... and the molecular orbitals are: σ, π, δ, etc. letter λ σ 0 π 1 δ 2 φ 3 γ 4 ψelec = F(ξ,η) (2π)-1/2 eimφ λ =|m| σ π δ

2.The Variation Theorem For any well-behaved wavefunction the average energy from the Hamiltonian of the system is always greater or close to the exact ground state energy (E)for that Hamiltonian, E0 ∫φdx Example:Devise a trial variation function for the particle in a one-dimensional box of length 1. A simple function that has the properties of the ground state is the parabolic function: p=x(1-x) for0sx≤I 0 =- 6m dr=fx(-xds= 0 - p*idx 5h2 ∫pdr 4r2m12 8ml2
2. The Variation Theorem For any well-behaved wavefunction φ, the average energy from the Hamiltonian of the system is always greater or close to the exact ground state energy (E0) for that Hamiltonian, * 0 * ˆ E d H d E ≥ ∫ ∫ = φ φ τ φ φ τ Example: Devise a trial variation function for the particle in a one-dimensional box of length l. 0 l A simple function that has the properties of the ground state is the parabolic function: φ = x(l − x) for 0≤x ≤l m l lx x dx dx d lx x m H d l 6 ( ) ( ) 2 ˆ 2 3 2 2 2 0 2 2 * h h = − − − = ∫ ∫ φ φ τ 30 ( ) 5 2 0 2 * l d x l x dx l = − = ∫ ∫ φ φ τ 2 8 2 2 2 4 2 5 * * ˆ ml h ml h d H d E = ≥ ∫ ∫ = φ φ τ π φ φ τ

Proof The Eigenfunctions of an φ(g≥E。)its ground state(w。→Eo) Hermitian operator consist 0=∑cw, of a complete set.V1.V2. 月w,=E, E,之E0 Ψ3.consist of an orthogonal normalized set ∫pidr = of wavefunctions odr fp'dr=∫∑ew,∑cwdr=∑c∑c∫w,y,dr ΣΣcc8,=∑k ∫。idr=∫∑ciwi∑cw,dr=∑ci∑c∫w,iwdr =∑∑ccwE,",dr=∑∑ce,EJw,w,dr=∑kfE ∑e'E, = ≥E。 3.Linear Variation Functions A linear variation function is a linear combination of =cf+c++cnfn=∑cf n linearly independent functions/,2,…a Based on this principle,the parameters are regulated by the minimization routine so as to obtain the wavefunction that 长E-9≥ ∫p*dz corresponds to the minimum energy.This is taken to be the wavefunction that closely 8= approximates the ground state. adjusting the parameter, 08 make =0 aci
j i i j j i j i i j i j i j j i j j i j j i i j j j i i i i i i j ij i j j i j j i i j j j i i i c c E d c c E d c E H d c H c d c c H d c c c d c c d c c d ∑ ∑ ∫ ∑ ∑ ∫ ∑ ∫ ∫ ∑ ∑ ∑ ∑ ∫ ∑ ∑ ∑ ∫ ∫ ∑ ∑ ∑ ∑ ∫ = = = = = = = * * 2 * * * * * 2 * * * * * ˆ ˆ ˆ ψ ψ τ ψ ψ τ φ φ τ ψ ψ τ ψ ψ τ δ φ φ τ= ψ ψ τ= ψ ψ τ The Eigenfunctions of an Hermitian operator consist of a complete set. ψ1, ψ2, ψ3 …consist of an orthogonal normalized set of wavefunctions φ φ τ φ φ τ ψ ψ φ ψ φ ε ψ d H d E H E E E c E ground state E i i i i i i i ∫ ∫ ∑ = = ≥ = ≥ → * * 0 0 0 0 ˆ ˆ ( ) its ( ) Proof 2 0 2 == ≥ E ∑ ∑ i i j i i c c E ε E adjusting the parameter, make = 0 ∂ ∂ i c ε Based on this principle, the parameters are regulated by the minimization routine so as to obtain the wavefunction that corresponds to the minimum energy. This is taken to be the wavefunction that closely approximates the ground state. * 0 * ˆ E d H d E ≥ ∫ ∫ = φ φ τ φ φ τ ε = 3. Linear Variation Functions ∑= = + + + = n j n n j j c f c f c f c f 1 1 1 2 2 φ ... A linear variation function is a linear combination of n linearly independent functions f1, f2, …fn

Example [中Hdr =C4+C2Ψ2 8= odr 「p'dr=「(cy+c4)'(c4+c22)dr =∫(G244+cc242+cc44+c222)dz =」(G44+2cc42+c42)dt =c2+2cc,S2+622 (Sy=∫4iy,dr=S) =c12S1+2c0S2+c22S2 (S1=S22=1) 「padr=c4tc,y)广a(c4+c业)dr (c'vHy+ccz+cc2 Hy+cW:HV2)dt CHn+2cc2Hn+c2Hz (H,=Hn=∫4iy,) (Hm=H2=1) let c'Hn+2cc,Hn+c'Hny c2S1+2cc2S2+622S2 X make 6→Eo 0= O8 1 dy y ox ac x 0c x2 0c (2cH+26,H2)-2GS+26,Sa) 2cH+2c,.)-S+2cc.+c2(2c5+2c,5)=0 CSu+2cC2S2+C2S2 (2cH1,+2c2H12)-E(2cS1+2c2S12)=0 (cH1+c2H2)-E(cS1+c2S2)=0 (Hu-ES])c +(H12-ES2)c2=0 () same as 0= OE OC2 (H21-ES21)G1+(H2-ES2)c2=0 (2)
( 1) ) ˆ 2 ( ) ˆ ˆ ˆ ˆ ( ( ) ˆ ( ) ˆ 11 22 * 22 2 11 1 2 12 2 2 1 2 * 2 2 1 2 * 2 1 2 2 * 1 1 2 1 * 1 2 1 1 1 2 2 * 1 1 2 2 * = = = + + = = = + + + = + + ∫ ∫ ∫ ∫ H H c H c c H c H H H H c H c c H c c H c H d H d c c H c c d ij ji ψ i ψ j ψ ψ ψ ψ ψ ψ ψ ψ τ φ φ τ ψ ψ ψ ψ τ Example 2 ( 1) 2 ( ) ( 2 ) ( ) ( ) ( ) 22 11 22 2 11 1 2 12 2 2 1 ji * 1 2 1 2 12 2 2 1 2 * 2 2 2 2 * 1 1 2 1 * 1 2 1 2 * 2 2 1 2 * 2 1 2 2 * 1 1 2 1 * 1 2 1 1 1 2 2 * 1 1 2 2 * = + + = = = + + = = + + = + + + = + + ∫ ∫ ∫ ∫ ∫ c S c c S c S S S c c c S c S d S c c c c d c c c c c c d d c c c c d ij ψ ψ j τ= ψ ψ ψ ψ ψ ψ τ ψ ψ ψ ψ ψ ψ ψ ψ τ φ φ τ ψ ψ ψ ψ τ φ φ τ φ φ τ φ ψ ψ ε d H d c c ∫ ∫ = + = * * 1 1 2 2 ˆ ( ) ( ) 0 (2) 0 21 21 1 22 22 2 2 − + − = ∂ ∂ = H ES c H ES c c same as ε ( ) ( ) 0 (1) ( ) ( ) 0 (2 2 ) (2 2 ) 0 (2 2 ) 0 2 2 (2 2 ) (2 2 ) (2 2 ) 1 1 0 11 11 1 12 12 2 1 11 2 12 1 11 2 12 1 11 2 12 1 11 2 12 1 11 2 12 22 2 11 1 2 12 2 2 1 22 2 11 1 2 12 2 2 1 1 11 2 12 1 11 2 12 2 1 11 2 12 1 2 1 1 0 − + − = + − + = + − + = + = + + + + + − = + − + ∂ ∂ − ∂ ∂ = ∂ ∂ = ⇒ H ES c H ES c c H c H E c S c S c H c H E c S c S c S c S c S c c S c S c H c c H c H c H c H c S c S x y c H c H x c x x y c y c x make E ε ε x y c S c c S c S c H c c H c H let = + + + + = 22 2 11 1 2 12 2 2 1 22 2 11 1 2 12 2 2 1 2 2 ε

seqular equation made equation resolved(c,c2≠O) Hu-ES Hv-ES2 =0 H21-ES21 H22-ES22 get E→get C1,c2→8et 中 The algebraic equation has 2 roots,E and E2. p=C+C2Ψ2++CnΨn Hu-ES H1-ES12 .. Hyn-ESin H21-ES21 H2-ES22 H2n-ES2n =0 Hn-ESn Hn2-ES2 Hm-ESom The algebraic equation has n roots,which can be shown to be real Arranging these roots in order of increasing value:E,≤E2≤..≤En From the variation theorem,we know that the lowest value of root (W)is the upper bound for the system's ground-state energy. E<W .Moreover,it can be proved that the linear variation method provides upper bounds to the energies of the lowest n states of the system. E2sW2E≤W3.…,En≤Wm We use the roots as approximations to the energies of the lowest states. If approximation to the energies of more states are wanted,we add more functions to the trial functionΦ,. The addition of more functions can be shown to increase the accuracy of the previously calculated energies
get E get c c get φ H ES H ES H ES H ES made equation resolved c c seqular equation ⇒ ⇒ = − − − − ≠ 1 2 21 21 22 22 11 11 12 12 1 2 , 0 ( , 0) 0 ... . . ... . . . ... . ... ... ... 1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 1 1 2 2 = − − − − − − − − − = + + + n n n n nn nn n n n n n n H ES H ES H ES H ES H ES H ES H ES H ES H ES φ cψ c ψ c ψ The algebraic equation has n roots, which can be shown to be real. Arranging these roots in order of increasing value: E1≤ E2≤… ≤En. The algebraic equation has 2 roots, E1 and E2. • From the variation theorem, we know that the lowest value of root (W1) is the upper bound for the system’s ground-state energy. E1≤W1 • We use the roots as approximations to the energies of the lowest states. • If approximation to the energies of more states are wanted, we add more functions fk to the trial function φ. • The addition of more functions fk can be shown to increase the accuracy of the previously calculated energies. E2≤ W2, E3≤ W3, … , En ≤ Wn, •Moreover, it can be proved that the linear variation method provides upper bounds to the energies of the lowest n states of the system

3.The solution of ForH达that is a e-Ta B 1S4= =Ψa R Wπ e-n =Ψb Vπ Note:we have as many linear combinations as we have atomic orbitals φ=CaΨa+CbΨ6 Trial functions =CaΨa+CbΨb seqular equation Hoa-ESaa Hab-ESab =0 Hpa-ESpa Hob-ESbb has the same form as ∴Ha=Ho, Hab=Ha (Ha-ESa)2=(Hb-ESb)月 Haa-ESaa=(Hab-ESab) 计 Ha-ESa=-(Hab-ESab) E= Haa+Hab_a+B 1+Sab 1+S Haa-ESoa=Hab-ESab E2 Hoe-Hab= -B 1-Sab 1-S
3. The solution of H2 + A B e- r r b a R θ For H2 + that is : Note : we have as many linear combinations as we have atomic orbitals a r A a e s ψ π = = − 1 b 1 ψ π = = − br B e s a a b b φ = c ψ + c ψ Trial functions ( ) ( ) ( ) has the same form as 2 2 , aa aa ab ab aa aa ab ab a b aa bb ab ba H ES H ES H ES H ES H H H H − = ± − − = − Qψ ψ ∴ = = = 0 − − − − = + ba ba bb bb aa aa ab ab a a b b H ES H ES H ES H ES seqular equation φ c ψ c ψ S S H H E if H ES H ES S S H H E if H ES H ES ab aa ab aa aa ab ab ab aa ab aa aa ab ab − − = − − = − = − + + = + + = − = − − 1 1 1 1 ( ) 2 1 α β α β

substituting E to seqular equation (Haa-ESaa)Ca+(Hab-ESab)Cb=O () (Hba-ESba)Ca+(Hob-ESBb)Co=O (2) Soa =Sbb=1 aa h。- HaatHab )c,+(HHga+Hab Sab )c 1+Sab 1+Sab (Haa(1+Sab)-(Haa+Hab))Ca+(Hab(1+Sab)-(Haa+Hab)Sab)Cp=O (Hoa(I+Sab)-(Moa+Hab))ca+(Hab(1+Sab)-(Hoa+Mab)Sab)Co=O (HaaSab-Hab)Ca+(Hab-Haa Sab)Cp=O Ca-Ch=0 Ca=Cb 4=ca。+C6。=Ca(。+6) nomalization condition ∫4g=1 (c(y。+ys)'ca(y。+wb)dx=1 Ic Wa+2c WaVs+cWs]dt=1 2c。2(1+Sb)=1 1 Ca= V21+S6) 1 (y。+6) V2(1+Sb) substituting E2 to seqular equation C。+C6=0 Ca=-Cb 2=CΨ。+CbΨ。=C(y。-Ψ6) 1 02= (ya-Ψ) V2(1-Sb)
( ) ( ) 0 (2) ( ) ( ) 0 (1) 1 − + − = − + − = ba ba a bb bb b aa aa a ab ab b H ES c H ES c H ES c H ES c substituting E to seqular equation ( ) 0 ( ) ( ) 0 ( (1 ) ( )) ( (1 ) ( ) ) 0 ( (1 ) ( )) ( (1 ) ( ) ) 0 ) 0 1 ) ( 1 ( 1 1 a a b b a a b a b a b aa ab ab a ab aa ab b aa ab aa ab a ab ab aa ab ab b aa ab aa ab a ab ab aa ab ab b ab b ab aa ab a ab ab aa ab aa aa bb c c c c c c c H S H c H H S c H S H H c H S H H S c H S H H c H S H H S c S c S H H c H S H H H S S φ = ψ + ψ = ψ +ψ − = = − + − = / + − / + + + / − + / = + − + + + − + = = + + + − + + − = = ( ) 2(1 ) 1 2(1 ) 1 2 (1 ) 1 [ 2 ] 1 ( ( )) ( ) 1 1 1 2 2 2 2 2 2 * 1 * 1 a b ab ab a a ab a a a a b a b a a b a a b S S c c S c c c d c c d nomalization condition φ ψ ψ ψ ψ ψ ψ τ ψ ψ ψ ψ τ φ φ + + = + ∴ = + = + + = + + = = ∫ ∫ ∫ ( ) 2(1 ) 1 ( ) 0 2 2 2 a b ab a a b b a a b a b a b S c c c c c c c substituting E to seqular equation φ ψ ψ φ ψ ψ ψ ψ − − = = + = − + = = −

E a+B 26* 1+S E2= Q-B H1s H1s 1-S 16 1 V2(1+Sb) (Ψ。+Ψ6) 1 V2(1-Sb) (Ψ。-Ψ6) Can we deduce the c and cp from the molecular symmetry? Overlap Sab= Wa widr integral coulombi H=∫g,iwd c integral =-1v2-11+1 2 ra R _1-1+2w.dr w,ar+0d-可v J≈5.5%EH Haa=EH+J≈En=a
S E + + = 1 1 α β S E − − = 1 2 α β ( ) 2(1 ) 1 ( ) 2(1 ) 1 a b ab b a b ab a S S φ ψ ψ φ ψ ψ − − = + + = + + - Can we deduce the ca and cb from the molecular symmetry? Overlap integral α ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ ∴ = + ≈ = ≈ = + − = + = − ∇ − + − = − ∇ − − + = − ∇ − − + = = ∫ ∫ ∫ ∫ ∫ ∫ ∫ aa H a H a H b H a a b a a a a a a a a b aa a a b aa a a ab a b H E J E J E d E J R r E d r d R d r d r r R H r r R H H H d S d 5.5% 1 1 1 1 ) 1 2 1 ( ) 1 1 1 2 1 ( 1 1 1 2 1 ˆ ˆ * * 2 * * * 2 2 * * coulombi c integral

resonance integral Hb=∫y。iy,dr a-vv Jgwartar -v.Ewdr+vvd-vdr 5+∫ EHSab +K =B Sb=∫y,y,dr=S Ham=EHtJ≈E。=a Hab EH Sab +K=B Ea= Hag +Hab 1+Sab Ep= Hoa-Hab 1-Sab E1= En+J+EnSab+K 1+Sab =EH* J+K 1+S J-K E2=EH+ 1-S
β ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ ψ ψ τ = = + = + − = + − = − ∇ − + − + = − ∇ − − + = ∫ ∫ ∫ ∫ ∫ ∫ ∫ ∫ E S K d R r S E S d r d R E d d r R d r d r r R H H H d H ab b a a ab H ab b a a b b a b a b a b a b a b a b ab a ab a b 1 1 1 ) 1 1 ) ( 1 2 1 ( ) 1 1 1 2 1 ( ˆ * * * * * 2 * * 2 * resonance integral S J K E E S J K E S E J E S K E S H H E S H H E H E S K H E J E S d S H H ab H H ab ab aa ab b ab aa ab a ab H ab aa H a ab a b − − = + + + = + + + + + = − − = + + = = + = = + ≈ = = = ∫ 1 1 1 1 1 2 1 * β α ψ ψ τ